Combining Sliding Mode and Fractional-Order Theory for Maximum Power Point Tracking Enhancement of Variable-Speed Wind Energy Conversion
Abstract
1. Introduction
2. Literature Review
Research Gap
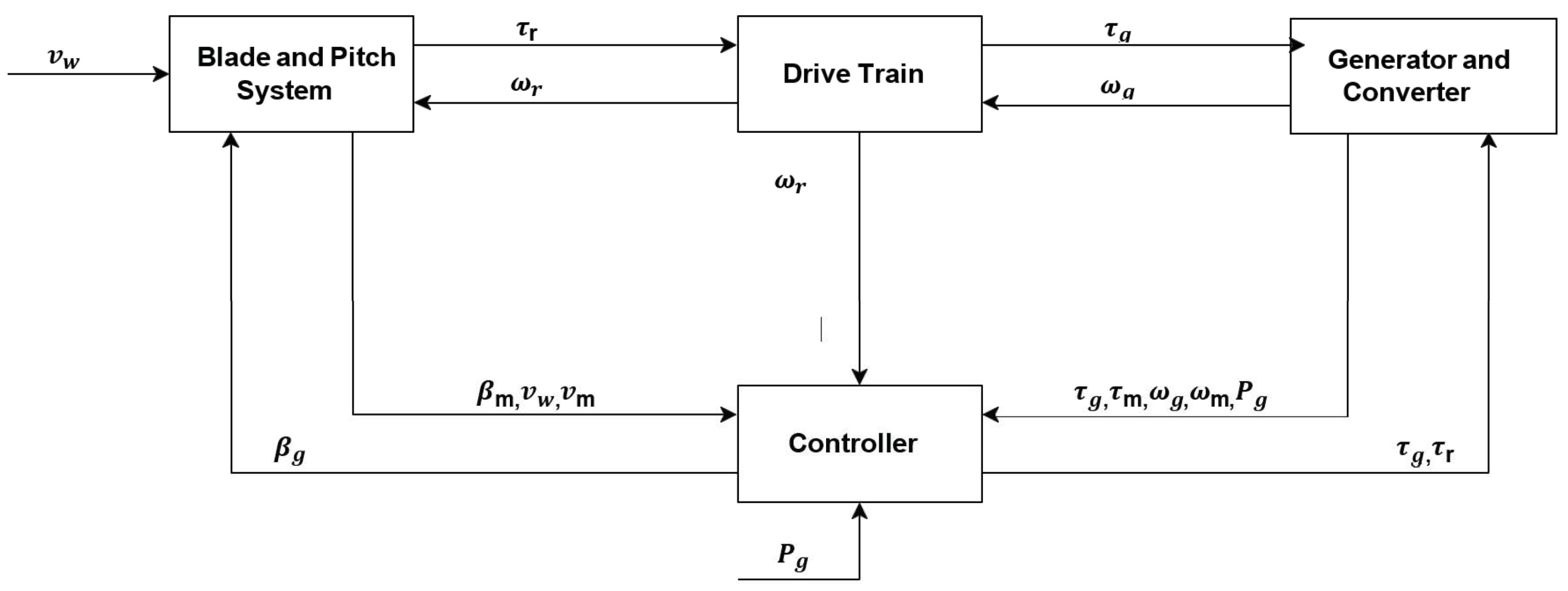
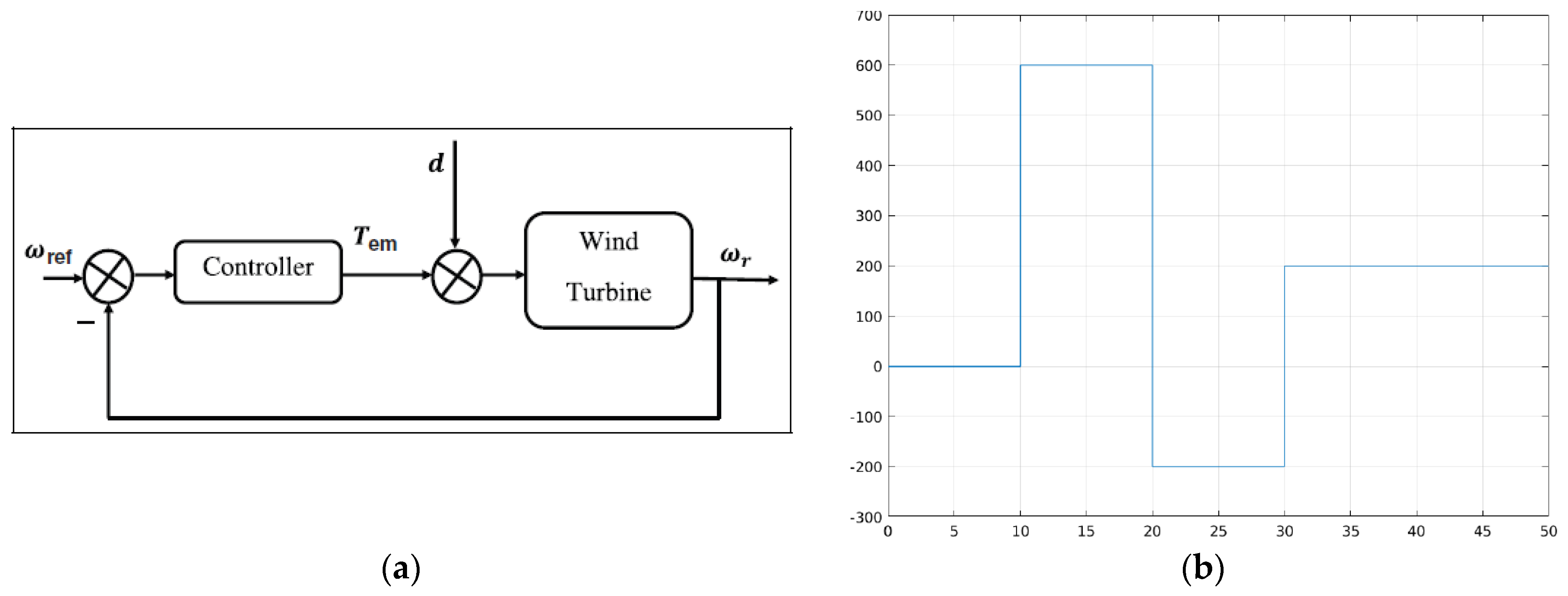
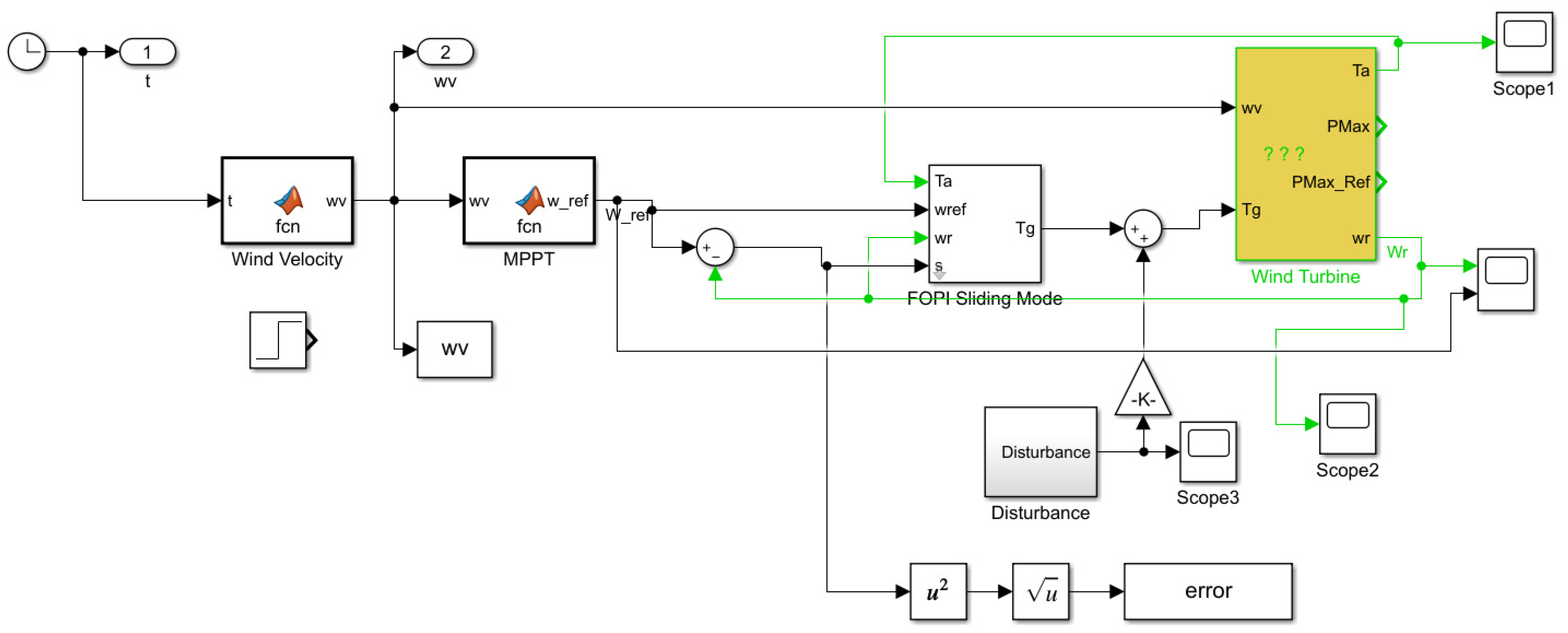
3. Materials and Methods
3.1. Mean Components of Wind Turbine
- Anemometer for measuring wind speed; the data are controlled by the controller;
- Blades to propel movement by harnessing the power of the wind;
- Brake, used on storm days or in case of maintenance (hydraulically, mechanically, or electrically);
- Controller to control the functions of the turbine (to turn on and shut off the turbine);
- Gear box, connecting the lower speed shaft with the higher one, which increases the speed from 60 rpm to more than 1000 rpm; in some cases, it could reach the 1800 rpm required to generate electricity;
- Generators to produce 60-cycle AC electricity;
- Low-speed shaft, which moves 30 to 60 rpm based on the wind speed;
- A nacelle at the top of the tower, which contains most of the turbine parts (generator, brake, speed shafts, and controller);
- High-speed shaft, which drives the generator;
- Pitch, which increases the turbine efficiency in case of low-speed wind, or decreases the efficiency in extreme cases;
- Rotor, which comprises the blades along with a hub;
- A tower made of concrete or steel, which produces electricity based on its height;
- Wind vane, which indicates the wind direction and passes the data to the yaw system to move the nacelle to face the wind direction;
- Yaw drive, which receives the data from the vane and keeps the blades facing the wind;
- Yaw motor, which supplies the yaw drive with power.
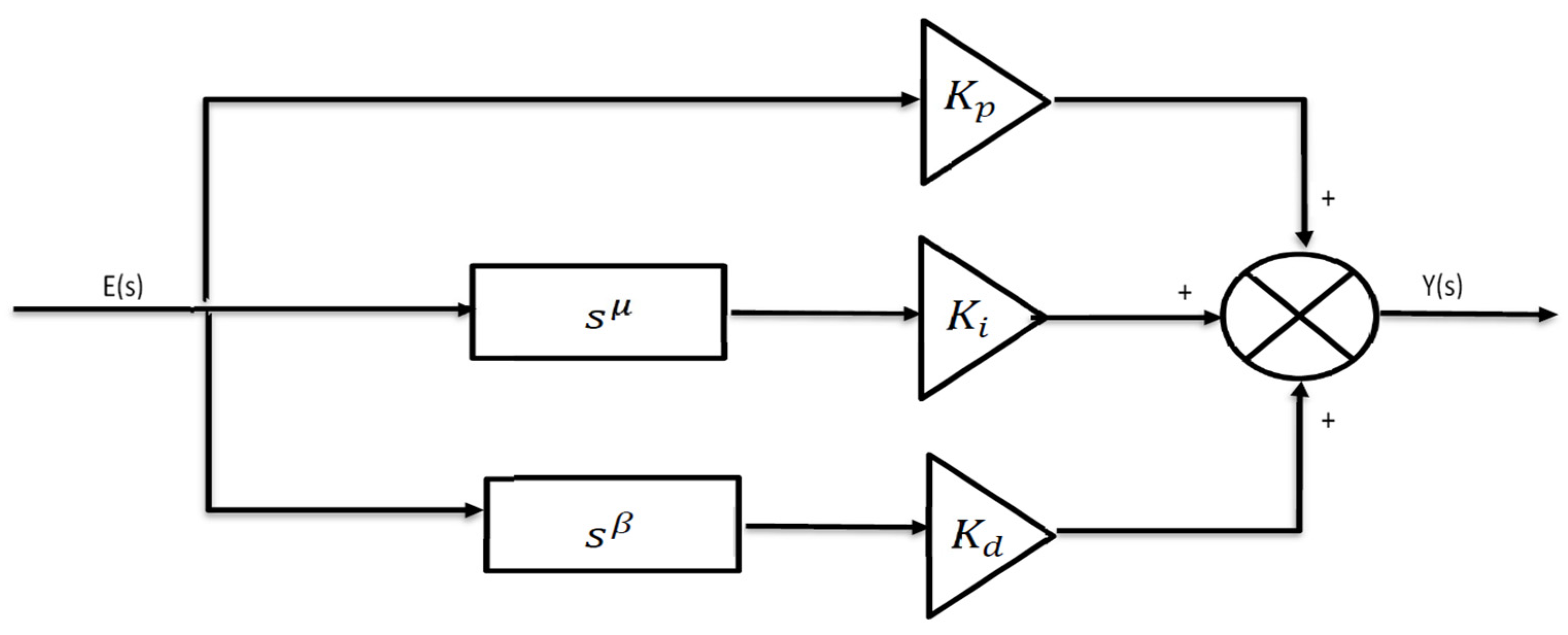
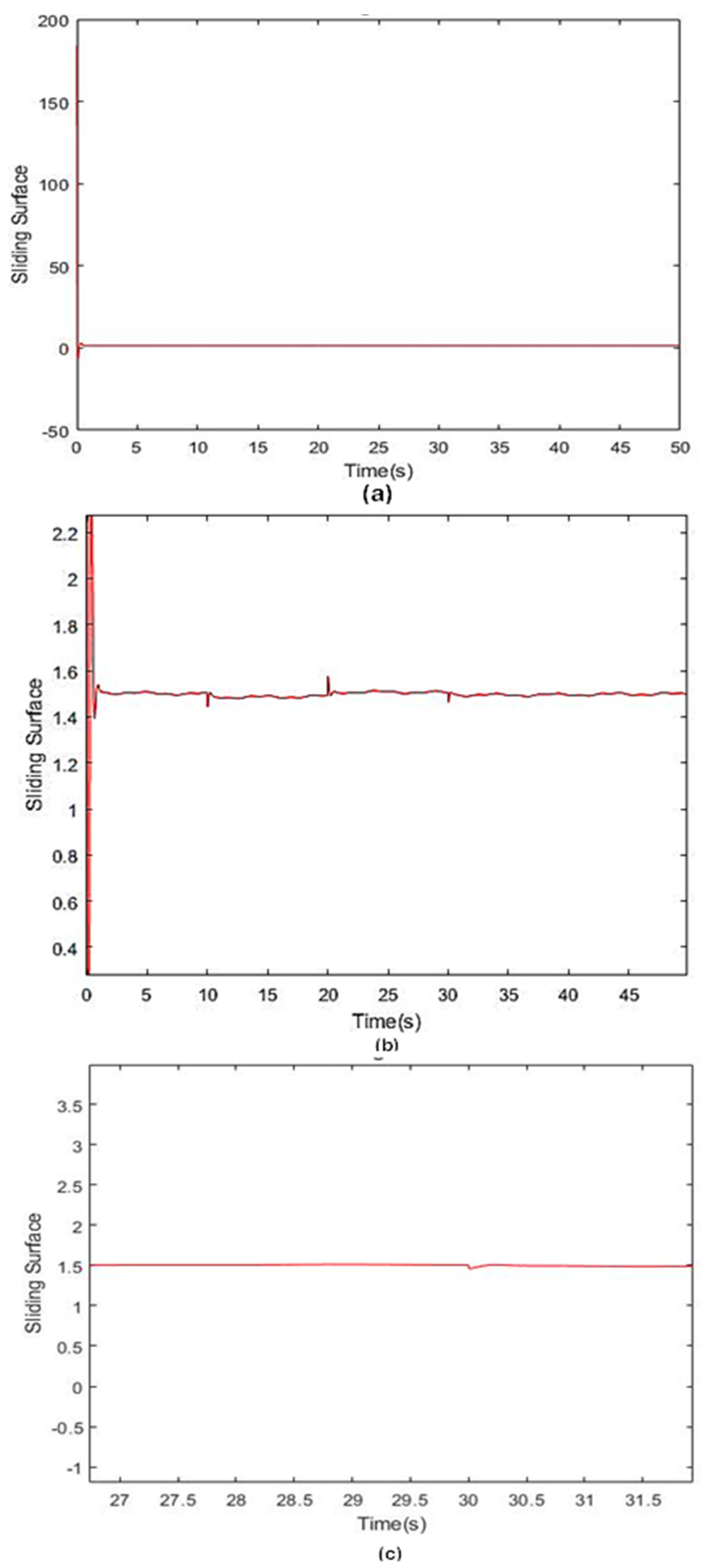
3.2. Fractional Order Slide Mode Control FOPI SMC_P
3.3. Controller Optimization for FOPID Using PSO
- Tracking Error: The deviation of the system output from the desired reference trajectory.
- Control Effort: The magnitude of the control signals, to ensure that they are within practical limits.
- Robustness: The ability of the controller to maintain performance in the presence of disturbances and model uncertainties.
- Initialization: An array of particles with random positions and velocities is created.
- Fitness Evaluation: Each particle’s fitness value is evaluated according to the desired optimization function.
- Update Best Positions: The algorithm updates the personal best and global best positions based on the current fitness evaluations.
- Update Velocities and Positions: The velocities and positions of the particles are updated using the iterative equations.
- Iteration: Steps 2–4 are repeated until the stopping criterion is met, typically based on the number of iterations or a convergence threshold.
4. Results
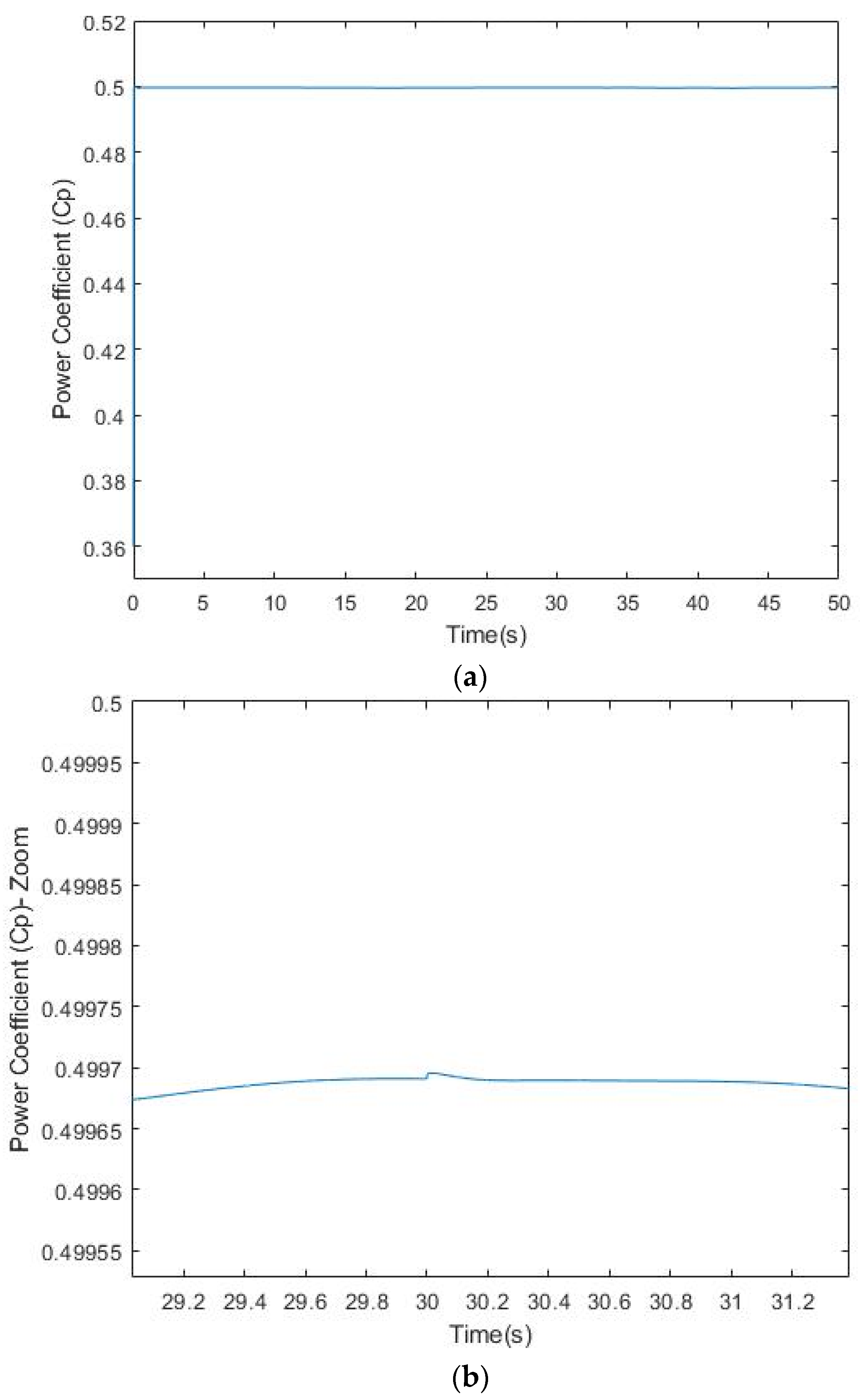
4.1. Maximum Power of Wind Turbine
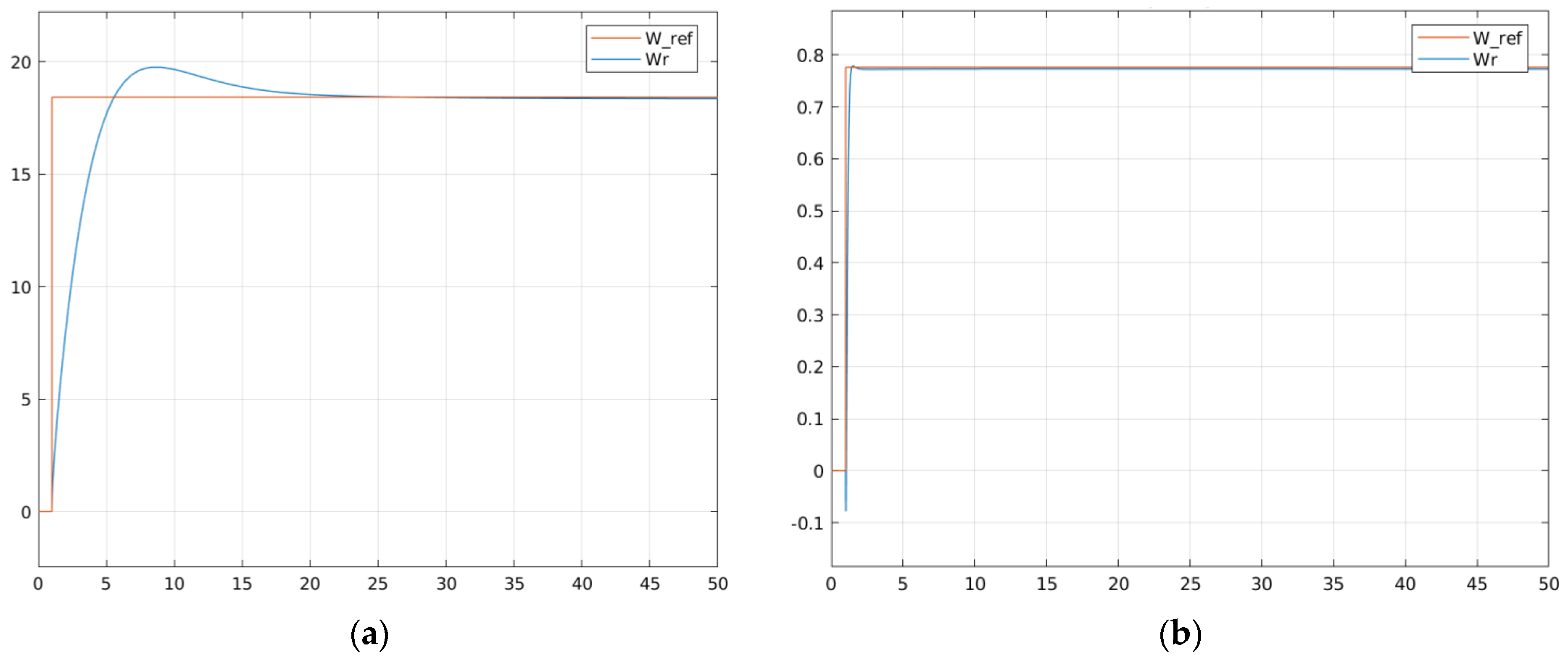
4.2. Response of Controllers with PSO
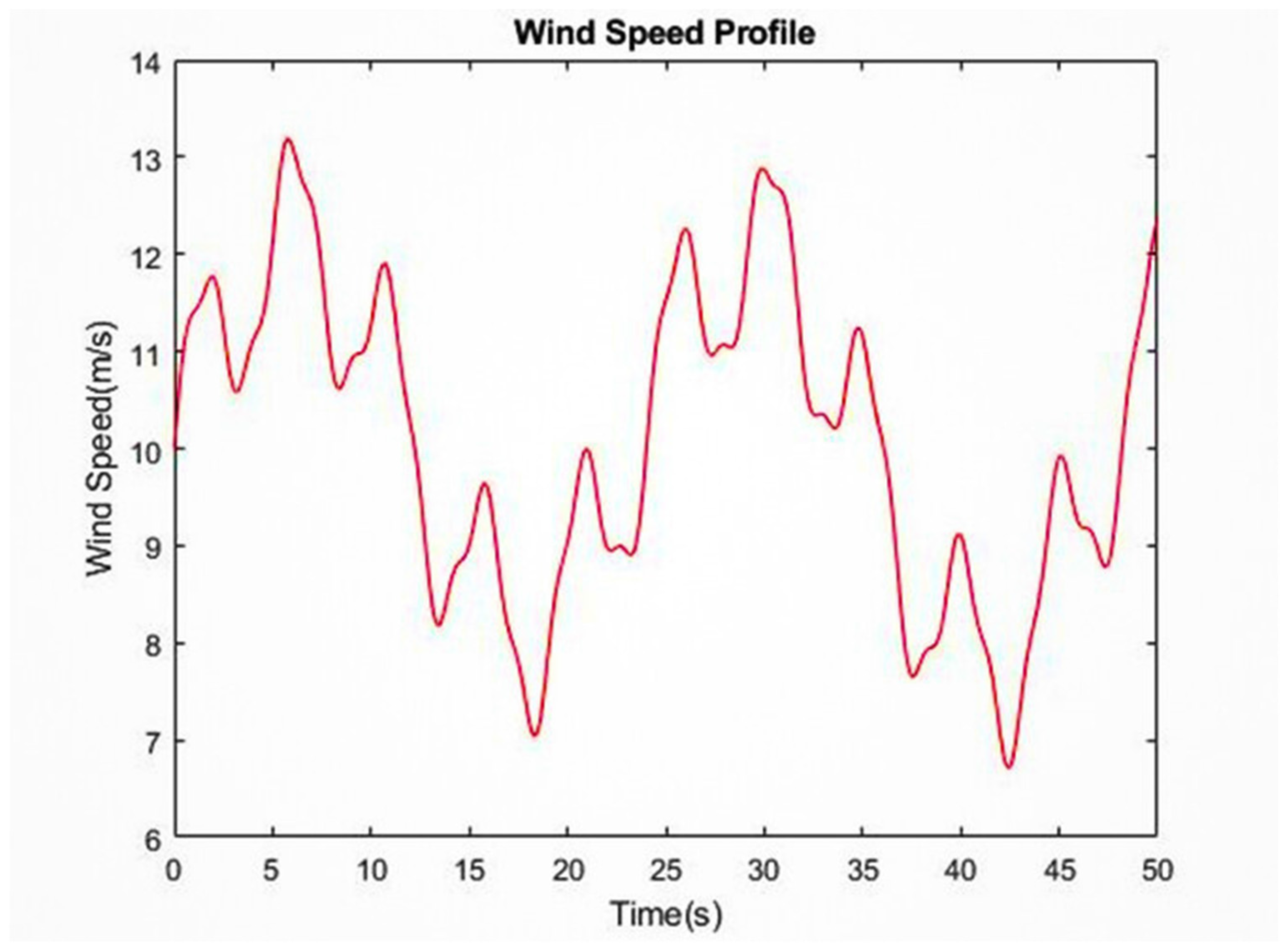
4.3. Wind Profile
4.4. Response of Controllers with Disturbance and PSO
4.5. Wind Profile Disturbance and Sensor Noise-FOPID SMC with OPT Optimization
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Benbouhenni, H.; Boudjema, Z.; Bizon, N.; Thounthong, P.; Takorabet, N. Direct power control based on modified sliding mode controller for a variable-speed multi-rotor wind turbine system using PWM strategy. Energies 2022, 15, 3689. [Google Scholar] [CrossRef]
- Shchur, I.; Klymko, V.; Xie, S.; Schmidt, D. Design features and numerical investigation of counter-rotating VAWT with co-axial rotors displaced from each other along the axis of rotation. Energies 2023, 16, 4493. [Google Scholar] [CrossRef]
- Benbouhenni, H.; Bizon, N. A new direct power control method of the DFIG-DRWT system using neural PI controllers and a four-level neural modified SVM technique. J. Appl. Res. Technol. 2023, 1, 36–55. [Google Scholar] [CrossRef]
- REN21. Renewable Global Status Report. 2020. Available online: https://www.ren21.net/reports/global-status-report/ (accessed on 23 March 2024).
- Chauhan, S.; Sameeullah, M.; Dahiya, R. Maximum Power Point Tracking scheme for variable speed wind generator. In Proceedings of the IEEE 6th India International Conference on Power Electronics (IICPE), Kurukshetra, India, 8–10 December 2014. [Google Scholar]
- Thongam, J.S.; Ouhrouche, M. MPPT control methods in wind energy conversion systems. Fundam. Adv. Top. Wind. Power 2011, 15, 339–360. [Google Scholar]
- Bougdour, S.; Elhouti, R.; Sefriti, S.; Boumhidi, I. Optimal predictive control model of wind turbine. In Proceedings of the 2021 Fifth International Conference on Intelligent Computing in Data Sciences (ICDS), Virtual, 20–22 October 2021; pp. 1–7. [Google Scholar]
- Ali, K.-M.; Barambones, O. Higher Order Sliding Mode Control of MIMO Induction Motors: A New Adaptive Approach. Mathematics 2023, 11, 4558. [Google Scholar] [CrossRef]
- Hu, L.; Xue, F.; Qin, Z.; Shi, J.; Qiao, W.; Yang, W.; Yang, T. Sliding mode extremum seeking control based on improved invasive weed optimization for MPPT in wind energy conversion system. Appl. Energy 2019, 248, 567–575. [Google Scholar] [CrossRef]
- Kazmi, S.M.; Goto, H.; Guo, H.J. Review and critical analysis of the research papers published to date on maximum power point tracking in wind energy conversion system. In Proceedings of the IEEE Energy Conversion Congress and Exposition, Atlanta, GA, USA, 12–16 September 2010; pp. 4075–4082. [Google Scholar]
- Liu, J.; Meng, H.; Hu, Y.; Lin, Z.; Wang, W. A novel MPPT method for enhancing energy conversion efficiency taking power smoothing into account. Energy Convers. Manag. 2015, 101, 738–748. [Google Scholar] [CrossRef]
- Cao, A.; Cen, L.; Chen, J. Optimal Torque Control for Large-Scale Wind Turbine Systems Based on Sliding Mode Control. In Proceedings of the 2018 37th Chinese Control Conference (CCC), Wuhan, China, 25–27 July 2018. [Google Scholar]
- Liu, D.; Xia, Y.; Li, R.; Liu, P. Integral sliding mode control of low-speed wind turbine. In Proceedings of the 2019 Chinese Automation Congress (CAC), Hangzhou, China, 22–24 November 2019. [Google Scholar]
- Maati, Y.A.E.; Bahir, L.E. Optimal Fault Tolerant Control of Large-Scale Wind Turbines in the Case of the Pitch Actuator Partial Faults. Complexity 2020, 2020, 1–17. [Google Scholar] [CrossRef]
- Van, T.L.; Nguyen, D.Q.; Duy, V.H.; Nguyen, H. Fast Maximum Power Point Tracking Control for Variable Speed Wind Turbines. In Proceedings of the International Conference on Advanced Engineering Theory and Applications, Ho Chi Minh, Vietnam, 7–9 December 2017; pp. 821–829. [Google Scholar]
- Porate, D.K.; Gawande, S.; Munshi, A.; Porate, K.; Kadwane, S.; Waghmare, M. Zero Direct-axis Current (ZDC) Control for Variable Speed Wind Energy Conversion System using PMSG. Energy Procedia 2017, 117, 943–950. [Google Scholar] [CrossRef]
- Kumar, S.S.; Jayanthi, K.; Kumar, N.S. Maximum power point tracking for a PMSG-based variable speed wind energy conversion system using optimal torque control. In Proceedings of the 2016 International Conference on Advanced Communication Control and Computing Technologies (ICACCCT), Ramanathapuram, India, 25–27 May 2016; pp. 347–352. [Google Scholar]
- Khiabani, A.G.; Heydari, A. Optimal torque control of permanent magnet synchronous motors using adaptive dynamic programming. IET Power Electron. 2020, 13, 2442–2449. [Google Scholar] [CrossRef]
- Karabacak, M.; Fernandez-Ramirez, L.M.; Kamal, T. A new hill climbing maximum power tracking control for wind turbines with inertial effect compensation. IEEE Trans. Ind. Electron. 2019, 66, 8545–8556. [Google Scholar] [CrossRef]
- Dida, A.; Attous, D.B. Adaptive hill-climb searching method for MPPT algorithm based DFIG system using fuzzy logic controller. Int. J. Syst. Assur. Eng. Manag. 2017, 8, 424–434. [Google Scholar] [CrossRef]
- Yaakoubi, A.; Amhaimar, L.; Attari, K.; Harrak, M.; Halaoui, M.; Asselman, A. Non-linear and intelligent maximum power point tracking strategies for small size wind turbines: Performance analysis and comparison. Energy Rep. 2019, 5, 545–554. [Google Scholar] [CrossRef]
- Tan, K.; Islam, S. Optimum control strategies in energy conversion of PMSG wind turbine system without mechanical sensors. IEEE Trans. Energy Convers. 2004, 19, 392–399. [Google Scholar] [CrossRef]
- Camblong, J.; Vechiu, I.; Guillaud, X.; Etxeberria, A.; Kreckelbergh, S. Wind turbine controller comparison on an island grid in terms of frequency control and mechanical stress. Renew. Energy 2014, 63, 37–45. [Google Scholar] [CrossRef]
- Oliveira, M.M.; Grigoletto, F.B. Fuzzy Sensorless MPPT Strategy for Small Wind Turbines. In Proceedings of the 2019 IEEE PES Innovative Smart Grid Technologies Conference-Latin America (ISGT Latin America), Gramado, Brazil, 15–18 September 2019. [Google Scholar]
- Ardjal, A.; Mansouri, R.; Bettayeb, M. Fractional sliding mode control of wind turbine for maximum power point tracking. Trans. Inst. Meas. Control 2019, 41, 447–457. [Google Scholar] [CrossRef]
- Barambones, O. Sliding Mode Control Strategy for Wind Turbine Power Maximization. Energies 2012, 5, 2310–2330. [Google Scholar] [CrossRef]
- Mahdavian, M.; Wattanapongsakorn, N.; Shahgholian, G.; Mozafarpoor, S.H.; Janghorbani, M.; Shariatmadar, S.M. Maximum power point tracking in wind energy conversion systems using tracking control system based on fuzzy controller. In Proceedings of the Electrical Engineering/Electronics, Computer, Telecommunications and Information Technology (ECTI-CON), 2014 11th International Conference, Nakhon Ratchasima, Thailand, 14–17 May 2014. [Google Scholar]
- Salim, O.M.; Zohdy, M.A.; Abdel-Aty-Zohdy, H.; Dorrah, H.T.; Kamel, A.M. Type-2 fuzzy logic pitch controller for wind turbine rotor blades. In Proceedings of the 2011 IEEE National Aerospace and Electronics Conference (NAECON), Dayton, OH, USA, 20–22 July 2011. [Google Scholar]
- Li, Y.; Chengxin, L. Overview of Maximum Power Point Tracking Control Method for Wind Power Generation System. IOP Conf. Ser. Mater. Sci. Eng. 2018, 428, 12007. [Google Scholar] [CrossRef]
- Sitharthan, R.; Parthasarathy, T.; Sheeba Rani, S. An improved radial basis function neural network control strategy-based maximum power point tracking controller for wind power generation system. Trans. Inst. Meas. Control 2019, 41, 3158–3170. [Google Scholar] [CrossRef]
- Sitharthan, R.; Karthikeyan, M.; Sundar, D.S. Adaptive hybrid intelligent MPPT controller to approximate effectual wind speed and optimal rotor speed of variable speed wind turbine. ISA Trans. 2020, 96, 479–489. [Google Scholar] [CrossRef]
- Fathy, A.; El-baksawi, O. Grasshopper optimization algorithm for extracting maximum power from wind turbine installed in Al-Jouf region. J. Renew. Sustain. Energy 2019, 11, 033303. [Google Scholar] [CrossRef]
- Li, B.X.; Zhao, X.F.; Liu, Y.W.; Zhao, X.; Robust, H. Control of fractional-order switched systems with order 0 < α < 2 and uncertainty. Fractal Fract. 2022, 6, 164. [Google Scholar]
- Wang, J.; Liu, Y.; Wu, H.Y.; Lu, S.; Zhou, M. Ensemble FARIMA prediction with stable infinite variance innovations for supermarket energy consumption. Fractal Fract. 2022, 6, 276. [Google Scholar] [CrossRef]
- Jia, T.Y.; Chen, X.Y.; He, L.P.; Zhao, F.; Qiu, J.L. Finite-time synchronization of uncertain fractional-order delayed memristive neural networks via adaptive sliding mode control and its application. Fractal Fract. 2022, 6, 502. [Google Scholar] [CrossRef]
- Zhang, X.F.; Dai, L.W. Image enhancement based on rough set and fractional order differentiator. Fractal Fract. 2022, 6, 214. [Google Scholar] [CrossRef]
- MWPS Powering the World. 2019. Available online: https://www.mwps.world/2011/07/27/inside-wind-turbine/ (accessed on 23 March 2024).
- Odgaard, P.F.; Stoustrup, J.; Kinnaert, M. Fault-tolerant control of wind turbines: A benchmark model. IEEE Trans. Control. Syst. Technol. 2013, 21, 1168–1182. [Google Scholar] [CrossRef]
- Mukhtar, A.; Tiwari, P.M.; Singh, H.P. Performance Improvement of Wind Turbine Control using Fractional Order PID Controller with PSO Optimized gains. In Proceedings of the International Conference on Advances in Computing, Communication & Materials (ICACCM), Dehradun, India, 10–11 November 2020; pp. 374–379. [Google Scholar]
- Santi, E.; Monti, A.; Li, D. Synergetic control for DC-DC boost converter: Implementation options. IEEE Trans. Ind. Appl. 2003, 39, 1803–1813. [Google Scholar] [CrossRef]
- Adhikary, N.; Mahanta, C. Integral backstepping sliding mode control for underactuated systems: Swing-up and stabilization of the Cart–Pendulum System. ISA Trans. 2013, 52, 870–880. [Google Scholar] [CrossRef] [PubMed]
- Slotine, J.J.; Li, W. Applied Nonlinear Control; Prentice Hall: Englewood Cliffs, NJ, USA, 1991. [Google Scholar]
- Podlubny, I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications; Academic Press: San Diego, CA, USA, 1998. [Google Scholar]
- Timis, D.D.; Muresan, C.I.; Dulf, E.H. Design and experimental results of an adaptive fractional-order controller for a quadrotor. Fractal Fract. 2022, 6, 204. [Google Scholar] [CrossRef]
- Kahla, S.; Soufi, Y.; Sedraoui, M. On-off control-based particle swarm optimization for maximum power point tracking of a wind turbine equipped by DFIG connected to the grid with energy storage. Int. J. Hydrogen Energy 2015, 40, 13749–13758. [Google Scholar] [CrossRef]














| Parameter | Description | Parameter | Description |
|---|---|---|---|
| Pr | Rated power | Jg | Generator inertia (high-speed shaft) |
| α | Empirical wind shear exponent | ηg | Efficiency of generator |
| H | Hub height | αgc | Generator and converter parameter |
| R | Radius of rotor | τr | Aerodynamic torque |
| ρ | Air density | Cq | Torque coefficient |
| ζ | Damping factor | θ∆ | Drive train torsion angle |
| ωn | Natural frequency | τg | Generator torque |
| Bdt | Torsion damping coefficient | ωr | Angular speed of the rotor |
| Kdt | Torsion stiffness | ωg | Angular speed of the generator |
| Jr | Rotor inertia (low-speed shaft) | λ | Tip speed ratio |
| Br | Rotor external damping | β | Blade pitch angle |
| Bg | Generator external damping | vw | Wind speed |
| ηdt | Drive train efficiency | Pg | Generated power |
| Ng | Gearbox ratio | vm | Mean wind speed |
| Tm | Mechanical torque | Te | Electrical torque |
| ω | Angular velocity | Cp | Power coefficient |
| θ | Blade angle |
| FOPID-Controller | FOPID-SMC | |
|---|---|---|
| Kp | 0.39138 | 0.83778 |
| Ki | 0.73452 | 0.01 |
| Lambda | 0.80659 | 0.01 |
| Kd | 0.01962 | 0.65638 |
| Mu | 0.6882 | 0.9234 |
| Time Domain | Without Controller | PID | FOPID | Basic Sliding Mode Control | FOPI–Sliding Mode Control | FOPID–Sliding Mode Control |
|---|---|---|---|---|---|---|
| Rise Times (s) | 10.1620 | 4.3681 | 3.0966 | 0.2105 | 0.2173 | 0.2262 |
| Settling Time (s) | 19.1035 | 28.9442 | 37.39 | 1.3753 | 1.4126 | 1.3468 |
| Peak Overshoot (%) | 0 | 7.6399 | 46 | 0.0087 | 0.0442 | 1.7527 |
| Steady-State Error | 1.5981 | 0.0361 | 0.0022 | 4.9342 × 10−4 | 0.0029 | 3.5838 × 10−4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-Dhaifallah, M.; Saif, A.-W.A.; Elferik, S.; Elkhider, S.M.; Aldean, A.S. Combining Sliding Mode and Fractional-Order Theory for Maximum Power Point Tracking Enhancement of Variable-Speed Wind Energy Conversion. Fractal Fract. 2024, 8, 447. https://doi.org/10.3390/fractalfract8080447
Al-Dhaifallah M, Saif A-WA, Elferik S, Elkhider SM, Aldean AS. Combining Sliding Mode and Fractional-Order Theory for Maximum Power Point Tracking Enhancement of Variable-Speed Wind Energy Conversion. Fractal and Fractional. 2024; 8(8):447. https://doi.org/10.3390/fractalfract8080447
Chicago/Turabian StyleAl-Dhaifallah, Mujahed, Abdul-Wahid A. Saif, Sami Elferik, Siddig M. Elkhider, and Abdalrazak Seaf Aldean. 2024. "Combining Sliding Mode and Fractional-Order Theory for Maximum Power Point Tracking Enhancement of Variable-Speed Wind Energy Conversion" Fractal and Fractional 8, no. 8: 447. https://doi.org/10.3390/fractalfract8080447
APA StyleAl-Dhaifallah, M., Saif, A.-W. A., Elferik, S., Elkhider, S. M., & Aldean, A. S. (2024). Combining Sliding Mode and Fractional-Order Theory for Maximum Power Point Tracking Enhancement of Variable-Speed Wind Energy Conversion. Fractal and Fractional, 8(8), 447. https://doi.org/10.3390/fractalfract8080447







