Evolution of Pore Structure and Fractal Characteristics in Red Sandstone under Cyclic Impact Loading
Abstract
1. Introduction
2. Methods
2.1. Materials and Experimental Procedures
- (1)
- Saturation treatment: prior to conducting NMR tests, the samples were subjected to a 48 h moisture saturation using a vacuum saturation device at a pressure of 0.1 MPa to ensure complete saturation of the pores.
- (2)
- NMR testing: Each specimen underwent NMR tests utilizing the AiniMR-150 NMR system manufactured by Suzhou Newmarket Analytical Instruments Co., Ltd. [3,31]. The CPMG sequence was applied with specific parameters: a 0.256 ms echo time (TE = 0.256 ms), 4096 echoes (NECH = 4096), a 6000 ms waiting time (TW = 6000 ms), and 32 scans. The porosity, T2 distribution, and MRIs were obtained.
- (3)
- Centrifugation and drying: After saturation and the NMR test, the samples were centrifuged at 4000 rpm for 90 min, followed by NMR testing. Subsequently, the specimens were placed in an oven and dried at 60 °C for 12 h before undergoing further NMR testing.
- (4)
- SHPB cyclic impact loading experiments: The SHPB equipment is mainly composed of a cylinder that generates power, a cone-shaped striker, an incident bar, a transmission bar, an absorption bar, and a data receiving and collecting system [4,8]. The pressure in the high-pressure gas chamber was set to 0.3 MPa, and the release pressure was released to drive the striker out at a speed of (3.27 ± 0.18) m/s.
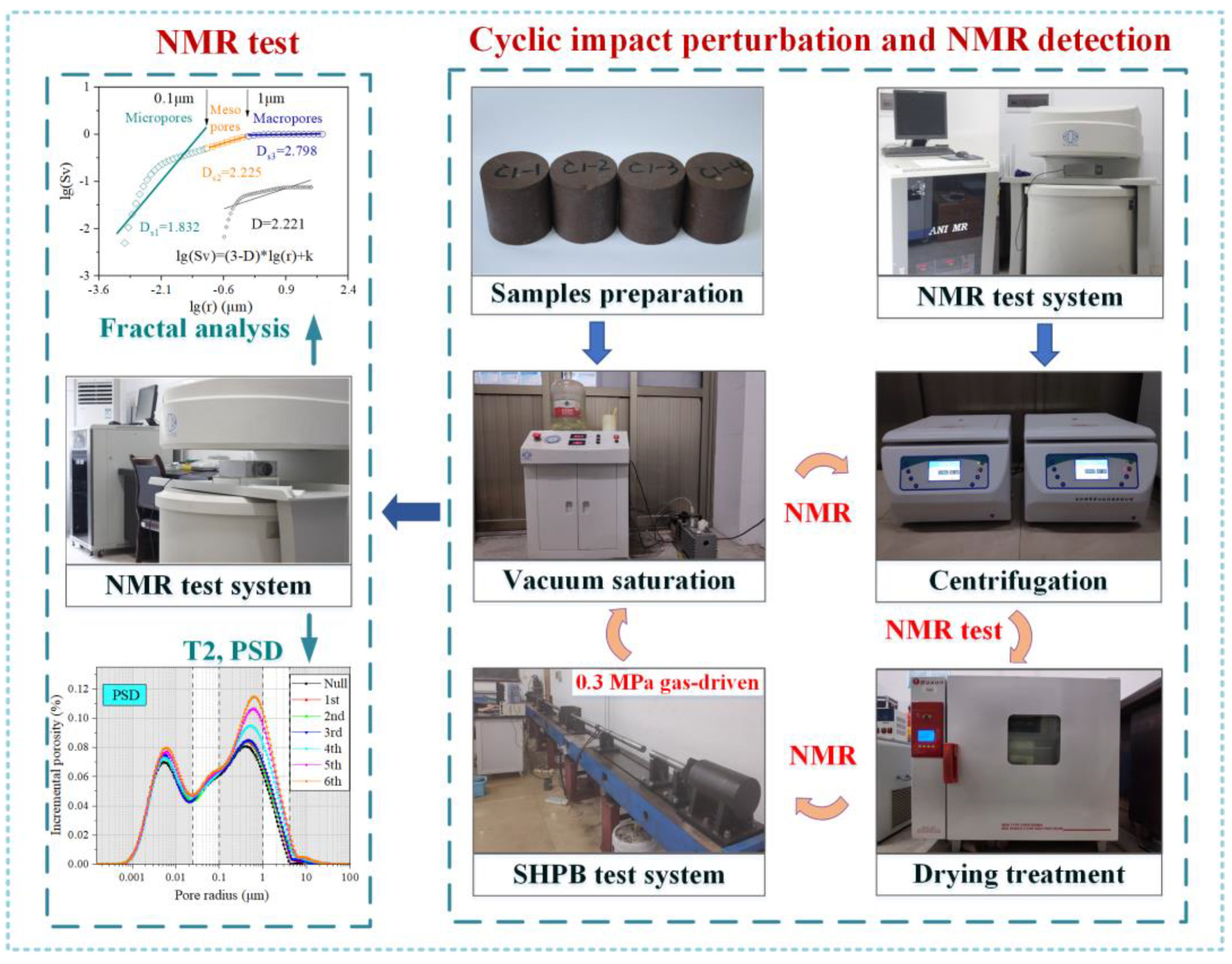
2.2. Multi-Exponential Decay Principle of NMR
3. Results
3.1. Evolution of Pore Structure
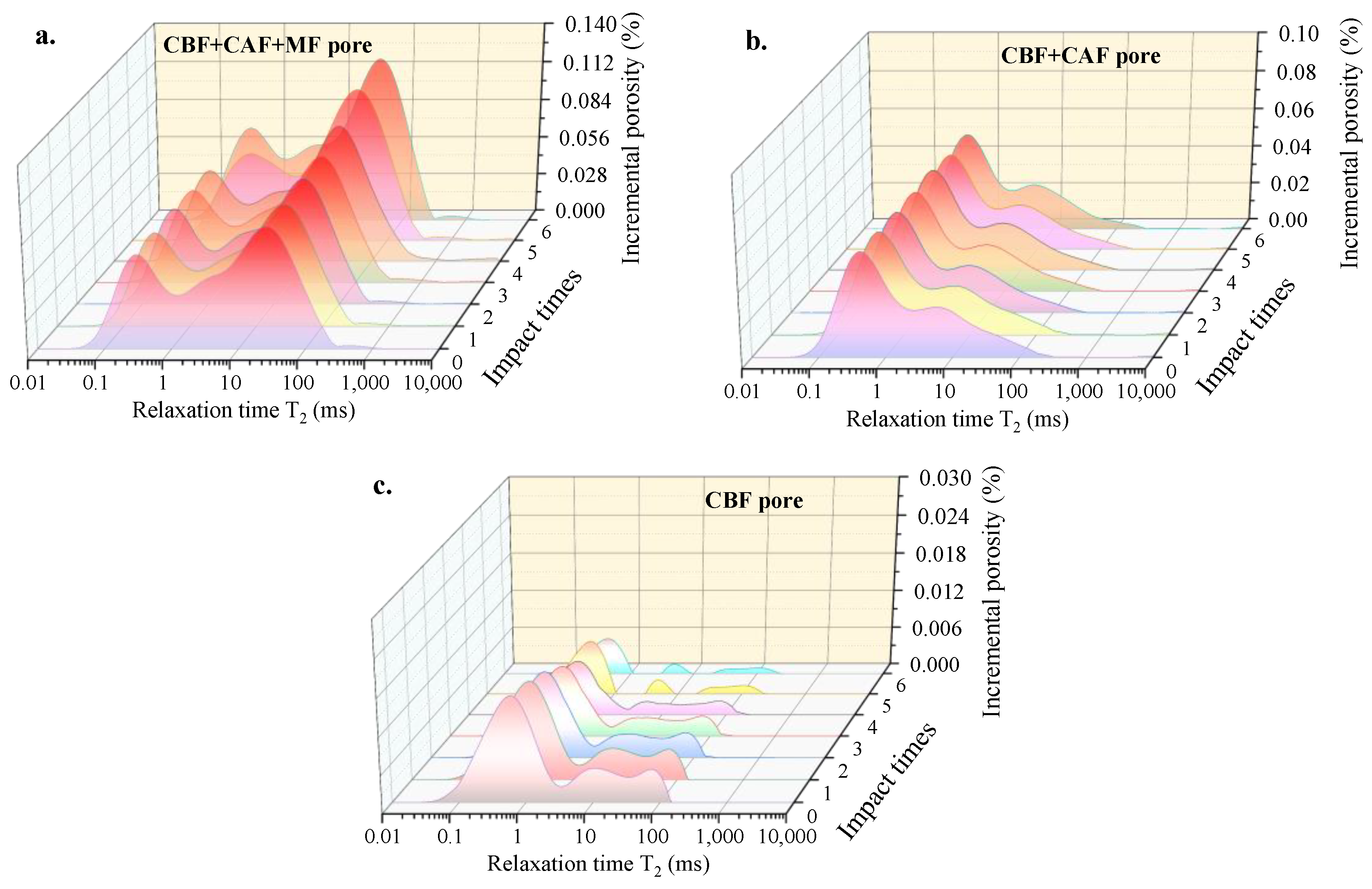
3.1.1. T2 Spectrum Distribution Measured According to Pore Connectivity
3.1.2. Quantitative Analysis of Pore Evolution Based on Pore Size
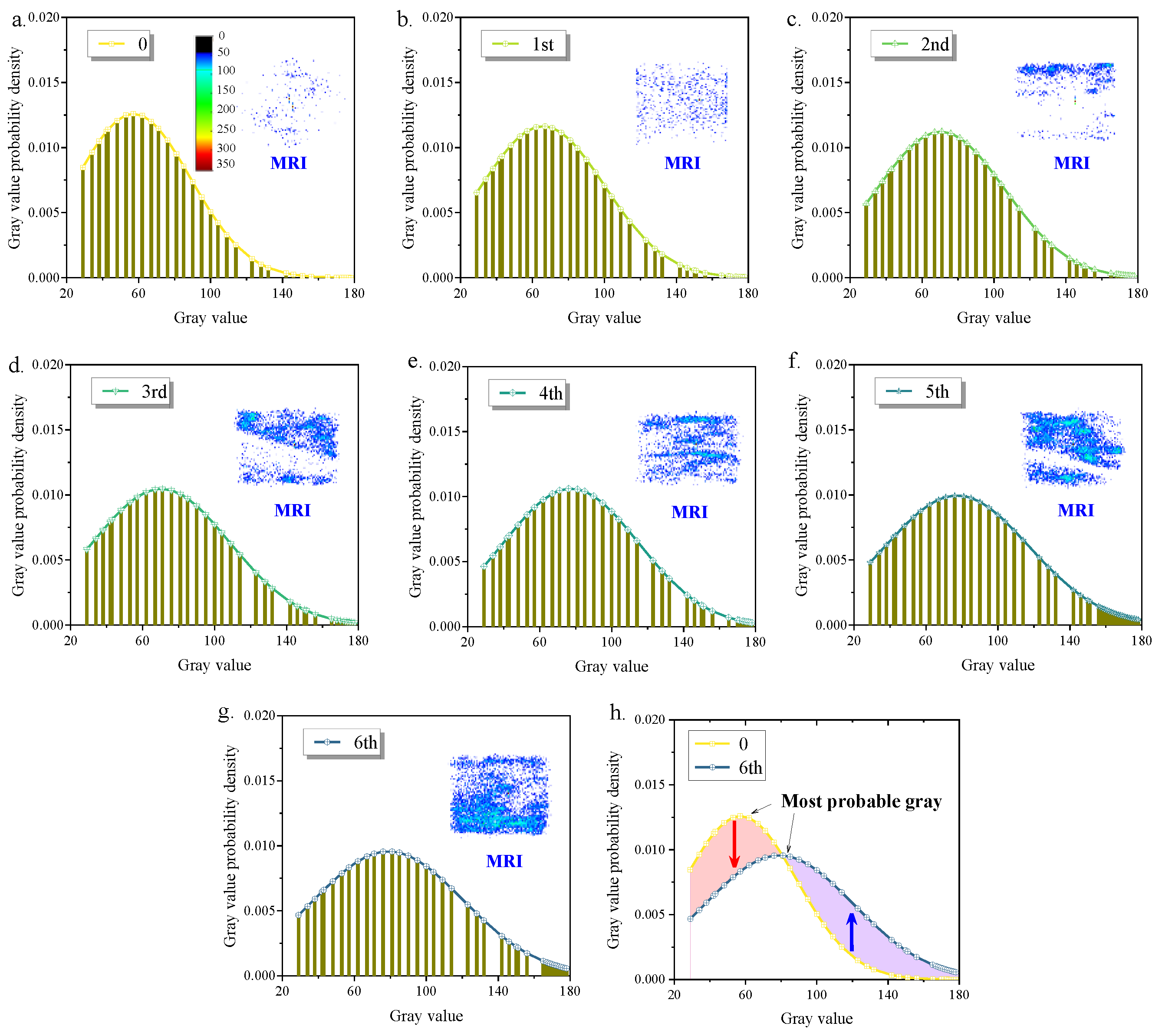
3.1.3. Pore Evolution Analysis Based on MRI
3.2. Fractal Characteristics of Pore Structure
4. Discussion
4.1. Correlation of Porosity and Fractal Dimension
4.2. Variation Correlation between Porosity and Fractal Dimension
5. Conclusions
- (1)
- The pore structure of red sandstone develops gradually under cyclic equal–amplitude impact loading, and the porosity increment increases with the accumulation of impacts. This increase is mainly observed in mesopores (0.1–1 μm) and macropores (>1 μm). After six impacts, macropores increased by 96.56%. The most probable developed pores are those with a pore size of about 1 μm.
- (2)
- The double T2 cutoff (T2c) value effectively evaluates pore connectivity. The T2c2 value distinguishes between the MF pores and the non–MF pores (CBF pores and CAF pores). Under cyclic impact, both T2c2 and T2c1 decrease, while the porosity of the MF pores increases by 37.8%, thereby enhancing the pore connectivity of the sandstone.
- (3)
- MRI visualizes the development of pores. The most probable gray value increases during cyclic impact. There is an increase in the number of macropores, which expand, forming pore clusters and even macro fissures.
- (4)
- Based on pore size and pore connectivity, the pores were analyzed, and their fractal dimension was calculated. The fractal dimension of various types of pores gradually decreased under cyclic impact. Additionally, the porosity of mesopores and macropores showed a non–linear correlation with their fractal dimension using the F–ps method. On the other hand, the porosity of the CAF and MF pores exhibited a linear correlation with their fractal dimension using the F–T2c method. Notably, micropores with small size or CBF pores with weak connectivity lack fractal features when analyzed from a surface geometry perspective.
- (5)
- Taking into account the magnitude of changes in the pore structure of rocks during equal–amplitude cyclic impact loading, a correlation model between ΦI and DI was established. Mesopores, macropores, and all pores exhibit a nonlinear power function relationship between ΦI and DI. In contrast, the CAF pores and MF pores show a linear correlation between ΦI and DI.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| T2 | Transverse relaxation time |
| r | Pore radius |
| 0 | Initial porosity |
| i | Porosity after ith impacts |
| Φcb | Porosity of CBF pores |
| Φca | Porosity of CAF pores |
| Φm | Porosity of MF pores |
| D | Fractal dimension |
| Dcb | Fractal dimension of CBF pores |
| Dca | Fractal dimension of CAF pores |
| Dm | Fractal dimension of MF pores |
| T2c | T2 cutoff |
| MRI | Magnetic resonance imaging |
| SHPB | Split Hopkinson pressure bar |
| NMR | Nuclear magnetic resonance |
| PSD | Pore size distribution |
| CBF | Clay–bound fluid |
| CAF | Capillary–bound fluid |
| MF | Movable fluid |
| F–T2c | Calculation of D value based on T2 cutoff |
| F–ps | Calculation of D value based on pore size |
| ΦI | The percent increase in porosity |
| DI | The percent increase in fractal dimension |
References
- Chu, F.; Liu, D.; Zhang, X.; Yu, H.; Zhu, G. Dynamic Response and Damage Regularity of Sandstone with Different Moisture States Under Cyclic Loading. Fractal Fract. 2022, 6, 226. [Google Scholar] [CrossRef]
- Li, R.; Zhu, J.; Qu, H.; Zhou, T.; Zhou, C. An Experimental Investigation on Fatigue Characteristics of Granite Under Repeated Dynamic Tensions. Int. J. Rock Mech. Min. Sci. 2022, 158, 105185. [Google Scholar] [CrossRef]
- Jiang, Z.; Yu, S.; Deng, H.; Deng, J.; Zhou, K. Investigation on Microstructure and Damage of Sandstone under Cyclic Dynamic Impact. IEEE Access 2019, 7, 133145–133158. [Google Scholar] [CrossRef]
- Liu, C.; Deng, H.; Wang, Y.; Lin, Y.; Zhao, H. Time-Varying Characteristics of Granite Microstructures After Cyclic Dynamic Disturbance Using Nuclear Magnetic Resonance. Crystals 2017, 7, 306. [Google Scholar] [CrossRef]
- Weng, L.; Wu, Z.; Liu, Q. Dynamic Mechanical Properties of Dry and Water-Saturated Siltstones Under Sub-Zero Temperatures. Rock Mech. Rock Eng. 2020, 53, 4381–4401. [Google Scholar] [CrossRef]
- Yang, R.; Xu, Y.; Chen, P.; Wang, J. Experimental Study on Dynamic Mechanics and Energy Evolution of Rubber Concrete Under Cyclic Impact Loading and Dynamic Splitting Tension. Constr. Build. Mater. 2020, 262, 120071. [Google Scholar] [CrossRef]
- Zhang, K.; Lai, J.; Bai, G.; Pang, X.; Ma, X.; Qin, Z.; Zhang, X.; Fan, X. Comparison of Fractal Models Using Nmr and Ct Analysis in Low Permeability Sandstones. Mar. Pet. Geol. 2020, 112, 104069. [Google Scholar] [CrossRef]
- Cao, R.; Wang, H.; Qiu, X.; Wang, C.; Lin, H.; Qiao, Q. Damage characteristics and fracture behavior of marble after cycle impact loading. Theor. Appl. Fract. Mech. 2023, 125, 103903. [Google Scholar] [CrossRef]
- Gao, X.; Xia, H.; Wang, X.; Zhao, C.; Yin, J.; Junyan, Y.; Yi, J. Experimental Study on Dynamic Mechanical Characteristics and Energy Evolution of Sandstone Under Cyclic Impact Loading. Shock Vib. 2022, 2022, 4805589. [Google Scholar] [CrossRef]
- Wang, X.; Dong, B.; Gao, X.; Li, P.; Wang, S.; Hu, B. Dynamic Behaviour and Energy Evolution of Granite in a Tunnel Under Cyclic Impact Loading. Rock Mech. Rock Eng. 2023, 56, 8997–9012. [Google Scholar] [CrossRef]
- Xia, W.; Xue, J.; Zhang, Y.; Jin, J.; Zhao, Z.; Cai, R. Dynamic Characteristics of Thermal Damage Granite under Cyclic Impact Loading. Geotech. Geol. Eng. 2023, 41, 2313–2323. [Google Scholar] [CrossRef]
- Luo, N.; Suo, Y.; Fan, X.; Yuan, Y.; Zhai, C.; Sun, W. Research on Confining Pressure Effect of Pore Structure of Coal-Rich in Coalbed Methane Under Cyclic Impact. Energy Rep. 2022, 8, 7336–7348. [Google Scholar] [CrossRef]
- Jiang, Z.; Deng, H.; Liu, T.; Tian, G.; Tang, L. Study on Microstructural Evolution of Marble under Cyclic Dynamic Impact Based On Nmr. IEEE Access 2019, 7, 138043–138055. [Google Scholar] [CrossRef]
- Shu, R.; Yin, T.; Li, X.; Yin, Z.; Tang, L. Effect of Thermal Treatment on Energy Dissipation of Granite Under Cyclic Impact Loading. Trans. Nonferrous Met. Soc. China 2019, 29, 385–396. [Google Scholar] [CrossRef]
- Li, H.; Qiao, Y.; He, M.; Shen, R.; Gu, Z.; Cheng, T.; Xiao, Y.; Tang, J. Effect of Water Saturation on Dynamic Behavior of Sandstone after Wetting-Drying Cycles. Eng. Geol. 2023, 319, 107105. [Google Scholar] [CrossRef]
- Wang, X.; Guo, L.J.; Xu, Z.; Liu, X.; Xu, J.; Pan, B.; Deng, D. Dynamic Response and Damage Evolution of Red Sandstone with Confining Pressure Under Cyclic Impact Loading. Fatigue Fract. Eng. Mater. Struct. 2023, 46, 1078–1092. [Google Scholar] [CrossRef]
- Radlinski, A.P.; Ioannidis, M.A.; Hinde, A.L.; Hainbuchner, M.; Baron, M.; Rauch, H.; Kline, S.R. Angstrom-to-Millimeter Characterization of Sedimentary Rock Microstructure. J. Colloid Interface Sci. 2004, 274, 607–612. [Google Scholar] [CrossRef] [PubMed]
- Deng, H.; Tian, G.; Yu, S.; Jiang, Z.; Zhong, Z.; Zhang, Y. Research on Strength Prediction Model of Sand-Like Material Based on Nuclear Magnetic Resonance and Fractal Theory. Appl. Sci. 2020, 10, 6601. [Google Scholar] [CrossRef]
- Pang, X.; Wang, G.; Kuang, L.; Li, H.; Zhao, Y.; Li, D.; Zhao, X.; Wu, S.; Feng, Z.; Lai, J. Insights into the Pore Structure and Oil Mobility in Fine-Grained Sedimentary Rocks: The Lucaogou Formation in Jimusar Sag, Junggar Basin, China. Mar. Pet. Geol. 2022, 137, 105492. [Google Scholar] [CrossRef]
- Lay Lian, T.; Radhakrishnan, P.; Daya Sagar, B.S. Morphological Decomposition of Sandstone Pore–Space: Fractal Power-Laws. Chaos Solitons Fractals 2004, 19, 339–346. [Google Scholar] [CrossRef]
- Li, J.; Tan, S.; Yang, C.; Chen, H.; Lin, Y. Analysis of Damage Characteristics for Skarn Subjected to Freeze-Thaw Cycles Based on Fractal Theory. Fractal Fract. 2023, 7, 354. [Google Scholar] [CrossRef]
- Vidales, A.M.; Miranda, E.N. Fractal Porous Media: Relations Between Macroscopic Properties. Chaos Solitons Fractals 1996, 7, 1365–1369. [Google Scholar] [CrossRef]
- Wu, X.; Cai, M.; Zhu, Y.; Guo, Q.; Wang, P.; Dong, J. An Experimental Study on the Fractal Characteristics of the Effective Pore Structure in Granite by Thermal Treatment. Case Stud. Therm. Eng. 2023, 45, 102921. [Google Scholar] [CrossRef]
- Zhang, Z.; Weller, A. Fractal Dimension of Pore-Space Geometry of an Eocene Sandstone Formation. Geophysics 2014, 79, D377–D387. [Google Scholar] [CrossRef]
- Guo, X.; Huang, Z.; Zhao, L.; Han, W.; Ding, C.; Sun, X.; Yan, R.; Zhang, T.; Yang, X.; Wang, R. Pore Structure and Multi-Fractal Analysis of Tight Sandstone Using Mip, Nmr and Nmrc Methods: A Case Study from the Kuqa Depression, China. J. Pet. Sci. Eng. 2019, 178, 544–558. [Google Scholar] [CrossRef]
- Wu, F.; Li, Y.; Burnham, B.; Zhang, Z.; Yao, C.; Yuan, L.; Zhang, F.; Deng, H.; Xi, Y.; He, J. Fractal-Based Nmr Permeability Estimation in Tight Sandstone: A Case Study of the Jurassic Rocks in the Sichuan Basin, China. J. Pet. Sci. Eng. 2022, 218, 110940. [Google Scholar] [CrossRef]
- Xin, Y.; Wang, G.; Liu, B.; Ai, Y.; Cai, D.; Yang, S.; Liu, H.; Xie, Y.; Chen, K. Pore Structure Evaluation in Ultra-Deep Tight Sandstones Using Nmr Measurements and Fractal Analysis. J. Pet. Sci. Eng. 2022, 211, 110180. [Google Scholar] [CrossRef]
- Feng, Z.; Zhao, Y.; Zhao, D. Investigating the Scale Effects in Strength of Fractured Rock Mass. Chaos Solitons Fractals 2009, 41, 2377–2386. [Google Scholar]
- Jiang, Z.; Cai, G.; Tian, G.; Liu, X. Effect of Aggregate Particle Size on Mortar Pore Structure. Constr. Build. Mater. 2022, 352, 128988. [Google Scholar] [CrossRef]
- Li, J.; Zhou, K.; Liu, W.; Deng, H. Nmr Research on Deterioration Characteristics of Microscopic Structure of Sandstones in Freeze–Thaw Cycles. Trans. Nonferrous Met. Soc. China 2016, 26, 2997–3003. [Google Scholar] [CrossRef]
- Jiang, Z.; He, H.; Tian, G.; Guo, W.; Li, Y.; Pan, Z. Pore Structure Quantification and Fractal Characterization of Msa Mortar Based On 1H Low-Field Nmr. Fractal Fract. 2024, 8, 42. [Google Scholar] [CrossRef]
- Wang, F.; Yang, K.; Cai, J. Fractal Characterization of Tight Oil Reservoir Pore Structure Using Nuclear Magnetic Resonance and Mercury Intrusion Porosimetry. Fractals-Complex Geom. Patterns Scaling Nat. Soc. 2018, 26, 1840017. [Google Scholar] [CrossRef]
- Xie, W.; Yin, Q.; Wang, G.; Yu, Z. Variable dimension Fractal-Based Conversion Method between the Nuclear Magnetic Resonance T 2 Spectrum and Capillary Pressure Curve. Energy Fuels 2021, 35, 351–357. [Google Scholar] [CrossRef]
- Rigby, S.P. Theoretical Aspects of the Estimation of Pore and Mass Fractal Dimensions of Porous Media on the Macroscopic Scale Using Nmr Imaging. Chaos Solitons Fractals 1998, 9, 1519–1527. [Google Scholar] [CrossRef]
- Mohnke, O.; Yaramanci, U. Pore Size Distributions and Hydraulic Conductivities of Rocks Derived from Magnetic Resonance Sounding Relaxation Data Using Multi-Exponential Decay Time Inversion. J. Appl. Geophys. 2008, 66, 73–81. [Google Scholar] [CrossRef]
- Saidian, M.; Prasad, M. Effect of Mineralogy on Nuclear Magnetic Resonance Surface Relaxivity: A Case Study of Middle Bakken and Three Forks Formations. Fuel 2015, 161, 197–206. [Google Scholar] [CrossRef]
- Valori, A.; Rodin, V.; Mcdonald, P.J. On the Interpretation of 1H 2-Dimensional Nmr Relaxation Exchange Spectra in Cements: Is there Exchange Between Pores with Two Characteristic Sizes or Fe3+ Concentrations? Cem. Concr. Res. 2010, 40, 1375–1377. [Google Scholar] [CrossRef]
- Godefroy, S.; Korb, J.P.; Fleury, M.; Bryant, R.G. Surface Nuclear Magnetic Relaxation and Dynamics of Water and Oil in Macroporous Media. Phys. Rev. E 2001, 64, 021605. [Google Scholar] [CrossRef]
- Xie, W.; Yin, Q.; Zeng, J.; Wang, G.; Feng, C.; Zhang, P. Fractal-Based Approaches to Pore Structure Investigation and Water Saturation Prediction from Nmr Measurements: A Case Study of the Gas-Bearing Tight Sandstone Reservoir in Nanpu Sag. Fractal Fract. 2023, 7, 273. [Google Scholar] [CrossRef]
- Peng, L.; Zhang, C.; Ma, H.; Pan, H. Estimating Irreducible Water Saturation and Permeability of Sandstones from Nuclear Magnetic Resonance Measurements by Fractal Analysis. Mar. Pet. Geol. 2019, 110, 565–574. [Google Scholar] [CrossRef]
- Zhang, P.; Lu, S.; Li, J.; Xue, H.; Li, W.; Zhang, P. Characterization of Shale Pore System: A Case Study of Paleogene Xin’gouzui Formation in the Jianghan Basin, China. Mar. Pet. Geol. 2017, 79, 321–334. [Google Scholar] [CrossRef]
- Zhang, P.; Lu, S.; Li, J.; Chang, X.; Zhang, J.; Pang, Y.; Lin, Z.; Chen, G.; Yin, Y.; Liu, Y. Quantitative Characterization of Shale Pore Connectivity and Controlling Factors Using Spontaneous Imbibition Combined with Nuclear Magnetic Resonance T2 and T1-T2. Pet. Sci. 2023, 20, 1947–1960. [Google Scholar] [CrossRef]





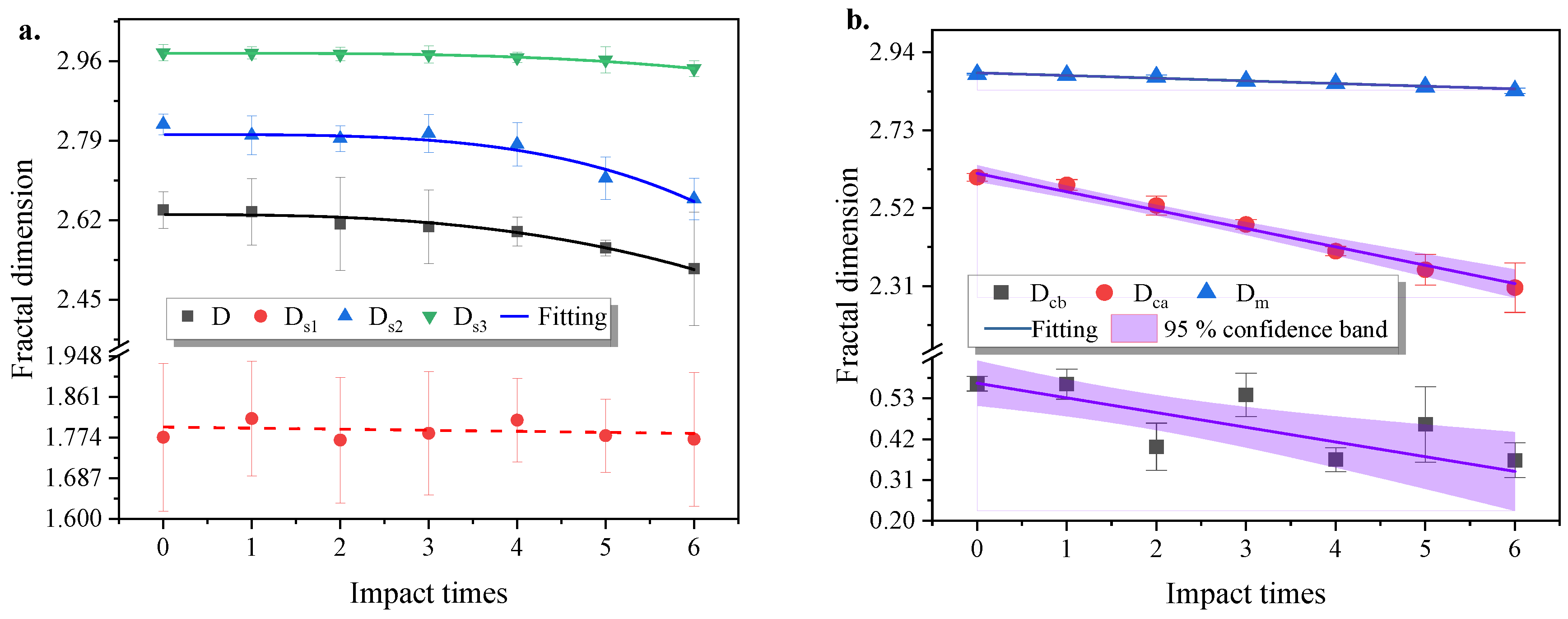




| Total Pores | Micropores | Mesopores | Macropores | |||||
|---|---|---|---|---|---|---|---|---|
| Number of Impacts | D (rmin < r < rmax) | Standard Deviation | Ds1 (rmin < r < 0.1 μm) | Standard Deviation | Ds2 (0.1 μm < r < 1 μm) | Standard Deviation | Ds3 (1 μm < r < rmax) | Standard Deviation |
| 0 | 2.642 | 0.039 | 1.775 | 0.158 | 2.825 | 0.022 | 2.979 | 0.018 |
| 1 | 2.638 | 0.071 | 1.815 | 0.123 | 2.802 | 0.042 | 2.978 | 0.013 |
| 2 | 2.612 | 0.099 | 1.769 | 0.134 | 2.795 | 0.028 | 2.976 | 0.014 |
| 3 | 2.607 | 0.079 | 1.783 | 0.132 | 2.805 | 0.040 | 2.975 | 0.018 |
| 4 | 2.596 | 0.031 | 1.811 | 0.090 | 2.782 | 0.047 | 2.968 | 0.011 |
| 5 | 2.561 | 0.017 | 1.778 | 0.078 | 2.710 | 0.045 | 2.963 | 0.028 |
| 6 | 2.516 | 0.121 | 1.770 | 0.143 | 2.666 | 0.044 | 2.944 | 0.017 |
| CBF Pores | CAF Pores | MF Pores | ||||
|---|---|---|---|---|---|---|
| Number of Impacts | Dcb (rmin < r < rc1) | Standard Deviation | Dca (rc1 < r < rc2) | Standard Deviation | Dm (rc1 < r < rmax) | Standard Deviation |
| 0 | 0.570 | 0.020 | 2.603 | 0.010 | 2.881 | 0.002 |
| 1 | 0.569 | 0.040 | 2.583 | 0.014 | 2.878 | 0.001 |
| 2 | 0.400 | 0.064 | 2.527 | 0.026 | 2.874 | 0.005 |
| 3 | 0.540 | 0.058 | 2.476 | 0.013 | 2.863 | 0.001 |
| 4 | 0.365 | 0.033 | 2.404 | 0.013 | 2.856 | 0.001 |
| 5 | 0.460 | 0.102 | 2.354 | 0.042 | 2.847 | 0.003 |
| 6 | 0.364 | 0.047 | 2.306 | 0.067 | 2.836 | 0.007 |
| Fitting Equation | R2 | p | |
|---|---|---|---|
| F–ps method | D = 2.632–8.4 × 10−4 × x2.761 | 0.981 | 0.002 |
| Ds1 = 1.797–0.002 × x | 0.163 | 0.625 > 0.05 | |
| Ds2 = 2.803–2.3 × 10−4 × x3.596 | 0.955 | 0.0003 | |
| Ds3 = 2.978–8.6 × 10−5 × x3.318 | 0.990 | 0.007 | |
| F–T2c method | Dcb = 0.571–0.040 × x | 0.806 | 0.010 |
| Dca = 2.614–0.049 × x | 0.978 | 0.007 | |
| Dm = 2.885–0.007 × x | 0.988 | 0.004 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qiao, H.; Wang, P.; Jiang, Z.; Liu, Y.; Tian, G.; Zhao, B. Evolution of Pore Structure and Fractal Characteristics in Red Sandstone under Cyclic Impact Loading. Fractal Fract. 2024, 8, 437. https://doi.org/10.3390/fractalfract8080437
Qiao H, Wang P, Jiang Z, Liu Y, Tian G, Zhao B. Evolution of Pore Structure and Fractal Characteristics in Red Sandstone under Cyclic Impact Loading. Fractal and Fractional. 2024; 8(8):437. https://doi.org/10.3390/fractalfract8080437
Chicago/Turabian StyleQiao, Huanhuan, Peng Wang, Zhen Jiang, Yao Liu, Guanglin Tian, and Bokun Zhao. 2024. "Evolution of Pore Structure and Fractal Characteristics in Red Sandstone under Cyclic Impact Loading" Fractal and Fractional 8, no. 8: 437. https://doi.org/10.3390/fractalfract8080437
APA StyleQiao, H., Wang, P., Jiang, Z., Liu, Y., Tian, G., & Zhao, B. (2024). Evolution of Pore Structure and Fractal Characteristics in Red Sandstone under Cyclic Impact Loading. Fractal and Fractional, 8(8), 437. https://doi.org/10.3390/fractalfract8080437






