Securing Bipartite Nonlinear Fractional-Order Multi-Agent Systems against False Data Injection Attacks (FDIAs) Considering Hostile Environment

Abstract

This study investigated the stability of bipartite nonlinear fractional-order multi-agent systems (FOMASs) in the presence of false data injection attacks (FDIAs) in a hostile environment. To tackle this problem we used signed graph theory, the Razumikhin methodology, and the Lyapunov function method. The main focus of our proposed work is to provide a method of stability for FOMASs against FDIAs. The technique of Razumikhin improves the Lyapunov-based stability analysis by supporting the handling of the intricacies of fractional-order dynamics. Moreover, utilizing signed graph theory, we analyzed both hostile and cooperative interactions between agents within the MASs. We determined the system stability requirements to ensure robustness against erroneous data injections through comprehensive theoretical investigation. We present numerical examples to illustrate the robustness and efficiency of our proposed technique.

1. Introduction

Networked system cooperation has been greatly improved through the fast developments of network and communication technologies [1,2]. In the field of multi-agent systems, cooperative control has received significant interest in areas such as automation [3], Mathematics [4], and Computer science [5]. This kind of technology has been utilized extensively in the military and the civilian sector for a range of operations, including designing smart power grid systems [6], controlling unmanned spacecraft [7], adjusting satellite placements [8], and guiding mobile robot formations [9]. In a multi-agent system, containment control having more than one leader is a specific field of interest. The use of this approach has gained greater attention in recent years. The primary object is to establish a control protocol to ensure that followers eventually converge to a desired region defined by the convex hull created by the leaders [10,11]. The research mentioned above explored traditional communication networks that encompass cooperative interactions. These networks are represented by directed graphs with non-negative adjacency weight matrices. However, practical situations, such as social networks [12], trust networks [13], natural predator–prey dynamics [14], games [15], and biological systems [16], commonly involve relationships that can be either cooperative or hostile. These interactions can be represented by signed digraphs, where positive weights show cooperative or trust relationships, and negative weights indicate hostile relationships between connected agents. The existence of hostile interactions leads to more complex actions in signed digraphs in contrast to conventional non-negative directed graphs [17]. Additionally, without a secure network and preservation, the system becomes susceptible to potential infiltration by adversaries who may interrupt communication channels. This could result in compromised control performance, such as a slow convergence rate, significant convergence error, and instability [18]. Additionally, the adversary’s capabilities are typically limited. Deception attacks [19] and DoS attacks [20] are two main categories of attacks on multi-agent dynamical systems based on their impact. Deception attacks involve manipulating transmitted information, while DoS attacks result in the loss or delay of transmitted information. Dibaji et al. highlighted that deception attacks, particularly false data injection (FDI) attacks [21], cause the most severe damage in such systems. Therefore, it is crucial to study deception attacks, especially FDI attacks, in multi-agent dynamical systems to safeguard against the manipulation of transmitted information [22]. In this overview, we provide a summary of the current research on coordinating the control of fractional-order multi-agent systems. Within the domain of continuous-time systems, several protocols have been suggested to address coordination issues in fractional-order multi-agent systems [23]. For example, in reference [24], researchers explored consensus mechanisms in the context of fractional-order multi-agent systems dealing with communication delays using frequency domain theory. Moreover, in [25], the academic community introduced conditions based on Linear Matrix Inequalities (LMIs) to facilitate containment control strategies designed for uncertain linear multi-agent systems. In a similar vein, [26] utilized a sliding-mode control approach to tackle the complex task of distributed consensus tracking within fractional-order multi-agent systems. These efforts collectively shed light on the ongoing work aimed at improving the understanding and implementation of effective coordination control mechanisms for fractional-order multi-agent systems within continuous-time frameworks. We examine several critical studies addressing the security of multi-agent systems in cyber-physical environments. Notably, the research on multi-agent systems for detecting false data injection attacks against the power grid provides essential methodologies for identifying and mitigating such threats [27]. Additionally, the observer-based event-triggered secure synchronization control for multi-agent systems under false data injection attacks offers valuable insights into maintaining secure synchronization in the presence of data corruption [28]. Furthermore, the cooperative control for cyber-physical multi-agent networked control systems with unknown false data injection and replay cyber-attacks highlights strategies for managing and securing networked control systems against sophisticated cyber-attacks [29]. These foundational studies form the basis of our approach, informing our strategies for enhancing the security and resilience of multi-agent systems. Motivated by the above study, we will address hostile-based nonlinear bipartite containment control fractional-order multi-agent systems under false data injection attacks (FDIAs). We will discuss both fixed and switching signed directed networks under FDIAs. Furthermore, we will check the stability of the system in the presence of false data injection attacks, and for this purpose, we use the Lyapunov function, Razumikhin methods, and signed graph theory. Our special contributions are listed below:

• In contrast to [28], our work contributes to the field by integrating delayed controllers to enhance the resilience and effectiveness of multi-agent systems against false data injection attacks.
• The use of false data injection in the dynamics of followers improves the detection and mitigation of such attacks in multi-agent systems, which were not considered in the previous study [17].
• Utilizing fractional-order multi-agent systems can enhance the robustness and accuracy of detecting and mitigating false data injection attacks as compared to [29].

The rest of this paper is as follows:

• Section 2: Provide background knowledge about multi-agent systems of fractional order, covering foundational concepts and initial details.
• Section 3: Present the formulation of the main result.
• Section 4: Present the stability analysis of the proposed multi-agent system.
• Section 5: Present practical examples to illustrate the effectiveness of our work.
• Section 6: Present the conclusion of the overall study.

2. Background Knowledge

This section presents the background knowledge about the study:

2.1. Signed Graph Theory

Consider a weighted signed digraph $\mathcal{G}=\{\mathcal{V},\mathcal{E}\}$, where $\mathcal{V}=\{v_1,v_2,\dots ,v_{\mathcal{M}}\}$ and $\mathcal{E}\subseteq \mathcal{V}\times \mathcal{V}$ are the vertices and edge set, respectively. The adjacency matrix $\mathcal{J}={\left[j_{uv}\right]}_{\mathcal{M}\times \mathcal{M}}$ is defined such that $j_{uv}\ne 0$ if $(v_u,v_v)\in \mathcal{E}$, and $j_{uv}=0$ otherwise. In this matrix, $j_{uv}>0$ and $j_{uv}<0$ represent cooperative and hostile relationships between nodes, respectively.

The Laplacian matrix of the graph $\mathcal{G}$, denoted by $L={\left[{\ell }_{uv}\right]}_{\mathcal{M}\times \mathcal{M}}$, is defined as follows:

• ${\ell }_{uv}=-j_{uv}$ if $u\ne v$
• ${\ell }_{uv}={\sum }_{v=1,v\ne u}^{\mathcal{M}}\left|j_{uv}\right|$ if $u=v$

A signed graph $\mathcal{G}$ is said to be structurally balanced if the set of nodes $\mathcal{V}$ can be partitioned into two disjoint subsets, ${\mathcal{V}}_1$ and ${\mathcal{V}}_2$, such that

• $j_{uv}\ge 0$ for any $v_u,v_v\in {\mathcal{V}}_1$ or $v_u,v_v\in {\mathcal{V}}_2$
• $j_{uv}\le 0$ for any $v_u\in {\mathcal{V}}_1$ and $v_v\in {\mathcal{V}}_2$

2.2. Necessary Lemmas and Definitions

Several essential definitions and lemmas are addressed in this section.

Definition 1 

([30]). The Caputo derivative of order α for the function $h\left(k\right)$ of order s, which is continuous and also differentiable, is defined as

$$D^{\alpha }h\left(k\right)={\displaystyle \frac{1}{\Gamma (s-\alpha )}}{\int }_{s_0}^s{\displaystyle \frac{h^s\left(u\right)}{{(s-u)}^{\alpha -s+1}}}du0\le s-1<\alpha \le s,s\in Z^{+}$$

Lemma 1 

([31]). A function $h\left(k\right)$ belonging to the set of absolutely continuous functions in ${\mathbb{R}}^n$ adheres to the following:

$$D^{\alpha }(h^T\left(k\right)h\left(k\right))\le 2h^T\left(k\right)D^{\alpha }h\left(k\right),\alpha \in (0,1)$$

Lemma 2 

([32]). If U, V, and W are matrices, then the inequality

$$\left(\begin{array}{ccc}U& & V\\ V^T& & W\end{array}\right)<0$$

(1)

is equivalent to inequalities U < 0 and $W-V^T{U}^{-1}V<0$.

Lemma 3 

([33]). The following inequality holds for positive scalar ξ and $W_1,W_2\in {\mathbb{R}}^n$:

$$2W_1^T{W}_2\le \xi W_1^T{W}_1+{\displaystyle \frac{1}{\xi }}{W}_2^T{W}_2$$

Consider the Banach space $B=B([-r,0]\to {\mathbb{R}}^n)$ of functions that exhibit continuity for interval $[-r,0]$. Also, consider a delayed system that is of a fractional order incorporating delays:

$$\begin{array}{cc}\hfill D^{\alpha }x\left(k\right)& =G(k,x_t)for0<\alpha <1\hfill \end{array}$$

(2)

$$\begin{array}{cc}\hfill x_{k_0}& =\phi \left(\theta \right),where{x}_t\left(\varphi \right)=x(k+\varphi ),\varphi ,\theta \in [-r,0]\hfill \end{array}$$

(3)

where $G:(\mathbb{R}\times \mathrm{bounded}\mathrm{set}\mathrm{of}\mathcal{B})\to (\mathrm{bounded}\mathrm{set}\mathrm{of}{\mathbb{R}}^n)$ satisfies condition $G(k,0)=0$. This condition holds for each $k\ge k_0$, time delay $r>0$, and $\phi \in \mathcal{B}$.

Lemma 4. 

For a quadratic Lyapunov function $V:{\mathbb{R}}^n\to \mathbb{R}$, there exist some $\eta >1$ and $a_1,a_2,a_3>0$ such that the following inequality holds:

• $a_1{\left|\right|s\left(k\right)\left|\right|}^2\le V\left(s\left(k\right)\right)\le a_2{\left|\right|s\left(k\right)\left|\right|}^2$ and always
• $V\left(s\right(k+\vartheta \left)\right)\le \eta V\left(s\right(k\left)\right),\vartheta \in [-r,0]$
• $D^{\alpha }z\left(s\left(k\right)\right)\le -a_3{\left|\right|s\left(k\right)\left|\right|}^2$

Hence, the necessary solution of the system defined by (2) and (3) may be made stable.

3. Issue Identification

Consider a bipartite fractional-order multi-agent system (FOMAS) with the following definitions:

• Follower: $\mathcal{F}$ agents labeled as $\overline{\mathcal{F}}=\{1,2,3\dots ,\mathcal{F}\}$;
• Leaders: $\mathcal{M}-\mathcal{F}$ agents labeled as $\overline{\mathcal{R}}=\{\mathcal{F}+1,\mathcal{F}+2\dots ,\mathcal{M}\}$.

The uth agent state $z_u\left(k\right)\in {\mathbb{R}}^n$ is governed by fractional differential equations that are defined as follows:

$$\begin{array}{cc}\hfill D^{\alpha }{z}_u\left(k\right)& =B{z}_u\left(k\right)+g(k,z_u\left(k\right))+W{\int }_{-r^{\prime }}^0{z}_u(k+\vartheta )d\vartheta +{\omega }_u(k-r^{″}),u\in \overline{\mathcal{F}}\hfill \end{array}$$

(4)

$$\begin{array}{cc}\hfill D^{\alpha }{z}_u\left(k\right)& =B{z}_u\left(k\right)+g(k,z_u\left(k\right))+W{\int }_{-r^{\prime }}^0{z}_u(k+\vartheta )d\vartheta ,u\in \overline{\mathcal{R}}\hfill \end{array}$$

(5)

Here, ${\omega }_u\left(k\right)$ represents the control input for agent u, and $r^{\prime }$ and $r^{″}$ are the delay in time and distributed delay, respectively. Matrices B and W belong to ${\mathbb{R}}^{n\times n}$, and g with $g(k,0)=0$ is the continuous odd function such that $g:\mathbb{R}\times {\mathbb{R}}^n\to {\mathbb{R}}^n$.

Definition 2 

([34]). The function $\eta \in {\mathbb{R}}^n$ is called convex if for each $x_1,x_2\in \eta$, for $0<\rho <1$, the following condition holds:

$$(1-\rho )x_1+\rho x_2\in \eta$$

And the convex hull formed by $x_1,x_2,\dots x_n\in {\mathbb{R}}^n.$ is defined as

$$co\{x_1,x_2\dots ,x_n{\displaystyle \}}=\left\{\sum _{u=1}^n{\eta }_u{x}_u\right|{\eta }_u\ge 0,\sum _{u=1}^n{\eta }_u=1\}$$

Definition 3. 

The bipartite containment control FOMAS defined by (4) and (5) will be obtained if some followers converge to $co\{z_u,u\in \overline{\mathcal{R}}\}$, and others converge to the negative of it.

For the main result, we need the following assumptions.

Assumption 1. 

For nonlinear function g, the following inequality holds:

$$\parallel g(k,x)-\sum _{u=1}^{\mathcal{M}-\mathcal{F}}{\eta }_{u}g(k,x_u)\parallel \le b\parallel x-\sum _{u=1}^{\mathcal{M}-\mathcal{F}}{\eta }_u{x}_u\parallel .$$

(6)

where $x_u\in {\mathbb{R}}^n$ b > 0, and ${\eta }_u$ is obtained from ${\sum }_{u=1}^{\mathcal{M}-\mathcal{F}}{\eta }_u=1$.

Assumption 2. 

$\mathcal{G}$ is a structurally balanced signed directed graph.

Assumption 3. 

In $\mathcal{G}$, each follower has a directed link with at least one leader.

All followers will be split into two subsets if Assumption 2 is true, with agents in subsets ${\overline{\mathcal{F}}}_1\mathrm{and}{\overline{\mathcal{F}}}_2$ interacting cooperatively while these subsets are in hostile connection with other subsets. Now, the FMAS implements bipartite containment control if, by Definition 3,

$$\begin{array}{c}\hfill \underset{k\to \infty }{lim}\parallel z_u\left(k\right)-co\{z_i\left(k\right),i\in \overline{\mathcal{R}}\}\parallel =0,\forall u\in {\overline{\mathcal{F}}}_1\\ \hfill \underset{k\to \infty }{lim}\parallel z_u\left(k\right)+co\{z_i\left(k\right),i\in \overline{\mathcal{R}}\}\parallel =0\forall u\in {\overline{\mathcal{F}}}_2.\end{array}$$

3.1. Attack Model

3.1.1. Identification of Compromised Agents

Firstly, we define a subset $\mathcal{A}$ that includes all the compromised agents. If an agent u is compromised, it belongs to subset $\mathcal{A}$, denoted as $u\in \mathcal{A}\subseteq \mathbb{F}$. To indicate which agents are compromised, we use an indicator vector ${\nu }^{\mathcal{A}}\in {\{0,1\}}^n$. The vector ${\nu }^{\mathcal{A}}$ is defined such that ${\nu }^{\mathcal{A}}={[{\nu }_1^{\mathcal{A}},{\nu }_2^{\mathcal{A}},...,{\nu }_n^{\mathcal{A}}]}^T$. The element ${\nu }_u^{\mathcal{A}}=1$ if and only if agent u is compromised, and ${\nu }_u^{\mathcal{A}}=0$ if agent u is not compromised. This can be formally expressed as

$$\left\{\begin{array}{c}{\nu }_u^{\mathcal{A}}=1 if u\in \mathcal{A}\hfill \\ {\nu }_u^{\mathcal{A}}=0 if u\notin \mathcal{A}\hfill \end{array}\right.$$

3.1.2. Characteristics of Vulnerable Agents

The specific characteristics that make agents vulnerable to attacks depend on various factors, including but not limited to the following:

• Connectivity: Agents with high connectivity or central roles in the network might be more vulnerable because compromising them can have a larger impact on the overall system.
• Lack of Security Measures: Agents that lack adequate security measures, such as encryption, authentication, or anomaly detection systems, are easier targets for attackers.
• Resource Constraints: Agents with limited computational resources might not be able to run advanced security algorithms, making them more susceptible to attacks.
• Behavioral Patterns: Agents with predictable or easily detectable patterns of behavior can be targeted more effectively by adversaries.

3.1.3. Attack Strategy Design

• State Update Equation: For any selected subset $\mathcal{A}$ of compromised agents, agent u will update its state according to the following equation:

  $$D^{\alpha }{z}_u\left(k\right)=B{z}_u\left(k\right)+g(k,z_u\left(k\right))+W{\int }_{-r^{\prime }}^0{z}_u(k+\vartheta )d\vartheta +{\omega }_u(k-r^{″})+{\omega }_u^a\left(k\right),u\in \overline{\mathcal{F}}$$

  (7)

  where ${\omega }_u^a\left(k\right)$ represents the false data injected by an adversary.
• False Data Injection: The false data ${\omega }_u^a\left(k\right)$ are designed as follows:

  $${\omega }_u^a\left(k\right)=\left\{\begin{array}{cc}\psi \left(k\right),\hfill & \mathrm{if}u\in \mathcal{A},\hfill \\ 0,\hfill & \mathrm{if}u\notin \mathcal{A}.\hfill \end{array}\right.$$

  (8)
  The term $\psi \left(k\right)\in {\mathbb{R}}^m$ is the concrete attack strategy.
• Attack Space Expansion: The dynamical interaction between agents with m-dimensional states greatly expands the attack space, allowing for more sophisticated and coordinated attack strategies.

We need the following assumptions regarding this type of attack.

Assumption 4. 

The adversary is capable of injecting false data undetected, and these false data are bounded.

Assumption 5. 

The attack is time-invariant.

3.2. Hostile Interactions in Signed Digraph

To better understand the practical implications of hostile interactions in signed digraphs, we consider a social network scenario where users exhibit both supportive and antagonistic relationships. This example illustrates the complexities and challenges introduced by such interactions.

3.2.1. Network Structure and Interaction Dynamics

In this social network, nodes represent users, and edges represent interactions. Positive edges (+) indicate support, while negative edges (−) indicate opposition. Consider the following network structure:

• Node A supports Node B (+);
• Node B opposes Node C (−);
• Node C supports Node D (+);
• Node D opposes Node A (−).

3.2.2. Dynamics of Hostile Interactions

• Feedback Loops: The presence of a negative feedback loop (A → B → C → D → A) introduces instability. Such loops can lead to persistent conflicts, making it difficult for the network to reach a consensus.
• Influence Propagation: If Node A is a key opinion leader, their opposition to Node B can trigger a cascade of antagonistic interactions, polarizing the network and hindering cooperative behavior.

3.2.3. Practical Implications

• System Design: Understanding these hostile interactions helps in designing interventions to promote stability and cooperation, such as targeted conflict resolution strategies or enhanced moderation policies.
• Policy Making: For policymakers, mitigating the effects of negative interactions is crucial in maintaining harmony and functionality in critical infrastructure networks.

4. Stability Analysis of Bipartite Containment Control under FDIA

In this section, we propose a stability analysis for both fixed and switching signed directed networks.

4.1. Fixed Signed Directed Networks

For attaining the bipartite containment control of the system defined by (4) and (5), first, we construct a controller that is under FDIAs:

$${\omega }_u(k-r^{″})=\mathcal{K}\sum _{v=1}^{\mathcal{M}}\left|j_{uv}\right|\left(sgn\left(j_{uv}\right)\right)z_v(k-r^{″})-z_u(k-r^{″})+{\omega }_u^a\left(k\right),u\in \overline{\mathcal{F}}$$

(9)

The gain constant $\mathcal{K}$ used in the above equation is taken to be positive, $j_{uv}\in \mathcal{J}$ where $\mathcal{J}$ is an adjacency matrix that is defined as

$$\mathcal{J}=\left(\begin{array}{ccc}{\mathcal{J}}_{\mathcal{F}\times \mathcal{F}}^{\left(1\right)}& & {\mathcal{J}}_{\mathcal{F}\times (\mathcal{M}-\mathcal{F})}^{\left(2\right)}\\ 0_{(\mathcal{M}-\mathcal{F})\times \mathcal{F}}& & 0_{(\mathcal{M}-\mathcal{F})\times (\mathcal{M}-\mathcal{F})}\end{array}\right)$$

(10)

Here, ${\omega }_u=0$$\forall u\in \overline{\mathcal{R}}$. Now, in using (10), the Laplacian matrix is defined as

$$L=\left(\begin{array}{ccc}{L}_{\mathcal{F}}& & L_{\mathcal{R}}\\ 0_{(\mathcal{M}-\mathcal{F})\times F}& & 0_{(\mathcal{M}-\mathcal{F})\times (\mathcal{M}-\mathcal{F})}\end{array}\right)$$

(11)

In the above equation, $L_F$ and $L_{\mathcal{R}}$ belong to ${\mathbb{R}}^{\mathcal{F}\times \mathcal{F}}$ and ${\mathbb{R}}^{\mathcal{F}\times (\mathcal{M}-\mathcal{F})}$, respectively. Suppose that Assumption 2 holds. Then, one can select

$$\Delta =diag({\Delta }_1,{\Delta }_2,\dots ,{\Delta }_{\mathcal{F}},{\Delta }_{\mathcal{F}+1},\dots ,{\Delta }_{\mathcal{M}})$$

where

$$\left\{\begin{array}{ccccc}\hfill {\Delta }_u=1& \hfill & \hfill \mathrm{if}& \hfill & \hfill u\in {\overline{\mathcal{F}}}_1\cup \overline{\mathcal{R}}\\ \hfill {\Delta }_u=-1& \hfill & \hfill \mathrm{if}& \hfill & \hfill u\in {\overline{\mathcal{F}}}_2\end{array}\right.$$

(12)

From Equation (12), we have

$$\overline{L}=\left(\begin{array}{cc}{\overline{L}}_{\mathcal{F}}& {\overline{L}}_{\mathcal{R}}\\ 0_{(\mathcal{M}-\mathcal{F})\times F}& 0_{(\mathcal{M}-\mathcal{F})\times (\mathcal{M}-\mathcal{F})}\end{array}\right)$$

(13)

where $\overline{L}=\Delta L\Delta$, and referring to [35], we have

$${\overline{L}}_{\mathcal{F}}={\left[{\overline{\ell }}_{uv}\right]}_{\mathcal{F}\times \mathcal{F}}=\left\{\begin{array}{ccccc}\hfill -|j_{uv}|,& \hfill & \hfill u\ne v,& \hfill & \hfill u=1,2,3\dots \mathcal{F}\\ \hfill \sum _{v=1,v\ne u}^{\mathcal{M}}\left|j_{uv}\right|,& \hfill & \hfill u=v,& \hfill & \hfill v=\mathcal{F}+1,\mathcal{F}+2,\dots ,\mathcal{M}\end{array}\right.$$

(14)

and ${\overline{L}}_{\mathcal{R}}={\left[{\overline{\ell }}_{uv}\right]}_{\mathcal{F}\times (\mathcal{M}-\mathcal{F})}$ with ${\overline{\ell }}_{uv}=-\left|j_{uv}\right|\le 0$.

4.1.1. Control Objective

The control object ensures that the states of followers remain within a region defined by the states of leaders despite the presence of compromised agents.

4.1.2. Detection and Mitigation of FDIA

Detection Mechanism:

• Implement residual analysis to detect anomalies in the state trajectories of agents.
• Employ statistical or machine learning-based methods to identify deviations indicative of FDIAs.

4.1.3. Control Design

• Redundancy: Incorporate redundant measurements and control paths to cross-verify data and control actions.
• Observer-Based Techniques: Design observers to estimate the true state of the system, reducing reliance on potentially compromised data.
• Adaptive Control: Implement adaptive control strategies that can adjust control parameters in real time to mitigate the effects of detected attacks.
• Fault-Tolerant Control: Develop control laws that are less sensitive to false data, ensuring system performance even when some agents are compromised.

4.1.4. Control Assumptions

• The set of compromised agents $\mathcal{A}$ is known or can be estimated.
• The system dynamics B, $g(k,z_u\left(k\right))$, and W are accurately known.
• The attack method $\psi \left(k\right)$ is either known or can be bounded.

4.1.5. Control Limitations

• High computational complexity of detection and control algorithms.
• Potential trade-offs between robustness and system performance.
• Assumptions on the attack model may not cover all possible FDIA scenarios.

Lemma 5 

([34]). If Assumption 3 is satisfied, ${\overline{L}}_{\mathcal{F}}$ is an invertible matrix. Moreover, the matrix $-{\overline{L}}_{\mathcal{F}}^{-1}{\overline{L}}_{\mathcal{R}}$ is non-negative, and each of its rows sums to 1.

Theorem 1. 

Under Assumptions 1, 2, and 3, the bipartite containment control of the fractional-order multi-agent system defined by (4) and (5) using controller (9) will be achieved if there exist a scalar $\mathcal{K}>0$ and symmetric matrices $A>0$ and $X>0$ satisfying the following inequalities:

$$\left(\begin{array}{ccc}{\Omega }_1& & 0\\ 0& & {\Omega }_2\end{array}\right)<0$$

(15)

$$\left(\begin{array}{ccc}{\Omega }_3& & {\mathcal{I}}_{\mathcal{F}}\otimes AW\\ {\mathcal{I}}_{\mathcal{F}}\otimes W^{T}A& & -\gamma {\mathcal{I}}_{\mathcal{F}}\otimes I_n\end{array}\right)<0$$

(16)

where

• ${\Omega }_1={\mathcal{I}}_{\mathcal{F}}\otimes (AB+B^{T}A+A^2+b^2{I}_n+\gamma I_n+X-\mathcal{K}{\lambda }_{1}A+4{\displaystyle \frac{{\nu }^{\mathcal{A}}\otimes A\psi \left(k\right)}{\delta }})$;
• ${\Omega }_2={\mathcal{I}}_{\mathcal{F}}\otimes (-\mathcal{K}A-\gamma I_n);$
• ${\Omega }_3={\mathcal{I}}_{\mathcal{F}}\otimes (\gamma I_n-{\displaystyle \frac{1}{r^{\prime }}}X)$, where $\gamma >0$ for any scalar, and ${\lambda }_1={\lambda }_{max}\left[{\overline{L}}_{\mathcal{F}}{\overline{L}}_{\mathcal{F}}^T\right]$.

Proof. 

Consider the coordinate transformation $h_u(.)={\Delta }_u{z}_u(.)$ specified in (12) being valid for any $u=1,2,\dots ,\mathcal{M}$. By applying the control protocol described in (9) to the system defined by Equations (4) and (5), we achieve the following result:

$$\begin{array}{cc}\hfill D^{\alpha }{h}_u\left(k\right)& =B{h}_u\left(k\right)+g(k,h_u\left(k\right))+W{\int }_{-r^{\prime }}^0{h}_u(k+\vartheta )d\vartheta \hfill \\ & +\mathcal{K}{\Delta }_u\sum _{v=1}^{\mathcal{M}}\left|j_{uv}\right|(sgn\left(j_{uv}\right){\Delta }_v{h}_v(k-r^{″})-{\Delta }_u{h}_u(k-r^{″}))+2{\omega }_u^a\left(k\right)u\in \overline{\mathcal{F}}\hfill \end{array}$$

(17)

$$\begin{array}{cc}\hfill D^{\alpha }{h}_u\left(k\right)& =B{h}_u\left(k\right)+g(k,h_u\left(k\right))+W{\int }_{-r^{\prime }}^0{h}_u(k+\vartheta )d\vartheta u\in \overline{\mathcal{R}}\hfill \end{array}$$

(18)

Notice that

$$\begin{array}{cc}\hfill \sum _{v=1}^{\mathcal{M}}\left|j_{uv}\right|sgn\left(j_{uv}\right)h_v(k-r^{″})-h_u(k-r^{″})& =\sum _{v=1,v\ne u}^{\mathcal{M}}{\displaystyle |}{j}_{uv}|sgn\left(j_{uv}\right)h_v(k-r^{″})-\sum _{v=1,v\ne u}^{\mathcal{M}}\left|j_{uv}\right|h_u(k-r^{″})\hfill \\ \hfill & =\sum _{v=1,v\ne u}^{\mathcal{M}}{\displaystyle |}{j}_{uv}{\displaystyle |}{h}_v(k-r^{″})-\sum _{v=1,v\ne u}^{\mathcal{M}}\left|j_{uv}\right|h_u(k-r^{″})\hfill \\ \hfill & =-\sum _{v=1,v\ne u}^{\mathcal{M}}{\ell }_{uv}{h}_v(k-r^{″})-{\ell }_{uu}{h}_u(k-r^{″})\hfill \\ \hfill & =-\sum _{v=1}^{\mathcal{M}}{\ell }_{uv}{h}_v(k-r^{″})\hfill \end{array}$$

Using this in Equations (17) and (18), we obtain

$$\begin{array}{cc}\hfill D^{\alpha }{h}_u\left(k\right)& =B{h}_u\left(k\right)+g(k,h_u\left(k\right))+W{\int }_{-r^{\prime }}^0{h}_u(k+\vartheta )d\vartheta \hfill \\ & \hfill -\mathcal{K}\sum _{v=1}^{\mathcal{M}}{\Delta }_u{\ell }_{uv}{\Delta }_v{h}_v(k-r^{″})+2{\omega }_u^a\left(k\right),u\in \overline{\mathcal{F}}\end{array}$$

(19)

$$\begin{array}{cc}\hfill D^{\alpha }{h}_u\left(k\right)& =B{h}_u\left(k\right)+g(k,h_u\left(k\right))+W{\int }_{-r^{\prime }}^0{h}_u(k+\vartheta )d\vartheta ,u\in \overline{\mathcal{R}}\hfill \end{array}$$

(20)

Let $H_{\mathcal{F}}(.)={(h_1^T(.),h_2^T(.),\dots h_{\mathcal{F}}^T(.))}^T$, $H_{\mathcal{R}}(.)={(h_{F+1}^T(.),h_{F+2}^T(.),\dots h_{\mathcal{M}}^T(.))}^T$,

$G(k,h_{\mathcal{F}})={(g^T(k,h_1),\dots g^T(k,h_{\mathcal{F}}))}^T$, and $G(k,h_{\mathcal{R}})={(g^T(k,h_{F+1}),\dots ,g^T(k,h_{\mathcal{M}}))}^T$ from (19) and (20):

$$\begin{array}{cc}\hfill D^{\alpha }{H}_{\mathcal{F}}\left(k\right)& =({\mathcal{I}}_{\mathcal{F}}\otimes B)H_{\mathcal{F}}\left(k\right)+G(k,H_{\mathcal{F}}\left(k\right))-\mathcal{K}({\overline{L}}_{\mathcal{F}}\otimes I_n)H_{\mathcal{F}}(k-r^{″})\hfill \\ & -\mathcal{K}({\overline{L}}_{\mathcal{R}}\otimes I_n)H_{\mathcal{R}}(k-r^{″})+{\int }_{-r^{\prime }}^0({\mathcal{I}}_{\mathcal{F}}\otimes W)H_{\mathcal{F}}(k+\vartheta )d\vartheta +2{\nu }^{\mathcal{A}}\otimes \psi \left(k\right)\hfill \end{array}$$

(21)

$$\begin{array}{cc}\hfill D^{\alpha }{H}_{\mathcal{R}}\left(k\right)& =(I_{\mathcal{M}-\mathcal{F}}\otimes B)H_{\mathcal{R}}\left(k\right)+G(k,H_{\mathcal{R}}\left(k\right))+{\int }_{-r^{\prime }}^0(I_{\mathcal{M}-\mathcal{F}}\otimes W)H_{\mathcal{R}}(k+\vartheta )d\vartheta \hfill \end{array}$$

(22)

Consider the bipartite containment control error as $\beta (.)=H_{\mathcal{F}}(.)-(-{\overline{L}}_{\mathcal{F}}^{-1}{\overline{L}}_{\mathcal{R}}\otimes I_n)H_{\mathcal{R}}(.)$. Then, the system defined by (21) and (22) becomes

$$\begin{array}{cc}\hfill D^{\alpha }\beta \left(k\right)& =({\mathcal{I}}_{\mathcal{F}}\otimes B)H_{\mathcal{F}}\left(k\right)+({\overline{L}}_{\mathcal{F}}^{-1}{\overline{L}}_{\mathcal{R}}\otimes B)H_{\mathcal{R}}\left(k\right)+G(k,H_{\mathcal{F}}\left(k\right))+({\overline{L}}_{\mathcal{F}}^{-1}{\overline{L}}_{\mathcal{R}}\otimes I_n)G(k,H_{\mathcal{R}}\left(k\right))\hfill \\ \hfill & -(\mathcal{K}{\overline{L}}_F\otimes I_n)({\mathcal{I}}_{\mathcal{F}}\otimes I_n)H_{\mathcal{F}}(k-r^{″})-(\mathcal{K}{\overline{L}}_{\mathcal{F}}\otimes I_n)({\overline{L}}_{\mathcal{F}}^{-1}{\overline{L}}_{\mathcal{R}}\otimes I_n)H_{\mathcal{R}}(k-r^{″})\hfill \\ \hfill & +{\int }_{-r^{\prime }}^0({\mathcal{I}}_{\mathcal{F}}\otimes W)H_{\mathcal{F}}(k+\vartheta )d\vartheta +{\int }_{-r^{\prime }}^0({\overline{L}}_{\mathcal{F}}^{-1}{\overline{L}}_{\mathcal{R}}\otimes W)H_{\mathcal{R}}(k+\vartheta )d\vartheta +2{\nu }^{\mathcal{A}}\otimes \psi \left(k\right)\hfill \\ \hfill D^{\alpha }\beta \left(k\right)& =({\mathcal{I}}_{\mathcal{F}}\otimes B)\beta \left(k\right)+G(k,H_{\mathcal{F}}\left(k\right))+({\overline{L}}_{\mathcal{F}}^{-1}{\overline{L}}_{\mathcal{R}}\otimes I_n)G(k,H_{\mathcal{R}}\left(k\right))\hfill \\ & (\mathcal{K}{\overline{L}}_{\mathcal{F}}\otimes I_n)\beta (k-r^{″})+{\int }_{-r^{\prime }}^0({\mathcal{I}}_{\mathcal{F}}\otimes W)\beta (k+\vartheta )d\vartheta +2{\nu }^{\mathcal{A}}\otimes \psi \left(k\right)\hfill \end{array}$$

(23)

We formed the following Lyapunov function:

$$V\left(\beta \left(k\right)\right)={\beta }^T\left(k\right)({\mathcal{I}}_{\mathcal{F}}\otimes A)\beta \left(k\right)$$

Now, in applying Lemmas 1 and 3 on Equation (23):

$$\begin{array}{cc}\hfill D^{\alpha }V\left(\beta \left(k\right)\right)& =D^{\alpha }\left[{\beta }^T\left(k\right)\right]({\mathcal{I}}_{\mathcal{F}}\otimes A)\beta \left(k\right)\le 2{\beta }^T\left(k\right)({\mathcal{I}}_{\mathcal{F}}\otimes A)\left[D^{\alpha }\beta \left(k\right)\right]\hfill \\ \hfill & =2{\beta }^T\left(k\right)({\mathcal{I}}_{\mathcal{F}}\otimes A)[({\mathcal{I}}_{\mathcal{F}}\otimes B)\beta \left(k\right)+G(k,H_{\mathcal{F}}\left(k\right))+({\overline{L}}_{\mathcal{F}}^{-1}{\overline{L}}_{\mathcal{R}}\otimes I_n)G(k,H_{\mathcal{R}}\left(k\right))\hfill \\ \hfill -& (\mathcal{K}{\overline{L}}_{\mathcal{F}}\otimes I_n)\beta (k-r^{″})+{\int }_{-r^{\prime }}^0({\mathcal{I}}_{\mathcal{F}}\otimes W)\beta (k+\vartheta )d\vartheta +2{\nu }^{\mathcal{A}}\otimes \psi \left(k\right)].\hfill \\ \hfill & ={\beta }^T\left(k\right)[{\mathcal{I}}_{\mathcal{F}}\otimes (AB+B^{T}A)]\beta \left(k\right)+2{\beta }^T\left(k\right)({\mathcal{I}}_{\mathcal{F}}\otimes A)[G(k,H_{\mathcal{F}}\left(k\right))+({\overline{L}}_{\mathcal{F}}^{-1}{\overline{L}}_{\mathcal{R}}\otimes I_n)G(k,H_{\mathcal{R}}\left(k\right))]\hfill \\ \hfill & 2{\beta }^T\left(k\right)(\mathcal{K}{\overline{\mathbb{L}}}_{\mathcal{F}}\otimes A)\beta (k-r^{″})+2{\beta }^T\left(k\right)({\mathcal{I}}_{\mathcal{F}}\otimes A)\left[{\int }_{-r^{\prime }}^0({\mathcal{I}}_{\mathcal{F}}\otimes W)\beta (k+\vartheta )d\vartheta \right]+4{\beta }^T\left(k\right){\nu }^{\mathcal{A}}\otimes A\psi \left(k\right)\hfill \\ \hfill & \le {\beta }^T\left(k\right)[{\mathcal{I}}_{\mathcal{F}}\otimes (AB+B^{T}A)]\beta \left(k\right)-2{\beta }^T\left(k\right)(\mathcal{K}{\overline{\mathbb{L}}}_{\mathcal{F}}\otimes A)\beta (k-r^{″})+{\beta }^T\left(k\right)({\mathcal{I}}_{\mathcal{F}}\otimes A^T)\beta \left(k\right)\hfill \\ \hfill & +{[G(k,H_{\mathcal{F}}\left(k\right))+({\overline{L}}_{\mathcal{F}}^{-1}{\overline{L}}_{\mathcal{R}}\otimes I_n)G(k,H_{\mathcal{R}}\left(k\right))]}^T[[G(k,H_{\mathcal{F}}\left(k\right))+({\overline{L}}_{\mathcal{F}}^{-1}{\overline{L}}_{\mathcal{R}}\otimes I_n)G(k,H_{\mathcal{R}}\left(k\right))]\hfill \\ \hfill & +2{\beta }^T\left(k\right)({\mathcal{I}}_{\mathcal{F}}\otimes A)\left[{\int }_{-r^{\prime }}^0({\mathcal{I}}_{\mathcal{F}}\otimes W)\beta (k+\vartheta )d\vartheta \right]+4{\beta }^T\left(k\right){\nu }^{\mathcal{A}}\otimes A\psi \left(k\right)\hfill \end{array}$$

(24)

Suppose that $-{\overline{L}}_{\mathcal{F}}^{-1}{\overline{L}}_{\mathcal{R}}={\left[{\overline{\ell }}_{pq}\right]}_{\mathcal{F}\times (\mathcal{M}-\mathcal{F})}$, and from Assumption 1,

$$\begin{array}{c}{[G(k,H_{\mathcal{F}}\left(k\right))-(-{\overline{L}}_{\mathcal{F}}^{-1}{\overline{L}}_{\mathcal{R}}\otimes I_n)G(k,H_{\mathcal{R}}\left(k\right))]}^T[[G(k,H_{\mathcal{F}}\left(k\right))-(-{\overline{L}}_{\mathcal{F}}^{-1}{\overline{L}}_{\mathcal{R}}\otimes I_n)G(k,H_{\mathcal{R}}\left(k\right))]\hfill \\ =\sum _{u=1}^{\mathcal{F}}{[g(k,h_u)-\sum _{v=1}^{\mathcal{M}-\mathcal{F}}{\overline{\ell }}_{uv}g(k,h_{\mathcal{F}+q})]}^T[\sum _{u=1}^{\mathcal{F}}g(k,h_u)-\sum _{v=1}^{\mathcal{M}-\mathcal{F}}{\overline{\ell }}_{uv}g(k,h_{\mathcal{F}+q})]\hfill \\ \le \sum _{u=1}^{\mathcal{F}}{b}^2{[h_u-\sum _{v=1}^{\mathcal{M}-\mathcal{F}}{\overline{\ell }}_{uv}{h}_{\mathcal{F}+q}]}^T[\sum _{u=1}^{\mathcal{F}}{h}_u-\sum _{v=1}^{\mathcal{M}-\mathcal{F}}{\overline{\ell }}_{uv}{h}_{\mathcal{F}+q}]\hfill \\ =b^2{[H_{\mathcal{F}}\left(k\right)-(-{\overline{L}}_{\mathcal{F}}^{-1}{\overline{L}}_{\mathcal{R}}\otimes I_n)H_{\mathcal{R}}\left(k\right)]}^T[H_{\mathcal{F}}\left(k\right)-(-{\overline{L}}_{\mathcal{F}}^{-1}{\overline{L}}_{\mathcal{R}}\otimes I_n)H_{\mathcal{R}}\left(k\right)]\hfill \\ =b^2{\beta }^T\left(k\right)\beta \left(k\right)\hfill \end{array}$$

(25)

Consider

$$\begin{array}{cc}\hfill 2{\beta }^T\left(k\right)(\mathcal{K}{\overline{L}}_{\mathcal{F}}\otimes A)\beta (k-r^{″})& =\mathcal{K}.2{\beta }^T\left(k\right)({\overline{L}}_{\mathcal{F}}\otimes A)({\mathcal{I}}_{\mathcal{F}}\otimes A^{{\displaystyle \frac{-1}{2}}})({\mathcal{I}}_{\mathcal{F}}\otimes A^{{\displaystyle \frac{1}{2}}})\beta (k-r^{″})\hfill \\ \hfill & \le \mathcal{K}.{\beta }^T\left(k\right)({\overline{L}}_{\mathcal{F}}\otimes A)({\mathcal{I}}_{\mathcal{F}}\otimes A^{{\displaystyle \frac{-1}{2}}})({\mathcal{I}}_{\mathcal{F}}\otimes A^{{\displaystyle \frac{-1}{2}}})({\overline{L}}_{\mathcal{F}}^{-T}\otimes A)\beta \left(k\right)\hfill \\ \hfill & +\mathcal{K}.{\beta }^T(k-r^{″})({\overline{L}}_{\mathcal{F}}\otimes A)({\mathcal{I}}_{\mathcal{F}}\otimes A^{{\displaystyle \frac{1}{2}}})({\mathcal{I}}_{\mathcal{F}}\otimes A^{{\displaystyle \frac{1}{2}}})\beta (k-r^{″})\hfill \\ \hfill & ={\beta }^T\left(k\right)(\mathcal{K}{\overline{L}}_{\mathcal{F}}{\overline{L}}_{\mathcal{F}}^{-T}\otimes A)\beta \left(k\right)+\mathcal{K}.{\beta }^T(k-r^{″})({\mathcal{I}}_{\mathcal{F}}\otimes A)\beta (k-r^{″})\hfill \end{array}$$

(26)

Using Equations (25) and (26) in Equation (24), we obtain

$$\begin{array}{cc}\hfill D^{\alpha }V\left(\beta \left(k\right)\right)& \le {\beta }^T\left(k\right)[{\mathcal{I}}_{\mathcal{F}}\otimes (AB+B^{T}A)]\beta \left(k\right)+{\beta }^T\left(k\right)({\mathcal{I}}_{\mathcal{F}}\otimes A^T)\beta \left(k\right)+b^2{\beta }^T\left(k\right)\beta \left(k\right)\hfill \\ \hfill & -{\beta }^T\left(k\right)(\mathcal{K}{\overline{L}}_{\mathcal{F}}{\overline{L}}_{\mathcal{F}}^{-T}\otimes A)\beta \left(k\right)-\mathcal{K}.{\beta }^T(k-r^{″})({\mathcal{I}}_{\mathcal{F}}\otimes A)\beta (k-r^{″})\hfill \\ \hfill & +2{\beta }^T\left(k\right)({\mathcal{I}}_{\mathcal{F}}\otimes A)\left[{\int }_{-r^{\prime }}^0({\mathcal{I}}_{\mathcal{F}}\otimes W)\beta (k+\vartheta )d\vartheta \right]+4{\beta }^T\left(k\right){\nu }^{\mathcal{A}}\otimes A\psi \left(k\right)\hfill \end{array}$$

By Lemma 5, ${\overline{L}}_{\mathcal{F}}$ is invertible. Then, ${\overline{L}}_{\mathcal{F}}{\overline{L}}_{\mathcal{F}}^T$ is a positive definite matrix. Therefore, we define ${\lambda }_1$ as the largest eigenvalue of ${\overline{L}}_{\mathcal{F}}{\overline{L}}_{\mathcal{F}}^T$, defined as

$${\lambda }_1={\lambda }_{max}\left\{{\overline{L}}_F{\overline{L}}_F^T\right\}$$

$$\begin{array}{cc}\hfill D^{\alpha }V\left(\beta \left(k\right)\right)& \le {\beta }^T\left(k\right)[{\mathcal{I}}_{\mathcal{F}}\otimes {\displaystyle (}AB+B^{T}A+A^T+b^2{I}_n-\mathcal{K}{\lambda }_{1}A+4{\displaystyle \frac{{\nu }^{\mathcal{A}}\otimes A\psi \left(k\right)}{\delta }}{\displaystyle )]}\beta \left(k\right)\hfill \\ & -\mathcal{K}.{\beta }^T(k-r^{″})({\mathcal{I}}_{\mathcal{F}}\otimes A)\beta (k-r^{″})+2{\beta }^T\left(k\right)({\mathcal{I}}_{\mathcal{F}}\otimes A)[{\int }_{-r^{\prime }}^0({\mathcal{I}}_{\mathcal{F}}\otimes W)\beta (k+\vartheta )]d\vartheta \hfill \end{array}$$

(27)

where $\delta =\beta \left(k\right)$ whenever

$$V(k+ϵ,g(k+ϵ\left)\right)<\varrho V(k,g(k\left)\right)\forall -r\le ϵ\le 0$$

(28)

where $r=max[r^{\prime },r^{″}]$. Now, for some $\varrho >1$, we can conclude that for any $\gamma >0$,

$$\begin{array}{cc}\hfill D^{\alpha }V\left(k\right)& \le {\beta }^T\left(k\right)[{\mathcal{I}}_{\mathcal{F}}\otimes (AB+B^{T}A+A^T+b^2{I}_M-\mathcal{K}{\lambda }_{1}A+4{\displaystyle \frac{{\nu }^{\mathcal{A}}\otimes A\psi \left(k\right)}{\delta }})]\beta \left(k\right)-\mathcal{K}.{\beta }^T(k-r^{″})({\mathcal{I}}_{\mathcal{F}}\otimes A)(k-r^{″})\hfill \\ \hfill & +2{\beta }^T\left(k\right){\int }_{-r^{\prime }}^0({\mathcal{I}}_{\mathcal{F}}\otimes A)({\mathcal{I}}_{\mathcal{F}}\otimes W)\beta (k+\vartheta )d\vartheta +\gamma [\varrho {\beta }^T\left(k\right)({\mathcal{I}}_{\mathcal{F}}\otimes I_n)\beta \left(k\right)-{\beta }^T(k-r^{″})({\mathcal{I}}_{\mathcal{F}}\otimes I_n)\beta (k-r^{″})]\hfill \\ \hfill & +{\int }_{r^{\prime }}^0\gamma [\varrho {\beta }^T\left(k\right)({\mathcal{I}}_{\mathcal{F}}\otimes I_n)\beta \left(k\right)-{\beta }^T(k+\vartheta )({\mathcal{I}}_{\mathcal{F}}\otimes I_n)\beta (k+\vartheta )]d\vartheta \hfill \\ \hfill & ={\beta }^T\left(k\right)[{\mathcal{I}}_{\mathcal{F}}\otimes (AB+B^{T}A+A^T+b^2{I}_n+\gamma \varrho I_n+X-\mathcal{K}{\lambda }_{1}A+4{\displaystyle \frac{{\nu }^{\mathcal{A}}\otimes A\psi \left(k\right)}{\delta }})]\beta \left(k\right)\hfill \\ \hfill & +\mathcal{K}.{\beta }^T(k-r^{″})({\mathcal{I}}_{\mathcal{F}}\otimes A)\beta (k-r^{″})-\gamma {\beta }^T(k-r^{″})({\mathcal{I}}_{\mathcal{F}}\otimes I_n)\beta (k-r^{″}){\int }_{-r^{\prime }}^0[{\beta }^T\left(k\right)({\mathcal{I}}_{\mathcal{F}}\otimes (\gamma \varrho I_n-{\displaystyle \frac{1}{r^{\prime }}}X))\beta \left(k\right)\hfill \\ \hfill & +2{\beta }^T\left(k\right)({\mathcal{I}}_{\mathcal{F}}\otimes A)({\mathcal{I}}_{\mathcal{F}}\otimes W)\beta (k+\vartheta )-\gamma {\beta }^T(k+\vartheta )({\mathcal{I}}_{\mathcal{F}}\otimes I_n)\beta (k+\vartheta )]d\vartheta \hfill \end{array}$$

$$\begin{array}{cc}\hfill & {\phi }_{r^{″}}^T\left(\begin{array}{ccc}{\mathcal{I}}_{\mathcal{F}}\otimes (AB+B^{T}A+A^T+b^2{I}_M+\gamma \varrho I_n+X-\mathcal{K}{\lambda }_{1}A+4{\displaystyle \frac{{\nu }^{\mathcal{A}}\otimes A\psi \left(k\right)}{\delta }})& & 0\\ 0& & {\mathcal{I}}_{\mathcal{F}}\otimes (-\mathcal{K}A-\gamma I_n)\end{array}\right){\phi }_{r^{″}}\hfill \\ \\ \hfill & {\int }_{-r^{\prime }}^0{\phi }_{\vartheta }^T\left(\begin{array}{ccc}{\mathcal{I}}_{\mathcal{F}}\otimes (\gamma \varrho I_n-{\displaystyle \frac{1}{r^{\prime }}}X)& & {\mathcal{I}}_{\mathcal{F}}\otimes AW\\ {\mathcal{I}}_{\mathcal{F}}\otimes W^{T}A& & -\gamma {\mathcal{I}}_{\mathcal{F}}\otimes I_n\end{array}\right){\phi }_{\vartheta }d\vartheta \hfill \end{array}$$

where ${\phi }_{r^{″}}=({\beta }^T\left(k\right),{\beta }^T(k-r^{″})),{\phi }_{\vartheta }=({\beta }^T\left(k\right),{\beta }^T(k+\vartheta )),$ and $\vartheta \in [-r^{\prime },0].$ Let $\varrho \to 1^{+}$. Then, we can obtain

$$\begin{array}{cc}\hfill D^{\alpha }V\left(k\right)& \le {\phi }_{r^{″}}^T\left(\begin{array}{ccc}{\Omega }_1& & 0\\ 0& & {\Omega }_2\end{array}\right){\phi }_{r^{″}}\hfill \\ \hfill & {\int }_{-r^{\prime }}^0{\phi }_{\vartheta }^T\left(\begin{array}{ccc}{\Omega }_3& & {\mathcal{I}}_{\mathcal{F}}\otimes AW\\ {\mathcal{I}}_{\mathcal{F}}\otimes W^{T}A& & -\gamma {\mathcal{I}}_{\mathcal{F}}\otimes I_n\end{array}\right){\phi }_{\vartheta }d\vartheta \hfill \end{array}$$

Now, from Lemma 2,

$$\left(\begin{array}{ccc}{\Omega }_1& & 0\\ 0& & {\Omega }_2\end{array}\right)<0$$

(29)

$$\left(\begin{array}{ccc}{\Omega }_3& & {\mathcal{I}}_{\mathcal{F}}\otimes AW\\ {\mathcal{I}}_{\mathcal{F}}\otimes W^{T}A& & -\gamma {\mathcal{I}}_{\mathcal{F}}\otimes I_n\end{array}\right)<0$$

(30)

where ${\lambda }_1={\lambda }_{max}\left[{\overline{L}}_{\mathcal{F}}{\overline{L}}_{\mathcal{F}}^T\right]$. By Lemma 2, relationships (15) and (16) hold, which indicates that $D^{\alpha }V\left(k\right)<0$ whenever $V(k+ϵ,g(k+ϵ\left)\right)<\varrho V(k,g(k\left)\right)$ for some $\varrho >1$ and $ϵ\in [-r,0]$. Lemma 4 states that system (23) is asymptotically stable, which means that control law (9) can attain the stability of the system defined by (4) and (5). □

Remark 1. 

In (9), we use delayed controllers because it can enhance the robustness of a multi-agent system. Delayed controllers allow agents to continue their work effectively even in scenarios where communication is disrupted or delayed.

Remark 2. 

In contrast, the irregularity in space and the restricted occurrence of extreme points in the gradients of fractional derivatives, compared to traditional integer-order systems, presents significant difficulties when studying fractional multi-agent systems (FMASs), especially with temporal delays. In traditional systems with integer-order derivatives, analyzing how they perform under delays often involves using a Lyapunov function that includes an integral component. However, when dealing with delayed FMASs, through using Caputo derivatives, this Lyapunov function becomes ineffective because fractional operators do not follow the same composition property as integer derivatives. That is, the derivative of a derivative may not be equal to the combined derivative of the sum. To address this issue, we propose a novel approach that leverages signed graph theory and the fractional Razumikhin method to control delayed FMASs with a bipartite containment objective. Our method overcomes the challenges posed by delays and fractional derivatives by employing a straightforward quadratic Lyapunov function. This technique is also adaptable to fractional-order multi-agent systems experiencing both communication and various types of distributed delays [36,37].

4.2. Switching Signed Directed Network

Let ${\mathcal{G}}^{\sigma \left(k\right)}=(\mathcal{V},{\mathcal{E}}^{\sigma \left(k\right)})$ be a switching signed directed graph, and at $k_{𝚥}$ (switching point), the switching signal (piecewise) $\sigma$ determines the interval $[k_0,\infty )$ for the set $N=\{1,2,3,\dots n\}$. For any $k_{𝚥}$, there exists a small point t such that $k_{𝚥+1}-k_{𝚥}\ge t$, preventing Zeno behavior. This ensures that the nth topology is activated for $k\in [k_{𝚥},k_{𝚥+1})$ when $\sigma \left(k\right)=n\in N$. The adjacency matrix is represented as ${\mathcal{J}}^{\sigma \left(k\right)}={\left[j_{uv}^{\sigma \left(k\right)}\right]}_{\mathcal{M}\times \mathcal{M}}$, and $L^{\sigma \left(k\right)}={\left[{\ell }_{uv}^{\sigma \left(k\right)}\right]}_{\mathcal{M}\times \mathcal{M}}$ represent the Laplacian matrices of ${\mathcal{G}}^{\sigma \left(k\right)}$. Furthermore, $G^{𝚤}=\mathcal{G}$ for any $\sigma \left(k\right)=𝚤\in N$.

To achieve the bipartite containment control of fractional-order multi-agent systems as described in (4) and (5) for a switching signed network, some assumptions are necessary. Here, we discuss them:

Assumption 6. 

The graph ${\mathcal{G}}^{\sigma \left(k\right)}$ is structurally balanced for any $\sigma \left(k\right)\in N$.

Assumption 7. 

Every follower has a directed link to at least one leader in ${\mathcal{G}}^{\sigma \left(k\right)}$.

We construct the delayed control protocol under FDIAs for attaining the bipartite containment control of the system defined by (4) and (5), which is defined as

$${\omega }_u(k-r^{″})=\mathcal{K}\sum _{v=1}^{\mathcal{M}}\left|j_{uv}^{\sigma \left(k\right)}\right|\left(sgn\left(j_{uv}^{\sigma \left(k\right)}\right)\right)z_v(k-r^{″})-z_u(k-r^{″})+{\omega }_u^a\left(k\right),u\in \overline{\mathcal{F}}$$

(31)

Remark 3. 

In using (10) and (12) for $\sigma \left(k\right)\in M$, the Laplacian matrix of ${\mathcal{G}}^{\sigma \left(k\right)}$ is denoted by

$$L^{\sigma \left(k\right)}=\left(\begin{array}{ccc}{L}_{\mathcal{F}}^{\sigma \left(k\right)}& & L_{\mathcal{R}}^{\sigma \left(k\right)}\\ 0_{(\mathcal{M}-\mathcal{F})\times F}& & 0_{(\mathcal{M}-\mathcal{F})\times (\mathcal{M}-\mathcal{F})}\end{array}\right)$$

(32)

In the above equation, $L_F^{\sigma \left(k\right)}$ and $L_{\mathcal{R}}^{\sigma \left(k\right)}$ belong to ${\mathbb{R}}^{\mathcal{F}\times \mathcal{F}}$ and ${\mathbb{R}}^{F\times (\mathcal{M}-\mathcal{F})}$, respectively. We can choose a matrix

$${\Delta }^{\sigma \left(k\right)}=diag({\Delta }_1,{\Delta }_2,\dots ,{\Delta }_{\mathcal{F}},\Delta F+1,\dots ,{\Delta }_{\mathcal{M}})$$

with

$$\left\{\begin{array}{ccccc}\hfill {\Delta }_u=1& \hfill & \hfill if& \hfill & \hfill u\in {\overline{\mathcal{F}}}_1\cup \overline{\mathcal{R}}\\ \hfill {\Delta }_u=-1& \hfill & \hfill if& \hfill & \hfill u\in {\overline{\mathcal{F}}}_2\end{array}\right.$$

(33)

Also,

$${\overline{L}}^{\sigma \left(k\right)}=\left(\begin{array}{cc}{\overline{L}}_{\mathcal{F}}^{\sigma \left(k\right)}& {\overline{L}}_{\mathcal{R}}^{\sigma \left(k\right)}\\ 0_{(\mathcal{M}-\mathcal{F})\times F}& 0_{(\mathcal{M}-\mathcal{F})\times (\mathcal{M}-\mathcal{F})}\end{array}\right)$$

(34)

where

$${\overline{\mathbb{L}}}^{\sigma \left(k\right)}={\Delta }^{\sigma \left(k\right)}{L}^{\sigma \left(k\right)}{\Delta }^{\sigma \left(k\right)}$$

$${\overline{L}}_{\mathcal{F}}^{\sigma \left(k\right)}={\left[{\overline{\ell }}_{uv}^{\sigma \left(k\right)}\right]}_{\mathcal{F}\times \mathcal{F}}=\left\{\begin{array}{ccccc}\hfill -|j_{uv}^{\sigma \left(k\right)}|,& \hfill & \hfill u\ne v& \hfill & \hfill u=1,...,\mathcal{F}\\ \hfill \sum _{v=1,v\ne u}^{\mathcal{M}}\left|j_{uv}^{\sigma \left(k\right)}\right|,& \hfill & \hfill u=v& \hfill & \hfill v=F+1,F+2,...,\mathcal{M}\end{array}\right.$$

(35)

and ${\overline{L}}_{\mathcal{R}}^{\sigma \left(k\right)}={\left[{\overline{\ell }}_{uv}^{\sigma \left(k\right)}\right]}_{\mathcal{F}\times (\mathcal{M}-\mathcal{F})}$ with ${\overline{\ell }}_{uv}^{\sigma \left(k\right)}=-\left|j_{uv}^{\sigma \left(k\right)}\right|\le 0$

Remark 4. 

If Assumption 3 is satisfied, ${\overline{L}}_{\mathcal{F}}^{\sigma \left(k\right)}$ is an invertible matrix. Moreover, the matrix ${\left({\overline{L}}_{\mathcal{F}}^{\sigma \left(k\right)}\right)}^{-1}{\overline{L}}_{\mathcal{R}}^{\sigma \left(k\right)}$ is non-negative, and each of its rows sums to 1 for any $\sigma \left(k\right)\in N$.

Theorem 2. 

Under Assumptions 1, 2, and 3, the bipartite containment control of fractional-order multi-agent systems (4) and (5) for switching signed network using controller (31) shall be achieved if there exist a scalar $\mathcal{K}>0$ and symmetric matrices $A>0$ and $X>0$ satisfying the following inequalities.

$$\left(\begin{array}{ccc}{\Omega }_1& & 0\\ 0& & {\Omega }_2\end{array}\right)<0$$

(36)

$$\left(\begin{array}{ccc}{\Omega }_3& & {\mathcal{I}}_{\mathcal{F}}\otimes AW\\ {\mathcal{I}}_{\mathcal{F}}\otimes W^{T}A& & -\gamma {\mathcal{I}}_{\mathcal{F}}\otimes I_n\end{array}\right)<0$$

(37)

where

• ${\Omega }_1={\mathcal{I}}_{\mathcal{F}}\otimes (AB+B^{T}A+A^T+b^2{I}_n+\gamma I_n+X-\mathcal{K}{\lambda }_{2}A+4{\displaystyle \frac{{\nu }^{\mathcal{A}}\otimes A\psi \left(k\right)}{\delta }})$;
• ${\Omega }_2={\mathcal{I}}_{\mathcal{F}}\otimes (-\mathcal{K}A-\gamma I_n);$
• ${\Omega }_3={\mathcal{I}}_{\mathcal{F}}\otimes (\gamma I_n-{\displaystyle \frac{1}{r^{\prime }}}X)$, where $\gamma >0$ for any scalar, and ${\lambda }_2=ma{x}_{\sigma \left(k\right)\in N}$$\left[{\lambda }_{max}{\left\{{\overline{L}}_{\mathcal{F}}^{\sigma \left(k\right)}{(\overline{L}}_{\mathcal{F}}^{\sigma \left(k\right)}\right)}^T\right\}]$.

Proof. 

The containment control error system is defined as $\beta (.)=H_{\mathcal{F}}(.)-({(-{\overline{L}}_{\mathcal{F}}^{\sigma \left(k\right)})}^{-1}{\overline{L}}_{\mathcal{R}}^{\sigma \left(k\right)}\otimes I_n)H_{\mathcal{R}}(.)$. Then, the system using controller (31) is defined as

$$\begin{array}{c}\hfill D^{\alpha }\beta \left(k\right)=({\mathcal{I}}_{\mathcal{F}}\otimes B)\beta \left(k\right)+H(k,H_{\mathcal{F}}\left(k\right))+({\left({\overline{L}}_{\mathcal{F}}^{\sigma \left(k\right)}\right)}^{-1}{\overline{L}}_{\mathcal{R}}^{\sigma \left(k\right)}\otimes I_n)H(k,H_{\mathcal{R}}\left(k\right))\\ \hfill -(\mathcal{K}{\overline{L}}_{\mathcal{F}}^{\sigma \left(k\right)}\otimes I_n)\beta (k-r^{″})+{\int }_{-r^{\prime }}^0({\mathcal{I}}_{\mathcal{F}}\otimes A)({\mathcal{I}}_{\mathcal{F}}\otimes W)\beta (k+\vartheta )d\vartheta +2{\nu }^{\mathcal{A}}\otimes \psi \left(k\right).\end{array}$$

(38)

We formed the following Lyapunov function for the purpose of stability:

$$V\left(\beta \left(k\right)\right)={\beta }^T\left(k\right)({\mathcal{I}}_{\mathcal{F}}\otimes A)\beta \left(k\right)$$

The Lyapunov function was selected based on its ability to handle the complexities of fractional-order systems and the particular characteristics of bipartite structures. This function provides a robust framework for stability analysis in such dynamic environments. Now, by using Theorem 1, one can obtain

$$\left(\begin{array}{ccc}{\mathcal{I}}_{\mathcal{F}}\otimes (AB+B^{T}A+A^T+b^2{I}_n+\gamma I_n+X-\mathcal{K}{\lambda }_{2}A+4{\displaystyle \frac{{\nu }^{\mathcal{A}}\otimes A\psi \left(k\right)}{\delta }})& & 0\\ 0& & {\mathcal{I}}_{\mathcal{F}}\otimes (-\mathcal{K}U-\gamma I_n)\end{array}\right)<0$$

(39)

$$\left(\begin{array}{ccc}{\mathcal{I}}_{\mathcal{F}}\otimes (\gamma I_n-{\displaystyle \frac{1}{r^{\prime }}}X)& & {\mathcal{I}}_{\mathcal{F}}\otimes AW\\ {\mathcal{I}}_{\mathcal{F}}\otimes W^{T}A& & -\gamma {\mathcal{I}}_{\mathcal{F}}\otimes I_n\end{array}\right)<0$$

(40)

where ${\lambda }_2=ma{x}_{\sigma \left(k\right)\in N}\left[{\lambda }_{max}{\left\{{\overline{L}}_{\mathcal{F}}^{\sigma \left(k\right)}{(\overline{L}}_{\mathcal{F}}^{\sigma \left(k\right)}\right)}^T\right\}]$. According to Lemma 2, relationships (36) and (37) hold, which indicates that $D^{\alpha }V\left(k\right)<0$ whenever $V(k+ϵ,g(k+ϵ\left)\right)<\varrho V(k,g(k\left)\right)$ for some $\varrho >1$ and $ϵ\in [-r,0]$. Lemma 4 states that system (38) is asymptotically stable, which means that control law (31) can attain the leader-following consensus of systems (4) and (5) when arbitrary switching is realized. □

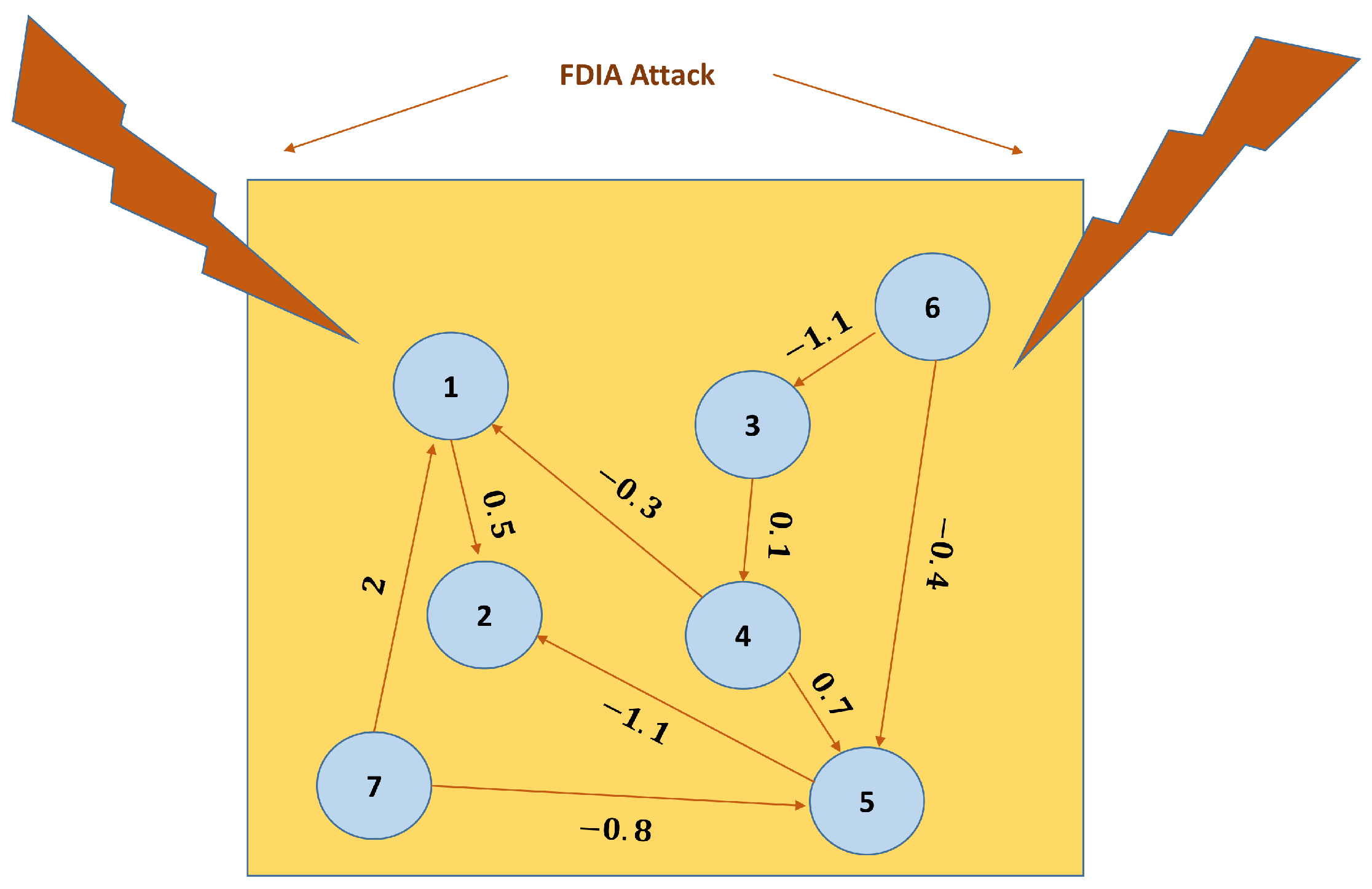
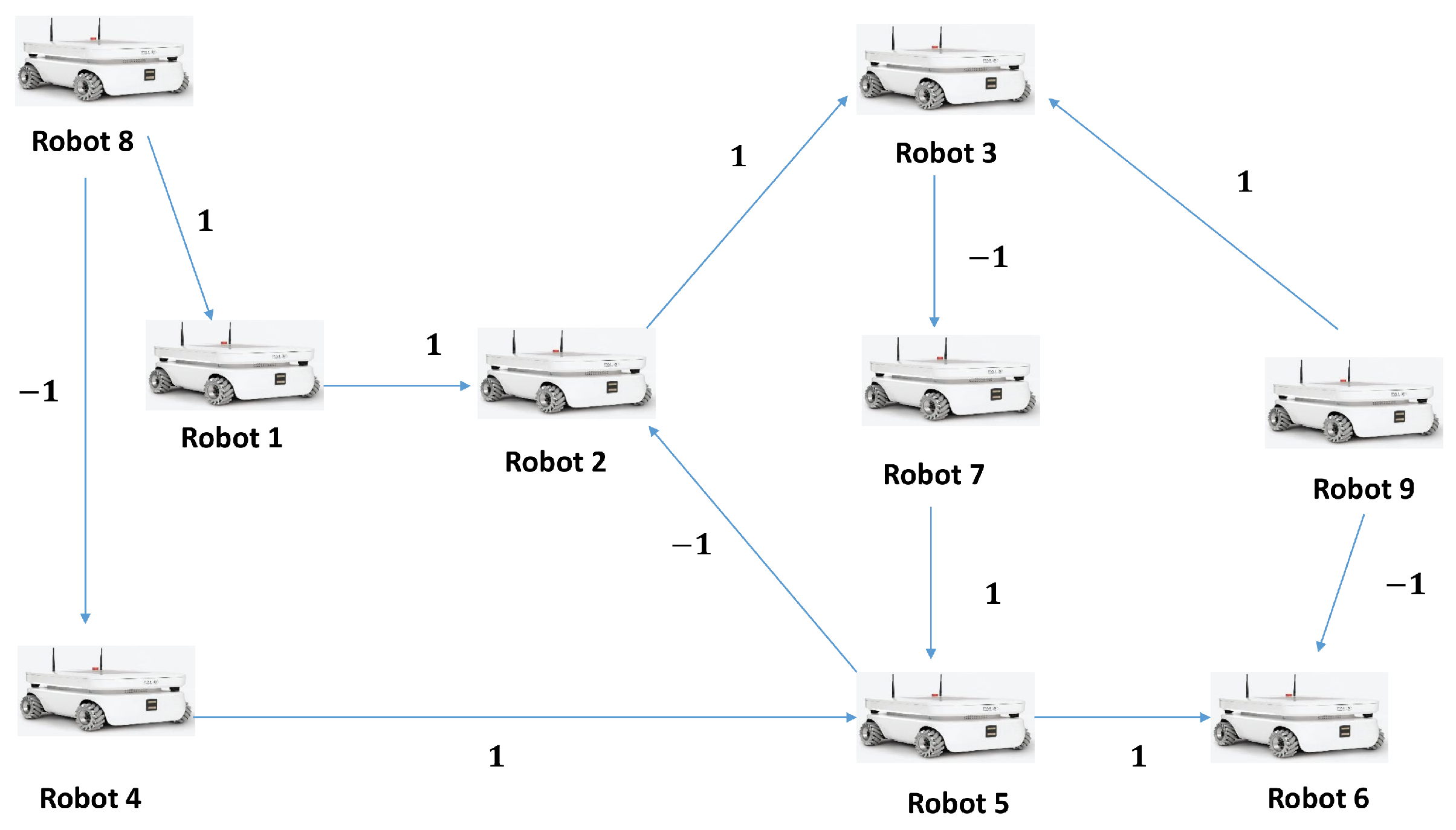
5. Numerical Illustration

Example 1. 

In the context of the bipartite containment control of a fractional-order multi-agent system defined by (4) and (5) for a fixed signed network containing two leaders and five followers, the topology of the problem is described in Figure 1. Take two bipartite subgroups that are defined as ${\overline{\mathcal{F}}}_1=\{1,2\}$ and $\overline{{\mathcal{F}}_2}=\{3,4,5\}$ for the structurally balanced signed directed graph $\mathcal{G}$.

Now, let B = $\left(\begin{array}{ccc}-6.3& & 0\\ 4& & -8\end{array}\right),$ W= $\left(\begin{array}{cc}-0.35& 0.05\\ 0.6& -0.6\end{array}\right)$, $\psi \left(k\right)=\left(\begin{array}{cc}0.23& 0.45\end{array}\right)$, $\delta =0.3$, and $g(k,z_u\left(k\right))={\displaystyle \frac{3}{2}}sin\left(z_u\left(k\right)\right),u=1,2,3\dots 7$, and we can take k = 0.6, which satisfies (6).

Now, from Figure 1, the adjacency matrices are as follows:

$$\mathcal{J}=\left(\begin{array}{ccccccc}0& 0& -0.5& 0& 0& 1& 0\\ 0.3& 0& 0& 0& 0& 0& 1.2\\ 0& 0& 0& 0& 0.4& -1& 0\\ 0& 0& 0.2& 0& 0& 0& -0.8\\ 0& -0.3& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0\end{array}\right)$$

$$\Delta =\left(\begin{array}{ccccccc}1& 0& 0& 0& 0& 0& 0\\ 0& 1& 0& 0& 0& 0& 0\\ 0& 0& -1& 0& 0& 0& 0\\ 0& 0& 0& -1& 0& 0& 0\\ 0& 0& 0& 0& -1& 0& 0\\ 0& 0& 0& 0& 0& 1& 0\\ 0& 0& 0& 0& 0& 0& 1\end{array}\right)$$

$$L=\left(\begin{array}{ccccccc}1.5& 0& 0.5& 0& 0& -1& 0\\ -0.3& 1.5& 0& 0& 0& 0& -1.2\\ 0& 0& 1.4& 0& -0.4& 1& 0\\ 0& 0& -0.2& 1& 0& 0& 0.8\\ 0& 0.3& 0& 0& 0.3& 0& 0\\ 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0\end{array}\right)$$

and $\overline{L}=\Delta L\Delta =\left(\begin{array}{ccccccc}1.5& 0& -0.5& 0& 0& -1& 0\\ -0.3& 1.5& 0& 0& 0& 0& -1.2\\ 0& 0& 1.4& 0& -0.4& -1& 0\\ 0& 0& -0.2& 1& 0& 0& -0.8\\ 0& -0.3& 0& 0& 0.3& 0& 0\\ 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0\end{array}\right)$ where ${\overline{L}}_{\mathcal{F}}=\left(\begin{array}{ccccc}1.5& 0& -0.5& 0& 0\\ -0.3& 1.5& 0& 0& 0\\ 0& 0& 1.4& 0& -0.4\\ 0& 0& -0.2& 1& 0\\ 0& -0.3& 0& 0& 0.3\end{array}\right)$ and ${\overline{L}}_{\mathcal{R}}=\left(\begin{array}{cc}-1& 0\\ 0& -1.2\\ -1& 0\\ 0& -0.8\\ 0& 0\end{array}\right)$ where ${\lambda }_1={\lambda }_{max}\left[{\overline{L}}_{\mathcal{F}}{\overline{L}}_{\mathcal{F}}^T\right]=3.2348$

If we take $\gamma =1.2$ and $r^{\prime }=0.625$ and then solve inequalities (15) and (16), we can obtain X = $\left(\begin{array}{cc}3.54& 2.61\\ 2.61& 3.74\end{array}\right)$, A= $\left(\begin{array}{cc}1.21& 0.32\\ 0.32& 1.21\end{array}\right)$, and $\mathcal{K}=1.14$, which satisfy inequalities (15) and (16). Take $\alpha =0.6$ and initial conditions

$$\begin{array}{c}\hfill z_1\left(1\right)={\left(\begin{array}{cc}0.5& -0.3\end{array}\right)}^T{z}_2\left(1\right)={\left(\begin{array}{cc}0.4& -1\end{array}\right)}^T\\ \hfill z_2\left(1\right)={[0.6,-0.4]}^T{z}_3\left(1\right)={[0.8,-2]}^T\\ \hfill z_4\left(1\right)={[0.3,-0.1]}^T{z}_5\left(1\right)={[0.5,-0.6]}^T\\ \hfill z_6\left(1\right)={[0.2,-0.6]}^T{z}_7\left(1\right)={[0.5,-1]}^T\end{array}$$

and then solve the system using ADAM’s optimizer. Then, the error trajectories of the FOMAS defined by (4) and (5) for a fixed signed directed network are given in Figure 2.

For error trajectories

$${\beta }_{p1}\left(k\right)=z_{p1}\left(k\right)-co\{z_{61},z_{71}\},$$

$${\beta }_{p2}\left(k\right)=z_{p2}\left(k\right)-co\{z_{61},z_{71}\},$$

and

$${\beta }_{p1}\left(k\right)=-(z_{p1}\left(k\right)+co\{z_{61},z_{71}\}),$$

$${\beta }_{p2}\left(k\right)=-(z_{p2}\left(k\right)+co\{z_{61},z_{71}\}),$$

we are now able to conclude that

$$\left\{\begin{array}{ccc}\hfill \underset{k\to \infty }{lim}\parallel z_u\left(k\right)-co\{z_i\left(k\right),i\in \overline{\mathcal{R}}\}\parallel =0,& \hfill & \hfill u\in \{1,2\},\\ \hfill \underset{k\to \infty }{lim}\parallel z_u\left(k\right)+co\{z_i\left(k\right),i\in \overline{\mathcal{R}}\}\parallel =0,& \hfill & \hfill u\in \{3,4,5\}.\end{array}\right.$$

This indicates that the system continues to operate under FDIAs and delays, but a larger number of delays and attacks can affect the speed of the convergence of the system. An attack signal is presented in Figure 3.

Example 2. 

In the context of the bipartite containment control of a fractional-order multi-agent system defined by (4) and (5) for a switching signed network containing two leaders and five followers, the switching topologies of digraphs ${\mathcal{G}}_1,{\mathcal{G}}_2,$ and ${\mathcal{G}}_3$ are described in Figure 4, Figure 5, and Figure 6, respectively. Take two bipartite subgroups that are defined as ${\overline{\mathcal{F}}}_1=\{1,2\}$ and $\overline{{\mathcal{F}}_2}=\{3,4,5\}$ for the structurally balanced signed directed graphs ${\mathcal{G}}_1,{\mathcal{G}}_2,$ and ${\mathcal{G}}_3$. Now, from Figure 4, Figure 5 and Figure 6, we have the following matrices:

$${\mathcal{J}}^{\left(1\right)}=\left(\begin{array}{ccccccc}0& 0& -0.2& 0& 0& 1.3& 0\\ 2& 0& 0& 0& 0& 0& 2.1\\ 0& 0& 0& 0& 0.5& -2& 0\\ 0& 0& 0.1& 0& 0& 0& -0.8\\ 0& -1.5& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0\end{array}\right)$$

$${\mathcal{J}}^{\left(2\right)}=\left(\begin{array}{ccccccc}0& 0& 0& -0.3& 0& 0& 2\\ 0.5& 0& 0& 0& -1.1& 0& 0\\ 0& 0& 0& 0& 0& -1.1& 0\\ 0& 0& 0.1& 0& 0& 0& 0\\ 0& 0& 0& 0.7& 0& -0.4& -0.8\\ 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0\end{array}\right)$$

$${\mathcal{J}}^{\left(3\right)}=\left(\begin{array}{ccccccc}0& 0& -0.3& 0& 0& 1.1& 0\\ 1.7& 0& 0& 0& 0& 0& 2\\ 0& 0& 0& 0& 0& -1.2& 0\\ 0& 0& 0.1& 0& 0& 0& 0\\ 0& -1.5& 0& 1& 0& 0& -0.5\\ 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0\end{array}\right)$$

$${\Delta }^{\left(1\right)}={\Delta }^{\left(2\right)}={\Delta }^{\left(3\right)}=\left(\begin{array}{ccccccc}1& 0& 0& 0& 0& 0& 0\\ 0& 1& 0& 0& 0& 0& 0\\ 0& 0& -1& 0& 0& 0& 0\\ 0& 0& 0& -1& 0& 0& 0\\ 0& 0& 0& 0& -1& 0& 0\\ 0& 0& 0& 0& 0& 1& 0\\ 0& 0& 0& 0& 0& 0& 1\end{array}\right)$$

Then,

$${\overline{\mathbb{L}}}_{\mathcal{F}}^{\left(1\right)}=\left(\begin{array}{ccccc}1.5& 0& -0.2& 0& 0\\ -2& 4.1& 0& 0& 0\\ 0& 0& 2.5& 0& -0.5\\ 0& 0& -0.1& 0.9& 0\\ 0& -1.5& 0& 0& 1.5\end{array}\right){\overline{\mathbb{L}}}_{\mathcal{R}}^{\left(1\right)}=\left(\begin{array}{cc}-1.3& 0\\ 0& -2.1\\ -2& 0\\ 0& -0.8\\ 0& 0\end{array}\right)$$

$${\overline{\mathbb{L}}}_{\mathcal{F}}^{\left(2\right)}=\left(\begin{array}{ccccc}2.3& 0& 0& -0.3& 0\\ -0.5& 1.6& 0& 0& -1.1\\ 0& 0& 1.1& 0& 0\\ 0& 0& -0.1& 0.1& 0\\ 0& 0& 0& -0.7& 1.9\end{array}\right){\overline{\mathbb{L}}}_{\mathcal{R}}^{\left(2\right)}=\left(\begin{array}{cc}0& -2\\ 0& 0\\ -1.1& 0\\ 0& 0\\ -0.4& -0.8\end{array}\right)$$

$${\overline{\mathbb{L}}}_{\mathcal{F}}^{\left(3\right)}=\left(\begin{array}{ccccc}1.3& 0& -0.3& 0& 0\\ -1.7& 1.9& 0& 0& 0\\ 0& 0& 1.2& 0& 0\\ 0& 0& -0.1& 0.1& 0\\ 0& -1.5& 0& -1& 3\end{array}\right){\overline{\mathbb{L}}}_{\mathcal{R}}^{\left(3\right)}=\left(\begin{array}{cc}-1.1& 0\\ 0& -2\\ -1.2& 0\\ 0& 0\\ 0& -0.5\end{array}\right)$$

Given ${\lambda }_{max}\left[{\overline{L}}_{\mathcal{F}}^{\left(1\right)}{\left({\overline{\mathbb{L}}}_{\mathcal{F}}^{\left(1\right)}\right)}^T\right]=23.2612,{\lambda }_{max}\left[{\overline{L}}_{\mathcal{F}}^{\left(2\right)}{\left({\overline{\mathbb{L}}}_{\mathcal{F}}^{\left(2\right)}\right)}^T\right]=6.8258,$ and ${\lambda }_{max}\left[{\overline{L}}_{\mathcal{F}}^{\left(3\right)}{\left({\overline{\mathbb{L}}}_{\mathcal{F}}^{\left(3\right)}\right)}^T\right]$ = 13.4871, from these three values, we have ${\lambda }_2=23.2612$. Now by solving inequalities (36) and (37), we can obtain A = $\left(\begin{array}{cc}1.31& 0.42\\ 0.42& 1.31\end{array}\right)$, X = $\left(\begin{array}{cc}3.64& 2.71\\ 2.71& 3.84\end{array}\right)$, and $\mathcal{K}=1.25$, which satisfy (36) and (37). Let $\alpha =0.6$. Then, the error trajectories of the FOMAS defined by (4) and (5) for a switching signed directed network are given in Figure 7.

Practical Example: Autonomous Warehouse Robots for Task Coordination

In a warehouse automation scenario, we consider a multi-agent system consisting of two leader robots and seven follower robots, designed to illustrate the proposed work. The communication topology is given in Figure 8. The system is organized into two groups: Group A includes robots 1, 2, and 3, while Group B consists of robots 4, 5, 6, and 7. The leaders are tasked with directing their respective groups to complete different sections of the warehouse, such as picking and sorting tasks, while managing potential conflicts between the two groups. In this setup, we apply the proposed control strategy to ensure that each follower robot maintains a desired formation around its leader and that the two groups manage their interactions effectively. From Figure 8, we have the following matrices:

$$\mathcal{J}=\left(\begin{array}{ccccccccc}0& 0& 0& 0& 0& 0& 0& 1& 0\\ 1& 0& 0& 0& -1& 0& 0& 0& 0\\ 0& 1& 0& 0& 0& 0& 0& 0& 1\\ 0& 0& 0& 0& 0& 0& 0& -1& 0\\ 0& 0& 0& 1& 0& 0& 1& 0& 0\\ 0& 0& 0& 0& 1& 0& 0& 0& -1\\ 0& 0& -1& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0\end{array}\right)$$

$$\Delta =\left(\begin{array}{ccccccccc}1& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 1& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 1& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& -1& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& -1& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& -1& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& -1& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 1& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 1\end{array}\right)$$

$$\mathrm{and}{\overline{\mathbb{L}}}_{\mathcal{F}}=\left(\begin{array}{ccccccc}1& 0& 0& 0& 0& 0& 0\\ -1& 2& 0& 0& -1& 0& 0\\ 0& -1& 2& 0& 0& 0& 0\\ 0& 0& 0& 1& 0& 0& 0\\ 0& 0& 0& -1& 2& 0& -1\\ 0& 0& 0& 0& -1& 2& 0\\ 0& 0& -1& 0& 0& 0& 1\end{array}\right) {\overline{\mathbb{L}}}_{\mathcal{R}}=\left(\begin{array}{cc}-1& 0\\ 0& 0\\ 0& -1\\ -1& 0\\ 0& 0\\ 0& -1\\ 0& 0\end{array}\right)$$

where ${\lambda }_1={\lambda }_{max}\left[{\overline{L}}_{\mathcal{F}}{\overline{L}}_{\mathcal{F}}^T\right]=9.7354$. Now, let the values of the other parameters involved in the system be the same as in Example 1. These parameters are chosen to satisfy the stability conditions of the system and ensure convergence to the desired formations. Then, through solving inequalities (15) and (16), we can obtain $\mathrm{X}=\left(\begin{array}{cc}3.04& 2.01\\ 2.01& 3.14\end{array}\right)$, $\mathrm{A}=\left(\begin{array}{cc}1.11& 0.22\\ 0.22& 1.21\end{array}\right)$, and $\mathcal{K}=1.13$ which satisfy inequalities (15) and (16). The Lypnove function stability graph is given in Figure 9. A series of experiments could be conducted using physical robots equipped with sensors and communication systems to enable real-time position tracking and control. The robots would be programmed to follow specified routes, maintaining their formations and managing interactions between Group A and Group B as they perform their tasks. These experiments would aim to demonstrate that the fractional-order control strategy can effectively manage both task completion and group interactions. It is anticipated that the followers will maintain stable positions relative to their leaders and that the two groups will avoid interference despite their competing objectives. The results of these experiments validate the theoretical findings from the fractional-order bipartite containment control model. The practical implementation confirms that the theoretical stability criteria are met, with the robots maintaining the desired formations and effectively managing the hostile interactions between groups. These results highlight the practical effectiveness of the fractional-order control strategy in real-world robotics applications, proving that the theoretical model can be successfully translated into a functional system.

6. Conclusions

Hostile-based nonlinear bipartite containment control (FOMASs) under FDIA is proposed in this paper. Both fixed and switching signed directed networks have been used for describing the interaction between agents. In assuming that the structural balance of the associated signed digraph remains intact when each follower is directed by at least one leader, robust controllers were developed to address bipartite containment control facing the issue of false data injection. These controllers can work in the presence of small delays and FDIAs. To check the stability of the system, we used the fractional Razumikhin technique and typical Lyapunov function approach. A reliable and feasible solution is proposed to tackle the problem arising from system delay switching topologies and fractional calculus. The validity and feasibility of the main findings are illustrated through concrete numerical examples. Practical examples are also provided for the effectiveness of our work.