Fractional Hermite–Hadamard–Mercer-Type Inequalities for Interval-Valued Convex Stochastic Processes with Center-Radius Order and Their Related Applications in Entropy and Information Theory
Abstract
1. Introduction
2. Preliminaries
- Stochastically continuous on , iffor every , where shows the limit of probability.
- Mean square continuous on , iffor every , where shows the value of the expectation related to the random variable .
- If , (14) gives an -.
- If , (14) gives an-tgs-.
- If , (14) gives an-P .
- If , (14) gives an exponential-type .
- If , (14) gives an-Godunova–Levin .
- If , (14) gives an-s-.
- If , (14) gives an-Godunova–Levin s-.
- If , (14) gives an n-polynomial .
- If , (14) gives an fractional n-polynomial .
- If , (14) gives an generalized n-polynomial .
3. Main Results
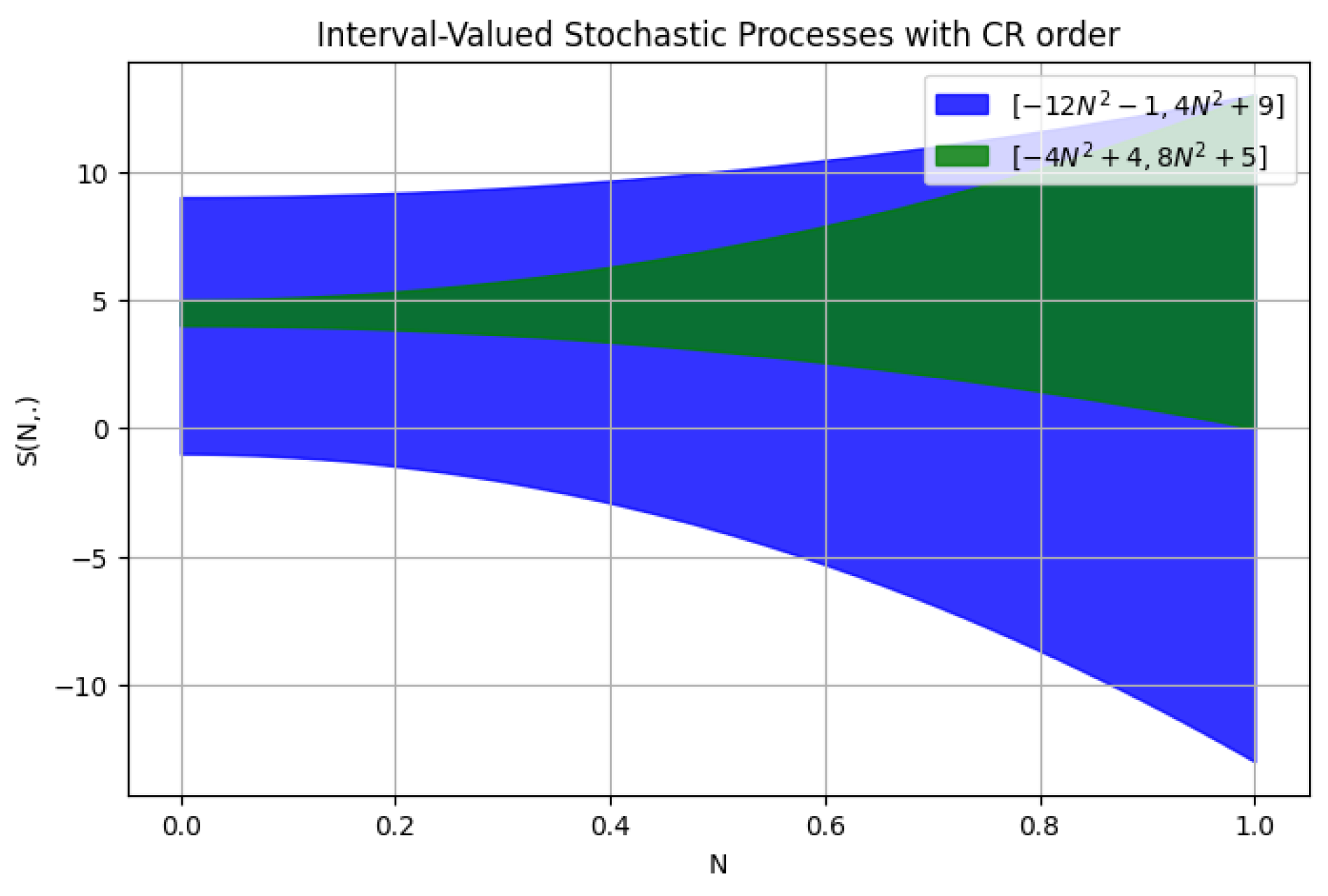
3.1. Jensen-Type Inclusion
- If , (18) gives a Jensen-type inclusion for of-.
- If , (18) gives a Jensen-type inclusion for of-tgs-.
- If , (18) gives a Jensen-type inclusion for of-P .
- If , (18) gives a Jensen-type inclusion for of exponential-type .
- If , (18) gives a Jensen-type inclusion for of-Godunova–Levin .
- If , (18) gives a Jensen-type inclusion for of-s-.
- If , (18) gives a Jensen-type inclusion for of-Godunova–Levin s-.
- If , (18) gives a Jensen-type inclusion for of-h-.
- If , (18) gives a Jensen-type inclusion for of n-polynomial .
- If , (18) gives a Jensen-type inclusion for of fractional n-polynomial .
- If , (18) gives a Jensen-type inclusion for of generalized n-polynomial .
3.2. Mercer-Type Inclusion
- If , (20) gives a Mercer-type inclusion for of-.
- If , (20) gives a Mercer-type inclusion for of-tgs-.
- If , (20) gives a Mercer-type inclusion for of-P .
- If , (20) gives a Mercer-type inclusion for of exponential-type .
- If , (20) gives a Mercer-type inclusion for of-Godunova–Levin .
- If , (20) gives a Mercer-type inclusion for of-s-.
- If , (20) gives a Mercer-type inclusion for of-Godunova–Levin s-.
- If , (20) gives a Mercer-type inclusion for of-h-.
- If , (20) gives a Mercer-type inclusion for of n-polynomial .
- If , (20) gives a Mercer-type inclusion for of fractional n-polynomial .
- If , (20) gives a Mercer-type inclusion for of generalized n-polynomial .
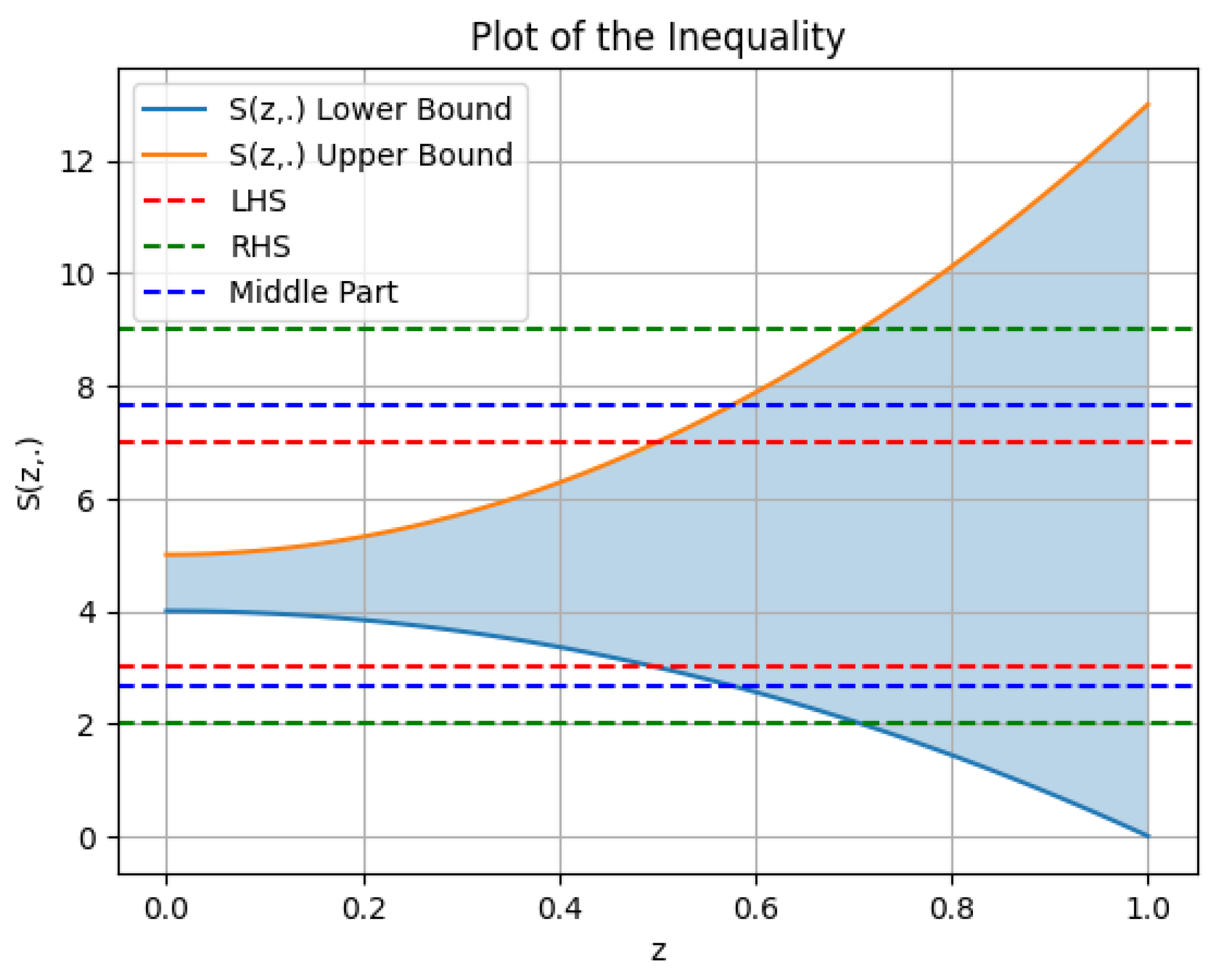
3.3. Hermite–Hadamard-Type Inclusion
- If , (23) gives a Hermite–Hadamard-type inclusion for of-.
- If , (23) gives a Hermite–Hadamard-type inclusion for of-tgs-.
- If , (23) gives a Hermite–Hadamard-type inclusion for of-P .
- If , (23) gives a Hermite–Hadamard-type inclusion for of exponential-type .
- If , (23) gives a Hermite–Hadamard-type inclusion for of-Godunova–Levin .
- If , (23) gives a Hermite–Hadamard-type inclusion for of-s-.
- If , (23) gives a Hermite–Hadamard-type inclusion for of-Godunova–Levin s-.
- If , (23) gives a Hermite–Hadamard-type inclusion for of-h-.
- If , (23) gives a Hermite–Hadamard-type inclusion for of n-polynomial .
- If , (23) gives a Hermite–Hadamard-type inclusion for of fractional n-polynomial .
- If , (23) gives a Hermite–Hadamard-type inclusion for of generalized n-polynomial .
- If , (26) gives a Hermite–Hadamard-type inclusion for of-.
- If , (26) gives a Hermite–Hadamard-type inclusion for of-tgs-.
- If , (26) gives a Hermite–Hadamard-type inclusion for of-P .
- If , (26) gives a Hermite–Hadamard-type inclusion for of exponential-type .
- If , (26) gives a Hermite–Hadamard-type inclusion for of-Godunova–Levin .
- If , (26) gives a Hermite–Hadamard-type inclusion for of-s-.
- If , (26) gives a Hermite–Hadamard-type inclusion for of-Godunova–Levin s-.
- If , (26) gives a Hermite–Hadamard-type inclusion for of-h-.
- If , (26) gives a Hermite–Hadamard-type inclusion for of n-polynomial .
- If , (26) gives a Hermite–Hadamard-type inclusion for of fractional n-polynomial .
- If , (26) gives a Hermite–Hadamard-type inclusion for of generalized n-polynomial .
- If , (29) gives a Hermite–Hadamard-type inclusion for of-.
- If , (29) gives a Hermite–Hadamard-type inclusion for of-tgs-.
- If , (29) gives a Hermite–Hadamard-type inclusion for of-P .
- If , (29) gives a Hermite–Hadamard-type inclusion for of exponential-type .
- If , (29) gives a Hermite–Hadamard-type inclusion for of-Godunova–Levin .
- If , (29) gives a Hermite–Hadamard-type inclusion for of-s-.
- If , (29) gives a Hermite–Hadamard-type inclusion for of-Godunova–Levin s-.
- If , (29) gives a Hermite–Hadamard-type inclusion for of-h-.
- If , (29) gives a Hermite–Hadamard-type inclusion for of n-polynomial .
- If , (29) gives a Hermite–Hadamard-type inclusion for of fractional n-polynomial .
- If , (29) gives a Hermite–Hadamard-type inclusion for of fractional n-polynomial .
- If , (30) gives a Hermite–Hadamard-type inclusion for of-.
- If , (30) gives a Hermite–Hadamard-type inclusion for of-tgs-.
- If , (30) gives a Hermite–Hadamard-type inclusion for of-P .
- If , (30) gives a Hermite–Hadamard-type inclusion for of exponential-type .
- If , (30) gives a Hermite–Hadamard-type inclusion for of-Godunova–Levin .
- If , (30) gives a Hermite–Hadamard-type inclusion for of-s-.
- If , (30) gives a Hermite–Hadamard-type inclusion for of-Godunova–Levin s-.
- If , (30) gives a Hermite–Hadamard-type inclusion for of-h-.
- If , (30) gives a Hermite–Hadamard-type inclusion for of n-polynomial .
- If , (30) gives a Hermite–Hadamard-type inclusion for of fractional n-polynomial .
- If , (30) gives a Hermite–Hadamard-type inclusion for of generalized n-polynomial .
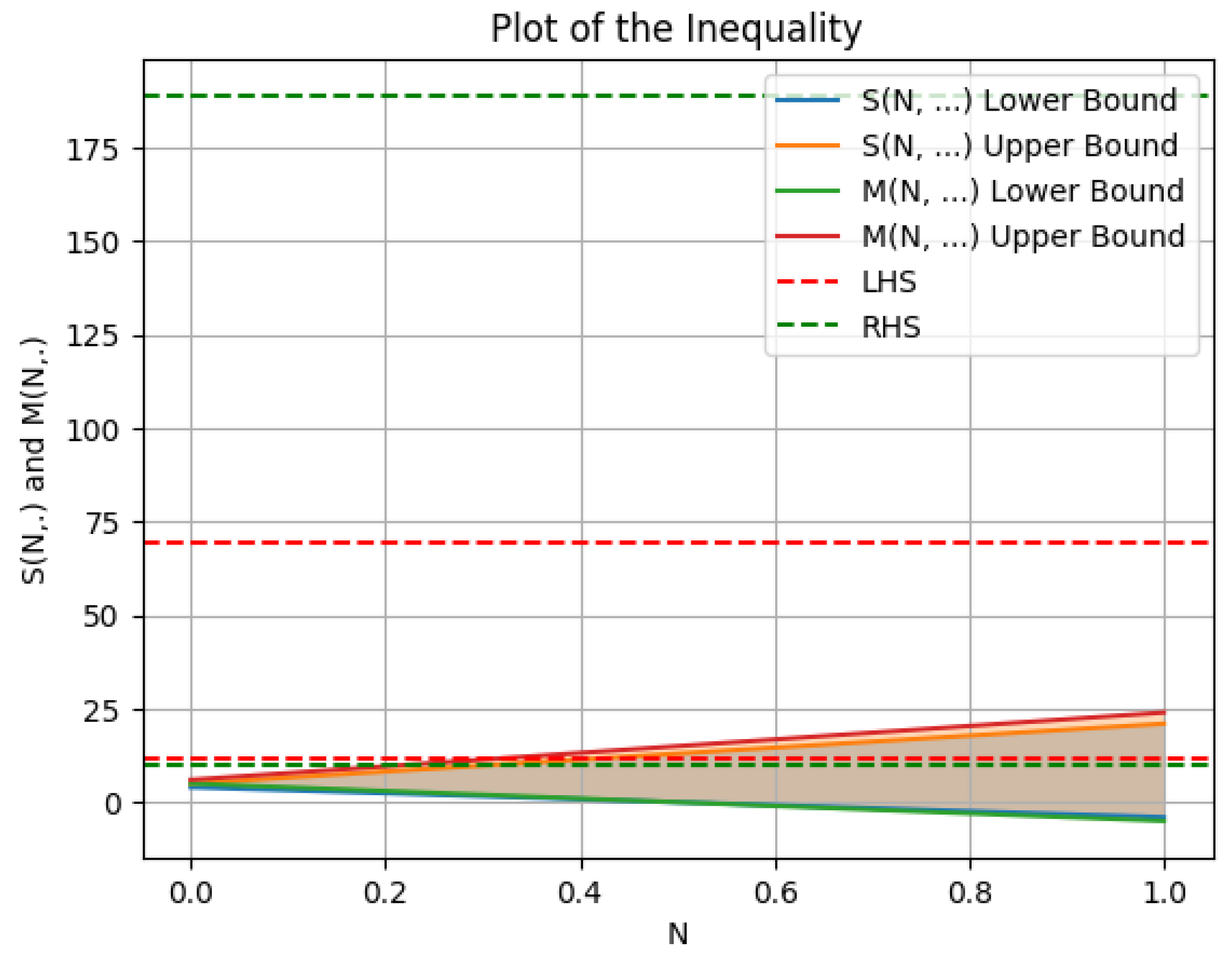
3.4. Fractional Hermite–Hadamard–Mercer-Type Inclusion
- If , (31) gives a Hermite–Hadamard–Mercer-type inclusion for of-.
- If , (31) gives a Hermite–Hadamard–Mercer-type inclusion for of-tgs-.
- If , (31) gives a Hermite–Hadamard–Mercer-type inclusion for of-P .
- If , (31) gives a Hermite–Hadamard–Mercer-type inclusion for of exponential-type .
- If , (31) gives a Hermite–Hadamard–Mercer-type inclusion for of-Godunova–Levin .
- If , (31) gives a Hermite–Hadamard–Mercer-type inclusion for of-s-.
- If , (31) gives a Hermite–Hadamard–Mercer-type inclusion for of-Godunova–Levin s-.
- If , (31) gives a Hermite–Hadamard–Mercer-type inclusion for of-h-.
- If , (31) gives a Hermite–Hadamard–Mercer-type inclusion for of n-polynomial .
- If , (31) gives a Hermite–Hadamard–Mercer-type inclusion for of fractional n-polynomial .
- If , (31) gives a Hermite–Hadamard–Mercer-type inclusion for of generalized n-polynomial .
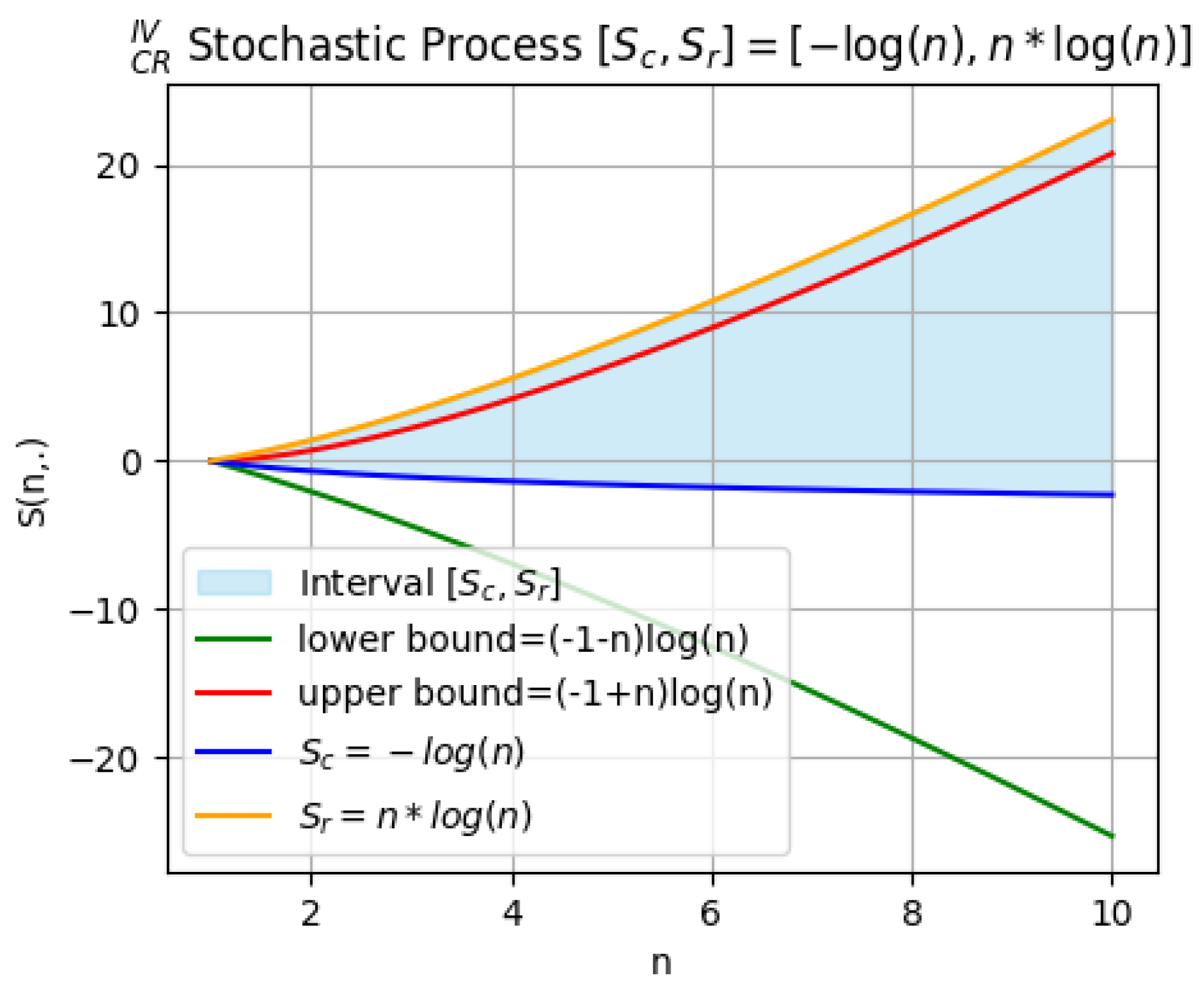
4. Applications
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Moore, R.E.; Kearfott, R.B.; Cloud, M.J. Introduction to Interval Analysis; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2009. [Google Scholar]
- Costa, T.M.; Román-Flores, H. Some integral inequalities for fuzzy-interval-valued functions. Inf. Sci. 2017, 420, 110–125. [Google Scholar] [CrossRef]
- Román-Flores, H.; Chalco-Cano, Y.; Lodwick, W. Some integral inequalities for interval-valued functions. Comput. Appl. Math. 2018, 37, 1306–1318. [Google Scholar] [CrossRef]
- Chalco-Cano, Y.; Lodwick, W.A.; Condori-Equice, W. Ostrowski-type inequalities and applications in numerical integration for interval-valued functions. Soft Comput. 2015, 19, 3293–3300. [Google Scholar] [CrossRef]
- Liu, W.; Shi, F.; Ye, G.; Zhao, D. The Properties of Harmonically cr-h-Convex Function and Its Applications. Mathematics 2022, 10, 2089. [Google Scholar] [CrossRef]
- Bhunia, A.K.; Samanta, S.S. A study of interval metric and its application in multi-objective optimization with interval objectives. Comput. Ind. Eng. 2014, 74, 169–178. [Google Scholar] [CrossRef]
- Liu, D.; Wang, S. An artificial neural network supported stochastic process for degradation modeling and prediction. Reliab. Eng. Syst. Saf. 2021, 214, 107738. [Google Scholar] [CrossRef]
- Ling, H.; Samarasinghe, S.; Kulasiri, D. Stochastic Neural Networks for Modelling Random Processes from Observed Data. In Artificial Neural Network Modelling; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Fahad, A.; Ayesha; Wang, Y.; Butt, S.I. Jensen-Mercer and Hermite-Hadamard-Mercer Type Inequalities for GA h-Convex Functions and Its Subclasses with Applications. Mathematics 2023, 11, 278. [Google Scholar] [CrossRef]
- Işcan, I. Construction of a new class of functions with their properties and certain inequalities n-fractional polynomial convex functions. Miskolc Math. Notes 2023, 24, 1389–1404. [Google Scholar] [CrossRef]
- Hadamard, J. Etude sur les propriétés des fonctions entières et en particulier d’une fonction considérée par Riemann. J. MathéMatiques Pures AppliquéEs 1893, 58, 171–215. [Google Scholar]
- Bombardelli, M.; Varo¸sanec, S. Properties of h-convex functions related to the Hermite-Hadamard-Fejer inequalities. Comput. Math. Appl. 2009, 58, 1869–1877. [Google Scholar] [CrossRef]
- Nagy, B. On a generalization of the Cauchy equation. Aequ. Math. 1974, 10, 165–171. [Google Scholar] [CrossRef]
- Nikodem, K. On convex stochastic processes. Aequ. Math. 1980, 20, 18–197. [Google Scholar] [CrossRef]
- Skowronski, A. On some properties of j-convex stochastic processes. Aequ. Math. 1992, 44, 249–258. [Google Scholar] [CrossRef]
- Pales, Z. Nonconvex functions and separation by power means. Math. Inequalities Appl. 2000, 3, 169–176. [Google Scholar] [CrossRef]
- Kotrys, D. Hermite-Hadamard inequality for convex stochastic processes. Aequ. Math. 2012, 83, 14–151. [Google Scholar] [CrossRef]
- Zhou, H.; Saleem, M.S.; Ghafoor, M.; Li, J. Generalization of h-convex stochastic processes and some classical inequalities. Math. Probl. Eng. 2020, 2020, 1583807. [Google Scholar] [CrossRef]
- Okur, N.; Işcan, I.; Dizdar, E.Y. Hermite-Hadamard type inequalities for p-convex stochastic processes. Int. J. Optim. Control Theor. Appl. 2019, 9, 148–153. [Google Scholar] [CrossRef]
- Maden, S.; Tomar, M.; Set, E. s-convex stochastic processes in the first sense. Pure Appl. Math. Lett. 2015, 2015, 1–7. [Google Scholar]
- Set, E.; Tomar, M.; Maden, S. s-convex stochastic processes in the second sense. Turk. J. Anal. Number Theory 2014, 2, 202–207. [Google Scholar] [CrossRef]
- Fu, H.; Saleem, M.S.; Nazeer, W.; Ghafoor, M.; Li, P. On Hermite-Hadamard type inequalities for n-polynomial convex stochastic processes. AIMS Math. 2021, 6, 6322–6339. [Google Scholar] [CrossRef]
- Rahman, M.S.; Shaikh, A.A.; Bhunia, A.K. Necessary and sufficient optimality conditions for non-linear unconstrained and constrained optimization problems with interval-valued objective function. Comput. Ind. Eng. 2020, 147, 106634. [Google Scholar] [CrossRef]
- Vivas-Cortez, M.; Ramzan, S.; Awan, M.U.; Javed, M.Z.; Khan, A.G.I. V-CR-γ-Convex Functions and Their Application in Fractional Hermite–Hadamard Inequalities. Symmetry 2023, 15, 1405. [Google Scholar] [CrossRef]
- Saeed, T.; Afzal, W.; Abbas, M.T.; De la Sen, M. Some New Generalizations of Integral Inequalities for Harmonical cr-(h1,h2)-Godunova–Levin Functions and Applications. Mathematics 2022, 10, 4540. [Google Scholar] [CrossRef]
- Afzal, W.; Nazeer, W.; Botmart, T.; Treanta, S. Some properties and inequalities for a generalized class of harmonical Godunova-Levin function via center radius order relation. AIMS Math. 2022, 8, 1696–1712. [Google Scholar] [CrossRef]
- Abbas, M.; Afzal, W.; Botmart, T.; Galal, A.M. Ostrowski and Hermite-Hadamard type inequalities for h-convex stochastic processes using center-radius order relation. AIMS Math. 2023, 8, 16013–16030. [Google Scholar] [CrossRef]
- Sayyari, Y.; Dehghanian, M. A new class of convex functions and applications in entropy and analysis. Chaos Solitons Fractals 2024, 181, 114677. [Google Scholar] [CrossRef]
- Toplu, T.; Kadakal, M. On n-polynomial convexity and some related inequalities. AIMS Math. 2020, 5, 1304. [Google Scholar] [CrossRef]
- Moore, R.E. Interval Analysis; Prentice-Hall: Englewood Cliff, NJ, USA, 1966. [Google Scholar]
- Jarad, F.; Sahoo, S.K.; Nisar, K.S.; Alzabut, J. New stochastic fractional integral and related inequalities of Jensen–Mercer and Hermite–Hadamard–Mercer type for convex stochastic processes. J. Inequalities Appl. 2023, 2023, 51. [Google Scholar] [CrossRef]
- Kadakal, M.; Işcan, I.; Kadakal, H. Construction of a new generalization for n-polynomial convexity with their certain inequalities. Hacet. J. Math. Stat. 2024, 2024, 1–13. [Google Scholar] [CrossRef]
- Afzal, W.; Breaz, D.; Abbas, M.; Cotîrlǎ, L.-I.; Khan, Z.A.; Rapeanu, E. Hyers–Ulam stability of 2D-convex mappings and some related new Hermite–Hadamard, Pachpatte, and Fejér type integral inequalities using novel fractional integral operators via totally interval-order relations with open problem. Mathematics 2024, 12, 1238. [Google Scholar] [CrossRef]
- Afzal, W.; Aloraini, N.; Abbas, M.; Ro, J.; Zaagan, A. Some novel Kulisch and Miranker type inclusions for generalized class of Godunova-Levin stochastic processes with open problem. AIMS Math. 2024, 9, 5122–5146. [Google Scholar] [CrossRef]
- Macías-Díaz, J.; Afzal, W.; Abbas, M. Some inequalities for the h-Godunova-Levin function using center radius (CR) order relation. J. Fract. Calc. Appl. 2024, 6, 518. [Google Scholar] [CrossRef]
- Lupulescu, V. Fractional calculus for interval-valued functions. Fuzzy Sets Syst. 2015, 265, 63–85. [Google Scholar] [CrossRef]
- Ekinci, A.; Ozdemir, M.E. Some new integral inequalities via Riemann Liouville integral operators. Appl. Comput. Math. 2019, 3, 288–295. [Google Scholar]
- Caputo, M.; Fabrizio, M.A. The new definition of fractional derivative without singular kernel. Prog. Fract. Differ. Appl. 2015, 1, 73–85. [Google Scholar]
- Rahman, G.; Nisar, K.S.; Abdeljawad, T. Tempered fractional integral inequalities for convex functions. Mathematics 2020, 8, 500. [Google Scholar] [CrossRef]
- Jarad, F.; Abdeljawad, T.; Alzabut, J. Generalized fractional derivatives generated by a class of local proportional derivatives. Eur. Phys. J. Spec. Top. 2017, 226, 3457–3471. [Google Scholar] [CrossRef]
- Huang, C.J.; Rahman, G.; Nisar, K.S.; Ghaffar, A.; Qi, F. Some Inequalities of Hermite-Hadamard type for k-fractional conformable integrals. Aust. J. Math. Anal. Appl. 2019, 16, 1–9. [Google Scholar]
- Baleanu, D.; Purohit, S.D.; Prajapati, J.C. Integral inequalities involving generalized Erdélyi-Kober fractional integral operators. Open Math. 2016, 14, 89–99. [Google Scholar] [CrossRef]
- Hilfer, R. Applications of Fractional Calculus in Physics; World Scientific: Singapore, 2000. [Google Scholar]
- Dokuyucu, M.A. Caputo and Atangana-Baleanu-Caputo fractional derivative applied to the garden equation. Turk. J. Sci. 2020, 5, 1–7. [Google Scholar]
- Rahman, G.; Khan, A.; Abdeljawad, T.; Nisar, K.S. The Minkowski inequalities via generalized proportional fractional integral operators. Adv. Differ. Equations 2019, 2019, 287. [Google Scholar] [CrossRef]
- Budak, H.; Tunc, T.; Sarikaya, M. Fractional Hermite-, Hadamard-type inequalities for interval-valued functions. Proc. Am. Math. Soc. 2020, 148, 705–718. [Google Scholar] [CrossRef]
- Butt, S.I.; Kashuri, A.; Tariq, M.; Nasir, J.; Aslam, A.; Gao, W. n–polynomial exponential type p–convex function with some related inequalities and their applications. Heliyon 2020, 6, e05420. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Saleem, M.S.; Nazeer, W.; Shah, A.F. New Hermite-Hadamard inequalities in fuzzy-interval fractional calculus via exponentially convex fuzzy interval-valued function. AIMS Math. 2021, 6, 12260–12278. [Google Scholar] [CrossRef]
- Zhou, H.; Saleem, M.S.; Nazeer, W.; Shah, A.F. Hermite-Hadamard type inequalities for interval-valued exponential type pre-invex functions via Riemann-Liouville fractional integrals. AIMS Math. 2022, 7, 2602–2617. [Google Scholar] [CrossRef]
- Cortez, M.V.; Saleem, M.S.; Shah, A.F.; Nazeer, W.; Hernndez, J.E. On Generalized Harmonically ψ-MT-Convex Functions via Local Fractional Integrals and some Applications. Appl. Math. 2023, 17, 417–429. [Google Scholar]
- Fang, Z.B.; Shi, R. On the (p,h)-convex function and some integral inequalities. J. Inequalities Appl. 2014, 2014, 45. [Google Scholar] [CrossRef][Green Version]
- Shi, F.; Ye, G.; Liu, W.; Zhao, D. cr-h-Convexity and Some Inequalities for CR h-Convex Function. Preprint. 2022. Available online: https://www.researchgate.net/publication/361244875 (accessed on 10 March 2022).
- Ogulmus, H.; Sarikaya, M.Z. Hermite-Hadamard-Mercer type inequalities for fractional integrals. Filomat 2021, 35, 2425–2436. [Google Scholar] [CrossRef]
- Kadakal, M.; Işcan, I. Exponential type convexity and some related inequalities. J. Inequalities Appl. 2020, 2020, 82. [Google Scholar] [CrossRef]
- Mohammed, P.O.; Abdeljawad, T.; Baleanu, D.; Alzabut, J. New fractional inequalities of Hermite–Hadamard type involving the incomplete gamma functions. J. Inequalities Appl. 2020, 2020, 263. [Google Scholar] [CrossRef]
- Alomari, M.; Darus, M. New inequalities of Simpson’s type for s-convex functions with applications. RGMIA Res. Rep. Collect. 2009, 12, 9. [Google Scholar]
- Cerone, P.; Dragomir, S.S. Ostrowski-type inequalities for functions whose derivatives satisfy certain convexity assumptions. Demonstr. Math. 2004, 37, 299–308. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shah, A.F.; Özcan, S.; Vivas-Cortez, M.; Saleem, M.S.; Kashuri, A. Fractional Hermite–Hadamard–Mercer-Type Inequalities for Interval-Valued Convex Stochastic Processes with Center-Radius Order and Their Related Applications in Entropy and Information Theory. Fractal Fract. 2024, 8, 408. https://doi.org/10.3390/fractalfract8070408
Shah AF, Özcan S, Vivas-Cortez M, Saleem MS, Kashuri A. Fractional Hermite–Hadamard–Mercer-Type Inequalities for Interval-Valued Convex Stochastic Processes with Center-Radius Order and Their Related Applications in Entropy and Information Theory. Fractal and Fractional. 2024; 8(7):408. https://doi.org/10.3390/fractalfract8070408
Chicago/Turabian StyleShah, Ahsan Fareed, Serap Özcan, Miguel Vivas-Cortez, Muhammad Shoaib Saleem, and Artion Kashuri. 2024. "Fractional Hermite–Hadamard–Mercer-Type Inequalities for Interval-Valued Convex Stochastic Processes with Center-Radius Order and Their Related Applications in Entropy and Information Theory" Fractal and Fractional 8, no. 7: 408. https://doi.org/10.3390/fractalfract8070408
APA StyleShah, A. F., Özcan, S., Vivas-Cortez, M., Saleem, M. S., & Kashuri, A. (2024). Fractional Hermite–Hadamard–Mercer-Type Inequalities for Interval-Valued Convex Stochastic Processes with Center-Radius Order and Their Related Applications in Entropy and Information Theory. Fractal and Fractional, 8(7), 408. https://doi.org/10.3390/fractalfract8070408







