Auto- and Cross-Correlation Multifractal Analysis of Sea Surface Temperature Variability
Abstract
1. Introduction
2. Materials and Methods
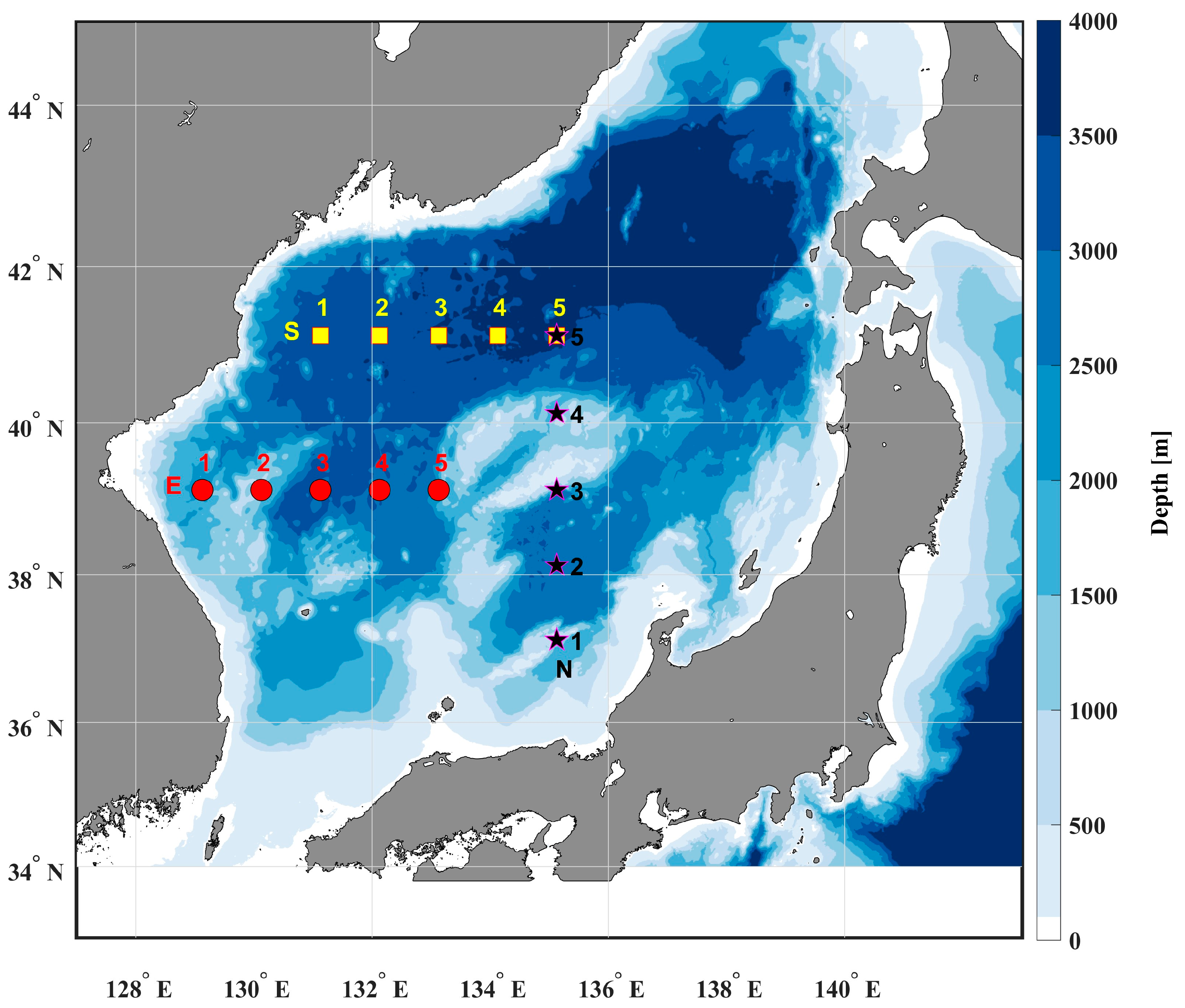
2.1. Data
2.2. Multifractal Methodology
2.2.1. Multifractal Cross-Correlation Analysis (MFCCA)
2.2.2. Multifractal Asymmetric Detrended Cross-Correlation Analysis
2.2.3. Multifractal Asymmetric Cross-Correlation Analysis (MF-ACCA)
2.3. Global Wavelet Spectrum
3. Analysis Results
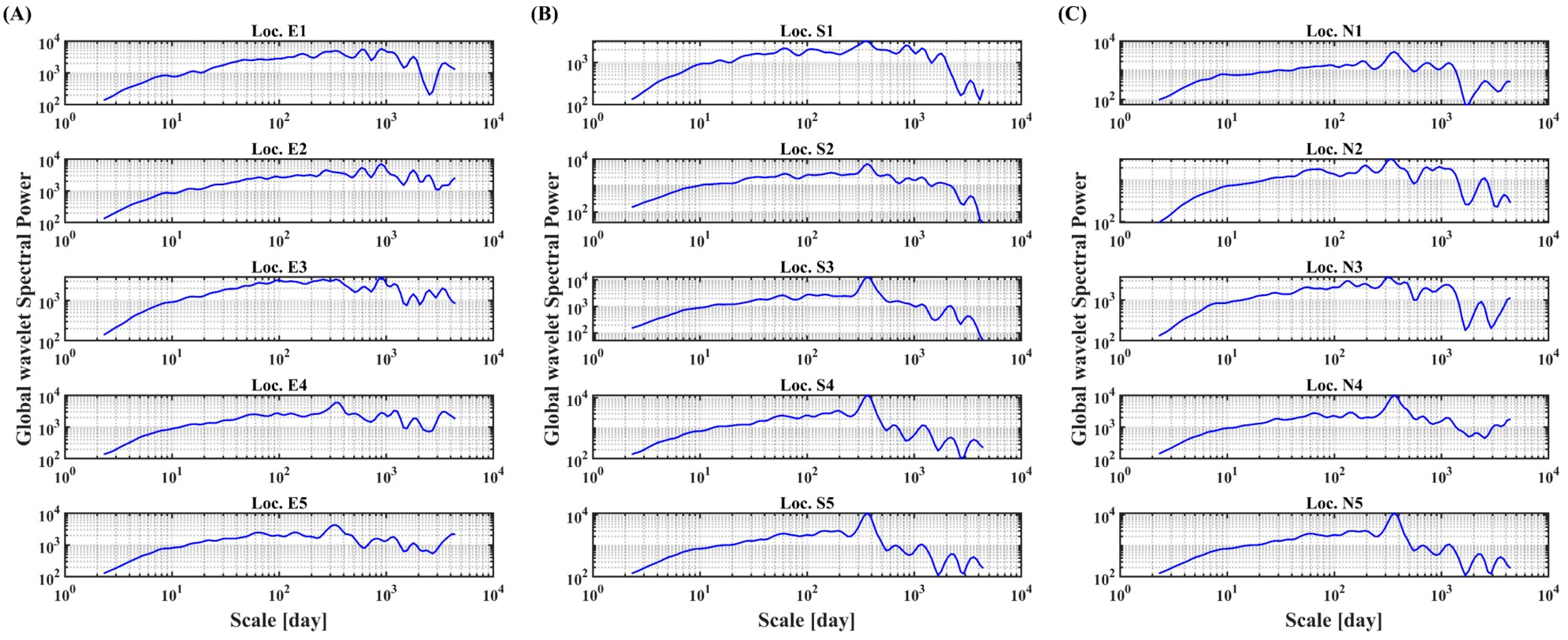
3.1. Spectral Pattern of SSTA
3.2. Multifractal Characteristics of SSTA
3.2.1. Multifractal Detrended Fluctuation Analysis
3.2.2. Asymmetric Multifractal Detrended Fluctuation Analysis
3.2.3. Multifractal Asymmetric Cross-Correlation Analysis (MF-ACCA)
4. Discussion
5. Conclusions
- Overall, the long-range auto-correlation was strongly persistent for the whole scale from 30 to 5000 days, meaning that the Hurst exponent was very close to 1. However, two locations of N1 and N2 near the KTS seemed to be random only for large scales from 1000 to 5000 days; their Hurst exponents were nearly 0.5 (Table A1).
- All considered SSTAs from different locations show scale- and location-dependent multifractal features (Table 1 and Table 2); the strength of multifractality was greater for small scales (30–1000 days) than for large scales (1000–5000 days), with the strongest in the S-line region (near the SPF) for small scales.
- A distinct crossover behavior appeared along S-line (SPF region), with an annual crossover scale (300–400 days), through which a long-range persistence changed into anti- or no-persistence for small scales (Figure 3). For large scales, the crossover behavior seemed continuous; a convex functional form was observed (Figure A2).
- All the asymmetric long-range auto-correlations were strongly persistent for small scales (Table 2), while some locations showed random behaviors (Table A2). The random behavior of auto-correlation structures for large scales was observed more frequently in negative (falling) trends than in positive (rising) trends.
- The crossover behaviors in the A-MFDFA analysis were the same as those in the MF-DFA analysis.
- The degree of asymmetry for three q-order detrended fluctuation functions was greater for large scales (1000 to 5000 days) than for small scales (30 to 1000 days); there seems to be nearly no asymmetry for small scales. As for the asymmetry of large scales, large fluctuations (with positive q-values, and ) showed a strong positive asymmetry, while small fluctuations (with negative q-value, ) showed a weak or moderate negative asymmetry.
- The strength of multifractality was a little stronger in the small scales than in the large scales; note that the overall weak multifractality was mainly due to the absence of long-range cross-correlations for negative q-values.
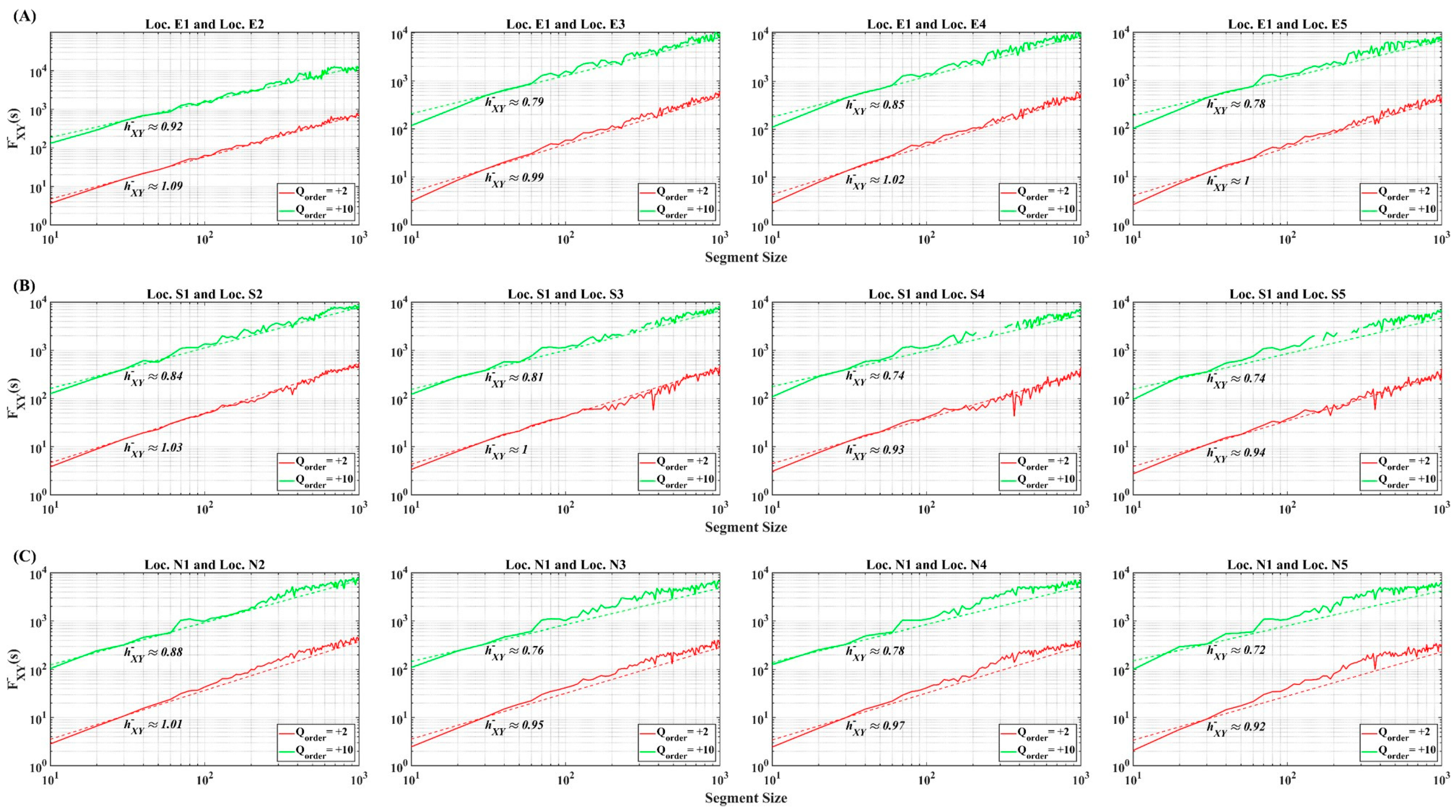
- Most asymmetric long-range cross-correlations were strongly persistent for small and large scales, characterized by the Hurst exponent of nearly one for both positive (rising) and negative (falling) trends. However, N-line clearly deviated from these persistent behaviors, especially for large scales (Table A3); the Hurst exponents were close to 0.5, indicating the randomness in cross-correlations, and the negative (falling) Hurst exponents were less persistent than the positive (rising) ones.
- The degree of asymmetry for two positive q-order detrended fluctuation functions was greater for large scales (1000 to 5000 days) than for small scales (30 to 1000 days). As for the directionality of asymmetry, there was a weak negative skewed asymmetry in the small scales, while a strong positive skewed asymmetry was observed in large scales (Table 4 and Table A3).
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A





Appendix B
| Location | Crossover Behavior | ||||
|---|---|---|---|---|---|
| E1 | 0.86 | 0.84 | 0.82 | 0.04 | not clear |
| E2 | 0.78 | 0.9 | 1.13 | 0.35 | not clear |
| E3 | 0.86 | 0.88 | 1.08 | 0.22 | not clear |
| E4 | 0.72 | 0.86 | 1.22 | 0.5 | not clear |
| E5 | 0.9 | 0.89 | 1 | 0.1 | not clear |
| S1 | 1.12 | 0.92 | 0.96 | 0.16 | not clear |
| S2 | 1.05 | 0.95 | 1.01 | 0.04 | strong (convex) |
| S3 | 0.85 | 0.79 | 0.69 | 0.16 | strong (convex) |
| S4 | 0.99 | 0.81 | 0.61 | 0.38 | not clear |
| S5 | 1.11 | 0.87 | 0.68 | 0.43 | strong (convex) |
| N1 | 0.44 | 0.5 | 0.66 | 0.22 | not clear |
| N2 | 0.41 | 0.56 | 0.89 | 0.48 | not clear |
| N3 | 0.63 | 0.68 | 0.86 | 0.23 | not clear |
| N4 | 1.29 | 1.1 | 1.11 | 0.18 | strong (convex) |
| N5 | 1.11 | 0.87 | 0.68 | 0.43 | weak (convex) |
| Location | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| E1 | 0.09 | 0.43 | 0.94 | 0.28 | 0.66 | 0.89 | 0.48 | 0.41 | 0.85 | 0.71 | 0.14 |
| E2 | 0.29 | 0.56 | 0.78 | 0.7 | 0.08 | 0.87 | 0.88 | −0.01 | 1.07 | 1.26 | −0.19 |
| E3 | 0.22 | 0.27 | 0.85 | 0.85 | 0 | 0.85 | 0.94 | −0.09 | 1.07 | 1.12 | −0.05 |
| E4 | 0.39 | 0.48 | 0.73 | 0.76 | −0.03 | 0.85 | 0.87 | −0.02 | 1.12 | 1.24 | −0.12 |
| E5 | 0.05 | 0.21 | 0.9 | 0.82 | 0.08 | 0.87 | 0.88 | −0.01 | 0.95 | 1.03 | −0.08 |
| S1 | 0.25 | 0.64 | 1.11 | 0.53 | 0.58 | 0.94 | 0.71 | 0.23 | 0.86 | 1.17 | −0.31 |
| S2 | 0.24 | 0.49 | 1.08 | 0.69 | 0.49 | 0.99 | 0.8 | 0.19 | 0.84 | 1.18 | −0.34 |
| S3 | 0.18 | 0.3 | 0.88 | 0.52 | 0.36 | 0.83 | 0.62 | 0.21 | 0.7 | 0.82 | −0.12 |
| S4 | 0.37 | 0.18 | 1 | 0.46 | 0.54 | 0.85 | 0.53 | 0.32 | 0.63 | 0.64 | −0.01 |
| S5 | 0.5 | 0.3 | 1.16 | 0.38 | 0.78 | 0.96 | 0.46 | 0.5 | 0.66 | 0.68 | −0.02 |
| N1 | 0.21 | 0.3 | 0.46 | 0.32 | 0.14 | 0.53 | 0.41 | 0.12 | 0.67 | 0.62 | 0.05 |
| N2 | 0.51 | 0.43 | 0.38 | 0.46 | −0.08 | 0.55 | 0.58 | −0.03 | 0.89 | 0.89 | 0 |
| N3 | 0.25 | 0.4 | 0.62 | 0.38 | 0.24 | 0.68 | 0.51 | 0.17 | 0.87 | 0.78 | 0.09 |
| N4 | 0.16 | 0.3 | 1.29 | 0.63 | 0.66 | 1.18 | 0.71 | 0.47 | 1.13 | 0.93 | 0.2 |
| N5 | 0.5 | 0.3 | 1.16 | 0.38 | 0.78 | 0.96 | 0.46 | 0.5 | 0.66 | 0.68 | −0.02 |
| Pairs | ||||||||
|---|---|---|---|---|---|---|---|---|
| E12 | 0.05 | 0.13 | 0.87 | 0.59 | 0.28 | 0.92 | 0.72 | 0.2 |
| E13 | 0.02 | 0.16 | 0.94 | 0.64 | 0.3 | 0.96 | 0.8 | 0.16 |
| E14 | 0.03 | 0.27 | 0.88 | 0.61 | 0.27 | 0.91 | 0.88 | 0.03 |
| E15 | 0.02 | 0.3 | 0.92 | 0.69 | 0.23 | 0.9 | 0.99 | −0.09 |
| S12 | 0.14 | 0.14 | 1.13 | 0.67 | 0.46 | 0.99 | 0.84 | 0.15 |
| S13 | 0.11 | 0.26 | 1.14 | 0.55 | 0.59 | 1.03 | 0.81 | 0.22 |
| S14 | 0.13 | 0.33 | 1.24 | 0.39 | 0.84 | 1.1 | 0.72 | 0.38 |
| S15 | 0.2 | 0.38 | 1.4 | 0.07 | 1.33 | 1.2 | 0.45 | 0.75 |
| N12 | 0.16 | 0.17 | 0.41 | 0.28 | 0.13 | 0.57 | 0.45 | 0.12 |
| N13 | 0.11 | 0.19 | 0.5 | 0.35 | 0.15 | 0.61 | 0.54 | 0.07 |
| N14 | 0.03 | 0.15 | 0.71 | 0.28 | 0.43 | 0.68 | 0.43 | 0.25 |
| N15 | 0.11 | 0.22 | 0.6 | 0.11 | 0.49 | 0.49 | −0.11 | 0.6 |
References
- Deser, C.; Alexander, M.A.; Xie, S.-P.; Phillips, A.S. Sea Surface Temperature Variability: Patterns and Mechanism. Annu. Rev. Mar. Sci. 2010, 2, 115–143. [Google Scholar] [CrossRef] [PubMed]
- Bulgin, C.E.; Merchant, C.J.; Ferreira, D. Tendencies, variability and persistence of sea surface temperature anomalies. Sci. Rep. 2020, 10, 7986. [Google Scholar] [CrossRef] [PubMed]
- Lopes, R.; Betrouni, N. Fractal and multifractal analysis: A review. Med. Image Anal. 2009, 13, 634–649. [Google Scholar] [CrossRef] [PubMed]
- Peng, C.-K.; Buldyrev, S.V.; Havlin, S.; Simons, M.; Stanley, H.E.; Goldberger, A.L. Mosaic organization of DNA nucleotides. Phys. Rev. E 1994, 49, 1685. [Google Scholar] [CrossRef] [PubMed]
- Kantelhardt, J.W.; Zschiegner, S.A.; Bunde, E.K.; Havlin, S.; Bunde, A.; Stanley, H.E. Multifractal detrended fluctuation anal-ysis of nonstationary time series. Phys. A 2002, 316, 87–114. [Google Scholar] [CrossRef]
- Podobnik, B.; Stanley, H.E. Detrended Cross-Correlation Analysis: A New Method for Analyzing Two Nonstationary Time Series. Phys. Rev. Lett. 2008, 100, 084102. [Google Scholar] [CrossRef] [PubMed]
- Gvozdanovic, I.; Podobnik, B.; Wang, D.; Eugene Stanley, H. 1/f behavior in cross-correlations between absolute returns in a US market. Phys. A 2012, 391, 2860–2866. [Google Scholar] [CrossRef]
- Horvatic, D.; Stanley, H.E.; Podobnik, B. Detrended cross-correlation analysis for non-stationary time series with periodic trends. Europhys. Lett. 2011, 94, 18007. [Google Scholar] [CrossRef]
- Marinho, E.B.S.; Sousa, A.M.Y.R.; Andrade, R.F.S. Using Detrended Cross-Correlation Analysis in geophysical data. Phys. A 2013, 392, 2195–2201. [Google Scholar] [CrossRef][Green Version]
- Shen, C.; Li, C.; Si, Y. A detrended cross-correlation analysis of meteorological and API data in Nanjing, China. Phys. A 2015, 419, 417–428. [Google Scholar] [CrossRef]
- Liao, W.; Wang, X.; Fan, Q.; Zhou, S.; Chang, M.; Wang, Z.; Wang, Y.; Tu, Q. Long-term atmospheric visibility, sunshine du-ration and precipitation trends in South China. Atmos. Environ. 2015, 107, 204–216. [Google Scholar] [CrossRef]
- Zhou, W.-X. Multifractal detrended cross-correlation analysis for two nonstationary signals. Phys. Rev. E 2008, 77, 066211. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; Ni, Z.; Ni, L. Multifractal detrended cross-correlation analysis between PM2.5 and meteorological factors. Phys. A 2015, 438, 114–123. [Google Scholar] [CrossRef]
- Hajian, S.; Movahed, M.S. Multifractal Detrended Cross-Correlation Analysis of sunspot numbers and river flow fluctuations. Phys. A 2010, 389, 4942–4957. [Google Scholar] [CrossRef]
- Cao, G.-X.; Cao, J.; Xu, L.-B.; He, L. Detrended cross-correlation analysis approach for assessing asymmetric multifractal detrended cross-correlations and their application to the Chinese financial market. Phys. A 2014, 393, 460–469. [Google Scholar] [CrossRef]
- Oswiecimka, P.; Drożdż, S.; Forczek, M.; Jadach, S.; Kwapień, J. Detrended cross-correlation analysis consistently extended to multifractality. Phys. Rev. E 2014, 89, 023305. [Google Scholar] [CrossRef] [PubMed]
- Park, K.; Chung, J.Y. Spatial and temporal scale variations of sea surface temperature in the East Sea using NOAA/AVHRR data. J. Oceanogr. 1999, 55, 271–288. [Google Scholar] [CrossRef]
- Park, W.-S.; Oh, I.S. Interannual and interdecadal variations of sea surface temperature in the East Asian marginal seas. Prog. Oceanogr. 2000, 47, 191–204. [Google Scholar] [CrossRef]
- Minobe, S.; Sako, A.; Nakamura, M. Interannual to interdecadal variability in the Japan Sea based on a new gridded upper water temperature dataset. J. Phys. Oceanogr. 2004, 34, 2382–2397. [Google Scholar] [CrossRef]
- Jeong, Y.; Nam, S.; Kwon, J.-I.; Uppara, U.; Jo, Y.-H. Surface warming slowdown with continued subsurface warming in the East Sea (Japan Sea) over recent decades, (2000–2014). Front. Mar. Sci. 2022, 9, 825368. [Google Scholar] [CrossRef]
- Kawamura, H.; Wu, P. Formation mechanism of Japan sea proper water in the flux center off Vladivostok. J. Geophys. Res. 1998, 103, 21611–21622. [Google Scholar] [CrossRef]
- Watanabe, T.; Hanawa, K.; Toba, Y. Analyses of year-to-year variation of water temperature along the coast of Japan Sea. Progr. Oceanogr. 1986, 17, 337–357. [Google Scholar] [CrossRef]
- Isoda, Y. Interannual SST variations to the north and south of the Polar front in the Japan Sea. La Mer 1994, 32, 285–293. [Google Scholar]
- Isoda, Y.; Korematsu, H. Interannual variation of water temperature, salinity, and oxygen vertical distribution in the Tsushima current region. Umi to Sora 1995, 71, 47–67. [Google Scholar]
- Ponomarev, V.I.; Dyakonova, I.; Palshin, N.; Rudykh, N.; Ishida, H. Multiscale Variability of oceanographic and meteoro-logical characteristics in the Japan (East) Sea area. In Past, Present and Future Environments of Pan-Japan Sea Region; Hayakawa, K., Ed.; MARUZEN Co., Ltd.: Kanazawa, Japan, 2006; pp. 407–417. [Google Scholar]
- Watanabe, Y.W.; Wakita, M.; Maeda, N.; Ono, T.; Gamo, T. Synchronous bidecadal periodic changes of oxygen phosphate and temperature between the Japan Sea deep water and the North Pacific intermediate water. Geophys. Res. Lett. 2003, 30, 2273. [Google Scholar] [CrossRef]
- Minobe, S. Interdecadal temperature variation of deep water in the Japan Sea (East Sea). In Proceedings of the Fourth Workshop CREAMS, R/V OKEAN, Vladivostok, Russia, 12–13 February 1996; pp. 81–88. [Google Scholar]
- Chu, P.C.; Chen, Y.; Lu, S. Temporal and spatial variabilities of Japan Sea surface temperature and atmospheric forcings. J. Oceanogr. 1998, 54, 273–284. [Google Scholar] [CrossRef]
- Dorman, C.E.; Friehe, C.A.; Khelif, D.; Scotti, A.; Edson, J.; Beardsley, R.C.; Limeburner, R.; Chen, S.S. Winter atmospheric conditions over the Japan/East Sea: The structure and impact of severe cold air outbreaks. Oceanography 2006, 19, 96–109. [Google Scholar] [CrossRef]
- Dorman, C.E.; Beardsley, R.C.; Dashko, N.A.; Friehe, C.A.; Kheilf, D.; Cho, K.; Limeburner, R.; Varlamov, S.M. Winter marine atmospheric conditions over the Japan Sea. J. Geophys. Res. Oceans 2004, 109, C12011. [Google Scholar] [CrossRef]
- Trusenkova, O.O.; Lobanov, V.B.; Kaplunenko, D.D. Variability of sea surface temperature in the Japan Sea and its relationship to the wind-curl field. Izv. Atmos. Ocean Phys. 2008, 44, 517. [Google Scholar] [CrossRef]
- Park, K.-A.; Park, J.-E.; Choi, B.-J.; Byun, D.-S.; Lee, E.-I. An Oceanic Current Map of the East Sea for Science Textbooks Based on Scientific Knowledge Acquired from Oceanic Measurements. Sea J. Korean Soc. Oceanogr. 2013, 18, 234–265. [Google Scholar]
- Kim, S.-Y.; Park, Y.-G.; Kim, Y.H.; Seo, S.; Jin, H.; Pak, G.; Lee, H.J. Origin, variability, and pathways of East Sea Intermediate Water in a high-resolution ocean reanalysis. J. Geophys. Res. Ocean. 2021, 126, e2020JC017158. [Google Scholar] [CrossRef]
- Ramirez, J.A.; Rodriguez, E.; Echeverria, J.C. A DFA approach for assessing asymmetric correlations. Phys. A 2009, 388, 2263–2270. [Google Scholar] [CrossRef]
- Cao, G.-X.; Cao, J.; Xu, L.-B. Asymmetric multifractal scaling behavior in the Chinese stock market: Based on asymmetric MF-DFA. Phys. A 2013, 392, 797–807. [Google Scholar] [CrossRef]
- Huang, B.; Liu, C.; Freeman, E.; Graham, G.; Smith, T.; Zhang, H.-M. Assessment and intercomparison of NOAA daily opti-mum interpolation sea surface temperature (DOISST) version 2.1. J. Clim. 2021, 34, 7421–7441. [Google Scholar] [CrossRef]
- Reynolds, R.W.; Smith, T.M.; Liu, C.; Chelton, D.B.; Casey, K.S.; Schlax, M.G. Daily high-resolution-blended analyses for sea surface temperature. J. Clim. 2007, 20, 5473–5496. [Google Scholar] [CrossRef]
- Farge, M. Wavelet transforms and their applications to turbulence. Annu. Rev. Fluid Mech. 1992, 24, 395–457. [Google Scholar] [CrossRef]
- Torrence, C.; Compo, G. A practical guide to wavelet analysis. Bull. Am. Meteorol. Soc. 1998, 79, 61–78. [Google Scholar] [CrossRef]
- Grinsted, A.; Moore, J.C.; Jevrejeva, S. Application of the cross wavelet transform and wavelet coherence to geophysical time series. Nonlin. Processes Geophys. 2004, 11, 561–566. [Google Scholar] [CrossRef]
- Wu, S.; Liu, Q. Some problems on the global wavelet spectrum. J. Ocean Univ. China 2005, 4, 398–402. [Google Scholar] [CrossRef]
- Jiang, Z.-Q.; Xie, W.-J.; Zhou, W.-X.; Sornette, D. Multifractal analysis of financial markets: A review. Rep. Prog. Phys. 2019, 82, 125901. [Google Scholar] [CrossRef]
- Gu, R.B.; Shao, Y.M.; Wang, Q.N. Is the efficiency of stock market correlated with multifractality? An evidence from the Shanghai stock market. Phys. A 2013, 392, 361–370. [Google Scholar] [CrossRef]
- Gu, R.B.; Zhang, B. Is efficiency of crude oil market affected by multifractality? Evidence from the WTI crude oil market. Energy Econ. 2016, 53, 151–158. [Google Scholar] [CrossRef]
- Lim, G.; Park, J.-J. Intrinsic Mode-Based Network Approach to Examining Multiscale Characteristics of Sea Surface Temperature Variability. Appl. Sci. 2024, 14, 1752. [Google Scholar] [CrossRef]
- Park, K.-A.; Chung, J.Y.; Kim, K. Sea surface temperature fronts in the East (Japan) Sea and temporal variations. Geophys. Res. Lett. 2004, 31, L07304. [Google Scholar] [CrossRef]
- Song, S.-Y.; Kim, Y.-J.; Lee, E.-J.; Yeh, S.-W.; Park, J.-H.; Park, Y.-G. Wintertime sea surface temperature variability modulated by Arctic Oscillation in the northwestern part of the East/Japan Sea and its relationship with marine heatwaves. Front. Mar. Sci. 2023, 10, 1198418. [Google Scholar] [CrossRef]
- Park, K.-A.; Ullman, D.S.; Kim, K.; Chung, J.Y.; Kim, K.-R. Spatial and temporal variability of satellite-observed Subpolar Front in the East/Japan Sea. Deep Res. Part I Oceanogr. Res. Pap. 2007, 54, 453–470. [Google Scholar] [CrossRef]
- Yoon, S.-T.; Park, J.-J. Warm bias of cold sea surface temperatures in the East Sea (Japan Sea). Front. Mar. Sci. 2022, 9, 923093. [Google Scholar] [CrossRef]


| Location | Crossover Behavior | ||||
|---|---|---|---|---|---|
| E1 | 0.93 | 1.04 | 1.4 | 0.47 | not clear |
| E2 | 0.96 | 1.07 | 1.3 | 0.34 | not clear |
| E3 | 0.84 | 0.96 | 1.22 | 0.38 | not clear |
| E4 | 0.83 | 0.98 | 1.33 | 0.5 | not clear |
| E5 | 0.76 | 0.92 | 1.2 | 0.44 | not clear |
| S1 | 0.86 | 0.98 | 1.19 | 0.33 | not clear |
| S2 | 0.79 | 0.93 | 1.22 | 0.43 | weak |
| S3 | 0.75 | 0.9 | 1.3 | 0.55 | strong |
| S4 | 0.64 | 0.84 | 1.29 | 0.65 | strong |
| S5 | 0.65 | 0.84 | 1.32 | 0.67 | strong |
| N1 | 0.82 | 0.96 | 1.19 | 0.37 | weak |
| N2 | 0.89 | 0.98 | 1.24 | 0.35 | not clear |
| N3 | 0.82 | 0.94 | 1.09 | 0.27 | weak |
| N4 | 0.81 | 0.95 | 1.22 | 0.41 | moderate |
| N5 | 0.65 | 0.84 | 1.32 | 0.67 | strong |
| Location | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| E1 | 0.55 | 0.42 | 0.86 | 0.96 | 0.1 | 0.99 | 1.09 | 0.1 | 1.41 | 1.38 | 0.03 |
| E2 | 0.37 | 0.36 | 0.95 | 0.93 | 0.02 | 1.08 | 1.03 | 0.05 | 1.32 | 1.29 | 0.03 |
| E3 | 0.44 | 0.4 | 0.85 | 0.8 | 0.05 | 0.99 | 0.93 | 0.06 | 1.29 | 1.2 | 0.09 |
| E4 | 0.54 | 0.39 | 0.79 | 0.88 | −0.09 | 0.97 | 0.99 | −0.02 | 1.33 | 1.27 | 0.05 |
| E5 | 0.39 | 0.48 | 0.78 | 0.74 | 0.04 | 0.93 | 0.92 | 0.01 | 1.17 | 1.22 | −0.05 |
| S1 | 0.39 | 0.29 | 0.81 | 0.91 | −0.1 | 0.96 | 1 | −0.04 | 1.2 | 1.2 | 0 |
| S2 | 0.43 | 0.45 | 0.79 | 0.79 | 0 | 0.92 | 0.94 | −0.02 | 1.22 | 1.24 | −0.02 |
| S3 | 0.53 | 0.56 | 0.73 | 0.78 | −0.05 | 0.89 | 0.9 | −0.01 | 1.26 | 1.34 | −0.08 |
| S4 | 0.66 | 0.65 | 0.64 | 0.65 | −0.01 | 0.85 | 0.84 | 0.01 | 1.3 | 1.3 | 0 |
| S5 | 0.61 | 0.71 | 0.68 | 0.65 | 0.03 | 0.85 | 0.83 | 0 | 1.29 | 1.36 | −0.07 |
| N1 | 0.37 | 0.38 | 0.81 | 0.86 | −0.05 | 0.93 | 0.98 | −0.05 | 1.18 | 1.27 | −0.06 |
| N2 | 0.38 | 0.32 | 0.9 | 0.88 | 0.02 | 0.97 | 0.98 | −0.01 | 1.28 | 1.2 | 0.08 |
| N3 | 0.29 | 0.43 | 0.83 | 0.76 | 0.07 | 0.94 | 0.92 | 0.02 | 1.12 | 1.19 | −0.07 |
| N4 | 0.38 | 0.46 | 0.82 | 0.77 | 0.05 | 0.97 | 0.93 | 0.04 | 1.2 | 1.23 | −0.03 |
| N5 | 0.61 | 0.71 | 0.68 | 0.65 | 0.03 | 0.85 | 0.85 | 0 | 1.29 | 1.36 | −0.07 |
| Location | Small Scales from 10 to 1000 Days | Large Scales from 1000 to 5000 Days | ||||
|---|---|---|---|---|---|---|
| E12 | 0.93 | 1.07 | 0.14 | 0.88 | 0.93 | 0.05 |
| E13 | 0.83 | 1 | 0.17 | 0.96 | 1 | 0.04 0.08 |
| E14 | 0.81 | 0.99 | 0.17 | 0.88 | 0.96 | |
| E15 | 0.77 | 0.99 | 0.22 | 0.95 | 0.99 | 0.04 |
| S12 | 0.82 | 1 | 0.18 | 1.13 | 0.98 | 0.15 |
| S13 | 0.73 | 0.94 | 0.21 | 1.11 | 1 | 0.11 |
| S14 | 0.66 | 0.87 | 0.21 | 1.2 | 1.08 | 0.12 |
| S15 | 0.66 | 0.88 | 0.22 | 1.35 | 1.19 | 0.16 |
| N12 | 0.87 | 0.99 | 0.12 | 0.39 | 0.54 | 0.15 |
| N13 | 0.79 | 0.94 | 0.15 | 0.52 | 0.64 | 0.12 |
| N14 | 0.76 | 0.95 | 0.19 | 0.69 | 0.69 | 0 |
| N15 | 0.73 | 0.93 | 0.2 | 0.56 | 0.41 | 0.15 |
| Pairs | ||||||||
|---|---|---|---|---|---|---|---|---|
| E12 | 0.13 | 0.17 | 0.92 | 0.92 | 0 | 1.05 | 1.09 | −0.04 |
| E13 | 0.15 | 0.2 | 0.85 | 0.79 | 0.06 | 1 | 0.99 | 0.01 |
| E14 | 0.18 | 0.17 | 0.79 | 0.85 | −0.06 | 0.97 | 1.02 | −0.05 |
| E15 | 0.21 | 0.22 | 0.77 | 0.78 | −0.01 | 0.98 | 1 | −0.02 |
| S12 | 0.17 | 0.19 | 0.79 | 0.84 | −0.05 | 0.96 | 1.03 | −0.07 |
| S13 | 0.21 | 0.19 | 0.68 | 0.81 | −0.13 | 0.89 | 1 | −0.11 |
| S14 | 0.21 | 0.19 | 0.61 | 0.74 | −0.13 | 0.82 | 0.93 | −0.11 |
| S15 | 0.22 | 0.2 | 0.61 | 0.74 | −0.13 | 0.83 | 0.94 | −0.11 |
| N12 | 0.1 | 0.13 | 0.86 | 0.88 | −0.02 | 0.96 | 1.01 | −0.05 |
| N13 | 0.12 | 0.19 | 0.8 | 0.76 | 0.04 | 0.92 | 0.95 | −0.03 |
| N14 | 0.17 | 0.19 | 0.76 | 0.78 | −0.02 | 0.93 | 0.97 | −0.04 |
| N15 | 0.18 | 0.2 | 0.74 | 0.72 | 0.02 | 0.92 | 0.92 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lim, G.; Park, J.-J. Auto- and Cross-Correlation Multifractal Analysis of Sea Surface Temperature Variability. Fractal Fract. 2024, 8, 239. https://doi.org/10.3390/fractalfract8040239
Lim G, Park J-J. Auto- and Cross-Correlation Multifractal Analysis of Sea Surface Temperature Variability. Fractal and Fractional. 2024; 8(4):239. https://doi.org/10.3390/fractalfract8040239
Chicago/Turabian StyleLim, Gyuchang, and Jong-Jin Park. 2024. "Auto- and Cross-Correlation Multifractal Analysis of Sea Surface Temperature Variability" Fractal and Fractional 8, no. 4: 239. https://doi.org/10.3390/fractalfract8040239
APA StyleLim, G., & Park, J.-J. (2024). Auto- and Cross-Correlation Multifractal Analysis of Sea Surface Temperature Variability. Fractal and Fractional, 8(4), 239. https://doi.org/10.3390/fractalfract8040239






