Abstract
This paper applies fractional calculus to a practical example in fluid mechanics, illustrating its impact beyond traditional integer order calculus. We focus on the classic problem of a rigid body rotating within a uniformly rotating container, which generates a liquid vortex from an undisturbed initial state. Our aim is to compare the time evolutions of the physical system in fractional and integer order models by examining the torque transmission from the rotating body to the surrounding liquid. This is achieved through closed-form, time-developing solutions expressed in terms of Mittag–Leffler and Bessel functions. Analysis reveals that the rotational velocity and, consequently, the vortex structure of the liquid are influenced by three distinct time zones that differ between integer and noninteger models. Anomalous diffusion, favoring noninteger fractions, dominates at early times but gradually gives way to the integer derivative model behavior as time progresses through a transitional regime. Our derived vortex formula clearly demonstrates how the liquid vortex is regulated in time for each considered fractional model.
1. Introduction
The anomalous diffusion observed in various physical, biological, and chemical systems cannot be fully captured by the standard integer derivative diffusion model. This limitation motivates researchers to explore alternative approaches [1,2]. One promising approach involves replacing the integer order derivative with a fractional order derivative. The nonlocal and memory-preserving properties of fractional derivatives are believed to better explain anomalous diffusion under certain conditions [3,4]. This study applies this concept to analyze the diffusion process and liquid vortex formation within a uniformly rotating container using fractional order derivatives in the Caputo sense.
Since fractional calculus is rapidly growing recently with the old models replaced by fractional ones in the light of a diverse choice of fractional derivative definitions, we mainly concentrate on recent studies. For instance, anomalous diffusion processes were investigated by means of fractional models in oil pollution [5], in tumor growth and oncological particularities [6,7], in antioxidant vegetable [8], in the voltage regulator of the power industry [9], in nuclear neutron transport [10], in enhancing low-frequency signal [11], in computer vision [12], in radioactive and transmutation linear chains [13], in optimizing current sequences in lithium-ion batteries [14,15], in structural analysis creep [16], in the transmission dynamics of Nipah virus [17], in chronic hepatitis B–related liver fibrosis [18], in cytokeratin [19], in the link formation of temporal networks [20], in slow decay phenomena of the Tesla Model S battery [21], in the slip flow of nanoparticles [22], and in the ultrasonic propagation of wave in a fractal porous material [23], among many others.
Since fractional order models are more complex than the classical integer order model, new and powerful solution techniques are also of the current focus. Analytical means of solutions include integral transforms via Laplace, Fourier, Mellin, and Mikusinski transforms, as can be referred to in [24,25]. Numerical ways of obtaining fractional solutions include the finite element solution of softening nonlocal response in a plate [26], the flower pollination algorithm [27], the shift Chebyshev-tau method in the evolution of a chaotic economic system [28], meshless methods [29], implicit differencing [30], the power series method [31], the optimal Adomian decomposition method [32], the optimal variational iteration method [33], and the hybrid local fractional technique based on homotopy and integral transform methods [34], among others.
While traditional time-developing models can be readily converted to fractional order models, grasping the underlying mechanisms of anomalous diffusion remains challenging. This study addresses this gap by focusing on a classic fluid mechanics problem: the vortex generation phenomenon induced by a rotating cylinder. The main objective is to shed light on competing time regimes and their influence on vortex formation. Therefore, we analyze this problem within the framework of a fractional order model using Caputo derivatives. The comparison between fractional and integer order models, the utilization of closed-form solutions involving Mittag–Leffler and Bessel functions, and the analysis of rotational velocity and vortex structure are well articulated. Specifically, leveraging exact analytical solutions obtained through Mittag–Leffler and Bessel functions, we shed light on the early, transitional, and late diffusion time regimes during vortex formation.
2. Vortex Generation Due to a Rotating Body of Liquid in Fractional Models
We are interested in axisymmetric torsional flow, i.e., in the motion of liquid in a cylinder of radius R rotating with a uniform angular velocity ; refer to the flow configuration in Figure 1.
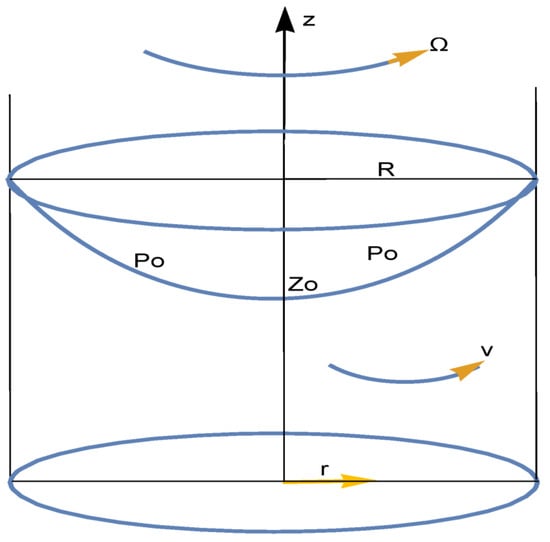
Figure 1.
Vortex generation in a rotating cylindrical container.
The methodology involves the conversion of the nonstationary integer order model to a fractional order initial value problem. Hence, the encapsulated liquid, taken as Newtonian with density and viscosity , is initially at rest governed by unidirectional transient flow equations and relevant initial and boundary conditions:
The flow of motion represented by system (1) matching to the integer derivative case can be recovered in many fluid dynamics textbooks; see, for instance, [35] (page 87, Section 3). Here, v and p are the rotational velocity and pressure of the liquid inside the body of rotation, which are made dimensionless in accordance with the scalings:
Moreover, the fractional order derivative with respect to power () is taken in the Caputo sense according to the definition [36]:
where denotes the gamma function. For the corresponding Riemann–Liouville fractional integral and other fractional features, one can look in [4]. One important function to be employed during the solution of fractional model (1) will be the so-called Mittag–Leffler function, whose definition is as follows [37]:
For the unsteady formation of a free surface or liquid vortex, at , the liquid is set into motion after the cylinder starts rotating about its axis with a constant angular velocity, and this transient, axisymmetric torsional flow can be solved by first finding the steady-state solution, which is as follows:
where is the elevation of the free surface at , and is the atmospheric pressure there. It is noted that the generated liquid vortex has a natural parabolic formula:
Later on, adding the steady and transient solutions, we form the following:
and with the help of a separable solution format,
the subsequent boundary value problem is established:
The eigenvalues are due to the solutions in (9), which can be accessed from the roots of a Bessel function:
Ten sample eigenvalues are given in Table 1, which are used in the present analysis.

Table 1.
First ten eigenvalues from (10).
Simultaneously, the time solution in (9) can be evaluated as follows:
As a result of the superposition of the obtained discrete solutions in (9), the following series solution is constructed:
where the coefficients can be determined from the initial condition and orthogonality properties of Bessel functions:
Hence, the free surface occurs at with the following liquid vortex formula:
3. Results and Discussion
The phenomenon of liquid vortex generation under the Caputo model of a fractional derivative will be exploited in this section with various fractional order derivatives.
It is previously noted that Figure 2 evidences how fractional order vortex velocities will be generated during the steady state from time fractions to , which are computed from the exact solutions:
in which is the Bessel function of the second kind. Even though the physical validity of the limiting case is questionable, Figure 2 is significant to demonstrate the fact that a fractional order model does not yield a much deviating circumferential vortex structure from the classical integer order model in the time-independent flow limit.
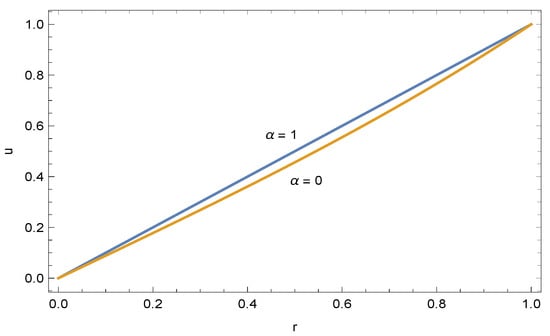
Figure 2.
Steady-state swirling velocity of the liquid vortex for models corresponding to and .
Next, the time development of the vortex speed inside the swirling tank for varying fractional order derivatives ranging from to is clarified. For this purpose, Figure 3a–d display the time evolution of diffusion starting from the quiescent flow up to the fully developed flow as a consequence of the sudden revolution of the cylindrical medium. Early on, transitional and fully set-up time regimes are exhibited at each fractional order depicted. The traditional integer order model produces the swirl velocities in time, as shown in Figure 3a, which can be found in many fluid mechanics books; see, for instance, [35]. Physically, the liquid vortex is generated as a result of the transmitted torque of the rotating cylinder to the liquid inside. Because of rigid body motion, the linear velocity distribution is achieved quickly as early as time from the start up. Anomalous diffusion is observed, on the other hand, for the fractional order derivative models in Figure 3b–d. As the fractional order decreases, a fast diffusion process occurs at early times, at which the torque of the rotating cylinder is transmitted to the liquid inside at an enhanced pace. This is compensated by a delayed diffusion at later times such that the occurrence of steady state is as early as time 1 for the integer order model, as opposed to the fractional order models for which the steady state is decelerated.
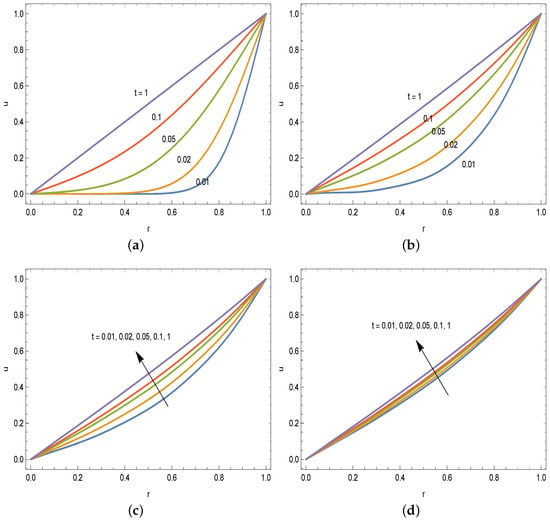
Figure 3.
Individual fractional order models with (a) , (b) , (c) , and (d) , and time evolution of tangential speed from the start up.
Early on, transitional and future time diffusions are better visualized from Figure 4a–d, in which the comparative time progression is shown among the chosen fractional order models. Anomaly in the diffusion in the early time zone is clearly scrutinized in Figure 4a,b wherein an increased torque transfer takes place. As time reaches around (refer to Figure 4c), the diffusion seems to settle for all fractional order models, pointing to a transition zone and an equal amount of torque transfer. At future times, competing diffusion is reversed now from a noninteger to an integer order model, having passed the transitional zone, and the diffusion (and thus the torque transfer) progresses to the steady time limit in Figure 4d in line with Figure 2.
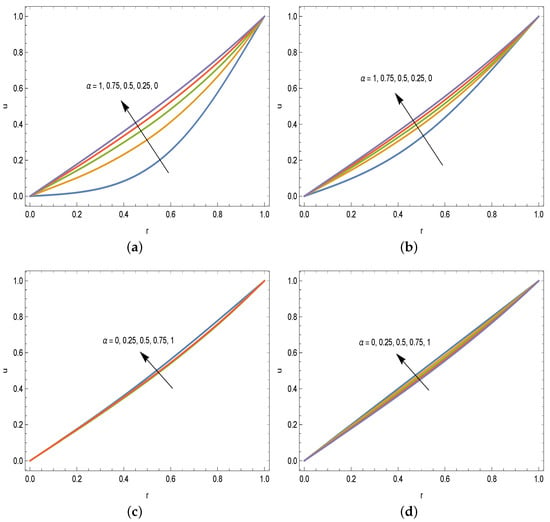
Figure 4.
Fractional time vortex velocities with different fractional time derivatives: (a) , (b) , (c) , and (d) .
Even though a physical explanation is an open question for the relation between the torque transfer and the order of fraction of the fractional model, one can anticipate the time developing wall skin friction in the spotted time regimes in Figure 5, which is evaluated from the following formula:
The competing time zones between the integer and fractional order models are apparent in Figure 5.
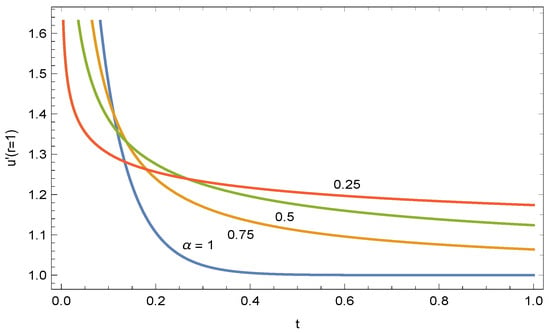
Figure 5.
Shear stress at the wall of the cylindrical container and fractional progress.
The free surface formation from the startup to the final steady state is then revealed in the three-dimensional Figure 6a–d obtained only from the dominant eigenvalue , making use of the following analytic formula:
The wiggly start of the figures at time zero will be attenuated by adding more terms into the series. Apart from that, the continuous time evolution of the vortex is vividly approximated. Together with these, Figure 7a–d further demonstrate the vortex formation inside the rotating tank from the full model. It is clear from Figure 6 and Figure 7 that vortex formation is rapid at early time stages for fractional orders rather than the integer order. At about , a transitional behavior is observed, and afterwards, an integer order model yields an accelerated vortex formation, in parallel with the earlier discussion on the vortex velocity distribution.
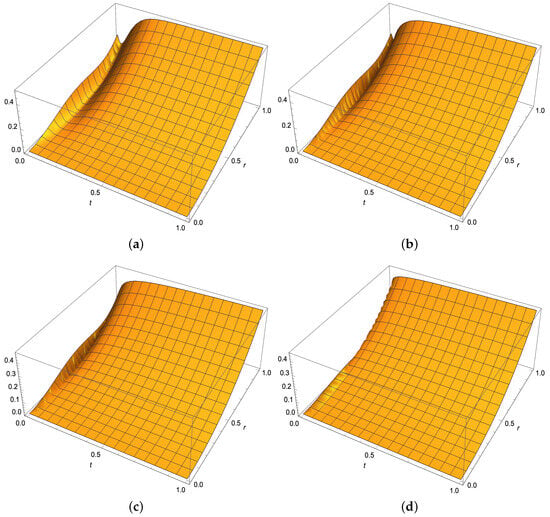
Figure 6.
Three-dimensional vortex shape formation from the dominant eigenvalue formula (17): (a) , (b) , (c) , and (d) .
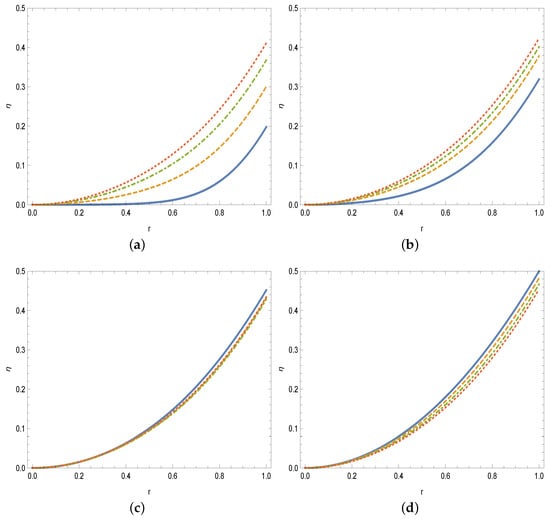
Figure 7.
Vortex shape formation from the full formula (14) at four fractional order models: unbroken , dashed , dot-dashed , and dotted ; (a) , (b) , (c) , and (d) .
The time development of a vortex at the contact of the surface in different fractional models is ultimately exhibited in Figure 8, which better summarizes each determined time zone in the fractional order models and the mutual vortex formation phenomenon. Hence, the background of a diffusion phenomenon and its possible implications for theory and practice are disclosed within the framework of the Caputo fractional derivative concept.
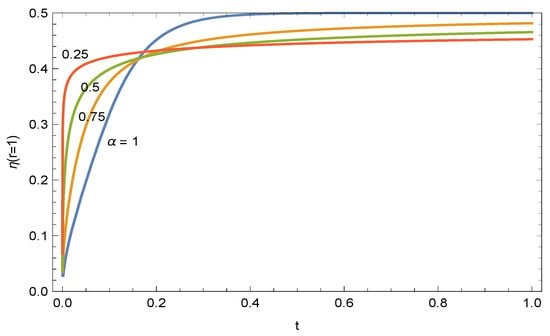
Figure 8.
Time progress of vortex at the wall.
4. Conclusions
The recent trend of converting integer order models to fractional order models in diverse fields raises challenges in interpreting the resulting time evolution. This study addresses this gap by revisiting a classic fluid mechanics problem: vortex formation within a cylindrical container driven by a rotating body [1]. We substitute the integer order time derivative with Caputo fractional derivatives to understand how this modification affects the physical phenomenon of torque transmission to the liquid. Our aim is to shed light on the competing time regimes present in the fractional order model.
First, we convert the nonstationary integer order model to a fractional order initial value problem. Analytical solutions are then obtained using Mittag–Leffler and Bessel functions, revealing that steady-state vortex velocities within the container span the range between zero and unity order fractional values.
Further analysis shows that the circumferential velocity and, consequently, the vortex structure are influenced by three distinct time zones bridging the integer and noninteger models. Early on, we observe anomalous diffusion, where the torque from the rotating body rapidly transmits to the surrounding liquid, leading to a faster fluid rotation and accelerated vortex formation in noninteger models. Around a dimensionless time of 0.2, the system dynamics become independent of the fractional order, transitioning back to the integer model behavior. As time progresses, diffusion decelerates for noninteger models while accelerating for the integer model. Our derived approximate and exact formulas within the fractional framework facilitate the analysis of free surface layer formation and vortex structure evolution.
Author Contributions
Conceptualization, M.T.; methodology, M.T.; software, M.T.; validation, M.T.; formal analysis, M.T.; investigation, M.T. and A.S.A.; resources, M.T.; data curation, M.T. and A.S.A.; writing—original draft preparation, M.T.; writing—review and editing, M.T.; visualization, M.T. and A.S.A.; supervision, M.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data can be obtained upon reasonable request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Sun, H.G.; Zhang, Y.; Baleanu, D.; Chen, W.; Chen, Y. A new collection of real world applications of fractional calculus in science and engineering. Commun. Nonlinear Sci. Numer. Simul. 2018, 64, 213–231. [Google Scholar] [CrossRef]
- Turkyilmazoglu, M.; Altanji, M. Fractional models of falling object with linear and quadratic frictional forces considering Caputo derivative. Chaos Solitons Fractals 2023, 166, 112980. [Google Scholar] [CrossRef]
- Ma, L.; Li, J. A bridge on Lomnitz type creep laws via generalized fractional calculus. Appl. Math. Model. 2023, 116, 786–798. [Google Scholar] [CrossRef]
- Turkyilmazoglu, M. Transient and passage to steady state in fluid flow and heat transfer within fractional models. Int. Numer. Methods Heat Fluid Flow 2023, 33, 728–750. [Google Scholar] [CrossRef]
- Patel, H.S.; Patel, T.; Pandit, D. An efficient technique for solving fractional-order diffusion equations arising in oil pollution. J. Ocean Eng. Sci. 2022, 8, 1–10. [Google Scholar] [CrossRef]
- Valentim, C.A.; Rabi, J.A.; David, S.A. Fractional Mathematical Oncology: On the potential of non-integer order calculus applied to interdisciplinary models. Biosystems 2021, 204, 104377. [Google Scholar] [CrossRef]
- Keshavarz, M.; Qahremani, E.; Allahviranloo, T. Solving a fuzzy fractional diffusion model for cancer tumor by using fuzzy transforms. Fuzzy Sets Syst. 2022, 443, 198–220. [Google Scholar] [CrossRef]
- Granella, S.J.; Bechlin, T.R.; Christ, D. Moisture diffusion by the fractional-time model in convective drying with ultrasound-ethanol pretreatment of banana slices. Innov. Food Sci. Emerg. Technol. 2022, 76, 102933. [Google Scholar] [CrossRef]
- Sowa, M.; Majka, L.; Wajda, K. Excitation system voltage regulator modeling with the use of fractional calculus. AEU Int. Electron. Commun. 2023, 159, 154471. [Google Scholar] [CrossRef]
- Roul, P.; Rohil, V.; Espinosa-Paredes, G.; Obaidurrahman, K. Numerical simulation of two-dimensional fractional neutron diffusion model describing dynamical behaviour of sodium-cooled fast reactor. Ann. Nucl. Energy 2022, 166, 108709. [Google Scholar] [CrossRef]
- Shaw, S.; Whiteman, J.R. Approximate Fourier series recursion for problems involving temporal fractional calculus. Comput. Methods Appl. Mech. Eng. 2022, 402, 115537. [Google Scholar] [CrossRef]
- Arora, S.; Mathur, T.; Agarwal, S.; Tiwari, K.; Gupta, P. Applications of fractional calculus in computer vision: A survey. Neurocomputing 2022, 489, 407–428. [Google Scholar] [CrossRef]
- Cruz-Lopez, C.A.; Espinosa-Paredes, G.; Francois, J.L. Development of the General Bateman Solution using fractional calculus: A theoretical and algorithmic approach. Comput. Phys. Commun. 2022, 273, 108268. [Google Scholar] [CrossRef]
- Guo, R.; Shen, W. Online state of charge and state of power co-estimation of lithium-ion batteries based on fractional-order calculus and model predictive control theory. Appl. Energy 2022, 327, 120009. [Google Scholar] [CrossRef]
- Liu, Z.; Chen, S.; Jing, B.; Yang, C.; Ji, J.; Zhao, Z. Fractional variable-order calculus based state of charge estimation of Li-ion battery using dual fractional order Kalman filter. J. Energy Storage 2022, 52, 104685. [Google Scholar] [CrossRef]
- Ribeiro, J.G.T.; Castro, J.T.P.; Meggiolaro, M.A. Modeling concrete and polymer creep using fractional calculus. J. Mater. Technol. 2021, 12, 1184–1193. [Google Scholar] [CrossRef]
- Baleanu, D.; Shekari, P.; Torkzadeh, L.; Ranjbar, H.; Jajarmi, A.; Nouri, K. Stability analysis and system properties of Nipah virus transmission: A fractional calculus case study. Chaos Solitons Fractals 2023, 166, 112990. [Google Scholar] [CrossRef]
- Sheng, R.; Zhang, Y.; Sun, W.; Ji, Y.; Zeng, M.; Yao, X.; Dai, Y. Staging Chronic Hepatitis B Related Liver Fibrosis with a Fractional Order Calculus Diffusion Model. Acad. Radiol. 2022, 29, 951–963. [Google Scholar] [CrossRef] [PubMed]
- Guo, Y.; Chen, J.; Zhang, Y.; Guo, Y.; Jiang, M.; Dai, Y.; Yao, X. Differentiating Cytokeratin 19 expression of hepatocellular carcinoma by using multi-b-value diffusion-weighted MR imaging with mono-exponential, stretched exponential, intravoxel incoherent motion, diffusion kurtosis imaging and fractional order calculus models. Eur. J. Radiol. 2022, 150, 110237. [Google Scholar]
- Rabbani, F.; Khraisha, T.; Abbasi, F.; Jafari, G.R. Memory effects on link formation in temporal networks: A fractional calculus approach. Phys. A Stat. Mech. Appl. 2021, 564, 125502. [Google Scholar] [CrossRef]
- Cai, R.Y.; Chen, Y.Q.; Chen, Y.Q.; Kou, C.H. NILT and Prony technique for new definitions of fractional calculus for modeling very slow decay phenomena. IFAC—PapersOnLine 2020, 53, 3689–3694. [Google Scholar] [CrossRef]
- Hejazi, H.A.; Khan, M.I.; Raza, A.; Smida, K.; Khan, S.U.; Tlili, I. Inclined surface slip flow of nanoparticles with subject to mixed convection phenomenon: Fractional calculus applications. J. Indian Chem. Soc. 2022, 99, 100564. [Google Scholar] [CrossRef]
- Fellah, Z.E.A.; Fellah, M.; Ogam, E.; Berbiche, A.; Depollier, C. Reflection and transmission of transient ultrasonic wave in fractal porous material: Application of fractional calculus. Wave Motion 2021, 106, 102804. [Google Scholar] [CrossRef]
- Costa, F.S.; Oliveira, E.C.; Plata, A.R.G. Fractional Diffusion with Time-Dependent Diffusion Coefficient. Rep. Math. Phys. 2021, 87, 59–79. [Google Scholar] [CrossRef]
- Fahad, H.M.; Fernandez, A. Operational calculus for Caputo fractional calculus with respect to functions and the associated fractional differential equations. Appl. Math. Comput. 2021, 409, 126400. [Google Scholar] [CrossRef]
- Patnaik, S.; Sidhardh, S.; Semperlotti, F. Geometrically nonlinear analysis of nonlocal plates using fractional calculus. Int. J. Mech. Sci. 2020, 179, 105710. [Google Scholar] [CrossRef]
- Yousri, D.; AbdElaziz, M.; Mirjalilic, S. Fractional-order calculus-based flower pollination algorithm with local search for global optimization and image segmentation. Knowl.-Based Syst. 2020, 197, 105889. [Google Scholar] [CrossRef]
- Wang, H.; Weng, C.; Song, Z.; Cai, J. Research on the law of spatial fractional calculus diffusion equation in the evolution of chaotic economic system. Chaos Solitons Fractals 2020, 131, 109462. [Google Scholar] [CrossRef]
- Bavi, O.; Hosseininia, M.; Heydari, M.M.; Bavi, N. SARS-CoV-2 rate of spread in and across tissue, groundwater and soil: A meshless algorithm for the fractional diffusion equation. Eng. Anal. Bound. Elem. 2022, 138, 108–117. [Google Scholar] [CrossRef]
- Ali, U.; Iqbal, A.; Sohail, M.; Abdullah, F.A.; Khan, Z. Compact implicit difference approximation for time-fractional diffusion-wave equation. Alex. Eng. J. 2022, 61, 4119–4126. [Google Scholar] [CrossRef]
- Cheng, X.; Wang, L.; Hou, J. Solving time fractional Keller–Segel type diffusion equations with symmetry analysis, power series method, invariant subspace method and q-homotopy analysis method. Chin. J. Phys. 2022, 77, 1639–1653. [Google Scholar] [CrossRef]
- Turkyilmazoglu, M. An Efficient Computational Method for Differential Equations of Fractional Type. CMES Comput. Model. Ineng. Sci. 2022, 133, 47–65. [Google Scholar] [CrossRef]
- Ibraheem, G.H.; Turkyilmazoglu, M.; AL-Jawary, M.A. Novel approximate solution for fractional differential equations by the optimal variational iteration method. J. Comput. Sci. 2022, 64, 101841. [Google Scholar] [CrossRef]
- Kumar, D.; Dubey, V.P.; Dubey, S.; Singh, J.; Alshehri, A.M. Computational analysis of local fractional partial differential equations in realm of fractal calculus. Chaos Solitons Fractals 2023, 167, 113009. [Google Scholar] [CrossRef]
- Schlichting, H. Boundary Layer Theory; McGraw-Hill: New York, NY, USA, 1979. [Google Scholar]
- Das, S. Functional Fractional Calculus for System Identification and Controls, 2nd ed.; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 2011. [Google Scholar]
- Agarwal, P.; Milovanovic, G.V.; Nisar, S.K. A Fractional Integral Operator Involving the Mittag-Leffler Type with Four Parameters. Facta Univ. Ser. Math. Inform. 2015, 30, 597–605. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).