An Error Analysis Study for the Distributed-Order Time-Fraction Model Using an Efficient Numerical Method
Abstract
1. Introduction
2. Preliminaries
3. Construction of the Approximate Function
4. Explain Approximation Solution for fKdV Using the Proposed Method
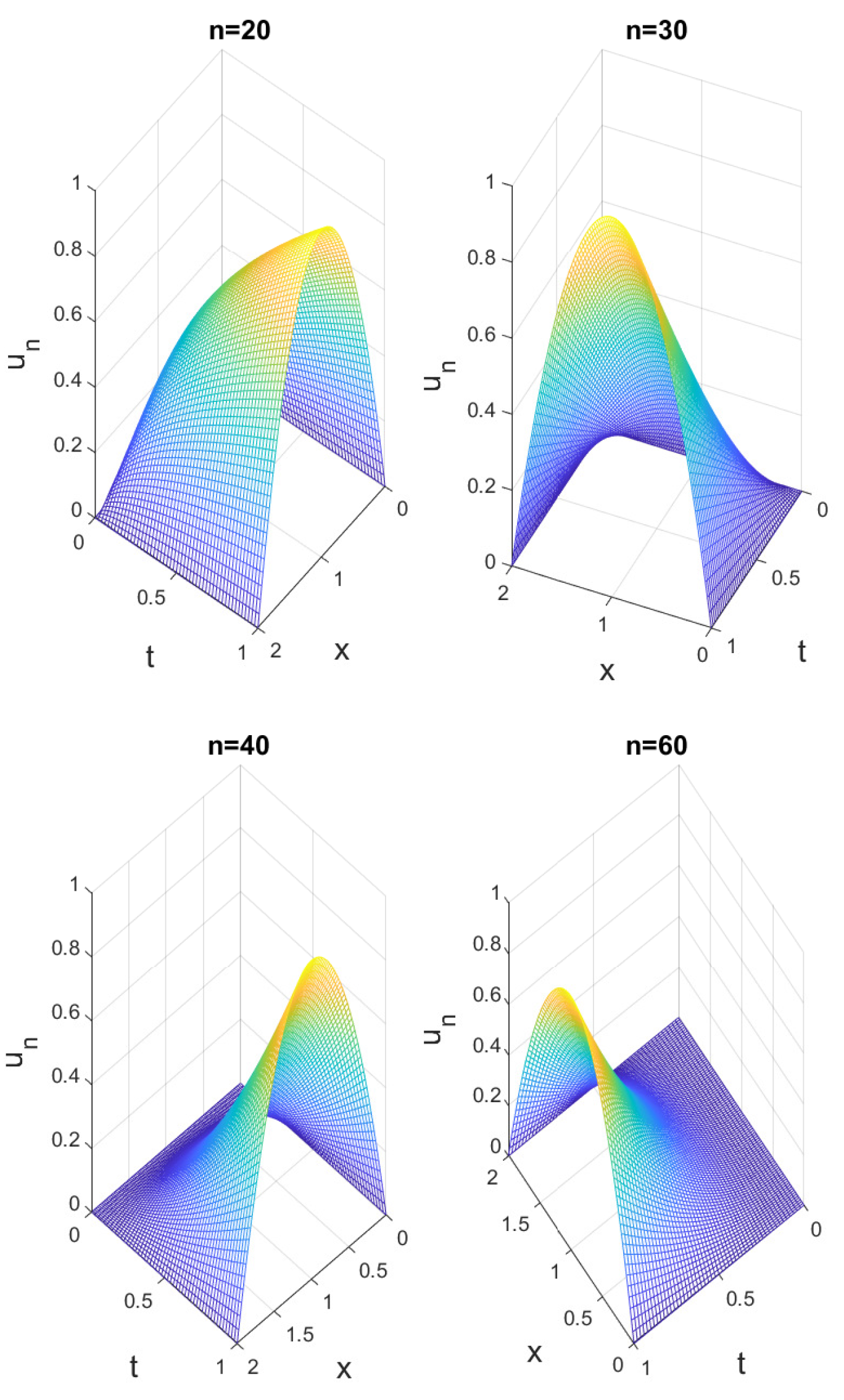
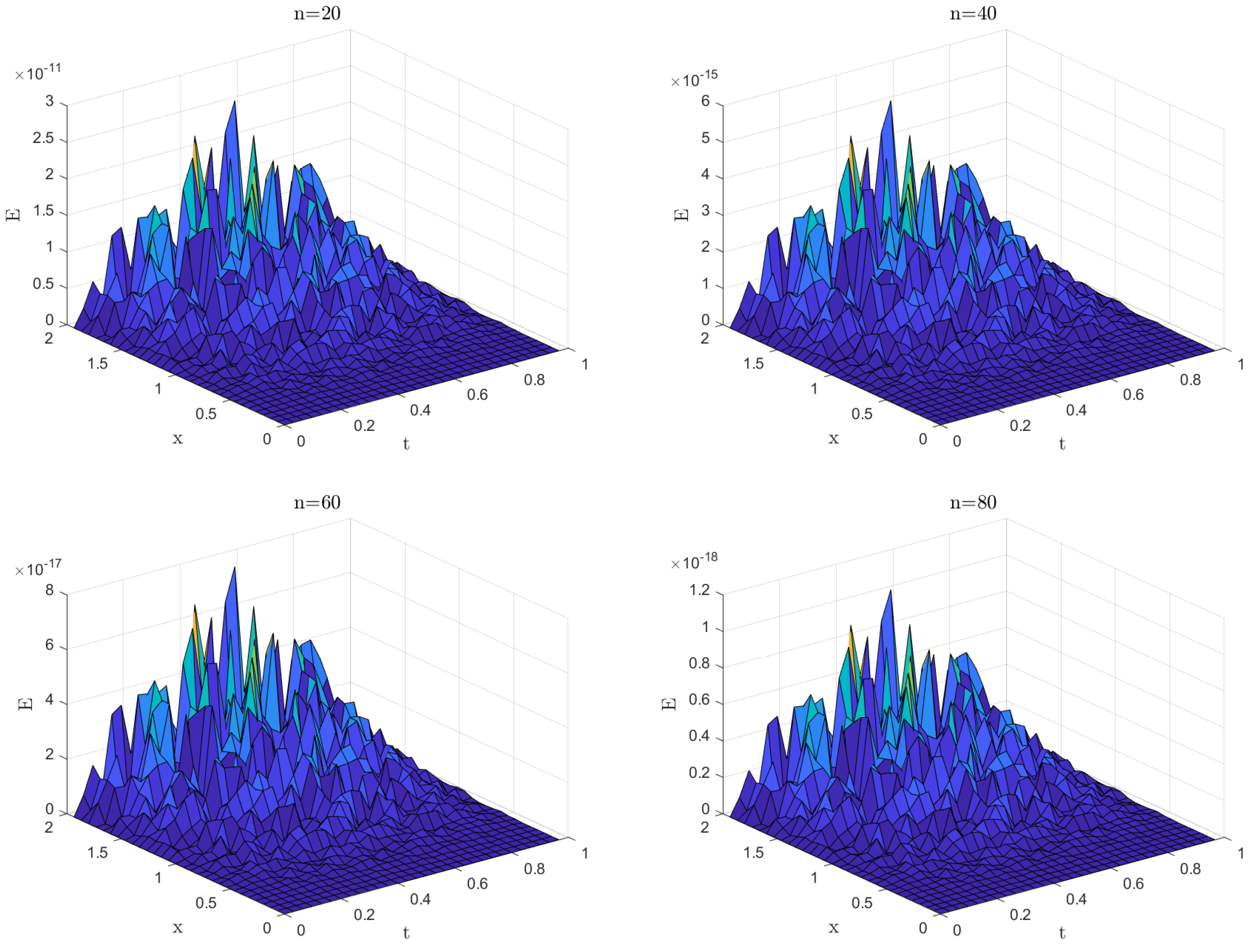
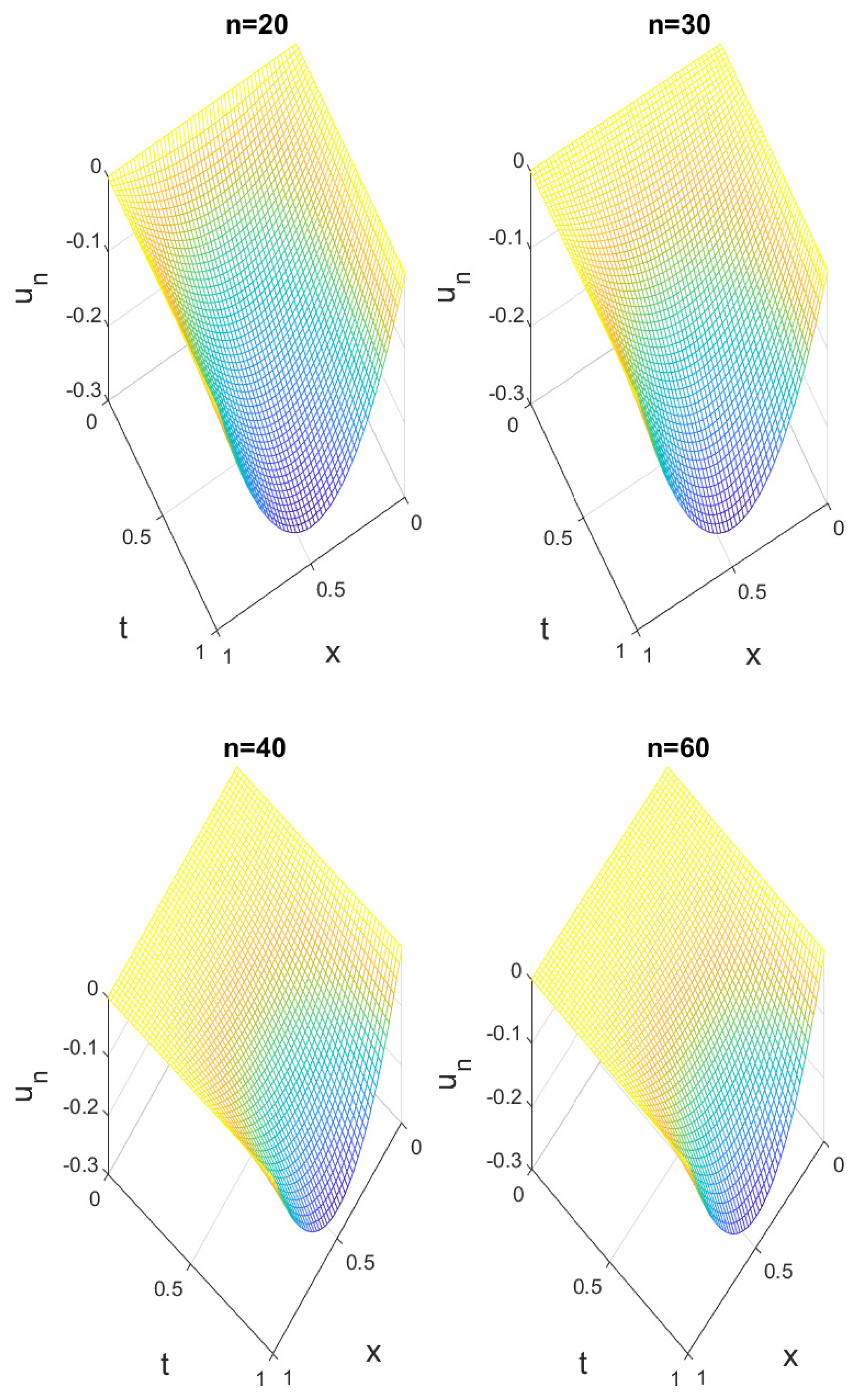
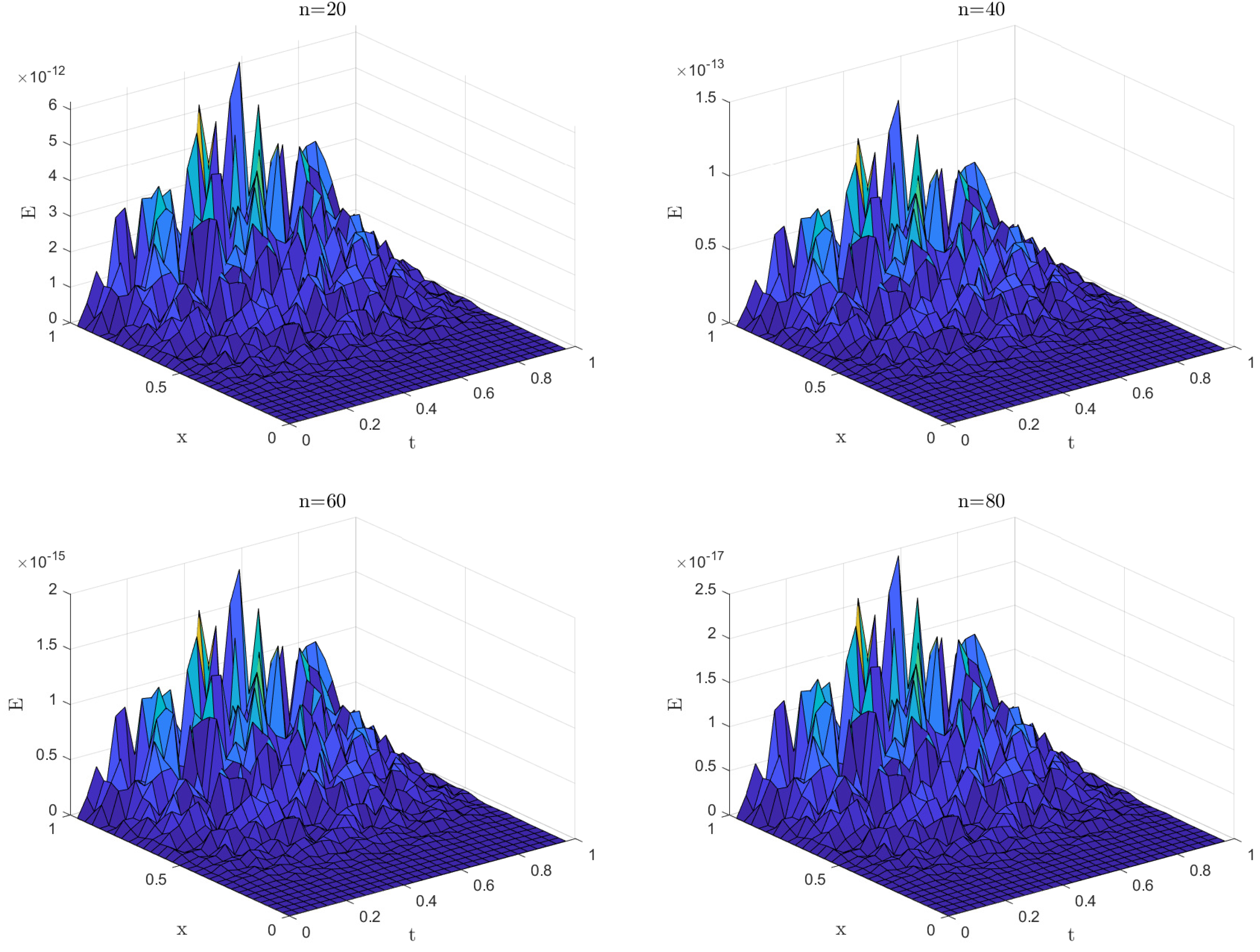
5. Numerical Simulation
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chen, Z.; Kosari, S.; Shafi, J.; Derakhshan, M.H. Stability Analysis Study of Time-Fractional Nonlinear Modified Kawahara Equation Based on the Homotopy Perturbation Sadik Transform. Fractal Fract. 2024, 8, 512. [Google Scholar] [CrossRef]
- Hashemi, M.S.; Abbasbandy, S. A geometric approach for solving Troesch’s problem. Bull. Malays. Math. Sci. Soc. 2017, 40, 97–116. [Google Scholar] [CrossRef]
- Inc, M.; Parto-Haghighi, M.; Akinlar, M.A.; Chu, Y.M. New numerical solutions of fractional-order Korteweg-de Vries equation. Results Phys. 2020, 19, 103326. [Google Scholar] [CrossRef]
- Kosari, S.; Xu, P.; Shafi, J.; Derakhshan, M.H. An efficient hybrid numerical approach for solving two-dimensional fractional cable model involving time-fractional operator of distributed order with error analysis. Numer. Algorithms 2024, 17, 1–20. [Google Scholar] [CrossRef]
- Pourbabaee, M.; Saadatmandi, A. A novel Legendre operational matrix for distributed order fractional differential equations. Appl. Math. Comput. 2019, 361, 215–231. [Google Scholar] [CrossRef]
- David, V.D.; Nazari, M.; Barati, V.; Salah, F.; Abdul Aziz, Z. Approximate analytical solution for the forced Korteweg-de Vries equation. J. Appl. Math. 2013, 2013, 795818. [Google Scholar] [CrossRef]
- Akylas, T.R. On the excitation of long nonlinear water waves by a moving pressure distribution. J. Fluid Mech. 1984, 141, 455–466. [Google Scholar] [CrossRef]
- Jun-Xiao, Z.; Bo-Ling, G. Analytic solutions to forced KdV equation. Commun. Theor. Phys. 2009, 52, 279. [Google Scholar] [CrossRef]
- Grimshaw, R.; Pelinovsky, E.; Tian, X. Interaction of a solitary wave with an external force. Phys. D Nonlinear Phenom. 1994, 77, 405–433. [Google Scholar] [CrossRef]
- Pelinovsky, E.; Talipova, T.; Kurkin, A.; Kharif, C. Nonlinear mechanism of tsunami wave generation by atmospheric disturbances. Nat. Hazards Earth Syst. Sci. 2001, 1, 243–250. [Google Scholar] [CrossRef]
- Derakhshan, M.H.; Rezaei, H.; Marasi, H.R. An efficient numerical method for the distributed-order time-fractional diffusion equation with the error analysis and stability properties. Math. Methods Appl. Sci. 2023, 214, 315–333. [Google Scholar] [CrossRef]
- Liao, S.J.; Cheung, K.F. Homotopy analysis of nonlinear progressive waves in deep water. J. Eng. Math. 2003, 45, 105–116. [Google Scholar] [CrossRef]
- Liao, S.J. An analytic approximate approach for free oscillations of self-excited systems. Int. J. -Non-Linear Mech. 2004, 39, 271–280. [Google Scholar] [CrossRef]
- Liao, S.J. On the analytic solution of magnetohydrodynamic flows of non-Newtonian fluids over a stretching sheet. J. Fluid Mech. 2003, 488, 189–212. [Google Scholar] [CrossRef]
- Grimshaw, R.H.; Maleewong, M. Transcritical flow over obstacles and holes: Forced Korteweg—De Vries framework. J. Fluid Mech. 2019, 881, 660–768. [Google Scholar] [CrossRef]
- Hereman, W. Shallow water waves and solitary waves. arXiv 2013, arXiv:1308.5383. [Google Scholar]
- Ali, R.; Saha, A.; Chatterjee, P. Analytical electron acoustic solitary wave solution for the forced KdV equation in superthermal plasmas. Phys. Plasmas 2017, 24, 122106. [Google Scholar] [CrossRef]
- Mandi, L.; Mondal, K.K.; Chatterjee, P. Analytical solitary wave solution of the dust ion acoustic waves for the damped forced modified Korteweg-de Vries equation in q-nonextensive plasmas. Eur. Phys. J. Spec. Top. 2019, 228, 2753–2768. [Google Scholar] [CrossRef]
- Ji, J.; Zhang, L.; Wang, L.; Wu, S.; Zhang, L. Variable coefficient KdV equation with time-dependent variable coefficient topographic forcing term and atmospheric blocking. Adv. Differ. Equ. 2019, 2019, 320. [Google Scholar] [CrossRef]
- Kurulay, M.; Bayram, M. Approximate analytical solution for the fractional modified KdV by differential transform method. Commun. Nonlinear Sci. Numer. Simul. 2010, 15, 1777–1782. [Google Scholar] [CrossRef]
- Ganji, D.D.; Nourollahi, M.; Rostamian, M. A comparison of variational iteration method with Adomian’s decomposition method in some highly nonlinear equations. Int. J. Sci. Technol. 2007, 2, 179–188. [Google Scholar]
- Rawashdeh, M. Improved approximate solutions for nonlinear evolutions equations in mathematical physics using the reduced differential transform method. J. Appl. Math. Bioinform. 2013, 3, 1. [Google Scholar]
- Yazid, N.M.; Tay, K.G.; Choy, Y.Y.; Sudin, A.M.; Tiong, W.K.; Ong, C.T. Numerical Solution of the Forced Korteweg-de Vries (fKDV) Equation. ARPN J. Eng. Appl. Sci. 2006, 11, 10757–10760. [Google Scholar]
- Lee, S. Dynamics of trapped solitary waves for the forced KdV equation. Symmetry 2018, 10, 129. [Google Scholar] [CrossRef]
- Taghipour, M.; Aminikhah, H. Numerical solution of distributed-order fractional Korteweg-de Vries equation via fractional Zigzag rising diagonal functions. Numer. Algorithms 2024, 96, 739–776. [Google Scholar] [CrossRef]
- Balamurugan, S.; Vigneshwaran, S. Exact Solutions for a Compound KDV-Burgers Equation with Forcing Term. Int. J. Math. Trends Technol. 2018, 56, 320–330. [Google Scholar]
- Hattam, L.L.; Clarke, S.R. Modulation theory for the steady forced KdV-Burgers equation and the construction of periodic solutions. Wave Motion 2015, 56, 67–84. [Google Scholar] [CrossRef]
- Zergania, S.; Leec, J.H.; Aziza, Z.A.; Viswanathan, K.K. KDV and FKDV Model for the Run-up of Tsunamis via Lattice Boltzmann Method. Int. J. Appl. Eng. Res. 2017, 12, 14338–14347. [Google Scholar]
- Saadatmi, A.; Khani, A.; Azizi, M.R. Numerical Calculation of Fractional Derivatives for the Sinc Functions via Legendre Polynomials. Math. Interdiscip. Res. 2019, 1, 71–86. [Google Scholar]
- Hildebr, F.B. Introduction to Numerical Analysis; Courier Corporation: North Chelmsford, MA, USA, 1987. [Google Scholar]
- Mashayekhi, S.; Ordokhani, Y.; Razzaghi, M. A hybrid functions approach for the Duffing equation. Phys. Scr. 2013, 88, 025002. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kosari, S.; Guan, H.; Derakhshan, M. An Error Analysis Study for the Distributed-Order Time-Fraction Model Using an Efficient Numerical Method. Fractal Fract. 2024, 8, 630. https://doi.org/10.3390/fractalfract8110630
Kosari S, Guan H, Derakhshan M. An Error Analysis Study for the Distributed-Order Time-Fraction Model Using an Efficient Numerical Method. Fractal and Fractional. 2024; 8(11):630. https://doi.org/10.3390/fractalfract8110630
Chicago/Turabian StyleKosari, Saeed, Hao Guan, and MohammadHossein Derakhshan. 2024. "An Error Analysis Study for the Distributed-Order Time-Fraction Model Using an Efficient Numerical Method" Fractal and Fractional 8, no. 11: 630. https://doi.org/10.3390/fractalfract8110630
APA StyleKosari, S., Guan, H., & Derakhshan, M. (2024). An Error Analysis Study for the Distributed-Order Time-Fraction Model Using an Efficient Numerical Method. Fractal and Fractional, 8(11), 630. https://doi.org/10.3390/fractalfract8110630







