Local Stability, Global Stability, and Simulations in a Fractional Discrete Glycolysis Reaction–Diffusion Model

Abstract

In the last few years, reaction–diffusion models associated with discrete fractional calculus have risen in prominence in scientific fields, not just due to the requirement for numerical simulation but also due to the described biological phenomena. This work investigates a discrete equivalent of the fractional reaction–diffusion glycolysis model. The discrete fractional calculus tool is introduced to the discrete modeling of diffusion problems in the Caputo-like delta sense, and a fractional discretization diffusion model is described. The local stability of the equilibrium points in the proposed discrete system is examined. We additionally investigate the global stability of the equilibrium point by developing a Lyapunov function. Furthermore, this study indicates that the L1 finite difference scheme and the second-order central difference scheme can successfully preserve the characteristics of the associated continuous system. Finally, an equivalent summation representing the model’s numerical formula is shown. The diffusion concentration is further investigated for different fractional orders, and examples with simulations are presented to corroborate the theoretical findings.

1. Introduction

Reaction–diffusion equations have recently gained popularity due to their applicability to a wide range of biological and chemical processes as well as their unique characteristics in terms of the propagation speed and the new oscillations not seen in standard two-species reaction–diffusion systems. The biochemical process that converts glucose to pyruvate is known as glycolysis, which is present in the vast majority of living creatures today [1]. Throughout this process, two molecules of pyruvate are generally created for every molecule of glucose. The prevalence of glycolysis in a wide range of animals on Earth suggests that it is a primitive metabolic route [2]. Glycolysis is a series of reactions that divide pyruvates (three-carbon molecules) into two components in order to obtain energy from glucose. The same reaction strategy underpins all glycolysis models. The model differs due to differences in the mechanism for the main enzyme reaction. Because such systems have spatial variables, they are widely utilized to analyze certain unusual behaviors, which can include self-replicating spikes, self-excitation, and spatiotemporal chaos. The need to comprehend dynamics is emphasized for this model in order to actualize a broader range of real-world scenarios. Numerous significant attempts have been made to explore the behavior of the reaction–diffusion glycolysis model. The application of a linear control rule to synchronize the reaction–diffusion glycolysis model is discussed in [3]. In [4], the numerical solution of a general glycolysis reaction–diffusion system was studied. In addition, the stability of the Selkov–Schnakenberg reaction–diffusion system was addressed in [5].

In modern-world experiences, fractional-order nonlinear equations are often employed to simulate a variety of physical phenomena [6,7,8,9]. Due to its numerous applications in the fields of chemistry, biology, physics, technology, thermal technology, electricity, mechanics, data processing, electrohydraulics, population modeling, machine learning, and control, the concept of fractional calculus continues to attract the attention of scientists [10,11,12,13]. Due to its use in and relevance to many fields of research and engineering, fractional reaction–diffusion models have gained attention in recent years. In this field, for example, in [14], a pair fractional reaction–diffusion model was explored. In fractional reaction–diffusion systems, they examined nonlinear oscillations and the stability domain. In [15], a solution to a specific fractional reaction-diffusion problem was proposed. In addition, several breakthroughs have been made in the research on the dynamics of the fractional reaction diffusion glycolysis model, for example, see [16,17,18]. In the works described earlier, the fractional component is dedicated to the time partial derivative; nevertheless, in some circumstances, the standard Laplacian cannot imitate the diffusion, and the mean square movement of the diffusing components does not progress linearly over time. Following numerous findings in biological systems, emphasis has been placed on fractional subdiffusion, which is defined as the mean square movement of a population propagating as a sublinear power law in time. It is now widely known that if particles are confined for arbitrarily extended periods of time, subdiffusion occurs (see [19,20,21]).

Discrete reaction–diffusion systems have received less attention than continuous reaction–diffusion systems. Discrete reaction–diffusion systems are formed of cells or lattices that contain chemical processes and are linked together via mass transfer across their membranes. Discrete reaction diffusion systems are more tightly linked to biological systems than continuous systems, and in reaction to a small disturbance, they may exhibit extremely intriguing and diverse patterns in a two-dimensional space [22,23,24]. However, fractional discrete reaction diffusion equations have received little attention [25]. In [26], a fractional discrete diffusion equation was proposed. The chaotic behavior of a variable-order fractional diffusion equation on discontinuous time scales was examined in [27]. In [28], the global dynamics for a class of discrete fractional epidemic models with reaction–diffusion were also investigated. Apparently, we have a gap in our understanding of the dynamics of such systems.

In recent decades, both integer and noninteger fractional orders of the well-known glycolysis reaction diffusion model have received extensive study. The majority of this work has focused on the dynamics and behavior of solutions ([29,30,31,32]). However, to the authors’ knowledge, this is the first investigation of the dynamics and stability of the discrete fractional reaction–diffusion glycolysis model. This prompted us to study the stability of the equilibrium state in a discrete fractional-order reaction–diffusion glycolysis model. A discrete fractional glycolisis reaction diffusion model in the Caputo-like delta sense is described in this study, employing a second-order central difference scheme and an L1 finite difference scheme. Both the local and global stability were explored, and simulations were conducted to test the model’s applicability.

The following is a summary of the paper’s content. Section 2 provides an introduction to fractional discrete calculus, as well as the fundamental concepts associated with the delta Caputo h-discrete difference operator. The mathematical model under examination is described in Section 3. The analysis of the local stability of the equilibrium state for the presence and absence of diffusion is highlighted in Section 4. The global stability of the equilibrium state, which relies on the fractional orders of the investigated model, is discussed in Section 5. Section 6 includes numerical simulations that back up the findings. Section 7 outlines a number of results.

2. Preliminaries

This section provides the necessary terminology and stability theory for the fractional discrete calculus.

Definition 1

([33]). Given that $\mathfrak{z}:\mathbb{N}\to \mathbb{R},$ the forward difference operator Δ is stated by

$$\Delta \mathfrak{z}\left(\mathfrak{r}\right)=\mathfrak{z}(\mathfrak{r}+1)-\mathfrak{z}\left(\mathfrak{r}\right);\mathfrak{r}\in \mathbb{N}.$$

(1)

Also, the recursive identification of the operator ${\Delta }^n,n=1,2,3,\dots$ is ${\Delta }^n\mathfrak{z}\left(\mathfrak{r}\right)=\Delta \left({\Delta }^{n-1}\mathfrak{z}\left(\mathfrak{r}\right)\right),\mathfrak{r}\in \mathbb{N}.$

In particular, the second-order difference operator of the function $\mathfrak{z}\left(t\right)$ is provided by

$${\Delta }^2\mathfrak{z}\left(\mathfrak{r}\right)=\mathfrak{z}(\mathfrak{r}+2)-2\mathfrak{z}(\mathfrak{r}+1)+\mathfrak{z}\left(\mathfrak{r}\right).$$

(2)

Theorem 1

([33]). We have the summation by parts formulae for the following two functions: $\mathfrak{z};\mathfrak{y}:\mathbb{R}\to \mathbb{R}$ and $\mathfrak{a};\mathfrak{b}\in \mathbb{N};\mathfrak{a}<\mathfrak{b};$

$$\begin{array}{cc}\sum _{\mathit{j}=\mathfrak{a}}^{\mathfrak{b}-1}\mathfrak{z}(\mathit{j})\Delta \mathfrak{y}(\mathit{j})& =\mathfrak{z}(\mathit{j})\mathfrak{y}(\mathit{j}){|}_{\mathfrak{a}}^{\mathfrak{b}}-\sum _{\mathit{j}=\mathfrak{a}}^{\mathfrak{b}-1}\mathfrak{y}(\mathit{j}+1)\Delta \mathfrak{z}(\mathit{j}),\hfill \end{array}$$

(3)

$$\begin{array}{cc}\hfill \sum _{\mathit{j}=\mathfrak{a}}^{\mathfrak{b}-1}\mathfrak{z}(\mathit{j}+1)\Delta \mathfrak{y}(\mathit{j})& =\mathfrak{z}(\mathit{j})\mathfrak{y}(\mathit{j}){|}_{\mathfrak{a}}^b-\sum _{\mathit{j}=\mathfrak{a}}^{b-1}\mathfrak{y}(\mathit{j})\Delta \mathfrak{z}(\mathit{j}).\hfill \end{array}$$

(4)

Definition 2

([34,35]). Let $\mathfrak{z}\in {(\hslash \mathbb{N})}_{\mathfrak{a}}\to \mathbb{R}$. For a given $\vartheta >0,$ the $\vartheta$-th order ℏ-sum is given by

$$\begin{array}{cc}\hfill {}_{\hslash }{\Delta }_{\mathfrak{a}}^{-\vartheta }\mathfrak{z}\left(\mathfrak{t}\right)& ={\displaystyle \frac{\hslash }{\mathsf{\Gamma }\left(\vartheta \right)}}\sum _{\frac{t}{\hslash }-\vartheta }^{s=\frac{\mathfrak{a}}{\hslash }}{(\mathfrak{t}-\sigma (s\hslash ))}^{(\vartheta -1)}\mathfrak{z}(s\hslash ),\sigma (s\hslash )=(s+1)\hslash ,\mathfrak{t}\in {(\hslash \mathbb{N})}_{\mathfrak{a}+\vartheta \hslash },\hfill \end{array}$$

the initial value is $a\in \mathbb{R}$, and the ℏ-falling factorial function is specified by

$${\mathfrak{t}}_{\hslash }^{\left(\vartheta \right)}={\hslash }^{\vartheta }{\displaystyle \frac{\mathsf{\Gamma }(\frac{\mathfrak{t}}{\hslash }+1)}{\mathsf{\Gamma }(\frac{\mathfrak{t}}{\hslash }+1-\vartheta )}},$$

while

$${(\hslash \mathbb{N})}_{\mathfrak{a}+\vartheta \hslash }=\{\mathfrak{a}+(1-\vartheta )\hslash ,\mathfrak{a}+(2-\vartheta )\hslash ,\dots \}.$$

Definition 3

([36,37]). Considering a function $\mathfrak{z}\left(t\right)$ given on ${(\hslash \mathbb{N})}_a$ and for a particular $\vartheta >0$, the Caputo ℏ-difference operator is represented by

$${}_{\hslash }^C{\Delta }_{\mathfrak{a}}^{\vartheta }\mathfrak{z}\left(\mathfrak{t}\right){=}_{\hslash }{\Delta }_{\mathfrak{a}}^{-(n-\vartheta )}{\Delta }_{\hslash }^n\mathfrak{z}\left(\mathfrak{t}\right),$$

(5)

where ${\Delta }_{\hslash }^n\mathfrak{z}\left(\mathfrak{t}\right)={\displaystyle \frac{\mathfrak{z}(\mathfrak{t}+\hslash )-\mathfrak{z}\left(\mathfrak{t}\right)}{\hslash }}.$

Lemma 1

([34]). The following inequality holds

$${}_{\hslash }^C{\Delta }_{\mathfrak{a}}^{\vartheta }{\mathfrak{z}}^2\left(t\right)\le 2\mathfrak{z}{(t+\vartheta \hslash )}_{\hslash }^C{\Delta }_{\mathfrak{a}}^{\vartheta }\mathfrak{z}\left(t\right),t\in {(\hslash \mathbb{N})}_{\mathfrak{a}+\vartheta \hslash },$$

(6)

where $0<\vartheta \le 1.$

Let us consider the nonlinear fractional-order difference system:

$${}_{\hslash }^C{\Delta }_{\mathfrak{a}}^{\vartheta }\mathfrak{z}\left(\mathfrak{t}\right)=\psi (\mathfrak{t}+\hslash \vartheta ,\mathfrak{z}(\mathfrak{t}+\hslash \vartheta )),\mathfrak{t}\in {(\hslash \mathbb{N})}_{\mathfrak{a}+\vartheta \hslash }.$$

(7)

Theorem 2

([38]). Assume that the equilibrium point of (7) is ${\mathfrak{z}}^{\ast }$. ${\mathfrak{z}}^{\ast }$ is asymptotically stable if all of the eigenvalues of ${\psi }^{\prime }\left({\mathfrak{z}}^{\ast }\right)$ are found in $S_{\hslash }^{\vartheta }$, where

$$S_{\hslash }^{\vartheta }=\left\{w\in \mathbb{C}:\left|Arg\left(w\right)\right|>{\displaystyle \frac{\vartheta \pi }{2}}\mathit{or}\left|w\right|>{\displaystyle \frac{2^{\vartheta }}{{\hslash }^{\vartheta }}}{cos}^{\vartheta }\left({\displaystyle \frac{Arg\left(w\right)}{\vartheta }}\right)\right\}.$$

(8)

Theorem 3

([34]). Assume that the equilibrium point of the system (21) is $\mathfrak{z}=0$. If there is a positively definite and decreasing scalar function, the equilibrium point is asymptotically stable, such that ${}_{\hslash }^C{\mathsf{\Delta }}_{\mathfrak{a}}^{\vartheta }V(\mathfrak{t},\mathfrak{z}\left(\mathfrak{t}\right))\le 0$.

3. The Fractional Discrete Glycolysis Reaction–Diffusion System

The model under consideration is approximated employing two commonly used approaches in this section. This is, to our knowledge, the first discrete model in the literature. The glycolysis reaction–diffusion system, as previously stated, was provided as a model. Refs. [4,5] cite it as follows:

$$\left\{\begin{array}{c}{\displaystyle \frac{\partial \mathfrak{z}}{\partial \mathfrak{t}}}=d_1\mathsf{\Delta }\mathfrak{z}+b\mathfrak{w}-\mathfrak{z}+{\mathfrak{z}}^2\mathfrak{w},\mathfrak{z}\in \mathsf{\Omega },\mathfrak{t}>0,\hfill \\ {\displaystyle \frac{\partial \mathfrak{w}}{\partial \mathfrak{t}}}=d_2\mathsf{\Delta }\mathfrak{w}+a-b\mathfrak{w}-{\mathfrak{z}}^2\mathfrak{w},\mathfrak{z}\in \mathsf{\Omega },\mathfrak{t}>0,\hfill \\ {\partial }_{\mathfrak{z}}={\partial }_{\mathfrak{w}}=0,\mathfrak{z}\in \partial \mathsf{\Omega },\mathfrak{t}>0,\hfill \\ u(\mathfrak{z},0)={\mathfrak{z}}_0\left(\mathfrak{z}\right)>0,\mathfrak{w}(\mathfrak{z},0)={\mathfrak{w}}_0\left(\mathfrak{z}\right)>0,\mathfrak{z}\in \mathsf{\Omega }.\hfill \end{array}\right.$$

(9)

In this case, the variables $\mathfrak{z}(\mathfrak{z},t)$ and $\mathfrak{w}(\mathfrak{z},t)$ denote the chemical concentrations, $d_1$ and $d_2$ are the diffusion coefficients, a is the dimensionless input flow, and b is the dimensionless constant rate for the low activity state. $\mathsf{\Omega }$ is a bounded domain in ${\mathbb{R}}^n$ with sufficiently smooth boundaries. For a two-cell system, this model has some stability findings (see [39,40]). The Sel’klov model, which has attracted a lot of interest recently ([41,42,43]), is known to exist for $b=0$.

Researchers have investigated time-fractional systems extensively; hence, the following fractional-time Glycolysis reaction-diffusion system was presented:

$$\left\{\begin{array}{c}{}_0^C{D}_{\mathfrak{t}}^{\delta }\mathfrak{z}-d_1\mathsf{\Delta }\mathfrak{z}=b\mathfrak{w}-\mathfrak{z}+{\mathfrak{z}}^2\mathfrak{w},\mathfrak{z}\in \mathsf{\Omega },\mathfrak{t}>0\hfill \\ {}_0^C{D}_{\mathfrak{t}}^{\delta }\mathfrak{w}-d_2\mathsf{\Delta }\mathfrak{w}=a-b\mathfrak{w}-{\mathfrak{z}}^2\mathfrak{w},\mathfrak{z}\in \mathsf{\Omega },\mathfrak{t}>0,\hfill \end{array}\right.$$

(10)

where $\mathsf{\Delta }={\sum }_{i=1}^n{\displaystyle \frac{{\partial }^2}{\partial {\mathfrak{z}}_i^2}}$, $0<\delta \le 1$ is the fractional order, and ${}_0^C{D}_{\mathfrak{t}}^{\delta }$ describes the Caputo fractional derivative. $d_1,d_2$, and $\sigma$ are strictly positive constants with the same initial conditions and Neumann boundary conditions.

Relying on the model (10) and the method of discretization employed in [26], provided that $\mathfrak{z}\in [0,L]$, we obtain ${\mathfrak{z}}_{i+1}={\mathfrak{z}}_i+k,i=0,\dots ,m$, and by applying (1), $\frac{{\partial }^2\mathfrak{z}(\mathfrak{z},t)}{\partial {\mathfrak{z}}^2}$ and $\frac{{\partial }^2\mathfrak{w}(\mathfrak{z},t)}{\partial {\mathfrak{z}}^2}$ may be approximated as

$$\left\{\begin{array}{c}{\displaystyle \frac{{\partial }^2\mathfrak{z}(\mathfrak{z},\mathfrak{t})}{\partial {\mathfrak{z}}^2}}\approx {\displaystyle \frac{{\mathfrak{z}}_{i+1}\left(\mathfrak{t}\right)-2{\mathfrak{z}}_i\left(\mathfrak{t}\right)+{\mathfrak{z}}_{i-1}\left(\mathfrak{t}\right)}{k^2}},\hfill \\ {\displaystyle \frac{{\partial }^2\mathfrak{w}(\mathfrak{z},\mathfrak{t})}{\partial {\mathfrak{z}}^2}}\approx {\displaystyle \frac{{\mathfrak{w}}_{i+1}\left(\mathfrak{t}\right)-2{\mathfrak{w}}_i\left(\mathfrak{t}\right)+{\mathfrak{w}}_{i-1}\left(\mathfrak{t}\right)}{k^2}}.\hfill \end{array}\right.$$

By defining the second-order difference operator of ${\mathfrak{z}}_i$ and ${\mathfrak{w}}_i$, we obtain

$$\left\{\begin{array}{c}{\displaystyle \frac{{\partial }^2\mathfrak{z}(\mathfrak{z},\mathfrak{t})}{\partial {\mathfrak{z}}^2}}\approx {\displaystyle \frac{{\mathsf{\Delta }}^2{\mathfrak{z}}_{i-1}\left(\mathfrak{t}\right)}{k^2}},\hfill \\ {\displaystyle \frac{{\partial }^2\mathfrak{w}(\mathfrak{z},\mathfrak{t})}{\partial {\mathfrak{z}}^2}}\approx {\displaystyle \frac{{\mathsf{\Delta }}^2{\mathfrak{w}}_{i-1}\left(\mathfrak{t}\right)}{k^2}}.\hfill \end{array}\right.$$

Thus, we introduce the following discrete-time reaction–diffusion fractional glycolysis system:

$$\left\{\begin{array}{c}{}_{\hslash }^C{\mathsf{\Delta }}_{{\mathfrak{t}}_0}^{\vartheta }{\mathfrak{z}}_i\left(\mathfrak{t}\right)={\displaystyle \frac{d_1}{k^2}}{\mathsf{\Delta }}^2{\mathfrak{z}}_{i-1}(\mathfrak{t}+\hslash \vartheta )+b{\mathfrak{w}}_i(\mathfrak{t}+\hslash \vartheta )-{\mathfrak{z}}_i(\mathfrak{t}+\hslash \vartheta )+{\mathfrak{z}}_i^2(t+\hslash \vartheta ){\mathfrak{w}}_i(\mathfrak{t}+\hslash \vartheta ),\hfill \\ {}_{\hslash }^C{\mathsf{\Delta }}_{{\mathfrak{t}}_0}^{\vartheta }{\mathfrak{w}}_i\left(\mathfrak{t}\right)={\displaystyle \frac{d_2}{k^2}}{\mathsf{\Delta }}^2{\mathfrak{w}}_{i-1}(\mathfrak{t}+\hslash \vartheta )+a-b{\mathfrak{w}}_i(\mathfrak{t}+\hslash \vartheta )-{\mathfrak{z}}_i^2(\mathfrak{t}+\hslash \vartheta ){\mathfrak{w}}_i(\mathfrak{t}+\hslash \vartheta ),\hfill \end{array}\right.$$

(11)

with the periodic boundary conditions

$$\left\{\begin{array}{c}{\mathfrak{z}}_0\left(t\right)={\mathfrak{z}}_m\left(\mathfrak{t}\right),{\mathfrak{z}}_1\left(\mathfrak{t}\right)={\mathfrak{z}}_{m+1}\left(\mathfrak{t}\right),\hfill \\ {\mathfrak{w}}_0\left(t\right)={\mathfrak{w}}_m\left(\mathfrak{t}\right),{\mathfrak{w}}_1\left(\mathfrak{t}\right)={\mathfrak{w}}_{m+1}\left(\mathfrak{t}\right),\hfill \end{array}\right.$$

(12)

and the initial condition

$${\mathfrak{z}}_i\left({\mathfrak{t}}_0\right)={\varphi }_1\left({\mathfrak{z}}_i\right)\ge 0,{\mathfrak{w}}_i\left({\mathfrak{t}}_0\right)={\varphi }_2\left({\mathfrak{z}}_i\right)\ge 0.$$

4. Local Stability

To analyze the asymptotic stability of the previously stated discrete fractional glycolysis model, we consider the single equilibrium produced by this system:

$$\left\{\begin{array}{c}{\displaystyle \frac{d_1}{k^2}}{\mathsf{\Delta }}^2{\mathfrak{z}}^{\ast }+b{\mathfrak{w}}^{\ast }-{\mathfrak{z}}^{\ast }+{\mathfrak{z}}^{2\ast }{\mathfrak{w}}^{\ast }=0,\hfill \\ {\displaystyle \frac{d_2}{k^2}}{\mathsf{\Delta }}^2{\mathfrak{w}}^{\ast }+a-b{\mathfrak{w}}^{\ast }-{\mathfrak{z}}^{2\ast }{\mathfrak{w}}^{\ast }=0.\hfill \end{array}\right.$$

(13)

Considering Theorem 1, the unique equilibrium point of system (11) is provided by

$$({\mathfrak{z}}^{\ast },{\mathfrak{w}}^{\ast })=\left(a,{\displaystyle \frac{a}{a^2+b}}\right).$$

(14)

4.1. Local Stability of the Free Diffusions System

In this section, we provide sufficient conditions for the system’s local asymptotic stability.

$$\left\{\begin{array}{c}{}_{\hslash }^C{\mathsf{\Delta }}_{{\mathfrak{t}}_0}^{\vartheta }\mathfrak{z}\left(\mathfrak{t}\right)=b\mathfrak{w}(\mathfrak{t}+\hslash \vartheta )-\mathfrak{w}(\mathfrak{t}+\hslash \vartheta )+u^2(\mathfrak{t}+\hslash \vartheta )\mathfrak{w}(\mathfrak{t}+\hslash \vartheta ),\hfill \\ {}_{\hslash }^C{\mathsf{\Delta }}_{{\mathfrak{t}}_0}^{\vartheta }\mathfrak{w}\left(\mathfrak{t}\right)=a-b\mathfrak{z}(\mathfrak{t}+\hslash \vartheta )-{\mathfrak{z}}^2(\mathfrak{t}+\hslash \vartheta )\mathfrak{w}(\mathfrak{t}+\hslash \vartheta ).\hfill \end{array}\right.$$

(15)

Theorem 4.

The conditions that follow must be satisfied for system (15) to be locally asymptotically stable at the positive steady state $({\mathfrak{z}}^{\ast },{\mathfrak{w}}^{\ast })$:

• If ${\left({\displaystyle \frac{a^2-b^2}{a^2+b^2}}-(a^2+b^2)\right)}^2\ge 4\left(a^2+b^2\right)$ and ${\displaystyle \frac{a^2-b^2}{a^2+b^2}}<a^2+b^2.$
• If ${\left({\displaystyle \frac{a^2-b^2}{a^2+b^2}}-(a^2+b^2)\right)}^2<4\left(a^2+b^2\right)$ and ${\displaystyle \frac{a^2-b^2}{a^2+b^2}}\le a^2+b^2.$

Proof. 

The characteristic equation for the eigenvalues is discovered around this stable state using linear stability analysis:

$$J({\mathfrak{z}}^{\ast },{\mathfrak{w}}^{\ast })=\left(\begin{array}{c}{\displaystyle \frac{\partial \psi }{\partial \mathfrak{z}}}{\displaystyle \frac{\partial \psi }{\partial \mathfrak{w}}}\\ {\displaystyle \frac{\partial \mathsf{\Psi }}{\partial \mathfrak{z}}}{\displaystyle \frac{\partial \mathsf{\Psi }}{\partial \mathfrak{w}}}\end{array}\right)=\left(\begin{array}{c}{\displaystyle \frac{2a^2}{a^2+b^2}}-1a^2+b^2\\ -{\displaystyle \frac{2a^2}{a^2+b^2}}-(a^2+b^2)\end{array}\right),$$

(16)

with

$$\psi (\mathfrak{z},\mathfrak{w})=b\mathfrak{w}(\mathfrak{t}+\hslash \vartheta )-\mathfrak{z}(\mathfrak{t}+\hslash \vartheta )+{\mathfrak{z}}^2(\mathfrak{t}+\hslash \vartheta )\mathfrak{w}(\mathfrak{t}+\hslash \vartheta ),$$

(17)

and

$$\mathsf{\Psi }(\mathfrak{z},\mathfrak{w})=a-b\mathfrak{w}(\mathfrak{t}+\hslash \vartheta )-{\mathfrak{z}}^2(\mathfrak{t}+\hslash \vartheta )\mathfrak{w}(\mathfrak{t}+\hslash \vartheta ).$$

(18)

From the Jacobian matrix, we can see that

$$\mathrm{tr}\left(J\right)={\displaystyle \frac{2a^2}{a^2+b^2}}-(a^2+b^2)-1,\det \left(J\right)=a^2+b^2,$$

(19)

and $J({\mathfrak{z}}^{\ast },{\mathfrak{w}}^{\ast })$ has the characteristic equation given by

$${\mathsf{\Lambda }}^2-\mathrm{tr}\left(J\right)\mathsf{\Lambda }+\det \left(J\right)=0,$$

(20)

or its discriminant is

$${\mathfrak{N}}_{\mathsf{\Lambda }}={\mathrm{tr}}^2\left(J\right)-4\det \left(J\right)={\left({\displaystyle \frac{a^2-b^2}{a^2+b^2}}-(a^2+b^2)\right)}^2-4\left(a^2+b^2\right).$$

(21)

As a consequence, we may conclude the following according to the sign of (21).

• If ${\mathfrak{N}}_{\mathsf{\Lambda }}>0$, it is evident that $\det \left(J\right)>0$. Thus, the sign of $\mathrm{tr}\left(J\right)$ determines the eigenvalues’ negativity, and the eigenvalues ${\mathsf{\Lambda }}_1$ and ${\mathsf{\Lambda }}_2$ are real and may be expressed as

  $${\mathsf{\Lambda }}_1={\displaystyle \frac{\mathrm{tr}\left(J\right)-\sqrt{{\mathfrak{N}}_{\mathsf{\Lambda }}}}{2}},{\mathsf{\Lambda }}_2={\displaystyle \frac{\mathrm{tr}\left(J\right)+\sqrt{{\mathfrak{N}}_{\mathsf{\Lambda }}}}{2}}.$$

  (22)

  -

  If $\mathrm{tr}\left(J\right)<0$, we have

  $${\mathsf{\Lambda }}_1={\displaystyle \frac{\mathrm{tr}\left(J\right)-\sqrt{{\mathfrak{N}}_{\mathsf{\Lambda }}}}{2}}<0.$$

  (23)

  Hence, $Arg\left({\mathsf{\Lambda }}_1\right)=\pi$. The two eigenvalues are real; therefore, $Arg\left({\mathsf{\Lambda }}_1\right)=Arg$$\left({\mathsf{\Lambda }}_2\right)=\pi .$ As a result, $({\mathfrak{z}}^{\ast },{\mathfrak{w}}^{\ast })$ is asymptotically stable according to Theorem 2.

  -

  If $\mathrm{tr}\left(J\right)>0$, then we have

  $${\mathsf{\Lambda }}_2={\displaystyle \frac{\mathrm{tr}\left(J\right)+\sqrt{{\mathfrak{N}}_{\mathsf{\Lambda }}}}{2}}>0.$$

  (24)

  Therefore, $Arg\left({\mathsf{\Lambda }}_2\right)=0$, and based on Theorem 2, system (15) is unstable.

• If ${\mathfrak{N}}_{\mathsf{\Lambda }}<0$, then

  $${\mathsf{\Lambda }}_1={\displaystyle \frac{\mathrm{tr}\left(J\right)-i\sqrt{-{\mathfrak{N}}_{\mathsf{\Lambda }}}}{2}},{\mathsf{\Lambda }}_2={\displaystyle \frac{\mathrm{tr}\left(J\right)+i\sqrt{-{\mathfrak{N}}_{\mathsf{\Lambda }}}}{2}}.$$

  (25)
  We may examine the solutions relying on the sign of $\mathrm{tr}\left(J\right)$.

  -

  If $\mathrm{tr}\left(J\right)<0$ or $\mathrm{tr}\left(J\right)>0$, consequently, system (15) is asymptotically stable following the same case that was previously analyzed.

  -

  If $\mathrm{tr}\left(J\right)=0$, then

  $$Arg\left({\displaystyle \frac{-i\sqrt{-{\mathfrak{N}}_{\mathsf{\Lambda }}}}{2}}\right)=Arg\left({\displaystyle \frac{i\sqrt{-{\mathfrak{N}}_{\mathsf{\Lambda }}}}{2}}\right)={\displaystyle \frac{\pi }{2}},$$

  and system (15) is asymptotically stable.

• If ${\mathfrak{N}}_{\mathsf{\Lambda }}=0$, it is impossible for $\mathrm{tr}\left(J\right)$ to equal zero, since $\det \left(J\right)>0$. The sign of the eigenvalues and that of $\mathrm{tr}\left(J\right)$ are the same. As a consequence, $({\mathfrak{z}}^{\ast },{\mathfrak{w}}^{\ast })$ is unstable if $\mathrm{tr}\left(J\right)>0$, and it is asymptotically stable for all $\vartheta \in (0,1]$, if $\mathrm{tr}\left(J\right)<0$.

The proof is complete. □

4.2. Local Stability of the Diffusion System

The steady state $({\mathfrak{z}}^{\ast },{\mathfrak{w}}^{\ast })$ may be stable in the presence of diffusion under specific parameter conditions. We follow the same procedure as in [44], beginning by examining the eigenvalues of this equation:

$${\mathsf{\Delta }}^2{\mathfrak{z}}_{i-1}(\mathfrak{t}+\hslash \vartheta )+{\mathsf{\Lambda }}_i{\mathfrak{z}}_i(\mathfrak{t}+\hslash \vartheta )=0,$$

(26)

with the periodic boundary conditions:

$${\mathfrak{z}}_0\left(\mathfrak{t}\right)={\mathfrak{z}}_m\left(\mathfrak{t}\right),{\mathfrak{z}}_1\left(\mathfrak{t}\right)={\mathfrak{z}}_{m+1}\left(\mathfrak{t}\right).$$

(27)

We obtain

$$\left\{\begin{array}{c}{}_{\hslash }^C{\mathsf{\Delta }}_{{\mathfrak{t}}_0}^{\vartheta }{\mathfrak{z}}_i\left(\mathfrak{t}\right)={\displaystyle \frac{d_1}{k^2}}{\mathsf{\Lambda }}_i{\mathfrak{z}}_i(\mathfrak{t}+\hslash \vartheta )+b{\mathfrak{w}}_i(\mathfrak{t}+\hslash \vartheta )-{\mathfrak{z}}_i(\mathfrak{t}+\hslash \vartheta )+{\mathfrak{z}}_i^2(\mathfrak{t}+\hslash \vartheta ){\mathfrak{w}}_i(\mathfrak{t}+\hslash \vartheta ),\hfill \\ {}_{\hslash }^C{\mathsf{\Delta }}_{{\mathfrak{t}}_0}^{\vartheta }{\mathfrak{w}}_i\left(\mathfrak{t}\right)={\displaystyle \frac{d_2}{k^2}}{\mathsf{\Lambda }}_i{\mathfrak{w}}_i(\mathfrak{t}+\hslash \vartheta )+a-b{\mathfrak{w}}_i(\mathfrak{t}+\hslash \vartheta )-{\mathfrak{z}}_i^2(\mathfrak{t}+\hslash \vartheta ){\mathfrak{w}}_i(\mathfrak{t}+\hslash \vartheta ).\hfill \end{array}\right.$$

(28)

When linearizing system (28) about the steady state $({\mathfrak{z}}^{\ast },{\mathfrak{w}}^{\ast })$, we obtain the following.

$$J_i=\left(\begin{array}{c}-\frac{d_1}{k^2}{\mathsf{\Lambda }}_i+{\displaystyle \frac{2a^2}{a^2+b^2}}-1a^2+b^2\\ -{\displaystyle \frac{2a^2}{a^2+b^2}}-\frac{d_2}{k^2}{\mathsf{\Lambda }}_i-(a^2+b^2)\end{array}\right).$$

(29)

Then, the following result is obtained.

Theorem 5.

We suppose that

$${\left({\displaystyle \frac{a^2-b^2}{a^2+b^2}}-(a^2+b^2)\right)}^2>4\left(a^2+b^2\right)\mathit{and}{\displaystyle \frac{a^2-b^2}{a^2+b^2}}<a^2+b^2;$$

system (11) is asymptotically stable at the steady state $({\mathfrak{z}}^{\ast },{\mathfrak{w}}^{\ast })$, if the following hold:

• If $d_1<d_2$ and $\frac{d_1}{k^2}{\mathsf{\Lambda }}_1\ge {\displaystyle \frac{2a^2}{a^2+b^2}}-1.$
• If $d_1>d_2$ and $\frac{d_1}{k^2}{\mathsf{\Lambda }}_1\ge {\displaystyle \frac{2a^2}{a^2+b^2}}-1$,
  and in addition, the eigenvalues

  $${\mu }_j\left({\mathsf{\Lambda }}_i\right)={\displaystyle \frac{tr\left(J_i\right){}_{\underline{+-}}\sqrt{tr{\left(J_i\right)}^2-4dert\left(J_i\right)}}{2}},j=1,2,$$
  satisfy $Arg\left({\mu }_j\left({\mathsf{\Lambda }}_i\right)\right)>{\displaystyle \frac{\vartheta \pi }{2}}.$

Proof. 

We linearize the system to investigate its local asymptotic stability. By applying basic linear operator theory and taking the system’s fractional nature into account, we may argue that $(u^{\ast },v^{\ast })$ is asymptotically stable if the eigenvalues of the linearized system satisfy the conditions of Theorem 2. We obtain

$$J_i=\left(\begin{array}{c}6\frac{d_1}{k^2}{\mathsf{\Lambda }}_i+{\displaystyle \frac{2a^2}{a^2+b^2}}-1a^2+b^2\\ -{\displaystyle \frac{2a^2}{a^2+b^2}}6\frac{d_2}{k^2}{\mathsf{\Lambda }}_i-(a^2+b^2)\end{array}\right)=J-\mu \left({\mathsf{\Lambda }}_i\right)I,$$

(30)

which has the eigenvalue equation

$${\mu }^2\left({\mathsf{\Lambda }}_i\right)-\mathrm{tr}\left(J_i\right)\mu \left({\mathsf{\Lambda }}_i\right)+\det \left(J_i\right)=0,$$

(31)

where

$$\mathrm{tr}\left(J_i\right)=-\left({\displaystyle \frac{d_1}{k^2}}+{\displaystyle \frac{d_2}{k^2}}\right){\mathsf{\Lambda }}_i+{\displaystyle \frac{a^2-b^2}{a^2+b^2}}-(a^2+b^2),$$

(32)

and

$$\det \left(J_i\right)={\displaystyle \frac{d_1}{k^2}}{\displaystyle \frac{d_2}{k^2}}{\mathsf{\Lambda }}_i^2+\left({\displaystyle \frac{d_1}{k^2}}(a^2+b^2)-{\displaystyle \frac{d_2}{k^2}}\left({\displaystyle \frac{a^2-b^2}{a^2+b^2}}\right)\right){\mathsf{\Lambda }}_i+a^2+b^2,$$

(33)

and its discriminant is

$$\begin{array}{cc}\hfill & {\mathfrak{N}}_i={\mathrm{tr}}^2\left(J_i\right)-4\det \left(J_i\right)\hfill \\ \hfill & ={\left(-\left({\displaystyle \frac{d_1}{k^2}}+{\displaystyle \frac{d_2}{k^2}}\right){\mathsf{\Lambda }}_i+{\displaystyle \frac{a^2-b^2}{a^2+b^2}}-(a^2+b^2)\right)}^2\hfill \\ \hfill & -4\left({\displaystyle \frac{d_1}{k^2}}{\displaystyle \frac{d_2}{k^2}}{\mathsf{\Lambda }}_i^2+\left({\displaystyle \frac{d_1}{k^2}}(a^2+b^2)-{\displaystyle \frac{d_2}{k^2}}\left({\displaystyle \frac{a^2-b^2}{a^2+b^2}}\right)\right){\mathsf{\Lambda }}_i+a^2+b^2\right),\hfill \\ \hfill & ={\left(\frac{d_1}{k^2}-\frac{d_2}{k^2}\right)}^2{\mathsf{\Lambda }}_i^2-2\left(\frac{d_1}{k^2}-\frac{d_2}{k^2}\right)\left({\displaystyle \frac{a^2-b^2}{a^2+b^2}}+(a^2+b^2)\right){\mathsf{\Lambda }}_i+{\mathsf{\Delta }}_{\mathsf{\Lambda }}.\hfill \end{array}$$

The stability of $({\mathfrak{z}}^{\ast },{\mathfrak{w}}^{\ast })$ depends on the sign of $\mathsf{\Delta }{1}_i$. The discriminant of $\mathsf{\Delta }{1}_i$ in relation to ${\mathsf{\Lambda }}_i$ is

$$\begin{array}{cc}\hfill {\mathfrak{N}}_{{\mathsf{\Lambda }}_i}& =4{\left(\frac{d_1}{k^2}-\frac{d_2}{k^2}\right)}^2{\left({\displaystyle \frac{a^2-b^2}{a^2+b^2}}+(a^2+b^2)\right)}^2\hfill \\ \hfill & -4{\left(\frac{d_1}{k^2}-\frac{d_2}{k^2}\right)}^2\left({\left({\displaystyle \frac{a^2-b^2}{a^2+b^2}}-(a^2+b^2)\right)}^2-4\left(a^2+b^2\right)\right)\hfill \\ \hfill & =32{\left(a\left({\displaystyle \frac{d_1}{k^2}}-{\displaystyle \frac{d_2}{k^2}}\right)\right)}^2.\hfill \end{array}$$

Clearly, ${\mathfrak{N}}_{{\mathsf{\Lambda }}_i}>0$, and because $d_1\ne d_2$, we distinguish two cases,

• If $d_1<d_2$, then ${\left({\displaystyle \frac{a^2-b^2}{a^2+b^2}}-(a^2+b^2)\right)}^2>4\left(a^2+b^2\right)$, and the two solutions of the equation ${\mathfrak{N}}_{{\mathsf{\Lambda }}_i}=0$ are both negative. Thus, ${\mathfrak{N}}_{{\mathsf{\Lambda }}_i}>0$, and the roots of (31) are

  $$\left\{\begin{array}{c}{\mu }_1\left({\mathsf{\Lambda }}_i\right)={\displaystyle \frac{\mathrm{tr}\left(J_i\right)+\sqrt{\mathrm{tr}{\left(J_i\right)}^2-4\det \left(J_i\right)}}{2}},\hfill \\ {\mu }_2\left({\mathsf{\Lambda }}_i\right)={\displaystyle \frac{\mathrm{tr}\left(J_i\right)-\sqrt{\mathrm{tr}{\left(J_i\right)}^2-4\det \left(J_i\right)}}{2}}.\hfill \end{array}\right.$$

  (34)
  It should be noted that the solutions are real, and $\mu {\left({\mathsf{\Lambda }}_i\right)}_1<0.$ In addition, if $\frac{d_1}{k^2}{\mathsf{\Lambda }}_1\ge {\displaystyle \frac{2a^2}{a^2+b^2}}-1$, then $\mu {\left({\mathsf{\Lambda }}_i\right)}_2<0.$ This leads to

  $$\left|Arg\left({\mu }_1\left({\mathsf{\Lambda }}_i\right)\right)\right|=\left|Arg\left({\mu }_2{\left({\mathsf{\Lambda }}_i\right)}_2\right)\right|=\pi ,$$

  (35)

  which ensures $({\mathfrak{z}}^{\ast },{\mathfrak{w}}^{\ast })$ is asymptotic stability.
• If $d_1>d_2$, we have $\frac{d_1}{k^2}{\mathsf{\Lambda }}_1\ge {\displaystyle \frac{2a^2}{a^2+b^2}}-1.$ This returns us to the previous scenario Again, for $\frac{d_1}{k^2}{\mathsf{\Lambda }}_1-\frac{3{\left(\frac{a}{5}\right)}^2-5}{1+{\left(\frac{a}{5}\right)}^2},$$\det \left(J_i\right)>0;$ hence, ${\lambda }_1$ and ${\lambda }_2$ are negative and must meet the conditions of Theorem 2.

□

5. Global Stability

In this section, we show how the constant steady-state solution is globally asymptotically stable.

Theorem 6.

If

$$-b{\mathfrak{w}}^{\ast }+2{\mathfrak{w}}^{\ast }{\mathfrak{z}}^{\ast 2}\le 0,$$

(36)

then system (11) is globally asymptotically stable.

Proof. 

To demonstrate this result, we employ the identical Lyapunov function as in [28]. We consider the following function for this purpose:

$$\mathfrak{l}\left(z\right)=z-1-ln\left(z\right),$$

where this function has a strict global minimum, i.e., $\mathfrak{l}\left(1\right)=0$. Let the following be a nonnegative function:

$$\mathfrak{L}\left(\mathfrak{t}\right)={\mathfrak{L}}_1\left(\mathfrak{t}\right)+{\mathfrak{L}}_2\left(\mathfrak{t}\right),$$

where

$${\mathfrak{L}}_1\left(\mathfrak{t}\right)=\sum _{i=1}^m{\mathfrak{z}}^{\ast }\mathfrak{l}\left({\displaystyle \frac{{\mathfrak{z}}_i}{{\mathfrak{z}}^{\ast }}}\right),{\mathfrak{L}}_2\left(t\right)=\sum _{i=1}^m{\mathfrak{w}}^{\ast }\mathfrak{l}\left({\displaystyle \frac{{\mathfrak{w}}_i}{{\mathfrak{w}}^{\ast }}}\right).$$

First, we calculate $L_1\left(t\right)$

$$\begin{array}{cc}\hfill {}_{\hslash }^C{\mathsf{\Delta }}_{{\mathfrak{t}}_0}^{\vartheta }{\mathfrak{L}}_1\left(\mathfrak{t}\right)& =\sum _{i=1}^m{}_{\hslash }^C{\mathsf{\Delta }}_{{\mathfrak{t}}_0}^{\gamma }{\mathfrak{z}}^{\ast }\mathfrak{l}\left({\displaystyle \frac{{\mathfrak{z}}_i\left(\mathfrak{t}\right)}{{\mathfrak{z}}^{\ast }}}\right),\hfill \\ \hfill & \le \sum _{i=1}^m\left(1-{\displaystyle \frac{{\mathfrak{z}}^{\ast }}{{\mathfrak{z}}_i(\mathfrak{t}+\hslash \vartheta )}}\right){}_{\hslash }^C{\mathsf{\Delta }}_{{\mathfrak{t}}_0}^{\gamma }{\mathfrak{z}}_i\left(\mathfrak{t}\right),\hfill \\ \hfill & \le \sum _{i=1}^m\left(1-{\displaystyle \frac{{\mathfrak{z}}^{\ast }}{{\mathfrak{z}}_i(\mathfrak{t}+\hslash \vartheta )}}\right)({\displaystyle \frac{d_1}{k^2}}{\mathsf{\Delta }}^2{\mathfrak{z}}_{i-1}(\mathfrak{t}+\hslash \vartheta )+b{\mathfrak{w}}_i(\mathfrak{t}+\hslash \vartheta )-{\mathfrak{z}}_i(\mathfrak{t}+\hslash \vartheta )\hfill \\ \hfill & +{\mathfrak{z}}_i^2(\mathfrak{t}+\hslash \vartheta ){\mathfrak{w}}_i(\mathfrak{t}+\hslash \vartheta )),\hfill \\ \hfill & \le \sum _{i=1}^m\left(1-{\displaystyle \frac{{\mathfrak{z}}^{\ast }}{{\mathfrak{z}}_i(\mathfrak{t}+\hslash \vartheta )}}\right)(b{\mathfrak{w}}_i(\mathfrak{t}+\hslash \vartheta )-b{\mathfrak{w}}^{\ast }-{\mathfrak{z}}_i(\mathfrak{t}+\hslash \vartheta )+{\mathfrak{z}}^{\ast }\hfill \\ \hfill & +{\mathfrak{z}}_i^2(\mathfrak{t}+\hslash \vartheta ){\mathfrak{w}}_i(\mathfrak{t}+\hslash \vartheta )-{\mathfrak{z}}^{2\ast }{\mathfrak{w}}^{\ast })\hfill \\ \hfill & +{\displaystyle \frac{d_1}{k^2}}\left(1-{\displaystyle \frac{{\mathfrak{z}}^{\ast }}{{\mathfrak{z}}_i(\mathfrak{t}+\hslash \vartheta )}}\right)({\mathfrak{z}}_{i+1}(\mathfrak{t}+\hslash \vartheta )-2{\mathfrak{z}}_i(\mathfrak{t}+\hslash \vartheta )+{\mathfrak{z}}_{i-1}(\mathfrak{t}+\hslash \vartheta )).\hfill \end{array}$$

Using (6), we obtain

$$\begin{array}{cc}\hfill {}_{\hslash }^C{\mathsf{\Delta }}_{{\mathfrak{t}}_0}^{\vartheta }{\mathfrak{L}}_1\left(\mathfrak{t}\right)& \le \sum _{i=1}^{m}b{\mathfrak{w}}^{\ast }\left(1-{\displaystyle \frac{{\mathfrak{z}}^{\ast }}{{\mathfrak{z}}_i(\mathfrak{t}+\hslash \vartheta )}}\right)\left(1-{\displaystyle \frac{{\mathfrak{w}}_i(\mathfrak{t}+\hslash \vartheta )}{{\mathfrak{w}}^{\ast }}}\right)\hfill \\ \hfill & -{\mathfrak{z}}^{2\ast }{\mathfrak{w}}^{\ast }\left(1-{\displaystyle \frac{{\mathfrak{z}}^{\ast }}{{\mathfrak{z}}_i(\mathfrak{t}+\hslash \vartheta )}}\right)\left(1-{\displaystyle \frac{{\mathfrak{z}}_i^2(\mathfrak{t}+\hslash \vartheta ){\mathfrak{w}}_i(\mathfrak{t}+\hslash \vartheta )}{{\mathfrak{z}}^{2\ast }{\mathfrak{w}}^{\ast }}}\right)\hfill \\ \hfill & +{\mathfrak{z}}^{\ast }\left(1-{\displaystyle \frac{{\mathfrak{z}}^{\ast }}{{\mathfrak{z}}_i(\mathfrak{t}+\hslash \vartheta )}}\right)\left(1-{\displaystyle \frac{{\mathfrak{z}}_i(\mathfrak{t}+\hslash \vartheta )}{{\mathfrak{z}}^{\ast }}}\right)+\sum _{i=1}^m{\displaystyle \frac{d_1}{k^2}}({\mathfrak{z}}_{i+1}(\mathfrak{t}+\hslash \gamma )\hfill \\ \hfill & -2{\mathfrak{z}}_i(\mathfrak{t}+\hslash \gamma )+{\mathfrak{z}}_{i-1}(\mathfrak{t}+\hslash \gamma ))-{\displaystyle \frac{d_1}{k^2}}{\mathfrak{z}}^{\ast }\left({\displaystyle \frac{{\mathfrak{z}}_{i+1}(\mathfrak{t}+\hslash \vartheta )}{{\mathfrak{z}}_i(\mathfrak{t}+\hslash \vartheta )}}+{\displaystyle \frac{{\mathfrak{z}}_{i-1}(\mathfrak{t}+\hslash \vartheta )}{{\mathfrak{z}}_i(\mathfrak{t}+\hslash \vartheta )}}-2\right),\hfill \\ \hfill & \le \sum _{i=1}^m-b{\mathfrak{w}}^{\ast }\left(\mathfrak{l}\left({\displaystyle \frac{{\mathfrak{z}}^{\ast }}{{\mathfrak{z}}_i(\mathfrak{t}+\hslash \vartheta )}}\right)+\mathfrak{l}\left({\displaystyle \frac{{\mathfrak{w}}_i(\mathfrak{t}+\hslash \vartheta )}{{\mathfrak{w}}^{\ast }}}\right)-\mathfrak{l}\left({\displaystyle \frac{{\mathfrak{w}}_i(\mathfrak{t}+\hslash \vartheta ){\mathfrak{z}}^{\ast }}{{\mathfrak{w}}^{\ast }{\mathfrak{z}}_i(\mathfrak{t}+\hslash \vartheta )}}\right)\right)\hfill \\ \hfill & +{\mathfrak{z}}^{2\ast }{\mathfrak{w}}^{\ast }\left(\mathfrak{l}\left({\displaystyle \frac{{\mathfrak{z}}^{\ast }}{{\mathfrak{z}}_i(\mathfrak{t}+\hslash \vartheta )}}\right)-\mathfrak{l}\left({\displaystyle \frac{{\mathfrak{w}}_i(\mathfrak{t}+\hslash \vartheta ){\mathfrak{z}}_i(\mathfrak{t}+\hslash \vartheta )}{{\mathfrak{z}}^{\ast }{\mathfrak{w}}^{\ast }}}\right)+\mathfrak{l}\left({\displaystyle \frac{{\mathfrak{z}}^2(\mathfrak{t}+\hslash \vartheta )\mathfrak{w}(\mathfrak{t}+\hslash \vartheta )}{{\mathfrak{z}}^{2\ast }{\mathfrak{w}}^{\ast }}}\right)\right)\hfill \\ \hfill & -{\mathfrak{z}}^{\ast }\left(\mathfrak{l}\left({\displaystyle \frac{{\mathfrak{z}}^{\ast }}{{\mathfrak{z}}_i(\mathfrak{t}+\hslash \vartheta )}}\right)+\mathfrak{l}\left({\displaystyle \frac{{\mathfrak{z}}_i(\mathfrak{t}+\hslash \vartheta )}{{\mathfrak{z}}^{\ast }}}\right)\right)\hfill \\ \hfill & +{\displaystyle \frac{d_1}{k^2}}\left({\mathfrak{z}}_{m+1}(\mathfrak{t}+\hslash \vartheta )-2{\mathfrak{z}}_m(\mathfrak{t}+\hslash \vartheta )+{\mathfrak{z}}_0(\mathfrak{t}+h\gamma )-{\mathfrak{z}}_1(\mathfrak{t}+\hslash \vartheta )\right)\hfill \\ \hfill & -{\mathfrak{z}}^{\ast }{\displaystyle \frac{d_1}{k^2}}\left({\displaystyle \frac{{\mathfrak{z}}_{i+1}(\mathfrak{t}+\hslash \vartheta )}{{\mathfrak{z}}_i(\mathfrak{t}+\hslash \vartheta )}}-2+{\displaystyle \frac{{\mathfrak{z}}_{i-1}(\mathfrak{t}+\hslash \vartheta )}{{\mathfrak{z}}_i(\mathfrak{t}+\hslash \vartheta )}}\right),\hfill \\ \hfill & \le \sum _{i=1}^m(-b{\mathfrak{w}}^{\ast }+{\mathfrak{z}}^{2\ast }{\mathfrak{w}}^{\ast }-{\mathfrak{z}}^{\ast })\mathfrak{l}\left({\displaystyle \frac{{\mathfrak{z}}^{\ast }}{{\mathfrak{z}}_i(\mathfrak{t}+\hslash \vartheta )}}\right)-b{\mathfrak{w}}^{\ast }\mathfrak{l}\left({\displaystyle \frac{{\mathfrak{z}}_i(\mathfrak{t}+\hslash \vartheta )}{{\mathfrak{z}}^{\ast }}}\right)-{\mathfrak{z}}^{\ast }\mathfrak{l}\left({\displaystyle \frac{{\mathfrak{w}}_i(\mathfrak{t}+\hslash \vartheta )}{{\mathfrak{w}}^{\ast }}}\right)\hfill \\ \hfill & +{\mathfrak{z}}^{2\ast }{\mathfrak{w}}^{\ast }\mathfrak{l}\left({\displaystyle \frac{{\mathfrak{z}}^2(\mathfrak{t}+\hslash \vartheta )\mathfrak{w}(\mathfrak{t}+\hslash \vartheta )}{{\mathfrak{z}}^{2\ast }{v}^{\ast }}}\right)-{\mathfrak{z}}^{2\ast }{\mathfrak{w}}^{\ast }\mathfrak{l}\left({\displaystyle \frac{{\mathfrak{w}}_i(\mathfrak{t}+\hslash \vartheta ){\mathfrak{z}}_i(\mathfrak{t}+\hslash \vartheta )}{{\mathfrak{z}}^{\ast }{\mathfrak{w}}^{\ast }}}\right)+{\mathfrak{z}}^{\ast }\mathfrak{l}\left({\displaystyle \frac{{\mathfrak{w}}_i(\mathfrak{t}+\hslash \vartheta ){\mathfrak{z}}^{\ast }}{{\mathfrak{w}}^{\ast }{\mathfrak{z}}_i(t+\hslash \vartheta )}}\right)\hfill \\ \hfill & -{\mathfrak{z}}^{\ast }{\displaystyle \frac{d_1}{k^2}}\left({\displaystyle \frac{{\mathfrak{z}}_{i+1}(\mathfrak{t}+\hslash \vartheta )}{{\mathfrak{z}}_i(\mathfrak{t}+\hslash \vartheta )}}-2+{\displaystyle \frac{{\mathfrak{z}}_{i-1}(\mathfrak{t}+\hslash \vartheta )}{{\mathfrak{z}}_i(\mathfrak{t}+\hslash \vartheta )}}\right).\hfill \end{array}$$

Now, we have

$$\begin{array}{cc}\hfill {}_{\hslash }^C{\mathsf{\Delta }}_{{\mathfrak{t}}_0}^{\vartheta }{\mathfrak{L}}_2\left(\mathfrak{t}\right)& =\sum _{i=1}^m{}_{\hslash }^C{\mathsf{\Delta }}_{{\mathfrak{t}}_0}^{\vartheta }{\mathfrak{w}}^{\ast }\mathfrak{l}\left({\displaystyle \frac{{\mathfrak{w}}_i\left(\mathfrak{t}\right)}{{\mathfrak{w}}^{\ast }}}\right),\hfill \\ \hfill & \le \sum _{i=1}^m\left(1-{\displaystyle \frac{{\mathfrak{w}}^{\ast }}{{\mathfrak{w}}_i(\mathfrak{t}+\hslash \vartheta )}}\right){}_{\hslash }^C{\mathsf{\Delta }}_{{\mathfrak{t}}_0}^{\vartheta }{\mathfrak{w}}_i\left(\mathfrak{t}\right),\hfill \\ \hfill & \le \sum _{i=1}^m\left(1-{\displaystyle \frac{{\mathfrak{w}}^{\ast }}{{\mathfrak{w}}_i(\mathfrak{t}+\hslash \vartheta )}}\right)\left({\displaystyle \frac{d_2}{k^2}}{\mathsf{\Delta }}^2{\mathfrak{w}}_{i-1}(\mathfrak{t}+\hslash \vartheta )+a-b{\mathfrak{w}}_i(\mathfrak{t}+\hslash \vartheta )-{\mathfrak{z}}_i^2(\mathfrak{t}+\hslash \vartheta ){\mathfrak{w}}_i(\mathfrak{t}+\hslash \vartheta )\right),\hfill \\ \hfill & \le \sum _{i=1}^m\left(1-{\displaystyle \frac{{\mathfrak{w}}^{\ast }}{{\mathfrak{w}}_i(\mathfrak{t}+\hslash \vartheta )}}\right)\left(b{\mathfrak{w}}^{\ast }+{\mathfrak{z}}^{2\ast }{\mathfrak{w}}^{\ast }-b{\mathfrak{w}}_i(\mathfrak{t}+\hslash \vartheta )-{\mathfrak{z}}_i^2(\mathfrak{t}+\hslash \vartheta ){\mathfrak{w}}_i(\mathfrak{t}+\hslash \vartheta )\right),\hfill \\ \hfill & +{\displaystyle \frac{d_2}{k^2}}\sum _{i=1}^m\left(1-{\displaystyle \frac{{\mathfrak{w}}^{\ast }}{{\mathfrak{w}}_i(\mathfrak{t}+\hslash \vartheta )}}\right)({\mathfrak{z}}_{i+1}\left(\mathfrak{t}\right)-2{\mathfrak{z}}_i\left(\mathfrak{t}\right)+{\mathfrak{z}}_{i-1}\left(\mathfrak{t}\right))+o\left(1\right),\hfill \\ \hfill & \le \sum _{i=1}^{m}b{\mathfrak{w}}^{\ast }\left(1-{\displaystyle \frac{{\mathfrak{w}}^{\ast }}{{\mathfrak{w}}_i(\mathfrak{t}+\hslash \vartheta )}}\right)\left(1-{\displaystyle \frac{{\mathfrak{w}}_i(\mathfrak{t}+\hslash \vartheta )}{{\mathfrak{w}}^{\ast }}}\right)\hfill \\ \hfill & +{\mathfrak{w}}^{\ast }{\mathfrak{z}}^{2\ast }\left(1-{\displaystyle \frac{{\mathfrak{w}}^{\ast }}{{\mathfrak{w}}_i(\mathfrak{t}+h\gamma )}}\right)\left(1-{\displaystyle \frac{{\mathfrak{w}}_i(\mathfrak{t}+\hslash \vartheta ){\mathfrak{z}}_i^2(\mathfrak{t}+\hslash \vartheta )}{{\mathfrak{w}}^{\ast }{u}^{2\ast }}}\right)\hfill \\ \hfill & +\sum _{i=1}^m{\displaystyle \frac{d_2}{k^2}}\left({\mathfrak{w}}_{i+1}(\mathfrak{t}+\hslash \vartheta )-2{\mathfrak{w}}_i(\mathfrak{t}+\hslash \vartheta )+{\mathfrak{w}}_{i-1}(\mathfrak{t}+\hslash \vartheta )\right)\hfill \\ \hfill & -{\displaystyle \frac{d_2}{k^2}}{\mathfrak{w}}^{\ast }\left({\displaystyle \frac{{\mathfrak{w}}_{i+1}(\mathfrak{t}+\hslash \vartheta )}{{\mathfrak{w}}_i(\mathfrak{t}+\hslash \vartheta )}}+{\displaystyle \frac{{\mathfrak{w}}_{i-1}(\mathfrak{t}+\hslash \vartheta )}{{\mathfrak{w}}_i(\mathfrak{t}+\hslash \vartheta )}}-2\right),\hfill \\ \hfill & \le \sum _{i=1}^m-b{\mathfrak{w}}^{\ast }\left(\mathfrak{l}\left({\displaystyle \frac{{\mathfrak{w}}^{\ast }}{{\mathfrak{w}}_i(\mathfrak{t}+\hslash \vartheta )}}\right)+\mathfrak{l}\left({\displaystyle \frac{{\mathfrak{w}}_i(\mathfrak{t}+\hslash \vartheta )}{{\mathfrak{w}}^{\ast }}}\right)\right)\hfill \\ \hfill & +{\mathfrak{w}}^{\ast }{\mathfrak{z}}^{2\ast }\left(-\mathfrak{l}\left({\displaystyle \frac{{\mathfrak{w}}^{\ast }}{{\mathfrak{w}}_i(\mathfrak{t}+\hslash \vartheta )}}\right)+\mathfrak{l}\left({\displaystyle \frac{{\mathfrak{z}}^{2\ast }}{{\mathfrak{z}}_i^2(\mathfrak{t}+\hslash \vartheta )}}\right)-\mathfrak{l}\left({\displaystyle \frac{{\mathfrak{w}}_i(\mathfrak{t}+\hslash \vartheta ){\mathfrak{z}}_i^2(\mathfrak{t}+\hslash \vartheta )}{{\mathfrak{w}}^{\ast }{\mathfrak{z}}^{2\ast }}}\right)\right)\hfill \\ \hfill & +{\displaystyle \frac{d_2}{k^2}}\left({\mathfrak{w}}_{m+1}(\mathfrak{t}+\hslash \vartheta )-2{\mathfrak{w}}_m(\mathfrak{t}+\hslash \vartheta )+{\mathfrak{w}}_0(\mathfrak{t}+\hslash \vartheta )-{\mathfrak{w}}_1(\mathfrak{t}+\hslash \vartheta )\right)\hfill \\ \hfill & -{\mathfrak{w}}^{\ast }{\displaystyle \frac{d_2}{k^2}}\left({\displaystyle \frac{{\mathfrak{w}}_{i+1}(\mathfrak{t}+\hslash \vartheta )}{{\mathfrak{w}}_i(\mathfrak{t}+\hslash \vartheta )}}-2+{\displaystyle \frac{{\mathfrak{w}}_{i-1}(\mathfrak{t}+\hslash \vartheta )}{{\mathfrak{w}}_i(\mathfrak{t}+\hslash \vartheta )}}\right),\hfill \\ \hfill & \le \sum _{i=1}^m(-b{\mathfrak{w}}^{\ast }-{\mathfrak{w}}^{\ast }{\mathfrak{z}}^{2\ast })\mathfrak{l}\left({\displaystyle \frac{{\mathfrak{w}}^{\ast }}{{\mathfrak{w}}_i(\mathfrak{t}+\hslash \vartheta )}}\right)-b{\mathfrak{w}}^{\ast }\mathfrak{l}\left({\displaystyle \frac{{\mathfrak{w}}_i(\mathfrak{t}+\hslash \vartheta )}{{\mathfrak{w}}^{\ast }}}\right)+{\mathfrak{w}}^{\ast }{\mathfrak{z}}^{2\ast }\mathfrak{l}\left({\displaystyle \frac{{\mathfrak{z}}_i^2(\mathfrak{t}+\hslash \vartheta )}{{\mathfrak{z}}^{2\ast }}}\right)\hfill \\ \hfill & -{\mathfrak{w}}^{\ast }{\mathfrak{z}}^{2\ast }\mathfrak{l}\left({\displaystyle \frac{{\mathfrak{w}}_i(\mathfrak{t}+\hslash \vartheta ){\mathfrak{z}}_i^2(\mathfrak{t}+\hslash \vartheta )}{{\mathfrak{w}}^{\ast }{\mathfrak{z}}^{2\ast }}}\right)-{\mathfrak{w}}^{\ast }{\displaystyle \frac{d_2}{k^2}}\left({\displaystyle \frac{{\mathfrak{w}}_{i+1}(\mathfrak{t}+\hslash \vartheta )}{{\mathfrak{w}}_i(\mathfrak{t}+\hslash \vartheta )}}-2+{\displaystyle \frac{{\mathfrak{w}}_{i-1}(\mathfrak{t}+\hslash \vartheta )}{{\mathfrak{w}}_i(\mathfrak{t}+\hslash \vartheta )}}\right).\hfill \end{array}$$

According to [28], we have

$$\begin{array}{cc}\hfill & {\displaystyle \frac{{\mathfrak{z}}_{i+1}(\mathfrak{t}+\hslash \vartheta )}{{\mathfrak{z}}_i(\mathfrak{t}+\hslash \vartheta )}}-2+{\displaystyle \frac{{\mathfrak{z}}_{i-1}(\mathfrak{t}+\hslash \vartheta )}{{\mathfrak{z}}_i(\mathfrak{t}+\hslash \vartheta )}}\ge 0,\hfill \\ \hfill & {\displaystyle \frac{{\mathfrak{w}}_{i+1}(\mathfrak{t}+\hslash \vartheta )}{{\mathfrak{w}}_i(\mathfrak{t}+\hslash \vartheta )}}-2+{\displaystyle \frac{{\mathfrak{w}}_{i-1}(\mathfrak{t}+\hslash \vartheta )}{{\mathfrak{w}}_i(\mathfrak{t}+\hslash \vartheta )}}\ge 0.\hfill \end{array}$$

We conclude that

$$\begin{array}{cc}\hfill {}_{\hslash }^C{\mathsf{\Delta }}_{{\mathfrak{t}}_0}^{\vartheta }\mathfrak{L}\left(\mathfrak{t}\right)& ={}_{\hslash }^C{\mathsf{\Delta }}_{{\mathfrak{t}}_0}^{\vartheta }{\mathfrak{L}}_1\left(\mathfrak{t}\right)+{}_{\hslash }^C{\mathsf{\Delta }}_{{\mathfrak{t}}_0}^{\vartheta }{\mathfrak{L}}_2\left(\mathfrak{t}\right),\hfill \\ \hfill & \le \sum _{i=1}^m(-b{\mathfrak{w}}^{\ast }+{\mathfrak{z}}^{2\ast }{\mathfrak{w}}^{\ast }-{\mathfrak{z}}^{\ast })\mathfrak{l}\left({\displaystyle \frac{{\mathfrak{z}}^{\ast }}{{\mathfrak{z}}_i(\mathfrak{t}+\hslash \vartheta )}}\right)+(-b{\mathfrak{w}}^{\ast }+2{\mathfrak{w}}^{\ast }{\mathfrak{z}}^{\ast 2})\mathfrak{l}\left({\displaystyle \frac{{\mathfrak{z}}_i(\mathfrak{t}+\hslash \vartheta )}{{\mathfrak{z}}^{\ast }}}\right)\hfill \\ \hfill & -(b{\mathfrak{w}}^{\ast }+{\mathfrak{z}}^{\ast })\mathfrak{l}\left({\displaystyle \frac{{\mathfrak{w}}_i(\mathfrak{t}+\hslash \vartheta )}{{\mathfrak{w}}^{\ast }}}\right)-(b{\mathfrak{w}}^{\ast }+{\mathfrak{w}}^{\ast }{\mathfrak{z}}^{\ast 2})\mathfrak{l}\left({\displaystyle \frac{{\mathfrak{w}}^{\ast }}{{\mathfrak{w}}_i(\mathfrak{t}+\hslash \vartheta )}}\right)\hfill \\ \hfill & -{\mathfrak{z}}^{2\ast }{\mathfrak{w}}^{\ast }\mathfrak{l}\left({\displaystyle \frac{{\mathfrak{w}}_i(\mathfrak{t}+\hslash \vartheta ){\mathfrak{z}}_i(\mathfrak{t}+\hslash \vartheta )}{{\mathfrak{z}}^{\ast }{\mathfrak{w}}^{\ast }}}\right)-{\mathfrak{z}}^{\ast }{\displaystyle \frac{d_1}{k^2}}\left({\displaystyle \frac{{\mathfrak{z}}_{i+1}(\mathfrak{t}+\hslash \vartheta )}{{\mathfrak{z}}_i(\mathfrak{t}+\hslash \vartheta )}}-2+{\displaystyle \frac{{\mathfrak{z}}_{i-1}(\mathfrak{t}+\hslash \vartheta )}{{\mathfrak{z}}_i(\mathfrak{t}+\hslash \vartheta )}}\right)\hfill \\ \hfill & -{\mathfrak{w}}^{\ast }{\displaystyle \frac{d_2}{k^2}}\left({\displaystyle \frac{{\mathfrak{w}}_{i+1}(\mathfrak{t}+\hslash \vartheta )}{{\mathfrak{w}}_i(\mathfrak{t}+\hslash \vartheta )}}-2+{\displaystyle \frac{{\mathfrak{w}}_{i-1}(\mathfrak{t}+\hslash \vartheta )}{{\mathfrak{w}}_i(\mathfrak{t}+\hslash \vartheta )}}\right).\hfill \end{array}$$

Hence, since $-b{\mathfrak{w}}^{\ast }+2{\mathfrak{w}}^{\ast }{\mathfrak{z}}^{\ast 2}\le 0$, then,

$${}_{\hslash }^C{\mathsf{\Delta }}_{{\mathfrak{t}}_0}^{\vartheta }\mathfrak{L}\left(\mathfrak{t}\right)\le 0$$

and ${}_{\hslash }^C{\mathsf{\Delta }}_{{\mathfrak{t}}_0}^{\vartheta }\mathfrak{L}\left(\mathfrak{t}\right)=0$ if and only if $({\mathfrak{z}}_i,{\mathfrak{w}}_i)=(0,0)$. $({\mathfrak{z}}^{\ast },{\mathfrak{w}}^{\ast })$ is therefore globally asymptotically stable under condition (36) according to Theorem 3. □

6. Simulations

Here, we demonstrate several simulations that illustrate certain theoretical aspects of the stability of the discrete fractional glycolysis reaction–diffusion system. Matlab was used to carry out all of the simulations in this section.

By changing the characteristics and order of the system, we are able to observe how it behaves. When we use the numerical solution shown below, system (11) looks like:

$$\left\{\begin{array}{c}{\mathfrak{z}}_i(n\hslash )={\varphi }_1\left({\mathfrak{z}}_i\right)+{\displaystyle \frac{{\hslash }^{\vartheta }}{\mathsf{\Gamma }\left(\vartheta \right)}}\sum _{\mathfrak{r}=1}^n{\displaystyle \frac{\mathsf{\Gamma }(n-\mathfrak{r}+\vartheta )}{\mathsf{\Gamma }(n-\mathfrak{r}+1)}}[d_1{\displaystyle \frac{{\mathfrak{z}}_{i+1}((\mathfrak{r}-1)\hslash )-2{\mathfrak{z}}_i((\mathfrak{r}-1)\hslash )+{\mathfrak{z}}_{i-1}((\mathfrak{r}-1)\hslash )}{k^2}}\hfill \\ +b{\mathfrak{z}}_i((\mathfrak{r}-1)\hslash )+{\mathfrak{z}}_i^2((\mathfrak{r}-1)\hslash ){\mathfrak{w}}_i((\mathfrak{r}-1)\hslash )],\hfill \\ {\mathfrak{w}}_i(n\hslash )={\varphi }_2\left({\mathfrak{z}}_i\right)+{\displaystyle \frac{{\hslash }^{\vartheta }}{\mathsf{\Gamma }\left(\vartheta \right)}}\sum _{\mathfrak{r}=1}^n{\displaystyle \frac{\mathsf{\Gamma }(n-\mathfrak{r}+\vartheta )}{\mathsf{\Gamma }(n-\mathfrak{r}+1)}}[d_2{\displaystyle \frac{{\mathfrak{w}}_{i+1}((\mathfrak{r}-1)\hslash )-2{\mathfrak{w}}_i((\mathfrak{r}-1)\hslash )+{\mathfrak{w}}_{i-1}((\mathfrak{r}-1)\hslash )}{k^2}}\hfill \\ +a-b{\mathfrak{z}}_i((\mathfrak{r}-1)\hslash )-{\mathfrak{w}}_i((\mathfrak{r}-1)\hslash )-{\mathfrak{z}}_i^2((\mathfrak{r}-1)\hslash ){\mathfrak{w}}_i((\mathfrak{r}-1)\hslash )],\hfill \\ 1\le i\le m,\hfill \\ n>0.\hfill \end{array}\right.$$

(37)

Example 1.

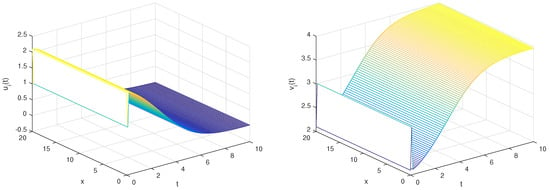
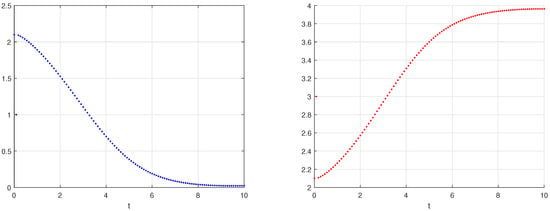
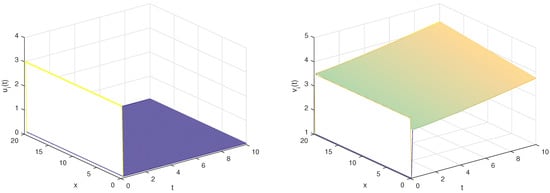
To demonstrate our point, we consider the following parameter values: $(d_1,d_2,a,b)=(1,2,0.1,0.01),N=100,\hslash =0.1,\mathfrak{t}\in [0,10],$ and $\mathfrak{z}\in [0,20]$ and the boundary conditions $({\mathfrak{z}}_0\left(\mathfrak{t}\right),$${\mathfrak{w}}_0\left(\mathfrak{t}\right))=(3,1),({\mathfrak{z}}_1\left(\mathfrak{t}\right),{\mathfrak{w}}_1\left(\mathfrak{t}\right))=(3,1)$. Also, we provide the following appropriate initial conditions:

$$\left\{\begin{array}{c}{\varphi }_1\left({\mathfrak{z}}_i\right)=3.5+{\displaystyle \frac{cos\left(\pi {\mathfrak{z}}_i\right)}{5}},\hfill \\ {\varphi }_2\left({\mathfrak{z}}_i\right)=2+{\displaystyle \frac{cos\left(\pi {\mathfrak{z}}_i\right)}{5}}.\hfill \end{array}\right.$$

We can see that all of the solutions to our model ultimately reach the same unique positive equilibrium $({\mathfrak{z}}^{\ast },{\mathfrak{w}}^{\ast })=(0.1,4)$. The unique equilibrium is hence asymptotically stable. For a, which denotes the dimensionless input flow, and b, which denotes the dimensionless constant rate for the low activity state, the conditions in Theorem 6 are clearly demonstrated, and this numerical finding is consistent with our earlier theoretical conclusions.

The results stated previously for various fractional orders are supported by Figure 1, Figure 2 and Figure 3, which describe the dynamic behavior of the system (11) and show that as the fractional order ϑ approaches 1, the model’s solution becomes more stable as it rapidly converges to the unique equilibrium.

7. Conclusions

In this study, a discrete equivalent of the fractional reaction–diffusion glycolysis model was investigated using the second-order central difference and L1 finite difference schemes. This unique approach’s capacity to keep the system confined and positive should be emphasized. Moreover, the local stability of the discrete system was explored. The results were consistent with those of the continuous system that serves as a continuous analog. This suggests that the discrete system generated by the considered schemes can preserve as continuous system characteristics like the positivity, boundedness, and global stability of the equilibrium point, which are first evaluated as a way to assess the stability of discrete fractional reaction diffusion systems using Lyapunov functions. Additionally, computations and simulations show the effectiveness and viability of the suggested system. In addition, the Lyapunov functional and the linearization approach may be utilized to solve the stability issue in discrete fractional reaction–diffusion models. More importantly, the results of this study might be easily extended to a variety of reaction–diffusion discrete fractional spatiotemporal systems, as well as other dynamical problems including chaos and synchronization control.