A Space-Time Finite Element Method for the Fractional Ginzburg–Landau Equation
Abstract
:1. Introduction
2. Preliminaries
3. The Fully Discrete Space-Time Finite Element Scheme
4. Well-Posedness
5. Error Estimate
6. Numerical Tests
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kilbas, A.; Srivastava, H.; Trujillo, J. Theory and Applications of Fractional Differential Equations; Elsevier Science: London, UK, 2006. J. Comput. Phys. 2017, 330, 863–883. [Google Scholar]
- Podlubny, I. Fractional Differential Equations; Academic Press: New York, NY, USA, 1999. [Google Scholar]
- Weitzner, H.; Zaslavsky, G. Some applications of fractional equations. Commun. Nonlinear Sci. Numer. Simul. 2003, 8, 273–281. [Google Scholar] [CrossRef] [Green Version]
- Tarasov, V.; Zaslavsky, G. Fractional Ginzburg-Landau equation for fractal media. Phys. A 2005, 354, 249–261. [Google Scholar] [CrossRef] [Green Version]
- Milovanov, A.; Rasmussen, J. Fractional generalization of the Ginzburg-Landau equation: An unconventional approach to critical phenomena in complex media. Phys. Lett. A 2005, 337, 75–80. [Google Scholar] [CrossRef] [Green Version]
- Mvogo, A.; Tambue, A.; Ben-Bolie, G.; Kofané, T. Localized numerical impulses solutions in diffuse neural networks modeled by the complex fractional Ginzburg-Landau equation. Commun. Nonlinear Sci. Numer. Simul. 2016, 39, 396–410. [Google Scholar] [CrossRef]
- Wang, P.; Huang, C. An implicit midpoint difference scheme for the fractional Ginzburg-Landau equation. J. Comput. Phys. 2016, 312, 31–49. [Google Scholar] [CrossRef] [Green Version]
- Hao, Z.; Sun, Z. A linearized high-order difference scheme for the fractional Ginzburg-Landau equation. Numer. Meth. Part. Differ. Equ. 2017, 33, 105–124. [Google Scholar] [CrossRef]
- Wang, N.; Huang, C. An efficient split-step quasi-compact finite difference method for the nonlinear fractional Ginzburg-Landau equations. Comput. Math. Appl. 2018, 75, 2223–2242. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhang, L.; Sun, H. A three-level finite difference method with preconditioning technique for two-dimensional nonlinear fractional complex Ginzburg-Landau equations. J. Comput. Appl. Math. 2021, 389, 113355. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, Q.; Sun, H. A fast compact difference method for two-dimensional nonlinear space-fractional complex Ginzburg-Landau equations. J. Comput. Math. 2021, 39, 682–706. [Google Scholar]
- Fei, M.; Li, W.; Yi, Y. Numerical analysis of a fourth-order linearized difference method for nonlinear time-space fractional Ginzburg-Landau equation. Electron. Res. Arch. 2022, 30, 3635–3659. [Google Scholar] [CrossRef]
- Zhang, Q.F.; Lin, X.; Pan, K.J.; Ren, Y. Linearized ADI schemes for two-dimensional space-fractional nonlinear Ginzburg-Landau equation. Comput. Math. Appl. 2020, 80, 1201–1220. [Google Scholar] [CrossRef]
- He, D.D.; Pan, K.J. An unconditionally stable linearized difference scheme for the fractional Ginzburg-Landau equation. Numer. Algor. 2018, 79, 899–925. [Google Scholar] [CrossRef]
- Ding, H.F.; Li, C.P. High-order numerical algorithm and error analysis for the two-dimensional nonlinear spatial fractional complex Ginzburg-Landau equation. Commun. Nonlinear Sci. Numer. Simulat. 2023, 120, 107160. [Google Scholar] [CrossRef]
- Ding, H.F.; Yi, Q. High-order numerical differential formulas of Riesz derivative with applications to nonlinear spatial fractional complex Ginzburg-Landau equations. Commun. Nonlinear Sci. Numer. Simulat. 2022, 110, 106394. [Google Scholar] [CrossRef]
- Li, M.; Huang, C.; Wang, N. Galerkin finite element method for the nonlinear fractional Ginzburg-Landau equation. Appl. Numer. Math. 2017, 118, 131–149. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, M.; Wang, Z. A linearized Crank-Nicolson Galerkin FEMs for the nonlinear fractional Ginzburg-Landau equation. Appl. Anal. 2019, 98, 2648–2667. [Google Scholar] [CrossRef]
- Yang, Z.; Yuan, Z.; Nie, Y.; Wang, J.; Zhu, X.; Liu, F. Finite element method for nonlinear Riesz space fractional diffusion equations on irregular domains. J. Comput. Phys. 2017, 330, 863–883. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Fan, E.Y.; Yin, B.L.; Li, H.; Wang, J.F. TT-M finite element algorithm for a two-dimensional space fractional Gray-Scott model. Comput. Math. Appl. 2020, 80, 1793–1809. [Google Scholar] [CrossRef]
- Nichell, R.; Sackman, J. Approximate solutions in linear coupled thermoelasticity. J. Appl. Mech. ASME Trans. 1968, 35, 255–266. [Google Scholar] [CrossRef]
- Oden, J. A general theory of finite elements II: Application. Int. J. Numer. Methods Eng. 1969, 1, 247–259. [Google Scholar] [CrossRef]
- Hulbert, G.; Hughes, T. Space-time finite element methods for second-order hyperbolic equations. Comput. Meth. Appl. Mech. Engrg. 1990, 84, 327–348. [Google Scholar] [CrossRef] [Green Version]
- Larsson, S.; Thomée, V.; Wahlbin, L. Numerical solution of parabolic integro-differential equations by the discontinuous Galerkin method. Math. Comput. 1998, 69, 45–71. [Google Scholar] [CrossRef] [Green Version]
- Karakashian, O.; Makridakis, C. A space-time finite element method for the nonlinear Schrödinger equation: The discontinuous Galerkin method. Math. Comp. 1998, 67, 479–499. [Google Scholar] [CrossRef] [Green Version]
- Li, H.; Liu, R. The space-time finite element methods for parabolic problems. Appl. Math. Mech. 2001, 22, 687–700. [Google Scholar] [CrossRef]
- Dong, Z.; Li, H. A space-time finite element method based on local projection stabilization in space and discontinuous Galerkin method in time for convection-diffusion-reaction equations. Appl. Math. Comput. 2021, 397, 125937. [Google Scholar] [CrossRef]
- Sharma, V.; Fujisawa, K.; Murakami, A. Space-time finite element method for transient and unconfined seepage flow analysis. Finite Elem. Anal. Des. 2021, 197, 103632. [Google Scholar] [CrossRef]
- Langer, U.; Schafelner, A. Adaptive space-time finite element methods for parabolic optimal control problems. J. Numer. Math. 2022, 30, 247–266. [Google Scholar] [CrossRef]
- Sharma, V.; Fujisawa, K.; Murakami, A.; Sasakawa, S. A methodology to control numerical dissipation characteristics of velocity based time discontinuous Galerkin space-time finite element method. Int. J. Numer. Methods Eng. 2022, 123, 5517–5545. [Google Scholar] [CrossRef]
- Popov, I.S. Space-time adaptive ADER-DG finite element method with LST-DG predictor and a posteriori sub-cell WENO finite-volume limiting for simulation of non-stationary compressible multicomponent reactive flows. J. Sci. Comput. 2023, 95, 44. [Google Scholar] [CrossRef]
- Mustapha, K. Time-stepping discontinuous Galerkin methods for fractional diffusion problems. Numer. Math. 2015, 130, 497–516. [Google Scholar] [CrossRef] [Green Version]
- Zheng, Y.; Zhao, Z. The time discontinuous space-time finite element method for fractional diffusion-wave equation. Appl. Numer. Math. 2020, 150, 105–116. [Google Scholar] [CrossRef]
- Liu, Y.; Yan, Y.; Khan, M. Discontinuous Galerkin time stepping method for solving linear space fractional partial differential equations. Appl. Numer. Math. 2017, 115, 200–213. [Google Scholar] [CrossRef] [Green Version]
- Liu, J.; Li, H.; Liu, Y.; He, S. Discontinuous space-time finite element method for a system of nonlinear fractional reaction-diffusion equations. Math. Numer. Sin. 2016, 38, 143–160. (In Chinese) [Google Scholar]
- Bu, W.; Shu, S.; Yue, X.; Xiao, A.; Zeng, W. Space-time finite element method for the multi-term time-space fractional diffusion equation on a two-dimensional domain. Comput. Math. Appl. 2019, 78, 1367–1379. [Google Scholar] [CrossRef]
- Yue, X.; Liu, M.; Shu, S.; Bu, W.; Xu, Y. Space-time finite element adaptive AMG for multi-term time fractional advection diffusion equations. Math. Meth. Appl. Sci. 2021, 44, 2769–2789. [Google Scholar] [CrossRef]
- Li, B.J.; Luo, H.; Xie, X.P. A space-time finite element method for fractional wave problems. Numer. Algor. 2020, 85, 1095–1121. [Google Scholar] [CrossRef] [Green Version]
- Mojtahedi, A.; Hokmabady, H.; Kouhi, M.; Mohammadyzadeh, S. A novel ANN-RDT approach for damage detection of a composite panel employing contact and non-contact measuring data. Compos. Struct. 2022, 279, 114794. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, F.; Anh, V. Galerkin finite element approximation of symmetric space-fractional partial differential equations. Appl. Math. Comput. 2010, 217, 2534–2545. [Google Scholar] [CrossRef]
- Ervin, V.; Roop, J. Variational formulation for the stationary fractional advection dispersion equation. Numer. Meth. Part. Differ. Equ. 2006, 22, 558–576. [Google Scholar] [CrossRef] [Green Version]
- Akrivis, G. Finite difference discretization of the cubic Schrödinger equation. IMA J. Numer. Anal. 1993, 13, 115–124. [Google Scholar] [CrossRef]
- Davis, P.J.; Rabinowitz, P. Methods of Numerical Integration; Academic Press: New York, NY, USA, 1975. [Google Scholar]
- Thomée, V. Galerkin Finite Element Methods for Parabolic Problems, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 1997. [Google Scholar]
- Akhmediev, N.; Afanasjev, V.; Soto-Crespo, J. Singularities and special soliton solutions of the cubic-quintic complex Ginzburg-Landau equation. Phys. Rev. E 1996, 53, 1190. [Google Scholar]
- Xu, Q.; Chang, Q. Difference methods for computing the Ginzburg-Landau equation in two dimensions. Numer. Meth. Part. Differ. Equ. 2011, 27, 507–528. [Google Scholar] [CrossRef]
- Guo, B.; Huo, Z. Well-posedness for the nonlinear fractional Schrodinger equation and inviscid limit behavior of solution for the fractional Ginzburg-Landau equation. Frac. Calc. Appl. Anal. 2013, 16, 226–242. [Google Scholar] [CrossRef]
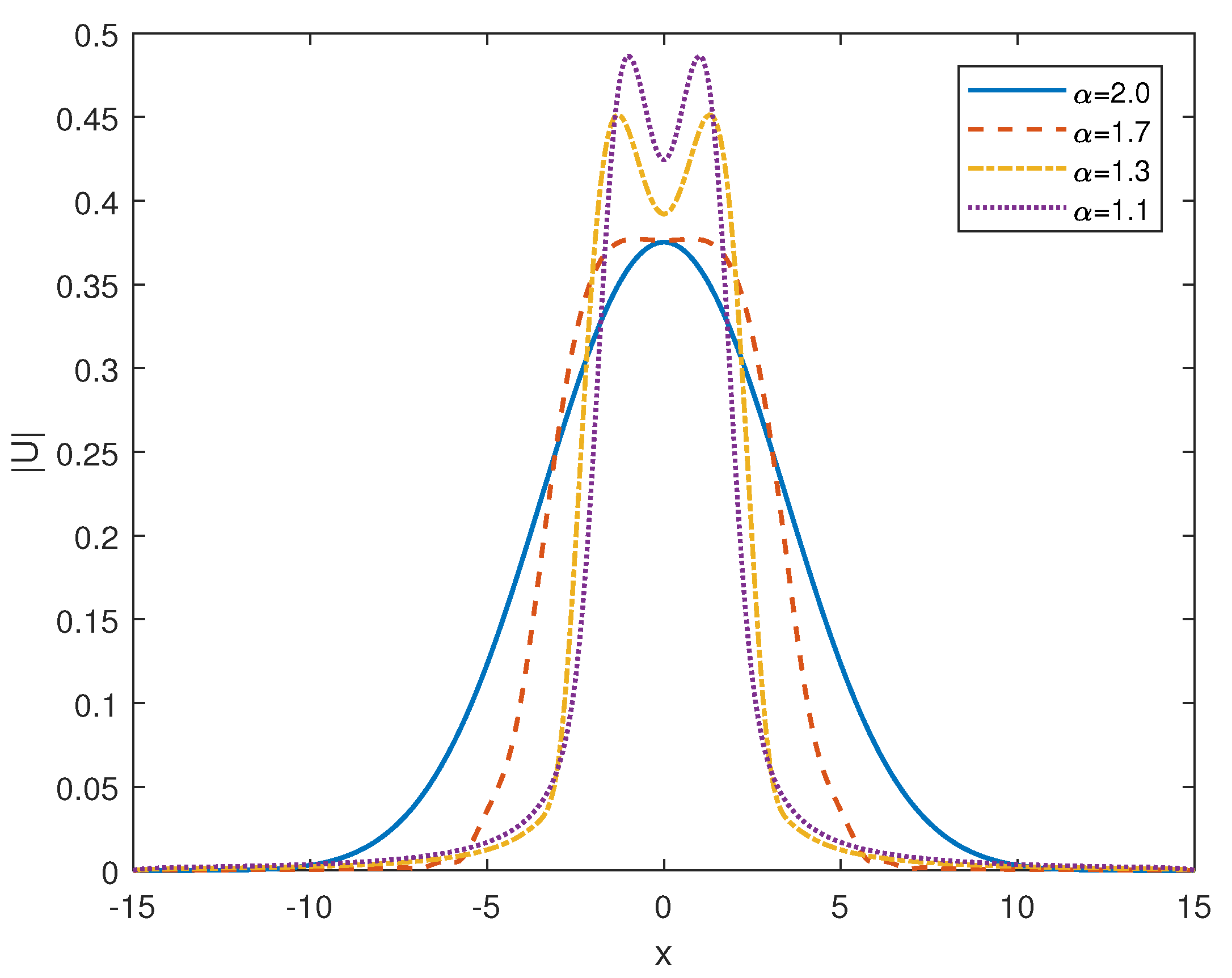





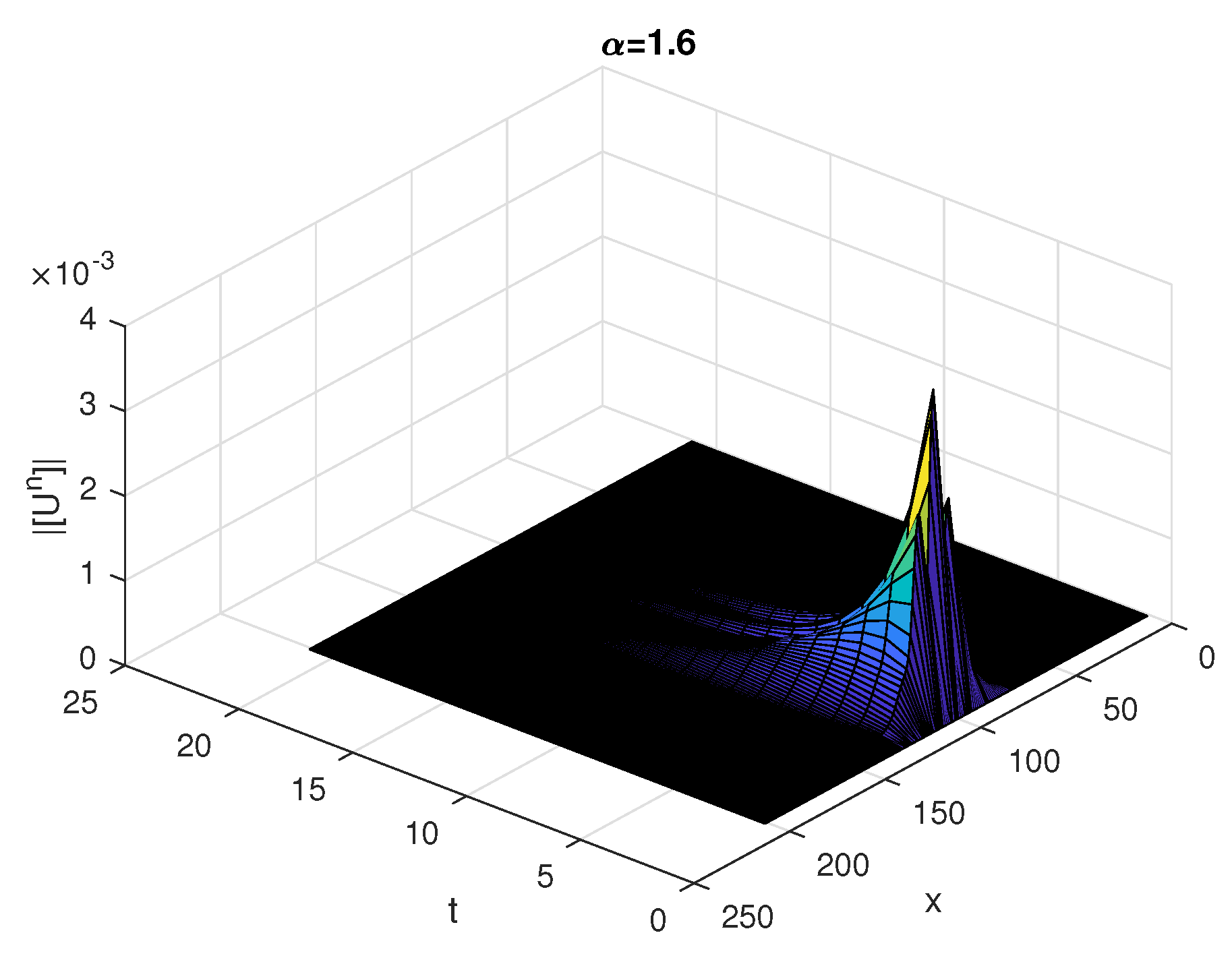
| 0.5000 | — | 0.5000 | — | ||
| 0.2500 | 1.7276 | 0.2500 | 1.6731 | ||
| 0.1250 | 1.8561 | 0.1250 | 1.9694 | ||
| 0.0625 | 1.8038 | 0.0625 | 2.0724 |
| 0.10000 | — | — | — | |||
| 0.05000 | 1.2823 | 1.2914 | 1.5740 | |||
| 0.02500 | 1.5018 | 1.5689 | 1.6221 | |||
| 0.01250 | 1.7936 | 1.7249 | 1.9787 | |||
| 0.00625 | 1.9910 | 1.9221 | 1.8903 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Li, H.; Liu, Y. A Space-Time Finite Element Method for the Fractional Ginzburg–Landau Equation. Fractal Fract. 2023, 7, 564. https://doi.org/10.3390/fractalfract7070564
Liu J, Li H, Liu Y. A Space-Time Finite Element Method for the Fractional Ginzburg–Landau Equation. Fractal and Fractional. 2023; 7(7):564. https://doi.org/10.3390/fractalfract7070564
Chicago/Turabian StyleLiu, Jincun, Hong Li, and Yang Liu. 2023. "A Space-Time Finite Element Method for the Fractional Ginzburg–Landau Equation" Fractal and Fractional 7, no. 7: 564. https://doi.org/10.3390/fractalfract7070564
APA StyleLiu, J., Li, H., & Liu, Y. (2023). A Space-Time Finite Element Method for the Fractional Ginzburg–Landau Equation. Fractal and Fractional, 7(7), 564. https://doi.org/10.3390/fractalfract7070564







