An Operational Approach to Fractional Scale-Invariant Linear Systems

Abstract

The fractional scale-invariant systems are introduced and studied, using an operational formalism. It is shown that the impulse and step responses of such systems belong to the vector space generated by some special functions here introduced. For these functions, the fractional scale derivative is a decremental index operator, allowing the construction of an algebraic framework that enables to compute the impulse and step responses of such systems. The effectiveness and accuracy of the method are demonstrated through various numerical simulations.

1. Introduction

The mathematical framework often used to define systems is based on shift-invariant derivatives [1,2], resulting from the works of Leibniz, Euler, Lagrange, and Liouville. However, a different concept was introduced by C. Braccini and G. Gambardella: the form-invariant linear filtering. It was a new kind of processing that was applied to several different fields such as optical pattern recognition, image restoration and reconstruction from projections [3]. This was the first step into the introduction of the scale-invariant linear systems, really done by B. Yazici and R. L. Kashyap for analysis and modelling 1/f phenomena and in general the self-similar processes, namely the scale stationary processes [4,5]. In parallel, physicists started studying the importance of scale in several physical systems [6,7,8,9,10,11,12,13]. Although the concept of scale is not very well defined, since it is a parameter expressing relative relations [6], the concept of scale-invariant system is well defined. While the shift-invariant systems are related and use in their definition the usual convolution [14] (D’Alembert’s) and corresponding derivatives, the scale-invariant systems are based on the Mellin’s convolution [15]. To fully define these systems the fractional scale-derivatives were introduced and studied [16], generalizing the classic Hadamard definitions [17]. These derivatives allow the formalization of linear scale-invariant systems of the autoregressive-moving average (ARMA) type [16,18]. With the use of the Mellin transform, the transfer functions of these systems assume a form identical to the one got from the shift-invariant systems through the use of the Laplace transform [19].

The objective of this paper is the study and search for the impulse and step responses of these systems. For this purpose, we first find a sequence of functions for which the fractional scale derivative behaves as a decremental index operator and then develop an algebraic framework similar to the one we used in the shift-invariant systems [20]. This approach allows us to closed forms for both the impulse and step responses of the systems.

The paper is organized as follows. Section 2 contains some preliminary results [16]. In Section 3 the sequence of functions ${\left\{u_k\left(\tau \right)\right\}}_k$ for which Hadamard right (left) derivative and fractional scale derivatives of type Grünwald-Letnikov are decremental index operators is founded. Section 3.2 contains the algebraic framework needed to solve fractional scale-invariant systems. In Section 4 we present an operational method based on algebraic framework introduced in Section 3. Numerical examples are solved in Section 5. Finally, Section 6 contains the main conclusions.

2. Scale–Invariant Systems and Derivatives

2.1. The Mellin Convolution

Definition 1. 

We call a linear system scale-invariant or dilation-invariant (DI) if its input–output relation is given by the Mellin convolution [16]

$$y\left(\tau \right)=x\left(\tau \right)★g\left(\tau \right)=\underset{0}{\overset{\infty }{\int }}x\left(\frac{\tau }{\eta }\right)g\left(\eta \right)\frac{d\eta }{\eta },$$

where $\tau \in {\mathbb{R}}^{+},$ and $g\left(\tau \right)$ is the impulse response: the response to $x\left(\tau \right)=\delta (\tau -1)$.

We demand that the impulse response, $g\left(t\right)$, be at least

• piecewise continuous,
• with bounded variation.

Similarly to the shift-invariant case, where the exponentials are the eigenfunctions, the powers $x\left(\tau \right)={\tau }^v,\tau \in {\mathbb{R}}^{+},v\in \mathbb{C},$ are the eigenfunctions of the dilation-invariant systems. In fact, if the input is $x\left(\tau \right)={\tau }^v,$ then the output is

$$y\left(\tau \right)=x\left(\tau \right)★g\left(\tau \right)=G\left(v\right){\tau }^v,$$

where $G\left(v\right)$ is the transfer function given by

$$G\left(v\right)=\underset{0}{\overset{\infty }{\int }}g\left(u\right)u^{-v-1}du,$$

(1)

which is a modifed version of the Mellin transform (MT) of the impulse response. The Mellin transform in (1), denoted by $\mathcal{M}\left[g\right(\tau \left)\right]\left(v\right)$, has a parameter sign change $-v\to v$ relatively to the usual Mellin transform [15,21,22].

Suppose that $\mathcal{M}\left[f\right(\tau \left)\right]\left(v\right)$ and $\mathcal{M}\left[g\right(\tau \left)\right]\left(v\right)$ exist in the regions of convergence (ROC) $a_1<Re\left(v\right)<b_1$ and $a_2<Re\left(v\right)<b_2$, respectively. An important property of Mellin convolution is

$$\mathcal{M}\left[f\left(\tau \right)★g\left(\tau \right)\right]\left(v\right)=F\left(v\right)G\left(v\right),max(a_1,a_2)<Re\left(v\right)<min(b_1,b_2),$$

where $F\left(v\right)$ and $G\left(v\right)$ are the Mellin transforms of f and g, respectively. The inverse Mellin transform related to (1) is

$$x\left(\tau \right)={\mathcal{M}}^{-1}\left[X\left(v\right)\right]={\displaystyle \frac{1}{2\pi i}}\underset{\gamma }{\int }X\left(v\right){\tau }^{v}dv,\tau \in {\mathbb{R}}^{+},$$

where $\gamma$ is vertical straight line in the ROC of the transform.

2.2. Scale-Derivatives

Definition 2. 

Let $\alpha \in \mathbb{R}$. We define the α-order scale derivative (SD) as the operator ${\mathfrak{D}}_s$ obeying the rule [16,23]

$${\mathfrak{D}}_s^{\alpha }{\tau }^v=v^{\alpha }{\tau }^v,\tau \in {\mathbb{R}}^{+},v\in \mathbb{C},$$

for $Re\left(v\right)>0$ (expansion or stretching case) or $Re\left(v\right)<0$ (shrinking case).

If a function $x\left(\tau \right)$ has Mellin transform $X\left(v\right)$, then it has fractional scale-derivative that is given by

$$\mathfrak{M}\left[{\mathcal{D}}_s^{\alpha }x\left(\tau \right)\right]=v^{\alpha }X\left(v\right),$$

(2)

for a suitable ROC. The way how we express $v^{\alpha }$ imposes a form for the derivative. To start, we notice that we can consider two situations corresponding to the sign of $Re\left(v\right)$. If it is positive, we obtain stretching derivatives, while if it is negative, we obtain the shrinking one. For both, we can express the inverse Mellin transform of $v^{\alpha }X\left(v\right)$ in two different forms: summation or integral.

2.2.1. Stretching Derivatives: $Re\left(v\right)>0$ [16]

Let $\epsilon \left(\tau \right)$ be Heaviside step function. We have two ways of expressing $v^{\alpha }$:

$$v^{\alpha }=\left\{\begin{array}{c}\underset{q\to 1^{+}}{lim}{\left[{\displaystyle \frac{(1-q^{-v})}{lnq}}\right]}^{\alpha }={\displaystyle \sum _{n=0}^{\infty }{\displaystyle \frac{{(-\alpha )}_n}{n!}}{q}^{-nv}}\hfill \\ \mathcal{M}\left[{\displaystyle \frac{{ln}^{-\alpha -1}\left(\tau \right)}{\Gamma (-\alpha )}}\epsilon (\tau -1)\right]\hfill \end{array}\right.$$

(3)

These expressions lead to the following scale derivative [16]:

$${\mathfrak{D}}_{s+}^{\alpha }x\left(\tau \right)=\left\{\begin{array}{c}\underset{q\to 1^{+}}{lim}{ln}^{-\alpha }\left(q\right){\displaystyle \sum _{n=0}^{\infty }}\frac{{(-\alpha )}_n}{n!}x\left(\tau q^{-n}\right)\hfill \\ {\displaystyle \frac{1}{\Gamma (-\alpha )}}{\displaystyle \underset{0}{\overset{\tau }{\int }}}\left[x\left(u\right)-{\displaystyle \sum _{n=0}^{N-1}}{(-1)}^n{\displaystyle \frac{{\mathfrak{D}}_{s+}^{N}x\left(\tau \right)}{n!}}{ln}^n(\tau /u)\right]{ln}^{-\alpha -1}(\tau /u){\displaystyle \frac{du}{u}}\hfill \end{array}\right.$$

(4)

(the last expression is valid for any real order, provided that we assume the summation to be null for $N\le 0$). These relations can alternatively be expressed by the Hadamard derivatives:

• Hadamard right derivative [17,24]

  $${\mathfrak{D}}_{s+}^{\alpha }x\left(\tau \right)={\displaystyle \frac{1}{\Gamma (N-\alpha )}}{\mathfrak{D}}_{s+}^N\underset{1}{\overset{\infty }{\int }}x(\tau /\eta ){ln}^{N-\alpha -1}\left(\eta \right){\displaystyle \frac{d\eta }{\eta }}.$$

  (5)
• Hadamard–Liouville right derivative [16]

  $${\mathfrak{D}}_{s+}^{\alpha }x\left(\tau \right)={\displaystyle \frac{1}{\Gamma (N-\alpha )}}\underset{1}{\overset{\infty }{\int }}\left[{\mathfrak{D}}_{s+}^{N}x\left(\tau \right)\right]{ln}^{N-\alpha -1}(\tau /u){\displaystyle \frac{du}{u}}.$$

These derivatives are equivalent from the Mellin transform point of view, although not from numerical aspects.

2.2.2. Shrinking Derivatives: $Re\left(v\right)<0$ [16]

We have again two ways of expressing $v^{\alpha }$:

$$v^{\alpha }=\left\{\begin{array}{c}\underset{q\to 1^{+}}{lim}{(-1)}^{\alpha }{\left[{\displaystyle \frac{(1-q^v)}{lnq}}\right]}^{\alpha }={\displaystyle {\displaystyle \sum _{n=0}^{\infty }}{\displaystyle \frac{{(-\alpha )}_n}{n!}}{q}^{nv}}\hfill \\ \mathcal{M}\left[{\displaystyle \frac{{ln}^{-\alpha -1}(1/\tau )}{\Gamma (-\alpha )}}\epsilon (1-\tau )\right]\hfill \end{array}\right.$$

These expressions lead to the following scale derivative [16]:

$${\mathfrak{D}}_{s-}^{\alpha }x\left(\tau \right)=\left\{\begin{array}{c}\underset{q\to 1^{+}}{lim}{(-1)}^{\alpha }{ln}^{-\alpha }\left(q\right){\displaystyle \sum _{n=0}^{\infty }}\frac{{(-\alpha )}_n}{n!}x\left(\tau q^n\right)\hfill \\ {\displaystyle \frac{1}{\Gamma (-\alpha )}}{\displaystyle \underset{\tau }{\overset{\infty }{\int }}}\left[x\left(u\right)-{\displaystyle \sum _{n=0}^{N-1}}{\displaystyle \frac{{\mathfrak{D}}_{s-}^{N}x\left(\tau \right)}{n!}}{ln}^n(u/\tau )\right]{ln}^{-\alpha -1}(u/\tau ){\displaystyle \frac{du}{u}}\hfill \end{array}\right.$$

(6)

that can alternatively be expressed by the Hadamard derivatives

• Hadamard left derivative [17,24]

  $${\mathfrak{D}}_{s-}^{\alpha }x\left(\tau \right)={\displaystyle \frac{1}{\Gamma (N-\alpha )}}{\mathfrak{D}}_{s-}^N\underset{0}{\overset{1}{\int }}x(\tau /\eta ){ln}^{N-\alpha -1}(1/\eta ){\displaystyle \frac{d\eta }{\eta }}.$$
• Hadamard–Liouville left derivative [16]

  $${\mathfrak{D}}_{s-}^{\alpha }x\left(\tau \right)={\displaystyle \frac{1}{\Gamma (N-\alpha )}}\underset{0}{\overset{1}{\int }}\left[{\mathfrak{D}}_{s-}^{N}x\left(\tau \right)\right]{ln}^{N-\alpha -1}(u/\tau ){\displaystyle \frac{du}{u}}.$$

2.3. ARMA Type Systems

Definition 3. 

We define the dilation (scale)-invariant fractional autoregressive-moving average (DI-FARMA) system through

$$\sum _{k=0}^{N_0}{a}_k{\mathfrak{D}}_{s\pm }^{{\alpha }_k}y\left(\tau \right)={\displaystyle \sum _{k=0}^{M_0}}{b}_k{\mathfrak{D}}_{s\pm }^{{\beta }_k}x\left(\tau \right),\tau \in {\mathbb{R}}^{+},$$

(7)

where ${\mathfrak{D}}_{s\pm }^{{\alpha }_k,\left({\beta }_k\right)},k=0,1,2,\cdots ,$ mean the fractional ${\alpha }_k\left({\beta }_k\right)$-order scale-derivatives and $N_0,M_0$ are the system orders. The parameters $a_k,b_k,k=0,1,\cdots ,$ are considered real numbers. Without losing generality, we set $a_{N_0}=1$.

The results in [25] can be easily adapted. As the power ${\tau }^v$ is the eigenfunction of (7), we obtain easily the transfer function

$$G\left(v\right)=\frac{{\displaystyle \sum _{k=0}^{M_0}}{b}_k{v}^{{\beta }_k}}{{\displaystyle \sum _{k=0}^{N_0}}{a}_k{v}^{{\alpha }_k}},$$

which is a bit difficult to manipulate [26]. In the following, we shall be considering the so-called “commensurate” systems described by differential equations with the format

$${\displaystyle \sum _{k=0}^{N_0}}{a}_k{\mathfrak{D}}_{s\pm }^{k\alpha }y\left(\tau \right)={\displaystyle \sum _{k=0}^{M_0}}{b}_k{\mathfrak{D}}_{s\pm }^{k\alpha }x\left(\tau \right),\tau \in {\mathbb{R}}^{+}.$$

The corresponding transfer function is

$$G\left(v\right)=\frac{{\displaystyle \sum _{k=0}^{M_0}}{b}_k{v}^{k\alpha }}{{\displaystyle \sum _{k=0}^{N_0}}{a}_k{v}^{k\alpha }},$$

where we assume that $M_0<N_0$, for simplicity. The objective of our work is to find the impulse and step responses of systems. As expected, we have two cases in agreement with the assumed ROC.

3. The Algebraic Framework for Solving DI-FARMA Systems

3.1. Sequence of Basic Functions for Fractional Scale Derivatives

Definition 4. 

Let $\mathcal{S}$ be an operator and ${\left\{u_k\left(\tau \right)\right\}}_{k\in \mathbb{Z}}$ a sequence of functions, verifying

$$\mathcal{S}{u}_k\left(\tau \right)=u_{k-1}\left(\tau \right),k\in \mathbb{Z}.$$

(8)

We say that $\mathcal{S}$ is decremental index operator of the sequence of functions ${\left\{u_k\left(\tau \right)\right\}}_{k\in \mathbb{Z}}$.

Remark 1. 

A well known example involves the generalized shift-invariant derivatives, $D,$ and the power functions, stating

$$D{\displaystyle \frac{t^n}{n!}}\epsilon \left(t\right)={\displaystyle \frac{t^{n-1}}{(n-1)!}}\epsilon \left(t\right),n\in \mathbb{Z}$$

It has been extended and studied by several researchers [27,28,29].

The main goal in this section is to find sequence of functions ${\left\{u_k\left(\tau \right)\right\}}_{k\in \mathbb{Z}}$ verifying (8) for the scale derivatives, mainly the Hadamard’s.

Hadamard Right (Left) Derivative

In the following we shall be addressing the stretching derivative case ($Re\left(v\right)>0$); the case of the shrinking derivative ($Re\left(v\right)<0$) is analogous. We remember the result shown in Section 2.2.1

$${\mathcal{M}}^{-1}\left[v^{-\alpha }\right]\left(\tau \right)={\displaystyle \frac{{ln}^{\alpha -1}\left(\tau \right)}{\Gamma \left(\alpha \right)}}\epsilon (\tau -1),Re\left(v\right)>0,$$

(9)

which will be used in this subsection.

Theorem 1. 

Let $u_k\left(\tau \right)$ be given by

$$u_k\left(\tau \right)=\frac{{ln}^{k\alpha -1}\left(\tau \right)}{\Gamma \left(k\alpha \right)}\epsilon (\tau -1),k\in \mathbb{N}.$$

(10)

Then,

$${\mathfrak{D}}_{s+}^{\alpha }{u}_k\left(\tau \right)=u_{k-1}\left(\tau \right),k\in \mathbb{N}.$$

(11)

Proof. 

Let $\alpha >0$, $1\le \tau$ and $k\in \mathbb{N}$. Using (9) with order $k\alpha$,

$$\mathcal{M}\left[\frac{{ln}^{k\alpha -1}\left(\tau \right)}{\Gamma \left(k\alpha \right)}\epsilon (\tau -1)\right]=v^{-k\alpha },\alpha >0,k\ge 1.$$

(12)

Following (2), the derivative ${\mathfrak{D}}_{s+}^{\alpha }\left(\frac{{ln}^{k\alpha -1}\left(\tau \right)}{\Gamma \left(k\alpha \right)}\epsilon (\tau -1)\right)$ is given by

$$\begin{array}{cc}\hfill {\mathfrak{D}}_{s+}^{\alpha }\left({\displaystyle \frac{{ln}^{k\alpha -1}\left(\tau \right)}{\Gamma \left(k\alpha \right)}}\epsilon (\tau -1)\right)& ={\mathcal{M}}^{-1}\left[v^{\alpha }\mathcal{M}\left[\frac{{ln}^{k\alpha -1}\left(\tau \right)}{\Gamma \left(k\alpha \right)}\epsilon (\tau -1)\right]\right]\left(\tau \right)\hfill \\ \hfill & ={\mathcal{M}}^{-1}\left[v^{-(k-1)\alpha }\right]\left(\tau \right)\hfill \end{array}$$

Finally, from (12) we obtain that

$${\mathfrak{D}}_{s+}^{\alpha }{\displaystyle \frac{{ln}^{k\alpha -1}\left(\tau \right)}{\Gamma \left(k\alpha \right)}}\epsilon (\tau -1)={\displaystyle \frac{{ln}^{(k-1)\alpha -1}\left(\tau \right)}{\Gamma \left(\right(k-1\left)\alpha \right)}}\epsilon (\tau -1).$$

for $\alpha >0$ and $k\ge 1$. □

Remark 2. 

For the next result, we need to observe that [30]

$$u_0\left(\tau \right)=\frac{{ln}^{-1}\left(\tau \right)}{\Gamma \left(0\right)}\epsilon (\tau -1)=\delta (ln\left(\tau \right))\epsilon (\tau -1)=\delta (\tau -1).$$

Lemma 1. 

Let $\alpha >0$ and $1\le \tau$. For $u_0\left(\tau \right)=\frac{{ln}^{-1}\left(\tau \right)}{\Gamma \left(0\right)}\epsilon (\tau -1)$,

$${\mathfrak{D}}_{s+}^{\alpha }{u}_0\left(\tau \right)={\displaystyle \frac{{ln}^{-\alpha -1}\left(\tau \right)}{\Gamma (-\alpha )}}\epsilon (\tau -1).$$

Proof. 

From Remark 2 and (5) we obtain

$${\mathfrak{D}}_{s+}^{\alpha }{u}_0\left(\tau \right)={\displaystyle \frac{1}{\Gamma (N-\alpha )}}{\mathfrak{D}}_{s+}^N{\int }_1^{\infty }\delta \left({\displaystyle \frac{\tau }{\eta }}-1\right){ln}^{N-\alpha -1}\left(\eta \right){\displaystyle \frac{d\eta }{\eta }}$$

Performing the variable change $\omega =\frac{\tau }{\eta }$ we have that

$${\int }_1^{\infty }\delta \left({\displaystyle \frac{\tau }{\eta }}-1\right){ln}^{N-\alpha -1}\left(\eta \right){\displaystyle \frac{d\eta }{\eta }}={\int }_0^{\tau }\delta (\omega -1){ln}^{N-\alpha -1}\left({\displaystyle \frac{\tau }{\omega }}\right){\displaystyle \frac{d\omega }{\omega }}.$$

It follows that

$${\displaystyle \frac{1}{\Gamma (N-\alpha )}}{\mathfrak{D}}_{s+}^N{\int }_0^{\tau }\delta (\omega -1){ln}^{N-\alpha -1}\left({\displaystyle \frac{\tau }{\omega }}\right){\displaystyle \frac{d\omega }{\omega }}=0,\tau <1$$

and

$${\displaystyle \frac{1}{\Gamma (N-\alpha )}}{\mathfrak{D}}_{s+}^N{\int }_0^{\tau }\delta (\omega -1){ln}^{N-\alpha -1}\left({\displaystyle \frac{\tau }{\omega }}\right){\displaystyle \frac{d\omega }{\omega }}={\displaystyle \frac{{ln}^{-\alpha -1}\left(\tau \right)}{\Gamma (-\alpha )}},\tau \ge 1.$$

Therefore

$${\mathfrak{D}}_{s+}^{\alpha }{u}_0\left(\tau \right)={\displaystyle \frac{{ln}^{-\alpha -1}\left(\tau \right)}{\Gamma (-\alpha )}}\epsilon (\tau -1).$$

□

The previous Lemma tells us that ${\mathfrak{D}}_{s+}^{\alpha }{u}_0\left(\tau \right)=u_{-1}\left(\tau \right)$. So, we wonder what about ${\mathfrak{D}}_{s+}^{\alpha }{u}_{-1}\left(\tau \right)$. For this, from the additivity of operator ${\mathfrak{D}}_{s+}^{\alpha }$ we have that

$$\begin{array}{cc}\hfill {\mathfrak{D}}_{s+}^{\alpha }{u}_{-1}\left(\tau \right)& ={\mathfrak{D}}_{s+}^{\alpha }\left({\mathfrak{D}}_{s+}^{\alpha }{u}_0\left(\tau \right)\right)\hfill \\ \hfill & ={\mathfrak{D}}_{s+}^{2\alpha }{u}_0\left(\tau \right)\hfill \\ \hfill & ={\displaystyle \frac{{ln}^{-2\alpha -1}\left(\tau \right)}{\Gamma (-2\alpha )}}\epsilon (\tau -1)\hfill \\ \hfill & =u_{-2}\left(\tau \right)\hfill \end{array}$$

(13)

The penultimate equality follows from Lemma 1 with the order of the derivative equal to $2\alpha$. Following this reasoning we obtain that ${\mathfrak{D}}_{s+}^{\alpha }{u}_{-k}\left(\tau \right)={\mathfrak{D}}_{s+}^{\alpha }{u}_{-k-1}\left(\tau \right)$, $k\in \mathbb{N}$. Finally, we conclude that

Corollary 1. 

$${\mathfrak{D}}_{s+}^{\alpha }{u}_k\left(\tau \right)={\mathfrak{D}}_{s+}^{\alpha }{u}_{k-1}\left(\tau \right),\mathrm{for}\mathrm{any}k\in \mathbb{Z}.$$

(14)

Therefore Hadamard right (left) derivative is a decremental index operator on the sequence of functions (10).

Remark 3. 

The condition $Re\left(v\right)<0$ leads to the $0<\tau \le 1$ case. The construction of the $u_k\left(\tau \right)$’s is similar to case $1\le \tau$. Here we get that

$$u_k\left(\tau \right)={\displaystyle \frac{{ln}^{k\alpha -1}\left(\frac{1}{\tau }\right)}{\Gamma \left(k\alpha \right)}}\epsilon (1-\tau ).$$

It is not difficult to verify that

$${\mathfrak{D}}_{s+}^{\alpha }{u}_k\left(\tau \right)=u_{k-1}\left(\tau \right),\mathrm{for}\mathrm{any}k\in \mathbb{Z}.$$

Remark 4. 

As we previously mentioned the Hadamard right (left) derivative and scale derivative of type Grünwald-Letnikov are equivalent. Despite this, in Appendix A we verify that the scale derivative of type Grünwald-Letnikov is a decremental index operators on the same sequence of functions (10).

In some situations, it is more convenient to use the step response instead of the impulse response because this one has a singularity at $\tau =1$. Therefore, another definition of $u_k\left(\tau \right)$ for which both Hadamard right (left) derivative and fractional scale derivative of type Grünwald-Letnikov are decremental index operators is possible and desired. For $1\le \tau$

$$u_k\left(\tau \right)={\displaystyle \frac{{ln}^{k\alpha }\left(\tau \right)}{\Gamma (k\alpha +1)}}\epsilon (\tau -1),k\in \mathbb{Z},$$

and when $0<\tau \le 1$

$$u_k\left(\tau \right)={\displaystyle \frac{{ln}^{k\alpha }\left(\frac{1}{\tau }\right)}{\Gamma (k\alpha +1)}}\epsilon (1-\tau ),k\in \mathbb{Z}.$$

The justification can be seen in Appendix B.

3.2. The Framework

Let $u_k\left(\tau \right),k\in \mathbb{Z}$, having Mellin transform $U_k\left(v\right)$. Then, for any $k,m\in \mathbb{N}$

$$\begin{array}{cc}\hfill \mathcal{M}\left[u_k\left(\tau \right)★u_m\left(\tau \right)\right]\left(v\right)& =U_k\left(v\right)U_m\left(v\right).\hfill \end{array}$$

As $U_k\left(v\right)=v^{k\alpha }$ and $U_m\left(v\right)=v^{m\alpha }$, hence

$$U_k\left(v\right)U_m\left(v\right)=v^{(k+m)\alpha },Re\left(v\right)>0,$$

and

$$u_k\left(\tau \right)★u_m\left(\tau \right)={\mathcal{M}}^{-1}\left[v^{(k+m)\alpha }\right]=u_{k+m}\left(\tau \right).$$

Therefore, we extend this product to any $k,m\in \mathbb{Z}$ as follows

$$u_k\left(\tau \right)★u_m\left(\tau \right)=u_{k+m}\left(\tau \right).$$

(15)

Remark 5. 

Observe that

$${\mathfrak{D}}_{s+}^{n\alpha }{u}_k\left(\tau \right)=u_{-n}\left(\tau \right)★u_k\left(\tau \right)=u_{k-n}\left(\tau \right),k\in \mathbb{Z},n\in \mathbb{N}.$$

Consider ${\left\{u_k\left(\tau \right)\right\}}_{k\in \mathbb{Z}}$ as a sequence of basic functions. Let $\mathcal{F}$ be the set of all the formal Laurent series

$$\mathcal{F}=\left\{{\displaystyle \sum _{k=-n}^{\infty }}{c}_k{u}_k\left(\tau \right):n\in {\mathbb{N}}_0,c_k\in \mathbb{C}\right\}.$$

Several properties of $\mathcal{F}$ and the product (15) can be founded in [20,31]. Observe that

• $u_0\left(\tau \right)$ is the neutral element of the Mellin convolution, $u_0\left(\tau \right)★u_k\left(\tau \right)=u_k\left(\tau \right)$;
• the inverse element of $u_k\left(\tau \right)$ is $u_{-k}\left(\tau \right)$, $u_k\left(\tau \right)★u_{-k}\left(\tau \right)=u_0\left(\tau \right)$.

By means of Cauchy series product, we can extend the Mellin product, $★,$ to any elements of $\mathcal{F}$ as follows. Let $a_j,b_j$, two sequences of real numbers and define

$$a={\displaystyle \sum _{j=-k_a}^{\infty }}{a}_j{u}_j\left(\tau \right),$$

and

$$b={\displaystyle \sum _{j=-k_b}^{\infty }}{b}_j{u}_j\left(\tau \right),$$

as elements of $\mathcal{F}$. Then

$$a★b=f={\displaystyle \sum _{n=-k_a-k_b}^{\infty }}{f}_n{u}_n\left(\tau \right),$$

where

$$f_n=\sum _{-k_a\le k\le n+k_b}{a}_k{b}_{n-k}.$$

This product is associative and commutative. Under this multiplication $\mathcal{F}$ is a field.

Definition 5. 

Let us define the function

$${\mathcal{E}}_{\gamma ,n}\left(\tau \right)={\displaystyle \sum _{k=n+1}^{\infty }}\left(\genfrac{}{}{0pt}{}{k-1}{n}\right){\gamma }^{k-n-1}{u}_k\left(\tau \right),\gamma \in \mathbb{C},n\in {\mathbb{N}}_0.$$

that we will call α–log-exponential function.

We could define an analogue to the Mittag-Leffler function [16], but this one is more useful.

Let us introduce also the sequential convolution

$${(u_{-1}\left(\tau \right)-\gamma u_0\left(\tau \right))}_{★}^{m+1}=\underset{m+1-times}{\underbrace{(u_{-1}\left(\tau \right)-\gamma u_0\left(\tau \right))★\cdots ★(u_{-1}\left(\tau \right)-\gamma u_0\left(\tau \right))}}.$$

It is not difficult to verify that

$$(u_{-1}\left(\tau \right)-\gamma u_0\left(\tau \right))★{\mathcal{E}}_{\gamma ,0}\left(\tau \right)=u_0\left(\tau \right),$$

and in general,

$${(u_{-1}\left(\tau \right)-\gamma u_0\left(\tau \right))}_{★}^{n+1}★{\mathcal{E}}_{\gamma ,n}\left(\tau \right)=u_0\left(\tau \right).$$

The $\alpha$–log-exponential function has some useful properties [31]:

• Derivative on a parameter

  $${\displaystyle \frac{D_{\gamma }^n}{n!}}{\mathcal{E}}_{\gamma ,0}\left(\tau \right)={\mathcal{E}}_{\gamma ,n}\left(\tau \right),$$

  where $D_{\gamma }$ means usual derivative with respect to $\gamma$.
• Convolution of two different $\alpha$–log-exponential functions, but with the same parameter $\gamma$

  $${\mathcal{E}}_{\gamma ,m}\left(\tau \right)★{\mathcal{E}}_{\gamma ,n}\left(\tau \right)={\mathcal{E}}_{\gamma ,m+n+1}\left(\tau \right).$$
• Convolution of two different $\gamma$ parameters $\alpha$–log-exponential functions
  For ${\gamma }_1\ne {\gamma }_2$,

  $${\mathcal{E}}_{{\gamma }_1,0}\left(\tau \right)★{\mathcal{E}}_{{\gamma }_2,0}\left(\tau \right)={\displaystyle \frac{{\mathcal{E}}_{{\gamma }_1,0}\left(\tau \right)-{\mathcal{E}}_{{\gamma }_2,0}\left(\tau \right)}{{\gamma }_1-{\gamma }_2}},$$

  $$\begin{array}{cc}\hfill {\mathcal{E}}_{{\gamma }_1,m}\left(\tau \right)★{\mathcal{E}}_{{\gamma }_2,n}\left(\tau \right)=\sum _{l=0}^m\frac{\left(\genfrac{}{}{0pt}{}{n+l}{l}\right){(-1)}^l}{{({\gamma }_1-{\gamma }_2)}^{1+n+l}}& {\mathcal{E}}_{{\gamma }_1,m-l}\left(\tau \right)+\sum _{k=0}^n\frac{\left(\genfrac{}{}{0pt}{}{m+k}{k}\right){(-1)}^k}{{({\gamma }_2-{\gamma }_1)}^{1+m+k}}{\mathcal{E}}_{{\gamma }_2,n-k}\left(\tau \right).\hfill \end{array}$$

Next, we will introduce and prove some other properties which will allow us to deduce that functions ${\mathcal{E}}_{\gamma ,m}\left(\tau \right)$ are the generating elements of solution space of fractional scale-invariant systems.

Theorem 2. 

Let $n\ge 1$. Then

$$u_{-1}\left(\tau \right)★{\mathcal{E}}_{\gamma ,n}\left(\tau \right)={\mathcal{E}}_{\gamma ,n-1}\left(\tau \right)+\gamma {\mathcal{E}}_{\gamma ,n}\left(\tau \right).$$

Proof. 

Observe that

$$\begin{array}{cc}\hfill u_{-1}\left(\tau \right)★{\mathcal{E}}_{\gamma ,n}\left(\tau \right)& =u_{-1}\left(\tau \right)★\sum _{k=n+1}^{\infty }\left(\genfrac{}{}{0pt}{}{k-1}{n}\right){\gamma }^{k-n-1}{u}_k\left(\tau \right)\hfill \\ \hfill & =\sum _{k=n+1}^{\infty }\left(\genfrac{}{}{0pt}{}{k-1}{n}\right){\gamma }^{k-n-1}{u}_{k-1}\left(\tau \right).\hfill \end{array}$$

Using the basic recurrence $\left(\genfrac{}{}{0pt}{}{k-1}{n}\right)=\left(\genfrac{}{}{0pt}{}{k-2}{n-1}\right)+\left(\genfrac{}{}{0pt}{}{k-2}{n}\right)$, we obtain

$$\begin{array}{cc}\hfill u_{-1}\left(\tau \right)★{\mathcal{E}}_{\gamma ,n}\left(\tau \right)& =\sum _{k=n+1}^{\infty }\left[\left(\genfrac{}{}{0pt}{}{k-2}{n-1}\right)+\left(\genfrac{}{}{0pt}{}{k-2}{n}\right)\right]{\gamma }^{k-n-1}{u}_{k-1}\left(\tau \right)\hfill \\ \hfill & =\sum _{k=n+1}^{\infty }\left(\genfrac{}{}{0pt}{}{k-2}{n-1}\right){\gamma }^{k-n-1}{u}_{k-1}\left(\tau \right)+\sum _{k=n+2}^{\infty }\left(\genfrac{}{}{0pt}{}{k-2}{n}\right){\gamma }^{k-n-1}{u}_{k-1}\left(\tau \right)\hfill \\ \hfill & =\sum _{k=n}^{\infty }\left(\genfrac{}{}{0pt}{}{k-1}{n-1}\right){\gamma }^{k-n}{u}_k\left(\tau \right)+\gamma \sum _{k=n+1}^{\infty }\left(\genfrac{}{}{0pt}{}{k-1}{n}\right){\gamma }^{k-n-1}{u}_k\left(\tau \right)\hfill \\ \hfill & ={\mathcal{E}}_{\gamma ,n-1}\left(\tau \right)+\gamma {\mathcal{E}}_{\gamma ,n}\left(\tau \right).\hfill \end{array}$$

□

Remark 6. 

Observe that letting $n=0$ in Theorem 2 we get

$$u_{-1}\left(\tau \right)★{\mathcal{E}}_{\gamma ,0}\left(\tau \right)=u_0\left(\tau \right)+\gamma {\mathcal{E}}_{\gamma ,0}\left(\tau \right)$$

(16)

Theorem 3. 

Let N and n be positive integers such that $N\le n$. Then we have

$$u_{-N}\left(\tau \right)★{\mathcal{E}}_{\gamma ,n}\left(\tau \right)=\sum _{k=0}^N\left(\genfrac{}{}{0pt}{}{N}{k}\right){\gamma }^{N-k}{\mathcal{E}}_{\gamma ,n-k}\left(\tau \right).$$

Proof. 

The proof is done by induction with $N\le n$. For the base step of the induction ($N=1$), we appeal to Lemma 2. For $N=2$, due to $u_{-2}\left(\tau \right)=u_{-1}\left(\tau \right)★u_{-1}\left(\tau \right)$ we have that

$$\begin{array}{cc}\hfill u_{-2}\left(\tau \right)★{\mathcal{E}}_{\gamma ,n}\left(\tau \right)& =u_{-1}\left(\tau \right)★\left(u_{-1}\left(\tau \right)★{\mathcal{E}}_{\gamma ,n}\left(\tau \right)\right)\hfill \\ \hfill & =u_{-1}\left(\tau \right)★\left({\mathcal{E}}_{\gamma ,n-1}\left(\tau \right)+\gamma {\mathcal{E}}_{\gamma ,n}\left(\tau \right)\right)\hfill \\ \hfill & ={\gamma }^2{\mathcal{E}}_{\gamma ,n}\left(\tau \right)+2\gamma {\mathcal{E}}_{\gamma ,n-1}\left(\tau \right)+{\mathcal{E}}_{\gamma ,n-2}\left(\tau \right).\hfill \end{array}$$

Suppose that theorem is valid for $N-1$. This is

$$u_{-N+1}\left(\tau \right)★{\mathcal{E}}_{\gamma ,n}\left(\tau \right)=\sum _{k=0}^{N-1}\left(\genfrac{}{}{0pt}{}{N-1}{k}\right){\gamma }^{N-k-1}{\mathcal{E}}_{\gamma ,n-k}\left(\tau \right).$$

(17)

Now, we will prove that theorem is valid for N. Observe that

$$\begin{array}{cc}\hfill u_{-N}\left(\tau \right)★{\mathcal{E}}_{\gamma ,n}\left(\tau \right)& =u_{-1}\left(\tau \right)★\left(u_{-N+1}\left(\tau \right)★{\mathcal{E}}_{\gamma ,n}\left(\tau \right)\right)\hfill \\ \hfill & =\sum _{k=0}^{N-1}\left(\genfrac{}{}{0pt}{}{N-1}{k}\right){\gamma }^{N-k-1}\left(u_{-1}\left(\tau \right)★{\mathcal{E}}_{\gamma ,n-k}\left(\tau \right)\right)\hfill \\ \hfill & =\sum _{k=0}^{N-1}\left(\genfrac{}{}{0pt}{}{N-1}{k}\right){\gamma }^{N-k-1}\left({\mathcal{E}}_{\gamma ,n-k-1}\left(\tau \right)+\gamma {\mathcal{E}}_{\gamma ,n-k}\left(\tau \right)\right)\hfill \\ \hfill & =\sum _{k=0}^N\left(\genfrac{}{}{0pt}{}{N}{k}\right){\gamma }^{N-k}{\mathcal{E}}_{\gamma ,n-k}\left(\tau \right).\hfill \end{array}$$

(18)

□

Theorem 4. 

Let $l\in \mathbb{N}$. Then

$$\begin{array}{cc}\hfill u_{-n-l}\left(\tau \right)★{\mathcal{E}}_{\gamma ,n}\left(\tau \right)& =\sum _{k=n+1}^{n+l}\left(\genfrac{}{}{0pt}{}{k-1}{n}\right){\gamma }^{k-n-1}{u}_{k-n-l}\left(\tau \right)+\sum _{k=0}^n\left(\genfrac{}{}{0pt}{}{n+l}{n-k}\right){\gamma }^{k+l}{\mathcal{E}}_{\gamma ,k}\left(\tau \right).\hfill \end{array}$$

(19)

Proof. 

The proof is by induction on $l\in \mathbb{N}$. For the base step of the induction ($l=1$) we have that

$$\begin{array}{cc}\hfill u_{-n-1}\left(\tau \right)★{\mathcal{E}}_{\gamma ,n}\left(\tau \right)& =u_{-1}\left(\tau \right)★\left(u_{-n}\left(\tau \right)★{\mathcal{E}}_{\gamma ,n}\left(\tau \right)\right)\hfill \\ \hfill & =u_{-1}\left(\tau \right)★\left(\sum _{k=0}^n\left(\genfrac{}{}{0pt}{}{n}{k}\right){\gamma }^k{\mathcal{E}}_{\gamma ,k}\left(t\right)\right)\hfill \\ \hfill & =u_0\left(\tau \right)+\gamma {\mathcal{E}}_{\gamma ,0}\left(\tau \right)+\sum _{k=1}^n\left(\genfrac{}{}{0pt}{}{n}{k}\right){\gamma }^k\left({\mathcal{E}}_{\gamma ,k-1}\left(\tau \right)+\gamma {\mathcal{E}}_{\gamma ,k}\left(\tau \right)\right)\hfill \\ \hfill & =u_0\left(\tau \right)+\sum _{k=0}^n\left(\genfrac{}{}{0pt}{}{n+1}{k+1}\right){\gamma }^{k+1}{\mathcal{E}}_{\gamma ,k}\left(\tau \right).\hfill \end{array}$$

In the penultimate equality we apply the Remark 6 to the first term of the sum. Suppose that the theorem is valid for $l-1$, this is

$$\begin{array}{cc}\hfill u_{-n-l+1}\left(\tau \right)★{\mathcal{E}}_{\gamma ,n}\left(\tau \right)& =\sum _{k=n+1}^{n+l-1}\left(\genfrac{}{}{0pt}{}{k-1}{n}\right){\gamma }^{k-n-1}{u}_{k-n-l+1}\left(\tau \right)+\sum _{k=0}^n\left(\genfrac{}{}{0pt}{}{n+l-1}{n-k}\right){\gamma }^{k+l-1}{\mathcal{E}}_{\gamma ,k}\left(\tau \right).\hfill \end{array}$$

(20)

Now, we will prove that theorem is valid for l. Observe that

$$\begin{array}{cc}\hfill u_{-n-l}\left(\tau \right)★& {\mathcal{E}}_{\gamma ,n}\left(\tau \right)=u_{-1}\left(\tau \right)★\left(u_{-n-l+1}\left(\tau \right)★{\mathcal{E}}_{\gamma ,n}\left(\tau \right)\right)\hfill \\ \hfill & =\sum _{k=n+1}^{n+l-1}\left(\genfrac{}{}{0pt}{}{k-1}{n}\right){\gamma }^{k-n-1}{u}_{k-n-l}\left(\tau \right)+\sum _{k=0}^n\left(\genfrac{}{}{0pt}{}{n+l-1}{n-k}\right){\gamma }^{k+l-1}(u_{-1}\left(\tau \right)★{\mathcal{E}}_{\gamma ,k}\left(\tau \right))\hfill \\ \hfill & =\sum _{k=n+1}^{n+l}\left(\genfrac{}{}{0pt}{}{k-1}{n}\right){\gamma }^{k-n-1}{u}_{k-n-l}\left(\tau \right)+\sum _{k=0}^n\left(\genfrac{}{}{0pt}{}{n+l}{n-k}\right){\gamma }^{k+l}{\mathcal{E}}_{\gamma ,k}\left(\tau \right).\hfill \end{array}$$

(21)

Again, Remark 6 is applied in the last equality. □

Theorem 4 suggests that impulse (step) response to a fractional scale-invariant system is a linear combination of functions ${\mathcal{E}}_{\gamma ,n}\left(t\right)$.

4. Impulse and Step Responses

4.1. The AR Case

Consider an AR system. Its impulse response is given by the solution of the equation

$$p\left({\mathfrak{D}}_{s+}^{\alpha }\right)y\left(\tau \right)=\delta (\tau -1),$$

(22)

where $p\left(x\right)=a_m{x}^m+a_{m-1}{x}^{m-1}+\cdots +a_{1}x+a_0$, $a_n\in \mathbb{C}$, $a_m=1$, and its roots ${\gamma }_1,{\gamma }_2,\dots ,{\gamma }_m$ have multiplicity 1. Consider that $y\left(\tau \right)\in \mathcal{F}$. In terms of the convolution ★, the Equation (22) can be rewritten as

$$\left(a_m{u}_{-m}\left(\tau \right)+a_{m-1}{u}_{-m+1}\left(\tau \right)+\cdots +a_1{u}_{-1}\left(\tau \right)+a_0{u}_0\left(\tau \right)\right)★y\left(\tau \right)=u_0\left(\tau \right).$$

Assume that impulse response is given by a linear combination of $\alpha$–log-exponential functions

$$r_{\delta }\left(\tau \right)=c_1{\mathcal{E}}_{{\gamma }_1,0}\left(\tau \right)+\cdots +c_m{\mathcal{E}}_{{\gamma }_m,0}\left(\tau \right).$$

From (19), it is not difficult to deduce that

$$u_{-m}\left(\tau \right)★{\mathcal{E}}_{{\gamma }_i,0}\left(\tau \right)=\sum _{k=1}^m{\gamma }_1^{k-1}{u}_{-m+k}\left(\tau \right)+{\gamma }_i^m{\mathcal{E}}_{{\gamma }_i,0}\left(t\right),\mathrm{for}\mathrm{any}m\in \mathbb{N}.$$

A simple computation leads to

$$\left(a_m{u}_{-m}\left(\tau \right)+a_{m-1}{u}_{-m+1}\left(\tau \right)+\cdots +a_0{u}_0\left(\tau \right)\right)★r_{\delta }\left(\tau \right)=\sum _{k=1}^m{c}_k\sum _{j=0}^{m-1}\sum _{i=0}^{m-j-1}{a}_{i+1}{\gamma }_k^i{u}_{-j}\left(\tau \right).$$

(23)

Now, in order to find the impulse response we obtain a linear system with m equations which can be reduced recursively to

$$\begin{array}{cc}\hfill c_1+c_2+c_3+\cdots +c_m& =0\hfill \\ \hfill {\gamma }_1{c}_1+{\gamma }_2{c}_2+{\gamma }_3{c}_3+\cdots +{\gamma }_m{c}_m& =0\hfill \\ \hfill ⋮\phantom{dddddddd}& =⋮\hfill \\ \hfill {\gamma }_1^{m-1}{c}_1+{\gamma }_2^{m-1}{c}_2+{\gamma }_3^{m-1}{c}_3+\cdots +{\gamma }_m^{m-1}{c}_m& =1.\hfill \end{array}$$

The coefficient matrix is invertible, since it has Vandermonde format and the roots ${\gamma }_j$ are distinct. Therefore, the system has a unique solution. Finally, using the $c_i$’s, we obtain $r_{\delta }\left(\tau \right)$, the solution to fractional system (22).

For the case of roots with multiplicity greater than one, we must propose an alternative solution. Consider that a given root, ${\gamma }_k,$ has multiplicity $m_k>1$. To obtain the solution, we need to add another linear combination of $\alpha$–log-exponentials to the previous solution

$$c_{k,0}{\mathcal{E}}_{{\gamma }_k,0}\left(\tau \right)+c_{k,1}{\mathcal{E}}_{{\gamma }_k,1}\left(\tau \right)+\cdots +c_{k,m_k}{\mathcal{E}}_{{\gamma }_1,m_k}\left(\tau \right)$$

With the obtained guess of the solution we are led to a linear system with m equations. The coefficient matrix is of generalized Vandermonde-type [32] having non null determinant. To fix ideas, consider the system (22) but with ${\gamma }_4,{\gamma }_5,\dots ,{\gamma }_m$ simple roots of $p\left(x\right)$ and ${\gamma }_1$ a root with multiplicity 3 (${\gamma }_1={\gamma }_2={\gamma }_3$). The proposed solution assumes the form

$$r_{\delta }\left(\tau \right)=c_1{\mathcal{E}}_{{\gamma }_1,0}\left(\tau \right)+c_2{\mathcal{E}}_{{\gamma }_2,1}\left(\tau \right)+c_3{\mathcal{E}}_{{\gamma }_3,2}\left(\tau \right)+c_4{\mathcal{E}}_{{\gamma }_4,0}\left(\tau \right)+\cdots +c_m{\mathcal{E}}_{{\gamma }_m,0}\left(\tau \right)$$

As in the previous case, from

$$\left(a_m{u}_{-m}\left(\tau \right)+a_{m-1}{u}_{-m+1}\left(\tau \right)+\cdots +a_1{u}_{-1}\left(\tau \right)+a_0{u}_0\left(\tau \right)\right)★r_{\delta }\left(\tau \right)=u_0\left(\tau \right)$$

we obtain a system of m linear equations that can be recursively reduced to the following system

$$\begin{array}{ccc}\hfill c_1+c_4+\cdots +c_m& =& 0\hfill \\ \hfill {\gamma }_1{c}_1+c_2+{\gamma }_4{c}_4+\cdots +{\gamma }_m{c}_m& =& 0\hfill \\ \hfill {\gamma }_1^2{c}_1+2{\gamma }_2{c}_2+{\gamma }_3{c}_3+{\gamma }_4^2{c}_4+\cdots +{\gamma }_m^2{c}_m& =& 0\hfill \\ \hfill ⋮\phantom{dddddddd}& =& ⋮\hfill \\ \hfill {\gamma }_1^{m-1}{c}_1+(m-1){\gamma }_2^{m-2}{c}_2+{\displaystyle \frac{(m-1)(m-2)}{2!}}{\gamma }_3^{m-1}{c}_3+{\gamma }_4^{m-1}{c}_4+\cdots +{\gamma }_m^{m-1}{c}_m& =& 1.\hfill \end{array}$$

This system has a coefficient matrix of generalized Vandermonde-type whose determinant is equal to

$$\prod _{3<i<j\le m}^{}{({\gamma }_i-{\gamma }_j)}^{m_i{m}_j},$$

where $m_i,m_j$ are the multiplicities of the roots ${\gamma }_i,{\gamma }_j$, respectively. It follows that the system has a unique solution.

We have proven that the solution to system (22) is an element of vector space generated by the set

$$\{{\mathcal{E}}_{\gamma ,n}\left(\tau \right):\gamma \in \mathbb{C},n\in {\mathbb{N}}_0\}.$$

(24)

Furthermore, in (p. 338, [31]) it is proved that the set (24) is linearly independent.

4.2. The ARMA Case

By means of the method above described, we can solve the more general problem

$$p\left({\mathfrak{D}}_{s+}^{\alpha }\right)y\left(\tau \right)=q\left({\mathfrak{D}}_{s+}^{\alpha }\right)\delta (\tau -1),$$

where $p\left(x\right)=a_m{x}^m+a_{m-1}{x}^{m-1}+\cdots +a_{1}x+a_0$ and $q\left(x\right)=b_r{x}^r+b_{r-1}{x}^{r-1}+\cdots +b_{1}x+b_0$ are polynomials of degree m and r, respectively, with constant coefficients in $\mathbb{C}$. We procedure as follows. Firstly, we compute the impulsive response $r_{\delta }\left(\tau \right)$. In different words, we solve the fractional system

$$p\left({\mathfrak{D}}_{s+}^{\alpha }\right)y\left(\tau \right)=\delta (\tau -1).$$

Later, the solution is given by the convolution

$$y\left(\tau \right)=\left(b_r{u}_{-r}\left(\tau \right)+b_{r-1}{u}_{-r+1}\left(\tau \right)+\cdots +b_1{u}_{-1}\left(\tau \right)+b_0{u}_0\left(\tau \right)\right)★r_{\delta }\left(\tau \right).$$

This is known as cascade connection of two systems

$$\begin{array}{cc}\hfill \mathrm{System}{S}_1:& p\left({\mathfrak{D}}_{s+}^{\alpha }\right)r_{\delta }\left(\tau \right)=\delta (\tau -1)\hfill \\ \hfill \mathrm{System}{S}_2:& y\left(\tau \right)=q\left({\mathfrak{D}}_{s+}^{\alpha }\right)r_{\delta }\left(\tau \right)\hfill \end{array}$$

(25)

5. Examples

In all the following examples, we will compute both impulse and step response, by means of operational method. In order to compare ours with the classic transform method, we include the computation of impulse response in Example 1 using the Mellin transform.

Example 1. 

Consider the fractional scale-invariant linear system

$$p\left({\mathfrak{D}}_{s+}^{\alpha }\right)y\left(\tau \right)=\delta (\tau -1).$$

(26)

with $p\left(x\right)=x^2+2$. The roots of $p\left(x\right)$ are $\sqrt{2}i$ and $-\sqrt{2}i$ of multiplicity 1.

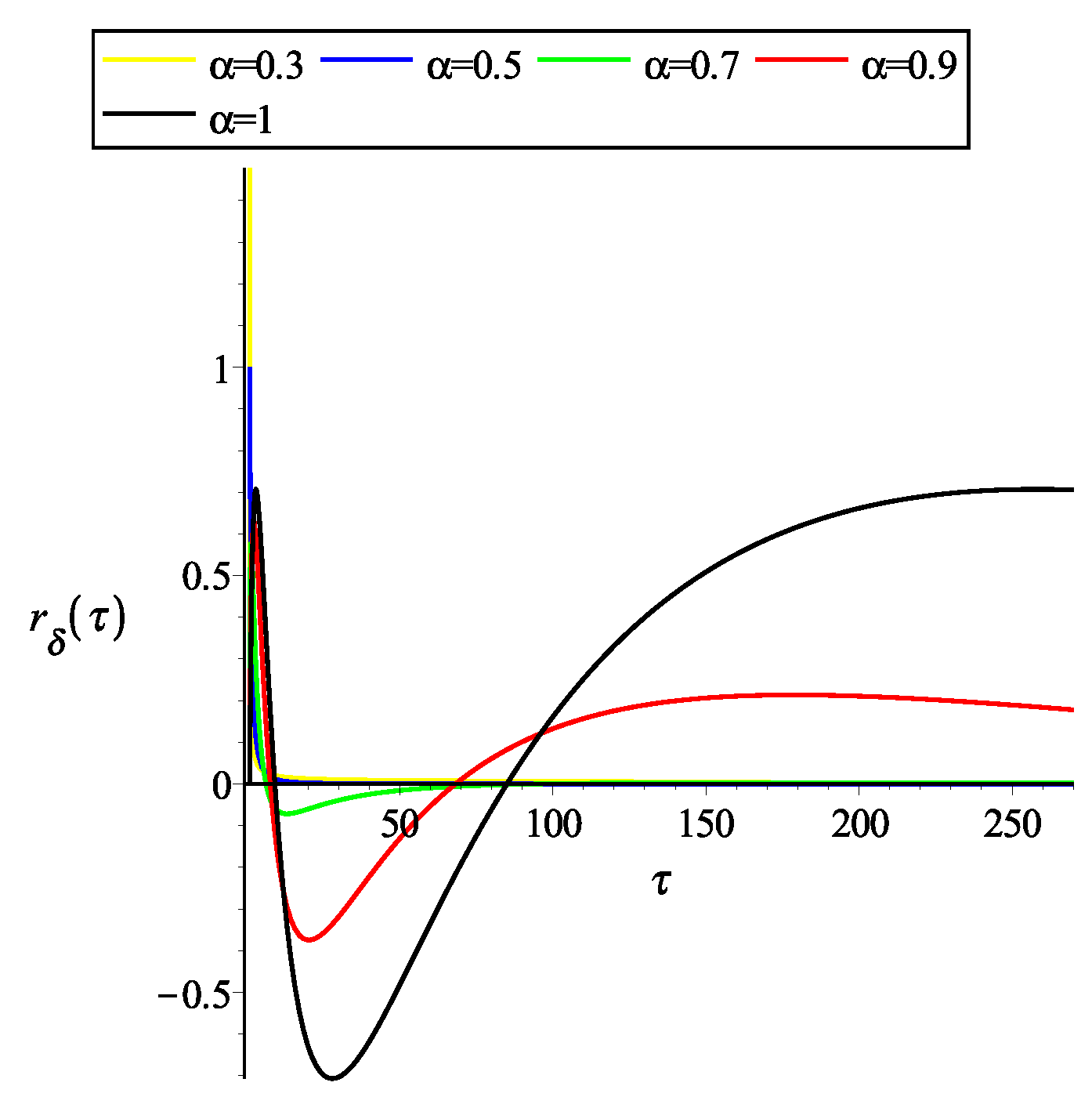
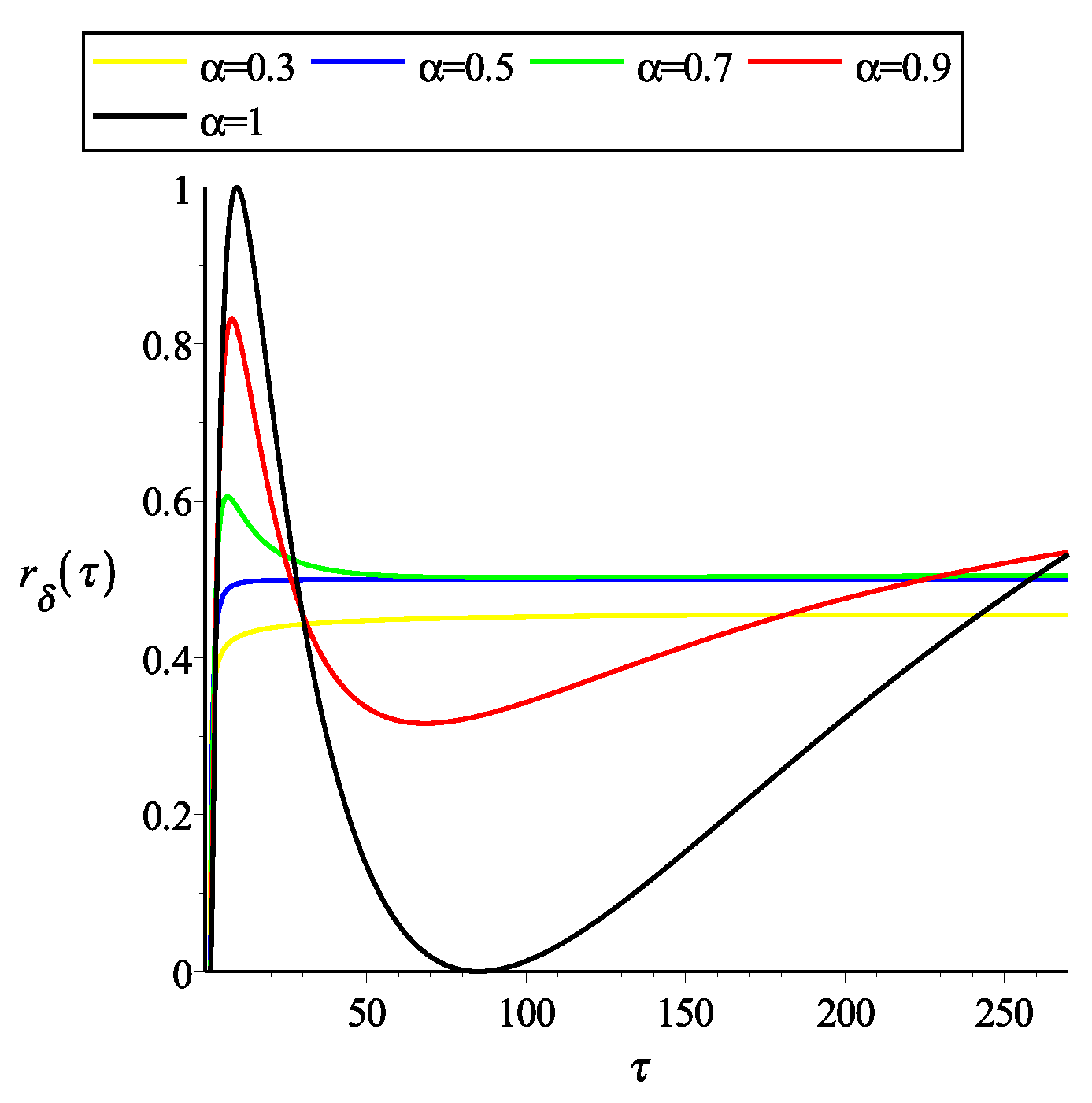
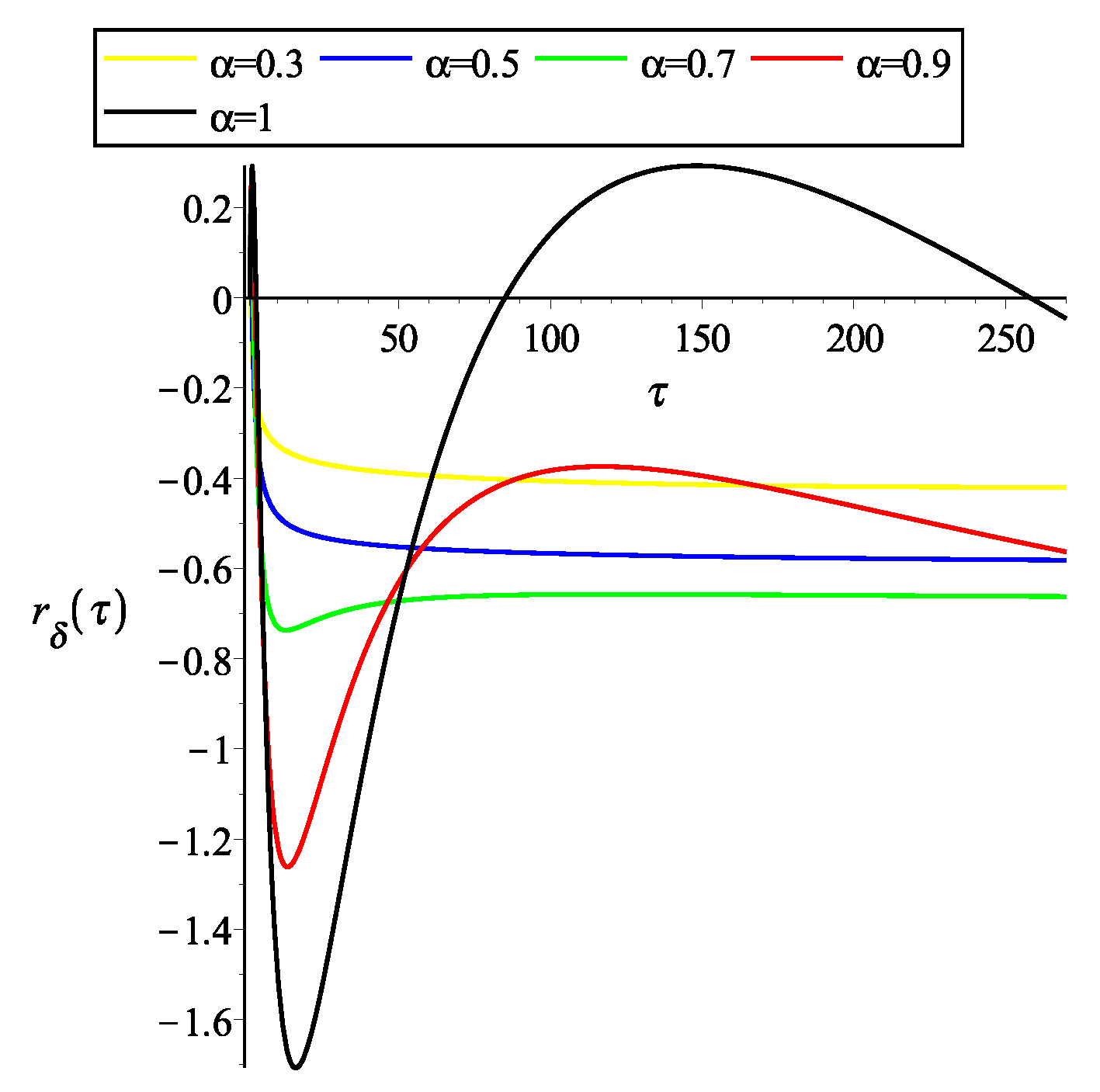
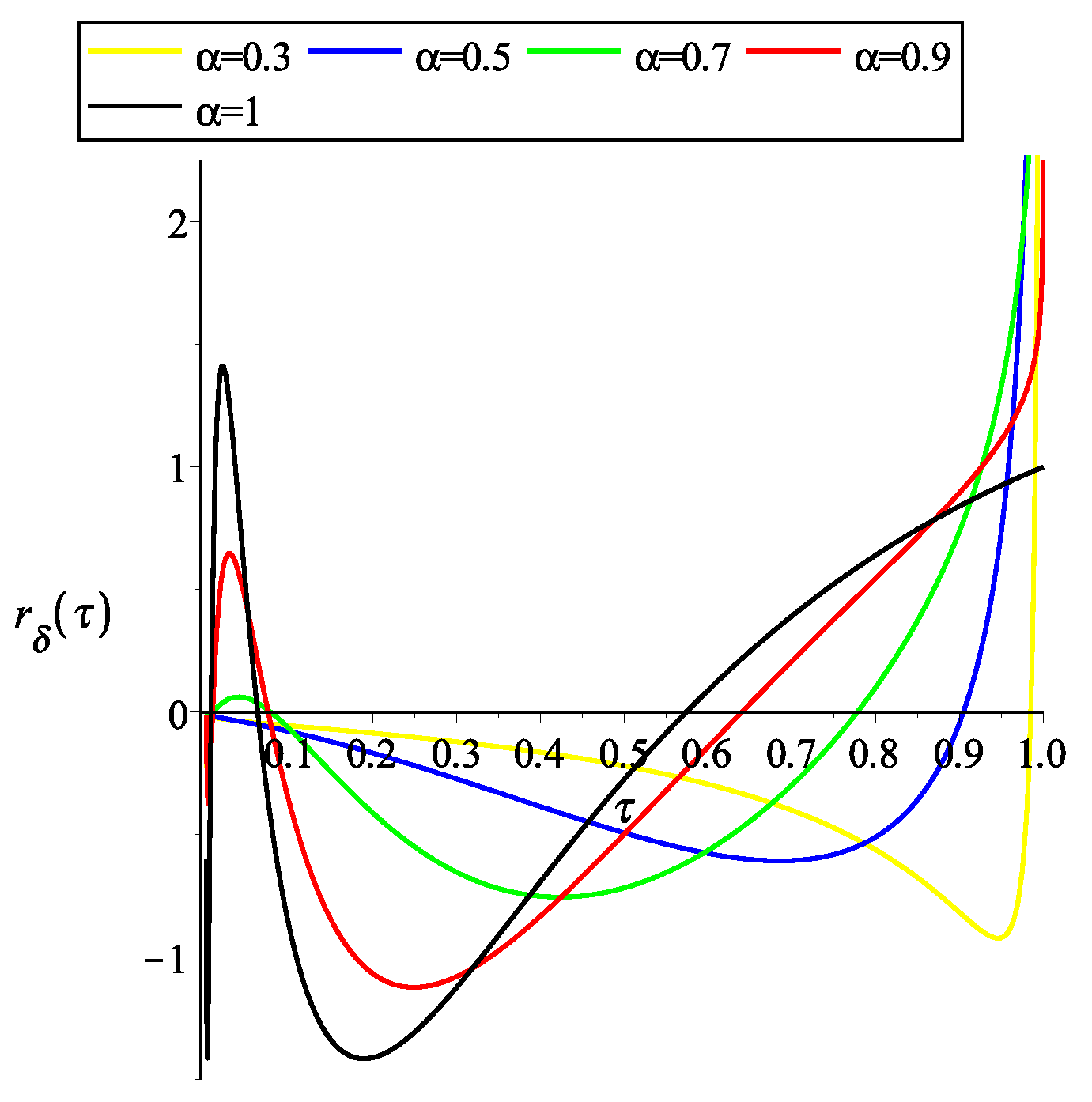
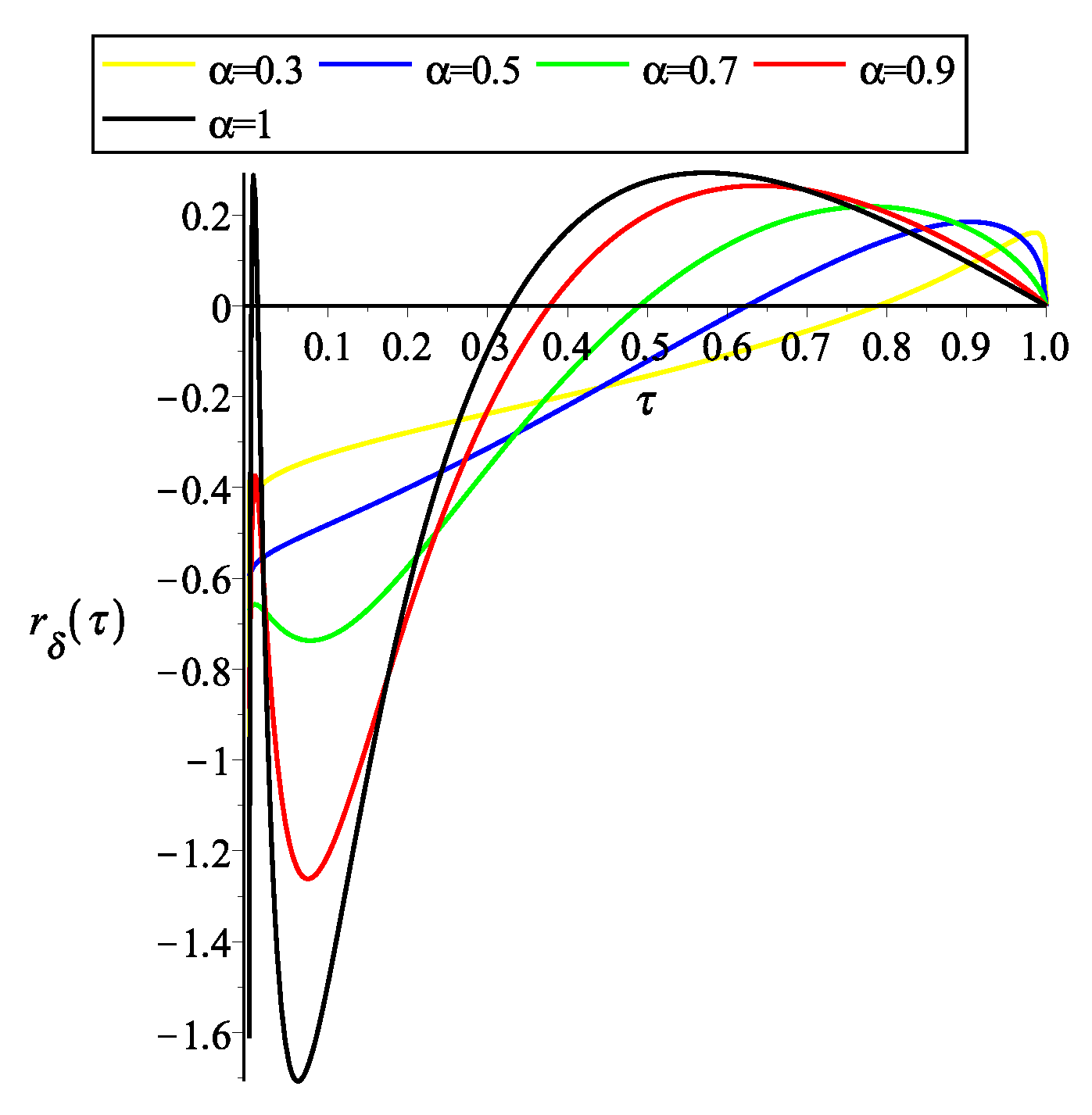
• Operational method:
  By means of our operational method, the system can be rewritten as

  $$\left(u_{-2}\left(\tau \right)+2u_0\left(\tau \right)\right)★y\left(\tau \right)=u_0\left(\tau \right).$$

  We propose the solution

  $$y\left(\tau \right)=c_1{\mathcal{E}}_{\sqrt{2}i,0}\left(\tau \right)+c_2{\mathcal{E}}_{-\sqrt{2}i,0}\left(\tau \right).$$

  Following the presented in Section 3.2 we obtain the system of equations

  $$\begin{array}{ccccc}{c}_1& +& c_2& =& 0\\ \sqrt{2}i{c}_1& -& \sqrt{2}i{c}_2& =& 1\end{array}.$$

  The solution to system of equations is $c_1=\frac{1}{2\sqrt{2}i}$ and $c_2=-\frac{1}{2\sqrt{2}i}$. Therefore, for $\tau \ge 1$ the impulse response is

  $$\begin{array}{cc}\hfill r_{\delta }\left(\tau \right)& ={\displaystyle \frac{1}{2\sqrt{2}i}}\left(\sum _{k=1}^{\infty }\left({\left(\sqrt{2}i\right)}^{k-1}-{(-\sqrt{2}i)}^{k-1}\right)\frac{{ln}^{k\alpha -1}\left(\tau \right)}{\Gamma \left(k\alpha \right)}\epsilon (\tau -1)\right)\hfill \\ \hfill & =\sum _{k=1}^{\infty }{(-2)}^{k-1}\frac{{ln}^{2k\alpha -1}\left(\tau \right)}{\Gamma \left(2k\alpha \right)}\epsilon (\tau -1),\hfill \end{array}$$

  and step response

  $$r_u\left(\tau \right)=\sum _{k=1}^{\infty }{(-2)}^{k-1}\frac{{ln}^{2k\alpha }\left(\tau \right)}{\Gamma (2k\alpha +1)}\epsilon (\tau -1).$$

  Remark 7. 

  When $\alpha =1$, $r_{\delta }\left(\tau \right)={\displaystyle \frac{1}{\sqrt{2}}}sin(\sqrt{2}ln\left(\tau \right))$ and $r_u\left(\tau \right)={\displaystyle \frac{1-cos(\sqrt{2}ln\left(\tau \right))}{2}}$.
  The Figure 1 and Figure 2 show the graphical representation of the solutions with $\tau \ge 1$ and several values of α.
  For $0<\tau \le 1$, the impulse response is

  $$r_{\delta }\left(\tau \right)=\sum _{k=1}^{\infty }{(-2)}^{k-1}\frac{{ln}^{2k\alpha -1}\left(\frac{1}{\tau }\right)}{\Gamma \left(2k\alpha \right)}\epsilon (1-\tau ),$$

  and step response

  $$r_u\left(\tau \right)=\sum _{k=1}^{\infty }{(-2)}^{k-1}\frac{{ln}^{2k\alpha }\left(\frac{1}{\tau }\right)}{\Gamma (2k\alpha +1)}\epsilon (1-\tau ).$$

  Remark 8. 

  When $\alpha =1$,

  $$r_{\delta }\left(\tau \right)={\displaystyle \frac{1}{\sqrt{2}}}sin(\sqrt{2}ln\left(\frac{1}{\tau })\right)\epsilon (1-\tau ),$$

  and

  $$r_u\left(\tau \right)={\displaystyle \frac{1-cos(\sqrt{2}ln\left(\frac{1}{\tau })\right)}{2}}\epsilon (1-\tau ).$$
  The Figure 3 and Figure 4 show the graphical representation of the solutions with $0<\tau \le 1$ and several values of α.
• Mellin transform:
  We only consider the case $\tau \ge 1$, the case $0<\tau \le 1$ is analog. By means of Mellin transform, the system (26) can be transformed to equation

  $$\begin{array}{cc}\hfill Y\left(v\right)& ={\displaystyle \frac{1}{v^{2\alpha }+2}}\hfill \\ \hfill & ={\displaystyle \frac{i}{2\sqrt{2}}}{\displaystyle \frac{1}{v^{\alpha }+\sqrt{2}i}}-{\displaystyle \frac{i}{2\sqrt{2}}}{\displaystyle \frac{1}{v^{\alpha }-\sqrt{2}i}}\hfill \\ \hfill & =v^{-\alpha }{\displaystyle \frac{\frac{i}{2\sqrt{2}}}{1+\frac{\sqrt{2}i}{v^{\alpha }}}}-v^{-\alpha }{\displaystyle \frac{\frac{i}{2\sqrt{2}}}{1-\frac{\sqrt{2}i}{v^{\alpha }}}}\hfill \end{array}$$

  Using the geometric series, with $\sqrt{2}<v^{\alpha }$, we obtain that

  $$\begin{array}{cc}\hfill Y\left(v\right)& ={\displaystyle \frac{i}{4}}{v}^{-\alpha }\sum _{k=0}^{\infty }{(-1)}^k{\left({\displaystyle \frac{2i}{v^{\alpha }}}\right)}^k-{\displaystyle \frac{i}{4}}{v}^{-\alpha }\sum _{k=0}^{\infty }{\left({\displaystyle \frac{2i}{v^{\alpha }}}\right)}^k\hfill \\ \hfill & =\sum _{k=1}^{\infty }{(-2)}^{k-1}{v}^{-2k\alpha }.\hfill \end{array}$$

  Computing the inverse Mellin transform we obtain the impulsive response

  $$\begin{array}{cc}\hfill r_{\delta }\left(\tau \right)& ={\mathcal{M}}^{-1}\left[\sum _{k=1}^{\infty }{(-2)}^{k-1}{v}^{-2k\alpha }\right]\hfill \\ \hfill & =\sum _{k=1}^{\infty }{(-2)}^{k-1}{\displaystyle \frac{{ln}^{2k\alpha -1}\left(\tau \right)}{\Gamma \left(2k\alpha \right)}}\epsilon (\tau -1).\hfill \end{array}$$

  For the step response we apply (A1) and obtain

  $$r_u\left(\tau \right)=\sum _{k=1}^{\infty }{(-2)}^{k-1}{\displaystyle \frac{{ln}^{2k\alpha }\left(\tau \right)}{\Gamma (2k\alpha +1)}}\epsilon (\tau -1).$$

Example 2. 

Consider the fractional scale-invariant linear system

$$p\left({\mathfrak{D}}_{s+}^{\alpha }\right)y\left(\tau \right)=q\left({\mathfrak{D}}_{s+}^{\alpha }\right)\delta (\tau -1),$$

with $p\left(x\right)=x^2+2$ and $q\left(x\right)=x-\sqrt{2}$. Observe that system is related with the Example 1. Following (25) we only need to compute the convolution

$$y\left(\tau \right)=\left(u_{-1}\left(\tau \right)-\sqrt{2}{u}_0\left(\tau \right)\right)★\left({\displaystyle \frac{1}{2\sqrt{2}i}}{\mathcal{E}}_{\sqrt{2}i,0}\left(\tau \right)-{\displaystyle \frac{1}{2\sqrt{2}i}}{\mathcal{E}}_{-\sqrt{2}i,0}\left(\tau \right)\right).$$

Simplifying we obtain that

$$\begin{array}{cc}\hfill y\left(\tau \right)& =\left(u_{-1}\left(\tau \right)-\sqrt{2}{u}_0\left(\tau \right)\right)★\left(\sum _{k=1}^{\infty }{(-2)}^{k-1}{u}_{2k}\left(\tau \right)\right)\hfill \\ \hfill & =\sum _{k=1}^{\infty }{(-2)}^{k-1}{u}_{2k-1}\left(\tau \right)-\sqrt{2}\sum _{k=1}^{\infty }{(-2)}^{k-1}{u}_{2k}\left(\tau \right).\hfill \end{array}$$

For $\tau \ge 1$, the impulse response is

$$\begin{array}{cc}\hfill r_{\delta }\left(\tau \right)& =\sum _{k=1}^{\infty }{(-2)}^{k-1}\frac{{ln}^{(2k-1)\alpha -1}\left(\tau \right)}{\Gamma \left(\right(2k-1\left)\alpha \right)}\epsilon (\tau -1)-\sqrt{2}\sum _{k=1}^{\infty }{(-2)}^{k-1}\frac{{ln}^{2k\alpha -1}\left(\tau \right)}{\Gamma \left(2k\alpha \right)}\epsilon (\tau -1),\hfill \end{array}$$

and step response

$$r_u\left(\tau \right)=\sum _{k=1}^{\infty }{(-2)}^{k-1}\frac{{ln}^{(2k-1)\alpha }\left(\tau \right)}{\Gamma \left(\right(2k-1)\alpha +1)}\epsilon (\tau -1)-\sqrt{2}\sum _{k=1}^{\infty }{(-2)}^{k-1}\frac{{ln}^{2k\alpha }\left(\tau \right)}{\Gamma (2k\alpha +1)}\epsilon (\tau -1).$$

The Figure 5 and Figure 6 show the graphical representation of the solutions with $\tau \ge 1$ and several values of α.

For $0<\tau \le 1$, the impulse response is

$$r_{\delta }\left(\tau \right)=\sum _{k=1}^{\infty }{(-2)}^{k-1}\frac{{ln}^{(2k-1)\alpha -1}\left(\frac{1}{\tau }\right)}{\Gamma \left(\right(2k-1\left)\alpha \right)}\epsilon (1-\tau )-\sqrt{2}\sum _{k=1}^{\infty }{(-2)}^{k-1}\frac{{ln}^{2k\alpha -1}\left(\frac{1}{\tau }\right)}{\Gamma \left(2k\alpha \right)}\epsilon (1-\tau ),$$

and step response

$$r_u\left(\tau \right))=\sum _{k=1}^{\infty }{(-2)}^{k-1}\frac{{ln}^{(2k-1)\alpha }\left(\frac{1}{\tau }\right)}{\Gamma \left(\right(2k-1)\alpha +1)}\epsilon (1-\tau )-\sqrt{2}\sum _{k=1}^{\infty }{(-2)}^{k-1}\frac{{ln}^{2k\alpha }\left(\frac{1}{\tau }\right)}{\Gamma (2k\alpha +1)}\epsilon (1-\tau ).$$

The Figure 7 and Figure 8 show the graphical representation of the solutions with $0<\tau \le 1$ and several values of α.

6. Conclusions

We have proved that both Hadamard right (left) derivative and fractional scale derivative of type Grünwald-Letnikov are decremental index operators on the same sequence of functions ${\left\{u_k\right\}}_{k\in \mathbb{Z}}$. The Mellin convolution suggested to us how to define an algebraic product, which allowed us to construct a simple mathematical method to resolve fractional scale-invariant systems. The method relies on the roots of characteristic polynomial and the resolution of a linear system of equations. As expected, in our simulations, there is no convergence issue.