Modeling the Transmission Dynamics of Coronavirus Using Nonstandard Finite Difference Scheme
Abstract
1. Introduction
2. Mathematical Model
3. Equilibria and Basic Reproduction Number ()
3.1. Equilibria of Model
3.2. Basic Reproduction Number
4. The NSFD Scheme
4.1. Positivity and Boundedness of NSFD Scheme
4.2. Local Stability of Equilibria
- ,
- ,
- , where denotes trace and indicates determinant of the Jacobian matrix.
- .
- .
- .
- .
- .
- .
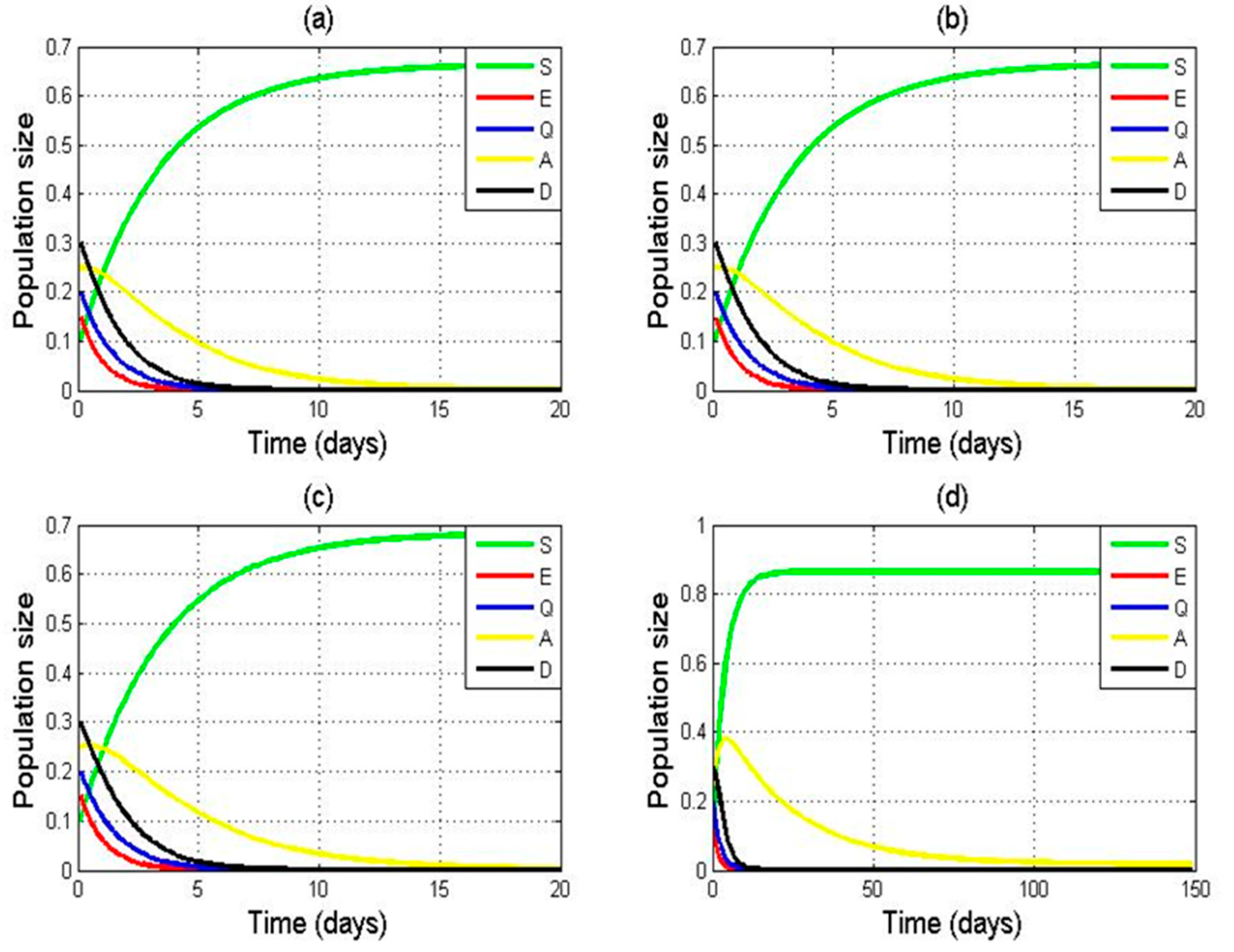
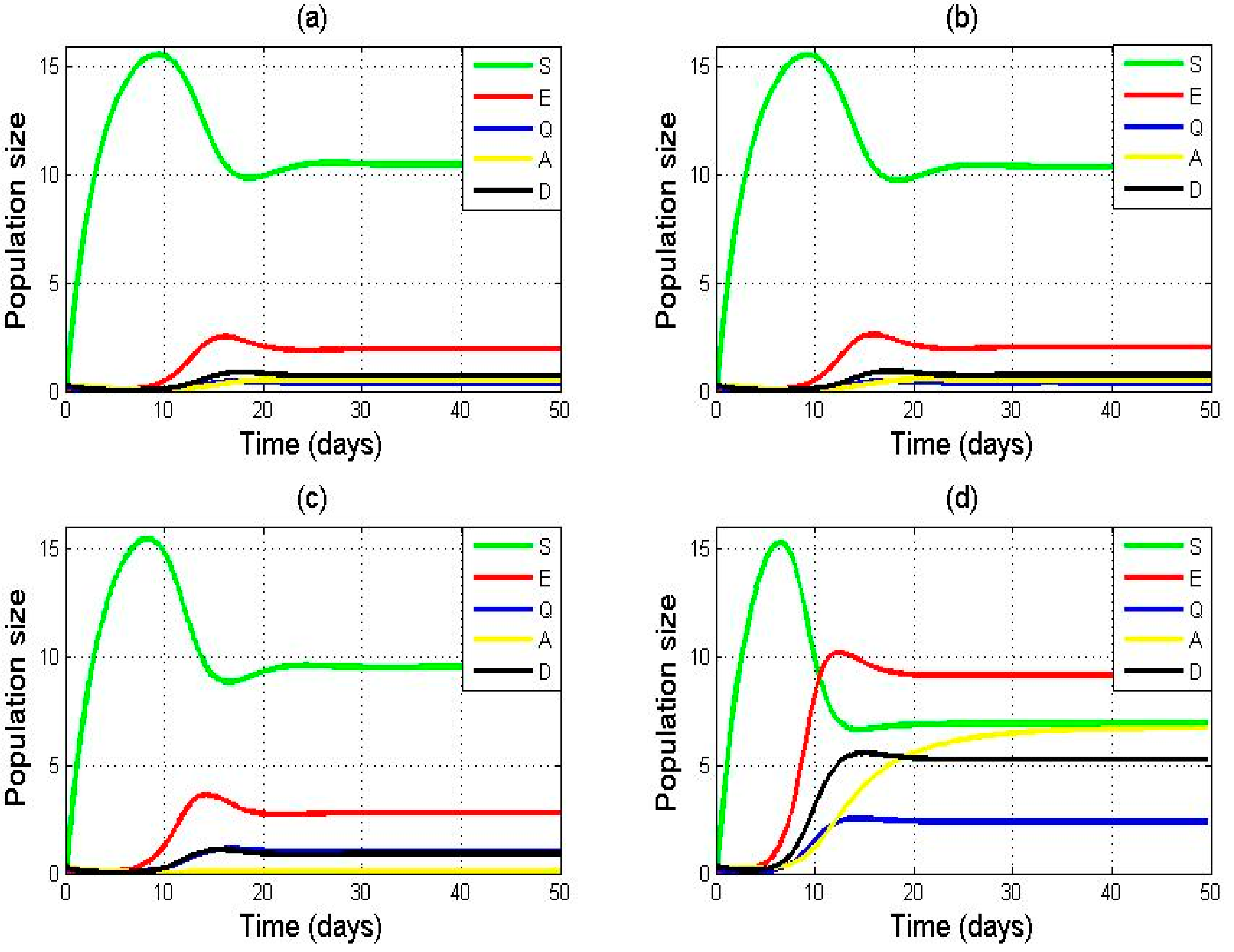
4.3. Global Stability of Equilibria
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Soresina, A.; Moratto, D.; Chiarini, M.; Paolillo, C.; Baresi, G.; Focà, E.; Badolato, R. Two X-linked agammaglobulinemia patients develop pneumonia as COVID-19 manifestation but recover. Pediatr. Allergy Immunol. 2020, 31, 565–569. [Google Scholar] [CrossRef]
- Liu, C.; Zhou, Q.; Li, Y.; Garner, L.V.; Watkins, S.P.; Carter, L.J.; Smoot, J.; Gregg, A.C.; Daniels, A.D.; Jervey, S.; et al. Research and development on therapeutic agents and vaccines for COVID-19 and related human coronavirus diseases. ACS Cent. Sci. 2020, 6, 315–331. [Google Scholar] [CrossRef]
- Bootsma, M.C.; Ferguson, N.M. The effect of public health measures on the 1918 influenza pandemic in US cities. Proc. Natl. Acad. Sci. USA 2007, 104, 7588–7593. [Google Scholar] [CrossRef]
- Imperial College COVID-19 Response Team. Impact of Non-Pharmaceutical Interventions (NPIs) to Reduce COVID-19 Mortality and Healthcare Demand; Imperial College: London, UK, 2020. [Google Scholar]
- Aba Oud, M.A.; Ali, A.; Alrabaiah, H.; Ullah, S.; Khan, M.A.; Islam, S. A fractional order mathematical model for COVID-19 dynamics with quarantine, isolation, and environmental viral load. Adv. Differ. Equ. 2021, 2021, 106. [Google Scholar] [CrossRef]
- Mahmoudi, M.R.; Heydari, M.H.; Qasem, S.N.; Mosavi, A.; Band, S.S. Principal component analysis to study the relations between the spread rates of COVID-19 in high risks countries. Alex. Eng. J. 2021, 60, 457–464. [Google Scholar] [CrossRef]
- Xu, R.; Cui, B.; Duan, X.; Zhang, P.; Zhou, X.; Yuan, Q. Saliva: Potential diagnostic value and transmission of 2019-n CoV. Int. J. Oral Sci. 2020, 12, 1–6. [Google Scholar] [CrossRef]
- Huang, C.; Wang, Y.; Li, X.; Ren, L.; Zhao, J.; Hu, Y.; Cao, B. Clinical features of patients infected with 2019 novel coronavirus in Wuhan, China. Lancet 2020, 395, 497–506. [Google Scholar] [CrossRef]
- Linton, N.M.; Kobayashi, T.; Yang, Y.; Hayashi, K.; Akhmetzhanov, A.R.; Jung, S.M.; Yuan, B.; Kinoshita, R.; Nishiura, H. Incubation Period and Other Epidemiological Characteristics of 2019 Novel Coronavirus Infections with Right Truncation: A Statistical Analysis of Publicly Available Case Data. J. Clin. Med. 2020, 9, 538. [Google Scholar] [CrossRef]
- Aliev, F.A.; Aliyev, N.A.; Hajiyeva, N.S.; Mahmudov, N.I. Some Mathematical Problems and Their Solutions for the Oscillating Systems with Liquid Dampers: A Review. Appl. Comput. Math. 2021, 20, 339–365. [Google Scholar]
- Adıgüzel, R.S.; Aksoy, U.; Karapınar, E.; Erhan, I.M. On the Solutions of Fractional Differential Equations via Geraghty Type Hybrid Contractions. Appl. Comput. Math. 2021, 20, 313–333. [Google Scholar]
- Pankov, P.S.; Zheentaeva, Z.K.; Shirinov, T. Asymptotic reduction of solution space dimension for dynamical systems. TWMS J. Pure Appl. Math. 2021, 12, 243–253. [Google Scholar]
- Musaev, H.K. The Cauchy problem for degenerate parabolic convolution equation. TWMS J. Pure Appl. Math. 2021, 12, 278–288. [Google Scholar]
- Tiantian, L.; Yakui, X. Global stability analysis of a delayed SEIQR epidemic model with quarantine and latent. Appl. Math. 2013, 4, 38059. [Google Scholar]
- Li, S.; Hussain, A.; Khan, I.U.; El Koufi, A.; Mehmood, A. The Continuous and Discrete Stability Characterization of Hepatitis B Deterministic Model. Math. Probl. Eng. 2022, 2022, 1893665. [Google Scholar] [CrossRef]
- Ahmed, I.; Modu, G.U.; Yusuf, A.; Kumam, P.; Yusuf, I. A mathematical model of Coronavirus Disease (COVID-19) containing asymptomatic and symptomatic classes. Results Phys. 2021, 21, 103776. [Google Scholar] [CrossRef]
- Ali, A.; Rabiei, F.; Shah, K.; Khodadadi, T. Qualitative analysis of fractal-fractional order COVID-19 mathematical model with case study of Wuhan. Alex. Eng. J. 2021, 60, 477–489. [Google Scholar] [CrossRef]
- Moore, S.; Hill, E.M.; Tildesley, M.J.; Dyson, L.; Keeling, M.J. Vaccination and non-pharmaceutical interventions for COVID-19: A mathematical modelling study. Lancet Infect. Dis. 2021, 21, 793–802. [Google Scholar] [CrossRef]
- Noeiaghdam, S.; Micula, S.; Nieto, J.J. A novel technique to control the accuracy of a nonlinear fractional order model of COVID-19: Application of the CESTAC method and the CADNA library. Mathematics 2021, 9, 1321. [Google Scholar] [CrossRef]
- Ahmed, A.; Salam, B.; Mohammad, M.; Akgul, A.; Khoshnaw, S.H. Analysis coronavirus disease (COVID-19) model using numerical approaches and logistic model. Aims Bioeng 2020, 7, 130–146. [Google Scholar] [CrossRef]
- Higazy, M. Novel fractional order SIDARTHE mathematical model of COVID-19 pandemic. Chaos Solitons Fractals 2020, 138, 110007. [Google Scholar] [CrossRef]
- Contreras, S.; Priesemann, V. Risking further COVID-19 waves despite vaccination. Lancet Infect. Dis. 2021, 21, 745–746. [Google Scholar] [CrossRef]
- Adak, D.; Majumder, A.; Bairagi, N. Mathematical perspective of COVID-19 pandemic: Disease extinction criteria in deterministic and stochastic models. Chaos Solitons Fractals 2021, 142, 110381. [Google Scholar] [CrossRef]
- Ahmad, S.; Owyed, S.; Abdel-Aty, A.H.; Mahmoud, E.E.; Shah, K.; Alrabaiah, H. Mathematical analysis of COVID-19 via new mathematical model. Chaos Solitons Fractals 2021, 143, 110585. [Google Scholar]
- Peter, O.J.; Qureshi, S.; Yusuf, A.; Al-Shomrani, M.; Idowu, A.A. A new mathematical model of COVID-19 using real data from Pakistan. Results Phys. 2021, 24, 104098. [Google Scholar] [CrossRef]
- Lin, Q.; Zhao, S.; Gao, D.; Lou, Y.; Yang, S.; Musa, S.S.; Wang, M.H.; Cai, Y.; Wang, W.; Yang, L.; et al. A conceptual model for the coronavirus disease 2019 (COVID-19) outbreak in Wuhan, China with individual reaction and governmental action. Int. J. Infect. Dis. 2020, 93, 211–216. [Google Scholar] [CrossRef]
- Abdo, M.S.; Shah, K.; Wahash, H.A.; Panchal, S.K. On a comprehensive model of the novel coronavirus (COVID-19) under Mittag-Leffler derivative. Chaos Solitons Fractals 2020, 135, 109867. [Google Scholar] [CrossRef]
- Yousaf, M.; Zahir, S.; Riaz, M.; Hussain, S.M.; Shah, K. Statistical analysis of fore- casting COVID-19 for upcoming month in Pakistan. Chaos Solitons Fractals 2020, 138, 109926. [Google Scholar] [CrossRef]
- Sabir, Z.; Asmara, A.; Dehraj, S.; Raja, M.A.Z.; Altamirano, G.C.; Salahshour, S.; Ali, M.R. A mathematical model of coronavirus transmission by using the heuristic computing neural networks. Eng. Anal. Bound. Elem. 2023, 146, 473–482. [Google Scholar] [CrossRef]
- Mickens, R.E. Nonstandard Finite Difference Models of Differential Equations; World Scientific: Singapore, 1994. [Google Scholar]
- Arino, J.; Driessche, P.V.D. The basic reproduction number in a multi-city compartmental epidemic model. In Positive Systems; Springer: Berlin/Heidelberg, Germany, 2023; pp. 135–142. [Google Scholar]
- Shokri, A.; Khalsaraei, M.M.; Molayi, M. Nonstandard dynamically consistent numerical methods for MSEIR model. J. Appl. Comput. Mech. 2022, 8, 196–205. [Google Scholar]
- Mickens, R.E. Applications of Nonstandard Finite Difference Schemes; World Scientific: Singapore, 2000. [Google Scholar]
- Mickens, R.E. Nonstandard finite difference schemes for differential equations. J. Differ. Equ. Appl. 2002, 8, 823–847. [Google Scholar] [CrossRef]
- Mickens, R.E. Dynamic consistency: A fundamental principle for constructing nonstandard finite difference schemes for differential equations. J. Differ. Equ. Appl. 2005, 11, 645–653. [Google Scholar] [CrossRef]
- Elaydi, S. An Introduction to Difference Equations, 3rd ed.; Springer: New York, NY, USA, 2005. [Google Scholar]
- Brauer, F.; Castillo-Chavez, C.; Castillo-Chavez, C. Mathematical Models in Population Biology and Epidemiology; Springer: New York, NY, USA, 2012; Volume 2, p. 508. [Google Scholar]
- Mehdizadeh Khalsaraei, M.; Shokri, A.; Noeiaghdam, S.; Molayi, M. Nonstandard finite difference schemes for an SIR epidemic model. Mathematics 2021, 9, 3082. [Google Scholar] [CrossRef]
- Shokri, A.; Mehdizadeh Khalsaraei, M.; Molayi, M. Dynamically consistent NSFD methods for predator-prey system. J. Appl. Comput. Mech. 2021, 7, 1565–1574. [Google Scholar]
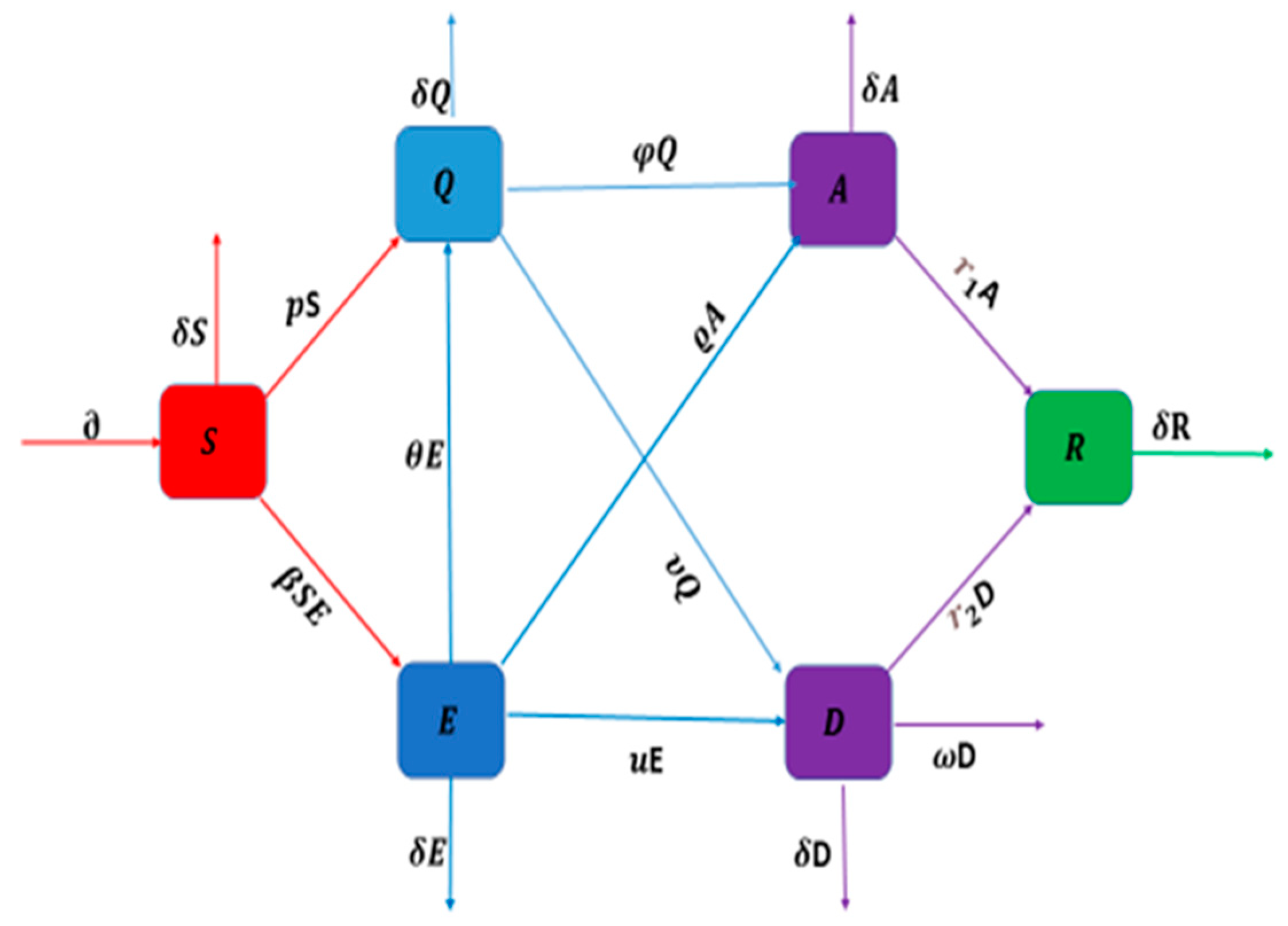
| Parameters | Parameters’ Description |
|---|---|
| Rate of contact between susceptible and exposed people | |
| Recruitment rate of mortality | |
| The rate of transmission from exposed to quarantined persons | |
| The rate of transmission from quarantined to symptomatic persons | |
| The rate of transmission from susceptible to quarantined persons | |
| The rate of mortality in symptomatic infected persons | |
| The rate of natural fatality | |
| The rate of transmission from quarantined to asymptomatic persons | |
| The rate of transmission from exposed to symptomatic persons | |
| The rate of recovered persons from asymptomatic disease | |
| The rate of recovered persons from symptomatic disease | |
| Transfer rate of exposed persons to asymptomatic persons |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khan, I.U.; Hussain, A.; Li, S.; Shokri, A. Modeling the Transmission Dynamics of Coronavirus Using Nonstandard Finite Difference Scheme. Fractal Fract. 2023, 7, 451. https://doi.org/10.3390/fractalfract7060451
Khan IU, Hussain A, Li S, Shokri A. Modeling the Transmission Dynamics of Coronavirus Using Nonstandard Finite Difference Scheme. Fractal and Fractional. 2023; 7(6):451. https://doi.org/10.3390/fractalfract7060451
Chicago/Turabian StyleKhan, Ihsan Ullah, Amjid Hussain, Shuo Li, and Ali Shokri. 2023. "Modeling the Transmission Dynamics of Coronavirus Using Nonstandard Finite Difference Scheme" Fractal and Fractional 7, no. 6: 451. https://doi.org/10.3390/fractalfract7060451
APA StyleKhan, I. U., Hussain, A., Li, S., & Shokri, A. (2023). Modeling the Transmission Dynamics of Coronavirus Using Nonstandard Finite Difference Scheme. Fractal and Fractional, 7(6), 451. https://doi.org/10.3390/fractalfract7060451








