A Self-Similar Infinite Binary Tree Is a Solution to the Steiner Problem

Abstract

We consider a general metric Steiner problem, which involves finding a set $\mathcal{S}$ with the minimal length, such that $\mathcal{S}\cup A$ is connected, where A is a given compact subset of a given complete metric space X; a solution is called the Steiner tree. Paolini, Stepanov, and Teplitskaya in 2015 provided an example of a planar Steiner tree with an infinite number of branching points connecting an uncountable set of points. We prove that such a set can have a positive Hausdorff dimension, which was an open question (the corresponding tree exhibits self-similar fractal properties).

1. Introduction

The Steiner problem, which has various (but more or less equivalent) formulations, involves finding a set $\mathcal{S}$ with a minimal length (a one-dimensional Hausdorff measure ${\mathcal{H}}^1$), such that $\mathcal{S}\cup A$ is connected, where A is a given compact subset of a given complete metric space X.

In [1], it is shown that under rather mild assumptions in the ambient space X (which are true in the Euclidean plane setting), a solution to the Steiner problem exists. Moreover, every solution $\mathcal{S}$ having a finite length has the following properties:

• $\mathcal{S}\cup A$ is compact.
• $\mathcal{S}\setminus A$ has, at most, a finite number of connected components, and each component has a strictly positive length.
• $\overline{\mathcal{S}}$ contains no loops (homeomorphic images of the circle ${\mathbb{S}}^1$).
• The closure of every connected component of $\mathcal{S}$ is a topological tree, which is a connected and locally connected compact set without loops. It has endpoints on A and, at most, many branching points. Each connected component of A has, at most, one endpoint on the tree, and all of the branching points have a finite number of branches leaving them.
• If A has a finite number of connected components, then $\mathcal{S}\setminus A$ has a finite number of connected components, the closure of each of which is a finite geodesic embedded graph with endpoints on A, and with, at most, one endpoint on each connected component of A.
• For every open set $U\subset X$, such that $A\subset U$, one has that the set ${\mathcal{S}}^{\prime }:=\mathcal{S}\setminus U$ is a subset of a finite geodesic embedded graph. Moreover, for a.e. $\epsilon >0$, one has that for $U=\{x:\mathrm{dist}(x,A)<\epsilon \}$, the set ${\mathcal{S}}^{\prime }$ is a finite geodesic embedded graph (in particular, it has a finite number of connected components and a finite number of branching points).

A solution to the Steiner problem is called the Steiner tree; the above properties explain such naming in the case of A being a totally disconnected set. We denote by $\mathbb{M}\left(A\right)$ the set of Steiner trees for A. From now, we will focus on $X={\mathbb{R}}^2$ (but the following properties also hold for ${\mathbb{R}}^d$) and assume that A is a totally disconnected set; we will refer to the points from A as terminals. In this case, ’geodesic’ is just a straight-line segment. A combination of the last enlisted property from [1] with well-known facts on Euclidean Steiner trees (see [2,3]) gives the following properties. The maximal degree (in a graph-theoretic sense) of a vertex in a Steiner tree is, at most, 3. Moreover, only terminals can have degrees 1 or 2, all of the other vertices have degrees of 3 and are referred to as Steiner points. Vertices with a degree of 3 are referred to as branching points, and the angle between any two adjacent edges of a Steiner tree is at least $2\pi /3$.

Note that a Steiner tree may be not unique, see the left-hand side of Figure 1.

Branching, particularly triple-branching points, is a well-known phenomenon in one-dimensional shape optimization problems. There have been several papers in the last decade that focused on the case of an infinite number of branching points for various variations of the irrigation problem [4,5,6]. The corresponding results for the Steiner problem were proven in [7] (see Theorem 1).

If every terminal point in a Steiner tree has degree one, then it is called full. In the Steiner tree problem, it is reasonable to focus on full trees since every non-full tree can be easily cut into full components. Conversely, it is relatively easy to glue several regular tripods (using terminals) and create a trivial example of a tree with an infinite number of branching points (note that a regular tripod is a union of three segments with a common end and pairwise angles equal to $2\pi /3$).

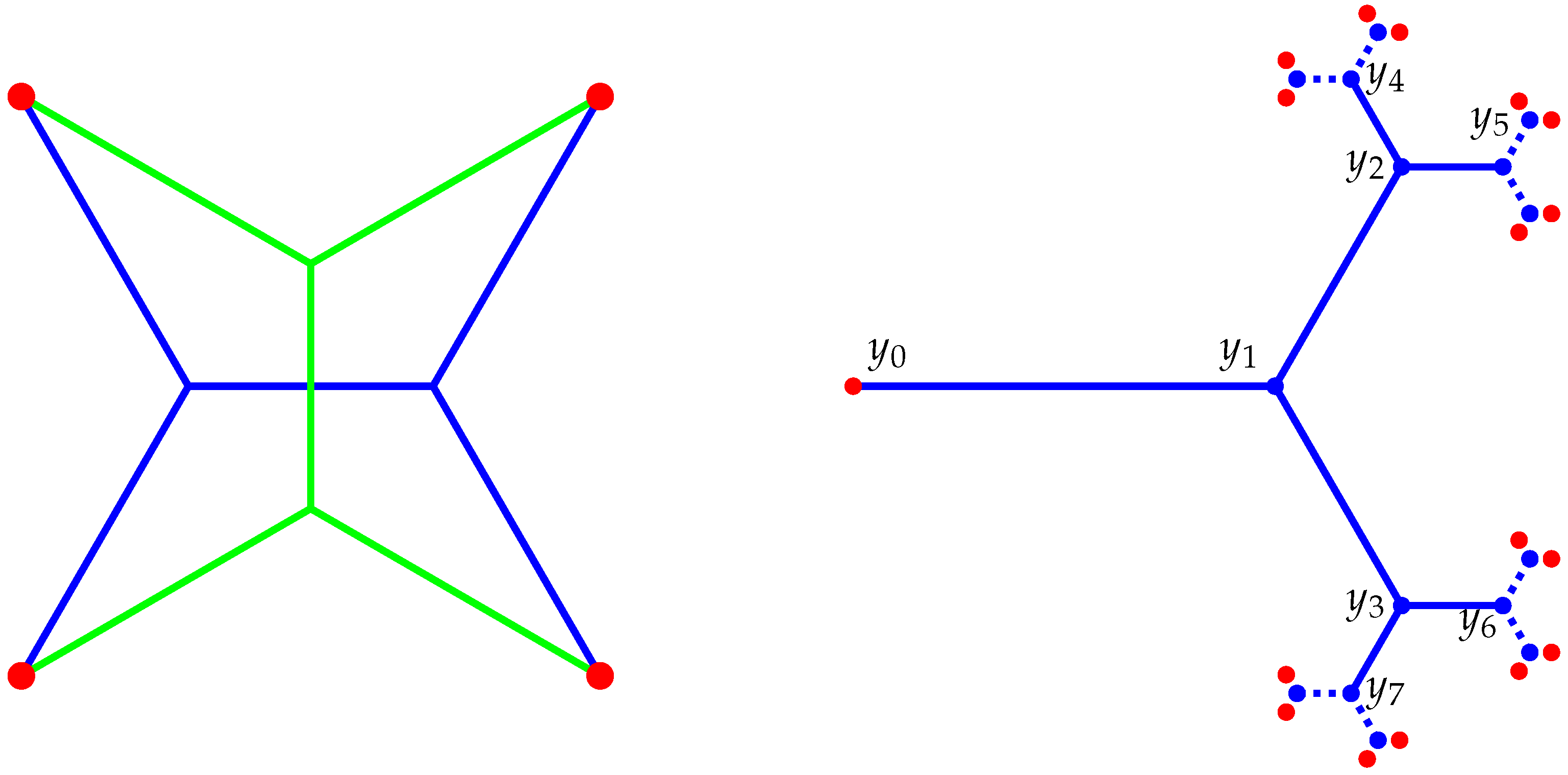
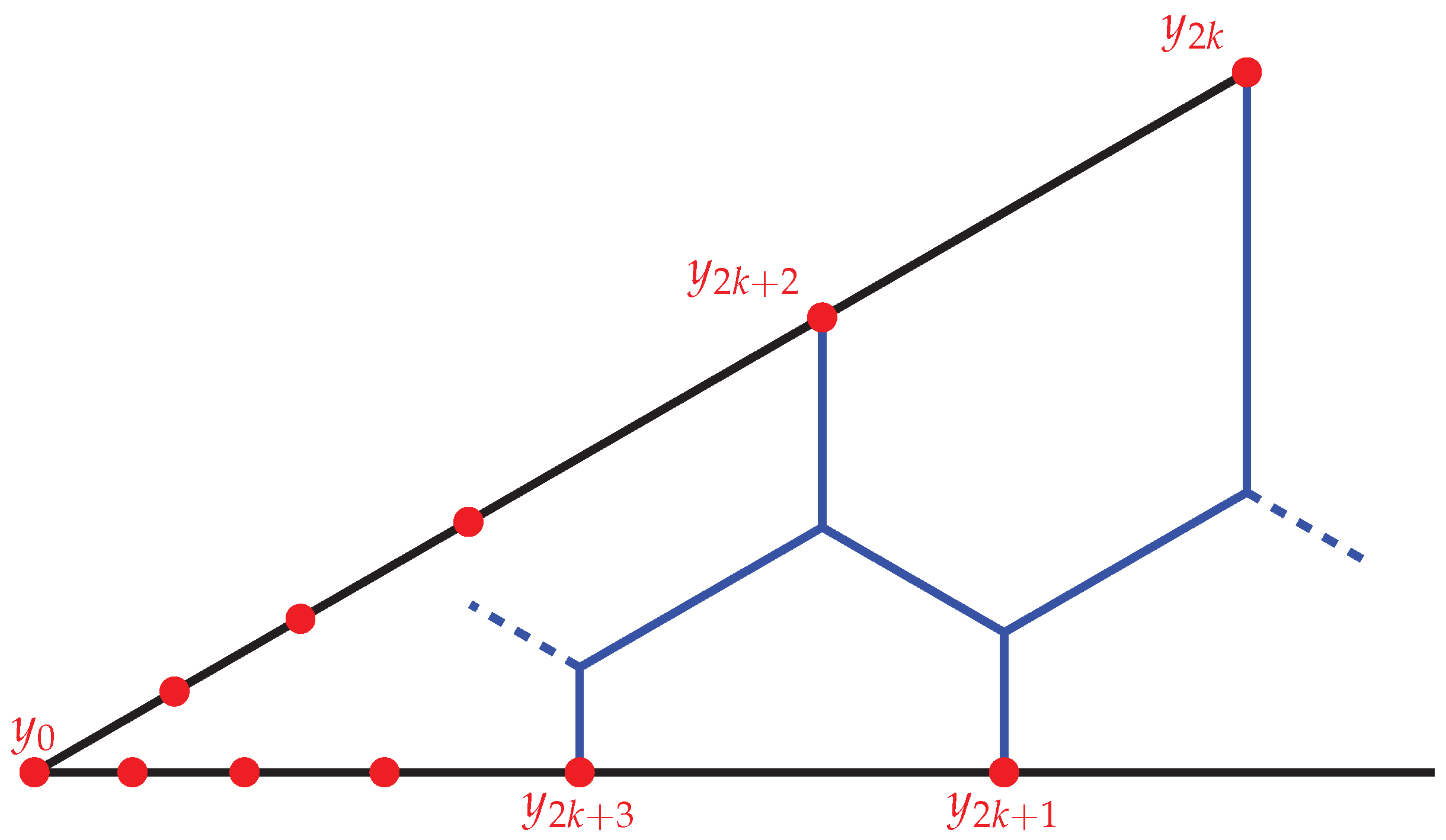
A Universal Steiner Tree

In this subsection, we provide the construction of a unique Steiner tree with an infinite number of Steiner points from [7].

Let $S_{\infty }$ be an infinite tree with vertices $y_0,y_1,y_2,\cdots$ and edges given by $y_0{y}_1$ and $y_k{y}_{2k}$, $y_k{y}_{2k+1}$, $k\ge 1$. Thus, $S_{\infty }$ is an infinite binary tree with an additional vertex $y_0$ attached to the common parent $y_1$ of all other vertices $y_k,k\ge 2$. The goal of [7] is to embed $S_{\infty }$ in the plane in such a way that the image of each finite subtree of $S_{\infty }$ will be a unique Steiner tree for the set of vertices having degrees of 1 or 2. We define the embedding below by specifying the positions of $y_0,y_1,y_2,\cdots$ in the plane.

Let $\Lambda ={\left\{{\lambda }_i\right\}}_{i=0}^{\infty }$ be a sequence of positive real numbers. An embedding $\Sigma (\Lambda )$ of $S_{\infty }$ is defined as a rooted binary tree where the root is denoted as $y_0=(0,0)$, the first descendant as $y_1=(1,0)$, and the ratio between the edges at the $(i+1)$-th and i-th levels is given by ${\lambda }_i$. For a small enough $\left\{{\lambda }_i\right\}$, the set $\Sigma (\Lambda )$ is a tree; see the right-hand side of Figure 1.

Let $A_{\infty }(\Lambda )$ be the union of the set of all leaves (limit points) of $\Sigma (\Lambda )$ and $\left\{y_0\right\}$.

Theorem 1 

(Paolini–Stepanov–Teplitskaya, [7]). A binary tree $\Sigma (\Lambda )$ is a unique Steiner tree for $A_{\infty }(\Lambda )$, provided by ${\lambda }_i<1/5000$ and ${\sum }_{i=1}^{\infty }{\lambda }_i<\pi /5040$.

The following corollary explains why a full binary Steiner tree is universal, i.e., it contains a subtree with a given combinatorial structure.

Corollary 1. 

In the conditions of Theorem 1, each connected closed subset S of $\Sigma (\Lambda )$ has a natural tree structure. Moreover, every S is the unique Steiner tree for the set P of the vertices with the degrees 1 and 2 of S.

Proof. 

Let $S\subset \Sigma (\Lambda )$ and $P\subset S$ satisfy the conditions of the corollary. The fact that S is a tree is straightforward. Let $S^{\prime }\ne S$ be any Steiner tree for S and assume that ${\mathcal{H}}^1\left(S^{\prime }\right)\le {\mathcal{H}}^1\left(S\right)$. Then it is clear that ${\mathcal{H}}^1((\Sigma (\Lambda )\setminus S)\cup S^{\prime })\le {\mathcal{H}}^1(\Sigma (\Lambda ))$, but on the other hand, $\left\{y_0\right\}\cup A_{\infty }\subset (\Sigma (\Lambda )\setminus S)\cup S^{\prime }$, which contradicts the minimality or the uniqueness in Theorem 1. □

After proving Theorem 1, the authors of [7] observed the following:

“Our proof requires that the sequence $\left\{{\lambda }_j\right\}$ vanish rather quickly (in fact, at least be summable). It is an open question if in the case of a constant sequence ${\lambda }_j=\lambda$ (with $\lambda >0$ small enough) the same construction still provides a Steiner tree. This seems to be quite interesting since the resulting tree would be, in that case, a self-similar fractal.”

The result of this paper is an affirmative answer.

Theorem 2. 

A binary tree $\Sigma (\Lambda )$ is a Steiner tree for $A_{\infty }(\Lambda )$ provided by a constant sequence ${\lambda }_i=\lambda <\frac{1}{300}$.

Clearly, in the conditions of Theorem 2, the set $\Sigma (\Lambda )$ is a self-similar fractal, such that

$${\mathcal{H}}^1(\Sigma (\Lambda ))=\sum _{i=0}^{\infty }{\left(2\lambda \right)}^i=\frac{1}{1-2\lambda }$$

and the Hausdorff dimension of $A_{\infty }$ is $-\frac{ln2}{ln\lambda }$. More about fractals and self-similarity in metric geometry can be found in [8].

The set of descendants of every vertex $y_k$ of $\Sigma (\Lambda )$ has an axis of symmetry containing $y_k$. The idea of the proof of Theorem 2 is to progressively show that there is a Steiner tree for $A_{\infty }$, which has more of such symmetries, and then to take a limit.

In fact, the proof uses a soft analysis in contrast to the previous one, which used a hard analysis. The proof uses symmetry arguments instead of stability arguments (the proof of Theorem 1 is based on a general estimation of a difference after a small perturbation). In fact, the proof of Theorem 1 allows us to use different ${\lambda }_i$ for different branches, which completely breaks the symmetries used in the proof of Theorem 2.

Another weakness in comparison with Theorem 1 is that we are not able to show the uniqueness of a Steiner tree.

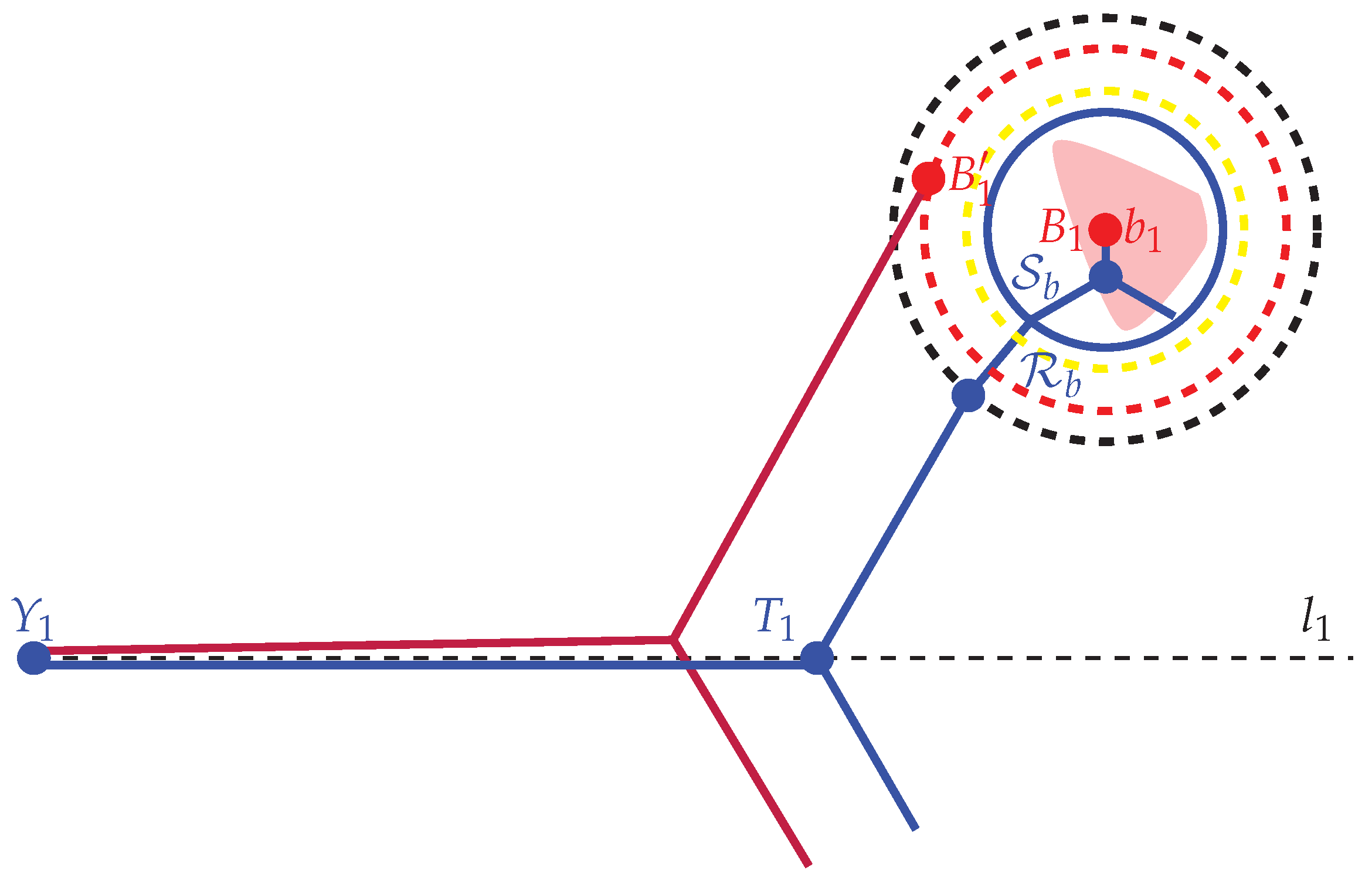
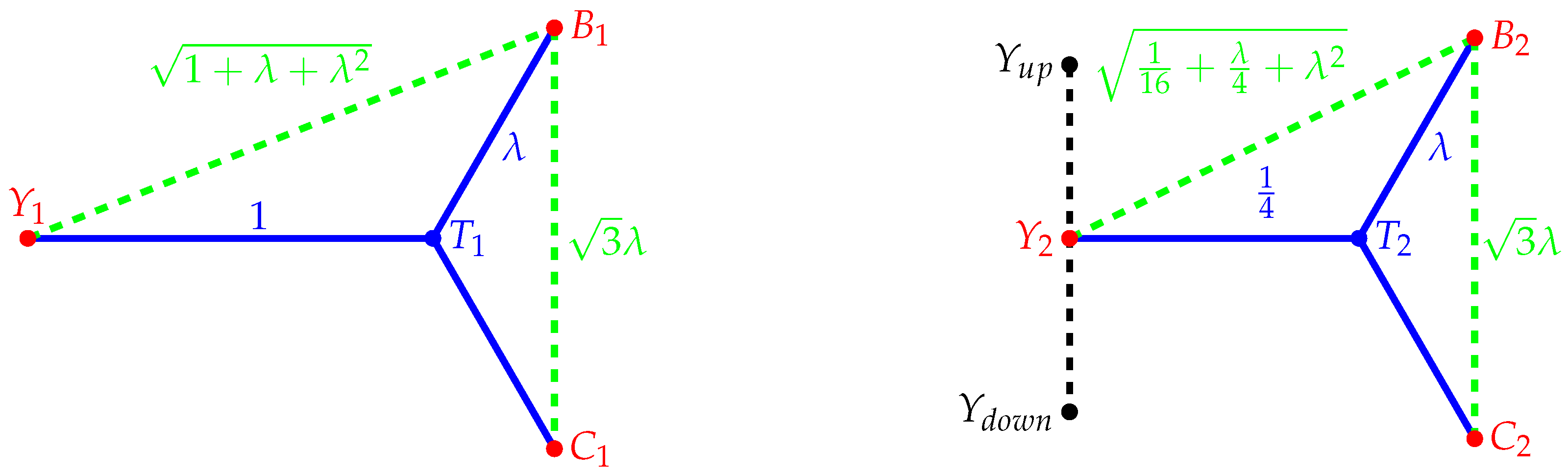
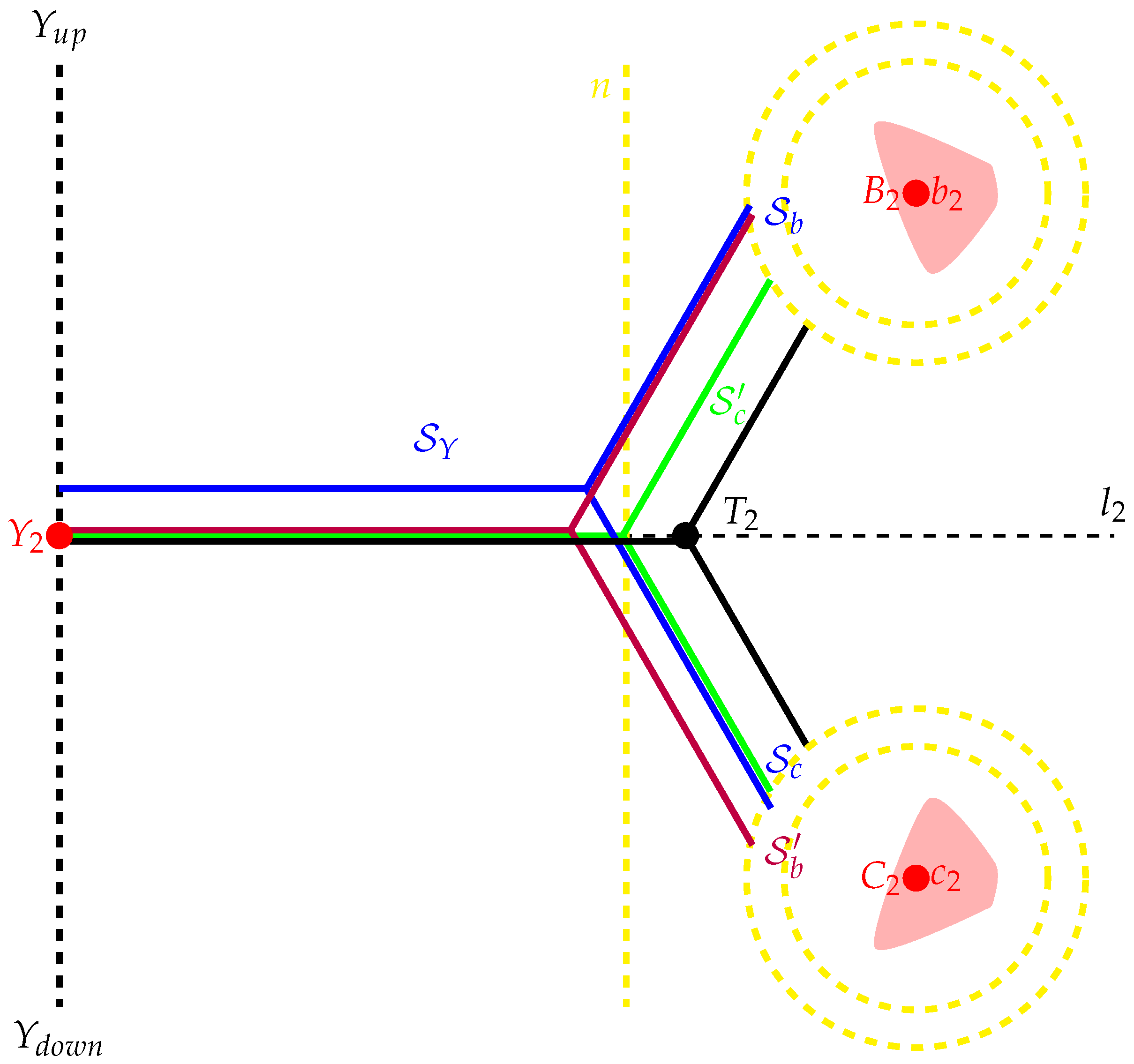
2. Results

Proof of Theorem 2. 

Let $\lambda <\frac{1}{300}$, $\epsilon =\frac{{\lambda }^2}{1-\lambda }$ be fixed during the proof. The following auxiliary constructions are drawn in Figure 2. Let $Y_1{B}_1{C}_1$ be an isosceles triangle with the Fermat–Torricelli point $T_1$, such that $|Y_1{T}_1|=1$, $|T_1{B}_1|=|T_1{C}_1|=\lambda$; then, by the cosine rule $|Y_1{B}_1|=|Y_1{C}_1|=\sqrt{1+\lambda +{\lambda }^2}$ and $|B_1{C}_1|=\sqrt{3}\lambda$. Analogously, let $Y_2{B}_2{C}_2$ be an isosceles triangle with the Fermat–Torricelli point $T_2$, such that $|Y_2{T}_2|=1/4$, $|T_2{B}_2|=|T_2{C}_2|=\lambda$; then $|Y_2{B}_2|=|Y_2{C}_2|=\sqrt{1/16+\lambda /4+{\lambda }^2}$ and $|B_2{C}_2|=\sqrt{3}\lambda$.

Let $b_i\subset B_{\epsilon }\left(B_i\right)$ and $c_i\subset B_{\epsilon }\left(C_i\right)$ be symmetric sets with respect to the axis of symmetry $l_i$ of $Y_i{B}_i{C}_i$, where $i=1,2$. Finally, let $Y_{up}$, $Y_{down}$ be such points that $Y_{up}{Y}_{down}\Vert B_2{C}_2$, $Y_2\in \left[Y_{up}{Y}_{down}\right]$ and $|Y_2{Y}_{up}|=|Y_2{Y}_{down}|=1/2$.

The following proposition is more-or-less known (see, for instance, Lemma A.6 in [7]), so we prove it in Appendix A. Recall that a regular tripod is a union of three segments with a common end and pairwise angles equal to $2\pi /3$.

Proposition 1. 

(i) 

For every $\mathcal{S}\in \mathbb{M}(\left\{Y_1\right\}\cup b_1\cup c_1)$, the set $\mathcal{S}\setminus B_{10\epsilon }\left(B_1\right)\setminus B_{10\epsilon }\left(C_1\right)$ is a regular tripod.

(ii) 

Every $\mathcal{S}\in \mathbb{M}(\left[Y_{up}{Y}_{down}\right]\cup b_2\cup c_2)$ is a regular tripod outside of $B_{10\epsilon }\left(B_2\right)\cup B_{10\epsilon }\left(C_2\right)$.

Lemma 1. 

There exists $\mathcal{S}\in \mathbb{M}(\left\{Y_1\right\}\cup b_1\cup c_1)$, which is symmetric with respect to $l_1$.

Proof. 

Let F be a point at the ray $\left[Y_1{T}_1\right)$, such that $|Y_{1}F|=1+\frac{3}{2}\lambda$ (see Figure 3), and denote by $DEF$ the equilateral triangle, such that $Y_1$ is the middle of the segment $\left[DE\right]$ and $B_1{C}_1$ is parallel to $DE$. Consider segments $\left[Z_l{Z}_r\right]\subset \left[DF\right]$ and $\left[V_l{V}_r\right]\subset \left[EF\right]$, such that $|Z_l{Z}_r|=\left[V_l{V}_r\right]=\lambda$ and $Z:=DF\cap T_1{B}_1,V:=EF\cap T_1{C}_1$ are centers of the segments. Note that $l_1$ is a symmetry axis of $DEF$, and $\left[Z_l{Z}_r\right]$ and $\left[V_l{V}_r\right]$ are also symmetric with respect to $l_1$.

By Proposition 1(i), every minimal set $\mathcal{S}$ is a regular tripod $Y_1{B}_1^{\prime }{C}_1^{\prime }$ out of $B_{10\epsilon }\left(B_1\right)\cup B_{10\epsilon }\left(C_1\right)$. We claim that the tripod $Y_1{B}_1^{\prime }{C}_1^{\prime }$ intersects segments $\left[Z_l{Z}_r\right]$ and $\left[V_l{V}_r\right]$. Indeed, consider Cartesian coordinates in which $Y_1=(0,0)$, $B_1=(1+\lambda /2,\sqrt{3}\lambda /2)$ and $C_1=(1+\lambda /2,-\sqrt{3}\lambda /2)$. Then $Z=(1+3\lambda /8,3\sqrt{3}\lambda /8)$, $Z_l=(1+3\lambda /8-\sqrt{3}\lambda /4,3\sqrt{3}\lambda /8+\lambda /4)$, and $Z_r=(1+3\lambda /8+\sqrt{3}\lambda /4,3\sqrt{3}\lambda /8-\lambda /4)$. Since the center $T_1^{\prime }$ of $Y_1{B}_1^{\prime }{C}_1^{\prime }$ lies inside triangle $Y_1{B}_1^{\prime }{C}_1^{\prime }$, it has an x-coordinate smaller than the x-coordinate of $B_1^{\prime }$ and a y-coordinate smaller than the y-coordinate of $B_1^{\prime }$.

We consider the following auxiliary data for the Steiner problem: $A_{mid}=\left[Z_l{Z}_r\right]\cup \left[V_l{V}_r\right]\cup \left\{Y_1\right\}$, $A_{up}=\left[Z_l{Z}_r\right]\cup b_1$, $A_{down}=\left[V_l{V}_r\right]\cup c_1$. By the results from [1], as mentioned in the introduction, every $\mathbb{M}\left(A_i\right)$ is not empty. Segments $\left[Z_l{Z}_r\right]$ and $\left[V_l{V}_r\right]$ split every $\mathcal{S}\in \mathbb{M}(\left\{Y_1\right\}\cup b_1\cup c_1)$ into three parts, connecting $A_{mid}$, $A_{up}$, and $A_{down}$, so

$${\mathcal{H}}^1\left(\mathcal{S}\right)\ge {\mathcal{H}}^1\left({\mathcal{S}}_{mid}\right)+{\mathcal{H}}^1\left({\mathcal{S}}_{up}\right)+{\mathcal{H}}^1\left({\mathcal{S}}_{down}\right),$$

(1)

where ${\mathcal{S}}_i\in \mathbb{M}\left(A_i\right)$. We claim that the equality in (1) holds.

It is known (see the barycentric coordinate system) that the sum of distances from a point inside a closed equilateral triangle to the sides does not depend on a point. Thus, $\mathbb{M}\left(A_{mid}\right)$ is a set of regular tripods, and each tripod is symmetric with respect to $l_1$. Moreover, for every point $x\in \left[Z_l{Z}_r\right]$, there is a unique regular tripod ${\mathcal{S}}_x\in \mathbb{M}\left(A_{mid}\right)$, and ${\mathcal{S}}_x$ is orthogonal to $\left[Z_l{Z}_r\right]$ at x.

Now consider any ${\mathcal{S}}_{down}\in \mathbb{M}\left(A_{down}\right)$. Let ${\mathcal{S}}_{up}$ be a set that is symmetric to ${\mathcal{S}}_{down}$ with respect to $l_1$; clearly, ${\mathcal{S}}_{up}\in \mathbb{M}\left(A_{up}\right)$. For $x\in {\mathcal{S}}_{down}\cap \left[V_l{V}_r\right]$, the set ${\mathcal{S}}_x\cup {\mathcal{S}}_{up}\cup {\mathcal{S}}_{down}$ connects $\left\{Y_1\right\}\cup b_1\cup c_1$, and reaches the equality in (1), so ${\mathcal{S}}_x\cup {\mathcal{S}}_{up}\cup {\mathcal{S}}_{down}$ is a Steiner tree for $\left\{Y_1\right\}\cup b_1\cup c_1$. By the construction, it is symmetric with respect to $l_1$. □

Lemma 2. 

There exists $\mathcal{S}\in \mathbb{M}(\left[Y_{up}{Y}_{down}\right]\cup b_2\cup c_2)$, which is symmetric with respect to $l_2$.

Proof. 

By Proposition 1(ii), every Steiner tree $\mathcal{S}$ coincides with a regular tripod outside of $B_{10\epsilon }\left(B_2\right)\cup B_{10\epsilon }\left(C_2\right)$. Clearly, its longest segment is perpendicular to $Y_{up}{Y}_{down}$ (see Figure 4). We want to show that it touches $Y_{up}{Y}_{down}$ in $Y_2$, i.e., one of the three segments is a subset of $l_2$. Assuming the contrary, suppose that $l_2\cap \mathcal{S}$ is a point, denote it by L, and let $n\Vert B_2{C}_2$ be the line containing L. Then n divides $\mathcal{S}$ into three connected components; denote them by ${\mathcal{S}}_Y$, ${\mathcal{S}}_b$, and ${\mathcal{S}}_c$, respectively.

Without the loss of generality, L belongs to ${\mathcal{S}}_c$.

Let us construct competitors ${\mathcal{S}}_1$ and ${\mathcal{S}}_2$, connecting $\left[Y_{up}{Y}_{down}\right]$, $b_2$, and $c_2$. Let ${\mathcal{S}}_1=\left[Y_{2}L\right]\cup {\mathcal{S}}_c\cup {\mathcal{S}}_c^{\prime }$, where ${\mathcal{S}}_c^{\prime }$ is a reflection of ${\mathcal{S}}_c$ with respect to $l_2$. Put $h:=\mathrm{dist}(Y_2,{\mathcal{S}}_Y\cap \left[Y_{up}{Y}_{down}\right])$. Thus

$${\mathcal{H}}^1\left({\mathcal{S}}_1\right)={\mathcal{H}}^1\left({\mathcal{S}}_Y\right)-\sqrt{3}h+2{\mathcal{H}}^1\left({\mathcal{S}}_c\right).$$

Let ${\mathcal{S}}_2:=\mathcal{T}\cup {\mathcal{S}}_b\cup {\mathcal{S}}_b^{\prime }$, where ${\mathcal{S}}_b^{\prime }$ is a reflection of ${\mathcal{S}}_b$, with respect to $l_2$, and $\mathcal{T}$ is a regular tripod connecting $Y_2$ with $n\cap {\mathcal{S}}_b$ and $n\cap {\mathcal{S}}_{b^{\prime }}$. Thus,

$${\mathcal{H}}^1\left({\mathcal{S}}_2\right)={\mathcal{H}}^1\left({\mathcal{S}}_Y\right)+\sqrt{3}h+2{\mathcal{H}}^1\left({\mathcal{S}}_b\right).$$

Since $\mathcal{S}$ is a Steiner tree, one has ${\mathcal{H}}^1\left(\mathcal{S}\right)\le {\mathcal{H}}^1\left({\mathcal{S}}_1\right)$, ${\mathcal{H}}^1\left(\mathcal{S}\right)\le {\mathcal{H}}^1\left({\mathcal{S}}_2\right)$ and clearly ${\mathcal{H}}^1\left(\mathcal{S}\right)=\frac{{\mathcal{H}}^1\left({\mathcal{S}}_1\right)+{\mathcal{H}}^1\left({\mathcal{S}}_2\right)}{2}$. Then ${\mathcal{H}}^1\left(\mathcal{S}\right)={\mathcal{H}}^1\left({\mathcal{S}}_1\right)={\mathcal{H}}^1\left({\mathcal{S}}_2\right)$, and so ${\mathcal{S}}_1,{\mathcal{S}}_2$ belong to $\mathbb{M}(\left[Y_{up}{Y}_{down}\right]\cup b_2\cup c_2)$. As ${\mathcal{S}}_1$ and ${\mathcal{S}}_2$ are symmetric with respect to $l_2$, the statement is proven. □

Now we are ready to prove Theorem 2, i.e., to show that for ${\lambda }_j=\lambda <\frac{1}{300}$, the set $\Sigma (\Lambda )$ is a Steiner tree for the set of terminals $A_{\infty }$.

Let $b_1$ and $c_1$ be the subsets of terminals that are descendants of $y_2$ and $y_3$, respectively. Since $\epsilon ={\lambda }^2+{\lambda }^3+\cdots +{\lambda }^k+\cdots$, we have $b_i\subset B_{\epsilon }\left(B_i\right)$, $c_i\subset B_{\epsilon }\left(C_i\right)$. Applying Lemma 1 to $Y_1=y_0$, $B_1=y_2$, $C_1=y_3$, $b_1$, and $c_1$, we show that there is a Steiner tree for $A_{\infty }$, which is symmetric with respect to the line $\left(y_0{y}_1\right)$.

Let $\left[Z_l{Z}_r\right]$ and $\left[V_l{V}_r\right]$ be the segments from the previous application of Lemma 1. Now define $b_2$ and $c_2$ as descendants of $y_4$ and $y_5$, respectively. Then, applying Lemma 2 to $\left[Y_{up}{Y}_{down}\right]=\left[Z_l{Z}_r\right]$, $B_2=y_4$, $C_2=y_5$, $b_2$, and $c_2$ (these data are similar to those required with the scale factor $\lambda$), we show that there is a Steiner tree containing $\left[y_0{y}_1\right]$ and branching at $y_1$ (because $y_1$ belongs to the axis of the symmetries of b and c).

Since ${\lambda }_i$ is constant, the upper and lower components of $\Sigma (\Lambda )\setminus \left[y_0{y}_1\right]$ are similar (with the scale factor $\lambda$) to $\Sigma (\Lambda )$. Thus, the second application of Lemmas 1 and 2 shows that there is a Steiner tree containing $\left[y_0{y}_1\right]\cup \left[y_1{y}_2\right]\cup \left[y_1{y}_3\right]$. This procedure recovers $\Sigma (\Lambda )$ step by step; so after the k-th step, we know that the length of every Steiner tree for $A_{\infty }$ is at least

$$\sum _{i=0}^{k-1}{\left(2\lambda \right)}^i.$$

Thus, the length of every Steiner tree for $A_{\infty }$ is at least the length of $\Sigma (\Lambda )$, which implies $\Sigma (\Lambda )\in \mathbb{M}\left(A_{\infty }\right)$. □

3. Conclusions

3.1. Recent Progress

Recall that our proof has two gaps; the first one is the absence of uniqueness and the second one is the crucial dependence on the symmetries of A. A few weeks before the revision, Paolini and Stepanov combined our arguments with an error estimation argument and obviated both gaps.

Theorem 3 

(Paolini–Stepanov [9]). A binary tree $\Sigma (\Lambda )$ is the unique Steiner tree for $A_{\infty }(\Lambda )$ provided by a constant sequence ${\lambda }_i=\lambda <\frac{1}{25}$.

3.2. Open Problems

Recall that the Steiner problem has a solution for a compact $A\subset {\mathbb{R}}^d$. Suppose that we omit the assumption that $A\subset {\mathbb{R}}^d$ is closed. The following arises.

Question 1 

([10]). Is it possible to find a bounded set A in $X={\mathbb{R}}^d$, such that the problem: “find $\mathcal{S}\subset X$ such that ${\mathcal{H}}^1\left(\mathcal{S}\right)$ is minimal among all sets for which $\mathcal{S}\cup A$ is connected” does not have a solution?

The second issue concerns another possible construction of a full Steiner tree with an infinite number of branching points. Consider $\lambda \in (0,1)$ and an angle of size $\alpha$ in the plane. Let $y_0$ be the vertex of the angle and $y_1,y_2$ be points on distinct sides of the angle. For $k\ge 1$, define $y_{2k+2}\in \left[y_{2k}{y}_0\right]$ and $y_{2k+1}\in \left[y_{2k-1}{y}_0\right]$ recurrently by $|y_{2k+2}{y}_0|=\lambda ·|y_{2k}{y}_0|$ and $|y_{2k+1}{y}_0|=\lambda ·|y_{2k-1}{y}_0|$ (see Figure 5). Let A be the union of $y_i$ for i from 0 to ∞. Clearly, A is compact (as a bounded countable set), so the Steiner problem admits a solution.

Question 2. 

Is the solution to the Steiner problem for A unique and full for an appropriate choice of α, λ, $y_1$, and $y_2$?

A computer simulation for small $\alpha$, $\lambda =1/2$, $|y_1{y}_0|=|y_2{y}_0|=1$ and $A_k:=\{y_0,y_1,\cdots y_k\}$ shows that the structure of a Steiner tree depends on k in a mysterious way. Thus, Question 2 requires quite a delicate analysis.