Cerofolini’s Model and the Fractal Adsorption Isotherms

Abstract

The close link between the roughness of a surface and its adsorptive properties in Cerofolini’s model yields, with an adequate choice of adsorption energy, the well-known Dubinin-Radushkevich or Freundlich adsorption isotherms. Assuming fractal behavior concerning both energetic and geometric surface heterogeneities described by the power-law expressions and fractal dimensions, the paper will develop some fractal adsorption isotherms. Using our theoretical approach, fractal isotherms will provide insights not only into the fractal behavior of the surface geometry but also into the fractal energetic heterogeneities, implying that a sorbent does not need to be porous to apply a fractal isotherm: adsorption on “flat” surfaces can also be described by fractal isotherms and fractal dimensions related to energetic disorders. For example, the theory will be applied to computing the energetic fractal dimensions of some nanoparticle catalysts, Rh/Al₂O₃, Rh/TiO₂, and Rh/WO₃.

1. Introduction

When an initially smooth solid surface is heated to a certain temperature, it becomes rough due to atom displacement from equilibrium sites and migration to higher energetic positions. The surface irregularities obtained will depend on the temperature; also, the geometric characteristics of a solid formed by powder sintering will depend on the treatment temperature; chemical reactions, such as etching, will also lead to heterogeneous surfaces. Many structures formed by these processes tend to be characterized by fractal properties, exhibiting self-similarity properties in a defined domain. Real surfaces are usually characterized by energetic disorder because of geometric irregularities and fractal patterns but also because of chemical irregularities: radicals on surfaces, basic and acid centers, and so on. That energetic heterogeneity is usually described as an adsorption energy distribution function depending on adsorption sites. Cerofolini [1,2], using the Boltzmann equation and a general distribution function of the excess energy of an adsorption site, developed the condensation approximation (CA) and the universal equation of adsorption on heterogeneous surfaces. At that moment, there was no relation between energetic and geometric heterogeneity; it was a matter of choice whether to consider energetic or geometric disorder. Later, in the 1980s, the relationship between pore dimensions and the free energy of adsorption on pores for different geometries was developed [3]. That was the first attempt to correlate the energy of adsorption with pore geometry in adsorption experiments and theory.

The change came in 1984, when David Avnir, Dina Farin, and Peter Pfeifer [4] reported that the surfaces of most materials are fractals at the molecular scale. In other words, the fractal theory could be used to describe geometric surface heterogeneities or surfaces with fractal structures of pores.

Following this observation, Henry’s law on fractal surfaces [5], the fractal-BET isotherm [6,7], Frenkel-Halsey-Hill [8], and Dubinin-Radushkevitch [9] fractal isotherms were developed.

All these isotherms considered surfaces as fractal porous structures characterized by a single number: the fractal dimension. In practice, it is hard to successfully apply this theoretical concept: experiments showed that surfaces are never mathematically self-similar; in other words, fractal behaviors can be observed only in the self-similarity domain [10]. Although there is no all-accepted threshold for a minimum self-similar domain to consider an object as a fractal, Pfeifer introduced the rule of r_max/r_min > 2^1/D, where r_min and r_max are the limits of the self-similarity domain, and D is the fractal dimension [11]. The fractal approach can be used even on “flat” surfaces, like graphitized carbon, where the fractal dimension is close to 2. But the solid surfaces are never totally flat or totally fractal [12]. Rudzinski et al. [13] introduced a new concept: “partially correlated surfaces”, which means surfaces with fractal properties on certain domains. Also, they assume a relation between geometric and energetic surface heterogeneities and provide a mathematical form for that. Applying a simple exponential relation between adsorption energy and radius, together with a pore size distribution, they obtained a generalized fractal isotherm.

Following the close relation between adsorption energy and surface geometry, our paper will develop some well-known adsorption isotherms, such as fractal Dubinin-Radushkevitch or Freundlich isotherms [14], assuming fractal surfaces that are characterized by fractal energetic heterogeneities. Using such fractal adsorption isotherms to fit experimental data, it will be proved that the slope of the log-log curve is not the fractal dimension but is rather proportional to both the fractal dimension and the energetic fractal dimension (if any). This means that it is necessary to use a complementary experimental technique (such as micrograph analysis) to compute the fractal dimension and, after that, using the adsorption isotherms, the energetic fractal dimension. These isotherms come to highlight the impact of energetic heterogeneity on fractal isotherms. They emphasize that directly computing the slope from log–log curves of fractal Dubinin-Radushkevitch, Freundlich, or Frankel-Halsey-Hill isotherms could obtain information about geometric and energetic fractal behavior. It is the aim of this paper to study how fractal energetic heterogeneity should be taken into account when fitting experimental isotherms. Also, the paper will demonstrate that choosing simple relations between geometric and energetic surface heterogeneities will lead to the same fractal isotherms as for porous surfaces. The theory will be applied to some nanoparticle catalysts (Rh/Al₂O₃, Rh/TiO₂, Rh/WO₃) to obtain information about their energetic heterogeneity.

2. Theory

2.1. Cerofolini’s Model

Cerofolini’s model [1,2] assumes that heterogeneous surfaces consist of atoms with various energies, which depend on their position on the surface. This assumption implies a close relation between roughness, fractal dimension, and its adsorptive properties.

Let’s consider u₀ the lowest atom’s energy, the energy of the fully coordinated atom, and u_i the energy of the atom occupying i site. The excess energy of the i atom will be u_i^ex = u_i − u₀. Cerofolini assumes that the number of atoms with energy u_i, N_i, is related to the number of atoms N₀ with u₀ energy by the Boltzmann equation [2]. The kinetic argument of the balance between the fully coordinated atom’s jump rate to the surface and the mobile surface atom’s jump rate to fully coordinated sites leads to the distribution function ϕ(u_i^(ex)), which can also be derived from the Boltzmann equation, where T is temperature and k is the Boltzmann’s constant:

$$\varphi \left(u_i^{\left(ex\right)}\right)=\left(\frac{1}{kT}\right)\mathrm{e}\mathrm{x}\mathrm{p}(-\frac{u_i^{\left(ex\right)}}{kT})$$

(1)

If ε_i is the energy of adsorption of i site, Cerofolini’s assumption predicts that there is a direct relation between excess energy and energy of adsorption, using the first two terms in the Taylor expansion:

$$u_i^{\left(ex\right)}={\alpha }^{\prime }\left({\epsilon }_i-{\epsilon }_0\right)+{\beta }^{\prime }{({\epsilon }_i-{\epsilon }_0)}^2$$

(2)

with α^′ and β^′ positive coefficients, and ε₀ is the energy of adsorption of the perfectly homogeneous flat surface. Using the condensation approximation (CA) and Equations (1) and (2), meaning that adsorption on heterogeneous surfaces proceeds from high-to-low adsorption energies, the overall adsorption isotherm can be obtained from the adsorption energy distribution χ(ε) as in the following:

$$\begin{gathered} {\chi }_{}\left({\epsilon }_i\right)=\varphi \left(u_i^{\left(ex\right)}\right)\frac{\partial u_i^{\left(ex\right)}}{\partial \epsilon }=\left[\alpha +2\beta \left({\epsilon }_i-{\epsilon }_0\right)\right]\exp \left\{-\left[\alpha \left({\epsilon }_i-{\epsilon }_0\right)+\beta {\left({\epsilon }_i-{\epsilon }_0\right)}^2\right]\right\} \\ \alpha =\frac{{\alpha }^{\prime }}{kT},\beta =\frac{{\beta }^{\prime }}{kT}, \\ \nu \left(p,T\right)={\int }_{{\epsilon }_c\left(p,T\right)}^{\infty }{\chi }_{}\left(\epsilon \right)d\epsilon , \\ {\epsilon }_c\left(p,T\right)=kTln\left(\frac{K}{p}\right)\mathrm{is} \mathrm{the} \mathrm{Langmuir} \mathrm{local} \mathrm{isotherm}, \\ \ln \nu \left(p,T\right)=A_0-A_{1}kTln\left(\raisebox{1ex}{$p^0$}\!\left/ \!\raisebox{-1ex}{$p$}\right.\right)-A_2{\left(kT\right)}^2{ln}^2\left(\raisebox{1ex}{$p^0$}\!\left/ \!\raisebox{-1ex}{$p$}\right.\right) \end{gathered}$$

(3)

where p⁰ is the saturated vapor pressure of adsorptive,

$$\begin{gathered} A_0=\left(\epsilon -{\epsilon }_0\right)\left[\alpha -\beta \left(\epsilon {-\epsilon }_0\right)\right],A_1=\left[\alpha -2\beta \left(\epsilon -{\epsilon }_0\right)\right] \\ {A}_2=\beta ,{\epsilon }_0=kTln\left(\raisebox{1ex}{$K$}\!\left/ \!\raisebox{-1ex}{$p^0$}\right.\right) \end{gathered}$$

(4)

When A₂ ≪ A₁ and β– > 0, Equation (3) becomes the Freundlich isotherm, whereas when A₂ ≫ A₁, the same equation will lead to the Dubinin Radushkevitch isotherm. Although in real experiments isotherms are a superposition of the Freundlich equation and the Dubinin Radushkevitch (DR) isotherm, at higher pressures the Freundlich term is much more important. At lower pressures, the DR-isotherm will prevail.

A more realistic hypothesis of adsorption should consider not only the adsorption energies but also the topography of the surface, including interactions between the adsorbed atom and direct lattice atoms, interactions with long distant atoms, and interactions with atoms in corners, tops, steps, and pits. This assumption will lead to α^′ and β^′ positive or negative coefficients and ε₀, the mean adsorption energy [15].

2.2. Geometric and Energetic Surface Heterogeneities. Partially Correlated Surfaces

Because the adsorption properties depend on surface topography and energetic surface disorder, isotherms must be described in terms of surface topographic properties, such as fractal properties.

The quest for a simple relation between energetic and geometric surface heterogeneities was the reason for introducing the fractal nature of heterogeneous solid surfaces as a source of Freundlich isotherm, or more generally, of experimental adsorption isotherms [16,17].

Modeling the fractal surface as a fractal structure of pores with a radius smaller than r_m, the normalized pore size distribution is mathematically described by [13]:

$$\rho \left(r\right)=\frac{3-D}{r_m^{3-D}}{r}^{2-D}$$

(5)

where D is the pore’s fractal dimension, and r_m is the maximum size of the pores where fractal properties are manifested.

There are results reported in the literature indicating that the function r(ε) has an exponentially decreasing dependence on ε [18,19,20,21,22,23], meaning that one can assume, as authors in Ref. [13] did, the existence of the following relation:

$$r=e^{-F\left(\epsilon \right)}$$

(6)

where F(ε) is a function depending on the adsorbate-adsorbent system. Using the Taylor expansion of function F(ε), Rudzinski et al. [13] obtained a general form of the adsorption energy distribution χ(ε) on fractal pores structures like:

$$\chi \left(\epsilon \right)=\left(3-D\right){\left(\frac{r_0}{r_m}\right)}^{\left(3-D\right)}\left[{\left(\frac{\partial F}{\partial \epsilon }\right)}_{{\epsilon }_0}+{\left(\frac{{\partial }^{2}F}{\partial {\epsilon }^2}\right)}_{{\epsilon }_0}\left(\epsilon -{\epsilon }_0\right)+\cdots \right]\mathrm{e}\mathrm{x}\mathrm{p}\{-\left(3-D\right){\left(\frac{\partial F}{\partial \epsilon }\right)}_{{\epsilon }_0}\left(\epsilon -{\epsilon }_0\right)-\frac{1}{2}(3-D){\left(\frac{{\partial }^{2}F}{\partial {\epsilon }^2}\right)}_{{\epsilon }_0}{\left(\epsilon -{\epsilon }_0\right)}^2+\cdots \},r_0=r\left({\epsilon }_0\right)$$

(7a)

Equation (7a) has the same form as the adsorption energy distribution used by Cerofolini to obtain Equation (3) in the CA assumption, but in this case, the geometric hypothesis of a fractal surface was considered.

In Ref. [13], Rudzinski et al. obtained the Dubinin-Radushkevitch isotherm in the CA approach by assuming:

$${\left(\frac{{\partial }^{2}F}{\partial {\epsilon }^2}\right)}_{{\epsilon }_0}\left({\epsilon }_c-{\epsilon }_0\right)\gg {\left(\frac{\partial F}{\partial \epsilon }\right)}_{{\epsilon }_0}$$

in the form:

$$\ln \nu \left(p,T\right)~{-1/2\left(3-D\right){\left(\frac{{\partial }^{2}F}{\partial {\epsilon }^2}\right)}_{{\epsilon }_0}}_{}{\left(kT\right)}^2{ln}^2\left(\raisebox{1ex}{$p^0$}\!\left/ \!\raisebox{-1ex}{$p$}\right.\right)+\left(3-D\right)\mathrm{l}\mathrm{n}\left(\frac{r_0}{r_m}\right)$$

(7b)

and the Freundlich isotherm, assuming:

$${\left(\frac{{\partial }^{2}F}{\partial {\epsilon }^2}\right)}_{{\epsilon }_0}\left({\epsilon }_c-{\epsilon }_0\right)\ll {\left(\frac{\partial F}{\partial \epsilon }\right)}_{{\epsilon }_0}$$

as:

$$\nu \left(p,T\right)={\left(\frac{r_0}{r_m}\right)}^{3-D}{\left(\frac{p}{p^0}\right)}^{\alpha kT},\alpha =\left[\left(3-D\right){\left(\frac{\partial F}{\partial \epsilon }\right)}_{{\epsilon }_0}\right]$$

(7c)

How about flat surfaces? It is hard to imagine a flat surface as a fractal structure of pores with fractal dimension D = 2. However, considering the exponentially decreasing dependence of ε in Equation (6), Rudzinski et al. [13] obtained fractal isotherms valid even for “flat” surfaces, suggesting that “flat” nonporous surfaces are porous at the molecular scale. Conner and Bennett [12] showed that although practical catalysts are not ideal fractals, fractal concepts may be useful in understanding surface roughness. Undoubtedly, for D = 2, Equation (5) implies ρ(r) is a constant, so where do the fractal properties come from in the case of flat surfaces? It is roughness at the molecular scale, but it is possible to assume that there is a fractal energetic disorder, too. Equation (6) has shown the deep relation between adsorption energy and geometry. If a surface roughness is expressed in terms of fractal dimension, the energetic heterogeneity of adsorbing centers is described by the energy distribution function χ(ε). Surface roughness implies adsorption energy heterogeneities. If the surface is fractal, we can presume that the energetic heterogeneities exhibit fractal behavior, too, but with a different fractal dimension. The energy of atoms depends on their coordination and symmetry, on geometric defects on their surface, and on surface impurities. We shall develop this hypothesis further in the paper.

The general form of the adsorption energy distribution on a fractal structure of pores, Equation (7a), is valid only for pore sizes smaller than a certain value of the pore radius, r = r_m.

What if the pore sizes are larger or the real fractal behavior deviates from the ideal one?

Rudzinski et al. [13] develop in their paper the adsorption energy distribution for a partially correlated surface, considering the more general expression of the fractal behavior as:

$$N=\frac{C{r}^{3-D}}{1+r^{3-D}},$$

(8)

where r is the pore size, D is the fractal dimension, C is a constant, and N is the number of spherical molecules necessary to cover the surface. Using Equation (8) and considering interactions between adsorbed molecules, they obtained the local isotherms for surfaces that were partially correlated and not ideal fractals.

3. Results and Discussions. Energetic Fractal Relations and Fractal Isotherms

We aim to develop some well-known fractal adsorption isotherms assuming fractal behavior not only of topographic surface properties but of both energetic and geometric surface heterogeneities described by the power-law expressions and fractal dimensions, using a generalized form of Equations (2) and (6). In Section 3.1 and Section 3.2, we will analyze some simple relations between excess energy and adsorption energy, while in Section 3.3, a fractal relation between adsorption energy and the pore size will be introduced. The energetic fractal dimension of some nanoparticle catalysts Rh/Al₂O₃, Rh/TiO₂, and Rh/WO₃ is computed in Section 3.4 using the fractal isotherm developed in Section 3.3.

3.1. A Simple Fractal Relation between Excess Energy and Adsorption Energy

Suppose there is a fractal behavior of the energetic surface heterogeneities with a mathematical transcription as a fractal relation between the excess energy u_i^(ex) and the adsorption energy ε_i on i site. In this case, the polynomial function of Equation (2) will be replaced by the scale-invariant power function:

$$u_i^{\left(ex\right)}={\alpha }^{\prime }{\left({\epsilon }_i-{\epsilon }_0\right)}^{\gamma }$$

(9)

where γ is a fractional, positive number describing the scaling of the energy excess with the adsorption energy of the site. Using Equations (1) and (9), and following the same mathematical calculus as above, the energy distribution function will be:

$$\chi \left({\epsilon }_i\right)=\varphi \left(u_i^{\left(ex\right)}\right)\frac{\partial u_i^{\left(ex\right)}}{\partial \epsilon }=\alpha \gamma {({\epsilon }_i-{\epsilon }_0)}^{\gamma -1}\exp \left[-\alpha {\left({\epsilon }_i-{\epsilon }_0\right)}^{\gamma }\right],$$

(10)

with ε_i ≥ ε₀, γ ≥ 1, α = α′/kT.

Considering the local Langmuir isotherm:

$${\epsilon }_c\left(p,T\right)=kTln\left(\frac{K}{p}\right)$$

(11)

where ε_c is the critical value of the energy of adsorption in the condensation approximation, k is Boltzmann’s constant, and K is a constant, the overall adsorption isotherm will be:

$$\nu \left(p,T\right)={\int }_{{\epsilon }_c(p,T)}^{\infty }\chi \left(\epsilon \right)d\epsilon ,$$

$$\ln \nu \left(p,T\right)=-\alpha {\left(kT\right)}^{\gamma }{\left[\ln (\raisebox{1ex}{$p^0$}\!\left/ \!\raisebox{-1ex}{$p$}\right.)\right]}^{\gamma }$$

(12)

which is, in fact, the well-known Dubinin-Astakov isotherm [24,25].

When γ = D − 3, Equation (12) leads, in fact, to a Dubinin-Radushkevitch-type fractal isotherm [9,13,14], whereas if γ = (D − 3)/3 Equation (12) leads to a fractal Frenkel-Halsey-Hill isotherm [8,9,14].

The fractal isotherm described by Equation (12) was obtained considering the fractal scaling law of the excess energy of the atom function of adsorption energy and not considering the topographic fractal behavior of the surface, such as a fractal pore structure, like in Section 2. It is proof that the fractal energetic disorder of the surface leads to the same adsorption equations as the geometric surface properties when considering proper scaling relations between excess energy and adsorption energy.

3.2. A Generalized Fractal Relation between Excess Energy and Adsorption Energy

Let’s generalize Equation (9) and consider another scaling relation between the excess energy and the adsorption energy [26]:

$$u_i^{\left(ex\right)}=kT\mathrm{l}\mathrm{n}{\left(\frac{{\epsilon }_u{-\epsilon }_0}{{\epsilon }_u-{\epsilon }_i}\right)}^{\gamma },$$

(13a)

where ε_u is the upper limit of the adsorption energy, ε₀ is the lower value of the adsorption energy, the energy of adsorption of a perfectly homogeneous plane surface, T is temperature, and k is Boltzmann’s constant.

Following the same mathematical procedure as above and using Equation (1), the energy distribution function will be:

$${\chi }_{}\left({\epsilon }_i\right)=\varphi \left(u_i^{\left(ex\right)}\right)\frac{\partial u_i^{\left(ex\right)}}{\partial \epsilon }=\gamma \frac{{({\epsilon }_u-{\epsilon }_i)}^{\gamma -1}}{{({\epsilon }_u-{\epsilon }_o)}^{\gamma }}$$

(13b)

In this case, the overall adsorption isotherm becomes:

$$\nu \left(p,T\right)={\int }_{{\epsilon }_c(p,T)}^{{\epsilon }_u}{\chi }_{}\left(\epsilon \right)d\epsilon ={\left(\frac{{\epsilon }_u-{\epsilon }_c}{{\epsilon }_u-{\epsilon }_0}\right)}^{\gamma },{\epsilon }_c=kTln(K/p),and {\epsilon }_0=kTln\left(K/p^0\right)$$

(14)

with p⁰ the saturated vapor pressure.

In terms of pressure using the Taylor expansion, that is:

$$\begin{gathered} \ln \nu \left(p,T\right)=\gamma ln\left(\frac{{\epsilon }_u}{{\epsilon }_u-{\epsilon }_0}\right)+\gamma ln\left(1-\frac{{\epsilon }_c}{{\epsilon }_u}\right)=const-\gamma \left[\frac{{\epsilon }_c}{{\epsilon }_u}+\frac{1}{2}{\left(\frac{{\epsilon }_c}{{\epsilon }_u}\right)}^2+\cdots \right], \\ ln\nu \left(p,T\right)=B_0-{\gamma B}_{1}ln{\left(\raisebox{1ex}{$p^0$}\!\left/ \!\raisebox{-1ex}{$p$}\right.\right)}^{}-{\gamma B}_2{ln}^2{\left(\raisebox{1ex}{$p^0$}\!\left/ \!\raisebox{-1ex}{$p$}\right.\right)}^{}-\cdots \end{gathered}$$

(15)

with B₀, B₁, B₂ positive coefficients.

When γ = D − 3, Equation (15) is a combination of the fractal Freundlich isotherm and the fractal Dubinin-Radushkevitch isotherms, as obtained by Rudzinski et al. in Ref. [13]. Again, energetic scaling laws lead to the well-known fractal isotherms without the necessity of considering fractal porous structures. Only a simple scaling relation between excess energy and the adsorption energy leads to the well-known fractal Freundlich isotherm or fractal Dubinin-Radushkevitch isotherm without considering porous fractal structure or complicated assumptions. It is not the porous fractal behavior of the surface that leads to the fractal isotherms but the fractal behavior of the adsorption energy. In this case, the exponent is not the geometric fractal dimension but an exponent characterizing the fractal energetic heterogeneities. This concept will be expanded upon further in the following sections.

3.3. A Fractal Relation between Adsorption Energy and Pore Size

As we already mentioned, there are reported experimental results in the literature indicating an exponentially decreasing dependence of r(ε) on ε [18,19,20,21,22,23]. Based on these results, Rudzinski et al. [13] supposed a simple relation between the adsorption energy and the pore size r, as described in Equation (6). Supposing the fractal surface is a fractal structure of pores described by the fractal geometry using the fractal dimension D, as in Equation (5) [13], we can imagine, too, a fractal behavior of the energetic surface heterogeneities, but characterized by a different fractal dimension. The deep relation between the fractal behavior of the surface and the fractal behavior of energetic surface heterogeneity can be motivated by the source of energetic surface heterogeneity. The adsorption energy distribution on the surface is related to surface defects, peaks, surface roughness, and surface impurities. Knowing that surfaces are fractal at the molecular scale and assuming that the distribution of adsorption energy depends on surface characteristics, one can assume fractal behavior for the adsorption energy. This fractal behavior can be mathematically described by choosing a simple scaling function with a fractional exponent between the pore size r and the adsorption energy ε:

$$r=a{\epsilon }^{D_e-3}$$

(16)

where a is a constant and D_e is the energetic fractal dimension describing the scaling properties of the adsorption energy. Experimental results indicating a decreasing dependence of r(ε) on ε [18,19,20,21,22,23] imply that D_e < 3.

The volume V of the layer of adsorbed molecules covering a fractal surface is:

$$V=C{r}^{3-D}$$

(17)

meaning that the total number of adsorption sites N will be proportional to V. Therefore, combining Equations (16) and (17), we obtain:

$$-\frac{\partial N}{\partial \epsilon }=-\xi \left(\frac{\partial V}{\partial r}\right)\frac{dr}{d\epsilon }={\xi a}^{3-D}C\left(3-D\right)\left(3-D_e\right){\epsilon }^{\left(D_e-3\right)\left(3-D\right)-1}$$

(18)

where ξ is a normalizing coefficient.

Defining r_m the maximum size of pores where fractal properties still exist and ε₁ as the corresponding adsorption energy, from Equation (16):

$$r_m=a{{\epsilon }_1}^{D_e-3}$$

the normalizing coefficient is obtained from the simple condition:

$${\int }_{{\epsilon }_1}^{\infty }\frac{\partial N}{\partial \epsilon }d\epsilon =1$$

leading to:

$$\xi =a^{D-3}{C}^{-1}{{\epsilon }_1}^{(3-D_e)(3-D)}={\left[C{r}_m^{3-D}\right]}^{-1}$$

The energy distribution function is:

$$\chi \left(\epsilon \right)=\frac{\partial N}{\partial \epsilon }=-{{\epsilon }_1}^{-1}(3-D)(3-D_e){\left(\raisebox{1ex}{$\epsilon $}\!\left/ \!\raisebox{-1ex}{${\epsilon }_1$}\right.\right)}^{\left(3-D\right)\left(D_e-3\right)-1}$$

(19)

where D is the geometric fractal dimension and D_e is the energetic fractal dimension.

Using Equation (19), for the highest energy sites, where adsorption occurs first, approximating $\left[\frac{\mathrm{l}\mathrm{n}(\raisebox{1ex}{$K$}\!\left/ \!\raisebox{-1ex}{$p$}\right.)}{\mathrm{l}\mathrm{n}(\raisebox{1ex}{$K$}\!\left/ \!\raisebox{-1ex}{$p^0$}\right.)}\right]~\mathrm{l}\mathrm{n}(\raisebox{1ex}{$p^0$}\!\left/ \!\raisebox{-1ex}{$p$}\right.)$, the overall adsorption isotherm will become:

$$\nu \left(p,T\right)={\int }_{{\epsilon }_c}^{\infty }\chi \left(\epsilon \right)d\epsilon ={\left(\raisebox{1ex}{${\epsilon }_c$}\!\left/ \!\raisebox{-1ex}{${\epsilon }_1$}\right.\right)}^{\left(3-D\right)\left(D_e-3\right)}=const{\left[\frac{\mathrm{l}\mathrm{n}\left(\raisebox{1ex}{$K$}\!\left/ \!\raisebox{-1ex}{$p^0$}\right.\right)}{\mathrm{l}\mathrm{n}\left(\raisebox{1ex}{$K$}\!\left/ \!\raisebox{-1ex}{$p$}\right.\right)}\right]}^{(3-D)(3-D_e)}=const{\left[ln\left(\raisebox{1ex}{$p^0$}\!\left/ \!\raisebox{-1ex}{$p$}\right.\right)\right]}^{-(D-3)(D_e-3)},$$

(20)

which is, in fact, the well-known Dubinin-Radushkevitch fractal isotherm, as in Refs. [9,13,14] for fractal surfaces, with an adjacent exponent related to energetic fractal behavior, D_e.

More of that, at higher adsorbate pressure, where $\left[\frac{\mathrm{l}\mathrm{n}\left(\raisebox{1ex}{$K$}\!\left/ \!\raisebox{-1ex}{$p$}\right.\right)}{\mathrm{l}\mathrm{n}\left(\raisebox{1ex}{$K$}\!\left/ \!\raisebox{-1ex}{$p^0$}\right.\right)}\right]~\frac{p^0}{p},$ the fractal Freundlich isotherm [8,9] is obtained:

$$\nu \left(p,T\right)=K{\left[\left(\raisebox{1ex}{$p^0$}\!\left/ \!\raisebox{-1ex}{$p$}\right.\right)\right]}^{-(D-3)(D_e-3)}$$

(21)

For the planar surface D = 2 and Equation (20) becomes:

$$\nu \left(p,T\right)=const{\left[ln\left(\raisebox{1ex}{$p^0$}\!\left/ \!\raisebox{-1ex}{$p$}\right.\right)\right]}^{D_e-3},$$

(22a)

the same Dubinin-Radushkevitch-type fractal isotherm, meaning that only the fractal energetic disorder is important, not the geometric properties (flat surface). This approximation explains Hobson’s observation [27,28] that the Dubinin-Radushkevitch fractal isotherm can describe even adsorption on “flat” surfaces. This observation is not proof that flat surfaces are porous.

When D_e = 2, Equation (21) becomes the fractal Dubinin-Radushkevitch-type isotherm [9,14]:

$$\nu \left(p,T\right)=const{\left[ln\left(\raisebox{1ex}{$p^0$}\!\left/ \!\raisebox{-1ex}{$p$}\right.\right)\right]}^{D-3},$$

(22b)

with D, the geometric fractal dimension, as above.

In conclusion, it seems that the fractal energetic disorder leads to the same well-known fractal isotherms as the assumption of the fractal system of pores—Equation (22a).

Fractal dimension computation by adsorption isotherms fitting must consider complementary techniques of fractal dimension measuring, such as micrograph analysis. In this case, the fractal dimension obtained by micrograph analysis can be assigned to the geometric fractal dimension, while the fractal dimension obtained using fractal isotherms could be, in fact, a combination of the geometric and energetic fractal dimensions, as in Equation (20).

3.4. Energetic Fractal Dimension Computation: “A Simple Application”

In our previous studies [28,29], we found that when analyzing the fractal behavior of rhodium nanoparticles synthesized by the polyol method, supported on alumina, titania, and tungsten trioxide (Rh/Al₂O₃, Rh/TiO₂, Rh/WO₃) (Figure 1), the TEM fractal dimensions could differ substantially from the fractal dimensions obtained by direct fitting of experimental isotherms (Figure 2) with the Dubinin-Radushkevitch fractal isotherm (Figure 3), Equation (22b). Preparation and characterization methods were presented in extenso in previous work [28,29].

Table 1. The fractal dimensions obtained by TEM analysis (using two different methods, the correlation function method (C) and the variable length-scale method (V), differ from the fractal dimensions obtained by fitting the experimental adsorption isotherms with the DR isotherms (in the capillary condensation regime) [28,29]. Reprinted with permission from Refs. [28,29]. Copyright 2021 IOSR Journals.

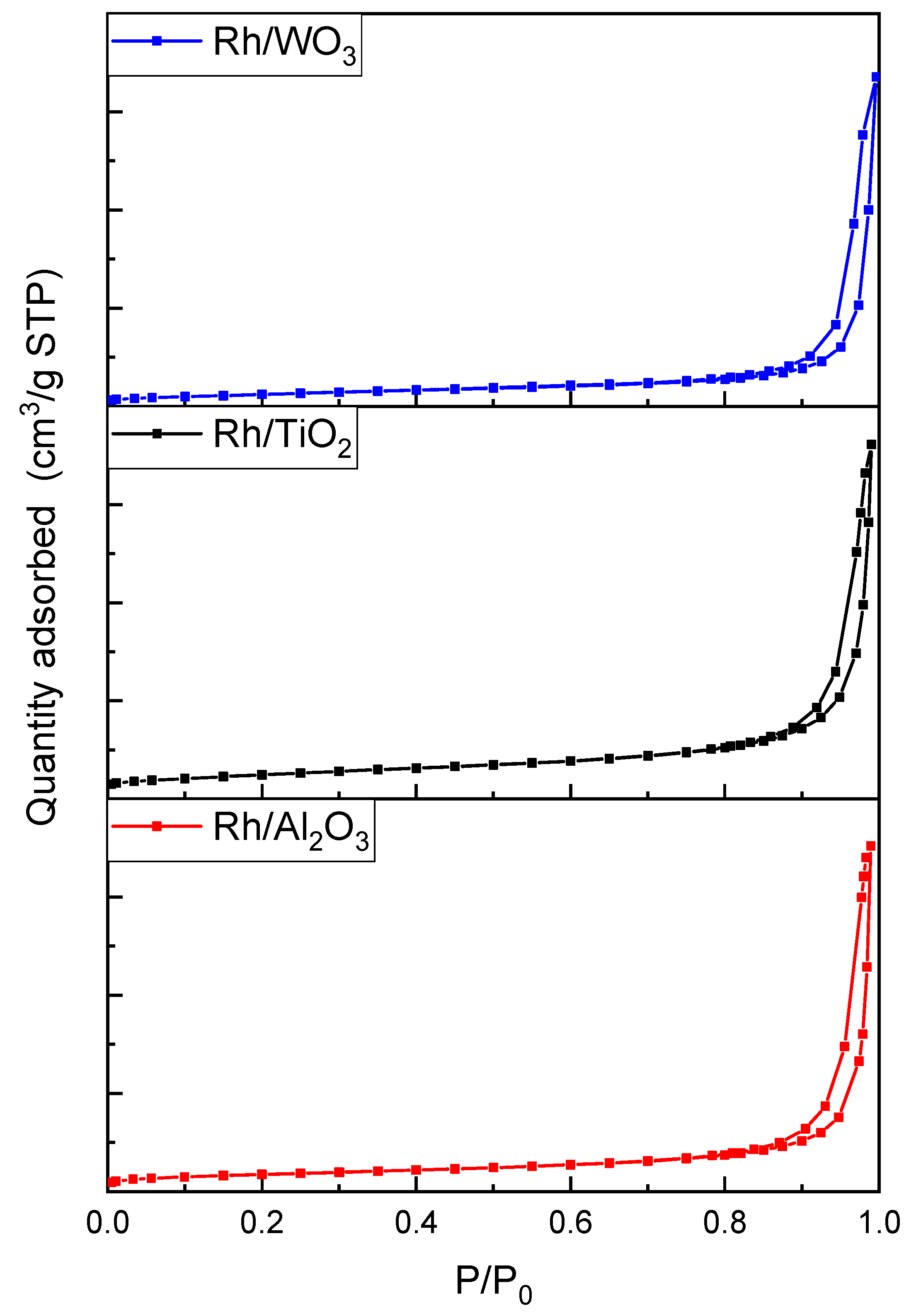
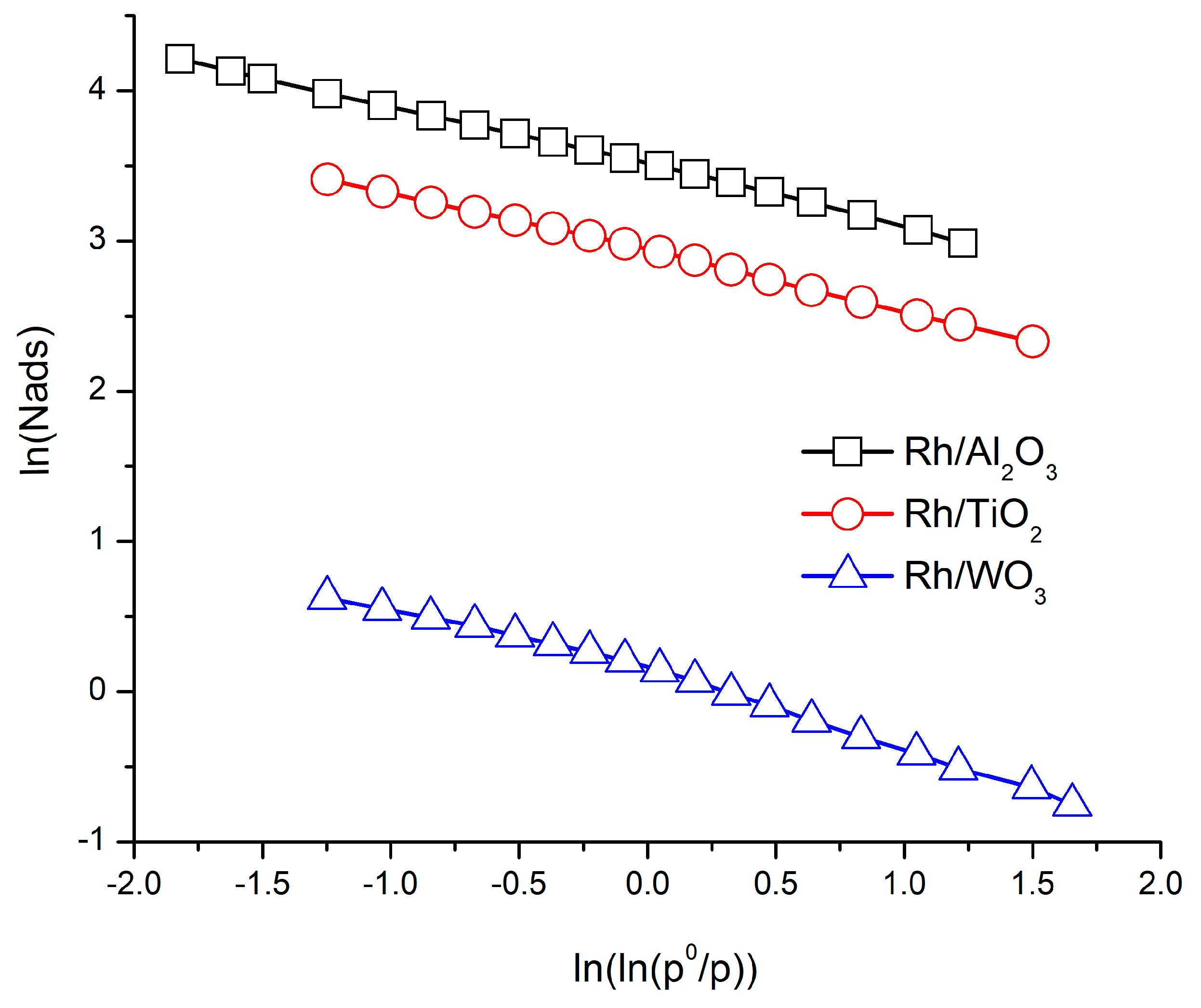
Sample	TEM Fractal Dimension	Method	Self-Similarity Domain (nm)	DR Fractal Dimension Equation (22a)	Self-Similarity Domain (p/p0)
Rh/Al2O3	2.872 ± 0.001 2.784 ± 0.051	C V	4.4–14.4 7.2–11.8	2.607 ± 0.004	0.033–0.850
Rh/TiO2	2.733 ± 0.001 2.832 ± 0.009	C V	4.9–14.4 5.4–17.3	2.604 ± 0.003	0.011–0.750
Rh/WO3	2.490 ± 0.001 2.469 ± 0.035 2.330 ± 0.001 2.226 ± 0.047	C C V V	0.2–2.7 2.7–13.8 4.5–11 11–29.3	2.448 ± 0.012 2.589 ± 0.014	0.005–0.200 0.200–0.750

briefly presents these results. TEM fractal dimensions were computed using the correlation function method [30] and the variable length scale method [31]. Both methods computed surface fractal dimensions. On the other hand, when fitting adsorption isotherms with the Dubinin-Radushkevitch-type fractal isotherm (Equation (22b)), the surface fractal dimension is computed.

All samples exhibit fractal behavior, as is depicted in Table 1. Simple calculus showed that Pfeifer’s condition of fractality [11] is obeyed.

Fitting adsorption isotherms (Figure 2) with the fractal isotherms depicted by Equation (21), considering TEM fractal dimension (Table 1) as the geometric fractal dimension, and computing the average TEM fractal dimension between the values obtained by different methods [28,29], the energetic fractal dimension D_e can be computed, as shown in

Table 2. The energetic fractal dimension D_e computed from Equation (17) and considering TEM fractal dimension as a geometric fractal dimension (see Table 1).

Sample	Energetic Fractal Dimension De	Standard Errors
Rh/Al2O3	0.715	0.023
Rh/TiO2	1.179	0.003
Rh/WO3	1.939	0.038
	2.430	0.065

.

Results presented in Table 2 show that if the TEM fractal dimension is equal to the Dubinin-Radushkevitch fractal dimension, then the surface is energetically uniform, and D_e = 2, the fractal behavior of the adsorption surface, is governed only by geometrical properties. This is the case of the Rh/WO₃ sample, where D_e is 1.939 ± 0.038 for the low self-similarity domain [28,29].

On the other hand, if the TEM fractal dimension is greater than the Dubinin-Radushkevitch fractal dimension, then the energetic fractal dimension is lower than 2, D_e < 2. In this case, not all the surface active sites are “visible” by the adsorbed molecule, the energetic fractal dimension is low, there are points on the surface hidden by pores or peaks, and the surface seems “flatter” than it is in reality when it is investigated by the adsorption method. It is the case of Rh/Al₂O₃ and Rh/TiO₂ (low self-similarity domain) [28,29].

If the energetic fractal dimension is greater than 2, the surface can be characterized by both geometrical and energetical fractal dimensions, each different from the other. This is the case of Rh/WO₃ (in the high self-similarity domain, D_e = 2.430) [28,29]. The energetic non-uniformity can be evidenced and quantitatively described by the energetic fractal dimension.

These observations are in accord with the results presented in Ref. [28], where the Rh/Al₂O₃ and Rh/TiO₂ samples have similar behavior, which can be explained by the blockage of the surface pores and irregularities by Rh-nanoparticles or/and by Rh encapsulation via SMSI (strong metal-support interaction). This behavior leads to energetic heterogeneity characterized by lower D_e and surfaces seeming “flatter” than TEM investigations depicted.

On the other hand, energetic non-uniformity described by the high energetic fractal dimension of the sample Rh/WO₃ can be related to the existence of weak, medium, and strong basic sites in approximately equal ratios on the surface [28].

The major application of these considerations and theoretical results is the possibility of discerning between the geometric fractal dimension and the energetic fractal dimension and computing a number, the energetic fractal dimension, to quantitatively describe this behavior. This observation leads to the opportunity of deepening the characterization of sorbents, not only from the geometrical point of view but also from the energetical one, knowing that all sorts of chemical irregularities are related to surface non-homogeneities: radicals on surfaces, basic and acid centers, and so on.

4. Conclusions

The major conclusion of this paper is that, by choosing the right relationship between the excess energy and the adsorption energy, as in Cerofolini’s assumption, all major fractal isotherms can be depicted. More so, the exponent involved in this relationship described the fractal properties of the surface, both geometric and energetic. This can be an argument for the fact that fractal properties are linked both to the geometric and energetic properties of the surface. Furthermore, considering energetic fractal behavior, fractal isotherms of adsorption on “flat” surfaces lead to the computation of energetic fractal dimensions. It seems that fractal energetic disorder, which can be related not only to geometrical disorder but to surface energetic heterogeneities, leads to the same well-known fractal isotherms as the assumption of the fractal system of pores. These theoretical results depicted the possibility of discerning between the geometric fractal dimension and the energetic fractal dimension and computing a number, the energetic fractal dimension, to quantitatively describe energetic surface heterogeneity. The theory was applied to compute the energetic fractal dimensions of some previously in extenso studied based nanoparticle catalysts, Rh/Al₂O₃, Rh/TiO₂, and Rh/WO₃ [28,29]. The importance of using complementary techniques to compute geometric fractal dimensions (such as micrograph analysis) is also emphasized. Results are in accord with previous studies [28,29] depicting the energetic non-uniformity of the Rh/WO₃ sample together with the behavior of Rh/Al₂O₃ and Rh/TiO₂, which seem “flatter” when investigated by the adsorption isotherm method, explaining the difference between the fractal dimension obtained by TEM analysis and by the adsorption–isotherm method.