Grid-Connected Inverter Based on a Resonance-Free Fractional-Order LCL Filter
Abstract
:1. Introduction
2. Caputo Fractional Calculus
3. Fractional-Order LCL (FOLCL) Filter
3.1. Mathematical Model
3.2. Characteristics Analysis
3.2.1. Theoretical Analysis
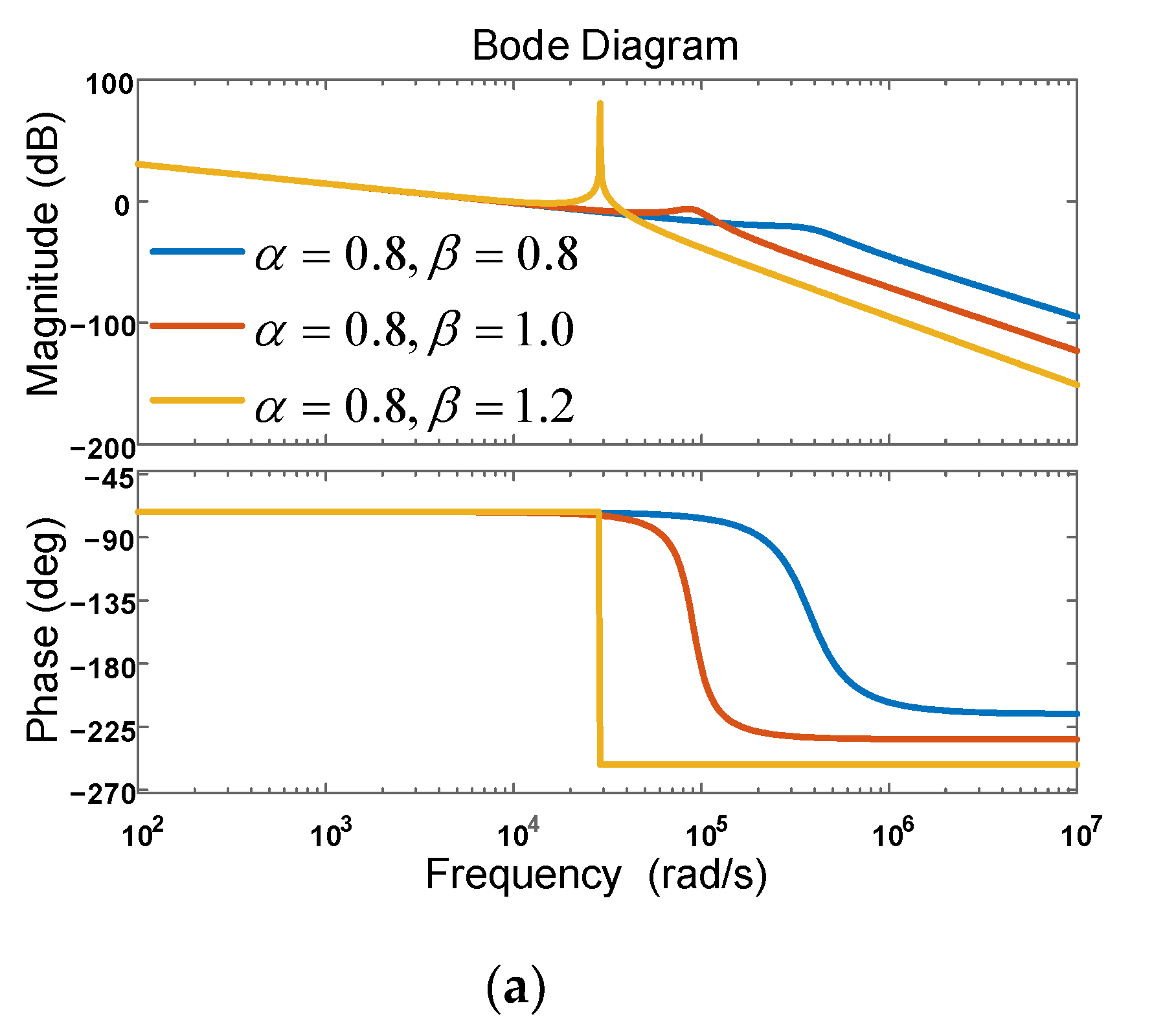
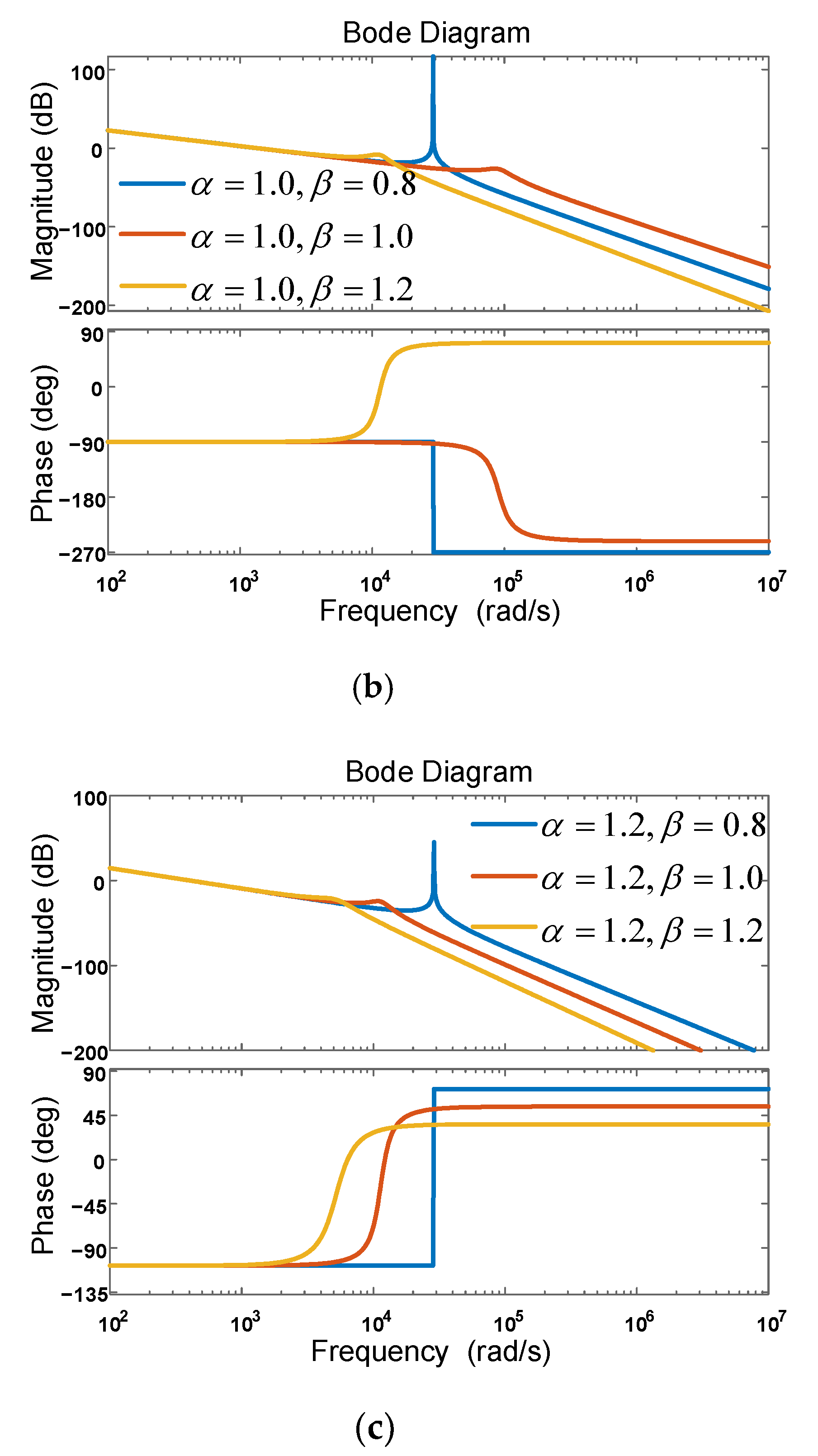
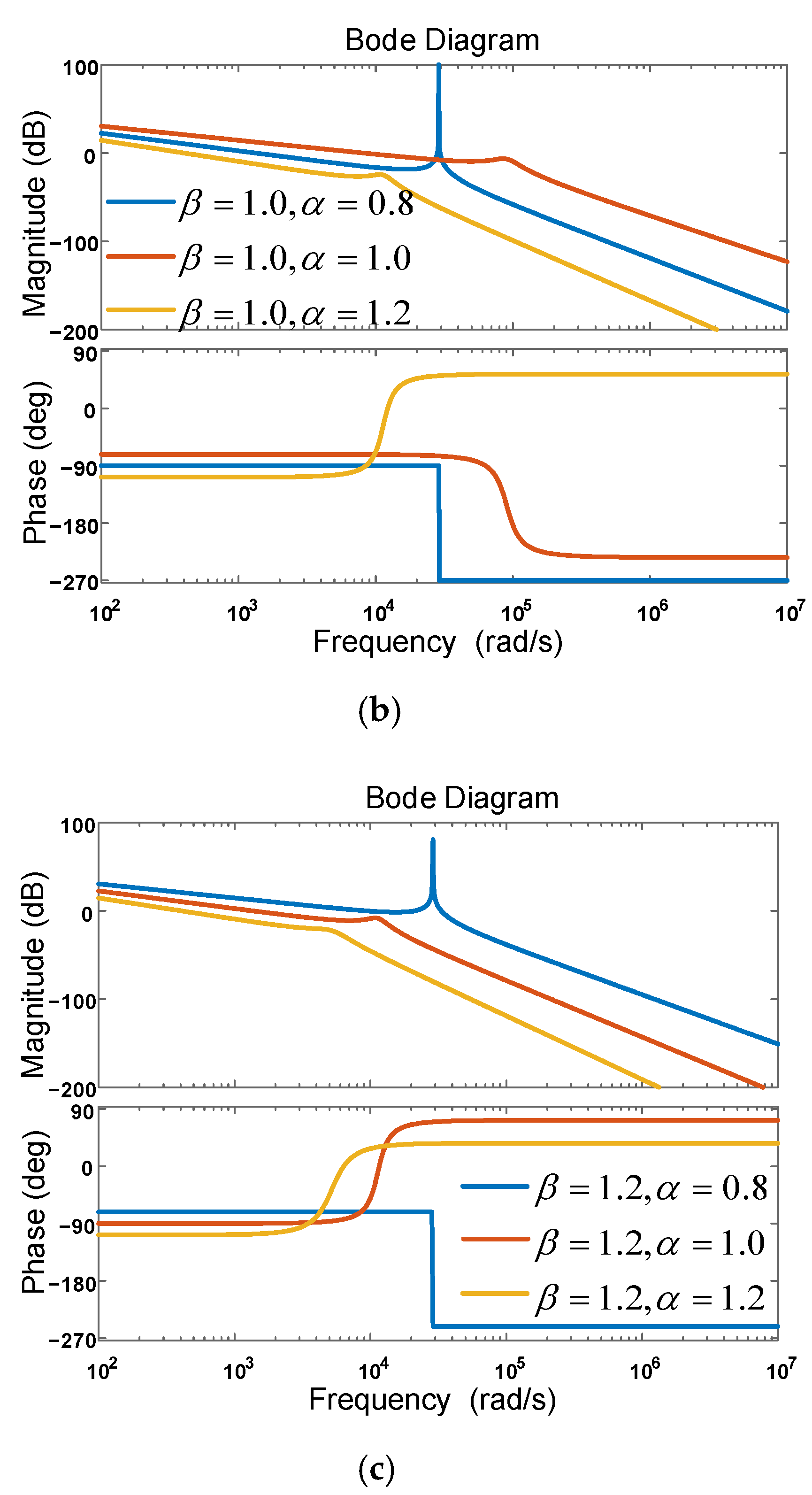
- When the resonant peak existed in the FOLCL filter, the resonant frequency was determined only by the values of and , independently of and . The resonant frequency was:
- When , the sufficient condition for the existence of resonance was . Compared with the IOLCL filter, the resonance could be effectively avoided by setting .
- When , and , there was a +180° phase jump at the resonance frequency. When , , and , there was a −180° phase jump at the resonance frequency.
3.2.2. Simulation Analysis
4. Single-Phase Grid-Connected Inverter (GCI) based on the FOLCL Filter
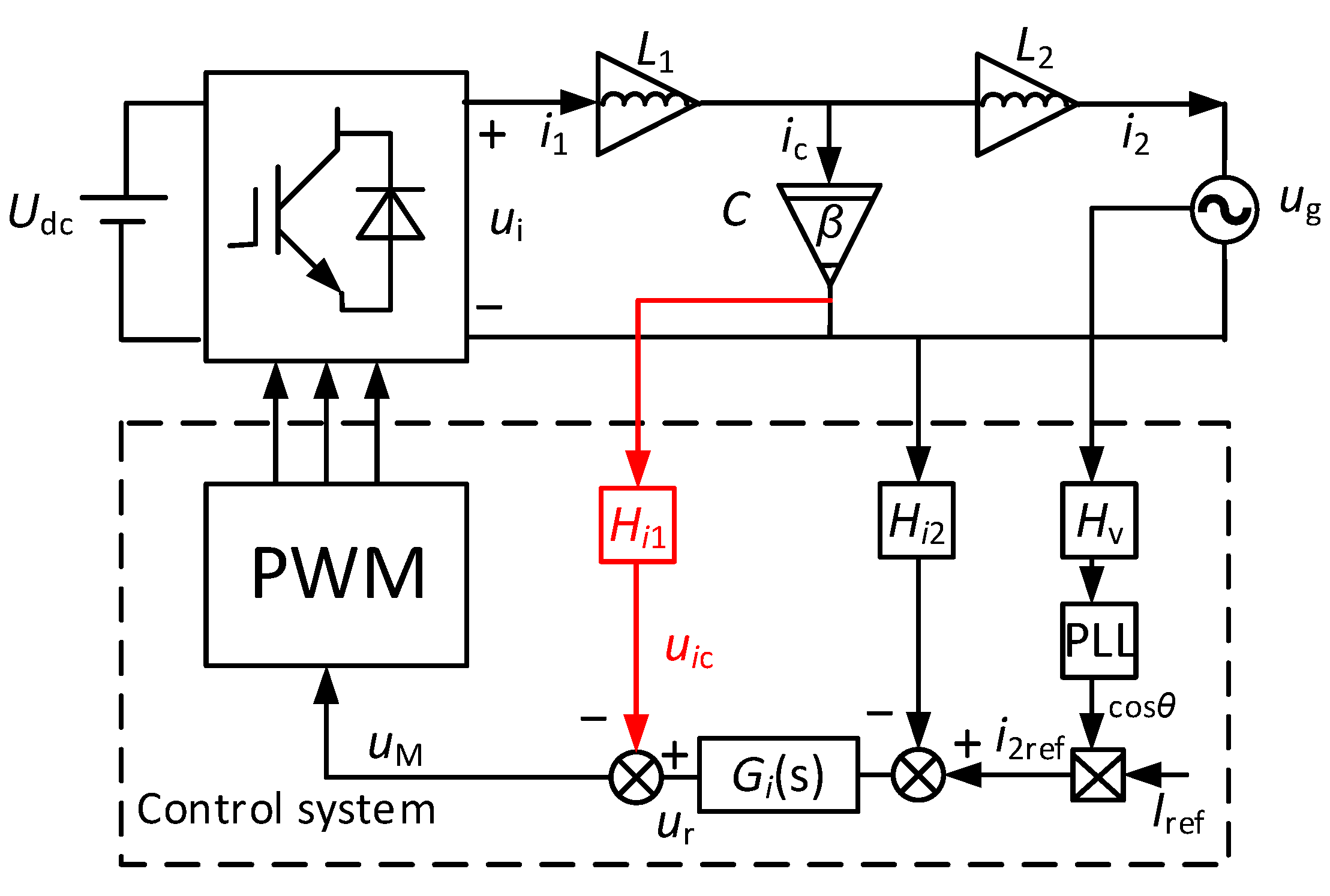
4.1. System Structure
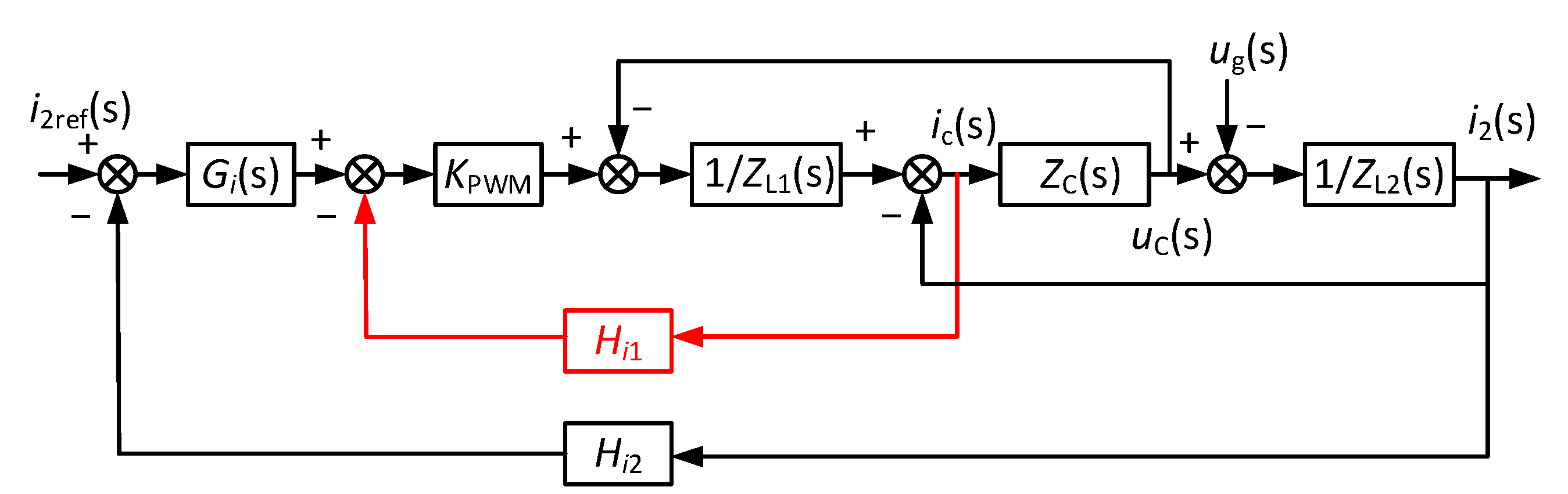
4.2. FOGCI Based on Capacitor Current Proportional Feedback
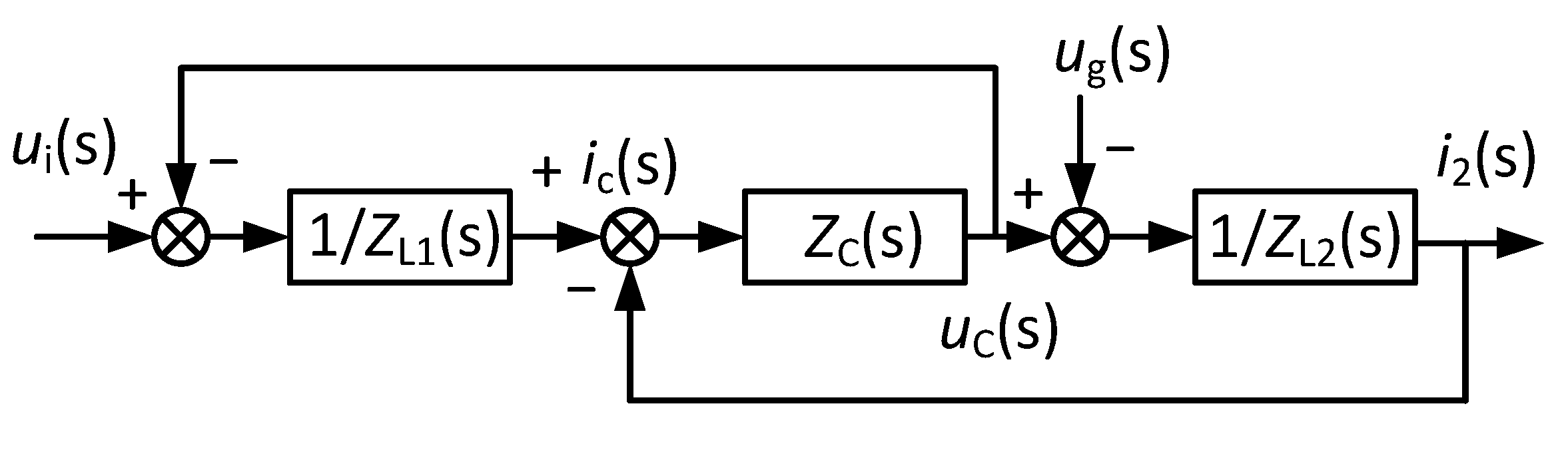
4.3. GCI without Capacitor Current Proportional Feedback
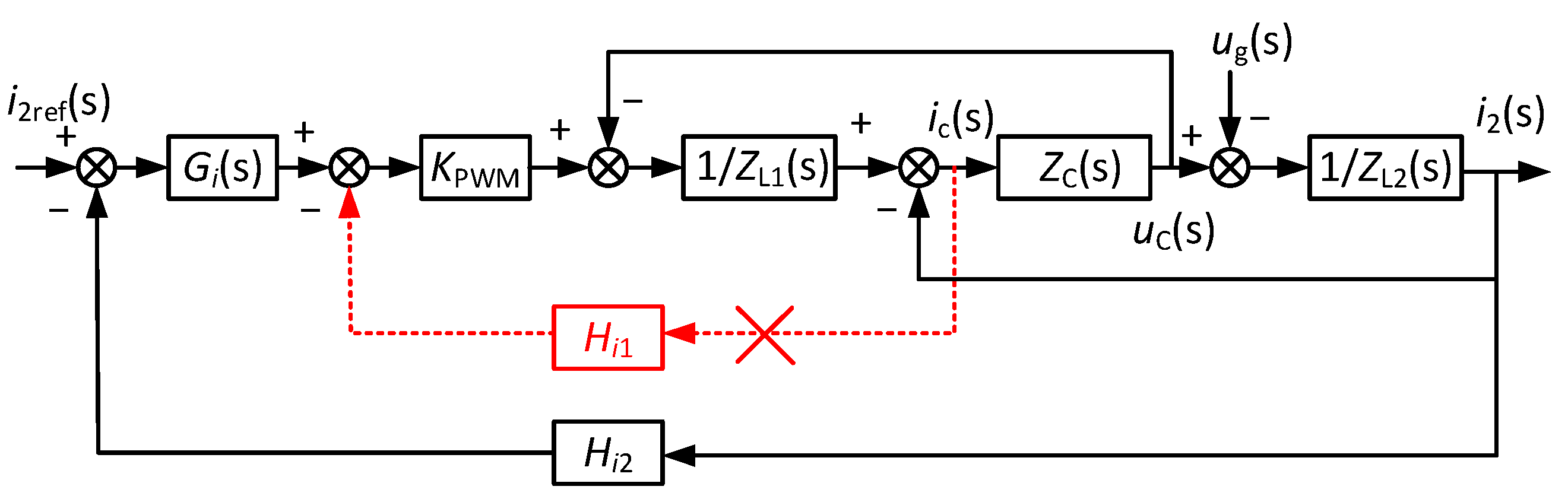
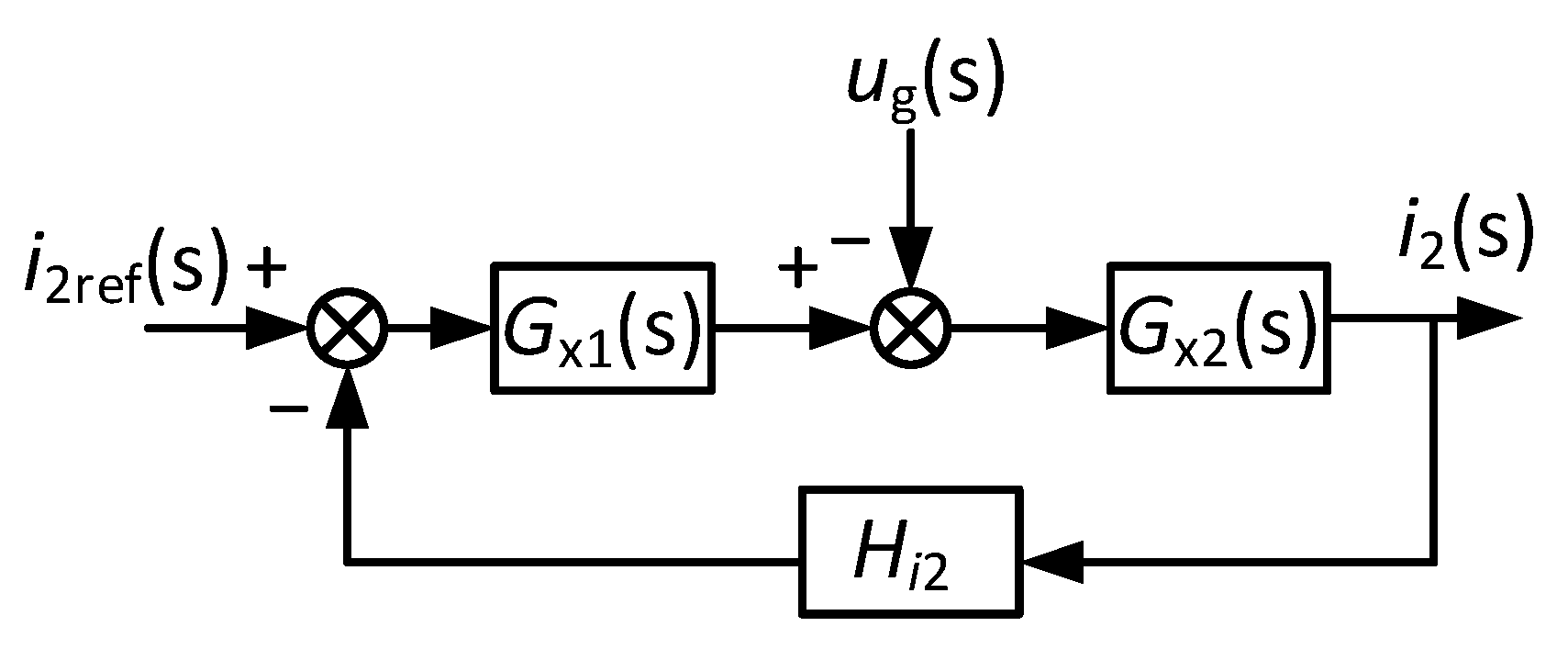
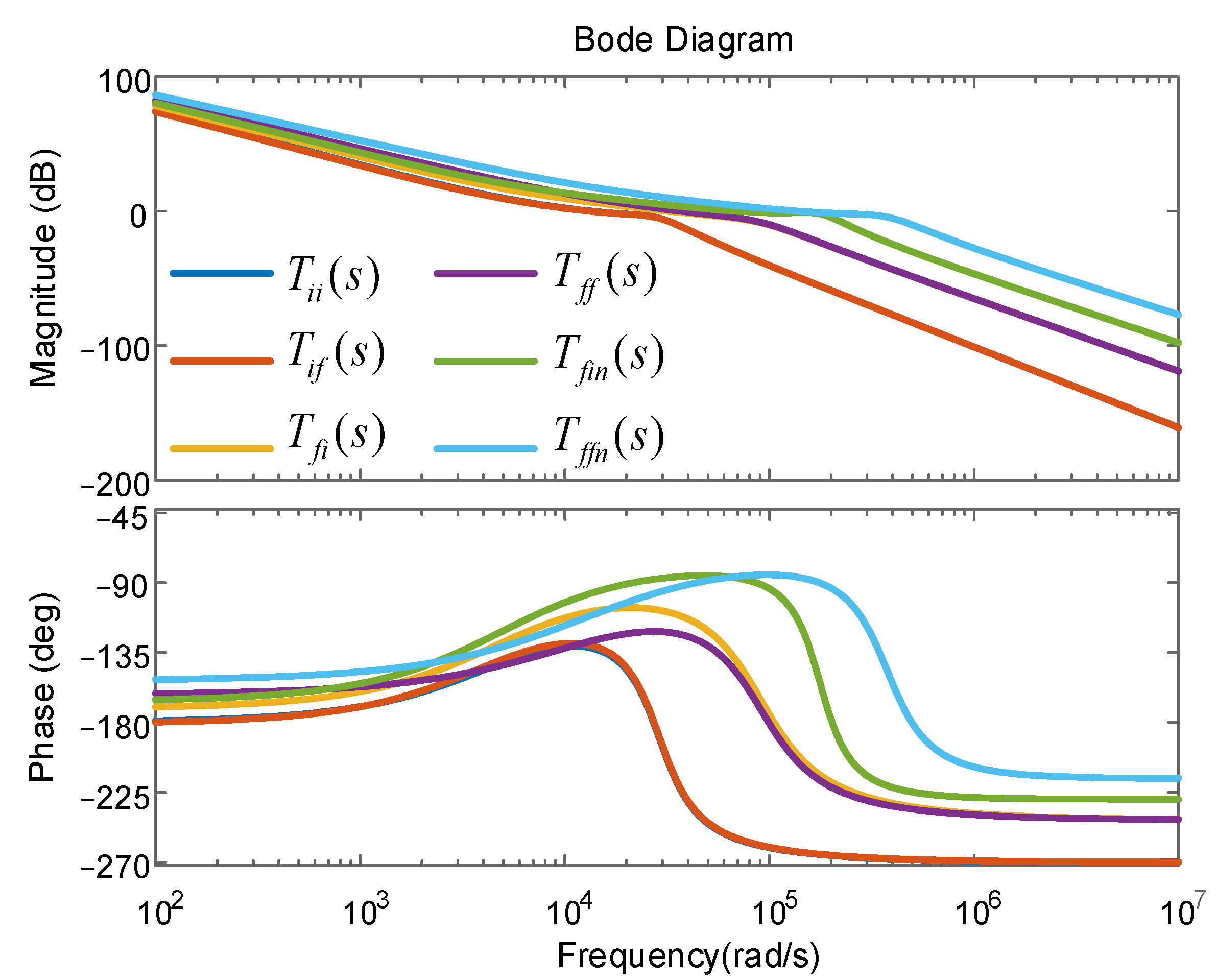
4.4. Characteristic Analyses of the GCI System
5. Simulation and Experimental Results
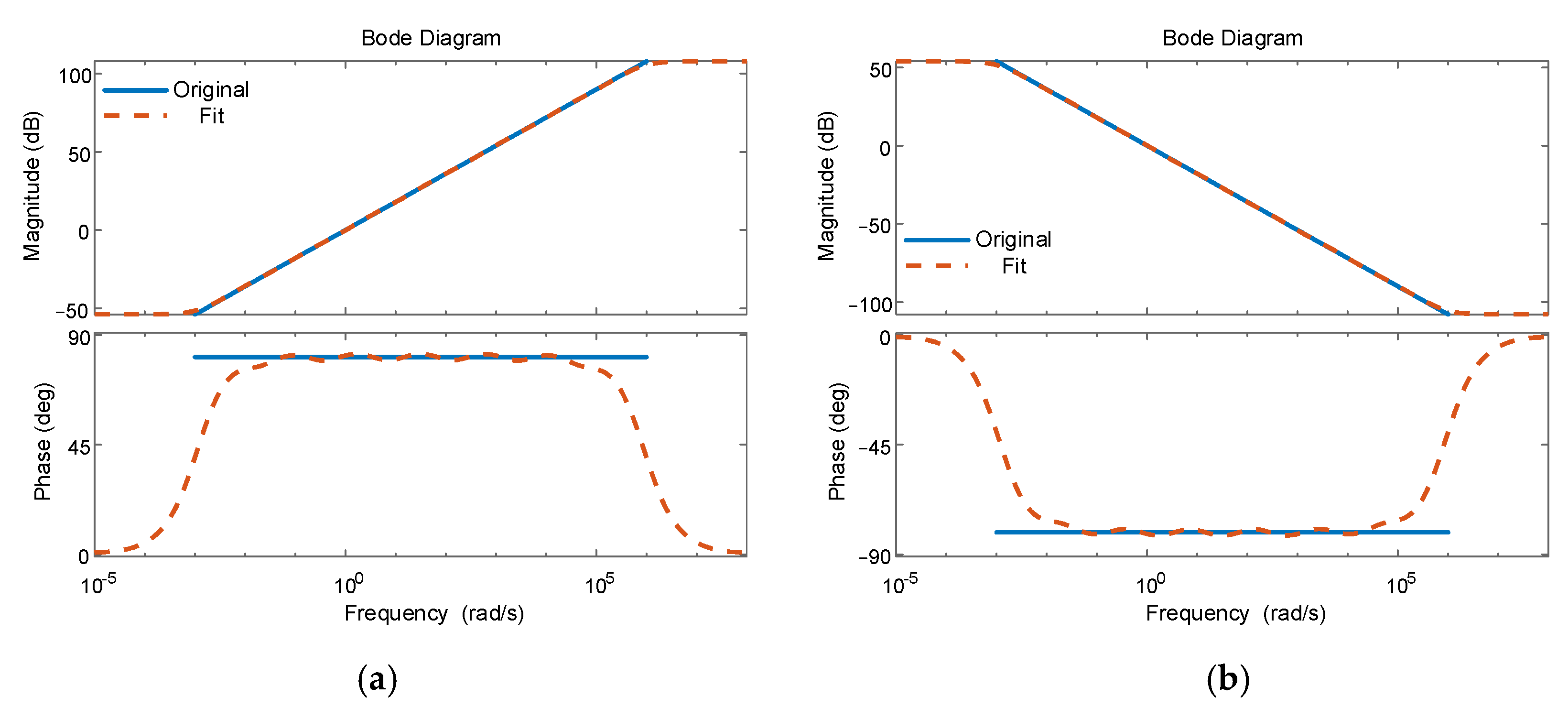
5.1. Fractional-Order Component Approximation
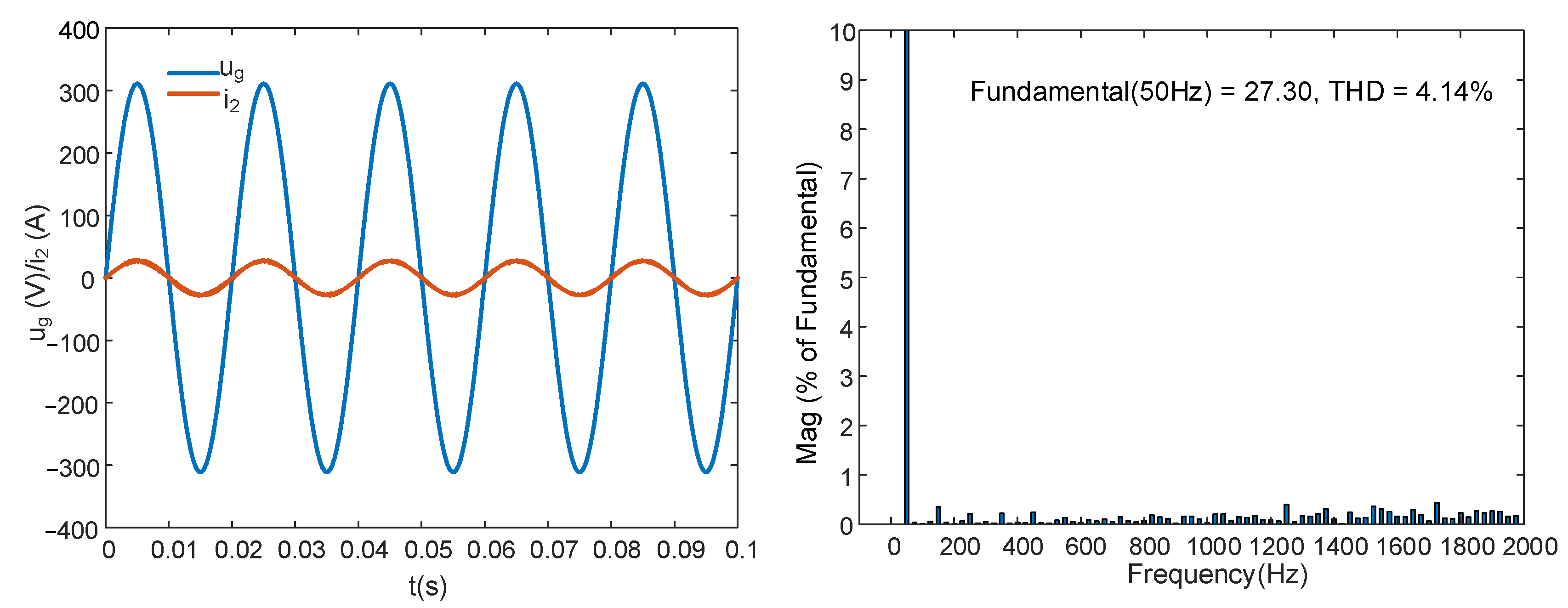
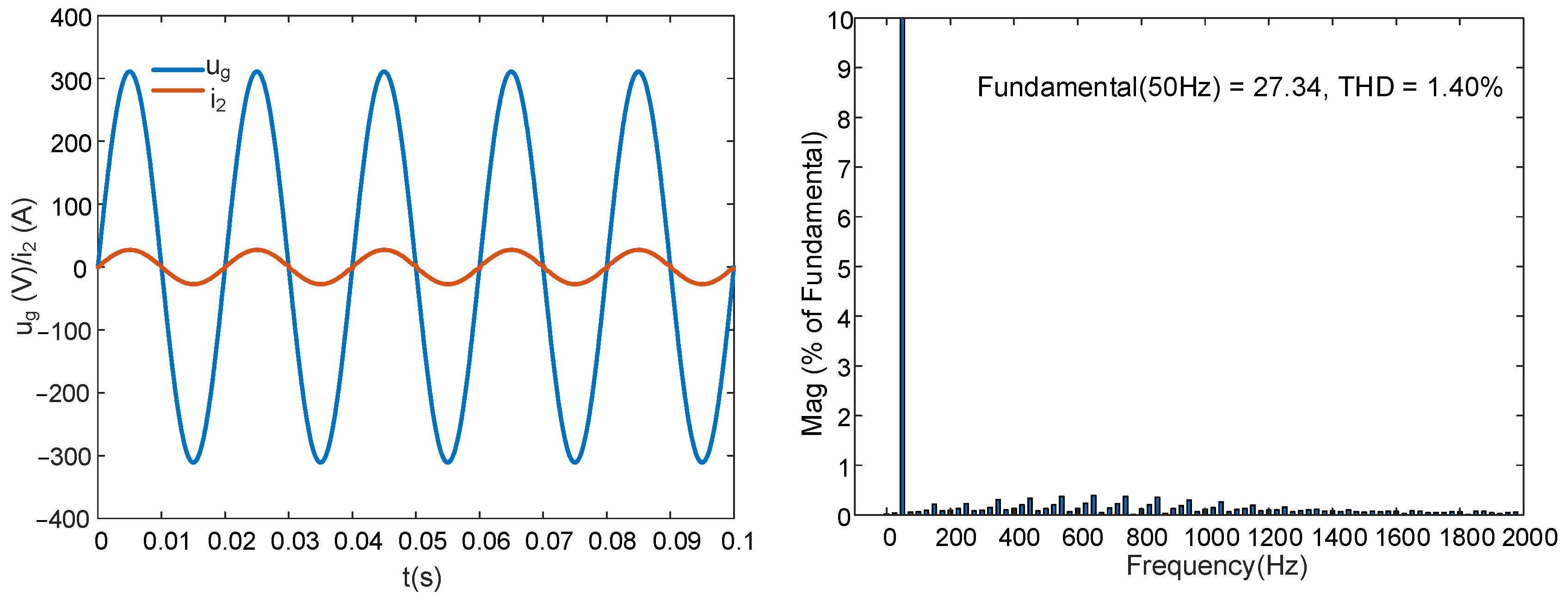
5.2. Simulation Results
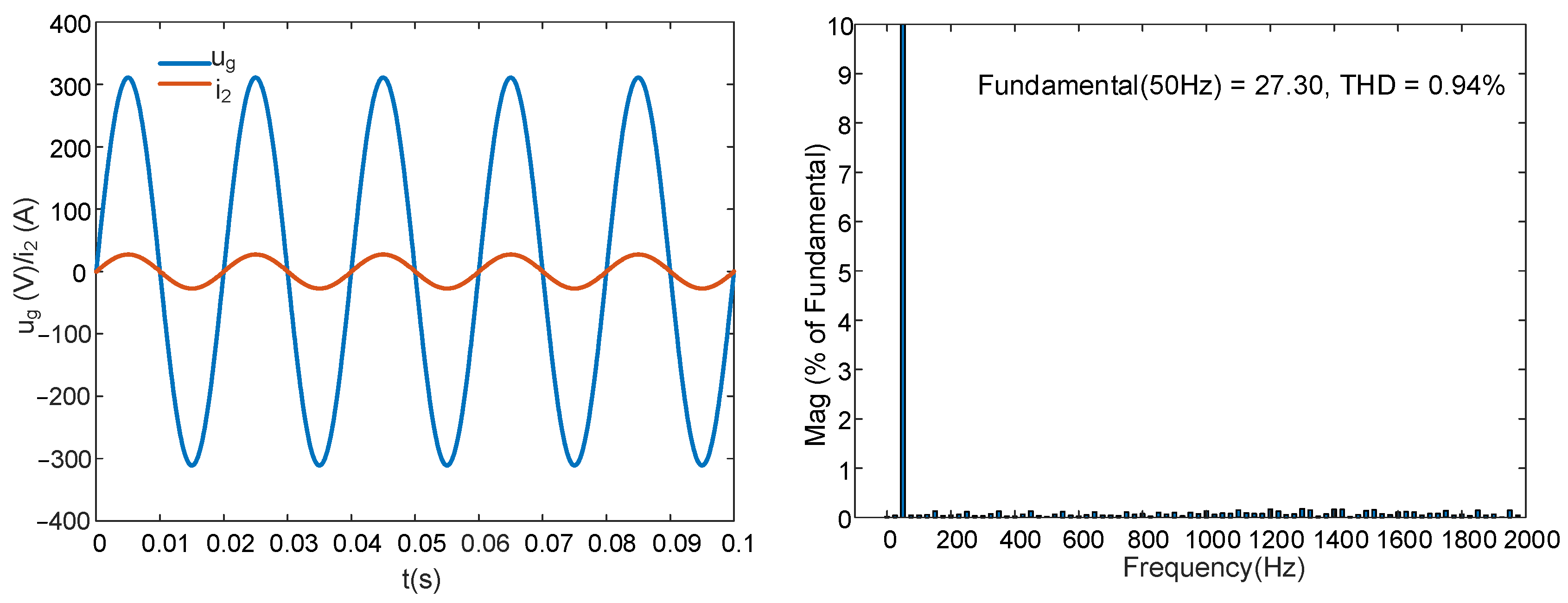
5.2.1. IOGCI and FOGCI with Capacitor Current Proportional Feedback
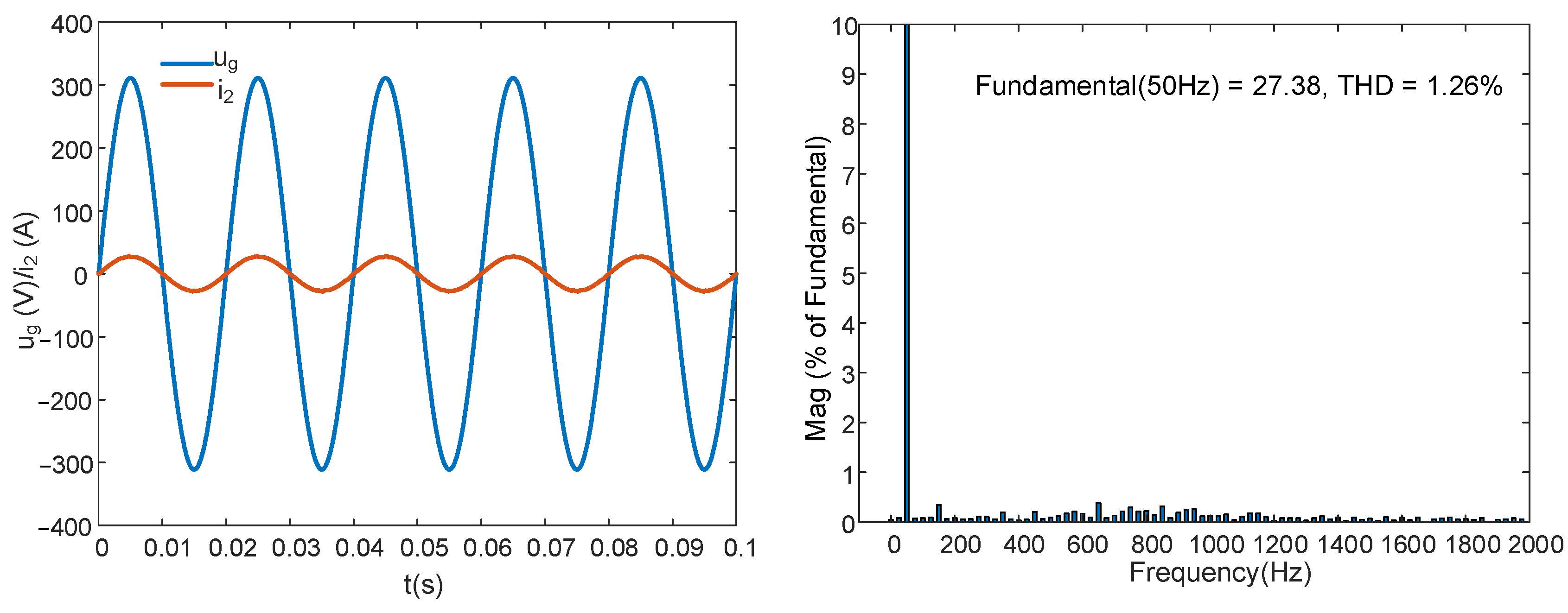
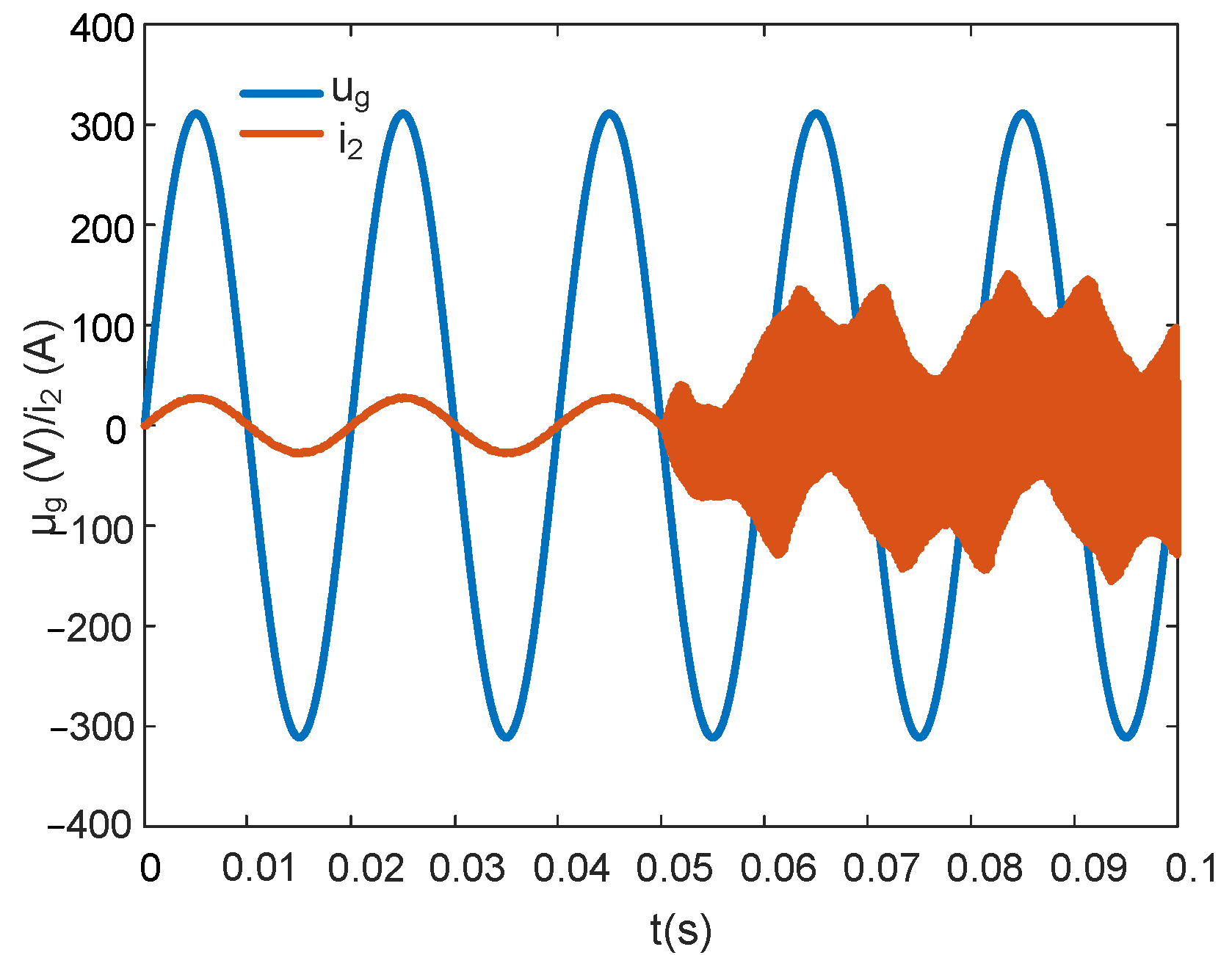
5.2.2. FOGCI without Capacitor Current Proportional Feedback
- With or without capacitor current proportional feedback, the FOGCI showed better system performance than the IOGCI.
- For GCI systems, the overall control effect of the FOPI controller was better than that of the IOPI controller.
- Compared with the FOGCI based on capacitor current proportional feedback when , the FOGCI without capacitor current proportional feedback when obtained lower grid current THD and simplified the control system.
- When , the FOGCI without capacitor current proportional feedback could not guarantee system stability.
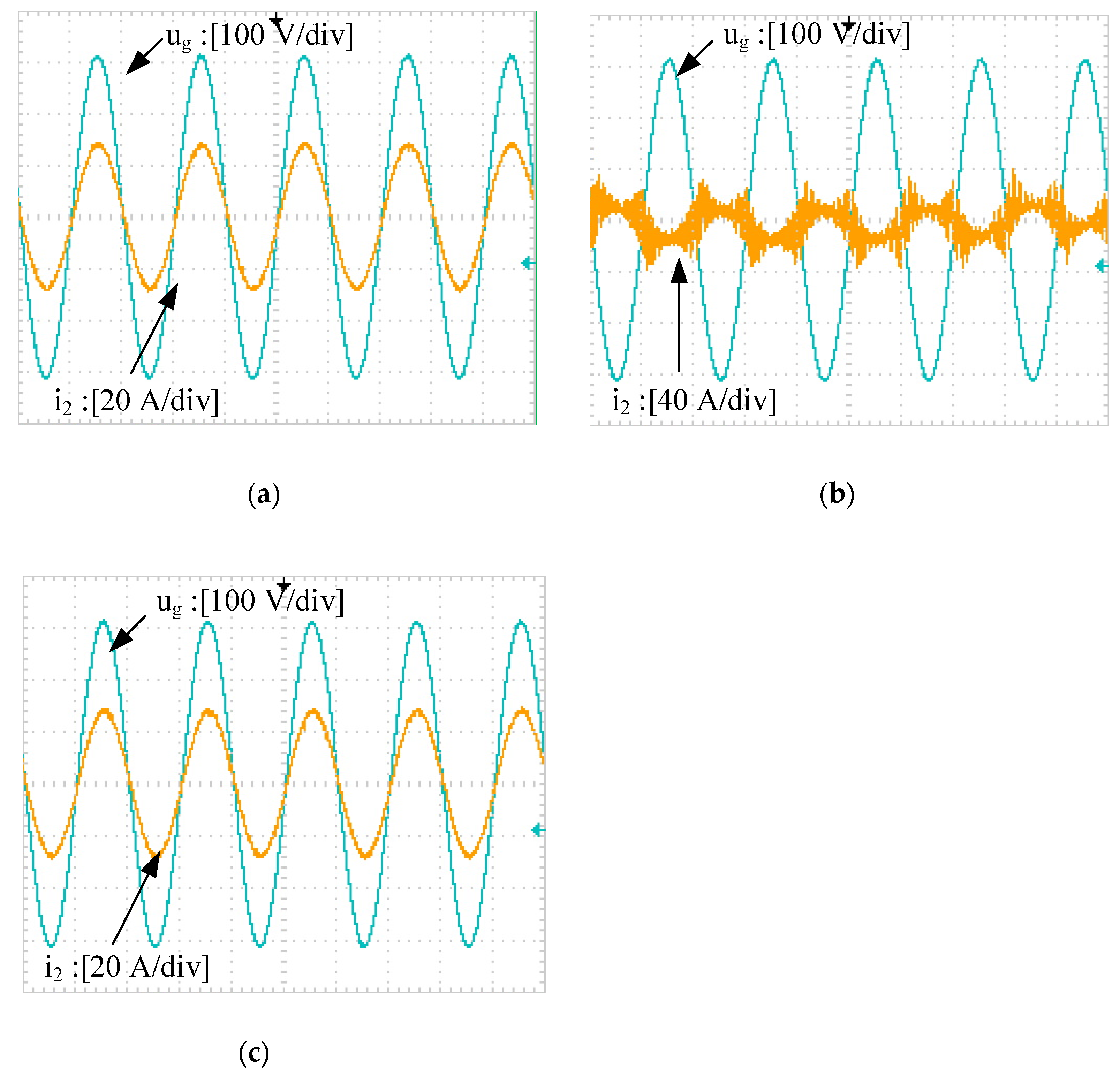
5.3. Experimental Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Blaabjerg, F.; Teodorescu, R.; Liserre, M.; Timbus, A.V. Overview of control and grid synchronization for distributed power generation systems. IEEE Trans. Ind. Electron. 2006, 53, 1398–1409. [Google Scholar] [CrossRef] [Green Version]
- Prodanovic, M.; Green, T.C. High-quality power generation through distributed control of a power park microgrid. IEEE Trans. Ind. Electron. 2006, 53, 1471–1482. [Google Scholar] [CrossRef] [Green Version]
- IEEE Standard Committee. IEEE Standard for Interconnection and Interoperability of Distributed Energy Resources with Associated Electric Power Systems Interfaces: 1547-2003; IEEE: Piscataway, NJ, USA, 2003. [Google Scholar]
- IEEE Standard Committee. IEEE Recommended Practices and Requirements for Harmonic Control in Electric Power System: 519-1992; IEEE: Piscataway, NJ, USA, 2004. [Google Scholar]
- Twining, E.; Holmes, D.G. Grid current regulation of a three-phase voltage source inverter with an LCL input filter. IEEE Trans. Power Electron. 2003, 18, 888–895. [Google Scholar] [CrossRef] [Green Version]
- Liserre, M.; Dell’Aquila, A.; Blaabjerg, F. Genetic algorithm-based design of the active damping for an LCL-filter three-phase active rectifier. IEEE Trans. Power Electron. 2004, 19, 76–86. [Google Scholar] [CrossRef]
- Liserre, M.; Blaabjerg, F.; Hansen, S. Design and control of an LCL-filter-based three-phase active rectifier. IEEE Trans. Ind. Appl. 2005, 41, 1281–1291. [Google Scholar] [CrossRef]
- Muhlethaler, J.; Schweizer, M.; Blattmann, R.; Kolar, J.W.; Ecklebe, A. Optimal Design of LCL Harmonic Filters for Three-Phase PFC Rectifiers. IEEE Trans. Power Electron. 2013, 28, 3114–3125. [Google Scholar] [CrossRef]
- Wu, W.M.; He, Y.B.; Tang, T.H.; Blaabjerg, F. A New Design Method for the Passive Damped LCL and LLCL Filter-Based Single-Phase Grid-Tied Inverter. IEEE Trans. Ind. Electron. 2013, 60, 4339–4350. [Google Scholar] [CrossRef]
- Liserre, M.; Teodorescu, R.; Blaabjerg, F. Stability of photovoltaic and wind turbine grid-connected inverters for a large set of grid impedance values. IEEE Trans. Power Electron. 2006, 21, 263–272. [Google Scholar] [CrossRef]
- Liserre, M.; Dell’Aquila, A.; Blaabjerg, F. Stability improvements of an LCL-filter based three-phase active rectifier. In Proceedings of the 33rd IEEE Annual Power Electronics Specialists Conference (PESC02), Carins, Australia, 23–27 June 2002; pp. 1195–1201. [Google Scholar]
- Bahrani, B.; Vasiladiotis, M.; Rufer, A. High-order vector control of grid-connected voltage-source converters with LCL-filters. IEEE Trans. Ind. Electron. 2014, 61, 2767–2775. [Google Scholar] [CrossRef]
- Wehmuth, G.R.; Busarello, T.D.C.; Peres, A. Step-by-step design procedure for LCL-type single-phase grid connected inverter using digital proportional-resonant controller with capacitor-current feedback. In Proceedings of the 13th Annual IEEE Green Technologies Conference (GreenTech), Denver, CO, 7–9 April 2021; pp. 448–454. [Google Scholar]
- Shen, G.Q.; Xu, D.H.; Cao, L.P.; Zhu, X.C. An improved control strategy for grid-connected voltage source inverters with an LCL filter. IEEE Trans. Power Electron. 2008, 23, 1899–1906. [Google Scholar] [CrossRef]
- He, J.W.; Li, Y.W. Generalized closed-loop control (GCC) schemes with embedded virtual imepdances for voltage source converters. In Proceedings of the IEEE Energy Conversion Congress and Exposition (ECCE), Phoenix, AZ, USA, 17–22 September 2011; pp. 479–486. [Google Scholar]
- Wang, T.C.Y.; Ye, Z.H.; Sinha, G.; Yuan, X.M. Output filter design for a grid-interconnected three-phase inverter. In Proceedings of the 34th Annual IEEE Power Electronics Specialists Conference, Acapulco, Mexico, 15–19 June 2003; pp. 779–784. [Google Scholar]
- Dannehl, J.; Liserre, M.; Fuchs, F.W. Filter-based active damping of voltage source converters with LCL filter. IEEE Trans. Ind. Electron. 2011, 58, 3623–3633. [Google Scholar] [CrossRef]
- Blasko, V.; Kaura, V. A novel control to actively damp resonance in input LC filter of a three phase voltage source converter. In Proceedings of the 11th Annual Applied Power Electronics Conference and Exposition (APEC 96), San Jose, CA, USA, 3–7 March 1996; pp. 545–551. [Google Scholar]
- Maamir, F.; Guiatni, M.; El Hachemi, H.; Ali, D. Auto-tuning of fractional-order PI controller using particle swarm optimization for thermal device. In Proceedings of the 2015 4th International Conference on Electrical Engineering (ICEE), Boumerdes, Algeria, 13–15 December 2015; pp. 174–179. [Google Scholar]
- De Keyser, R.; Muresan, C.I.; Ionescu, C.M. A novel auto-tuning method for fractional order PI/PD controllers. ISA Trans. 2016, 62, 268–275. [Google Scholar] [CrossRef] [PubMed]
- Erenturk, K. Fractional-order PIλDμ and active disturbance rejection control of nonlinear two-mass drive system. IEEE Trans. Ind. Electron. 2013, 60, 3806–3813. [Google Scholar] [CrossRef]
- Xu, J.H.; Li, X.C.; Meng, X.R.; Qin, J.B.; Liu, H. Modeling and analysis of a single-phase fractional-order voltage source pulse width modulation rectifier. J. Power Sources 2020, 479, 12. [Google Scholar] [CrossRef]
- Freeborn, T.J.; Maundy, B.; Elwakil, A.S. Measurement of supercapacitor fractional-order model parameters from voltage-excited step response. IEEE Jour. Emer. Select. Top. Circu. Syste. 2013, 3, 367–376. [Google Scholar] [CrossRef]
- Chen, X.; Xi, L.; Zhang, Y.N.; Ma, H.; Huang, Y.H.; Chen, Y.Q. Fractional techniques to characterize non-solid aluminum electrolytic capacitor for power electronic applications. Nonlinear Dyn. 2019, 98, 3125–3141. [Google Scholar] [CrossRef]
- Allagui, A.; Freeborn, T.J.; Elwakil, A.S.; Fouda, M.E.; Maundy, B.J.; Radwan, A.G.; Said, Z.; Abdelkareem, M.A. Review of fractional-order electrical characterization of supercapacitor. J. Power Sources 2018, 400, 457–467. [Google Scholar] [CrossRef]
- Machado, J.A.T.; Galhano, A. Fractional order inductive phenomena based on the skin effect. Nonlinear Dyn. 2012, 68, 107–115. [Google Scholar] [CrossRef]
- Jesus, I.S.; Machado, J.A.T. Development of fractional order capacitor based on electrolyte processes. Nonlinear Dyn. 2009, 56, 45–55. [Google Scholar] [CrossRef] [Green Version]
- Kartci, A.; Agambayev, A.; Herencsar, N.; Salama, K.N. Series-, parallel-, and inter-connection of solid-state arbitrary fractional-order capacitor: Theoretical study and experimental verification. IEEE Access 2018, 6, 10933–10943. [Google Scholar] [CrossRef]
- Bertsias, P.; Psychalinos, C.; Radwan, A.G.; Elwakil, A.S. High-frequency capacitorless fractional-order CPE and FI emulator. Circuits Syst. Signal Process. 2018, 37, 2694–2713. [Google Scholar] [CrossRef]
- Sarafraz, M.S.; Tavazoei, M.S. Passive realization of fractional-order impedances by a fractional element and RLC components: Conditions and procedure. IEEE Trans. Circuits Syst. I-Regul. Pap. 2017, 64, 585–595. [Google Scholar] [CrossRef]
- Radwan, A.G.; Soliman, A.M.; Elwakil, A.S. Design equations for fractional-order sinusoidal oscillators: Four practical circuit examples. Int. J. Circuit Theory Appl. 2008, 36, 473–492. [Google Scholar] [CrossRef]
- Semary, M.S.; Fouda, M.E.; Hassan, H.N.; Radwan, A.G. Realization of fractional-order capacitor based on passive symmetric network. J. Adv. Res. 2019, 18, 147–159. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Chen, Y.F.; Zhang, B.; Qiu, D.Y. A Modeling and analysis method for fractional-order DC-DC converters. IEEE Trans. Power Electron. 2017, 32, 7034–7044. [Google Scholar] [CrossRef]
- Wu, C.J.; Si, G.Q.; Zhang, Y.B.; Yang, N.N. The fractional-order state-space averaging modeling of the Buck Boost DC/DC converter in discontinuous conduction mode and the performance analysis. Nonlinear Dyn. 2015, 79, 689–703. [Google Scholar] [CrossRef]
- Tan, C.; Liang, Z.S. Modeling and simulation analysis of fractional-order Boost converter in pseudo-continuous conduction mode. Acta Phys. Sin. 2014, 63, 10. [Google Scholar] [CrossRef]
- Ahmad, W. Power factor correction using fractional capacitors. In Proceedings of the IEEE International Symposium on Circuits and Systems, Bangkok, Thailand, 25–28 May 2003; pp. 5–7. [Google Scholar]
- Sharma, M.; Rajpurohit, B.S.; Agnihotri, S.; Rathore, A.K. Development of fractional order modeling of voltage source converters. IEEE Access 2020, 8, 131750–131759. [Google Scholar] [CrossRef]
- Xu, J.H.; Li, X.C.; Liu, H.; Meng, X.R. Fractional-order modeling and analysis of a three-phase voltage source PWM rectifier. IEEE Access 2020, 8, 13507–13515. [Google Scholar] [CrossRef]
- El-Khazali, R. Fractional-order LCαL filter-based grid connected PV systems. In Proceedings of the 62nd IEEE International Midwest Symposium on Circuits and Systems (MWSCAS), Dallas, TX, USA, 4–7 August 2019; pp. 533–536. [Google Scholar]
- Podlubny, I. Fractional-order systems and PIλDμ-controllers. IEEE Trans. Autom. Control 1999, 44, 208–214. [Google Scholar] [CrossRef]
- Martinez, R.; Bolea, Y.; Grau, A.; Martinez, H. LPV model for PV cells and fractional control of DC/DC converter for photovoltaic systems. In Proceedings of the 20th IEEE International Symposium on Industrial Electronics (ISIE), Gdansk, Poland, 27–30 June 2011. [Google Scholar]
- Jiang, P.; Lv, H.J.; Wang, L.Y. Study on Control of Single Phase Grid-Connected Inverter Based on Fractional Order PI Controller. In Proceedings of the 2nd International Conference on Materials Science, Machinery and Energy Engineering (MSMEE), Dalian, China, 13–14 May 2017; pp. 1414–1420. [Google Scholar]
- Ghoudelbourk, S.; Azar, A.T.; Dib, D. Three-level (NPC) shunt active power filter based on fuzzy logic and fractional-order PI controller. Int. J. Autom. Control 2021, 15, 149–169. [Google Scholar] [CrossRef]
- Podlubny. Fractional Differential Equations.; USA Academic: New York, NY, USA, 1999. [Google Scholar]
- Monje, C.A.; Chen, Y.; Vinagre, B.M.; Xue, D. Fractional Order Systems and Controls: Fundamentals and Applications; Springer: London, UK, 2010. [Google Scholar]
- Petras. Fractional calculus. In Fractional-Order Nonlinear Systems; Higher Education: Beijing, China, 2011. [Google Scholar]
- Ruan, X.; Wang, X.; Pan, D. Control Techniques for LCL-Type Grid-Connected Inverters; Springer: Singapore, 2017. [Google Scholar]





| Characteristics | IOLCL Filter | FOLCL Filter | Statement |
| Number of variables | ) | ) | is the order of the inductor and is the order of the capacitor |
| Transfer function | |||
| Resonance peak | exists | is a sufficient condition for the existence of a resonance peak in the FOLCL filter | |
| Loop Gain | Magnitude Margin | Phase Margin |
| 4.29 dB | 48.0° | |
| 4.42 dB | 49.9° | |
| 11.4 dB | 71.1° | |
| 9.91 dB | 56.7° | |
| 5.03 dB | 93.2° | |
| 10.1 dB | 93.7° |
| Parameters | Symbols | Numerical Value | Parameters | Symbols | Numerical Value |
| DC input voltage | 360 V | Filter capacitor | 10 μF | ||
| RMS value of grid voltage | 220 V | Grid-side inductor | 150 μH | ||
| Rated power of inverter | 6 kW | Carrier magnitude | 3.05 V | ||
| Grid frequency | 50 Hz | Capacitor current sampling coefficient | 0.1 or 0 | ||
| Switching frequency | 10 kHz | Grid current sampling coefficient | 0.15 | ||
| Inverter-side inductor | 600 μH |
| GCI Model | Controller | Kp | Ki | λ |
| FOGCI (α + β = 2, capacitor current proportional feedback was used) | IOPI | 0.443 | 2250 | 1 |
| FOPI | 0.442 | 2248 | 0.90 | |
| IOGCI (capacitor current proportional feedback was used) | IOPI | 0.450 | 2200 | 1 |
| FOPI | 0.450 | 2582 | 1.01 | |
| FOGCI (α + β ≠ 2, capacitor current proportional feedback was not used) | IOPI FOPI | 0.630 0.550 | 2500 2400 | 1 0.90 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Cai, J. Grid-Connected Inverter Based on a Resonance-Free Fractional-Order LCL Filter. Fractal Fract. 2022, 6, 374. https://doi.org/10.3390/fractalfract6070374
Wang X, Cai J. Grid-Connected Inverter Based on a Resonance-Free Fractional-Order LCL Filter. Fractal and Fractional. 2022; 6(7):374. https://doi.org/10.3390/fractalfract6070374
Chicago/Turabian StyleWang, Xiaogang, and Junhui Cai. 2022. "Grid-Connected Inverter Based on a Resonance-Free Fractional-Order LCL Filter" Fractal and Fractional 6, no. 7: 374. https://doi.org/10.3390/fractalfract6070374
APA StyleWang, X., & Cai, J. (2022). Grid-Connected Inverter Based on a Resonance-Free Fractional-Order LCL Filter. Fractal and Fractional, 6(7), 374. https://doi.org/10.3390/fractalfract6070374







