Stationary Response of a Kind of Nonlinear Stochastic Systems with Variable Mass and Fractional Derivative Damping

Abstract

Viscoelasticity and variable mass are common phenomena in Micro-Electro-Mechanical Systems (MEMS), and could be described by a fractional derivative damping and a stochastic process, respectively. To study the dynamic influence cased by the viscoelasticity and variable mass, stationary response of a kind of nonlinear stochastic systems with stochastic variable-mass and fractional derivative, damping is investigated in this paper. Firstly, an approximately equivalent system of the studied nonlinear stochastic system is presented according to the Taylor expansion technique. Then, based on stochastic averaging of energy envelope, the corresponding Fokker–Plank–Kolmogorov (FPK) equation is deduced, which gives an approximated analytical solution of stationary response. Finally, a nonlinear oscillator with variable mass and fractional derivative damping is proposed in numerical simulations. The approximated analytical solution is compared with Monte Carlo numerical solution, which could verify the effectiveness of the obtained results.

1. Introduction

As the rapid development of Micro-Electro-Mechanical Systems (MEMS) in recent years, the size of micro-devices is declining to micron, even nanometer, scale. In nanometer scale, some particular microscopic phenomena always occurs, such as viscoelastic damping and variable mass. For example, in materials like plastics and nano-wires, the most adequate kind of damping is viscoelastic, which is usually described by the fractional derivative damping [1,2,3,4]. Thus, the dynamics of the micro-system with fractional derivative damping have attracted amount of attention, such as the stability, stochastic response, bifurcation analysis, and so on [5,6,7]. However, except for fractional derivative damping, variable mass is another common phenomenon in MEMS of nanometer scale, which will be considered altogether. According to the MEMS application, the stationary response of nonlinear stochastic systems with a variable mass and a fractional derivative damping is studied in this paper.

Variable mass phenomenon commonly occurs in physics and engineering fields, such as comet, jet planes, and rockets, which are all missing mass in their motions [8]. Within these applications, the variable mass was always modeled by continuous functions in deterministic systems, whose dynamics researches were developed in the last decades [9]. All the above variable mass phenomena are described by deterministic functions according to their inherent regularity. However, in the micro world, variable mass phenomenon is always characterized as a stochastic one. When the size of micro-devices is declining to micron, even nanometer, scale, the random adsorption and desorption of the particles around the micro-devices could significantly increase or decrease its quality, resulting in the variable mass phenomenon [10,11]. It is able to change the dynamical characteristics of the micro-devices and cause the damage or even failure of the device performance. For example, the variable mass of atomic force microscope probe can affect its detection accuracy [12]. Thus, the stochastic dynamics of nonlinear systems with variable mass have also attracted the attention of scholars.

The first step to study nonlinear stochastic systems with variable mass is to construct a model of variable mass. Since the size and mass of MEMS itself are very tiny, the random adsorption and desorption of surrounding particles would significantly change the system’s mass. Thus, this variable mass phenomenon should be described as a stochastic process. The initial models of random variable mass oscillator were always simplified by dichotomous or trichotomous noise [13,14,15,16,17]. However, the variable mass modeling method based on dichotomous or trichotomous noise limits the mass change within two or three states, which can not fully show the randomness of the variable mass of micro-devices. In order to better simulate the randomness of the variable mass, many scholars used Gaussian white noise to model the mass disturbance. Wang et al. [18] utilized Gaussian white noise to describe the random mass disturbance and proposed the stochastic averaging technique of the variable mass system based on Hamilton theory, which provided a method to analyze the random responses of stochastic systems with Gaussian-white-noise-based variable mass. Then, Qiao et al. [19,20] presented a group of stochastic stability conditions of the variable mass system under the Gaussian white noise excitation by using the stochastic averaging method and the maximum Lyapunov exponent method. Li [21] analyzed the stochastic response of a vibro-impact system with variable mass under the Gaussian white noise excitation, as well as its stochastic P-bifurcation characteristics.

Motivated by the above discussion, fractional derivative damping and variable mass are both considered in this paper. In this case, the stationary response of a kind of nonlinear stochastic system with fractional derivative damping and variable mass is studied. Based on the Taylor expansion technique, an approximately equivalent equation of the nonlinear stochastic system is given. Then, the corresponding stochastic averaging method is provided by following the diffusion approach to energy envelope. By constructing the corresponding Fokker–Plank–Kolmogorov (FPK) equation, an approach to calculate its approximate analytical solution of a stationary response is proposed. Besides, the effectiveness of the obtained results is verified by simulation of the Monte Carlo numerical solution.

The rest of this paper is organized as follows: in Section 2, some preliminaries are introduced including the fractional derivative and problem statement; then, the approximately equivalent system is proposed in Section 3; a stochastic averaging method is proposed in Section 4; an example is listed to verify the obtained results in Section 5; and, finally, the conclusions are given in Section 6.

2. Preliminaries

2.1. Fractional Derivative

A fractional derivative is a generalization of the integer-order derivatives, which have been widely applied in different fields, such as dynamics, engineering, computer science, etc. [22,23,24,25,26,27,28]. Fractional derivative damping is usually utilized to describe the viscoelastic damping model. Fractional derivative owns three common definitions, named Grunwald–Letnikov (G-L), Riemann–Liouville (R-L) and Caputo definitions [29,30]. These definitions are introduced in the following.

Definition 1

([31]). The R-L fractional derivative of a continuous function $x:(0,+\infty )⟶\mathrm{R}$ with order $q>0$ is defined as:

$${}_0^R{D}_{t^{}}^{q}x\left(t\right)=\frac{1}{\Gamma (k-q)}\frac{{\mathrm{d}}^k}{\mathrm{d}{\mathrm{t}}^k}{\int }_0^t\frac{x\left(s\right)}{{(t-s)}^{q-k+1}}\mathrm{ds},$$

(1)

where k is a positive integer and $k-1\le q\le k$, and $\Gamma (·)$ is the gamma function, i.e.,

$$\Gamma \left(a\right)={\int }_0^{+\infty }{s}^{a-1}{e}^{-s}\mathrm{d}s.$$

The G-L definition is a discrete form of fractional derivative, which is equivalent to the discretized R-L definition and is introduced as follows.

Definition 2

([32]). The G-L fractional derivative of function $x:(0,+\infty )⟶\mathrm{R}$ with order $q>0$ is denoted by

$$\begin{array}{ccc}\hfill {}_0^G{D}_t^{q}x\left(t\right)& =& \frac{1}{h^q}\sum _{i=0}^n{(-1)}^i\left(\begin{array}{c}q\\ i\end{array}\right)x(t-ih),h\to 0^{+}.\hfill \end{array}$$

(2)

In addition, the Caputo definition of a fractional derivative is introduced in the following Definition 3.

Definition 3

([33]). The Caputo fractional derivative of a continuous function $x:(0,+\infty )⟶\mathrm{R}$ with order $q>0$ is defined as:

$${}_0^C{D}_{t^{}}^{q}x\left(t\right)=\frac{1}{\Gamma (k-q)}{\int }_0^t\frac{x^{\left(k\right)}\left(s\right)}{{(t-s)}^{q-k+1}}\mathrm{ds},$$

(3)

where k is an positive integer and $k-1\le q\le k$.

The Caputo definition owns the practical physical meaning in the initial values and has more advantages than R-L or G-L definition. Thus, Caputo fractional derivative is employed to describe the fractional derivative damping (viscoelastic damping) in this paper.

Moreover, the Laplace transformation of the Caputo fractional derivative is given as,

$$L\left\{{}_0^C{D}_t^{q}x\left(t\right)\right\}=s^{q}X\left(s\right)-\sum _{i=0}^{k-1}{s}^{q-i-1}{x}^{\left(i\right)}\left(0\right),$$

(4)

where $L\{·\}$ is a Laplace transform operator with satisfying $X\left(s\right)=L\left\{x\right(t\left)\right\}$, and k is an positive integer with $k-1\le q\le k$. Especially, with null initial conditions, the Laplace transformation of the Caputo fractional derivative is obtained as

$$L\left\{{}_0^C{D}_t^{q}x\left(t\right)\right\}=s^{q}X\left(s\right).$$

(5)

2.2. Problem Statement

Consider the following single-degree-of-freedom nonlinear stochastic system [19] with a variable mass and a fractional derivative damping,

$$m\ddot{x}+\zeta {}_0^C{D}_t^{q}x+g\left(x\right)=\epsilon f\left(x\right){\xi }_f\left(t\right),$$

(6)

where differentiable $g\left(x\right)$ is the nonlinear restoring force with $g\left(0\right)=0$ and $g^{\prime }\left(0\right)>0$, $\epsilon$ is a small constant, $f\left(x,\dot{x}\right)$ is an amplitude of the stochastic excitation, ${\xi }_f\left(t\right)$ represents Gaussian white noise and satisfies $E\left[{\xi }_f\left(t\right){\xi }_f\left(t+\tau \right)\right]=2D_f\delta \left(\tau \right),$ and $D_f$ is the intensity of the noise ${\xi }_f\left(t\right)$. Besides, m represents a variable mass described by

$$m=\overline{m}+\sigma {\xi }_m\left(t\right),$$

(7)

where $\overline{m}$ is a positive parameter, ${\xi }_m\left(t\right)$ denotes Gaussian white noise with satisfying $E\left[{\xi }_m\left(t\right){\xi }_m\left(t+\tau \right)\right]=2D_m\delta \left(\tau \right)$ and $D_m$ is the intensity of the noise ${\xi }_m\left(t\right)$. In this paper, it is assumed that both stochastic processes ${\xi }_f\left(t\right)$ and ${\xi }_m\left(t\right)$ are independent with each other. In addition, $\ddot{x}$ represents the second derivative, and $\zeta {}_0^C{D}_t^{q}x$ denotes the fractional derivative damping force with $0<q<2$ and $\zeta >0$, which satisfies the Caputo definition in Definition 3.

To study the stationary response of System (6), the corresponding stochastic averaging method is studied. Due to the variable mass and fractional derivative damping, the classical stochastic averaging method could not be applied directly. Thus, the studied System (6) should be transformed into an approximately equivalent system, such that the equivalent form satisfies an improved stochastic averaging method. In the next section, the approximately equivalent form of System (6) is investigated.

3. Approximately Equivalent System

3.1. Approximately Equivalent Equation of the Fractional Derivative Damping

According to the above section, the conventional stochastic averaging method is not available for System (6). Thus, the approximately equivalent form of System (6) is studied in this section. First, an approximately equivalent method of the fractional derivative damping ${}_0^C{D}_t^{q}x$ is proposed as follows.

Theorem 1.

The fractional derivative damping ${}_0^C{D}_t^{q}x$ in System (6) can be approximately rewritten by

$${}_0^C{D}_t^{q}x\approx \left(1-\frac{3q}{2}+\frac{q^2}{2}\right)\mathrm{Re}\left(r_{\ast }^q\right)x+\left[q\left(2-q\right)\mathrm{Re}\left(r_{\ast }^{q-1}\right)\right]\dot{x}+\frac{q\left(q-1\right)\mathrm{Re}\left(r_{\ast }^{q-2}\right)}{2}\ddot{x}.$$

(8)

where $r_{\ast }$ is the characteristic root with the largest real part of the following characteristic equation,

$$\overline{m}{s}^2+\zeta s^q+g^{\prime }\left(0\right)=0.$$

(9)

Proof of Theorem 1.

The restoring force $g\left(x\right)$ is differentiable and satisfies $g\left(0\right)=0,g^{\prime }\left(0\right)>0$. Thus, the linearized homogeneous equation of System (6) in the neighborhood of the origin becomes

$$\overline{m}\ddot{x}+{\zeta }_0^C{D}_t^{q}x+g^{\prime }\left(0\right)x=0.$$

(10)

Then, according to the Laplace transformation in Equation (5), the characteristic equation of System (10) can be obtained as Equation (9).

Due to $m,\zeta ,g^{\prime }\left(0\right)>0$, the real parts of characteristic roots in characteristic Equation (9) must be negative. Suppose that $\Omega$ is the set of the characteristic roots in characteristic Equation (9), and $r_{\ast }$ is the characteristic root with the largest real part, i.e., $r_{\ast }=\underset{r\in \Omega }{\mathrm{argmax}}\mathrm{Re}\left(r\right).$

In dynamic analysis, $r_{\ast }$ is a critical index especially for stability analysis. Thus, the approximately equivalent equation of the fractional derivative damping $s^q$ can be obtained based on the Taylor expansion technique around the characteristic root $r_{\ast }$, i.e.,

$$s^q=r_{\ast }^q+q{r}_{\ast }^{q-1}\left(s-r_{\ast }\right)+\frac{q\left(q-1\right)r_{\ast }^{q-2}}{2}{\left(s-r_{\ast }\right)}^2+o\left({\left(s-r_{\ast }\right)}^2\right).$$

(11)

Omitting the higher term of ${\left(s-r_{\ast }\right)}^2$ in System (11), it is approximately equivalent to

$$s^q\approx r_{\ast }^q+q{r}_{\ast }^{q-1}\left(s-r_{\ast }\right)+\frac{q\left(q-1\right)r_{\ast }^{q-2}}{2}{\left(s-r_{\ast }\right)}^2.$$

(12)

Denote ${\overline{r}}_{\ast }$ as the conjugate of $r_{\ast }$. Then, ${\overline{r}}_{\ast }$ is also a characteristic root and satisfies Equation (12). Because $r_{\ast }$ and ${\overline{r}}_{\ast }$ both satisfy Equation (12), it gives the following equation, i.e.,

$$\begin{array}{c}\hfill \begin{array}{cc}{s}^q\hfill & \approx \frac{r_{\ast }^q+{{\overline{r}}_{\ast }}^q}{2}+q\frac{r_{\ast }^{q-1}+{{\overline{r}}_{\ast }}^{q-1}}{2}s-q\frac{r_{\ast }^q+{{\overline{r}}_{\ast }}^q}{2}+\frac{q\left(q-1\right)}{2}\left[\frac{r_{\ast }^{q-2}+{{\overline{r}}_{\ast }}^{q-2}}{2}{s}^2+\frac{r_{\ast }^q+{{\overline{r}}_{\ast }}^q}{2}-\left(r_{\ast }^{q-1}+{{\overline{r}}_{\ast }}^{q-1}\right)s\right]\hfill \\ \hfill & =\left(1-\frac{3q}{2}+\frac{q^2}{2}\right)\mathrm{Re}\left(r_{\ast }^q\right)+\left[\left(2q-q^2\right)\mathrm{Re}\left(r_{\ast }^{q-1}\right)\right]s+\frac{q\left(q-1\right)\mathrm{Re}\left(r_{\ast }^{q-2}\right)}{2}{s}^2.\hfill \end{array}\end{array}$$

(13)

According to the inverse Laplace transformation of System (13), it obtains Equation (8) as follows,

$$\begin{array}{c}\hfill {}_0^C{D}_t^{q}x\approx \left(1-\frac{3q}{2}+\frac{q^2}{2}\right)\mathrm{Re}\left(r_{\ast }^q\right)x+\left[q\left(2-q\right)\mathrm{Re}\left(r_{\ast }^{q-1}\right)\right]\dot{x}+\frac{q\left(q-1\right)\mathrm{Re}\left(r_{\ast }^{q-2}\right)}{2}\ddot{x}.\end{array}$$

This completes the proof. □

Remark 1.

The approximately equivalent equation of the fractional derivative damping ${}_0^C{D}_t^{q}x$ in Theorem 1 is accurate in the neighborhood of the characteristic root $r_{\ast }$. Thus, the approximately equivalent Equation (8) is much more effective when the difference of real parts of characteristic roots in characteristic Equation (9) is relatively small.

3.2. Approximately Equivalent Equation of the Nonlinear Stochastic System

According to the approximately equivalent Equation (8) of the fractional derivative damping, the approximately equivalent equation of the nonlinear stochastic System (6) could be obtained in this subsection.

Substituting the approximately equivalent Equation (8) into System (6), it obtains the following updated system,

$$\left(m_e+\sigma {\xi }_m\left(t\right)\right)\ddot{x}+{\zeta }_e\dot{x}+g_e\left(x\right)=\epsilon f\left(x\right){\xi }_f\left(t\right),$$

(14)

where the corresponding parameters can be obtained based on Equations (6) and (8), and are listed as follows,

$$\left\{\begin{array}{c}{m}_e=\overline{m}+\frac{\zeta q\left(q-1\right)\mathrm{Re}\left(r_{\ast }^{q-2}\right)}{2},\\ {\zeta }_e=\zeta \left[q\left(2-q\right)\mathrm{Re}\left(r_{\ast }^{q-1}\right)\right],\\ g_e\left(x\right)=g\left(x\right)+\zeta \left(1-\frac{3q}{2}+\frac{q^2}{2}\right)\mathrm{Re}\left(r_{\ast }^q\right)x,\\ r_{\ast }=\underset{r\in \Omega }{\mathrm{argmax}}\mathrm{Re}\left(r\right).\end{array}\right.$$

(15)

Referring to System (14), $y_1\left(t\right)=x\left(t\right)$ and $y_2\left(t\right)=m_e\dot{x}\left(t\right)$ are denoted as the generalized displacement and momentum respectively. Then it gives

$$\left\{\begin{array}{c}{\dot{y}}_1=\frac{y_2}{m_e+\sigma {\xi }_m\left(t\right)},\\ {\dot{y}}_2=-{\zeta }_e\frac{y_2}{m_e+\sigma {\xi }_m\left(t\right)}-g_e\left(y_1\right)+\epsilon f\left(y_1\right){\xi }_f\left(t\right).\end{array}\right.$$

(16)

Due to the mass disturbance $\sigma {\xi }_m\left(t\right)$, stochastic averaging method can not be employed in System (16). However, if the mass disturbance $\sigma {\xi }_m\left(t\right)$ is small enough, the following approximated equation is obtained based on the Taylor expansion technique,

$$\frac{1}{m_e+\sigma {\xi }_m\left(t\right)}=\frac{1}{m_e}-\frac{\sigma {\xi }_m\left(t\right)}{{m_e}^2}+o\left(\sigma {\xi }_m\left(t\right)\right).$$

(17)

According to Equation (17), by omitting the higher term of the $\sigma$ term in System (16), it gives the approximately equivalent equation of the nonlinear stochastic System (6), i.e.,

$$\left\{\begin{array}{c}{\dot{y}}_1=\frac{y_2}{m_e}-\frac{y_2\sigma {\xi }_m\left(t\right)}{{m_e}^2},\\ {\dot{y}}_2=-\frac{{\zeta }_e}{m_e}{y}_2-g_e\left(y_1\right)+\epsilon f\left(y_1\right){\xi }_f\left(t\right).\end{array}\right.$$

(18)

The approximately equivalent Equation (18) is close to the traditional form of second-order stochastic systems. Thus, the corresponding stochastic averaging method is available, which is presented in the next section.

4. Stochastic Averaging of a Nonlinear Stochastic System with Variable Mass and Fractional Derivative Damping

In this section, a stochastic averaging of a nonlinear stochastic system with variable mass and fractional derivative damping is proposed based on the diffusion approach to the energy envelope. Then, according to the obtained stochastic averaging, the stationary response of such a nonlinear stochastic system is discussed.

According to the approximately equivalent Equation (18), the corresponding Stratonovich stochastic differential equation can be obtained [18],

$$\left\{\begin{array}{c}d{y}_1=\frac{y_2}{m_e}dt-\frac{y_2\sigma \sqrt{2D_m}}{{m_e}^2}\circ d{B}_m\left(t\right),\\ {\dot{y}}_2=\left[-\frac{{\zeta }_e}{m_e}{y}_2-g_e\left(y_1\right)\right]dt+\epsilon \sqrt{2D_f}f\left(y_1\right)\circ d{B}_f\left(t\right),\end{array}\right.$$

(19)

where $B_m\left(t\right)$ and $B_f\left(t\right)$ are independent standard Wiener processes. Because $y_1,y_2$ in the above Stratonovich stochastic differential equation are independent of $B_m\left(t\right),B_f\left(t\right)$, no Wong-–Zakai correction term exists. Then, the corresponding $\mathrm{It}\widehat{\mathrm{o}}$ stochastic differential equations of System (18) is given,

$$\left\{\begin{array}{c}d{y}_1=\frac{y_2}{m_e}dt-\frac{y_2\sigma \sqrt{2D_m}}{{m_e}^2}d{B}_m\left(t\right),\\ {dy}_2=\left[-\frac{{\zeta }_e}{m_e}{y}_2-g_e\left(y_1\right)\right]dt+\epsilon \sqrt{2D_f}f\left(y_1\right)d{B}_f\left(t\right).\end{array}\right.$$

(20)

Define a quasi Hamiltonian of System (20) as,

$$H=\frac{y_2^2}{2m_e}+{\int }_0^{y_1}{g}_e\left(t\right)dt.$$

(21)

Then, System (20) can be rewritten as the following form,

$$\left\{\begin{array}{c}d{y}_1=\frac{\partial H}{\partial y_2}dt-\frac{\sigma \sqrt{2D_m}}{m_e}\frac{\partial H}{\partial y_2}d{B}_m\left(t\right),\\ d{y}_2=\left[-{\zeta }_e\frac{\partial H}{\partial y_2}-\frac{\partial H}{\partial y_1}\right]dt+\epsilon \sqrt{2D_f}f\left(y_1\right)d{B}_f\left(t\right).\end{array}\right.$$

(22)

According to the $\mathrm{It}\widehat{\mathrm{o}}$ differential rule and Systems (21) and (22), the $\mathrm{It}\widehat{\mathrm{o}}$ equation of the quasi Hamiltonian H can be obtained,

$$\begin{array}{c}\hfill \begin{array}{cc}dH=\hfill & \left[-{\zeta }_e{\left(\frac{\partial H}{\partial y_2}\right)}^2+{\epsilon }^2{D}_f{f}^2\left(y_1\right)\frac{{\partial }^{2}H}{\partial {y_2}^2}+\frac{D_m{\sigma }^2}{{m_e}^2}{\left(\frac{\partial H}{\partial y_2}\right)}^2\frac{{\partial }^{2}H}{\partial {y_1}^2}\right]dt\hfill \\ \hfill & +\epsilon \sqrt{2D_f}f\left(y_1\right)\frac{\partial H}{\partial y_2}d{B}_f\left(t\right)-\frac{\sigma \sqrt{2D_m}}{m_e}\frac{\partial H}{\partial y_1}\frac{\partial H}{\partial y_2}d{B}_m\left(t\right).\hfill \end{array}\end{array}$$

(23)

It is noted that H is a slowly varying process and $y_1$ is a rapidly varying process. Based on the Khasminskii’s theorem [34], the slowly varying process H weakly converges to a Markov process. Then, the $\mathrm{It}\widehat{\mathrm{o}}$ equation of the approximate Markov process (20) can be obtained by the time averaging of Equation (23), i.e.,

$$dH=m^H\left(H\right)dt+{\sigma }_1^H\left(H\right)d{B}_1\left(t\right)+{\sigma }_2^H\left(H\right)d{B}_2\left(t\right).$$

(24)

In Equation (24), $m^H$ and ${\sigma }_1^H,{\sigma }_2^H$ are respectively drift and diffusion coefficients, which are introduced in [18] and described by

$$m^H\left(H\right)=\frac{1}{T\left(H\right)}{\int }_{\Theta }^{}\left[-{\zeta }_e{\left(\frac{\partial H}{\partial y_2}\right)}^2+{\epsilon }^2{D}_f{f}^2\left(y_1\right)\frac{{\partial }^{2}H}{\partial {y_2}^2}+\frac{D_m{\sigma }^2}{{m_e}^2}{\left(\frac{\partial H}{\partial y_2}\right)}^2\frac{{\partial }^{2}H}{\partial {y_1}^2}\right]{\left(\frac{\partial H}{\partial y_2}\right)}^{-1}d{y}_1,$$

(25)

and

$${\left[{\sigma }_1^H\left(H\right)\right]}^2+{\left[{\sigma }_2^H\left(H\right)\right]}^2=\frac{1}{T\left(H\right)}{\int }_{\Theta }^{}\left[{\epsilon }^{2}2D_f{f}^2\left(y_1\right)\frac{{\partial }^{2}H}{\partial {y_2}^2}+\frac{2D_m{\sigma }^2}{{m_e}^2}{\left(\frac{\partial H}{\partial y_2}\right)}^2\frac{{\partial }^{2}H}{\partial {y_1}^2}\right]{\left(\frac{\partial H}{\partial y_2}\right)}^{-1}d{y}_1,$$

(26)

where the region of integration $\Theta$ is denoted by

$$\Theta =\left\{y_1:H\left(y_1,y_2=0\right)={\int }_0^{y_1}{g}_e\left(t\right)dt\le H\right\},$$

(27)

and

$$T\left(H\right)={\int }_{\Theta }^{}{\left(\frac{\partial H}{\partial y_2}\right)}^{-1}d{y}_1.$$

(28)

The stationary probability density solution $p\left(H\right)$ of Equation (24) can be obtained by solving the FPK equation as follows,

$$\frac{\partial }{\partial t}p\left(H\right)=-\frac{\partial }{\partial H}\left[m^H\left(H\right)p\left(H\right)\right]+\frac{1}{2}\frac{{\partial }^2}{\partial H^2}\left\{\left[{\left({\sigma }_1^H\left(H\right)\right)}^2+{\left({\sigma }_2^H\left(H\right)\right)}^2\right]p\left(H\right)\right\}.$$

(29)

Substituting in $\frac{\partial }{\partial t}p\left(H\right)=0$, the solution $p\left(H\right)$ is given by

$$p\left(H\right)=Cexp\left\{-{\int }_0^H\frac{-2m^H\left(s\right)+\frac{d}{ds}\left[{\left({\sigma }_1^H\left(s\right)\right)}^2+{\left({\sigma }_2^H\left(s\right)\right)}^2\right]}{{\left({\sigma }_1^H\left(s\right)\right)}^2+{\left({\sigma }_2^H\left(s\right)\right)}^2}ds\right\},$$

(30)

where C is a normalization constant defined by

$$C={\left\{{\int }_0^{+\infty }exp\left\{-{\int }_0^H\frac{-2m^H\left(s\right)+\frac{d}{ds}\left[{\left({\sigma }_1^H\left(H\right)\right)}^2+{\left({\sigma }_2^H\left(H\right)\right)}^2\right]}{{\left({\sigma }_1^H\left(H\right)\right)}^2+{\left({\sigma }_2^H\left(H\right)\right)}^2}ds\right\}dH\right\}}^{-1}.$$

(31)

Then, the joint probability density of generalized displacement and momentum is

$$p\left(y_1,y_2\right)={\left.\frac{p\left(H\right)}{T\left(H\right)}\right|}_{H=H\left(y_1,y_2\right)}.$$

(32)

In addition, the marginal probability densities of the generalized displacement and momentum can be calculated by the following integrations,

$$p_{Y_1}\left(y_1\right)={\int }_{-\infty }^{+\infty }p\left(y_1,y_2\right)d{y}_2,p_{Y_2}\left(y_2\right)={\int }_{-\infty }^{+\infty }p\left(y_1,y_2\right)d{y}_1.$$

(33)

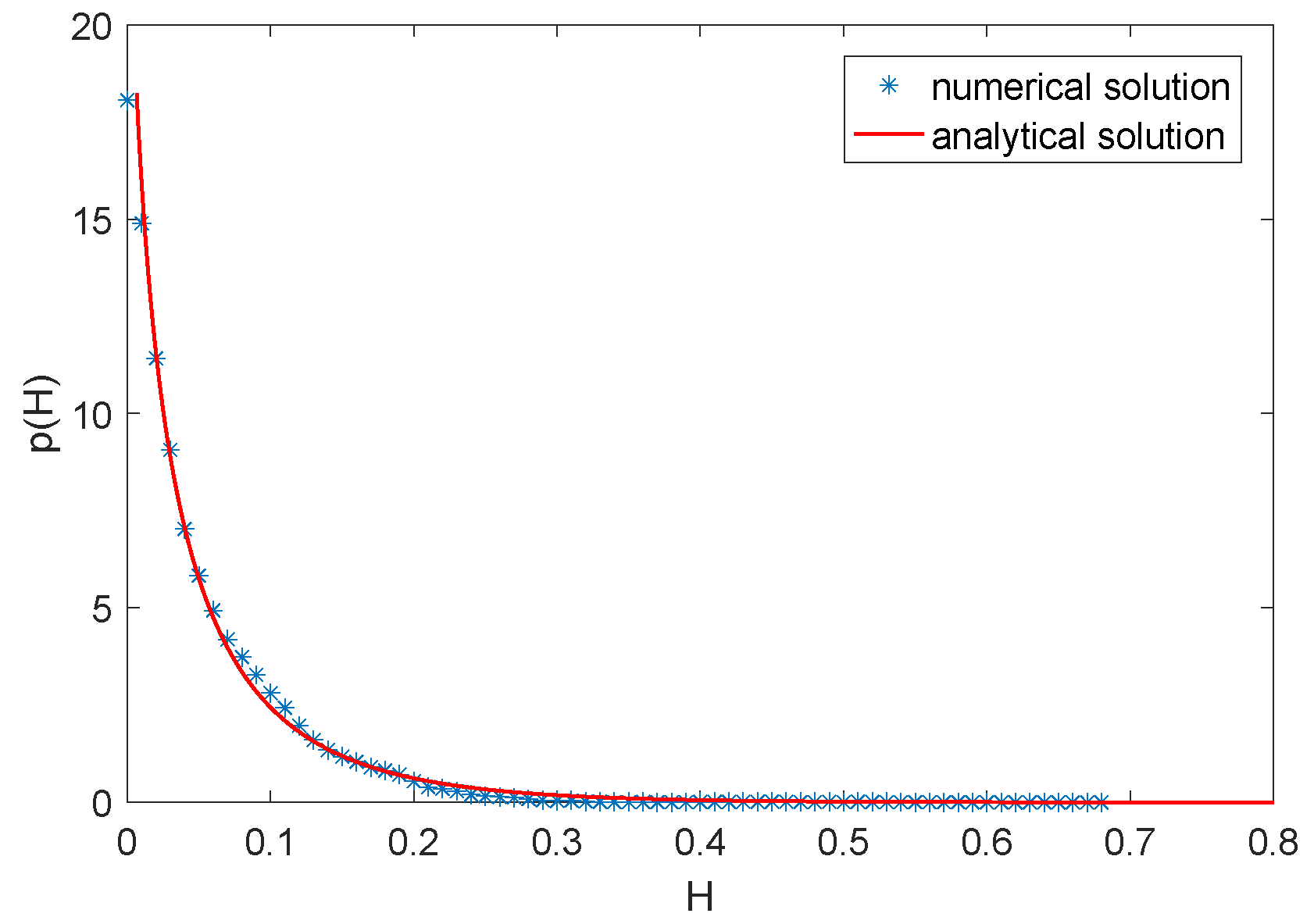
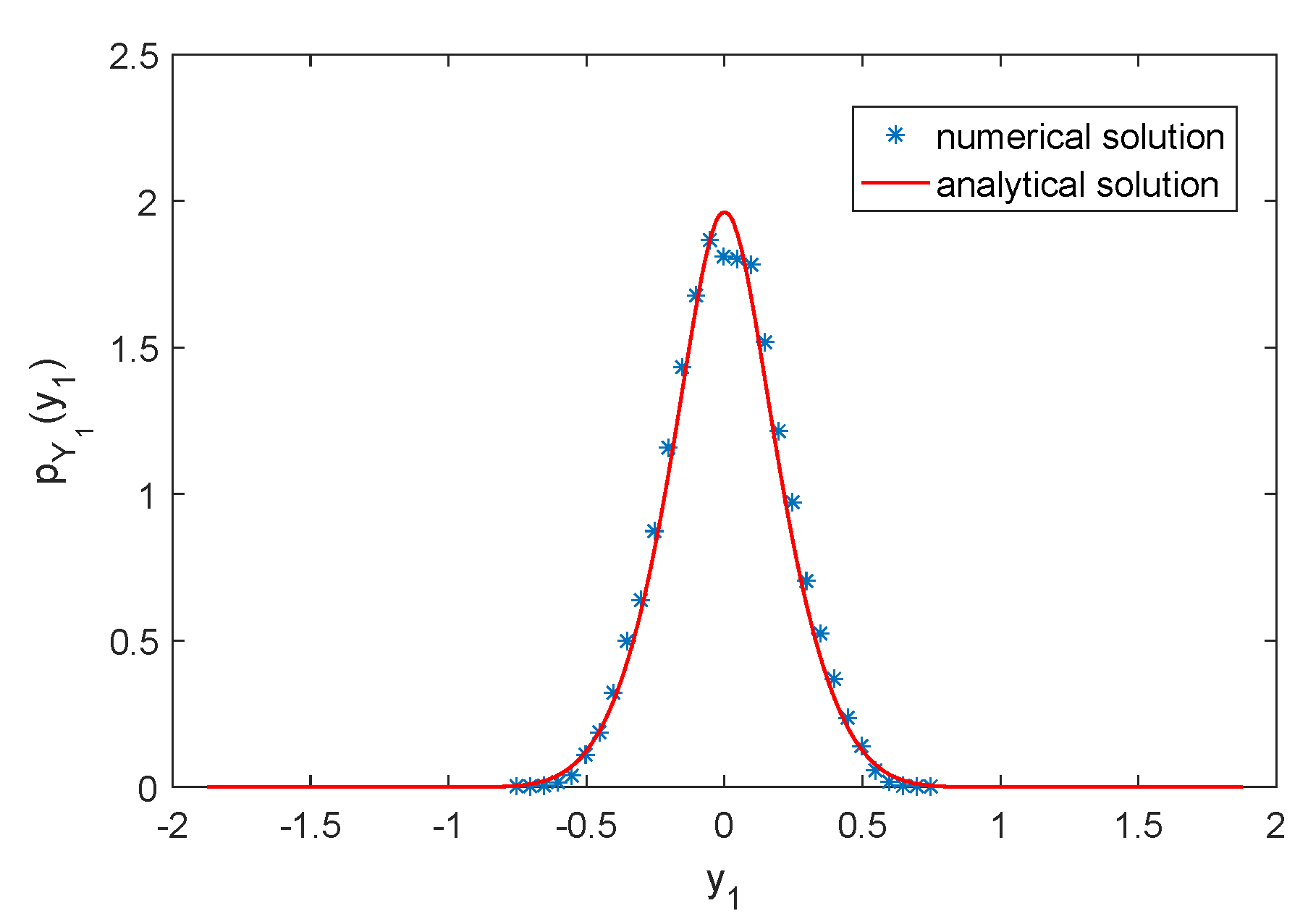
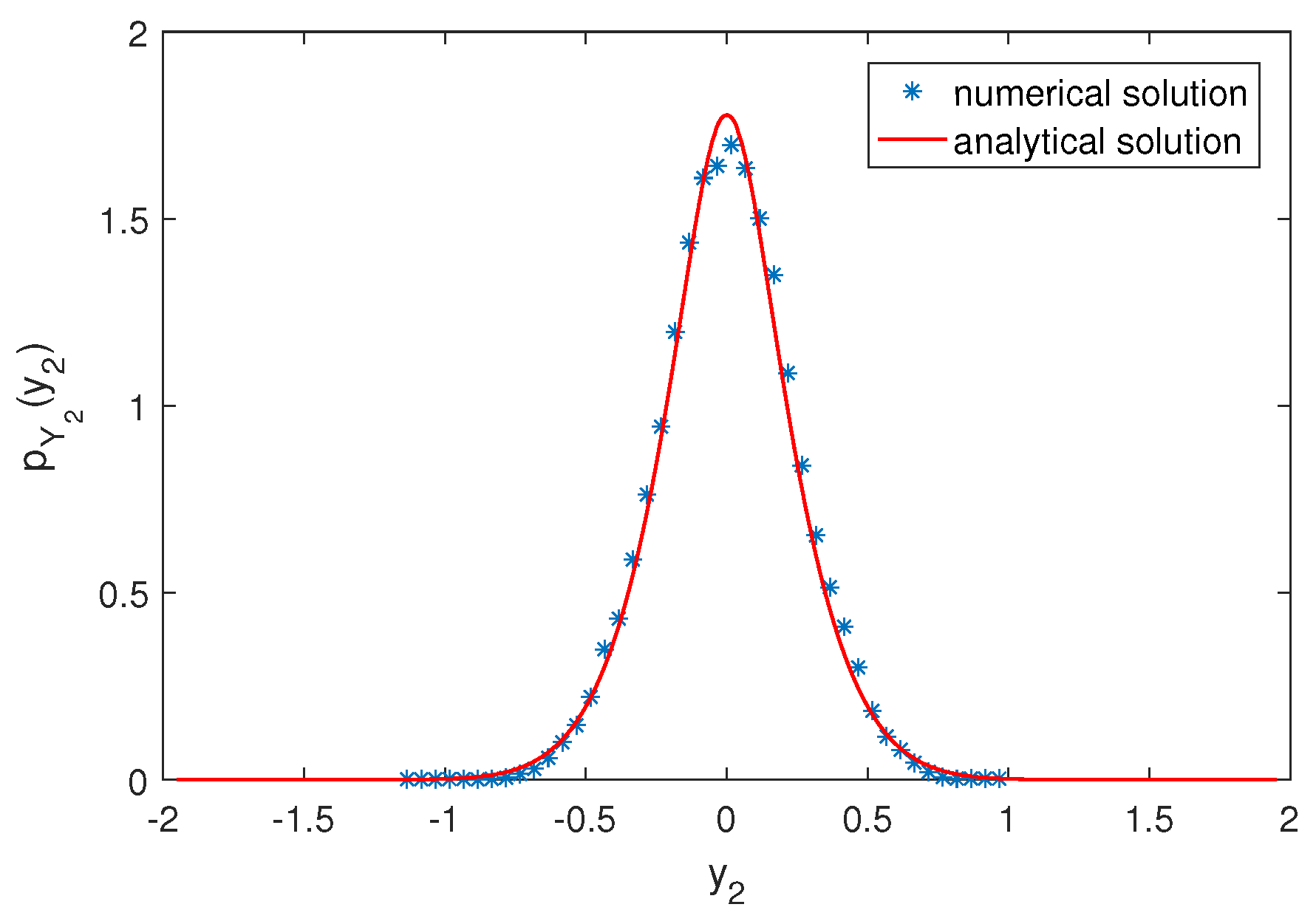
5. Numerical Examples

In this section, an example is given to show the effectiveness of the proposed results. Consider the following nonlinear oscillator with variable mass and fractional derivative damping,

$$(\overline{m}+\sigma {\xi }_m\left(t\right))\ddot{x}+\zeta {}_0^C{D}_t^{q}x+k_{1}x+k_2{x}^3=\epsilon f\left(x\right){\xi }_f\left(t\right).$$

(34)

The corresponding parameters are initially determined as

$$\overline{m}=1,\sigma =0.1,D_m=0.05,\zeta =0.1,q=0.5,k_1=1,k_2=2,\epsilon f\left(x\right)=0.2,D_f=0.1.$$

According to the characteristic Equation (9), the characteristic roots are approximately calculated as $-0.035\pm 1.035$. The highest differential order of System (34) is 2, which is equal to the number of the corresponding characteristic roots. The characteristic roots of System (34) are approximately $-0.035\pm 1.035$, who own the same real parts. In this case, the proposed approximate method is accurate. Then, based on Equation (8) and Theorem 1, it has the approximately equivalent equation rewritten by

$$\left(1.0088+0.1{\xi }_m\left(t\right)\right)\ddot{x}+0.0713\dot{x}+1.0826x+2x^3=0.2{\xi }_f\left(t\right).$$

(35)

which means $m_e=1.0088$, ${\zeta }_e=0.0713$, $g_e\left(x\right)=1.0826x+2x^3$ referring to System (14). Due to Equation (21), the quasi Hamiltonian is constructed as

$$H=\frac{y_2^2}{2.0176}+0.5413y_1^2+0.5y_1^4.$$

(36)

Then, according to Equations (21)–(28), it gives,

$$T\left(H\right)={\int }_{-A}^A\frac{2.0176}{\sqrt{2.0176H-2.0176\left(0.5413y_1^2+0.5y_1^4\right)}}d{y}_1,$$

(37)

and

$$F\left(H\right)=\frac{2}{T\left(H\right)}{\int }_{-d\left(H\right)}^{d\left(H\right)}\sqrt{2.0176H-2.0176\left(0.5413y_1^2+0.5y_1^4\right)}d{y}_1,$$

(38)

where

$$d\left(H\right)=\sqrt{\left[{\left(1.0826^2+8H\right)}^{1/2}-1.0826\right]/2}.$$

(39)

The drift and diffusion coefficients are obtained by

$$\begin{array}{c}\hfill \begin{array}{c}{m}^H\left(H\right)=\frac{0.2^2\times 0.1}{1.0088}-\frac{0.0713}{1.0088}F\left(H\right)+\frac{2\times {0.1}^2\times 0.05}{1.0088^{3}T\left(H\right)}\times \dots \hfill \\ {\int }_{-d\left(H\right)}^{d\left(H\right)}\left(1.0826+6y_1^2\right)\sqrt{2.0176H-2.0176\left(0.5413y_1^2+0.5y_1^4\right)}d{y}_1,\hfill \end{array}\end{array}$$

(40)

and

$$\begin{array}{c}\hfill \begin{array}{c}{\left[{\sigma }_1^H\left(H\right)\right]}^2+{\left[{\sigma }_2^H\left(H\right)\right]}^2=\frac{2\times {0.2}^2\times 0.1}{1.0088}F\left(H\right)+\frac{4\times {0.1}^2\times 0.05}{1.0088^{3}T\left(H\right)}\times \dots \hfill \\ {\int }_{-d\left(H\right)}^{d\left(H\right)}{\left(1.0826y_1+2y_1^3\right)}^2\sqrt{2.0176H-2.0176\left(0.5413y_1^2+0.5y_1^4\right)}d{y}_1.\hfill \end{array}\end{array}$$

(41)

According to Equation (30), the stationary probability density solution $p\left(H\right)$ of quasi Hamiltonian (36) can be obtained, which is shown in Figure 1. In Figure 1, the solid curve is the analytical solution of $p\left(H\right)$ in quasi Hamiltonian (36) based on the proposed stochastic averaging method. The ’*’ is the numerical solution of the stationary probability density solution $p\left(H\right)$ according to the Monte Carlo simulations. In addition, Figure 2 and Figure 3 show the stationary probability densities of $y_1$ and $y_2$ in Equation (33), respectively. Similarly, the solid curve and the ’*’ represent the corresponding analytical solution and numerical solution, respectively. In Section 3, the approximately equivalent equations of the fractional derivative damping and the mass disturbance are given to deduce the corresponding stochastic averaging method. Multiple approximation methods may have an influence in the accuracy of the obtained method. According to Figure 1, Figure 2 and Figure 3, the numerical solutions agree well with the analytical solutions, which could verify the effectiveness of the proposed approximate analytical method of the stochastic averaging.

6. Conclusions

In this paper, a class of nonlinear stochastic systems with variable mass and fractional derivative damping is studied in order to reveal the dynamic properties related to viscoelasticity and variable mass. Especially, the stationary response of the studied model is analyzed based on a group of approximately equivalent systems and stochastic averaging. Firstly, an approximately equivalent equation of the fractional derivative damping is proposed based on the Taylor expansion technique, such that the fractional derivative damping could be transformed into an approximate second-order system. Besides, the approximately equivalent equation of the nonlinear stochastic system is provided with the first-order Taylor approximation of the mass disturbance. Then, according to the obtained approximately equivalent equation, the corresponding stochastic averaging method is given based on the diffusion approach to energy envelope. In this case, the analytic method of the stationary probability density solution is proposed by solving the obtained FPK equation. At last, an example of nonlinear oscillator with variable mass and fractional derivative damping is given to illustrate the effectiveness of the obtained results.