Map of a Bending Problem for Self-Similar Beams into the Fractal Continuum Using the Euler–Bernoulli Principle

Abstract

The bending of self-similar beams applying the Euler–Bernoulli principle is studied in this paper. A generalization of the standard Euler–Bernoulli beam equation in the ${\mathcal{F}}_{d_{\mathcal{H}}}^3$ continuum using local fractional differential operators is obtained. The mapping of a bending problem for a self-similar beam into the corresponding problem for a fractal continuum is defined. Displacements, rotations, bending moments and shear forces as functions of fractal parameters of the beam are estimated, allowing the mechanical response for self-similar beams to be established. An example of the structural behavior of a cantilever beam with a load at the free end is considered to study the influence of fractality on the mechanical properties of beams.

1. Introduction

Beam deflection is one of the most important issues of structural engineering. From the classical theory of Euler–Bernoulli [1], it follows that the bending $u_3^{\mathcal{E}}$ in beams with length L under load $q_3^{\mathcal{E}}$ is given by [2]

$$\begin{array}{c}\hfill \frac{d^2}{d{x}_1^2}\left[EI\frac{d^2{u}_3^{\mathcal{E}}}{d{x}_1^2}\right]=q_3^{\mathcal{E}}\mathrm{for}0\le x_1\le L,\end{array}$$

(1)

where E is the Young’s modulus, I is the second moment area and $\mathcal{E}$ denotes the quantities in the Euler–Bernoulli beam theory. Extensive theoretical [3,4], numerical [5,6] and experimental studies [7] have been performed to describe such structural phenomena.

It is well-known that the product $EI$ is the bending stiffness [8] related to the geometry and mechanical properties of a beam, and its complex morphology plays an important role in the transverse force behavior and displacement. This heterogeneity can possess self-similar properties and non-integer dimensions [9,10]. The functions defined on such fractal beams are discontinuous [11], or their derivatives do not exist at some points [12,13]. Therefore, it is impossible to describe the mechanical behavior of such beams using standard calculus, and it is necessary to develop new paradigms to map physical problems on nowhere differentiable fractals into appropriate problems within a continuum framework [14].

In order to solve this problem the notions of fractal geometry [15,16], fractional space [17,18] and fractal continuums [14,19,20,21,22] have been used to generalize the concepts of ordinary calculus, which have proved to be convenient to model discontinuous point and even non-differentiable continuous functions.

In [23,24,25], fractional space models were applied to compute the fractional bending of a Euler–Bernoulli beam, and in [14,26], the fractional continuum and fractal continuum were used to describe the stress, strain, and kinematics of fractional and fractal continuum deformations, respectively. Meanwhile, in [22], the concept of an equivalent continuum solution for the Euler–Bernoulli self-similar beam using ordinary calculus on pre-fractals was introduced.

An efficient fractional equation that relates the deflection with the load applied to a beam using the Euler–Bernoulli theory was introduced in refs. [27,28] as:

$$\begin{array}{c}\hfill D_{x_1}^{\alpha }\left\{{\ell }_f^{\alpha -1}{D}_{x_1}^{\alpha }\left[{\ell }_f^{2\alpha -2}{D}_{x_1}^{\alpha }\left({\ell }_f^{\alpha -1}{D}_{x_1}^{\alpha }{u}_3^{\mathcal{E}}\right)\right]\right\}EI=q_3^{\mathcal{E}},\end{array}$$

(2)

where $D_{x_1}^{\alpha }$ is Caputo’s fractional differential operator of order $\alpha \in {\Re }^{+}$ and ${\ell }_f\ge 0$ is the variable length scale [29,30]. When we have that $\alpha =1$, Equation (2) reduces to the standard form given by Equation (1).

Self-similar beams have important potential applications, as it has been persistently hypothesised that higher degrees of structural hierarchy are responsible for increased resilience to pressure bearing (for a given mass of construction material). Moreover, it was shown that fractal-like suture joints can be used to tailor mechanical properties, load resistance and flaw tolerance [31]. In [32], a potential biomechanical application of Menger sponge fractal NiTi structures as bone implants was investigated. Another application of self-similar beams for antennas in telecommunication engineering was presented in [33].

In [34], a mechanical approach for a fractal bar that takes into account the irregularity of fractal domain was formulated. The ${\mathcal{F}}_{d_{\mathcal{H}}}^3$ continuum was defined using the approximation of non-differentiable functions defined on fractals by differentiable analytic envelopes introduced in the previous work [35]. This formulation was applied to solve the hydrodynamic and Maxwell equations in fractal continuums [36,37].

On the basis of the above-mentioned approach, we consider the concepts of stresses and strains within a fractal continuum framework using the fractal continuum ${\mathcal{F}}_{d_{\mathcal{H}}}^3$ introduced in [14] to obtain a more complete description of the structural behavior of self-similar beams. We study the transversal displacements in a Menger sponge-like fractal beam with a cross-section identical to the Sierpinski carpet, which is a self-similar path-connected fractal [38,39,40].

In the fractal geometry framework ${\mathcal{F}}_3^{d_{\mathcal{H}}}$, the fractal features of a beam are characterized by the set of fractal dimension numbers, such as Hausdorff $d_{\mathcal{H}}$, chemical $d_{\ell }$ and cross-section $d_{\mathcal{I}}$ dimensions, as well as co-dimension $\zeta$ (other dimensional numbers of fractal objects can be found in [41,42] and references therein). In what follows, we apply the ${\mathcal{F}}_{d_{\mathcal{H}}}^3$continuum to model a discontinuous Menger sponge-like fractal beam within the mechanics of the elastic fractal continuum ${\mathcal{F}}_{d_{\mathcal{H}}}^3$ [14,34,35,36,37] that uses local fractional differential operators.

In this work, a new formulation for the bending of a fractal beam applying the Euler–-Bernoulli principle is defined. The formulation obtained allows us to calculate the exact values of the spatial distribution of the beam response along its length.

Our paper is outlined as follows. In Section 2, we present the fractal aspects required. In Section 3 we develop the main formulation of this work. In Section 4 some engineering implications are discussed, and the conclusions and outlook are presented in Section 5.

2. Fractal Aspects

The main aim of the section is to summarize and define the basic concepts used in this work.

2.1. Fractal Domain ${\mathcal{F}}_3^{d_{\mathcal{H}}}$

Fractals provide an accurate modelling of irregular objects that have complex structures with statistical scale invariance in a range of length scales ${\xi }_0<L<{\xi }_C$, where ${\xi }_0$ and ${\xi }_C$ are the lower and upper cutoffs, respectively [43]. A fractal is characterized by the non-integer Hausdorff dimension $d_{\mathcal{H}}$, which exceeds or is equal to the topological dimension $d_t$, and at the same time is less than the dimension n of the Euclidean space ${\Re }^n$ where it lies [44], so we have that $d_t\le d_{\mathcal{H}}<n$. Hence, the properties of the fractal domain ${\mathcal{F}}_3^{d_{\mathcal{H}}}\subset {\Re }^3$ are described by non-differentiable and discontinuous functions in ${\Re }^3$ [10].

The Hausdorff dimension $d_{\mathcal{H}}$ can be obtained as the number of boxes $ϵ$ needed to cover the fractal linear size L with the scaling law $N_{L/ϵ}\sim {\left(L/ϵ\right)}^{d_{\mathcal{H}}}$ [45]. The value of $d_{\mathcal{H}}$ is constant within the bounded range of length scales ${\xi }_0\le ϵ<L\le {\xi }_C$. Meanwhile, the fractal mass M scales with respect to the linear size $L\in ({\xi }_0,{\xi }_C)$ as in [46]:

$$\begin{array}{c}\hfill M={\rho }_0{\xi }_0^3{\left(\frac{L}{{\xi }_0}\right)}^{d_{\mathcal{H}}},\end{array}$$

(3)

where ${\rho }_0$ is the mass density. On the one hand, the fractal topology is characterized by the chemical dimension $d_{\ell }$, which is defined by the scaling law $N_{L/{ϵ}_{\ell }}\sim {\left(L/{ϵ}_{\ell }\right)}^{d_{\ell }}$ [47], where $d_{\ell }$ is the number of $d_{\ell }$-dimensional boxes of size ${ϵ}_{\ell }$ needed to cover the fractal according to the scale invariance principle, and ${ϵ}_{\ell }$ is measured with respect to the geodesic metric over the fractal, so we have $2\le d_{\ell }\le 3$ for fractals with $d_t\le d_{\mathcal{H}}<3$. Moreover, the integer part of the chemical dimension $\lfloor d_{\ell }\rfloor$ defines the number of orthogonal fractional coordinates in the fractal domain [14]. The fractal dimension of a cross-section $d_{\mathcal{I}}$ is given by the intersection between the fractal and a Cartesian plane in ${\Re }^3$ [35,36], and it characterizes the scale dependence of the fractal area of the cross-section $A_{\mathcal{F}}$ with respect to the linear size L as:

$$\begin{array}{c}\hfill A_{\mathcal{F}}={\xi }_0^2{\left(\frac{L}{{\xi }_0}\right)}^{d_{\mathcal{I}}}.\end{array}$$

(4)

The fractal distance on $x_i\left(L\right)$ is defined as:

$$\begin{array}{c}\hfill x_i\left(L\right)={\xi }_0{\left(\frac{L}{{\xi }_0}\right)}^{{\zeta }_i},\end{array}$$

(5)

where

$$\begin{array}{c}\hfill {\zeta }_i=d_{\mathcal{H}}-d_{\mathcal{I}}\end{array}$$

(6)

is the co-dimension of the cross-section [34]. Hence, we can rewrite Equation (3) as:

$$\begin{array}{c}\hfill M={\rho }_0{x}_i\left(L\right)A_{\mathcal{F}}={\rho }_0{\xi }_0^3{\left(\frac{L}{{\xi }_0}\right)}^{d_{\mathcal{H}}}.\end{array}$$

(7)

Figure 1 shows a Menger sponge with a Sierpinski carpet-type cross-section after the fourth iteration. The Hausdorff dimension of the pre-fractals used to generate the Menger sponge is defined by (see [48] and references therein):

$$\begin{array}{c}\hfill d_{\mathcal{H}}=\frac{log\left({(L/{\xi }_0)}^n-{\beta }^n\right)}{log(L/{\xi }_0)},\end{array}$$

(8)

where $L/{\xi }_0$ is the size of boxes covering the fractal mass, $\beta$ is the number of deleted boxes of the fractal mass and $n=1,2,3,$ defines the Hausdorff dimension for the Cantor middle-$\mu$ set, Sierpinski carpet and Menger sponge, respectively. Here, $0<\mu <1$ is the length of open interval which is eliminated in the kth iteration of the corresponding Cantor middle-$\mu$ set [49].

2.2. Fractal Continuum Domain ${\mathcal{F}}_{d_{\mathcal{H}}}^3$

The fractal continuum is defined in [34,35] as a three-dimensional object ${\mathcal{F}}_{d_{\mathcal{H}}}^3\subset {\Re }^3$ filled with continuous matter. ${\mathcal{F}}_{d_{\mathcal{H}}}^3$ is equipped with its particular fractional norm, metric, measure and rules for integro-differential calculus, and its properties are defined as differentiable analytic envelopes of non-analytic functions describing the properties of the fractal material under study [14]. The topological dimension of ${\mathcal{F}}_{d_{\mathcal{H}}}^3$ is given by $d_t=3>d_{\mathcal{H}}$. In order to map a path-connected fractal with $\lfloor d_{\ell }\rfloor <3$ (for example, the Menger sponge for which $d_{\ell }=d_{\mathcal{H}}\approx 2.72$ and $\lfloor d_{\ell }\rfloor =2$) in ${\mathcal{F}}_{d_{\mathcal{H}}}^3$, at first two mutually orthogonal fractal coordinates (${\chi }_i,A_{{\mathcal{F}}_i}$) associated with the infinitesimal volume element in the fractal continuum are defined (for details, see [34,36]). Three orthogonal fractal coordinates $({\chi }_1,{\chi }_2,{\chi }_3)$ correspond to the decomposition of (7) in ${\chi }_i\in {\mathcal{F}}_{d_{\mathcal{H}}}^3$ [14] so that:

$$\begin{array}{c}\hfill \begin{array}{c}{\chi }_1={\xi }_0{\left(x_1/{\xi }_0\right)}^{{\zeta }_1},\hfill \\ {\chi }_2={\xi }_0{\left(x_2/{\xi }_0\right)}^{{\zeta }_2},\hfill \\ {\chi }_3={\xi }_0{\left(x_3/{\xi }_0\right)}^{{\zeta }_3},\hfill \end{array}\end{array}$$

(9)

where $x_i$ are the Cartesian coordinates in ${\Re }^3$, and ${\zeta }_i$ is the fractal dimension of the coordinate ${\chi }_i$, such that $d_{{\chi }_i}=d_{\mathcal{H}}-d_{{\mathcal{I}}_i}={\zeta }_i$. Therefore, we have $x_i\mapsto {\chi }_i={\xi }_0{\left(x_i/{\xi }_0\right)}^{{\zeta }_i}$. For a geometrical interpretation, see Figure 5 in [14], which presents the mapping ${\mathcal{F}}_3^{d_{\mathcal{H}}}\mapsto {\mathcal{F}}_{d_{\mathcal{H}}}^3$.

2.3. Elastic Fractal Continuum

The fractal continuum elasticity in small-strain regimes was proposed by Balankin in [34]. We consider the problem of static deformation under the assumption that material is linearly elastic and small fractional deformation holds, so it is governed by the following equations:

$$\begin{array}{c}\hfill \begin{array}{ccc}di{v}_{\mathcal{H}}{\sigma }_{ij}+b_i\hfill & =\hfill & 0,\hfill \\ {\epsilon }_{ij}\hfill & =\hfill & \frac{1}{2}\left({\nabla }_j^{\mathcal{H}}{\upsilon }_i+{\nabla }_i^{\mathcal{H}}{\upsilon }_j\right)=\frac{1}{2}\frac{1}{c_1}\left(\frac{\partial {\upsilon }_i}{\partial x_j}+\frac{\partial {\upsilon }_j}{\partial x_i}\right),\hfill \\ {\sigma }_{ij}\hfill & =\hfill & {\mathcal{C}}_{ijkl}{\epsilon }_{kl},\hfill \\ u_i\hfill & =\hfill & {\widehat{u}}_i,\hfill \\ {\sigma }_{ij}{n}_j\hfill & =\hfill & {\widehat{t}}_i,\hfill \end{array}\end{array}$$

(10)

where ${\sigma }_{ij}$ is the Cauchy stress tensor and $b_i$ is the body force; ${\epsilon }_{ij}$ is the infinitesimal strain tensor; ${\mathcal{C}}_{ijkl}$ is the stiffness tensor; $n_j$ is the outward unit normal vector; t is the Cauchy traction vector; x is a material variable, u is the displacement and ${\mathsf{\Omega }}_u$ and ${\mathsf{\Omega }}_{\sigma }$ are parts of boundary ${\mathcal{F}}_{d_{\mathcal{H}}}^3$ where the displacements and the tractions are applied, respectively. We have $c_1={\zeta }_1{\left(x_1/{\xi }_0\right)}^{{\zeta }_1-1}$ [34,35,36], and ${\upsilon }_i\in {\mathcal{F}}_{d_{\mathcal{H}}}^3$ is defined by [14] as:

$$\begin{array}{c}\hfill \begin{array}{c}{\upsilon }_1={\zeta }_1{\left(x_1/{\xi }_0\right)}^{{\zeta }_1-1}{u}_1,\hfill \\ {\upsilon }_2={\zeta }_2{\left(x_2/{\xi }_0\right)}^{{\zeta }_2-1}{u}_2,\hfill \\ {\upsilon }_3={\zeta }_3{\left(x_3/{\xi }_0\right)}^{{\zeta }_3-1}{u}_3;\hfill \end{array}\end{array}$$

(11)

therefore, we have that $u_i\mapsto {\upsilon }_i={\zeta }_i{\left(x_i/{\xi }_0\right)}^{{\zeta }_i-1}{u}_i$.

In Equation (10), the notation ${\nabla }_i^{\mathcal{H}}$ denotes the Hausdorff derivative introduced by Chen in [50] and modified in [34,35]:

$$\begin{array}{c}\hfill {\nabla }_i^{\mathcal{H}}f=\underset{{\chi }_i\to {\chi }_i^{\prime }}{lim}\frac{f\left({\chi }_i^{\prime }\right)-f\left({\chi }_i\right)}{{\chi }_i^{\prime }-{\chi }_i}=\underset{x_i\to x_i^{\prime }}{lim}\frac{f\left(x_i^{\prime }\right)-f\left(x_i\right)}{\mathrm{\Delta }\left(x_i^{\prime },x_i\right)}=\frac{\partial }{\partial {\chi }_i}f\left({\chi }_i\right)=\frac{1}{{\zeta }_i}{\left(\frac{x_i}{{\xi }_0}\right)}^{1-{\zeta }_i}\frac{\partial }{\partial x_i}f,\end{array}$$

(12)

where $\partial /\partial x_i$ denotes the conventional partial derivative, the exponent ${\zeta }_i=d_{\mathcal{H}}-d_{\mathcal{I}}$ is the co-dimension of cross-section, and:

$$\begin{array}{c}\hfill di{v}_{\mathcal{H}}f={\chi }_1\frac{\partial f_1}{\partial x_1}+{\chi }_2\frac{\partial f_2}{\partial x_2}+{\chi }_3\frac{\partial f_3}{\partial x_3},\end{array}$$

(13)

where f is a continuous differentiable function of $x_j\in {\Re }^3$. It is a straightforward matter to see that the standard solution of (11) is a special case of the fractal generalization when ${\zeta }_i=d_{\mathcal{H}}-d_{\mathcal{I}}=1$.

3. Differential Equations of the Euler–Bernoulli Beam in the ${\mathcal{F}}_{d_{\mathcal{H}}}^3$ Continuum

The main goal of this section is to introduce a new model of fractal bending by applying the Euler–Bernoulli beam theory to the fractal continuum ${\mathcal{F}}_{d_{\mathcal{H}}}^3$.

3.1. Euler–Bernoulli Beam Equation in Fractal Continuum ${\mathcal{F}}_{d_{\mathcal{H}}}^3$

The governing equations of the Euler–Bernoulli bending principle of mechanics in the fractal continuum are obtained under the similar assumptions as in the standard or Euclidean case (for details, see [51]). Hence, the displacement field of the Euler=-Bernoulli beam in the fractal space framework is given as:

$$\begin{array}{c}\hfill \begin{array}{ccc}{\upsilon }_1^{\mathcal{E}}({\chi }_1,{\chi }_3)\hfill & =\hfill & -{\chi }_3\frac{d{\upsilon }_3^{\mathcal{E}}}{d{\chi }_1},\hfill \\ {\upsilon }_2^{\mathcal{E}}({\chi }_1,{\chi }_3)\hfill & =\hfill & 0,\hfill \\ {\upsilon }_3^{\mathcal{E}}({\chi }_1,{\chi }_3)\hfill & =\hfill & {\upsilon }_3^{\mathcal{E}}\left({\chi }_1\right),\hfill \end{array}\end{array}$$

(14)

where ${\upsilon }_3^{\mathcal{E}}$ is the transverse deflection of the point (${\chi }_1,0$) of a point at the mid-plane, where ${\chi }_3=0$ (see Figure 2).

Using Equations (9) and (11) in Equation (14), the following equation for the fractal continuum beam is obtained (see Figure 3):

$$\begin{array}{c}\hfill \begin{array}{ccc}{\upsilon }_1^{\mathcal{E}}({\chi }_1,{\chi }_3)\hfill & =\hfill & -{\zeta }_3{\xi }_0^{{\zeta }_1}{\left(\frac{x_3}{{\xi }_0}\right)}^{2{\zeta }_3-1}\frac{d{u}_3^{\mathcal{E}}}{d{x}_1^{{\zeta }_1}},\hfill \\ {\upsilon }_2^{\mathcal{E}}({\chi }_1,{\chi }_3)\hfill & =\hfill & 0,\hfill \\ {\upsilon }_3^{\mathcal{E}}({\chi }_1,{\chi }_3)\hfill & =\hfill & {\zeta }_3{\left(\frac{x_3}{{\xi }_0}\right)}^{{\zeta }_3-1}{u}_3^{\mathcal{E}}\left({\xi }_0^{1-{\zeta }_1}{x}_1^{{\zeta }_1}\right)={\zeta }_3{\left(\frac{x_3}{{\xi }_0}\right)}^{{\zeta }_3-1}{u}_3^{\mathcal{E}}\left(x_1^{{\zeta }_1}\right);\hfill \end{array}\end{array}$$

(15)

therefore, when ${\zeta }_i=1$, the displacement field can be obtained in the standard calculus manner.

Equation (15) implies that the straight lines normal to the mid-plane before deformation remain straight and normal to the mid-plane after deformation, as shown in Figure 2. Therefore, both transverse shear and transverse normal strains are neglected. It is well-known that the virtual strain energy $\delta U$ of a beam is given as:

$$\begin{array}{c}\hfill \delta U={\int }_0^L{\int }_A{\sigma }_{11}\delta {\epsilon }_{11}dAd{\chi }_1,\end{array}$$

(16)

where $\delta$ is the variational symbol, A is the cross-sectional area of the uniform beam, L is the length of the beam, ${\sigma }_{11}$ is the axial stress, and ${\epsilon }_{11}$ is the normal strain. Note that the strain energy associated with the shearing strain is zero in the Euler–Bernoulli beam theory. Using the linear strain-displacement relation (see Equation (14)), we have that:

$$\begin{array}{c}\hfill {\epsilon }_{11}=\frac{\partial {\upsilon }_1^{\mathcal{E}}}{\partial {\chi }_1}=-{\chi }_3\frac{d^2{\upsilon }_3^{\mathcal{E}}}{d{\chi }_1^2}\end{array}$$

(17)

and as the bending moment is:

$$\begin{array}{c}\hfill M_{11}^{\mathcal{E}}={\int }_A{\chi }_3{\sigma }_{11}dA,\end{array}$$

(18)

from Equation (16), we obtain that:

$$\begin{array}{c}\hfill \delta U=-{\int }_0^L{M}_{11}^{\mathcal{E}}\frac{d^2\delta {\upsilon }_3^{\mathcal{E}}}{d{\chi }_1^2}d{\chi }_1.\end{array}$$

(19)

Assuming that the transverse load $q_3^{\mathcal{E}}$ acts at the centroidal axis of the beam and that there are no other applied loads, the virtual potential energy of the load $q_3$ is given by:

$$\begin{array}{c}\hfill \delta V={\int }_0^{L}q\delta {\upsilon }_3^{\mathcal{E}}d{\chi }_1.\end{array}$$

(20)

The principle of virtual displacements states that if a body is in equilibrium, then the total virtual work done, $\delta W=\delta U+\delta V$, is zero [51]. Thus, we have:

$$\begin{array}{c}\hfill \delta W=-{\int }_0^L\left(M_{11}^{\mathcal{E}}\frac{d^2\delta {\upsilon }_3^{\mathcal{E}}}{d{\chi }_1^2}+q\delta {\upsilon }_3^{\mathcal{E}}\right)d{\chi }_1=0.\end{array}$$

(21)

Integrating by parts twice the first term in Equation (21), we get:

$$\begin{array}{c}\hfill {\int }_0^L\left(-\frac{d^2{M}_{11}^{\mathcal{E}}}{d{\chi }_1^2}-q\right)\delta {\upsilon }_3^{\mathcal{E}}d{\chi }_1+{\left[M_{11}^{\mathcal{E}}\frac{d\delta {\upsilon }_3^{\mathcal{E}}}{d{\chi }_1}-\frac{d{M}_{11}^{\mathcal{E}}}{d{\chi }_1}\delta {\upsilon }_3^E\right]}_0^L=0.\end{array}$$

(22)

Since $\delta {\upsilon }_3$ is arbitrary for $0<{\chi }_1<L$, the following equilibrium equation holds:

$$\begin{array}{c}\hfill -\frac{d^2{M}_{11}^{\mathcal{E}}}{d{\chi }_1^2}=q_3^{\mathcal{E}}\mathrm{for}0<{\chi }_1<L,\end{array}$$

(23)

and as the shear force is $q_3^{\mathcal{E}}=-d{Q}_{11}^{\mathcal{E}}/d{\chi }_1$ [52], equilibrium Equation (23) can be rewritten in the following form:

$$\begin{array}{c}\hfill -\frac{d{M}_{11}^{\mathcal{E}}}{d{\chi }_1}+Q_{11}^{\mathcal{E}}=0.\end{array}$$

(24)

Hooke’s law implies that:

$$\begin{array}{c}\hfill {\sigma }_{11}=E{\epsilon }_{11}=-E{\chi }_3\frac{d^2{\upsilon }_3^{\mathcal{E}}}{d{\chi }_1^2};\end{array}$$

(25)

therefore, from Equation (18), it follows that:

$$\begin{array}{c}\hfill M_{11}^{\mathcal{E}}=\left[-E{\int }_A{\chi }_3^{2}dA\right]\frac{d^2{\upsilon }_3^{\mathcal{E}}}{d{x}_1^2}=-EI\frac{d^2{\upsilon }_3^{\mathcal{E}}}{d{\chi }_1^2},\end{array}$$

(26)

where $I={\int }_A{\chi }_3^{2}dA$ is the second moment of area around the ${\chi }_2$-axis. The substitution of Equation (26) into Equation (23) yields the following fractal Euler–Benoulli bending beam equation:

$$\begin{array}{c}\hfill \frac{d^2}{d{\chi }_1^2}\left[EI\frac{d^2{\upsilon }_3^{\mathcal{E}}}{d{\chi }_1^2}\right]=q_3^{\mathcal{E}}\mathrm{for}0<{\chi }_1<L,\end{array}$$

(27)

and the mapping of the Euler–Bernoulli bending equation for fractal beams into the fractal continuum ${\mathcal{F}}_{d_{\mathcal{H}}}^3$ yields

$$\begin{array}{c}\hfill {\zeta }_3{\left(\frac{x_3}{{\xi }_0}\right)}^{{\zeta }_3-1}{\xi }_0^{4{\zeta }_1-4}\frac{d^2}{d{x}_1^{2{\zeta }_1}}\left[EI\frac{d^2{u}_3^{\mathcal{E}}}{d{x}_1^{2{\zeta }_1}}\right]=q_3^{\mathcal{E}}.\end{array}$$

(28)

It is worth noting that when ${\zeta }_i=1$, Equation (28) coincides with Equation (1).

3.2. ${\mathcal{F}}_{d_{\mathcal{H}}}^3$ Continuum for Rotation ${\varphi }^{\mathcal{E}}$, Bending Moment $M^{\mathcal{E}}$ and Shear Force $Q^{\mathcal{E}}$ of Self-Similar Beams

The complete static response of a self-similar beam is given by the displacement, rotation, bending moment and shear force governed by the external loads and the boundary conditions [8] and can be described by the following equations [8,52]:

$$\begin{array}{c}\hfill \begin{array}{ccc}{\varphi }_{11}^{\mathcal{E}}\hfill & =\hfill & \frac{d{\upsilon }_3^{\mathcal{E}}}{d{\chi }_1},\hfill \\ M_{11}^{\mathcal{E}}\hfill & =\hfill & EI\frac{d{\varphi }_{11}}{d{\chi }_1}=EI\frac{d^2{\upsilon }_3^{\mathcal{E}}}{d{\chi }_1^2},\hfill \\ Q_{11}^{\mathcal{E}}\hfill & =\hfill & \frac{d{M}_{11}^{\mathcal{E}}}{d{\chi }_1}=EI\frac{d^3{\upsilon }_3^{\mathcal{E}}}{d{\chi }_1^3},\hfill \\ q_3^{\mathcal{E}}\hfill & =\hfill & \frac{d{Q}_{11}^{\mathcal{E}}}{d{\chi }_1}=EI\frac{d^4{\upsilon }_3^{\mathcal{E}}}{d{\chi }_1^4}.\hfill \end{array}\end{array}$$

(29)

Using Equations (9) and (11), we can map Equation (29) into the fractal continuum, so we have:

$$\begin{array}{c}\hfill \begin{array}{ccc}{\varphi }_{11}^{\mathcal{E}}\hfill & =\hfill & {\zeta }_3{\left(\frac{x_3}{{\xi }_0}\right)}^{{\zeta }_3-1}{\xi }_0^{{\zeta }_1-1}\frac{d{u}_3}{d{x}_1^{{\zeta }_1}},\hfill \\ M_{11}^{\mathcal{E}}\hfill & =\hfill & {\zeta }_3{\left(\frac{x_3}{{\xi }_0}\right)}^{{\zeta }_3-1}{\xi }_0^{2{\zeta }_1-2}EI\frac{d^2{u}_3^{\mathcal{E}}}{d{x}_1^{2{\zeta }_1}},\hfill \\ Q_{11}^{\mathcal{E}}\hfill & =\hfill & {\zeta }_3{\left(\frac{x_3}{{\xi }_0}\right)}^{{\zeta }_3-1}{\xi }_0^{3{\zeta }_1-3}EI\frac{d^3{u}_3^{\mathcal{E}}}{d{x}_1^{3{\zeta }_1}},\hfill \\ q_3^{\mathcal{E}}\hfill & =\hfill & {\zeta }_3{\left(\frac{x_3}{{\xi }_0}\right)}^{{\zeta }_3-1}{\xi }_0^{4{\zeta }_1-4}EI\frac{d^4{u}_3^{\mathcal{E}}}{d{x}_1^{4{\zeta }_1}}.\hfill \end{array}\end{array}$$

(30)

4. Bending on a Cantilever Fractal Beam

In this section, we apply the proposed model for a self-similar beam with classical boundary conditions in order to show the fractal influence in bending beam problems.

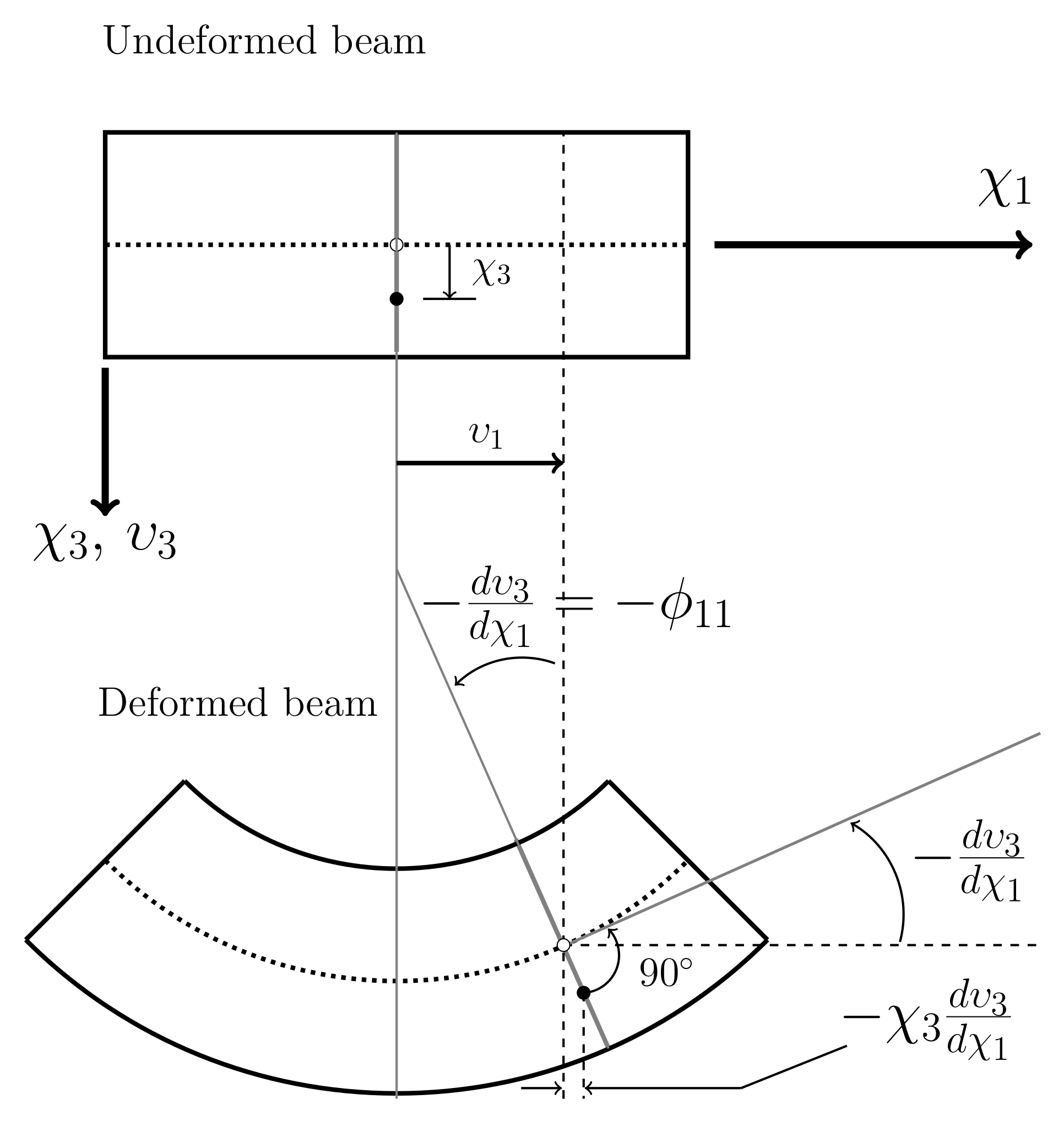
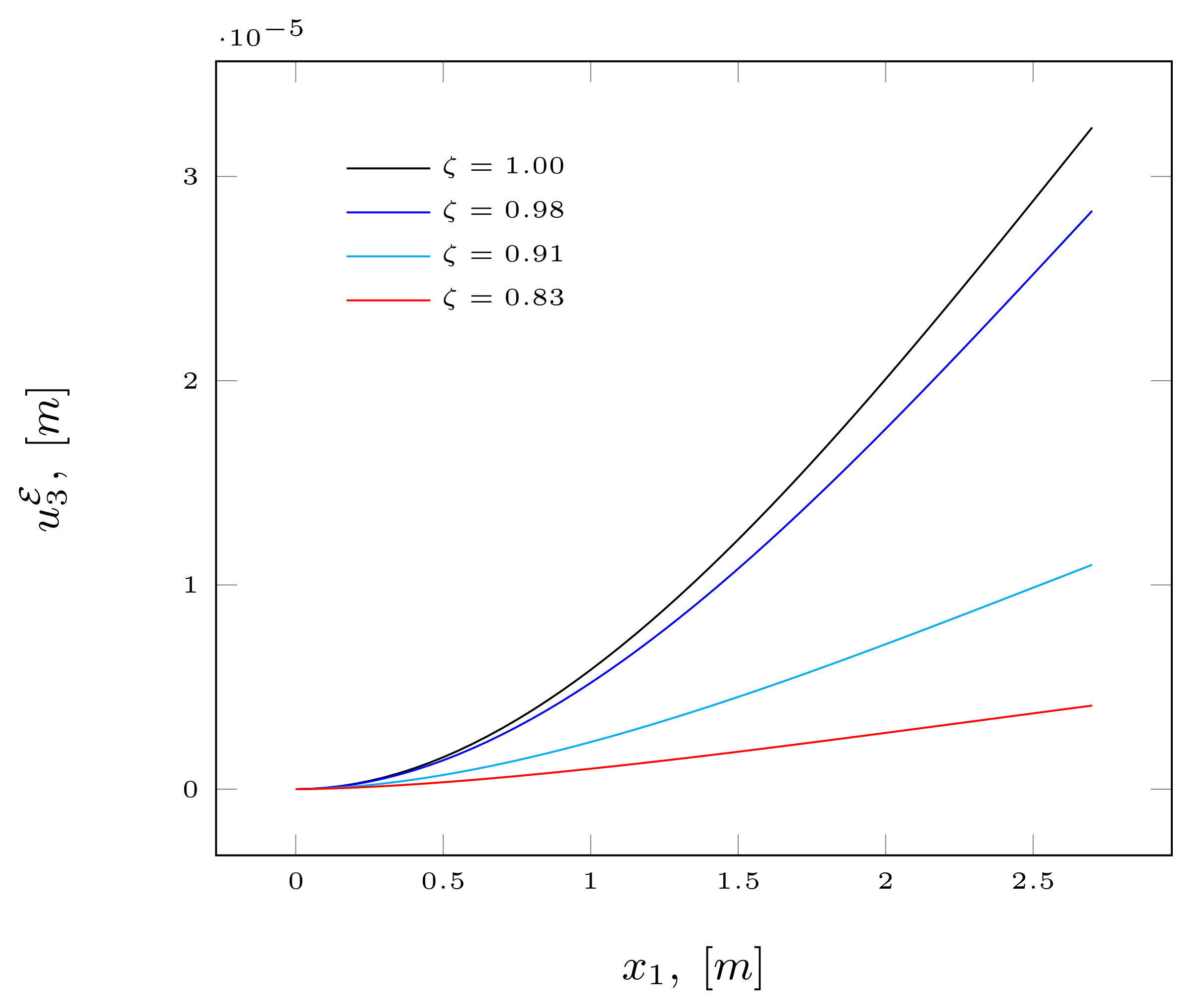
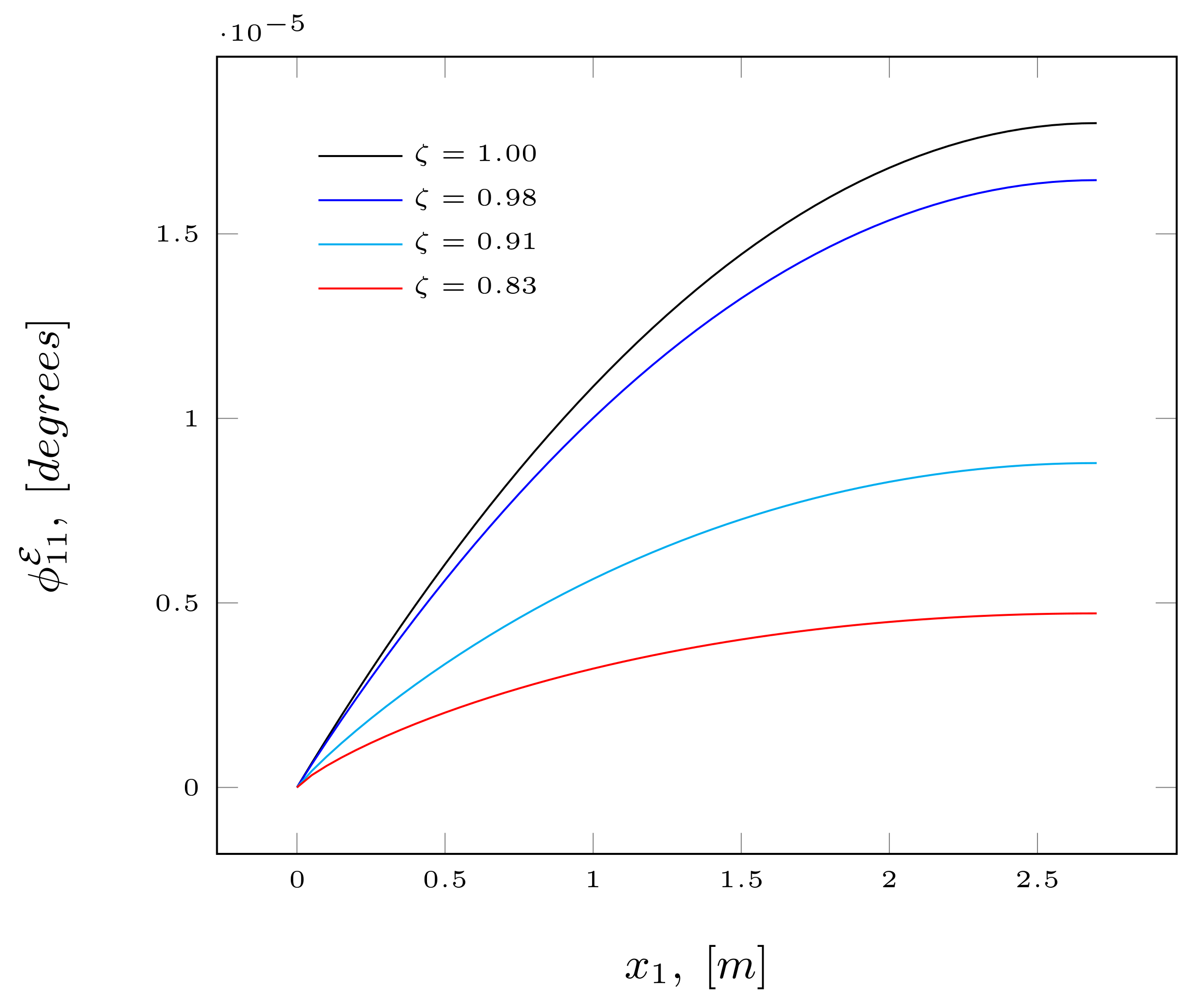
4.1. Structural Behavior

We consider a cantilever fractal beam with a load at the free end, as sketched in Figure 3. The beam is a fourth iteration Menger sponge part, and each cube that integrates it is generated at the second iteration, where all the pre-fractals have the same Hausdorff dimension, nonetheless with different length scales of self-similarity, as shown in Figure 1. The fractal parameters of the beam are presented in

Table 1. Fractal parameters of the cantilever fractal beam.

Parameter	$\mathit{\mu }=0$	$\mathit{\mu }=1/9$	$\mathit{\mu }=3/9$	$\mathit{\mu }=1/3$
$d_{\mathcal{H}}$	3	2.98	2.86	2.72
$d_{\mathcal{I}}$	2	1.99	1.94	1.89
${\zeta }_i$	1	0.98	0.91	0.83
${\xi }_0$	0	$2.7/3^4$	$2.7/3^4$	$2.7/3^4$
${\xi }_0^{1-\zeta }{L}^{\zeta }$	2.70	2.58	1.87	1.30
I	$675\times {10}^{-6}$	$674.897\times {10}^{-6}$	$666.667\times {10}^{-6}$	$599.177\times {10}^{-6}$

, where $\mu$ denotes the amount of mass removed in the Cantor set used to generate the Menger sponge (recall that the Sierpinski carpet and the Menger sponge are two- and three-dimensional versions of the Cantor set); in particular, when $\mu =0$, the Menger sponge has $d_{\mathcal{H}}=3$, and the beam is a Euclidean solid beam. The beam was considered with the data from [27], i.e.,: $L=2.7$ m, $h=b=0.3$ m, $E=30\times {10}^9$ N/m${}^2$, and $q=100$ N. The values of dimensions $d_{\mathcal{H}}$ and $d_{\mathcal{I}}$ are calculated using Equation (8), the values of ${\zeta }_i$ follow from Equation (6), ${\xi }_0$ is the lower cutoff for any fractal with $0<\mu <1$ and the parameter I depends on the cross-section area described by Equation (4).

By applying the boundary conditions ${\upsilon }_3({\chi }_1=0)=0$, ${\varphi }_2({\chi }_1=0)=0$, $M_2({\chi }_1=L)=0$ and $q_3({\chi }_1=L)=q$ in Equation (27), the transverse displacement of the self-similar beam ${\mathcal{F}}_3^{d_{\mathcal{H}}}$ in fractal coordinates is:

$$\begin{array}{c}\hfill {\upsilon }_3^{\mathcal{E}}=\frac{q_3^{\mathcal{E}}{\chi }_1^2}{6EI}(3L-{\chi }_1).\end{array}$$

(31)

The equation obtained by mapping Equation (31) into the fractal continuum ${\mathcal{F}}_{d_{\mathcal{H}}}^3$ is:

$$\begin{array}{c}\hfill {\upsilon }_3^{\mathcal{E}}=\frac{q_3^{\mathcal{E}}{\xi }_0^{2-2{\zeta }_1}{x}_1^{2{\zeta }_1}}{6EI}\left(3{\xi }_0^{1-{\zeta }_1}{L}^{{\zeta }_1}-{\xi }_0^{1-{\zeta }_1}{x}_1^{{\zeta }_1}\right).\end{array}$$

(32)

Four deflections of a cantilever self-similar beam with the values of $\zeta =0.98$, $\zeta =0.91$ and $\zeta =0.83$ are plotted in Figure 4.

Therefore, the slope and the bending moment of beam are determined by substituting Equation (32) into Equation (29), whose behaviors are sketched in Figure 5 and Figure 6, respectively. Note that the shear forces are constant for both the Euclidean and the fractal geometries: (a) ${\zeta }_1=1,Q_{11}=-1$, (b) ${\zeta }_1=0.98,Q_{11}=-1.15$, (c) ${\zeta }_1=0.91,Q_{11}=-3.09$ and (d) ${\zeta }_1=0.83,Q_{11}=-9.56$.

4.2. Discussion of Results Obtained

First of all, in Figure 4, the transversal displacement is a function of the co-dimension (${\zeta }_1$), as the length scale of beam is defined as ${\xi }_0^{1-{\zeta }_1}{L}^{{\zeta }_1}$, where the Hausdorff dimensions of the beam and cross-section play a fundamental role (see Equation (6)). It was found that deflection is shorter for self-similar beams in comparison with Euclidean beams.

Additionally, it was found that the biggest slope corresponds to the Euclidean beam in comparison with the self-similar beams, and the difference between the classical and fractal-continuum solutions increases as the value of ${\zeta }_1$ decreases (see Figure 5).

The bending stiffness $EI$ is affected by the fractal geometry of the beam (see Figure 6). For all cases analysed, the fractal bending stiffness is greater than the Euclidean bending stiffness with the following adjusted trend:

$$\begin{array}{c}\hfill EI\approx 1\times {10}^{7}ln\left({\zeta }_1\right)+2\times {10}^7.\end{array}$$

(33)

Furthermore, the introduced model has an exact analytical solution, and the classical solution is a particular case of the formulation proposed.

5. Conclusions

A generalized formulation of the Euler–Bernoulli bending beam from a fractal medium into a fractal continuum was developed. Displacement, rotation, bending moment and shear force of fractal beams were established by applying the kinematics of fractal continuum deformations. The static bending behaviour of cantilever fractal beams was found using the ${\mathcal{F}}_{d_{\mathcal{H}}}^3$ continuum. The following effects of the fractal parameters on the mechanical properties of self-similar beams were obtained:

i

Parameters $\zeta ,{\xi }_0$, ${\xi }_0^{1-\zeta }{L}^{\zeta }$, $A_{\mathcal{F}}$ and $d_{\mathcal{I}}$ control the stiffness of the fractal beam;

ii

The bending stiffness $EI$ is influenced by the fractal geometry of the beam, specifically, by the cross-section area along its length, so that it increases as its co-dimension decreases according to Equation (33);

iii

The scale effect depends on boundary conditions, fractal mass of the pre-fractals and the length scales of similarity;

iv

The fractal continuum model allows the exact solutions to be obtained, subject to the values of order ${\zeta }_i$;

v

The solution to the classical model is obtained when ${\zeta }_i=1$;

vi

The model can be applied to other tri-dimensional fractals such as Cantor tartan [53,54], Cantor cubes [55] and Vicsek fractals [56];

vii

The model can be extended to describe the structural dynamic behavior of fractal beams, such as free vibration and modal analysis.