Influence of Groundwater Depth on Pile–Soil Mechanical Properties and Fractal Characteristics under Cyclic Loading
Abstract
:1. Introduction
2. Materials and Methods
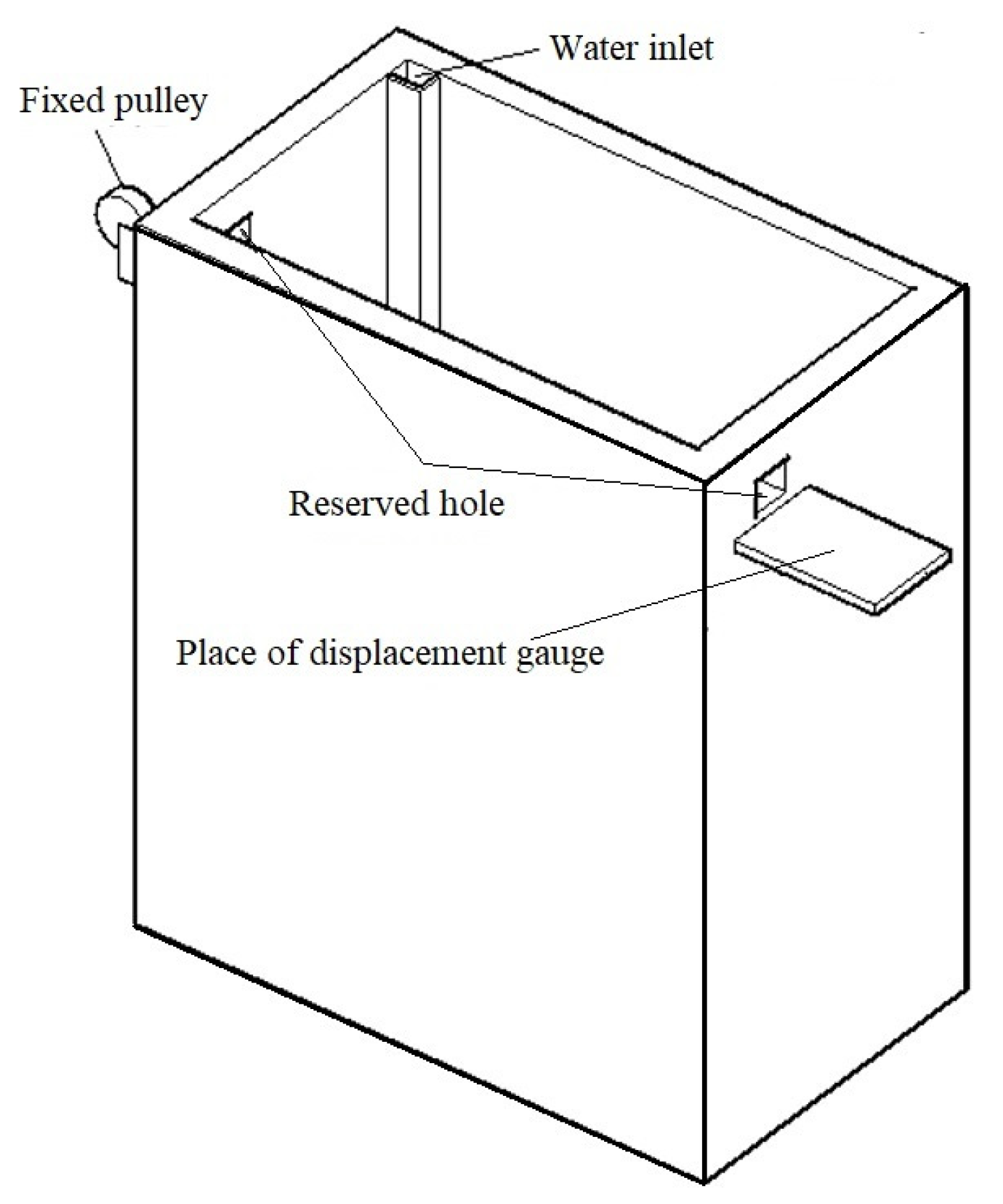
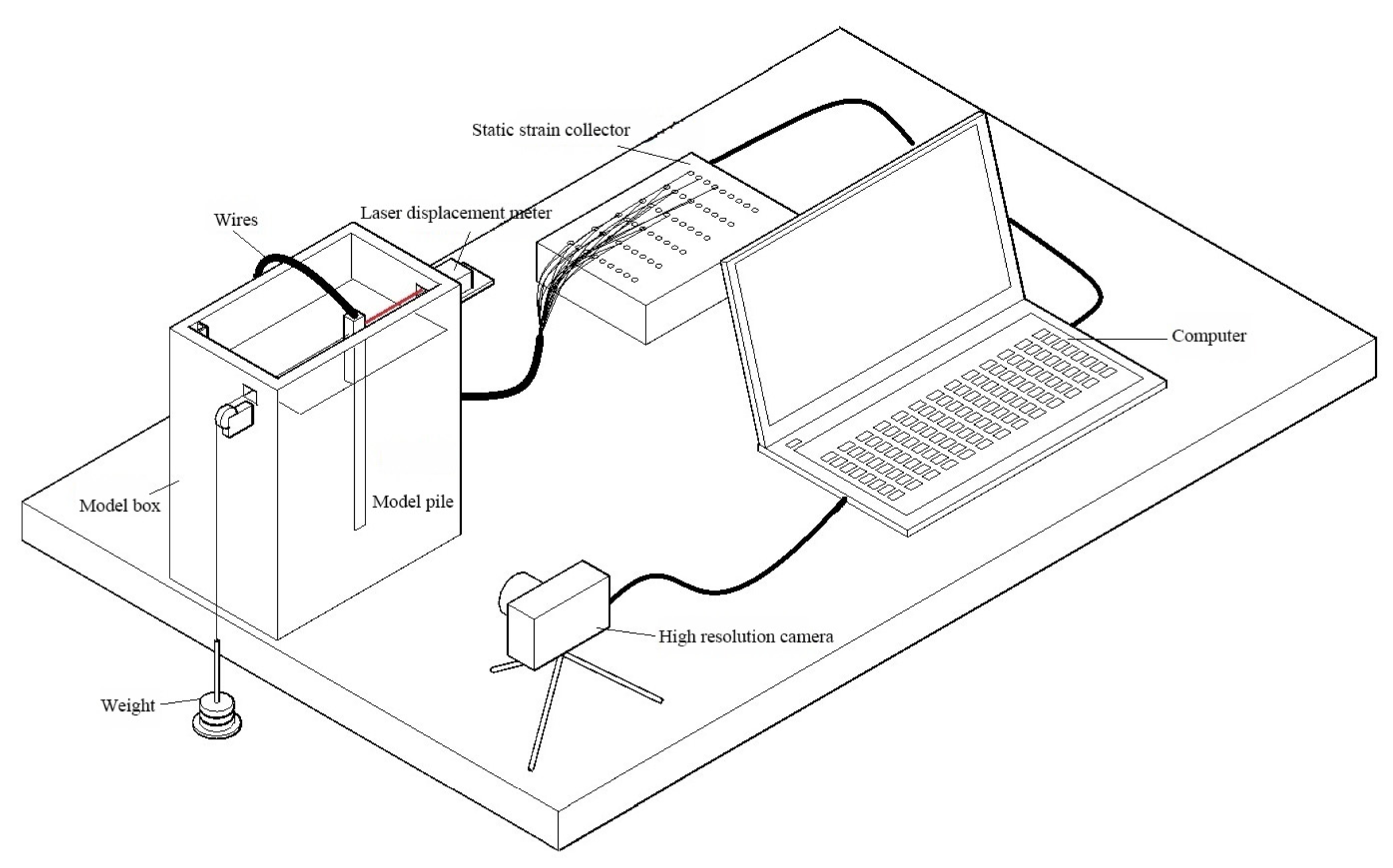
2.1. Model Box
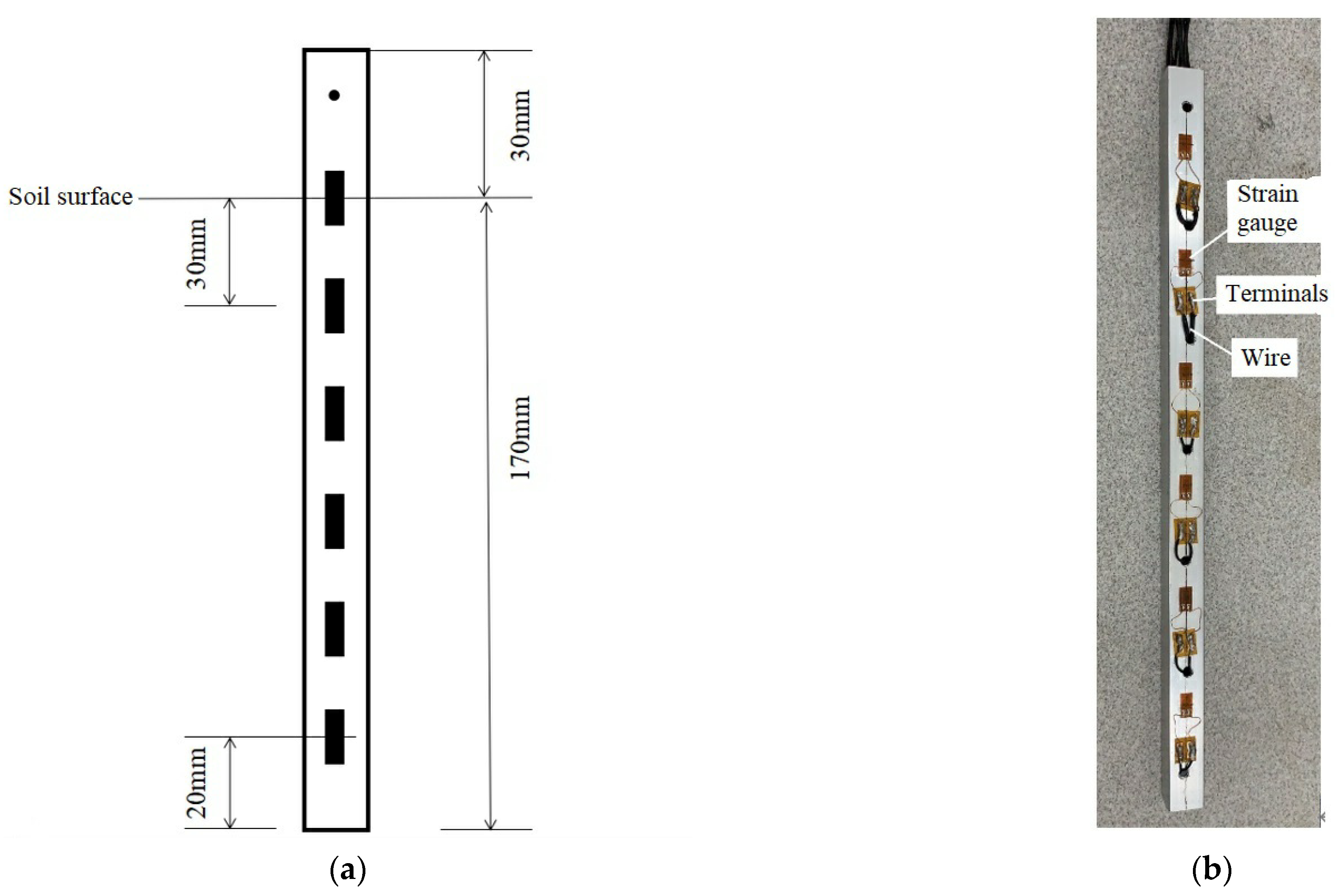
2.2. Test Model Pile
2.3. Test Soil
| Specific Gravity ds (g/cm3) | Minimum Dry Density ρdmin (g/cm3) | Maximum Dry Density ρdmax (g/cm3) | Minimum Void Ratio emin | Maximum Void Ratio emax | Internal Friction Angle (°) |
|---|---|---|---|---|---|
| 2.64 | 1.332 | 1.628 | 0.604 | 0.855 | 36 |

2.4. Acquisition System
2.5. Cyclic Loading Test Plan
2.6. Theoretical Method
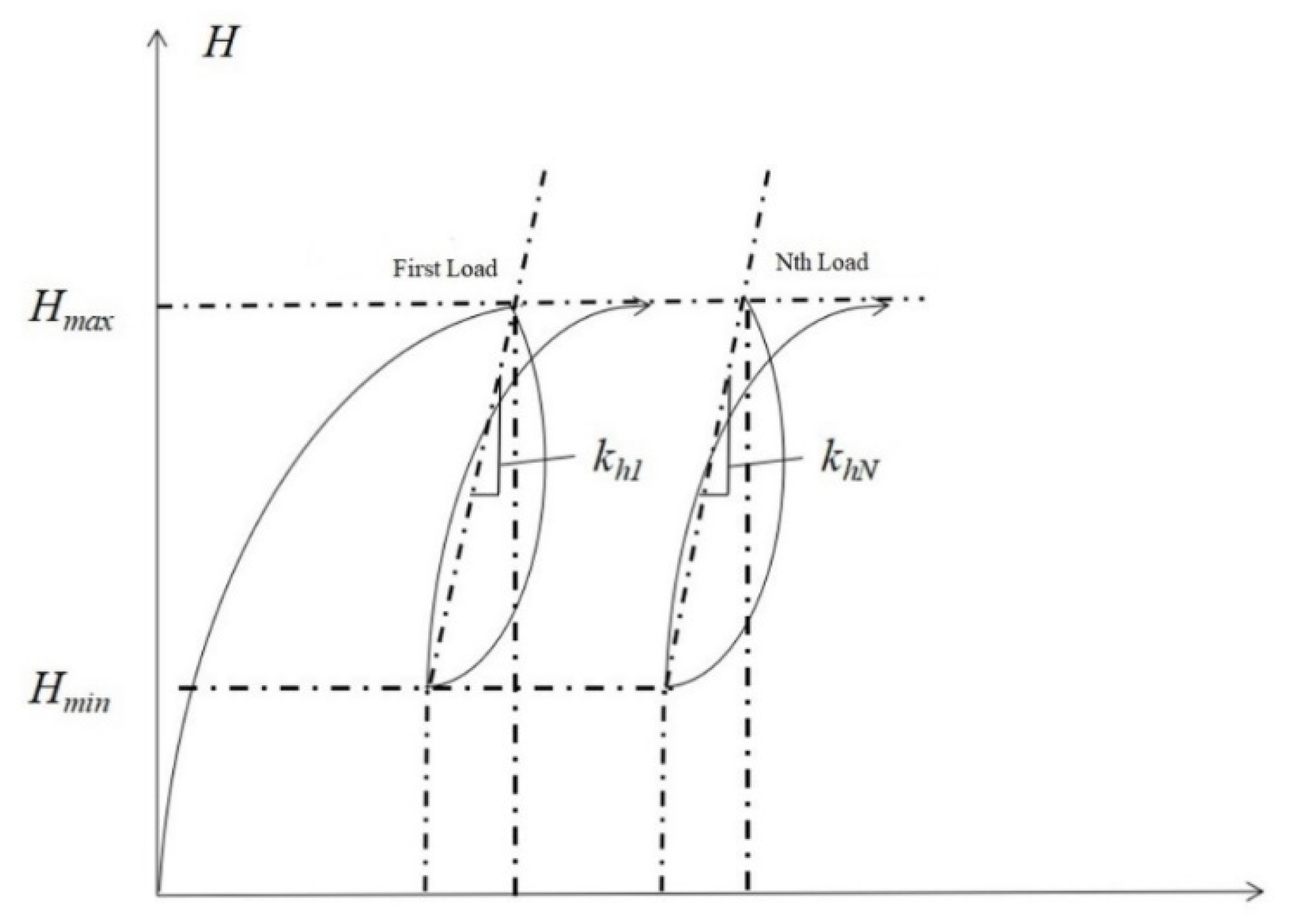
2.6.1. Cyclic Secant Stiffness
2.6.2. Fractal Dimension
3. Results and Discussion
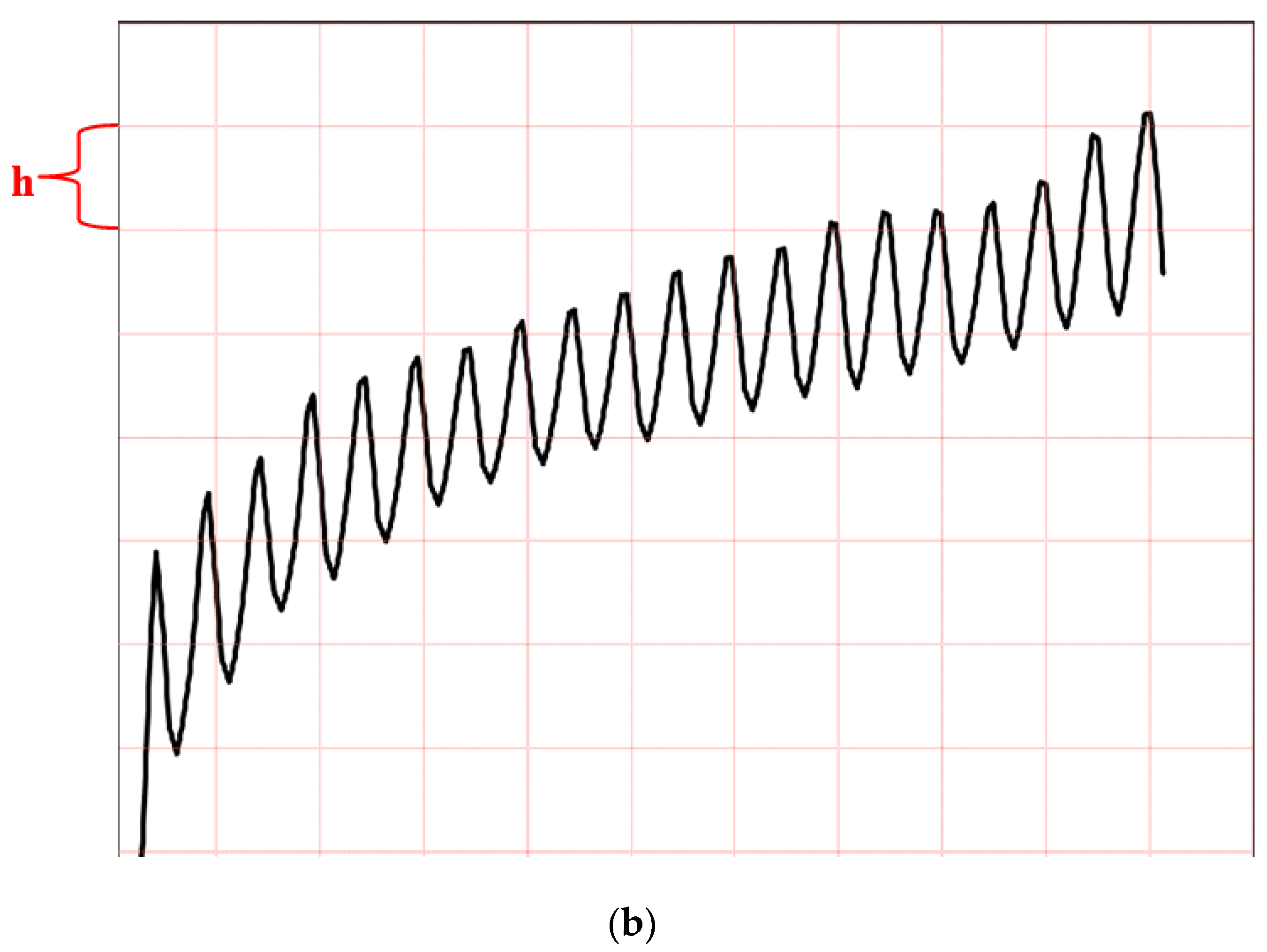
3.1. Analysis of Cumulative Displacement of Pile Top Cyclic Loading
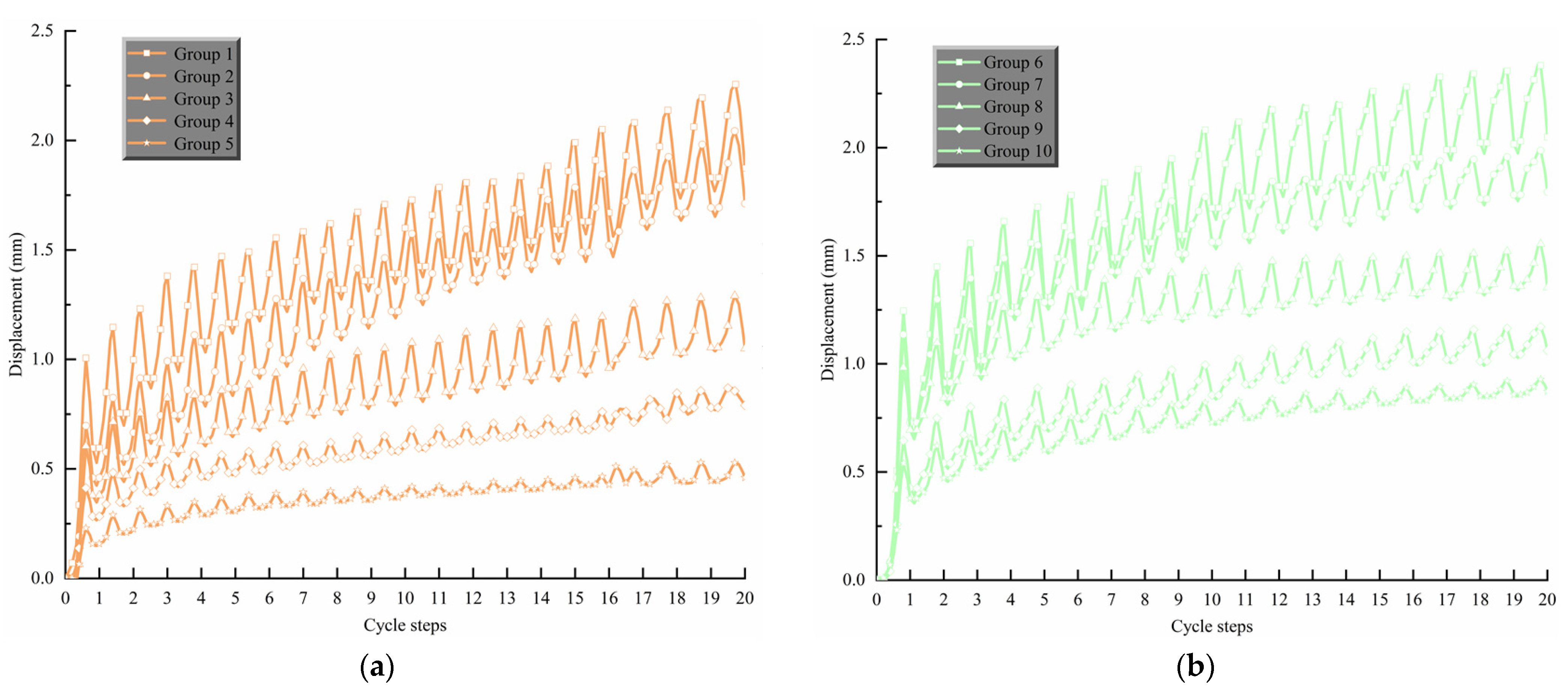
3.2. Analysis of Cyclic Stiffness of Sand around Pile
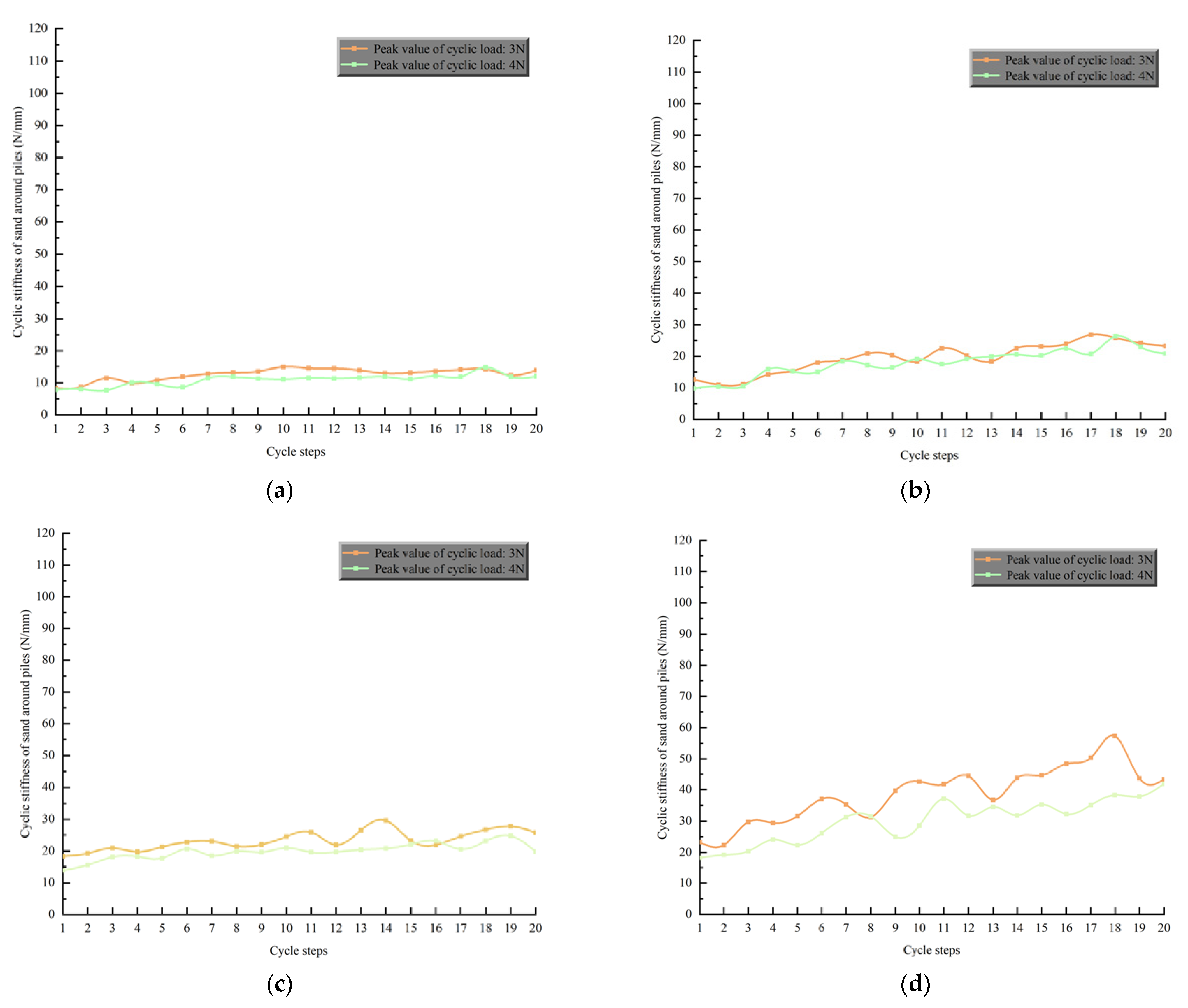
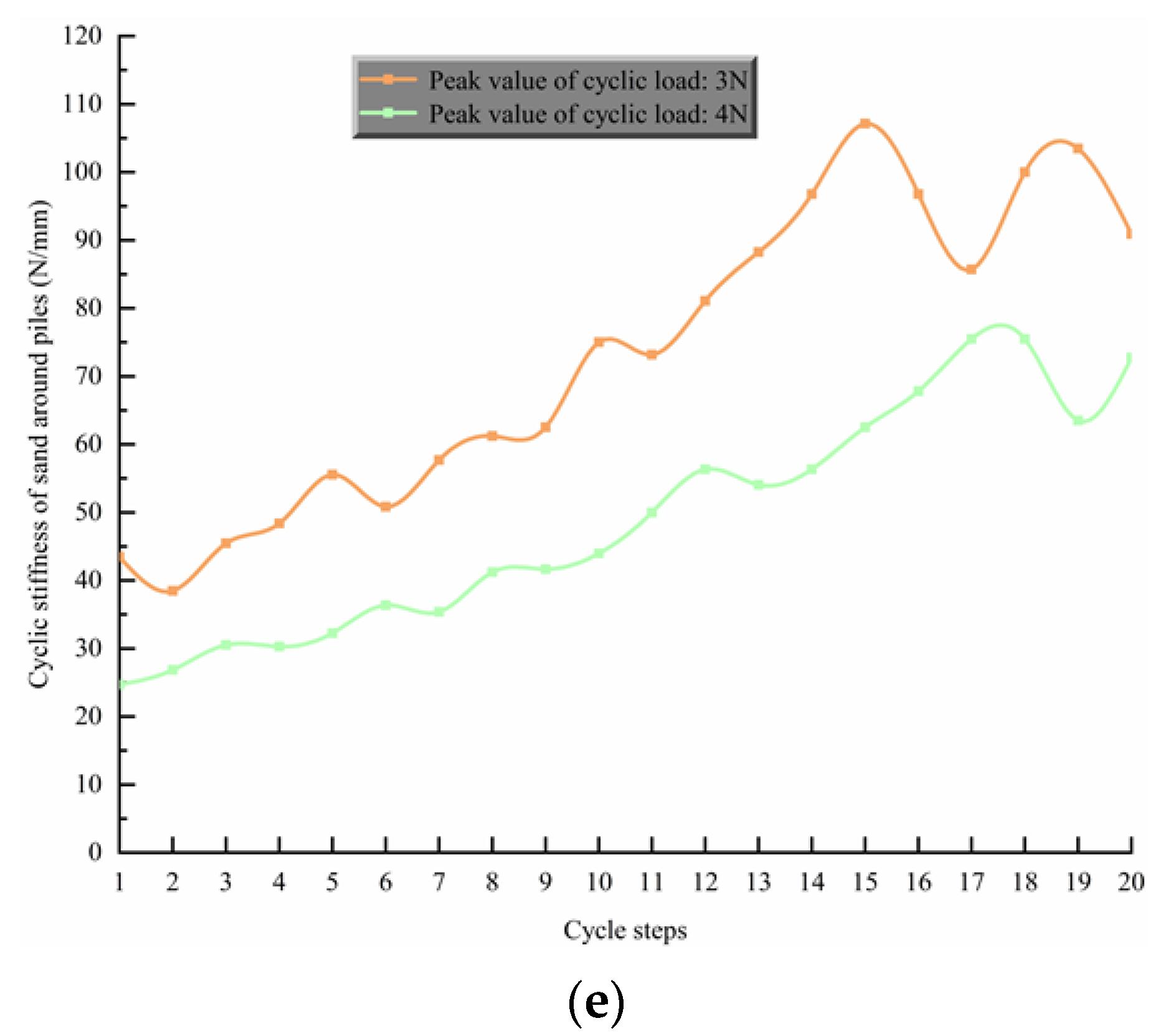
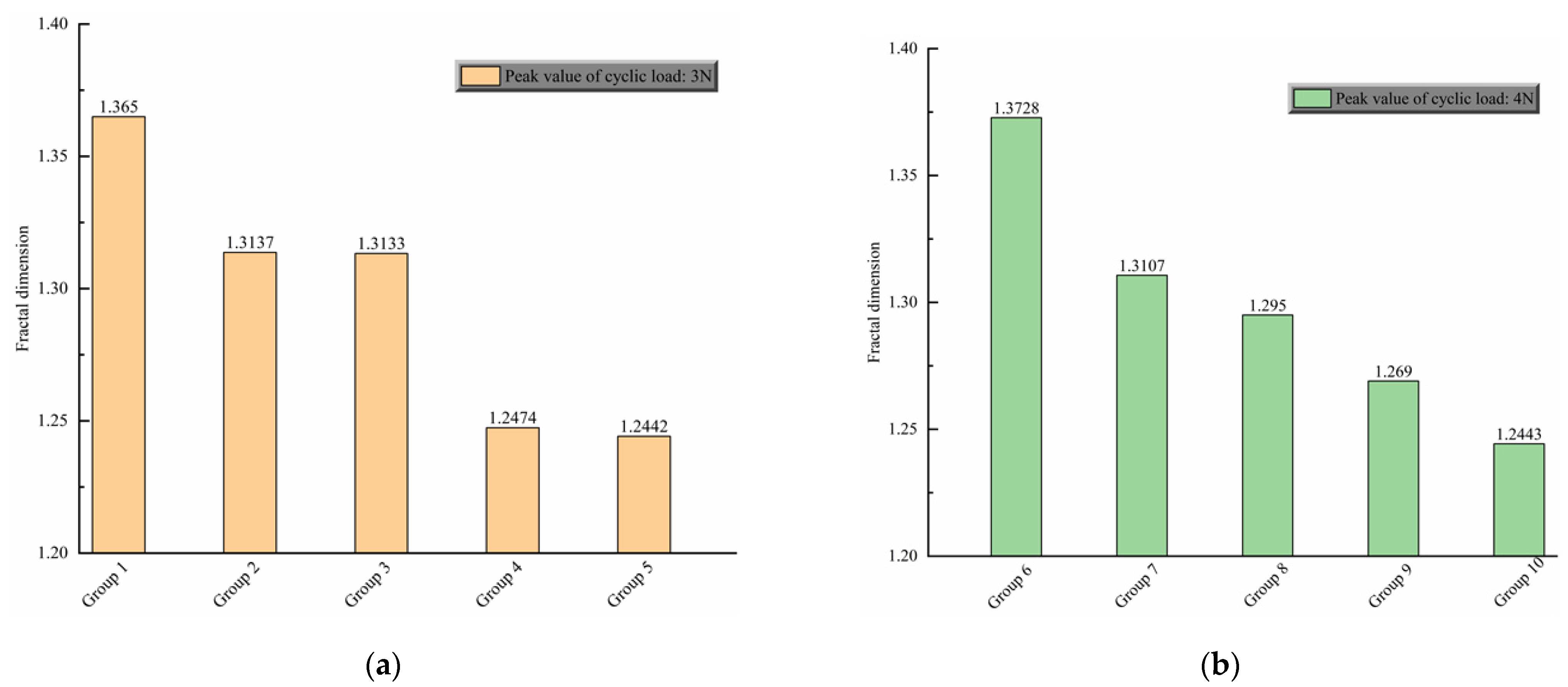
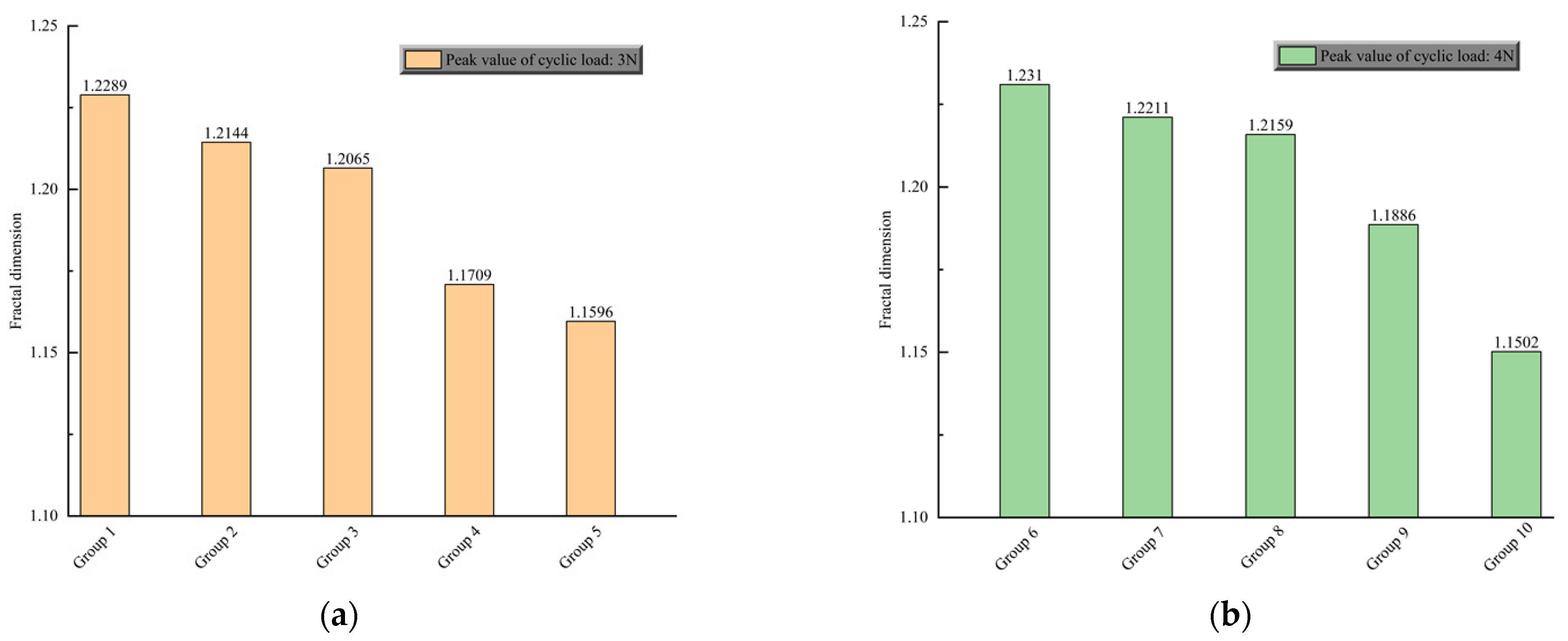
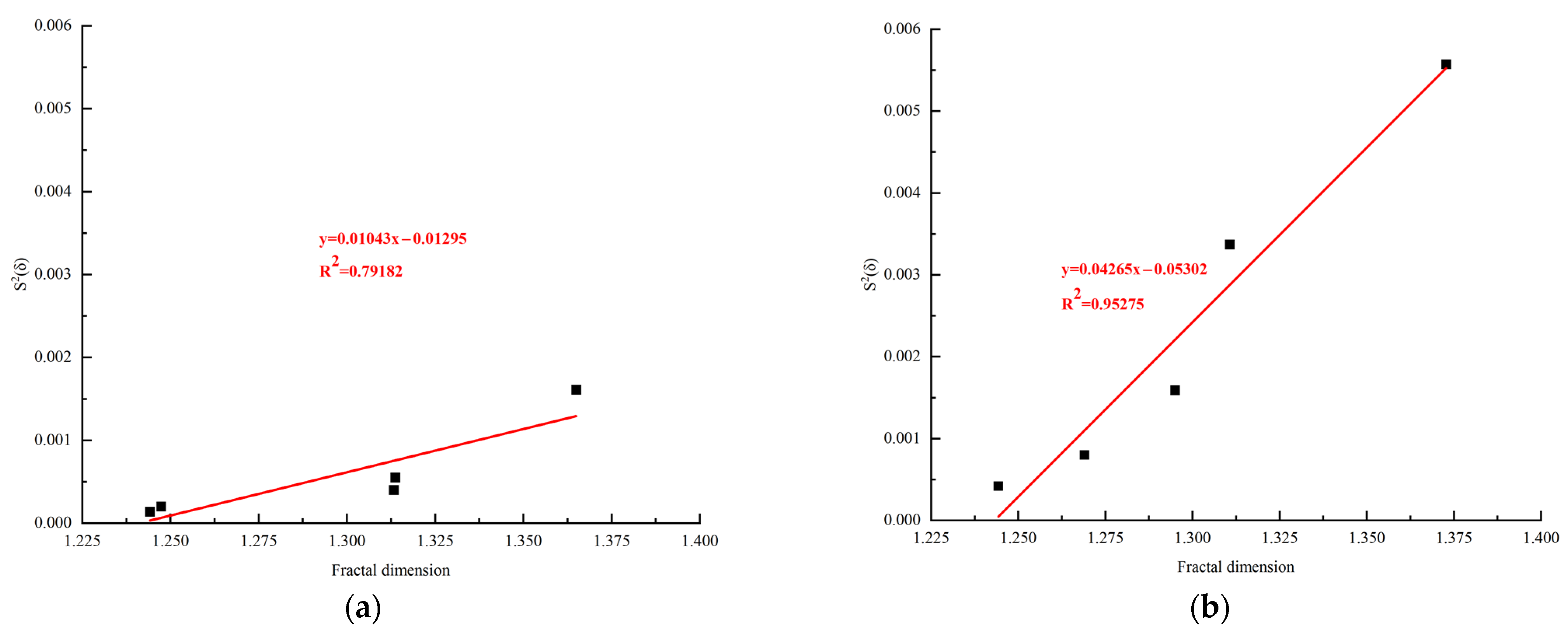
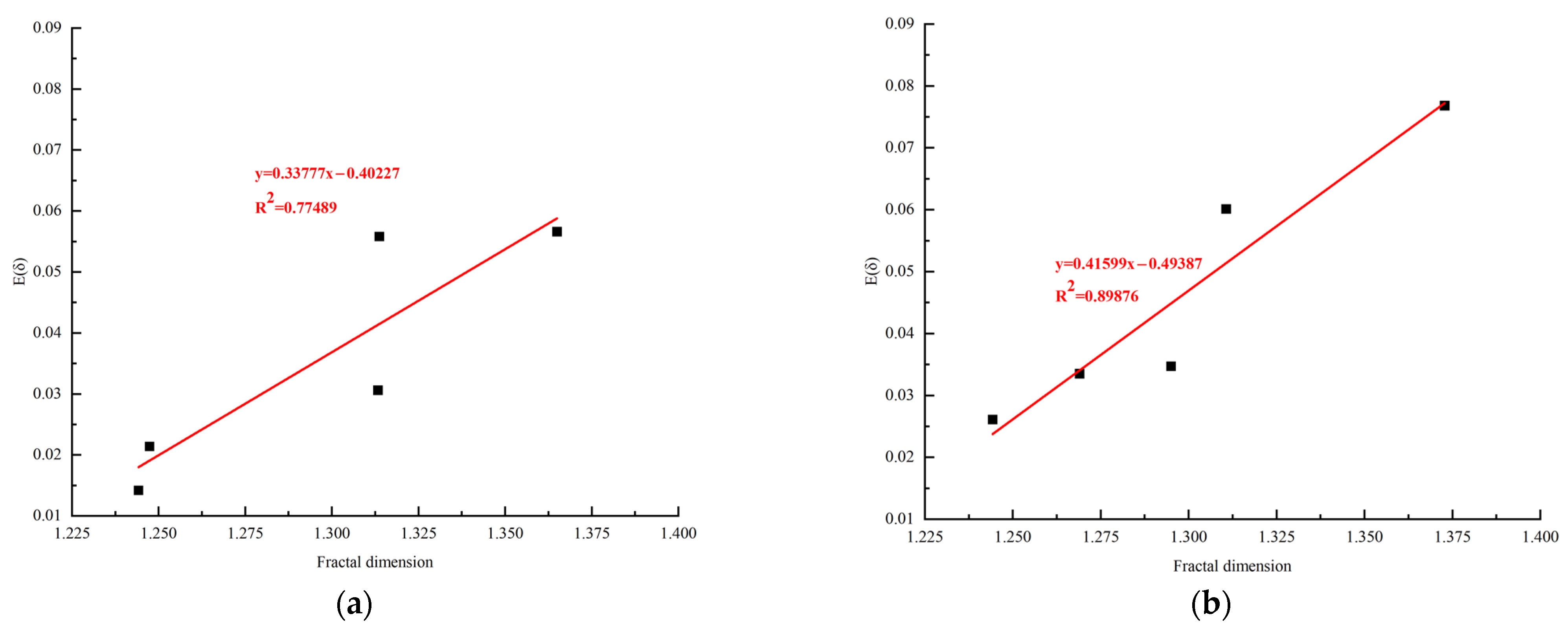
3.3. Analysis of Fractal Dimension
3.4. Comparative Analysis of the Change Law of Soil Displacement Field
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sunday, K.; Brennan, F. A review of offshore wind monopiles structural design achievements and challenges. Ocean Eng. 2021, 235, 109409. [Google Scholar] [CrossRef]
- van der Male, P.; Vergassola, M.; van Dalen, K.N. Decoupled Modelling Approaches for Environmental Interactions with Monopile-Based Offshore Wind Support Structures. Energies 2020, 13, 5195. [Google Scholar] [CrossRef]
- O’Kelly-Lynch, P.; Long, C.; McAuliffe, F.D.; Murphy, J.; Pakrashi, V. Structural design implications of combining a point absorber with a wind turbine monopile for the east and west coast of Ireland. Renew. Sustain. Energy Rev. 2020, 119, 109583. [Google Scholar] [CrossRef]
- Rathod, D.; Krishnanunni, K.T.; Nigitha, D. A Review on Conventional and Innovative Pile System for Offshore Wind Turbines. Geotech. Geol. Eng. 2020, 38, 3385–3402. [Google Scholar] [CrossRef]
- Vicedo, J.S.; Barba, J.G.; Frades, J.L.; Valdecantos, V.N. Scale Tests to Estimate Penetration Force and Stress State of the Silica Sand in Windfarm Foundations. Energies 2021, 14, 5904. [Google Scholar] [CrossRef]
- Schweizer, J.; Antonini, A.; Govoni, L.; Gottardi, G.; Archetti, R.; Supino, E.; Berretta, C.; Casadei, C.; Ozzi, C. Investigating the potential and feasibility of an offshore wind farm in the Northern Adriatic Sea. Appl. Energy 2016, 177, 449–463. [Google Scholar] [CrossRef]
- Wang, X.F.; Zeng, X.W.; Yang, X.; Li, J.L. Feasibility study of offshore wind turbines with hybrid monopile foundation based on centrifuge modeling. Appl. Energy 2018, 209, 127–139. [Google Scholar] [CrossRef]
- Zou, X.J.; Cao, X.; Zhou, C.L.; Zhou, M.; Zhang, X.H. Experimental study on the bearing capacity of large-diameter monopile in sand under water flow condition. Ocean Eng. 2021, 224, 108708. [Google Scholar] [CrossRef]
- McAdam, R.A.; Byrne, B.W.; Houlsby, G.T.; Beuckelaers, W.J.A.P.; Burd, H.J.; Gavin, K.G.; Igoe, D.J.P.; Jardine, R.J.; Martin, C.M.; Wood, A.M.; et al. Monotonic laterally loaded pile testing in a dense marine sand at Dunkirk. Geotechnique 2020, 70, 986–998. [Google Scholar] [CrossRef]
- Wang, J.Y.; Sun, G.D.; Chen, G.S.; Yang, X. Finite element analyses of improved lateral performance of monopile when combined with bucket foundation for offshore wind turbines. Appl. Ocean Res. 2021, 111, 102647. [Google Scholar] [CrossRef]
- Li, J.L.; Zhang, Y.; Wang, X.F.; Sun, Z.Z. Assessment of offshore wind turbine with an innovative monopile foundation under lateral loading. Ocean Eng. 2021, 237, 109583. [Google Scholar] [CrossRef]
- Li, F.; Zhu, Z.Y.; Tian, P.S.; Hu, D.; Li, Y.F. The behavior of monopile embedded in sand under scour and cyclic loading conditions. Mar. Georesour. Geotechnol. 2022, 40, 52–63. [Google Scholar] [CrossRef]
- Que, X.C.; Zhu, Z.D.; Niu, Z.H.; Lu, W.N. Estimating the strength and deformation of columnar jointed rock mass based on physical model test. Bull. Eng. Geol. Environ. 2021, 80, 1557–1570. [Google Scholar] [CrossRef]
- Shao, J.L.; Zhang, Q.; Wu, X.T.; Lei, Y.; Wu, X.A.; Wang, Z.Y. Investigation on the Water Flow Evolution in a Filled Fracture under Seepage-Induced Erosion. Water 2020, 12, 3188. [Google Scholar] [CrossRef]
- Bai, B.; Zhou, R.; Cai, G.Q.; Hu, W.; Yang, G.C. Coupled thermo-hydro-mechanical mechanism in view of the soil particle rearrangement of granular thermodynamics. Comput. Geotech. 2021, 137, 104272. [Google Scholar] [CrossRef]
- Bai, B.; Nie, Q.K.; Zhang, Y.K.; Wang, X.L.; Hu, W. Cotransport of heavy metals and SiO2 particles at different temperatures by seepage. J. Hydrol. 2021, 597, 125771. [Google Scholar] [CrossRef]
- Yang, B.B.; Liu, J.W.; Zhao, X.M.; Zheng, S. Evaporation and cracked soda soil improved by fly ash from recycled materials. Land Degrad. Dev. 2021, 32, 2823–2832. [Google Scholar] [CrossRef]
- Yuan, B.X.; Li, Z.H.; Su, Z.L.; Luo, Q.Z.; Chen, M.J.; Zhao, Z.Q. Sensitivity of Multistage Fill Slope Based on Finite Element Model. Adv. Civ. Eng. 2021, 2021, 6622936. [Google Scholar] [CrossRef]
- Wu, Y.; Cui, J.; Huang, J.S.; Zhang, W.; Yoshimoto, N.; Wen, L.W. Correlation of Critical State Strength Properties with Particle Shape and Surface Fractal Dimension of Clinker Ash. Int. J. Geomech. 2021, 21. [Google Scholar] [CrossRef]
- Shen, J.H.; Hu, M.J.; Wang, X.; Zhang, C.Y.; Xu, D.S. SWCC of Calcareous Silty Sand Under Different Fines Contents and dry Densities. Front. Environ. Sci. 2021, 9, 303. [Google Scholar] [CrossRef]
- Liu, M.M.; Yang, M.; Wang, H.J. Bearing behavior of wide-shallow bucket foundation for offshore wind turbines in drained silty sand. Ocean Eng. 2014, 82, 169–179. [Google Scholar] [CrossRef]
- Liu, Z.Y.; Xue, J.F. The deformation behaviour of an anisotropically consolidated kaolin clay under lateral cyclic loading. Mar. Georesour. Geotechnol. 2021. [Google Scholar] [CrossRef]
- Maleksaeedi, E.; Nuth, M. Evaluation of capillary water retention effects on the development of the suction stress characteristic curve. Can. Geotech. J. 2020, 57, 1439–1452. [Google Scholar] [CrossRef]
- Yang, B.; Su, Y.; He, N.; Zhang, B.; Zhou, X.S.; Zhang, Y. Experimental study on the stable morphology and self-attraction effect of subaqueous barchan dunes. Adv. Powder Technol. 2020, 31, 1032–1039. [Google Scholar] [CrossRef]
- Zhang, C.; Lu, N. Unified Effective Stress Equation for Soil. J. Eng. Mech. 2020, 146, 04019135. [Google Scholar] [CrossRef]
- Guo, Y.C.; Ye, Y.Y.; Guan-Lin; Lv, J.F.; Bai, Y.L.; Zeng, J.J. Effective usage of high strength steel tubes: Axial compressive behavior of hybrid FRP-concrete-steel solid columns. Thin Walled Struct. 2020, 154, 106796. [Google Scholar] [CrossRef]
- Lozano-Minguez, E.; Kolios, A.J.; Brennan, F.P. Multi-criteria assessment of offshore wind turbine support structures. Renew. Energy 2011, 36, 2831–2837. [Google Scholar] [CrossRef] [Green Version]
- Liu, F.; Chen, G.X.; Li, L.J.; Guo, Y.C. Study of impact performance of rubber reinforced concrete. Constr. Build. Mater. 2012, 36, 604–616. [Google Scholar] [CrossRef]
- Liu, F.; Zheng, W.H.; Li, L.J.; Feng, W.X.; Ning, G.F. Mechanical and fatigue performance of rubber concrete. Constr. Build. Mater. 2013, 47, 711–719. [Google Scholar] [CrossRef]
- Damgaard, M.; Bayat, M.; Andersen, L.V.; Ibsen, L.B. Assessment of the dynamic behaviour of saturated soil subjected to cyclic loading from offshore monopile wind turbine foundations. Comput. Geotech. 2014, 61, 116–126. [Google Scholar] [CrossRef]
- Devolder, B.; Rauwoens, P.; Troch, P. Application of a buoyancy-modified k-omega SST turbulence model to simulate wave run-up around a monopile subjected to regular waves using OpenFOAM (R). Coast. Eng. 2017, 125, 81–94. [Google Scholar] [CrossRef] [Green Version]
- Guo, Y.C.; Xie, J.H.; Zhao, J.B.; Zuo, K.X. Utilization of unprocessed steel slag as fine aggregate in normal- and high-strength concrete. Constr. Build. Mater. 2019, 204, 41–49. [Google Scholar] [CrossRef]
- Zhang, X.Y.; Tang, L.; Ling, X.Z.; Chan, A.H.C.; Lu, J.C. Using peak ground velocity to characterize the response of soil-pile system in liquefying ground. Eng. Geol. 2018, 240, 62–73. [Google Scholar] [CrossRef]
- Cao, X.L.; Dai, G.L.; Gong, W.M.; Zhou, F.X.; Xu, J. Resistance of saturated soil to a laterally vibrating pile. Soil Dyn. Earthq. Eng. 2021, 141, 106496. [Google Scholar] [CrossRef]
- Xie, J. Impedance of Inner Saturated Soil to Horizontally Vibrating Large-Diameter Pipe Piles. Shock Vib. 2021, 2021, 1845109. [Google Scholar] [CrossRef]
- Ding, X.M.; Qu, L.M.; Yang, J.C.; Wang, C.L. Experimental study on the pile group-soil vibration induced by railway traffic under the inclined bedrock condition. Acta Geotech. 2020, 15, 3613–3620. [Google Scholar] [CrossRef]
- Ren, L.W.; Yang, Q.W.; Kong, G.Q.; Dun, Z.L.; Wang, X.Y. Model Tests on Y-Shaped Piles under Compressive and Lateral Loading in Saturated Sand. Geofluids 2021, 2021, 6978602. [Google Scholar] [CrossRef]
- Fattah, M.Y.; Zabar, B.S.; Mustafa, F.S. Effect of saturation on response of a single pile embedded in saturated sandy soil to vertical vibration. Eur. J. Environ. Civ. Eng. 2020, 24, 381–400. [Google Scholar] [CrossRef]
- Li, J.H.; Zhang, B.; Shen, C.; Fu, X.L.; Li, W.C. Experimental Study on Local Scour Depth around Monopile Foundation in Combined Waves and Current. Sustainability 2021, 13, 13614. [Google Scholar] [CrossRef]
- Li, Q.; Askarinejad, A.; Gavin, K. Impact of scour on lateral resistance of wind turbine monopiles: An experimental study. Can. Geotech. J. 2021, 58, 1770–1782. [Google Scholar] [CrossRef]
- Cui, C.Y.; Meng, K.; Xu, C.S.; Liang, Z.M.; Li, H.J.; Pei, H.F. Analytical solution for longitudinal vibration of a floating pile in saturated porous media based on a fictitious saturated soil pile model. Comput. Geotech. 2021, 131, 103942. [Google Scholar] [CrossRef]
- Achmus, M.; Kuo, Y.S.; Abdel-Rahman, K. Behavior of monopile foundations under cyclic lateral load. Comput. Geotech. 2009, 36, 725–735. [Google Scholar] [CrossRef]
- Lombardi, D.; Bhattacharya, S.; Wood, D.M. Dynamic soil-structure interaction of monopile supported wind turbines in cohesive soil. Soil Dyn. Earthq. Eng. 2013, 49, 165–180. [Google Scholar] [CrossRef]
- Arshad, M.; O’Kelly, B.C. Analysis and Design of Monopile Foundations for Offshore Wind-Turbine Structures. Mar. Georesour. Geotechnol. 2016, 34, 503–525. [Google Scholar] [CrossRef]
- Feng, W.H.; Liu, F.; Yang, F.; Li, L.J.; Jing, L. Experimental study on dynamic split tensile properties of rubber concrete. Constr. Build. Mater. 2018, 165, 675–687. [Google Scholar] [CrossRef]
- Luo, R.P.; Yang, M.; Li, W.C. Numerical study of diameter effect on accumulated deformation of laterally loaded monopiles in sand. Eur. J. Environ. Civ. Eng. 2020, 24, 2440–2452. [Google Scholar] [CrossRef]
- Malakshah, R.R.; Moradi, M.; Ghalandarzadeh, A. Centrifuge Modelling of Monopiles in Calcareous Sand Subjected to Cyclic Lateral Loading. Int. J. Civ. Eng. 2022, 20, 195–206. [Google Scholar] [CrossRef]
- Namazi, H. Complexity-based analysis of the correlation between stride interval variability and muscle reaction at different walking speeds. Biomed. Signal. Process. 2021, 69, 102956. [Google Scholar] [CrossRef]
- Phinyomark, A.; Larracy, R.; Scheme, E. Fractal Analysis of Human Gait Variability via Stride Interval Time Series. Front. Physiol. 2020, 11, 333. [Google Scholar] [CrossRef]
- Tabares-Ospina, H.A.; Angulo, F.; Osorio, M. New Method to Calculate the Energy and Fractal Dimension of the Daily Electrical Load. Fractals 2020, 28, 2050135. [Google Scholar] [CrossRef]
- Yan, B.W.; Chan, P.W.; Li, Q.S.; He, Y.C.; Shu, Z.R. Characterising the fractal dimension of wind speed time series under different terrain conditions. J. Wind Eng. Ind. Aerodyn. 2020, 201, 104165. [Google Scholar] [CrossRef]
- Shu, Z.R.; Chan, P.W.; Li, Q.S.; He, Y.C.; Yan, B.W. Quantitative assessment of offshore wind speed variability using fractal analysis. Wind Struct. 2020, 31, 363–371. [Google Scholar] [CrossRef]
- Yang, B.B.; Liu, Y. Application of Fractals to Evaluate Fractures of Rock Due to Mining. Fractal Fract. 2022, 6, 96. [Google Scholar] [CrossRef]
- Yang, B.B.; Du, S.T.; Zhao, X.M.; Tang, D.Q.; Yang, C.D. Decision Making of Curriculum Attainment Degree for Engineering Geology Based on Fuzzy Set Theory. Adv. Civ. Eng. 2021, 2021, 1743778. [Google Scholar] [CrossRef]
- Wang, L.; Luo, R.Y.; Zhang, W.; Jin, M.M.; Tang, S.W. Effects of Fineness and Content of Phosphorus Slag on Cement Hydration, Permeability, Pore Structure and Fractal Dimension of Concrete. Fractals 2021, 29, 2140004. [Google Scholar] [CrossRef]
- Xiao, J.; Qu, W.J.; Jiang, H.B.; Li, L.; Huang, J.; Chen, L. Fractal Characterization and Mechanical Behavior of Pile-Soil Interface Subjected to Sulfuric Acid. Fractals 2021, 29, 2140010. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, H.; Huang, M.H.; Yin, H.B.; Jiang, K.; Xiao, K.T.; Tang, S.W. Influence of Different Alkali Sulfates on the Shrinkage, Hydration, Pore Structure, Fractal Dimension and Microstructure of Low-Heat Portland Cement, Medium-Heat Portland Cement and Ordinary Portland Cement. Fractal Fract. 2021, 5, 79. [Google Scholar] [CrossRef]
- Wang, L.; Lu, X.; Liu, L.S.; Xiao, J.; Zhang, G.; Guo, F.X.; Li, L. Influence of MgO on the Hydration and Shrinkage Behavior of Low Heat Portland Cement-Based Materials via Pore Structural and Fractal Analysis. Fractal Fract. 2022, 6, 40. [Google Scholar] [CrossRef]
- Wang, L.; Guo, F.X.; Yang, H.M.; Wang, Y.; Tang, S.W. Comparison of Fly Ash, Pva Fiber, Mgo and Shrinkage-Reducing Admixture on the Frost Resistance of Face Slab Concrete Via Pore Structural and Fractal Analysis. Fractals 2021, 29, 2140002. [Google Scholar] [CrossRef]
- Duan, H.Q.; Zhang, S. Fractal Characteristics of Coal Specimens’ Surface Cracks in Triaxial Conventional Compression and Cyclic Loading Tests. Geotech. Geol. Eng. 2020, 38, 19–29. [Google Scholar] [CrossRef]
- Kim, N.S.; Lee, J.H.; Chang, S.P. Equivalent multi-phase similitude law for pseudodynamic test on small scale reinforced concrete models. Eng. Struct. 2009, 31, 834–846. [Google Scholar] [CrossRef]
- Stanier, S.A.; Blaber, J.; Take, W.A.; White, D.J. Improved image-based deformation measurement for geotechnical applications. Can. Geotech. J. 2016, 53, 727–739. [Google Scholar] [CrossRef]
- White, D.J.; Take, W.A.; Bolton, M.D. Soil deformation measurement using particle image velocimetry (PIV) and photogrammetry. Geotechnique 2003, 53, 619–631. [Google Scholar] [CrossRef]
- Gudehus, G.; Nubel, K. Evolution of shear bands in sand. Geotechnique 2004, 54, 187–201. [Google Scholar] [CrossRef]
- Georgescu, M.R.; Meslem, A.; Nastase, I.; Sandu, M. Numerical and experimental study of the International Space Station crew quarters ventilation. J. Build. Eng. 2021, 41, 102714. [Google Scholar] [CrossRef]
- Yuan, B.X.; Sun, M.; Xiong, L.; Luo, Q.Z.; Pradhan, S.P.; Li, H.Z. Investigation of 3D deformation of transparent soil around a laterally loaded pile based on a hydraulic gradient model test. J. Build. Eng. 2020, 28, 101024. [Google Scholar] [CrossRef]
- Zhang, X.; Huang, M.S.; Hu, Z.P. Model tests on cumulative deformation characteristics of a single pile subjected to lateral cyclic loading in sand. Rock Soil Mech. 2019, 40, 933–941. [Google Scholar] [CrossRef]
- Prabakar, J.; Sridhar, R.S. Effect of random inclusion of sisal fibre on strength behaviour of soil. Constr. Build. Mater. 2002, 16, 123–131. [Google Scholar] [CrossRef]
- Lu, N.; Zhang, C. Soil Sorptive Potential: Concept, Theory, and Verification. J. Geotech. Geoenviron. 2019, 145, 04019006. [Google Scholar] [CrossRef]
- Wang, H.; Wang, L.Z.; Hong, Y.; Masin, D.; Li, W.; He, B.; Pan, H.L. Centrifuge testing on monotonic and cyclic lateral behavior of large-diameter slender piles in sand. Ocean Eng. 2021, 226, 108299. [Google Scholar] [CrossRef]
- Yuan, B.X.; Sun, M.; Wang, Y.X.; Zhai, L.H.; Luo, Q.Z.; Zhang, X.Q. Full 3D Displacement Measuring System for 3D Displacement Field of Soil around a Laterally Loaded Pile in Transparent Soil. Int. J. Geomech. 2019, 19, 04019028. [Google Scholar] [CrossRef]
- Yuan, B.X.; Xiong, L.; Zhai, L.H.; Zhou, Y.F.; Chen, G.F.; Gong, X.; Zhang, W. Transparent Synthetic Soil and Its Application in Modeling of Soil-Structure Interaction Using Optical System. Front. Earth Sci. 2019, 7, 276. [Google Scholar] [CrossRef]


| Parameter | Scale (Model/Prototype) |
|---|---|
| Cross-sectional area | 1/n2 |
| Pile length | 1/n |
| Bending stiffness | 1/n4 |
| Pile Length | Width of Pile Section | Pile Thickness | Moment of Inertia I | Bending Stiffness |
|---|---|---|---|---|
| L | D | d | (mm4) | EI |
| (mm) | (mm) | (mm) | (N·m2) | |
| 200 | 10 | 1 | 492 | 29.5 |
| Loading Conditions | Group | Hmax = 3 N Hmin = 0 N | Group | Hmax = 4 N Hmin = 0 N |
|---|---|---|---|---|
| Groundwater depth conditions | 1 | Saturated sand | 6 | Saturated sand |
| 2 | Dry sand | 7 | Dry sand | |
| 3 | Groundwater depth 140 mm | 8 | Groundwater depth 140 mm | |
| 4 | Groundwater depth 90 mm | 9 | Groundwater depth 90 mm | |
| 5 | Groundwater depth 40 mm | 10 | Groundwater depth 40 mm |
| Maximum and Minimum Values of Cyclic Loading | Group | y1min (mm) | y20min (mm) | E(δ) (mm) | S2(δ) | COV |
|---|---|---|---|---|---|---|
| Hmax = 3 N Hmin = 0 N | 1 | 0.595 | 1.67 | 0.0566 | 16.1 × 10−4 | 1.29 |
| 2 | 0.46 | 1.52 | 0.0558 | 5.5 × 10−4 | 1.51 | |
| 3 | 0.379 | 0.961 | 0.0306 | 4 × 10−4 | 0.754 | |
| 4 | 0.284 | 0.691 | 0.0214 | 2 × 10−4 | 0.482 | |
| 5 | 0.159 | 0.429 | 0.0142 | 1.4 × 10−4 | 0.313 | |
| Hmax = 4 N Hmin = 0 N | 6 | 0.735 | 2.195 | 0.0768 | 55.7 × 10−4 | 2.11 |
| 7 | 0.728 | 1.87 | 0.0601 | 33.7 × 10−4 | 1.60 | |
| 8 | 0.694 | 1.353 | 0.0347 | 15.9 × 10−4 | 0.904 | |
| 9 | 0.426 | 1.062 | 0.0335 | 8 × 10−4 | 0.977 | |
| 10 | 0.378 | 0.873 | 0.0261 | 4.2 × 10−4 | 0.753 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuan, B.; Li, Z.; Chen, W.; Zhao, J.; Lv, J.; Song, J.; Cao, X. Influence of Groundwater Depth on Pile–Soil Mechanical Properties and Fractal Characteristics under Cyclic Loading. Fractal Fract. 2022, 6, 198. https://doi.org/10.3390/fractalfract6040198
Yuan B, Li Z, Chen W, Zhao J, Lv J, Song J, Cao X. Influence of Groundwater Depth on Pile–Soil Mechanical Properties and Fractal Characteristics under Cyclic Loading. Fractal and Fractional. 2022; 6(4):198. https://doi.org/10.3390/fractalfract6040198
Chicago/Turabian StyleYuan, Bingxiang, Zhijie Li, Weijie Chen, Jin Zhao, Jianbing Lv, Jie Song, and Xudong Cao. 2022. "Influence of Groundwater Depth on Pile–Soil Mechanical Properties and Fractal Characteristics under Cyclic Loading" Fractal and Fractional 6, no. 4: 198. https://doi.org/10.3390/fractalfract6040198
APA StyleYuan, B., Li, Z., Chen, W., Zhao, J., Lv, J., Song, J., & Cao, X. (2022). Influence of Groundwater Depth on Pile–Soil Mechanical Properties and Fractal Characteristics under Cyclic Loading. Fractal and Fractional, 6(4), 198. https://doi.org/10.3390/fractalfract6040198







