A Numerical Study of the Fractional Order Dynamical Nonlinear Susceptible Infected and Quarantine Differential Model Using the Stochastic Numerical Approach

Abstract

The theme of this study is to present the impacts and importance of the fractional order derivatives of the susceptible, infected and quarantine (SIQ) model based on the coronavirus with the lockdown effects. The purpose of these investigations is to achieve more accuracy with the use of fractional derivatives in the SIQ model. The integer, nonlinear mathematical SIQ system with the lockdown effects is also provided in this study. The lockdown effects are categorized into the dynamics of the susceptible, infective and quarantine, generally known as SIQ mathematical system. The fractional order SIQ mathematical system has never been presented before, nor solved by using the strength of the stochastic solvers. The stochastic solvers based on the Levenberg-Marquardt backpropagation scheme (LMBS) along with the neural networks (NNs), i.e., LMBS-NNs have been implemented to solve the fractional order SIQ mathematical system. Three cases using different values of the fractional order have been provided to solve the fractional order SIQ mathematical model. The data to present the numerical solutions of the fractional order SIQ mathematical model is selected as 80% for training and 10% for both testing and validation. For the correctness of the LMBS-NNs, the obtained numerical results have been compared with the reference solutions through the Adams–Bashforth–Moulton based numerical solver. In order to authenticate the competence, consistency, validity, capability and exactness of the LMB-NNs, the numerical performances using the state transitions (STs), regression, correlation, mean square error (MSE) and error histograms (EHs) are also provided.

1. Introduction

There are a number of dangerous and transmitted diseases like dengue, HIV and Ebola [1,2,3]. The coronavirus is a transmitted disease and has played a significant role in human lives for the last two years. It badly affected the economies, industries, sports, social activities, education sectors and each part of life [4,5]. The coronavirus disease spread quickly, and a number of casualties happened in a short time. The basic role of the coronavirus spreading is due to travel or transportations of individuals from defective countries to different areas [6,7]. The vaccination process was started as a hope to control this series viral disease. It is stated in the literature that the individual’s migration has a vital role in the spreading of the infection. It has also been noted that immigration is not only an issue of the infections, but the other reasons may also affect the spread of the virus [8].

A number of the approaches have been used to solve the mathematical form of the coronavirus along with different features. Rhodes et al. [9] proposed the mathematical ODEs for the communal distresses due to coronavirus. Benvenuto et al. [10] implemented the ARIMA system for the coronavirus. Mustafa et al. [11] presented a mathematical system to forecast and analyze the coronavirus transmission. Sivakumar [12] analyzed the predictive control for the coronavirus in India. Nesteruk [13] assessed the dynamics of the coronavirus pandemic in Ukraine using the double data sets. Thompson [14] studied the epidemiologic system with the use of significant apparatus using the coronavirus interferences. Libotte [15] presented an administration plan for the coronavirus vaccine. Sadiq et al. [16] investigated the impacts of nanomaterial to handle the coronavirus disease. Gumel et al. [17] discovered a mathematical system for the coronavirus disease. Ortenzi et al. [18] presented a transdisciplinary discipline study of coronavirus in Italy. Sánchez et al. [19] designed a susceptible, infected, treatment and recovered (SITR) mathematical model using the sense of corona virus. In other studies, Sabir et al. [20] provided the stochastic performances of the SITR model-based coronavirus. Moore et al. [21] designed a mathematical coronavirus system to investigate a vaccination impact and a non-pharmaceutical intervention. Umar [22] studied theoretical performances to treat coronavirus. Anirudh [23] provided the transmission dynamics prediction based on the coronavirus. Chen et al. [24] provided the social distance effects using the mathematical form of the dynamics of coronavirus. Zhang et al. [25] expressed the coronavirus dynamics using the stochastic perturbation behavior. Soumia et al. [26] described the possible inhibitors of coronavirus.

In this study, the fractional order derivatives of susceptible, infected and quarantine (SIQ) model based on the coronavirus with the lockdown effects are presented using the stochastic numerical performances of the Levenberg–Marquardt backpropagation scheme (LMBS) along with the neural networks (NNs), i.e., LMBS-NNs.

The design of the fractional order SIQ model is presented in Section 2. The details of the stochastic applications are provided in Section 3. The LMBS-NNs structure is explained in Section 4. The simulations of the fractional order SIQ model are provided in Section 5. Finally, the conclusion is drawn in the Section 6.

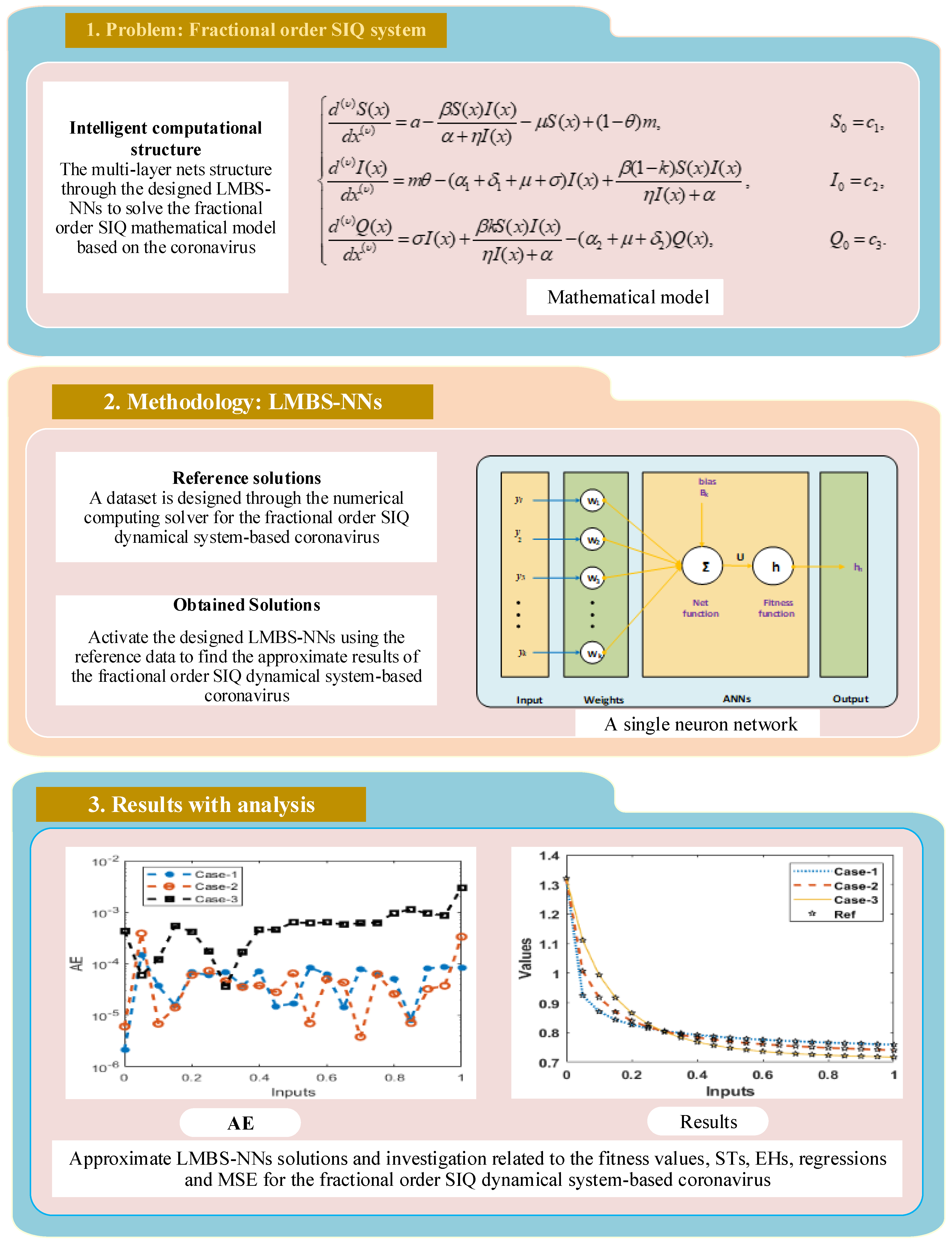
2. Mathematical Design of the Fractional Order SIQ System

In this section, the lockdown impacts as protective measures have been provided in the SIQ model. The lockdown effects are categorized into the dynamics of the susceptible, infective and quarantine classes-based system of differential equations. The mathematical form of the SIQ model is provided as [27]:

$$\left\{\begin{array}{ll}\frac{dS(x)}{dx}=a-\frac{\beta S(x)I(x)}{\alpha +\eta I(x)}-\mu S(x)+(1-\theta )m,& S_0=c_1,\\ \frac{dI(x)}{dx}=m\theta -({\alpha }_1+{\delta }_1+\mu +\sigma )I(x)+\frac{\beta (1-k)S(x)I(x)}{\eta I(x)+\alpha },& I_0=c_2,\\ \frac{dQ(x)}{dx}=\sigma I(x)+\frac{\beta kS(x)I(x)}{\eta I(x)+\alpha }-({\alpha }_2+\mu +{\delta }_2)Q(x),& Q_0=c_3.\end{array}\right.$$

(1)

The necessary and exhaustive detail of the SIQ mathematical model together with the description of each parameter is given in

Table 1. Description of each comprehensive detail of each specification of the SIQ mathematical model.

Parameters	Details
$a$	Recruitment rate
$\alpha$	Half saturation constant
$\eta$	Positive value
m	Migrants number
$\beta$	Transmission infection rate
$\mu$	Natural death rate
${\delta }_1$	Recovery of infective population
k	Contact tracing rate
$\theta$	Infected migrants’ rate
$\sigma$	0.59 per day
${\alpha }_2$	Disease associated quarantine’s population death rate
${\alpha }_1$	Disease related infective population’s death rate
${\delta }_2$	Quarantined population recovered rate
c1, c2 and c3	Contents: Initial conditions (ICs)

. Moreover, the selection of the appropriate values given in the system (1) provided in [27] along with the theoretical details of optimal control, global and local stabilities.

In the current study, the numerical investigations of the fractional order derivatives of SIQ model based on the coronavirus with the lockdown effects (1) have been provided by using the artificial intelligence (AI) with the design of LMBS-NNs. The design of the fractional order derivatives of SIQ model is formulated for the in-depth analysis of the super slow evolution as well as superfast transitions by replacing the ordinary integer order derivation in set of Equation (1) by fractional orders. The modified system (1) is given as follows:

$$\left\{\begin{array}{ll}\frac{d^{(\upsilon )}S(x)}{d{x}^{(\upsilon )}}=a-\frac{\beta S(x)I(x)}{\alpha +\eta I(x)}-\mu S(x)+(1-\theta )m,& S_0=c_1,\\ \frac{d^{(\upsilon )}I(x)}{d{x}^{(\upsilon )}}=m\theta -({\alpha }_1+{\delta }_1+\mu +\sigma )I(x)+\frac{\beta (1-k)S(x)I(x)}{\eta I(x)+\alpha },& I_0=c_2,\\ \frac{d^{(\upsilon )}Q(x)}{d{x}^{(\upsilon )}}=\sigma I(x)+\frac{\beta kS(x)I(x)}{\eta I(x)+\alpha }-({\alpha }_2+\mu +{\delta }_2)Q(x),& Q_0=c_3.\end{array}\right.$$

(2)

where $\upsilon$ shows the FO derivative in the above system.

3. Novel Topographies and Outline of the Stochastic Solvers

The numerical stochastic operators through the LMBS-NNs are provided to solve the fractional order derivatives of SIQ model based on the coronavirus with the lockdown effects. The local and global operator performances through the stochastic computing solvers have been exploited to solve the numerous nonlinear, complex, stiff and singular systems [28].

The aim of this study is to perform the numerical representations of the fractional order derivatives of SIQ model based on the coronavirus with the lockdown effects using the stochastic procedures of the LMBS-NNs. It is observed that the time-fractional order derivatives have a number of applications to define the system conditions. The derivative order form represents the remembrance, but the memory function represents the derivative of fractional order. These fractional derivatives indicate the real-world applications [29,30]. Some novel features of the LMBS-NNs for the mathematical fractional order system using the SIQ model are presented as:

• A novel design of the fractional order SIQ model based on the coronavirus with the lockdown effects is presented;
• The stochastic measures have not been applied before to solve the fractional order SIQ model based on the coronavirus with the lockdown effects;
• The numerical investigations through the stochastic paradigms are successfully presented using the fractional order SIQ mathematical model;
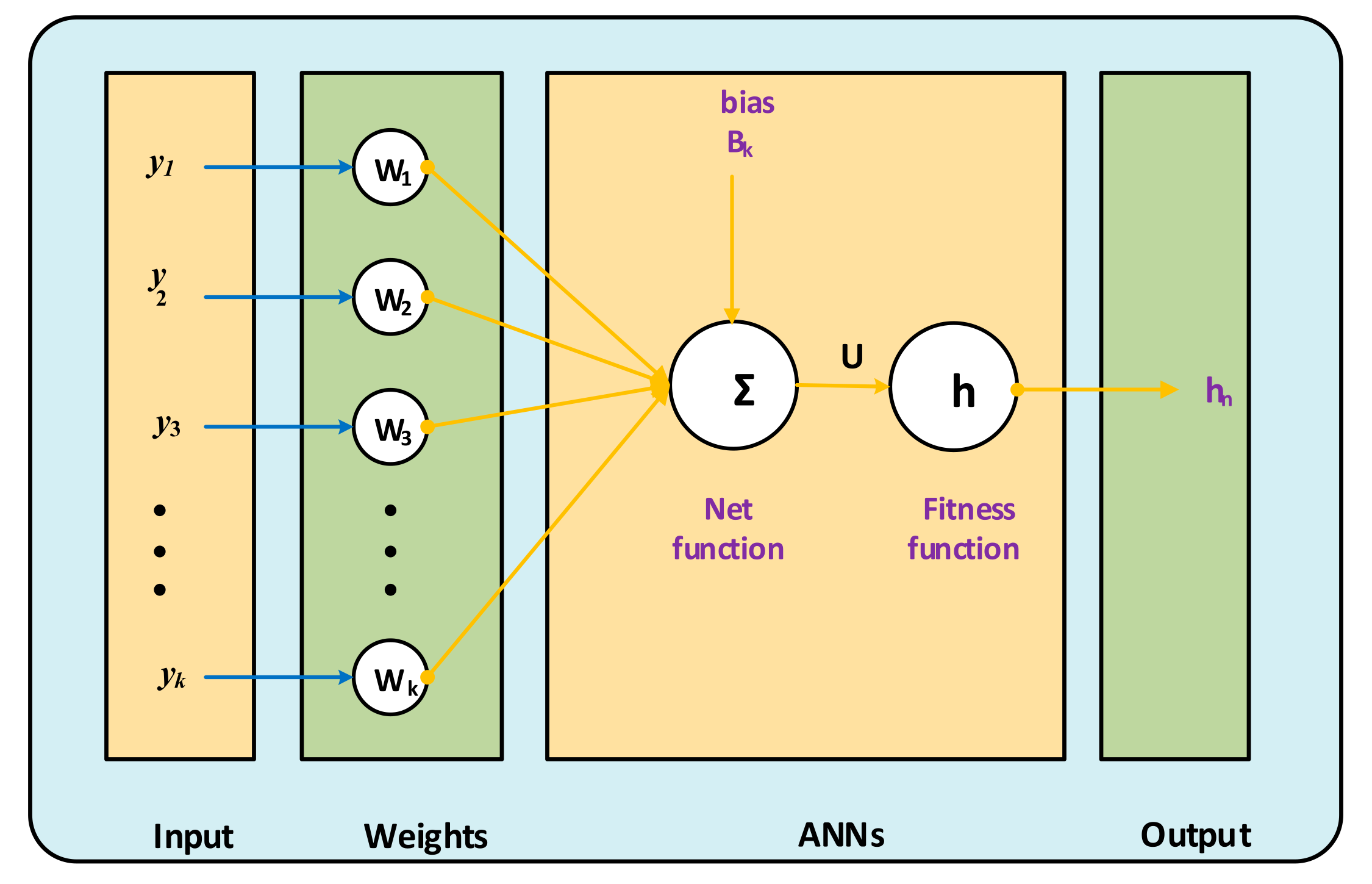
• AI with the design of LMBS-NNs is presented to solve the nonlinear fractional order SIQ mathematical model;
• Three different fractional order variations based on the SIQ model have been numerically solved to authenticate the reliability of the proposed scheme;
• The brilliance of the stochastic computing solver based LMBS-NNs is provided using the comparison of the obtained and reference (Adams–Bashforth–Moulton) solutions;
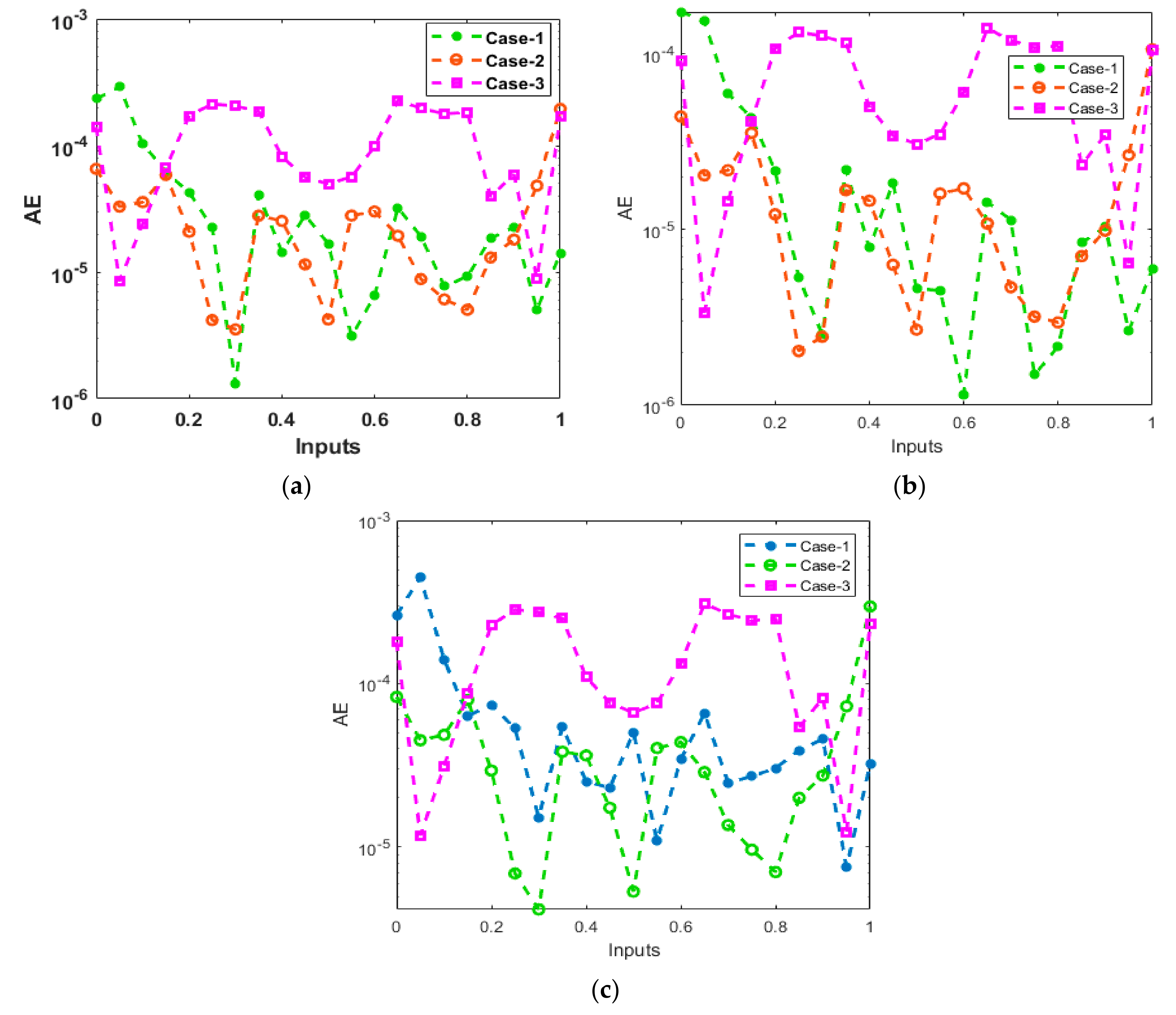
• The accuracy of the scheme is observed through the absolute error (AE) performances that is achieved in good order to solve the fractional order SIQ mathematical model;
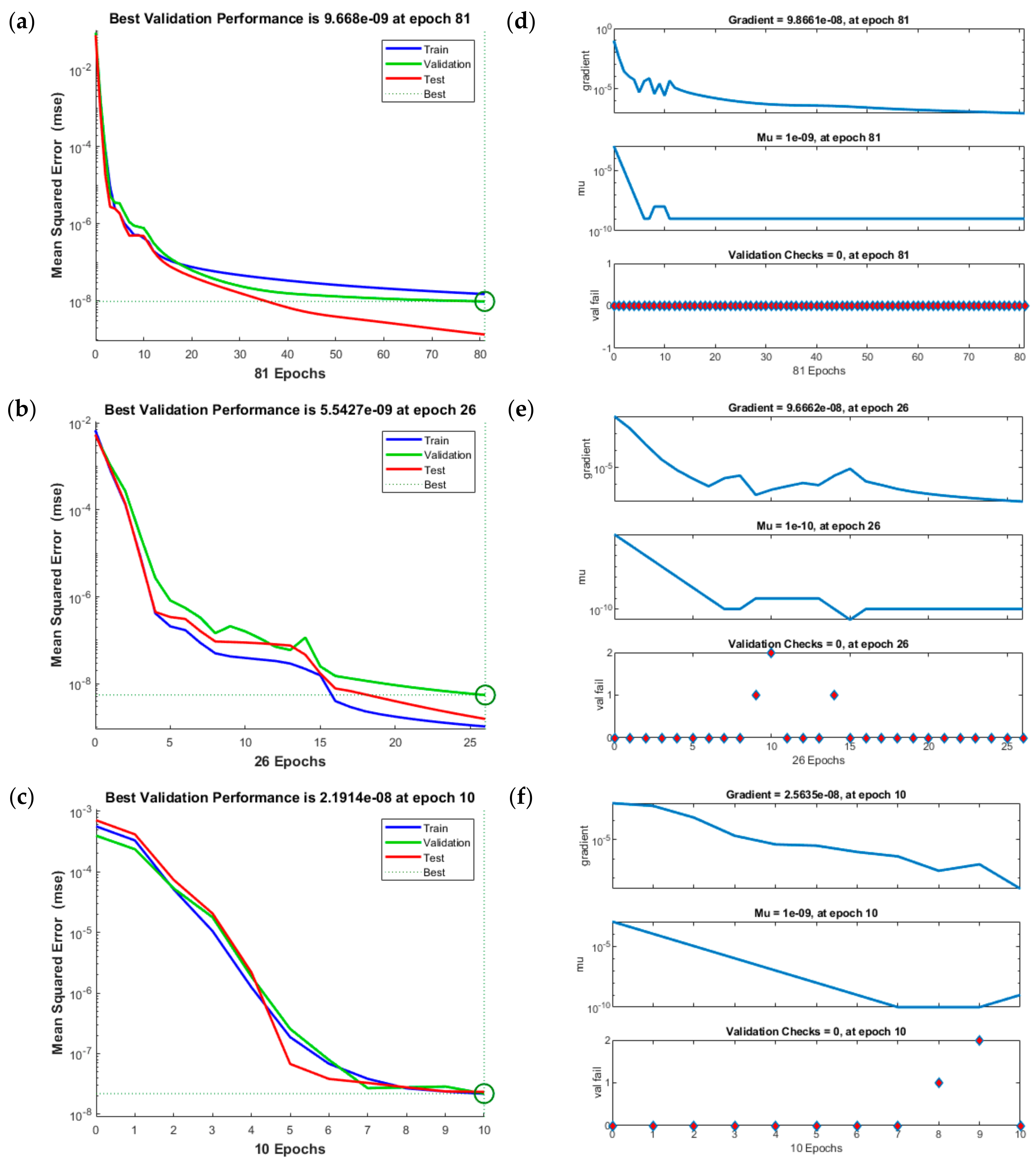
• The regression, STs, MSE and EHs and correlation performances approve the dependability and constancy of the designed LMBS-NNs to solve the fractional order SIQ mathematical model.

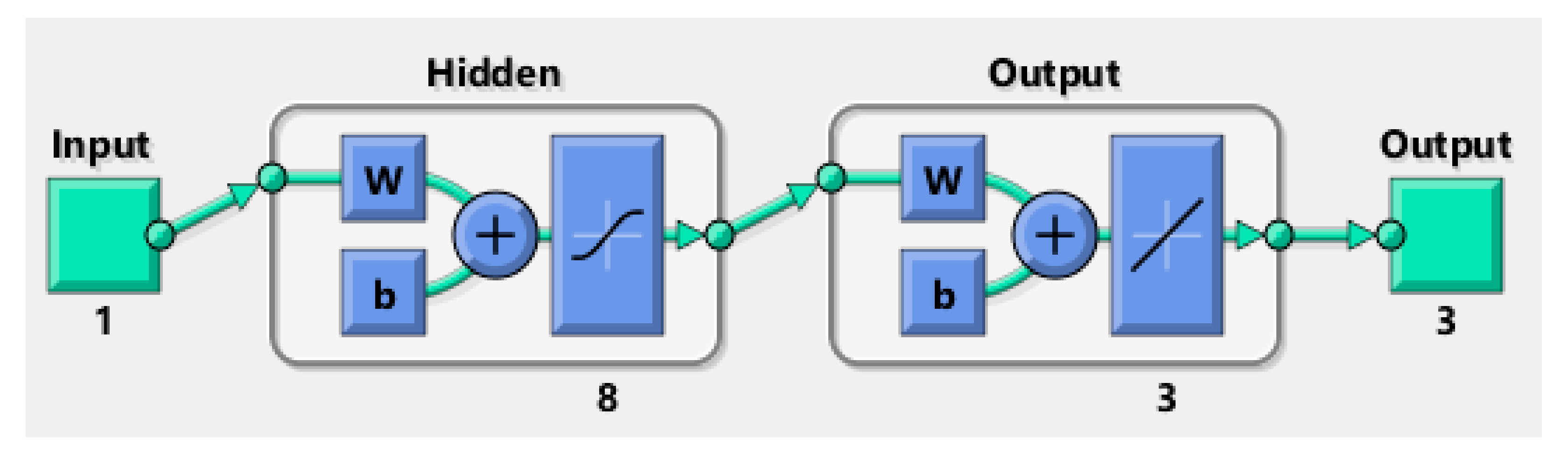
4. Proposed Procedures: LMBS-NNs

The proposed LMBS-NNs structure for solving the fractional order SIQ mathematical model is explained in this section. The methodology is designed in two parts. First, the essential performances of the LMB-NNs operator are provided. Next, the execution method via LMBS-NNs is implemented to solve the fractional order SIQ mathematical model. The proposed LMBS-NN are executed with analysis on the similar pattern as given in reported studies [31,32].

Figure 1 presents the multi-layer optimization procedures using the numerical stochastic LMBS-NNs, while the single layer neuron structure is plotted in Figure 2. The LMBS-NNs procedures are provided using ‘nftool’ command in Matlab with the selection of data as 80% for training and 10% for both testing and authorization.

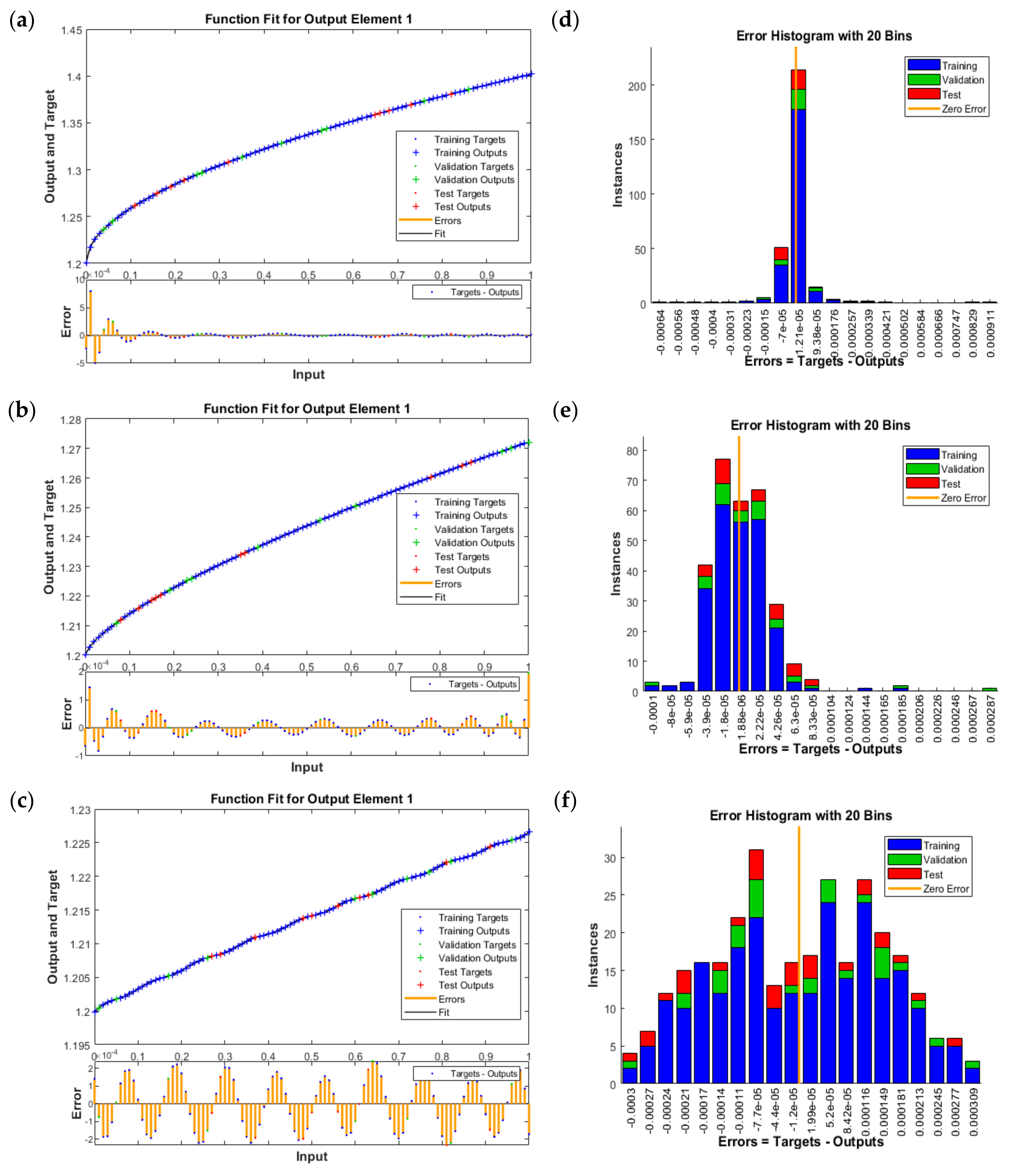
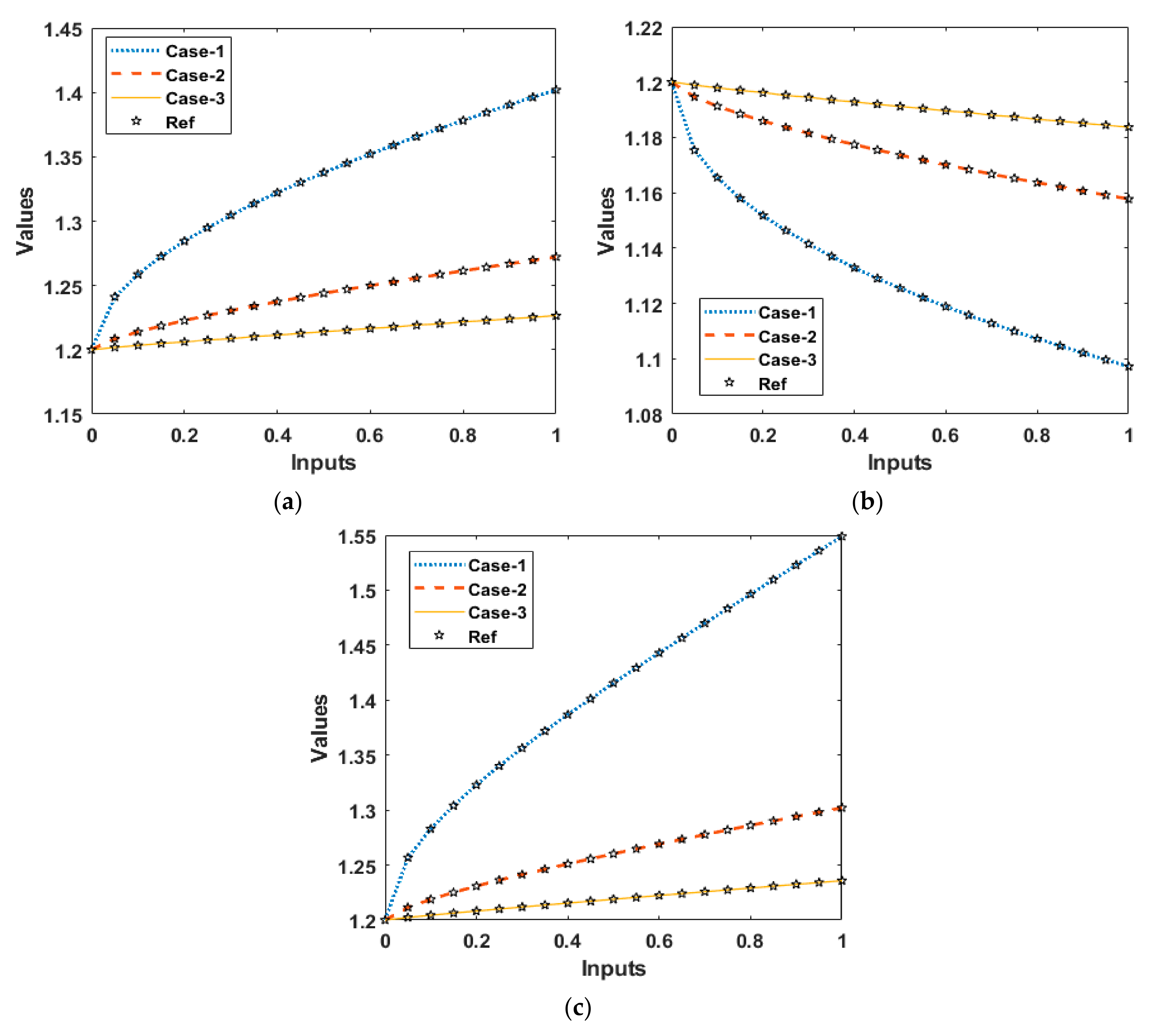
5. Results through the Designed Method

This section shows the numerical performances of three different fractional order variations to solve the nonlinear SIQ mathematical system using the proposed LMBS-NNs. The mathematical representation of each variation is presented in the below cases as:

• Case 1: Consider a fractional order coronavirus based SIQ mathematical model by taking the appropriate values $\upsilon =0.5,$ $a=2.6,$ $\beta =2.1,$ $\alpha =5,$ $\sigma =0.59$, $\eta =1$, ${\alpha }_1=1.78$, ${\delta }_1=0.4$, $\mu =5.2,$ ${\alpha }_2=1.78$, ${\delta }_2=0.4$, $\theta =0.9$, k = 0.1, $m=14$, $c_1=1.32$, $c_2=2.29$ and $c_3=3.5$ is provided as:

  $$\left\{\begin{array}{ll}\frac{d^{(0.5)}S(x)}{d{x}^{(0.5)}}=4-5.2S(x)-\frac{2.1S(x)I(x)}{5+I(x)},& S_0=1.32,\\ \frac{d^{(0.5)}I(x)}{d{x}^{(0.5)}}=12.6-7.97I(x)+\frac{1.89I(x)S(x)}{I(x)+5},& I_0=2.29,\\ \frac{d^{(0.5)}Q(x)}{d{x}^{(0.5)}}=0.59I(x)+\frac{0.21S(x)I(x)}{5+I(x)}-7.38Q(x),& Q_0=3.5.\end{array}\right.$$

  (3)
• Case 2: Consider a fractional order coronavirus based SIQ mathematical model by taking the appropriate values $\upsilon =0.7,$ $a=2.6,$ $\beta =2.1,$ $\alpha =5,$ $\sigma =0.59$, $\eta =1$, ${\alpha }_1=1.78$, ${\delta }_1=0.4$, $\mu =5.2,$ ${\alpha }_2=1.78$, ${\delta }_2=0.4$, $\theta =0.9$, k = 0.1, $m=14$, $c_1=1.32$, $c_2=2.29$ and $c_3=3.5$ is provided as:

  $$\left\{\begin{array}{ll}\frac{d^{(0.7)}S(x)}{d{x}^{(0.7)}}=4-5.2S(x)-\frac{2.1S(x)I(x)}{5+I(x)},& S_0=1.32,\\ \frac{d^{(0.7)}I(x)}{d{x}^{(0.7)}}=12.6-7.97I(x)+\frac{1.89I(x)S(x)}{I(x)+5},& I_0=2.29,\\ \frac{d^{(0.7)}Q(x)}{d{x}^{(0.7)}}=0.59I(x)+\frac{0.21S(x)I(x)}{5+I(x)}-7.38Q(x),& Q_0=3.5.\end{array}\right.$$

  (4)
• Case 3: Consider a fractional order coronavirus based SIQ mathematical model by taking the appropriate values $\upsilon =0.9,$ $a=2.6,$ $\beta =2.1,$ $\alpha =5,$ $\sigma =0.59$, $\eta =1$, ${\alpha }_1=1.78$, ${\delta }_1=0.4$, $\mu =5.2,$ ${\alpha }_2=1.78$, ${\delta }_2=0.4$, $\theta =0.9$, $k=0.1$, $m=14$, $c_1=1.32$, $c_2=2.29$ and $c_3=3.5$ is provided as:

  $$\left\{\begin{array}{ll}\frac{d^{(0.9)}S(x)}{d{x}^{(0.9)}}=4-5.2S(x)-\frac{2.1S(x)I(x)}{5+I(x)},& S_0=1.32,\\ \frac{d^{(0.9)}I(x)}{d{x}^{(0.9)}}=12.6-7.97I(x)+\frac{1.89I(x)S(x)}{I(x)+5},& I_0=2.29,\\ \frac{d^{(0.9)}Q(x)}{d{x}^{(0.9)}}=0.59I(x)+\frac{0.21S(x)I(x)}{5+I(x)}-7.38Q(x),& Q_0=3.5.\end{array}\right.$$

  (5)

The numerical presentations through the simulations of coronavirus based SIQ mathematical model is presented by using the stochastic LMBS-NNs procedures with 8 numbers of neurons along with the selection of data as 80% for training and 10% for both testing and authorization. The hidden, output and input neuron’s structure is given in Figure 3.

The graphical representations are plotted in Figure 4, Figure 5 and Figure 6 to solve the fractional order coronavirus based SIQ mathematical model by using the LMBS-NNs procedures. In order to check the best performances and STs, the graphical illustrations are provided in Figure 4 and Figure 5. The MSE and STs values for training, best curves and authentication are derived in Figure 4 to solve the fractional order coronavirus based SIQ mathematical model. The obtained values of MSE based on the best performances of the fractional order coronavirus based SIQ mathematical model have been calculated at epochs 294, 1000 and 155 that are calculated as 1.2309 × 10⁻⁸, 5.17679 × 10⁻⁹ and 1.9259 × 10⁻⁷, respectively. The gradient measures are also plotted in Figure 4 to solve the fractional order coronavirus based SIQ mathematical model using the LMBS-NNs. These gradient performances have been calculated as 5.1656 × 10⁻⁶, 1.9123 × 10⁻⁶ and 2.0104 × 10⁻⁵ for case 1, 2 and 3. These graphical representations indicate the convergence of proposed LMBS-NNs to solve the fractional order coronavirus based SIQ mathematical model using the LMBS-NNs. Figure 5, Figure 6, Figure 7 and Figure 8 represents the values of the fitting curves to solve each case of fractional order coronavirus based SIQ mathematical model. These plots represent the comparative performances of the reference and obtained results. The error plots from the substantiation, testing and training to solve each case of fractional order coronavirus based SIQ mathematical model are provided in Figure 5 (a to c) while, the EHs are plotted in Figure 5d–f. The EHs are calculated as 2.38 × 10⁻⁴, 7.10 × 10⁻⁵ and 4.29 × 10⁻⁴ for case 1, 2 and 3, respectively. The regression measures are provided in Figure 6a–c based on the fractional order coronavirus based SIQ mathematical model. The correlation is provided to validate the regression performance in Figure 6. It is clear in understanding that the correlation plots are calculated as 1 for the fractional order coronavirus based SIQ mathematical model. The training, testing and authentication representations denote the correctness of the stochastic LMBS-NNs procedure to solve the fractional order coronavirus based SIQ mathematical model. The convergence through MSE using the complexity, training, authentication, iterations, testing and backpropagation is provided in

Table 2. LMBS-NNs procedure to solve the fractional order coronavirus based SIQ mathematical model.

Case	MSE			Gradient	Performance	Epoch	Mu	Time
	Training	Testing	Validation
1	2.01 × 10−8	4.14 × 10−6	1.23 × 10−8	5.17 × 10−6	1.98 × 10−8	300	1 × 10−8	06
2	2.37 × 10−9	1.64 × 10−7	5.17 × 10−9	1.91 × 10−6	2.38 × 10−9	1000	1 × 10−8	06
3	1.45 × 10−7	5.21 × 10−6	1.92 × 10−7	2.01 × 10−5	1.37 × 10−7	161	1 × 10−7	03

Figure to solve the fractional order coronavirus based SIQ mathematical model. The brief description of the parameters tabulated is provided as follows; the validation performance means that the value of fitness, i.e., MSE, for the data samples used for the validation, i.e., 10% of total samples, validation checks being the controlling paper for the networks to stop further learning of the weights, Mu being the adaptive Levenberg–Marquardt parameter for convergence controlling coefficient of the algorithm, gradient being the first order optimality parameter, performance means fitness on MSE and time in seconds being the time complexity of adaption of the networks.

The plots of the result comparisons and AE values are provided in Figure 7 and Figure 8. The numerical representations are provided to solve the fractional order coronavirus based SIQ mathematical model using the stochastic LMBS-NNs. The reference and obtained numerical performances are plotted in Figure 7 through the overlapping of the results. The result overlapping authenticates the exactness of the LMBS-NNs to solve the fractional order coronavirus based SIQ mathematical model. The AE values to solve the SIQ model are performed in Figure 8. The AE for the susceptible individuals S(x) calculated as 10⁻⁴ to 10⁻⁷, 10⁻⁴ to 10⁻⁶ and 10⁻⁴ to 10⁻⁵ for case 1 to 3. The AE for the infected individuals I(x) calculated as 10⁻⁴ to 10⁻⁶, 10⁻⁴ to 10⁻⁷ and 10⁻⁴ to 10⁻⁶ for case 1 to 3. Similarly, the AE for the quarantine individuals Q(x) calculated as 10⁻⁴ to 10⁻⁶, 10⁻⁴ to 10⁻⁵ and 10⁻³ to 10⁻⁵ for case 1 to 3. These AE values represent the exactness of the proposed LMBS-NNs to solve the fractional order coronavirus based SIQ mathematical model.

6. Concluding Remarks

In this work, the numerical presentations of the coronavirus based SIQ mathematical model are presented. The aim of this study is to provide the fractional order study using the dynamics of coronavirus based SIQ mathematical model to get more accurate performances of the system. The integer nonlinear mathematical SIQ system with the lockdown effects was also provided in this study. The fractional order coronavirus based SIQ mathematical model is classified into three dynamics, susceptible, infective and quarantine, generally known as the SIQ mathematical system. The numerical performances of the fractional order coronavirus based SIQ mathematical model have never been presented nor solved by using the stochastic Levenberg-Marquardt backpropagation neural networks. Three cases using different values of the fractional order have been provided to solve the fractional order SIQ mathematical model. The data to present the numerical solutions of the fractional order SIQ mathematical model were selected as 80% for training and 10% for both testing and authorization. Eight numbers of neurons were used to present the numerical performances of the fractional order SIQ mathematical system. The numerical results of the fractional order SIQ mathematical system have been compared with the Adams–Bashforth–Moulton solver. To reduce the MSE, the obtained numerical results have been performed by using the LMBS-NNs. The reliability and competence of LMBS-NNs and the numerical performances have been illustrated using the STs, regression, correlation, EHs and MSE. The correctness of the LMBS-NNs based on the fractional order SIQ mathematical model is observed via the matching of reference and obtained results. The performance of the scheme is verified based on the consistency and dependability of the proposed LMBS-NNs.

In future work, the LMBS-NNs can be implemented to present the numerical measures of the lonngren-wave, fluid mechanics systems, bioinformatics studies as well as information security models.