Abstract
This paper studies the influence of space-fractional and multiplicative noise on the exact solutions of the space-fractional stochastic dispersive modified Benjamin–Bona–Mahony equation, driven in Ito’s sense by a multiplicative Wiener process. The bifurcation of the exact solutions is investigated, and novel fractional stochastic solutions are presented. The dependence of the solutions on the initial conditions is discussed. Due to the significance of the fractional stochastic modified Benjamin–Bona–Mahony equation in describing the propagation of surface long waves in nonlinear dispersive media, the derived solutions are significantly more helpful for and influential in comprehending diverse, crucial, and challenging physical phenomena. The effect of the Wiener process and the fractional order on the exact solutions are studied.
1. Introduction
Many problems in the world can be identified through physical and mathematical models. It has been shown that models are practically related to nonlinear partial differential equations (NPDEs), which can be used to describe many real-life phenomena. Several mathematical models have been determined for physical processes in the field of scientific research, and this has led to the comprehensive study of the behaviors of nonlinear waves receiving attention. The category of shallow water equations is one of the most important tools for modeling the behavior of waves, which has been applied and integrated with the mathematical process of the study of atmospheric and oceanic models. Several phenomena of shallow water waves have been obtained from NPDEs [1,2,3,4]. For more detail related to the equations closely connected to the developing topics, we direct the reader to [5,6,7,8,9]. Closed-form solutions for nonlinear partial differential equations (PDEs) are crucial for understanding intricate phenomena. In this regard, it is necessary to find wave solutions, in particular. Researchers have presented new methods and refined existing approaches. Various significant methods have been introduced, such as the Darboux transformation [10], Weierstrass elliptic functions methods [11,12], Bäcklund transformation [13], Lie group [14,15,16,17], Hirota’s method [18,19], and the bifurcation method [20,21,22,23,24,25,26]. The analytical and numerical solutions for various types of NPDEs have been investigated using traditional Lie symmetry approaches; see, for instance [27].
Numerous branches of science, including physics and engineering, have emphasized the benefits of taking random effects into account when analyzing, simulating, and modeling complicated processes. The reason for this is that the noise may provide statistical characteristics and significant phenomena that cannot be ignored [28,29,30,31]. Further, when stochastic terms are introduced to PDEs, exact solutions are more difficult to find than deterministic PDEs. Models based on fractional derivatives have been successful in describing nonlinear physical phenomena. A continuing interest in fractional calculus resides in its applicability. In fields such as physics, mechanics, chemistry, and biology, fractional calculus is extremely useful [32,33,34,35].
We consider the fractional-space stochastic nonlinear dispersive modified Benjamin–Bona–Mahony equation. It takes the form
where is a non-zero real number, refers to the conformable fractional derivative of order , is the intensity of the noise, and is the standard Brownian motion; see Appendix A and Appendix B for more details about the conformable fractional derivative and Wiener process. To our knowledge, the space-fractional stochastic dispersive modified Benjamin–Bona–Mahony equation has not been studied in the literature, which motivates us to examine it. We attempt to prove and discuss several possibilities for the solution to this equation via dynamical system analysis. In other words, this equation can be considered a generalization or an extension for the classical nonlinear dispersive modified Benjamin–Bona–Mahony as , i.e.,
This equation initially appeared in [3] to characterize an approximation for surface long waves in nonlinear dispersive media. Equation (2) can also be employed to describe acoustic-gravity waves’ incompressible fluids, acoustic waves in a harmonic crystal, and hydromagnetic waves in a cold plasma [36,37]. Notice that Equation (1) provides a good description for all phenomena descried by Equation (2) because the multiplicative noise implies a statistical characteristic that can not be ignored. Equation (2) has been studied in several works. A modified simple method has been applied to construct a traveling wave solution for Equation (2) [38]. A modified exp-function method has been utilized to construct some analytical solutions for Equation (2) [39]. Ref. [40] contains some wave solutions for Equation (2) with time-fractional by employing the extended sub-equation method. In [41], the author constructed a topological soliton solution for Equation (2). The method was applied to formulate wave solutions for Equation (2) in [42,43]. Elbrolosy and Elmandouh [44] used the enhanced modified simple equation of Equation (2), and they obtained some solitary wave solutions. Alharbi et al. [45] used the adaptive moving mesh PDEs method to solve Equation (2) numerically. In [46], the authors applied semianalytical and numerical simulations for Equation (2). In [47], Wang constructed an abundant wave solution for Equation (2) by applying two effective methods: the variational direct method and He’s frequency formulation method. Shakeel et al. [48] presented some hyperbolic, trigonometric, and rational function solutions for Equation (2) by utilizing a new generalization of the exp-function method. The modified auxiliary equation method was used to announce some new solutions for Equation (2) [49]. Tian et al., in [50], employed the simplest equation method to find some wave solutions for Equation (2). In [51], Seadawy constructed traveling wave solutions for Equation (2) by employing the generalized direct algebraic, modified F-expansion, and improved simple equation methods.
This work is organized as follows: Section 2 contains the qualitative analysis for the dynamical system corresponding to the fractional stochastic Equation (1). Section 3 includes some new fractional stochastic solutions for Equation (1), and we study the degeneracy of the solution based on the variation of the initial conditions. Section 4 clarifies the effects of the strength of the noise , the fractional order , and their combined effect. Section 5 summarizes the results.
2. Mathematical Analysis
We consider the transformation
which has been applied in several works, such as [52]. After some calculations, we have
where indicates the derivative with respect to . Inserting the expressions (4) into (1), we obtain
Based on our assumption that is normally distributed, . Consequently, the expectation of both sides of Equation (5) implies
Integrating the last equation with respect to , we obtain
where the integration constant is ignored. Let ; then, Equation (7) is written down as a dynamic system in the form
System (8) is a conservative system because . It is also a Hamiltonian system since it can be derived from the Hamilton canonical equation using a Hamiltonian function
Based on , the Hamiltonian function (9) is a first integral, i.e., it takes a constant value along any trajectory of the system (8). Hence, we have
where E is constant. Thus, the problem of finding a solution for Equation (1) is reduced to finding the solution of the Hamiltonian system (8). Therefore, we insert the first equation in system (8) into the first integral (10) and separate the variables; we obtain the 1-differential form
where is a quartic polynomial given by
The integration of both sides of Equation (11) demands the range of the parameters , and e. Thus, we apply the qualitative theory of the planar dynamic system [53] to obtain this range. The equilibria for system (8) are the solution of . If , then it has a single fixed point at the origin , while if , then it has three equilibrium points and . The classification of these points is investigated by evaluating the eigenvalues of the Jacobi matrix associated with system (8) at these equilibria. The Jacobi matrix is
The eigenvalues of the matrix (13) evaluated at the equilibrium points are
Taking into account the existence conditions for these equilibrium points, we have the next two cases:
Case 1.
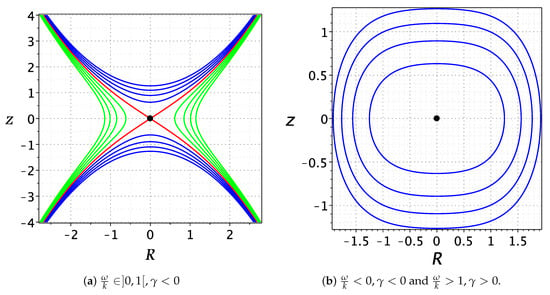
System (8) has a single equilibrium point O if . It is saddle if and it is center when either or . The phase portrait for this case is introduced by Figure 1.

Figure 1.
Phase portrait for system (8) when . The black solid circles indicate the equilibrium points.
Case 2.
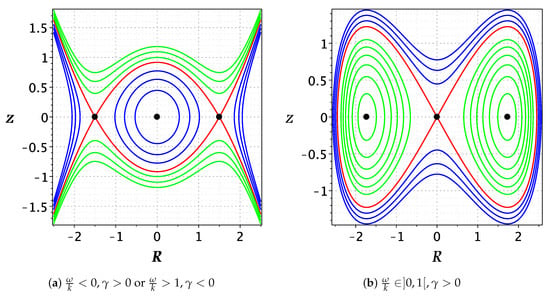
System (8) possesses three equilibrium points if . They are . If or , then O is the center and are the saddle points, while if , the point O is the saddle and are the center. The phase portrait for this case is outlined by Figure 2.

Figure 2.
Phase portrait for system (8) when . The black solid circles indicate the equilibrium points.
Phase Portrait Description
This subsection aims to present a short description of the phase portrait of the system (8). The values of the constant E at the equilibrium points are
The phase orbits are also the energy level curves, which are parameterized by the parameter E, i.e.,
The description of the phase portrait is summarized as the following:
- System (8) has three equilibrium points O and when . For or , the equilibrium point O is the center, while are the saddle points. The phase plane, which is illustrated by Figure 2a, for this case, consists of three different types of orbits based on the values of E. The family of is unbounded orbits in green. The red orbit is a heteroclinic orbit or sometimes is named a connecting orbit due to it connecting the two saddle points . The family of orbits, , in blue, is composed of three separated subfamilies of orbits. Two of them are unbounded and arise outside the heteroclinic orbit, while the inside one is periodic around the center point O. In the case in which , the equilibrium point O is saddle, while the others are centers. All the orbits are bounded for all possible values of the parameter E. The family is a super periodic family of orbit. When , there are two ovals in the homoclinic orbit connecting the saddle point O with itself. For , there are two families of periodic orbits in green. Each of them appears in the left and right oval of the homoclinic orbit.
It is worth mentioning that the phase orbits do not intersect with each other. Moreover, each of them corresponds to a certain value of E as well as specific initial conditions. From this point, we can study the transformation between the phase orbits for the distinct initial conditions. Let us outline that in the following:
- In Figure 1b, if , the family of periodic orbits degenerates into the equilibrium point O.
- In Figure 2a, if , the periodic family of orbits in blue degenerates to the equilibrium point, and the two unbounded orbits in blue turn into the extension parts of the unbounded orbits in red. If , the periodic orbits in blue degenerate to the heteroclinic orbits in red, and the unbounded family of orbits in green is converted to the heteroclinic orbit in red as .
- In Figure 2b, if , the super periodic orbits in blue are converted to the homoclinic orbit in red, and the two periodic families in green are transformed into the homoclinic orbit as . Furthermore, the two periodic families of orbits in green will be shrunk into the two equilibrium points as .
These items are significant as seen in the construction of the solutions.
3. Construction of the Solutions
Based on the bifurcation analysis in Section 2, we integrate both sides of the 1-differential form (11) to obtain the required solutions taking into account only the integration along the bounded orbit and a possible interval of real propagation. This restriction enables us to construct only real bounded solutions, which are desirable in real-world applications. Thus, let us consider the following cases:
Case 3.
Case 4.
If, the polynomialhas four real simple zeros, namely, , where; therefore, it reads, where. The interval of real propagation is. We selectbecause it corresponds to a bound orbit. Assuming, the integration of both sides along the chosen interval gives
Hence, Equation (1) admits the solution
Solution (21) is a novel solution for Equation (1).
Case 5.
If, the polynomial (12) has two real zeros repeated twice, i.e., the zeros are not simple. Consequently, we have . The interval of possible real propagation is . Postulating and integrating both sides in the 1-differential form (11) along this interval, we obtain
Therefore, Equation (1) has a new solution in the form
Case 6.
If, the system (8) has a family of super periodic orbits in blue, see Figure 2b. The polynomial has two real zeros, namely, , while the others are conjugate imaginary (say), ; therefore, it is written as , where . The interval of real wave propagation is . Postulating , the integration of both sides of the 1-differential form (11) implies
Then, Equation (1) has a new solution in the form
Case 7.
If, system (8) has a homoclinic orbit in red, seeFigure 2b. The polynomialhas two simple roots (say), and one is double at the origin; so, it has the form. The interval of real wave propagation is. Let us assume. The integration of both sides along this interval gives
Hence, Equation (1) has a solution
Case 8.
; there are two separated families of periodic orbits in green, see Figure 2b. Therefore, the polynomialhas four real zeros (say), where. It is expressed as, where. The interval of real propagation is. Assumingand integrating both sides of Equation (11), we obtain
Hence, Equation (1) has a novel solution in the form
Degeneracy of the Solutions
We study the degeneracy of the Jacobi-elliptic solutions utilizing the transmission between the phase orbits, or equivalently, we study the dependence of the solutions on the initial conditions. Let us clarify this in the following:
4. Physical Interpretation
This section aims to explain the effect of the noise, fractional-order derivatives, and their combination on the obtained solutions.
The choice of the parameters , and agrees with Case 3. The solution (19) is reduced to
A study of the influence of noise, fractional order, and their combination is conducted.
- (a)
- Influence of the noise:Figure 3a illustrates how the noise influences the solution (19) at different values of . The representation of solution (19) illustrates how the noise impacts the blue curve, which represents the deterministic case. Figure 3b illustrates how the deterministic solution differs from the fractional stochastic solution.
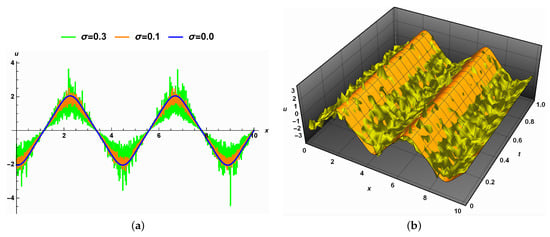 Figure 3. The effect of the noise on the solution (19) when .
Figure 3. The effect of the noise on the solution (19) when . - (b)
- Influence of the fractional order :Figure 4a describes the 2D representation of the solution (19) for different values of the fractional order in the absence of noise, i.e., . The amplitude of the solution is approximately fixed, while the width of the solution grows as the fractional order derivative increases. Figure 4b outlines the representation of the solution in both cases in which the order of the derivatives is fractional (yellow) and integer (orange).
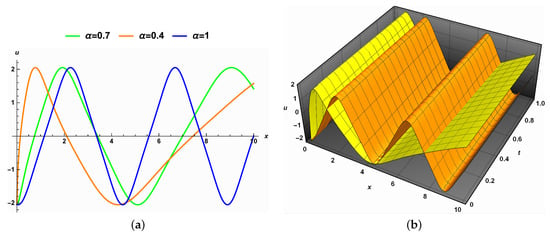 Figure 4. The effect of the fractional order on the solution (19) when .
Figure 4. The effect of the fractional order on the solution (19) when . - (c)
- Combined effects:As shown in Figure 5a, there are some changes in the amplitude due to the effect of the noise, while the width increases as the value of the fractional order increases, and the noise causes a small change in width. The same conclusion can be stated for Figure 5b.
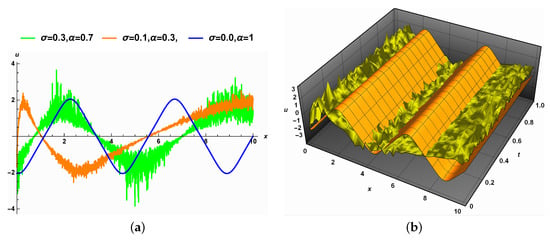 Figure 5. The combined effect of the noise and the fractional order on the solution (19).
Figure 5. The combined effect of the noise and the fractional order on the solution (19).
Let us choose , and . This choice of parameters leads to the solution (27), which is a 1-soliton solution in the absence of the noise and the fractional order . We investigate the influence of the noise, fractional order, and their combination as the following:
- (a)
- Influence of the noise:Figure 6a displays the representation of the solution (27). The solution is perturbed around the solution in the deterministic case with , and this causes some small changes in the width of the solution and large changes in the amplitude, as the strength of the noise grows. Furthermore, the 3D representation in Figure 6b outlines the same conclusion.
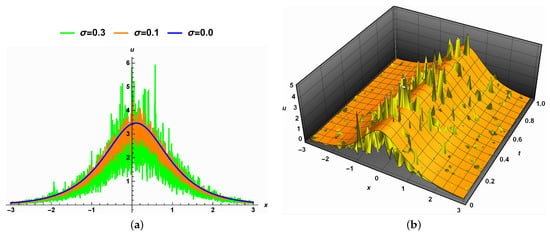 Figure 6. The effect of the noise on the solution (27) when .
Figure 6. The effect of the noise on the solution (27) when . - (b)
- Influence of the fractional order:Figure 7a clarifies the 2D representation of the solution (27) for different values of the fractional order in the deterministic case, i.e., in the absence of the noise. As the fractional order increases, the width of the solution increases, while the amplitude remains relatively unchanged. Figure 7b illustrates the 3D representation of the solution (27) when without the presence of noise, i.e., .
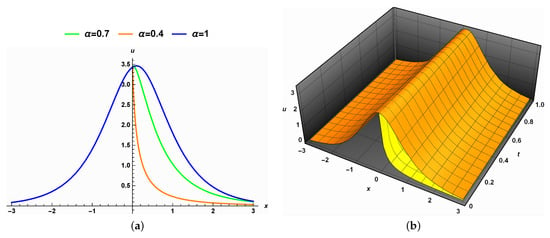 Figure 7. The effect of the fractional order on the solution (27) when .
Figure 7. The effect of the fractional order on the solution (27) when . - (c)
- Effect of the combination of the noise and the fractional order:Figure 8a illustrates the representation of the solution (27) for distinct values of and in addition to the classical case that is represented in blue. The existence of both combines the two previous effects. The amplitude and the width of the solution increase as and grow. Figure 8b outlines the representation of the solution (27), and it gives the same conclusion.
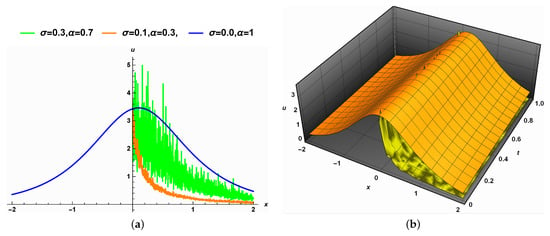 Figure 8. The combined effect of the noise and the fractional order on the solution (27).
Figure 8. The combined effect of the noise and the fractional order on the solution (27).
We can similarly examine the effect of the noise with strength and the fractional order on the other obtained solutions.
5. Conclusions
We studied the influence of the space-fractional and multiplicative noise on the exact solutions of the space-fractional stochastic dispersive modified Benjamin–Bona–Mahony equation, driven in Ito’s sense by a multiplicative Wiener process. The bifurcation of the fractional exact solutions for this equation was investigated. New fractional stochastic solutions were provided. We focused on constructing only real solutions on certain intervals, which are named intervals of real propagation. This type of solution is significant because it is acceptable in real-world applications. On the another hand, the exact obtained solutions acquired their significance from their ability to comprehend diverse crucial challenges in the propagation of surface long waves in nonlinear dispersive media, as described by the fractional stochastic Benjamin–Bona–Mahony equation. The dependence of the gained analytical solutions on the initial conditions was clarified. Moreover, we linked the solutions together by employing the degeneracy properties of the solutions. We illustrated the influence of the strength of the noise and the fractional order on the solutions. We considered two solutions to examine the impact of the noise alone, the fractional order alone, and their combination on these solutions. These effects were seen through looking at the amplitude and the width of the solutions, as the strength of the noise and the fractional order grew. Figure 3 shows that the noise caused some disturbance to the solution (19) in the deterministic case. Figure 4 illustrates the impact of the fractional order on the width and the amplitude of the solution (19) in the absence of the noise, while Figure 5 clarifies the combined effects of the noise and the fractional order on the solution (19); i.e., the width increased as the value of the fractional order increased, while the noise caused a small change in the width. Figure 6 shows that the noise caused small changes in the width and large changes in the amplitude of the solution (27) as the intensity of the noise increased. Figure 7 shows that the growth of the fractional order increased the width, while the amplitude remained unchanged. Figure 8 shows the combined effects of the noise and fractional order on the solution (27). It also shows that the amplitude and the width of the solutions increased as grew.
We will address our equation forced by additive noise in the future work. In addition, some numerical studies will be considered.
Author Contributions
Methodology, A.E. and E.F.; Software, A.E. and E.F.; Formal analysis, A.E. and E.F.; Writing—original draft, A.E. and E.F.; Writing—review & editing, A.E. and E.F. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
No data were used to support the findings of the study.
Acknowledgments
This work was supported by the Deanship of Scientific Research, Vice Presidency for Graduate Studies and Scientific Research, King Faisal University, Saudi Arabia (Project No. GRANT 1830), through its KFU Research summer initiative.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Conformable Derivatives
In engineering and physical science, fractional calculus provides a better selection for describing real-world problems. Scholars have proposed novel fractional calculus operators in recent decades, such as the Riemann–Liouville, Caputo, and conformable fractional operators. The conformal fractional operator overcomes some of the limitations of other fractional operators and provides basic properties of classical calculus, such as the derivative of the quotient of two functions, the chain rule, the product of two functions, the mean value theorem, and Rolle’s Theorem. The application of conformable derivatives is simple and very efficient. Furthermore, it allows us better understand the behavior of physical phenomena.
Definition A1
([54]). Let be a function; then, the conformable fractional derivative of order ν is defined as
for all and .
We display some conformable derivative properties that are significant in our work. Let the two functions be conformable differential for , and are two constants. Then, we have the following properties:
- ,
- , ,
- ;
- ;
- .
- Let h and g be two functions, such that is differentiable map, and g is defined in the range of g; then, .
Appendix B. Wiener Process
In this appendix, we introduce the definition of the standard Wiener process [55].
Definition A2.
A stochastic process is named a standard Wiener process if
- ,
- is a continuous function for ,
- For , are independent,
- has a normal distribution with mean zero and variance .
are verified.
References
- Peregrine, D.H. Long waves on a beach. J. Fluid Mech. 1967, 27, 815–827. [Google Scholar] [CrossRef]
- Korteweg, D.J.; De Vries, G. XLI. On the change of form of long waves advancing in a rectangular canal, and on a new type of long stationary waves. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1895, 39, 422–443. [Google Scholar] [CrossRef]
- Benjamin, T.B.; Bona, J.L.; Mahony, J.J. Model equations for long waves in nonlinear dispersive systems. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Sci. 1972, 272, 47–78. [Google Scholar]
- Peregrine, D.H. Calculations of the development of an undular bore. J. Fluid Mech. 1966, 25, 321–330. [Google Scholar] [CrossRef]
- Easwaran, C.V.; Majumbar, S.R. The evolution of perturbations of the renormalized long wave equation. J. Math. Phys. 1988, 29, 390–392. [Google Scholar] [CrossRef]
- Biswas, A. 1-soliton solution of the B (m, n) equation with generalized evolution. Commun. Nonlinear Sci. Numer. Simul. 2009, 14, 3226–3229. [Google Scholar] [CrossRef]
- Camassa, R.; Holm, D.D. An integrable shallow water wave equation with peaked solitons. Phys. Rev. Lett. 1974, 19, 1095–1097. [Google Scholar]
- Biswas, A. 1-Soliton solution of Benjamin–Bona–Mahoney equation with dual-power law nonlinearity. Commun. Nonlinear Sci. Numer. Simul. 2010, 15, 2744–2746. [Google Scholar] [CrossRef]
- Musette, M.; Lambert, F.; Decuyper, J.C. Soliton and antisoliton resonant interactions. J. Phys. A Math. Gen. 1987, 20, 6223. [Google Scholar] [CrossRef]
- Adler, V.E.; Postnikov, V.V. On vector analogs of the modified Volterra lattice. J. Phys. A Math. Theor. 2008, 41, 455203. [Google Scholar] [CrossRef]
- Fan, E. Soliton solutions for a generalized Hirota–Satsuma coupled KdV equation and a coupled MKdV equation. Phys. Lett. A 2001, 282, 18–22. [Google Scholar] [CrossRef]
- Fan, E.; Hon, B.Y. Double periodic solutions with Jacobi elliptic functions for two generalized Hirota–Satsuma coupled KdV systems. Phys. Lett. A 2002, 292, 335–337. [Google Scholar] [CrossRef]
- Rogers, C.; Rogers, C.; Schief, W.K. Bäcklund and Darboux Transformations: Geometry and Modern Applications in Soliton Theory; Cambridge University Press: Cambridge, UK, 2002; Volume 30. [Google Scholar]
- Olver, P.J. Applications of Lie Groups to Differential Equations; Springer Science and Business Media: Berlin/Heidelberg, Germany, 1993; Volume 107. [Google Scholar]
- Bluman, G.; Anco, S. Symmetry and Integration Methods for Differential Equations; Springer Science and Business Media: Berlin/Heidelberg, Germany, 2008; Volume 154. [Google Scholar]
- Ibragimov, N.H. Transformation Groups Applied to Mathematical Physics; Springer Science and Business Media: Berlin/Heidelberg, Germany, 1984; Volume 3. [Google Scholar]
- Kumar, S.; Almusawa, H.; Dhiman, S.K.; Osman, M.S.; Kumar, A. A study of Bogoyavlenskii’s (2 + 1)-dimensional breaking soliton equation: Lie symmetry, dynamical behaviors and closed-form solutions. Results Phys. 2021, 29, 104793. [Google Scholar] [CrossRef]
- Hirota, R. The Direct Method in Soliton Theory (No. 155); Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Hu, X.B.; Li, C.X.; Nimmo, J.J.; Yu, G.F. An integrable symmetric (2 + 1)-dimensional Lotka–Volterra equation and a family of its solutions. J. Phys. A Math. Gen. 2004, 38, 195. [Google Scholar] [CrossRef]
- Elbrolosy, M.E.; Elmandouh, A.A. Dynamical behaviour of nondissipative double dispersive microstrain wave in the microstructured solids. Eur. Phys. J. Plus 2021, 136, 955. [Google Scholar] [CrossRef]
- Nuwairan, M.A.; Elmandouh, A.A. Qualitative analysis and wave propagation of the nonlinear model for low-pass electrical transmission lines. Phys. Scr. 2021, 96, 095214. [Google Scholar] [CrossRef]
- Elmandouh, A.A. Integrability, qualitative analysis and the dynamics of wave solutions for Biswas–Milovic equation. Eur. Phys. J. Plus 2021, 136, 638. [Google Scholar] [CrossRef]
- Elmandouh, A.A. Bifurcation and new traveling wave solutions for the 2D Ginzburg–Landau equation. Eur. Phys. J. Plus 2020, 135, 648. [Google Scholar] [CrossRef]
- Elmandouh, A.A.; Elbrolosy, M.E. New traveling wave solutions for Gilson–Pickering equation in plasma via bifurcation analysis and direct method. Math. Methods Appl. Sci. 2022. [Google Scholar] [CrossRef]
- Tamang, J.; Abdikian, A.; Saha, A. Phase plane analysis of small amplitude electron-acoustic supernonlinear and nonlinear waves in magnetized plasmas. Phys. Scr. 2020, 95, 105604. [Google Scholar] [CrossRef]
- Elbrolosy, M.E. Qualitative analysis and new soliton solutions for the coupled nonlinear Schrödinger type equations. Phys. Scr. 2021, 96, 125275. [Google Scholar] [CrossRef]
- Verma, A.; Jiwari, R.; Koksal, M.E. Analytic and numerical solutions of nonlinear diffusion equations via symmetry reductions. Adv. Differ. Equ. 2014, 2014, 229. [Google Scholar] [CrossRef]
- Arnold, L. Trends and open problems in the theory of random dynamical systems. In Probability towards 2000; Springer: New York, NY, USA, 1998; pp. 34–46. [Google Scholar]
- Weinan, E.; Li, X.; Vanden-Eijnden, E. Some recent progress in multiscale modeling. Multiscale Model. Simul. 2004, 39, 3–21. [Google Scholar]
- Mohammed, W.W.; Iqbal, N.; Botmart, T. Additive noise effects on the stabilization of fractional-space diffusion equation solutions. Mathematics 2022, 10, 130. [Google Scholar] [CrossRef]
- Mohammed, W.W.; Alshammari, M.; Cesarano, C.; Albadrani, S.; El-Morshedy, M. Brownian Motion Effects on the Stabilization of Stochastic Solutions to Fractional Diffusion Equations with Polynomials. Mathematics 2022, 10, 1458. [Google Scholar] [CrossRef]
- Das, S. Functional Fractional Calculus; Springer: Berlin, Germany, 2011; Volume 1. [Google Scholar]
- Dong, J.; Xu, M. Space–time fractional Schrödinger equation with time-independent potentials. J. Math. Anal. Appl. 2008, 344, 1005–1017. [Google Scholar] [CrossRef]
- Bayın, S.Ş. On the consistency of the solutions of the space fractional Schrödinger equation. J. Math. Phys. 2012, 53, 042105. [Google Scholar] [CrossRef]
- Elbrolosy, M.E.; Elmandouh, A.A. Dynamical behaviour of conformable time-fractional coupled Konno-Oono equation in magnetic field. Math. Probl. Eng. 2022, 2022, 3157217. [Google Scholar] [CrossRef]
- Saut, J.C.; Tzvetkov, N. Global well-posedness for the KP-BBM equations. Appl. Math. Res. eXpress 2004, 2004, 1–16. [Google Scholar] [CrossRef]
- Varlamov, V.; Liu, Y. Cauchy problem for the Ostrovsky equation. Discret. Contin. Dyn. Syst.-A 2004, 10, 731. [Google Scholar] [CrossRef]
- Khan, K.; Akbar, M.A.; Islam, S.R. Exact solutions for (1 + 1)-dimensional nonlinear dispersive modified Benjamin-Bona-Mahony equation and coupled Klein-Gordon equations. SpringerPlus 2014, 3, 724. [Google Scholar] [CrossRef] [PubMed]
- Baskonus, H.M.; Bulut, H. Analytical studies on the (1 + 1)-dimensional nonlinear dispersive modified Benjamin–Bona–Mahony equation defined by seismic sea waves. Waves Random Complex Media 2015, 25, 576–586. [Google Scholar] [CrossRef]
- Batool, F.; Akram, G. Application of extended Fan sub-equation method to (1 + 1)-dimensional nonlinear dispersive modified Benjamin-Bona-Mahony equation with fractional evolution. Opt. Quantum Electron. 2017, 49, 375. [Google Scholar] [CrossRef]
- Guner, O. Soliton solution of the generalized modified BBM equation and the generalized Boussinesq equation. J. Ocean Eng. Sci. 2017, 2, 248–252. [Google Scholar] [CrossRef]
- Zayed, E.M.E.; Al-Joudi, S. Applications of an Extended G′/G-expansion Method to Find Exact Solutions of Nonlinear PDEs in Mathematical Physics. Math. Probl. Eng. 2010, 2010, 768573. [Google Scholar] [CrossRef]
- Manafianheris, J. Exact Solutions of the BBM and MBBM Equations by the Generalized G′/G expansion Method Equations. Int. J. Genet. Eng. 2012, 19, 1789–1796. [Google Scholar] [CrossRef]
- Islam, M.S.; Roshid, M.M.; Rahman, A.L.; Akbar, M.A. Solitary wave solutions in plasma physics and acoustic gravity waves of some nonlinear evolution equations through enhanced MSE method. J. Phys. Commun. 2019, 3, 125011. [Google Scholar] [CrossRef]
- Alharbi, A.; Abdelrahman, M.A.; Almatrafi, M.B. Analytical and numerical investigation for the DMBBM equation. Comput. Model. Eng. Sci. 2020, 122, 743–756. [Google Scholar] [CrossRef]
- Khater, M.M.; Salama, S.A. Semi–analytical and numerical simulations of the modified Benjamin–Bona–Mahony model. J. Ocean Eng. Sci. 2022, 7, 264–271. [Google Scholar] [CrossRef]
- Wang, K.J. Variational principle and diverse wave structures of the modified Benjamin-Bona-Mahony equation arising in the optical illusions field. Axioms 2022, 11, 445. [Google Scholar] [CrossRef]
- Shakeel, M.; El-Zahar, E.R.; Shah, N.A.; Chung, J.D. Generalized Exp-Function Method to Find Closed Form Solutions of Nonlinear Dispersive Modified Benjamin–Bona–Mahony Equation Defined by Seismic Sea Waves. Mathematics 2022, 10, 1026. [Google Scholar] [CrossRef]
- Alotaibi, T.; Althobaiti, A. Exact Solutions of the Nonlinear Modified Benjamin-Bona-Mahony Equation by an Analytical Method. Fractal Fract. 2022, 6, 399. [Google Scholar] [CrossRef]
- Tian, Y.; Cui, J.; Zhang, R. Exact traveling wave solutions of the strain wave and (1+ 1)-dimensional Benjamin–Bona–Mahony equations via the simplest equation method. Mod. Phys. Lett. B 2022, 36, 2250103. [Google Scholar] [CrossRef]
- Ali, A.; Seadawy, A.R. Dispersive soliton solutions for shallow water wave system and modified Benjamin-Bona-Mahony equations via applications of mathematical methods. J. Ocean Eng. Sci. 2021, 6, 85–98. [Google Scholar] [CrossRef]
- Al-Askar, F.M.; Mohammed, W.W.; Alshammari, M. Impact of brownian motion on the analytical solutions of the space-fractional stochastic approximate long water wave equation. Symmetry 2022, 14, 740. [Google Scholar] [CrossRef]
- Nemytskii, V.; Stepanov, V. Qualitative Theory of Differential Equations; Dover: New York, NY, USA, 1989. [Google Scholar]
- Khalil, R.; Al Horani, M.; Yousef, A.; Sababheh, M. A new definition of fractional derivative. J. Comput. Appl. Math. 2014, 264, 65–70. [Google Scholar] [CrossRef]
- Platen, E.; Bruti-Liberati, N. Numerical Solution of Stochastic Differential Equations with Jumps in Finance; Springer Science, Business Media: Berlin/Heidelberg, Germany, 2010; Volume 64. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).