Abstract
Risk management is very important for individual investors or companies. There are several ways to measure the risk of investment. Prices of risky assets vary rapidly and randomly due to the complexity of finance market. Random interval is a good tool to describe uncertainty including both randomness and imprecision. Considering the uncertainty of financial market, we employ random intervals to describe returns of a risk asset and define an interval-valued risk measurement, which considers the tail risk. It is called the interval-valued conditional value-at-risk (ICVaR, for short). Similar to the classical conditional value-at-risk, ICVaR satisfies the sub-additivity. Under the new risk measure ICVaR, as a manner similar to the classical Mean-CVaR portfolio model, two optimal interval-valued portfolio selection models are built. The sub-additivity of ICVaR guarantees the global optimal solution to the Mean-ICVaR portfolio model. Based on the real data from mainland Chinese stock markets and international stock markets, the case study shows that our models are interpretable and consistent with the practical scenarios.
1. Introduction
A portfolio is a collection of stocks, bonds, and financial derivatives held by investors or financial institutions to spread risk. Since Markowitz published the pioneering paper on Mean-Variance model in 1952, there have been a large number of papers on the applications and extension of the classical models. It is known that one major drawback of Markowitz’s model is that the solutions are sensitive to the underlying parameters, i.e., mean and covariance matrix of assets. In order to overcome the sensitivity, some robust portfolio models are proposed. For example, Blanchet et al. [1] (2021) studied a distributionally robust version of Markowitz’s Mean–Variance model, in which the Wasserstein distance is used to describe the discrepancy between probability measures. For more research on the robustness of portfolio selection models, readers can refer to some references in [1].
Risk measurement is very important for investors or financial analysts and must be considered in portfolio selection models. Besides variance, there are some other ways to measure the risk of assets. For example, Konnor and Yamazaki [2] (1991) studied the optimal portfolio problem based on absolute deviation or semi-variance, which is easier to calculate than variance of portfolio. Value at risk (VaR, for short) is a financial risk measurement that has been developed and widely used (see, e.g., [3,4,5]). Hamel et al. [6] extended real-valued VaR to a set-valued case. As a risk measure, VaR is convenient and easy to calculate. However, VaR has no nice mathematical properties such as convexity and sub-additivity, which are crucial to solve the optimal problem. The Mean-VaR portfolio model may not have a global optimal solution since VaR is not a convex risk measurement. In order to overcome the drawback of VaR, the conditional value-at-risk (CVaR, for short) was proposed, which is a coherent risk measurement with nice mathematical properties [7,8]. Based on Mean-CVaR portfolio selection models, Liu et al. [9] (2017) studied one-period and multi-period distributionally robust Mean-CVaR portfolio selection problems, in which the uncertainties in terms of both the distribution and the first two order moments were considered.
Because of the asymmetry of information and the incompleteness of financial markets, the price of risky assets shows a more complex form than a scalar variable. Classical models usually consider the daily opening price or daily closing price of risky assets instead of the interval of high and low prices. The latter contains more information than a scalar variable. In order to describe the complexity, randomness, and inaccuracy of the financial market, the tool of interval-valued or fuzzy variable is a good choice. For example, Ida [10] (2003) studied portfolio selection with interval coefficients. Ida [11] (2004) considered a portfolio problem with both interval and fuzzy coefficients. Giove et al. [12] (2006) studied the interval portfolio model based on regret function. Zhang and Li [13] (2009) considered the portfolio selection models based on interval-valued semi-variance. Reyes et al. [14] (2019) estimated the systematic risk in capital asset pricing with interval-valued data. Hu et al. [15] (2020) proposed an optimal interval-valued portfolio model based on possibility measure. Yan et al. [16] (2017) built a nonlinear portfolio selection model with interval-valued downside semi-variance constraints. Mohagheghi et al. [17] (2017) employed an interval type-2 fuzzy optimization approach to study the problem of research and development project evaluation and project portfolio selection. In addition, there are some references that deal with the portfolio selection without using the usual risk measure such as variance, semi-variance, VaR and CVaR. For example, Mansini and Speramza [18] (1999) built the portfolio model with minimum transaction lots, which is independent of the risk function. Under the interval framework, one can also consider interval-valued return, interval-valued VaR (IVaR, for short), and interval-valued CVaR (see, e.g., [19], 2017). Compared with classical VaR and CVaR, the so-called IVaR and ICVaR contain more information other than closing prices or opening prices.
Motivated by interval-valued risk measurement ICVaR and a classical Mean-CVaR portfolio selection model, it is natural to extend the Mean-CVaR portfolio selection to an interval-valued case. Thus, as far as we know, there is no literature dealing with a portfolio problem based on the risk measure ICVaR. The purpose of this paper is to establish the Mean-ICVaR portfolio selection model and solve it, which is not only the supplement and extension of quantitative portfolio theory, but also the need to consider the complexity and uncertainties of an actual financial market. Compared with existing references of interval-valued portfolio selection models, the innovation of this paper is that we shall use ICVaR to depict risk instead of others, such as semi-absolute variance ([13]) or downside semi-variance ([16]), etc. ICVaR is sub-additive, which is in line with the principle of portfolio diversification. At the same time, it guarantees that the local optimal solution is just the global solution of the Mean-ICVaR model.
In this paper, based on the risk measure ICVaR, two interval-valued optimal portfolio selection models are established. One is the optimal portfolio (Model 1, see (9)) by maximizing the return for a given level of risk , and the other is the optimal portfolio (Model 2, see (11)) by minimizing the risk for a given level of return . Model 1 and Model 2 are a natural extension of the classic portfolio model, which can comprehensively reflect the complexity of financial market. In order to solve the interval-valued programming problems, we shall use the satisfactory crisp equivalent form proposed by Sengupta et al. [20] (2001) and transform the interval-valued problem into the real-valued one. In the two models, there is an index denoted by , which can be given by investors and indicate their risk appetite. In Model 1, the higher the value of , the higher the tolerance of investors to risk. In Model 2, based on actual data coming from practical financial markets, a case study is given. We collect daily closing prices, daily highest prices, and daily lowest prices of some stocks coming from several different countries over a period of time. The range of daily return of a risky asset can be represented as an interval-valued random variable denoted by R. By using a historical simulation method, the expectation , IVaR and IVaR are estimated. The results of the case study show that our model is valid and reasonable.
The remainder of the paper is organized as follows: Section 2 is the preliminaries of interval-valued variables and interval-valued programming. Section 3 contributes to the interval-valued portfolio selection models based on ICVaR. Section 4 is devoted to the application of our models in real financial market. Section 6 is the concluding remarks and discussion.
2. Preliminaries
In this section, we list the knowledge of interval-valued variables and interval-valued programming needed later.
2.1. Operations and Order of Intervals
Let be the set of all real numbers, real closed intervals. Let , . If , the interval degenerates to a one-element set .
For any intervals and any real number , the Minkowski addition and scalar-multiplication are defined as follows (see e.g., [21]):
Let , which are called the midpoint and half-width (or simply be termed as ‘width’) of the interval A, respectively. Then, A can also be determined by and .
Ranking intervals is a crucial step to study interval-valued optimization problems. There are infinitely many ways to rank intervals [22]. The popular and natural way is using the endpoints or their functions such as midpoint and width. In this paper, we use the rule “midpoint-first, left-second” to rank intervals for calculating the IVaR and ICVaR. For example, for two intervals and , define if . If and , then . if and only if and . Multiple intervals can be ranked well according to this rule.
2.2. Interval-Valued Optimization
We shall employ the method introduced in [20] (2001) to solve interval-valued optimization portfolio. In [20], at first, the authors defined an index to describe the acceptability for ranking two intervals. Let ⧀ be a partial order of intervals. For any closed intervals A and B, define
where . The value of function , denoted by , may be interpreted as the grade of acceptability of ‘the interval A is less than the interval B’.
The grade of acceptability of may be classified and interpreted further on the basis of comparative position of midpoint and width of interval B with respect to those of interval A as follows:
If , then the premise ‘A is less than B’ is not accepted. If , then the interpreter accepts the premise ‘A is less than B’ with different grades of satisfaction ranging from zero to one (excluding zero and one). If , the interpreter is absolutely satisfied with the premise ‘’.
2.3. A Satisfactory Crisp Equivalent System of
Let and x be a nonnegative singleton variable. In order to solve linear programming problems with interval coefficients, Sengupta et al. [20] proposed a satisfactory crisp equivalent form for the interval inequality relations or
The satisfactory crisp equivalent form of is given as follows ([20]):
where may be interpreted as an optimistic threshold given and fixed by the decision maker. Similarly, for , the satisfactory crisp equivalent form is:
Now, we consider the maximizing interval-valued linear programming problem:
According to [20], the principle of -index indicates that, for the maximization (minimization) problem, an interval with a higher midpoint is superior (inferior) to an interval with a lower mid-value. Therefore, in order to obtain the max (min) of the interval-valued objective function, considering the midpoint is our primary concern. We reduce the interval objective function its central value and use conventional LP (Linear Programming) techniques for its solution. We also consider the width but as a secondary attribute, only to confirm whether it is within the acceptable limit of the decision maker. If it is not, one has to reduce the extent of width (uncertainty) according to his satisfaction and thus to obtain a less wide interval from the non-dominated alternatives accordingly. Thus, by the satisfactory crisp equivalent form (3), the following LP problem (6) is the necessary equivalent form of the model (5):
Similarly, the minimizing interval linear programming can be constructed as follows:
According to (4), the interval-valued programming problem (7) can be transformed to the following real valued linear programming model: (8):
Note: In the above, as you can see, there are three symbols ‘≺’, ‘’ and ‘≤’ for interval-comparison. ‘≺’ is the ‘midpoint-first, left-second’ order of interval for calculating the value of IVaR and ICVaR. ‘’ and ‘≤’ are used together to transfer the interval-valued programming models (5) and (7) into real valued linear programming problems (6) and (8), respectively.
3. Portfolio Selection Based on Icvar
We consider the portfolio problem with n risky assets. Due to the volatility and complexity of financial market, the profit is uncertain. There are several tools to describe uncertainty, for example, random variable, fuzzy variable, set-valued variable, etc. Here, the return is considered as a random interval, which includes not only randomness but also imprecision.
3.1. Interval-Valued Risk Measure
3.1.1. Interval-Valued Random Variable
Let be a complete probability space and be the real space equipped with the Borel sigma-algebra . () denotes the family of all nonempty closed (nonempty, closed and convex, respectively) subsets of . The mapping is called measurable set-valued mapping or a random set if, for any element , .
V is called an interval-valued random variable or random interval if V is measurable and takes a value in .
For any , the distribution function of V is defined by
where ≺ is the partial order according to the rule ‘midpoint-first, left-second’. V is called integrably bounded if . The real valued random variable f is called an integrable selection of V if and .
For an integrably bounded random set V,
where denotes the family of all integrable real valued random variables, the closure is taken in . For two random sets V and U, it is well known that if and only if ([21]).
The expectation of V is defined by
which is closed in .
A random set V is an interval-valued random variable if and only if , where both f and g are real valued random variables (see, e.g., [23]).
For an integrably bounded interval-valued random variable , obviously it holds that .
3.1.2. IVaR and ICVaR
In a manner similar to the usual value-at-risk and conditional value-at-risk, we define the interval-valued value-at-risk (IVaR) and interval-valued conditional value-at-risk (ICVaR) as follows:
Definition 1.
Let be a complete probability space. R is the random interval-valued return of a risky asset. Given confidence level , the value-at-risk is defined by
where inf is taken according to the order ≺.
Definition 2.
Let be a complete probability space. R is the random interval-valued return of a risky asset. Given confidence level , is the value-at-risk. The conditional value-at-risk is defined by
Similar to the real-valued CVaR, ICVaR describes the tail risk.
Remark 1.
The expectation of a random interval is linear for positive coefficients (c.f. [21]). As a manner similar to the real-valued CVaR, it can be proved that the risk measure ICVaR satisfies the sub-additivity.
3.2. Portfolio Models
Let the rate of return of asset be an interval-valued random variable, be the rate of return of the i-th security at the j-th period, and ,
Given the confidence level , () is the value-at-risk (conditional value-at-risk, resp.) of the i-th risky asset at the j-th period, , . Let () be the proportion of the i-th asset in the portfolio. By Remark 1, the value of a portfolio is less than the linear composition of with weights (), which consists with the rule that the portfolio can spread the risk.
Now, we build two models of portfolio selection as follows:
- Model 1We consider the optimal portfolio problem under a given acceptable maximum of risk level:where is the expectation return of the i-th asset, is the acceptable maximum risk in the j-period, , which are subjective and given by the investors.By (6), the corresponding real-valued linear programming problem of (9) is represented as (10) below:where is the midpoint of interval A and the semi-width of A. is a given index in advance, which can describe the degree of risk appetite of investors. The larger , the lower the risk aversion:
- Model 2Correspondingly, by (8), the interval-valued linear programming problem (11) is represented as the following real-valued linear programming model (12) belowwhere and have the same meaning as that in (10).
Remark 2.
Due to the complexity of practical market and random intervals, it is difficult to obtain the distribution function of the return of a risk asset. Therefore, it is almost impossible to calculate the exact values of , , , , etc. In the following case study, we use historical data to estimate the related values. For mathematical expectation, the moment estimator (13) is employed, which is consistent. For example, let be the given observations of random variable R, and the estimation of is given as follows:
4. Case Study
This section presents two case studies based on the data from different stock markets. We use a historical simulation method to estimate the expectation, IVaR and ICVaR without any special assumption about the financial market. Therefore, there is nothing technically difficult to replicate the study for different data sets. The software R is employed to make the empirical analysis.
The data used in the case studies are stock’s daily closing price, daily highest price, and daily lowest price during the research period. The closing price of shares on day j is denoted by . denotes the highest price on day j, and denotes the lowest price on day j. According to the daily closing price, the highest price, and the lowest price of the stock, we calculate the exact value and the interval value of the return rate. Denote the real valued returns by , , , . is the interval of return on day j. As usual, the real valued return does not obey normal distribution. Then, it is not suitable to compute the real valued VaR by using the variance–covariance method. By using a historical simulation method, we estimate the values of real-valued VaR, CVaR and IVaR, ICVaR based on historical data. There are many methods to rank intervals. Here, the “midpoint-first, left-second” of the intervals ranking method is used to estimate IVaR and ICVaR under the confidence level . By the satisfactory crisp equivalent system, interval-valued programming problems are transformed into real-valued ones. Then, the optimal solutions of the corresponding portfolio models are obtained.
- Case 1In the case study 1, we selected the stocks of ten listed companies of financial markets on the Chinese mainland as samples. The listed companies include oil, bank, coal, liquor, security, medicine, technology industry, and so on. The ticker symbols of stocks are listed in Table 1. Daily prices were collected in the period from January 2016 to September 2020 (Data source: http://www.finance.sina.cn (accessed on 1 October 2021)). In Table 2, you can find that returns of all assets are not normally distributed. We will use historical simulation method to estimate expectation of return.

Table 1.
Sample assets.
Table 1.
Sample assets.
| Number | ST01 | ST02 | ST03 | ST04 | ST05 |
| Ticker | SH600028 | SH600085 | SH600188 | SH600536 | SH601939 |
| Number | ST06 | ST07 | ST08 | ST09 | ST10 |
| Ticker | SZ000333 | SZ6000735 | SZ000776 | SZ000858 | SZ002428 |

Table 2.
Jarque–Bera test, data from Chinese Mainland markets.
Table 2.
Jarque–Bera test, data from Chinese Mainland markets.
| Number | ST01 | ST02 | ST03 | ST04 | ST05 |
| Number | ST06 | ST07 | ST08 | ST09 | ST10 |
In Table 3, when the maximum risk level is different, the selection of assets is different. When taking the lower acceptable risk level , the investor prefers the stock ST05 (CCB, China Construction Bank) and ST08 (GF Securities Co., Ltd) since these two stocks have stable returns and lower risk compared with the stock ST06 and ST09, which implies that the investor is more conservative than one who takes . Table 3 also shows that the less , the more allocation to assets with lower risk. Correspondingly, the weights of ST06 (Mediea Group) and ST09 (Wuliangye Group) increase with respect to . The result implies that ST06 and ST09 have higher returns but accompanied with higher risk, which is consistent with the actual situation of the market.

Table 3.
Portfolio, Model 1 with the same .
In Table 4, given the minimum return constraint , and , to minimize the risk, it is obvious that ST05 has the highest proportion in each scenario, very different from the case in Model 1. Its lower risk property explains this result. In addition, one can figure out that the weight of stock ST05 increases with respect to . However, the proportion of ST07 behaves on the contrary. In a word, the solution is sensitive to the constraints and also depends on the index . One can also figure out the law from Table 5 and Table 6.

Table 4.
Portfolio, Model 2 with the same .

Table 5.
Portfolio, Model 1 with different for different .

Table 6.
Portfolio, Model 2 with different for different .
- Case 2In Case study 2, the data set comes from international stock markets. We selected six stocks from the London Stock Exchange, Hong Kong Stock Exchange, NASDAQ Stock Exchange, and New York Stock Exchange. The daily stock closing price, the highest price and the lowest price from January 2020 to August 2022 (Data source: https://www.10jqka.com.cn/ (accessed on 20 August 2022)) were collected. The listed companies include bank, security, technology industry, auto industry, and so on. Since the data of the same period as that in Case study 1 from the Chinese Mainland markets are not available, we study the two sets of data separately.
Table 7 is the detailed information of six stocks from international markets.

Table 7.
International Sample Assets.
In order to visually present the daily returns of six stocks, we give the time series of return as Figure 1. The blue (red) curve represents the highest (lowest, respectively) daily return of the underlying stock. The green curve is the daily return based on daily closing prices. It can be seen that the first stock ST01(Barclays Bank PLC.) is very special. It is almost a straight line except some sharp jumps (−11.9% on 19 March 2021, −9.86% on 14 April 2021, −7.01% on 30 April 2021, −4.87% on 3 March 2022, −7.19% on 4 March 2022, and −9.35% on 7 March 2022). Maybe there was something important that happened. We will see that there is no allocation to stock ST01 (Barclays Bank PLC) according to the results of Model 1 and Model 2 because smaller volatility means less opportunity for big profits.
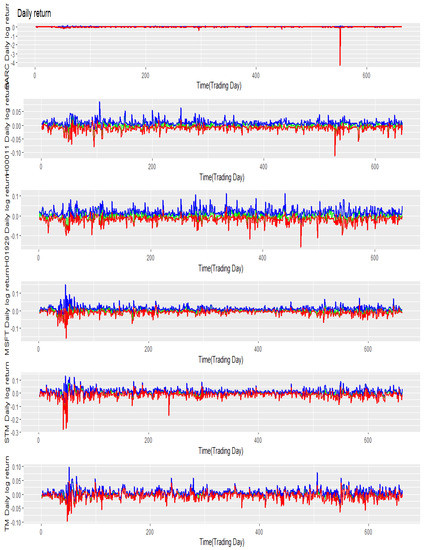
Figure 1.
Return Time Series Plot, data from international market.
According to the result of the Jarque–Bera test in Table 8, none of the daily returns are normally distributed.

Table 8.
Jarque–Bera test, data from international market.
Table 9 presents the daily return , the lower daily return , the higher daily return , and the midpoint . As you can see, the stock ST04 (Microsoft Corporation) has the best return, followed by stock ST06 (Toyota Motor Corporation). The stock ST01 (Barclays Bank PLC.) has the worst return.

Table 9.
Return, data from international market.
Table 10 shows the values of the lower bound of ICVaR, the upper bound of ICVaR, midpoint, and width. One can see that stock ST01 has the biggest ICVaR since there were several sharp drops. ICVaR is computed in terms of the quantile given level . The stock ST02 (Hang Seng Bank Ltd.) has the smallest ICVaR, followed by ST06 and then ST04. That is why you will find that the investment shares are allocated to these three stocks according to Model 1 and Model 2.

Table 10.
ICVaR, data from international market.
Table 11 presents the result of Model 1 (9) under given constraint and . Here, we take since it is a small sample size. That is, all data from January 2022 to August 2022 are considered in one investment period. Then, one constraint condition is needed. In order to show the validity of Model 1, we solve the problem under serval different constraints with two levels of for comparison. Table 11 shows that the solution is sensitive to the constraint . When taking (wide interval), all investment shares are allocated to ST02 since ST02 has lower risk and better return. If taking (less tolerance for risk), then the allocation is dispersed to ST02, ST04, and ST06. Among them, ST06 accounted for the main investment share since compared with ST02, it has much better return. In addition, compared with ST04, ST06 has much lower ICVaR.

Table 11.
Solution of Model 1, data from international markets.
Similar to Model 1, for Model 2 (11), we also take . The constraint condition is denoted by . For comparison, we take three different constraints. Solutions of Model 2 under three different constraints with five levels of are given in Table 12. Given the smallest return acceptable, investors select ST02 and ST06. It is reasonable since ST02 has the lowest ICVaR and is followed by that of ST06, which is consistent with minimizing the objective function. As the value of decreases, the investment share of ST02 decreases, while the investment share of ST06 and the optimal value of objective function increase. It can be explained that smaller means that the investors have less tolerance of lower than expected portfolio returns. High returns are often accompanied by high risks. Therefore, less leads to higher optimal ICVaR of the portfolio.

Table 12.
Solution of Model 2, data from international markets.
The size of indicates the degree of risk preference of investors. From the results of the case study, such as in Table 3, Table 4 and Table 12, it is seen that the investment share allocation changes significantly with different values of under appropriate constraint conditions. This means that a different risk preference has different weights for portfolio selection. In the process of solving the model, we need to give appropriate constraints, which must be based on the relevant returns and values of ICVaR calculated by historical data. For example, in Table 11, the constraint , it almost covers the of six stocks, which leads to the entire investment in ST04. A similar thing will happen if selecting a too big or too small in Model 2. Thus, it is important to select appropriate constraints and for making a portfolio selection decision for investors. As the analysis above, our models make sense and are interpretable.
5. Discussion
Our models only considered the historical transaction data. However, the risk of asset is affected by many factors. It is not only related to the industry, but also closely related to the size and financial status of the company, trading time, national policy, and so on. The object function is the expected return, which is an average during a long-term period. The result of the models is just advice. For investors, before making a decision, it is necessary to consider other information such as current policy and assets and liabilities of enterprises. Indebtedness ratio is an important indicator to determine the stability and sustainability of enterprises, which could affect the stock returns and play a significant role in the decision-making process. Regarding this knowledge, one can refer to the professional article written by Valaskova et al. [24].
The authors thanks the anonymous referee’s valuable advice, who pointed out an interesting research direction to extend the IVaR and ICVaR by considering interval-valued distortion risk measure. Under the framework of single valued theory, the distortion risk measure extends VaR and CVaR, which is widely studied and applied to risk management; see, e.g., [25]. However, for an interval-valued case, to our knowledge, there is no literature on the distortion risk. To define the interval-valued distortion risk measure as a manner similar to the classical distortion risk measure, the key point is to define an appropriate interval-valued distortion function, which should be non-decreasing in the framework of interval-valued theory. It may be related to the interval-valued Choquet integral (see, e.g., [26]). However, compared with single valued variables, there is a delicate problem on arithmetic of intervals. That is, arithmetics of Minkowski addition and scalar multiplication of intervals are not linear. If we define , then . In order to overcome this drawback, the Hukuhara difference was proposed, which guarantees the difference between two identical sets to be an empty set. However, the Hukuhara difference may not exist between two sets, even for two intervals. We have some ideas to overcome this problem. We are thinking about the distortion risk measure under the framework of interval-valued theory. According to our preliminary conclusion, the interval-valued distortion risk measure is expected to generalize the IVaR and ICVaR. Since more complex theory related to interval analysis and capacity integral is involved, it is inconvenient to discuss it in detail here. We will dedicate ourselves to the work in another paper in the near future.
6. Conclusions
This paper contributes to the optimal selection under an interval-valued environment. At first, the interval-valued conditional value-at-risk (ICVaR) was defined, which satisfies the sub-additivity. In addition, then, based on the risk measure, two interval-valued portfolio selection models were constructed, where both the return and risk of a risky asset are random intervals. A random interval includes both randomness and imprecision, which can describe the uncertainty better than a vector-valued random variable. The“midpoint-first, left-second” method was employed to rank the intervals for estimating IVaR and ICVaR by a historical simulation method. Of course, one can use other methods to rank intervals, such as “midpoint-first, right-second” or possibility degree, etc. A different ranking method will lead to different IVaR and ICVaR for the risky asset. Upon solving the maximization and minimization problem of interval values, the satisfactory crisp equivalent system of ([20]) was used. In Model 1 and Model 2, the -index can describe investors’ subjective preference or aversion to risk, which is an innovation different from the classical portfolio model. The smaller the index, the higher the risk aversion of investors. An investor can select an appropriate value of according to his (or her) risk tolerance level. The results of empirical analysis also confirm this conclusion. However, the real finance market is very complicated. Our models are based on the practical data of markets. Due to the complexity of markets, the distribution function of random return is difficult to obtain. Then, we use the historical simulation method to estimate the expectation, IVaR and ICVaR without any other deep investigation, and assumption on the financial markets. According to the analysis of the case study, the results show that our models are interpretable and consistent with the practical scenarios. It is expected that the models have certain guiding significance for investors’ choices.
Author Contributions
This research was designed and performed by all authors. The data were collected by K.Z. J.Z. contributed to writing—original draft. J.Z. and K.Z. contributed to model solving and writing—review and editing. All authors have read and agreed to the submitted version of the manuscript.
Funding
This work is supported by the Natural Science Foundation of Beijing Municipality (No. 1192015).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data of stocks in Chinese markets are publicly available at http://www.finance.sina.cn (accessed on 1 October 2021). The data of stocks in international stock market are publicly available at https://www.10jqka.com.cn/ (accessed on 20 August 2022).
Acknowledgments
The authors are grateful to the editor and referees for valuable comments which led to improvements in this work. Special gratitude goes to two anonymous referees for recommending references [24,25].
Conflicts of Interest
The authors declare no conflict of interest.
Sample Availability
Samples are available from the authors.
Abbreviations
The following abbreviations are used in this manuscript:
| VaR | value-at-risk |
| CVaR | conditional value-at-risk |
| IVaR | interval-valued value-at-risk |
| ICVaR | interval-valued conditional value-at-risk |
References
- Blanchet, J.; Chen, L.; Zhou, X. Distributionally robust mean-variance portfolio selection with Wasserstein distances. Manag. Sci. 2021, 1–29. [Google Scholar] [CrossRef]
- Konno, H.; Yamazaki, H. Mean-absolute deviation portfolio optimization model and its applications to Tokyo stock market. Manage. Sci. 1991, 37, 519–531. [Google Scholar] [CrossRef]
- Castellacci, G.; Siclari, M. The practice of Delta-Gamma VaR: Implementing the quadratic portfolio model. Eur. J. Oper. Res. 2003, 150, 529–545. [Google Scholar] [CrossRef]
- Costello, A.; Asem, E.; Gardner, E. Comparison of historically simulated VaR: Evidence from oil prices. Energy Econ. 2008, 30, 2154–2166. [Google Scholar] [CrossRef]
- Ramazan, G.; Faruk, S. High volatility, thick tails and extreme value theory in value-at-risk estimation. Insur. Math. Econ. 2003, 33, 337–356. [Google Scholar]
- Hamel, A.H.; Rudloff, B.; Yankova, M. Set-valued average value at risk and its computation. Math. Financ. Econ. 2013, 7, 229–246. [Google Scholar] [CrossRef]
- Mansini, R.; Ogryczak, W.; Speranza, M.G. Conditional value at risk and related linear programming models for portfolio optimization. Ann. Oper. Res. 2007, 152, 227–256. [Google Scholar] [CrossRef]
- Rockafellar, R.T.; Uryasev, S. Optimization of conditional value-at-risk. J. Risk 2000, 2, 21–41. [Google Scholar] [CrossRef]
- Liu, J.; Chen, Z.; Lisser, A.; Xu, Z. Closed-form optimal portfolios of distributionally robust mean-CVaR problems with unknown mean and variance. Appl. Math. Optim. 2017. [Google Scholar] [CrossRef]
- Ida, M. Portfolio selection problem with interval coefficients. Appl. Math. Lett. 2003, 16, 709–713. [Google Scholar] [CrossRef]
- Ida, M. Solutions for the portfolio selection problem with interval and fuzzy coefficients. Reliab. Comput. 2004, 1, 389–400. [Google Scholar] [CrossRef]
- Giove, S.; Funari, S.; Nardelli, C. An interval portfolio selection problem based on regret function. Eur. J. Oper. Res. 2006, 170, 253–264. [Google Scholar] [CrossRef]
- Zhang, J.; Li, S. The portfolio selection problem with random interval-valued return rates. Int. J. Innov. Comput. I. 2009, 5, 47–56. [Google Scholar]
- Reyes, D.M.A.; de Souza, R.M.C.R.; Cysneiros, F.J.A. Estimating risk in capital asset pricing for interval-valued data. Int. J. Bus. Inf. Syst. 2019, 32, 522–535. [Google Scholar] [CrossRef]
- Hu, J.; Ma, F.; Sui, Y. A mean-variance portfolio selection model with interval-valued possibility measures. Math. Probl. Eng. 2020, 2020, 4135740. [Google Scholar] [CrossRef]
- Yan, D.; Hu, Y.; Lai, K. A nonlinear interval portfolio selection model and its application in banks. J. Syst. Sci. Complex 2017. [Google Scholar] [CrossRef]
- Mohagheghi, V.; Mousavi, S.M.; Vahdani, B.; Shahriari, M.R. R & D project evaluation and project portfolio selection by a new interval type-2 fuzzy optimization approach. Neural Comput. Appl. 2017, 28, 3869–3888. [Google Scholar]
- Mansini, R.; Speranza, M.G. Heuristic algorithms for the portfolio selection problem with minimum transaction lots. Eur. J. Oper. Res. 1999, 114, 219–233. [Google Scholar]
- Li, Z.; Zhang, J.; Wang, X. Interval-valued risk measure models and empirical analysis. In Proceedings of the Fuzzy Systems Association, International Conference on Soft Computing & Intelligent Systems, Otsu, Japan, 27–30 June 2017. [Google Scholar]
- Sengupta, A.; Pal, T.K.; Chakraborty, D. Interpretation of inequality constraints involving interval coefficients and a solution to interval linear programming. Fuzzy Set Syst. 2001, 119, 129–138. [Google Scholar] [CrossRef]
- Li, S.; Ogura, Y.; Kreinovich, V. Limit Theorems and Applications of Set-Valued and Fuzzy Sets-Valued Random Variables; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2002. [Google Scholar]
- Wang, W.; Wang, Z. Total orderings defined on the set of all fuzzy numbers. Fuzzy Set Syst. 2014, 243, 131–141. [Google Scholar]
- Zhang, J.; Mitoma, I.; Okazaki, Y. Submartingale property of set-valued stochastic integration associated with Poisson process and related integral equations on Banach spaces. J. Nonlinear Convex A. 2021, 22, 775–799. [Google Scholar]
- Valaskova, K.; Kliestik, T.; Gajdosikova, D. Distinctive determinants of financial indebtedness: Evidence from Slovak and Czech enterprises. Equilibrium. Q. J. Econ. Econ. Policy 2021, 16, 639–659. [Google Scholar] [CrossRef]
- Wirch, J.L.; Hardy, M.R. Distortion risk measures: Coherence and stochastic dominance. In Proceedings of the 5th International Congress on Insurance: Mathematics and Economics, State College, PA, USA, 25 July 2001; pp. 15–17. [Google Scholar]
- Jang, L.C. A note on convergence properties of interval-valued capacity functionals and Choquet integrals. Inf. Sci. 2012, 183, 151–158. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).