Existence Results for the Solution of the Hybrid Caputo–Hadamard Fractional Differential Problems Using Dhage’s Approach
Abstract
:1. Introduction
2. Preliminaries
- If for each , the set has convex values, then we say that the set-valued map is convex.
- The set-valued map is said to be an upper semi-continuous map if for every belongs to and for every open set with , there is a neighborhood of such that .
- The set-valued map has a fixed point if . The collection of all fixed points of is represented by .
- Assume to be a metric space. For each , the Pompeiu–Hausdorff metric is defined aswhere, and .
- The set-valued map is said to be Lipschitzian if holds for every where is a Lipschitz constant. If , then we say that the Lipschitz map is a contractive map.
- We say that is measurable if the function is measurable .
- The graph of is defined by . It is noticeable that the graph of is said to be closed if for every arbitrary sequence and with and , we obtain . If is an upper semi-continuous map, then is a closed set.
- A set-valued map is completely continuous operator if the is relatively compact . Furthermore, we assume that by the complete continuity assumption, the map has a closed graph. Then, the multi-valued map is upper semi-continuous.
- The set-valued map has a Caratheodory property if the function is upper semi-continuous and the function is measurable for every . Furthermore, A Caratheodory multi-valued mapping has -Caratheodory property if for every there exists provided thatfor all and for every .
- The selections of at are represented by
- 1.
- is a Lipschitzian map so that is a Lipschitz constant;
- 2.
- is completely continuous;
- 3.
- , where .
- (i)
- The operator equation has a solution contained in or;
- (ii)
- There exists with so that for some .
- 1.
- is a Lipschitzian map so that is a Lipschitz constant;
- 2.
- has compactness and an upper-semi continuity property;
- 3.
- with .
- (i)
- there exists a solution contained in for the inclusion or;
- (ii)
- the set is an unbounded set.
3. Main Results
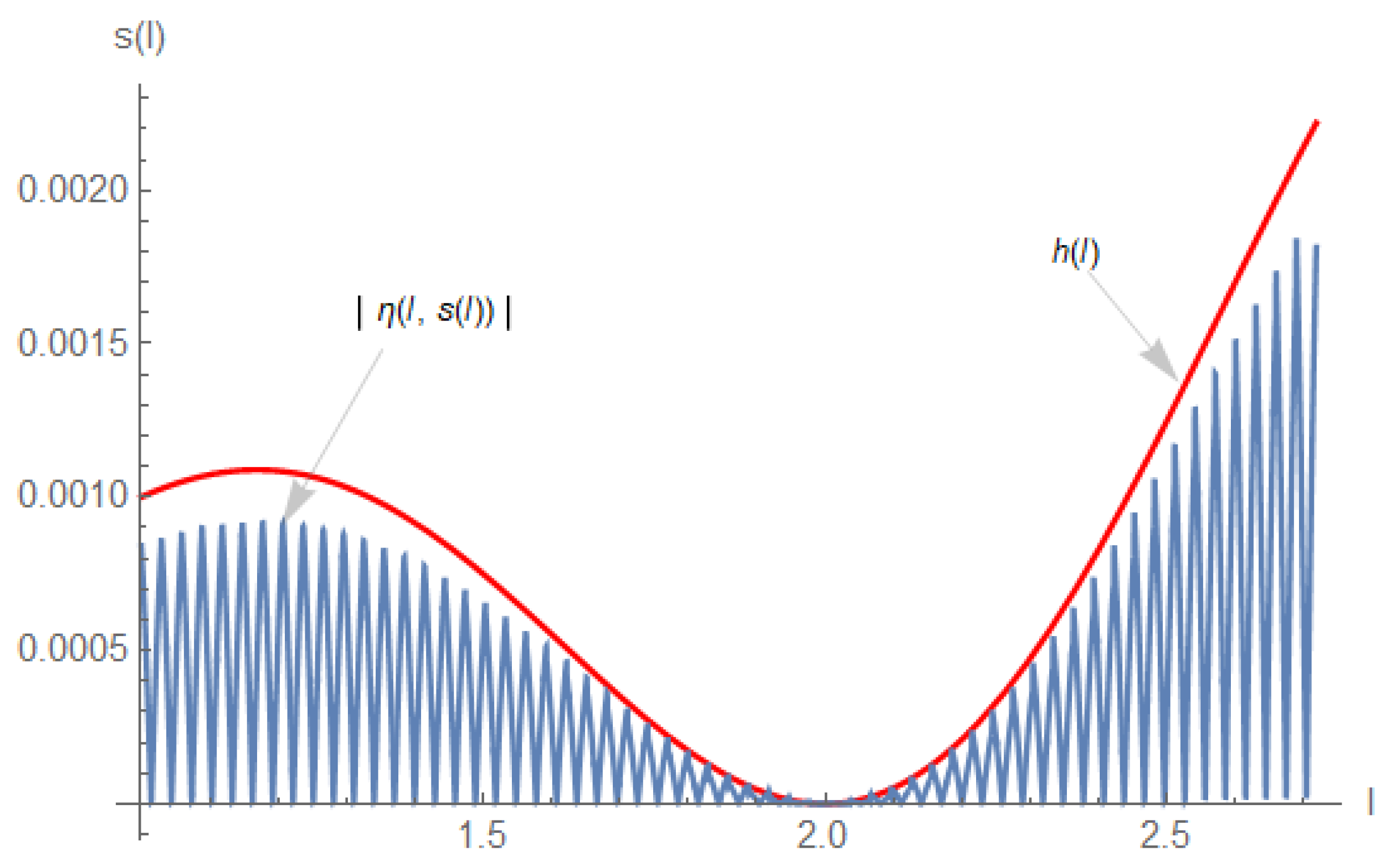
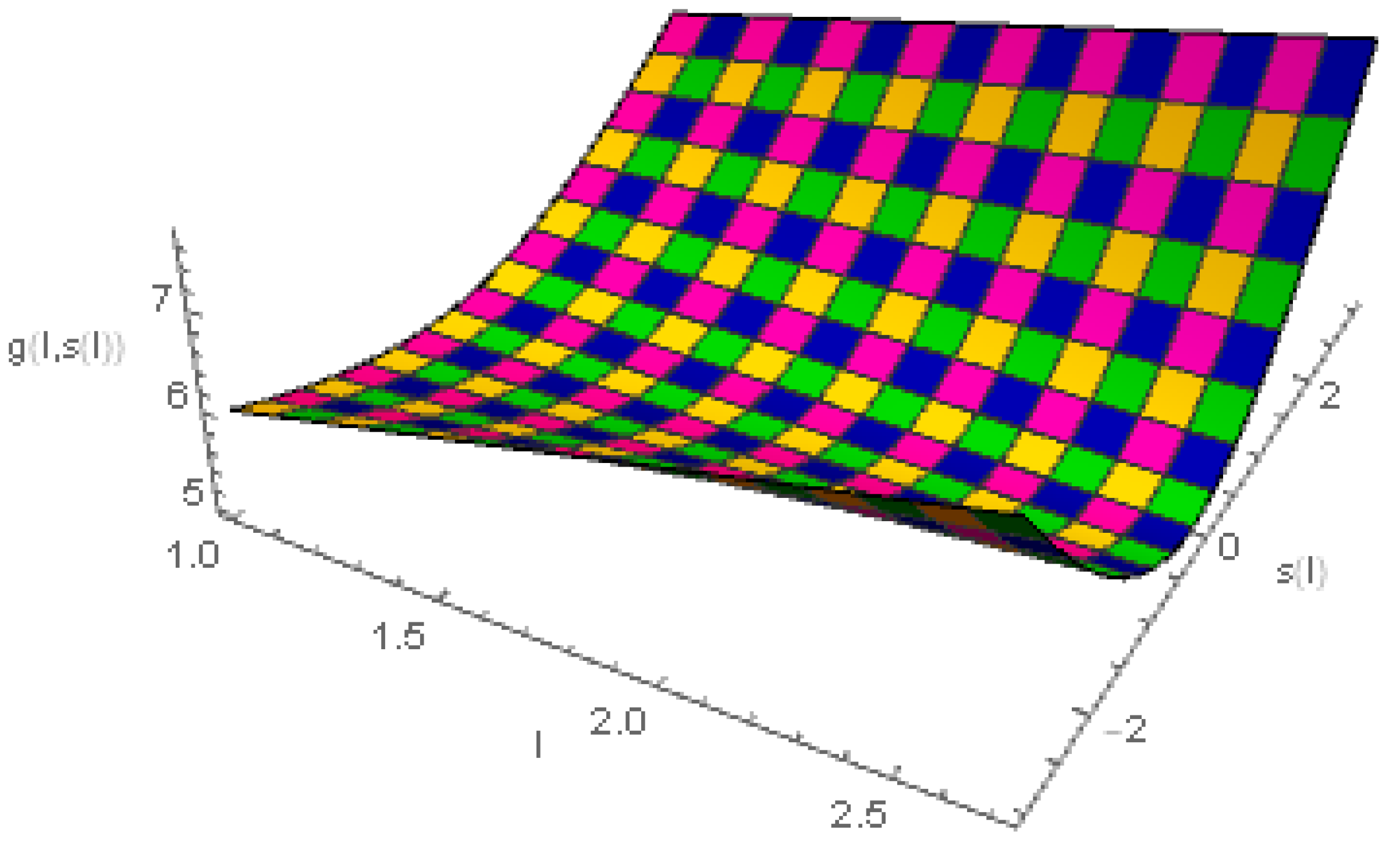
4. Examples
5. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| Caputo–Hadamard Fractional Derivative | |
| Caputo–Hadamard Fractional Integral | |
| CH-FBVP | Caputo–Hadamard Fractional Boundary Value Problem |
| CH–FIBVP | Caputo–Hadamard Fractional Inclusion Boundary Value Problem |
| Normed Space | |
| Set of all Subsets of | |
| Pompeiu–Hausdorff metric | |
| Selections of at |
References
- Hilfer, R. Application of Fractional Calculus in Physics; World Scientific: Singapore, 2000. [Google Scholar]
- Kilbas, A.A.; Srivastava, H.M.; Rujillo, J.J. Theory and Applications of Fractional Diferential Equations; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Mohammadi, H.; Rezapour, S. Two existence results for nonlinear fractional diferential equations by using fixed point theory on ordered gauge spaces. J. Adv. Math. Stud. 2013, 6, 154–158. [Google Scholar]
- Baleanu, D.; Etemad, S.; Rezapour, S. A hybrid Caputo fractional modeling for thermostat with hybrid boundary value conditions. Bound. Value Probl. 2020, 2020, 64. [Google Scholar] [CrossRef] [Green Version]
- Baleanu, D.; Nazemi, S.Z.; Rezapour, S. Attractivity for a k-dimensional system of fractional functional diferential equations and global attractivity for a k-dimensional system of nonlinear fractional diferential equations. J. Inequal. Appl. 2014, 2014, 31. [Google Scholar] [CrossRef] [Green Version]
- Baleanu, D.; Nazemi, S.Z.; Rezapour, S. The existence of solution for a k-dimensional system of multi-term fractional integro-diferential equations with anti-periodic boundary value problems. Abstr. Appl. Anal. 2014, 2014, 896871. [Google Scholar] [CrossRef] [Green Version]
- Wang, G.; Ren, X.; Zhang, L.; Ahmad, B. Explicit iteration and unique positive solution for a Caputo–Caputo–Hadamard fractional turbulent fow model. IEEE Access 2019, 7, 109833–109839. [Google Scholar] [CrossRef]
- Wang, G.; Pei, K.; Chen, Y.Q. Stability analysis of nonlinear Caputo–Hadamard fractional diferential system. J. Franklin Inst. 2019, 356, 6538–6546. [Google Scholar] [CrossRef]
- Wang, G.; Pei, K.; Agarwal, R.P.; Zhang, L.; Ahmad, B. Nonlocal Caputo–Hadamard fractional boundary value problem with Caputo–Hadamard integral and discrete boundary conditions on a half-line. J. Comput. Appl. Math. 2018, 343, 230–239. [Google Scholar] [CrossRef]
- Pei, K.; Wang, G.; Sun, Y. Successive iterations and positive extremal solutions for a Caputo–Hadamard type fractional integro-diferential equations on infnite domain. Appl. Math. Comput. 2017, 312, 158–168. [Google Scholar]
- Abbas, S.; Benchohra, M.; Hamani, S.; Henderson, J. Upper and lower solutions method for Caputo–Hadamard fractional differential inclusions. Math. Moravica 2019, 23, 107–118. [Google Scholar] [CrossRef]
- Benchohra, M.; Graef, J.R.; Guerraiche, N.; Hamani, S. Nonlinear boundary value problems for fractional differential inclusions with Caputo-Hadamard derivatives on the half line. AIMS Math. 2016, 6, 6278–6292. [Google Scholar] [CrossRef]
- Hamani, S.; Henderson, J. Boundary value problems for fractional differential inclusions with nonlocal conditions. Mediterr. J. Math. 2016, 13, 967–979. [Google Scholar] [CrossRef]
- Benhamidaa, W.; Hamania, S.; Hendersonb, J. Boundary Value Problems For Caputo-Hadamard fractional differential equations. Adv. Theory Nonlinear Anal. Its Appl. 2018, 2, 138–145. [Google Scholar]
- Benchohra, M.; Hamani, S.; Zhou, Y. Oscillation and nonoscillation for Caputo–Hadamard impulsive fractional differential inclusions. Adv. Differ. Equations 2019, 2019, 74. [Google Scholar] [CrossRef]
- Dhage, B.C.; Lakshmikantham, V. Basic results on hybrid diferential equation. Nonlinear Anal. Hybrid Syst. 2010, 4, 414–424. [Google Scholar] [CrossRef]
- Zhao, Y.; Sun, S.; Han, Z.; Li, Q. Theory of fractional hybrid diferential equations. Comput. Math. Appl. 2011, 62, 1312–1324. [Google Scholar] [CrossRef] [Green Version]
- Sun, S.; Zhao, Y.; Han, Z.; Li, Y. The existence of solutions for boundary value problem of fractional hybrid differential equations. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 4961–4967. [Google Scholar] [CrossRef]
- Hilal, K.; Kajouni, A. Boundary value problems for hybrid diferential equations with fractional order. Adv. Differ. Equations 2015, 2015, 183. [Google Scholar] [CrossRef] [Green Version]
- Baleanu, D.; Hedayati, V.; Rezapour, S.; Al Qurashi, M.M. On two fractional diferential inclusions. SpringerPlus 2016, 5, 882. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Infante, G.; Webb, J. Loss of positivity in a nonlinear scalar heat equation. Nonlinear Differ. Equ. Appl. 2006, 13, 249–261. [Google Scholar] [CrossRef]
- Nieto, J.J.; Pimentel, J. Positive solutions of a fractional thermostat model. Bound. Value Probl. 2013, 2013, 5. [Google Scholar] [CrossRef] [Green Version]
- Miller, K.S.; Ross, B. An Introduction to Fractional Calculus and Fractional Diferential Equations; Wiley: New York, NY, USA, 1993. [Google Scholar]
- Deimling, K. Multi-Valued Diferential Equations; de Gruyter: Berlin, Germany, 1992. [Google Scholar]
- Aubin, J.; Cellina, A. Diferential Inclusions: Set-Valued Maps and Viability Theory; Springer: Berlin, Germany, 1984. [Google Scholar]
- Dhage, B.C. Nonlinear functional boundary value problems involving Carathedory. Kyungpook Math. J. 2006, 46, 427–441. [Google Scholar]
- Lasota, A.; Opial, Z. An application of the Kakutani–Ky Fan theorem in the theory of ordinary diferential equations. Bull. Acad. Pol. Sci. Set. Sci. Math. Astronom. Phys. 1965, 13, 781–786. [Google Scholar]
- Dhage, B.C. Existence results for neutral functional diferential inclusions in Banach algebras. Nonlinear Anal. 2006, 64, 1290–1306. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yaseen, M.; Mumtaz, S.; George, R.; Hussain, A. Existence Results for the Solution of the Hybrid Caputo–Hadamard Fractional Differential Problems Using Dhage’s Approach. Fractal Fract. 2022, 6, 17. https://doi.org/10.3390/fractalfract6010017
Yaseen M, Mumtaz S, George R, Hussain A. Existence Results for the Solution of the Hybrid Caputo–Hadamard Fractional Differential Problems Using Dhage’s Approach. Fractal and Fractional. 2022; 6(1):17. https://doi.org/10.3390/fractalfract6010017
Chicago/Turabian StyleYaseen, Muhammad, Sadia Mumtaz, Reny George, and Azhar Hussain. 2022. "Existence Results for the Solution of the Hybrid Caputo–Hadamard Fractional Differential Problems Using Dhage’s Approach" Fractal and Fractional 6, no. 1: 17. https://doi.org/10.3390/fractalfract6010017
APA StyleYaseen, M., Mumtaz, S., George, R., & Hussain, A. (2022). Existence Results for the Solution of the Hybrid Caputo–Hadamard Fractional Differential Problems Using Dhage’s Approach. Fractal and Fractional, 6(1), 17. https://doi.org/10.3390/fractalfract6010017







