Electrical Circuits RC, LC, and RLC under Generalized Type Non-Local Singular Fractional Operator
Abstract
1. Introduction
2. Fractional Electrical Circuits
2.1. Fractional RC Electrical Circuits under Non-Local M-Derivative in the Sense of Caputo
2.2. Fractional Inductance-Capacitance (LC) Electrical Circuits under Non-Local M-Derivative in the Sense of Caputo
2.3. Fractional RLC Electrical Circuits under Non-Local M-Derivative in the Sense of Caputo
3. Comparative Analysis and Concluding Remarks
- We have carried out an efficient extension of a physical problem through a non-local singular fractional operator by providing the solutions including three arbitrary parameters , , and ;
- A detailed analysis has been introduced for the Resistance-Capacitance (RC), Inductance-Capacitance (LC), and Resistance-Inductance-Capacitance (RLC) electric circuits utilizing a generalized type fractional operator in the sense of Caputo called non-local M-derivative;
- Due to the fact that all solutions obtained in this study depend on three parameters unlike the other studies in the literature, the solutions we have obtained are more general results;
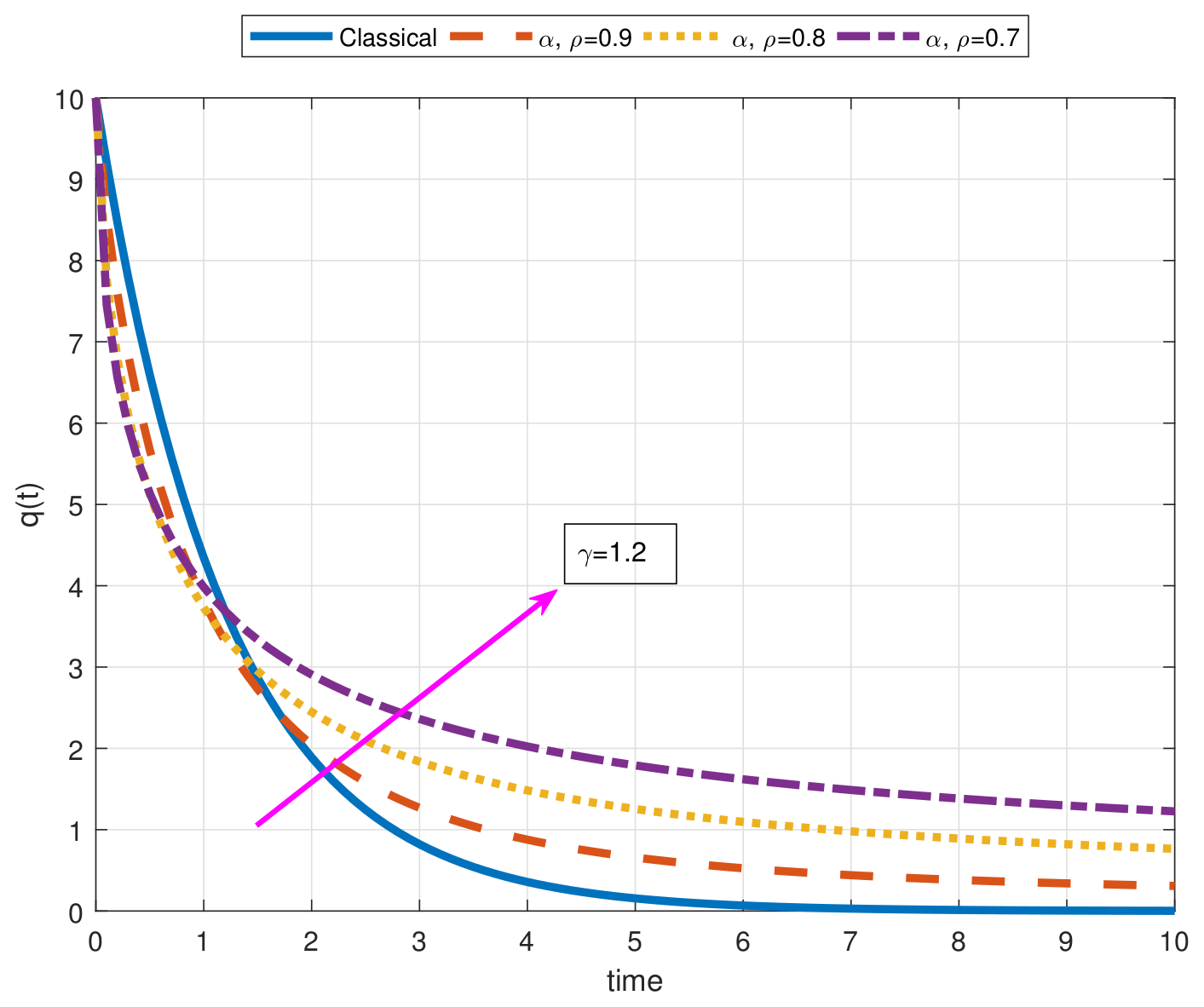
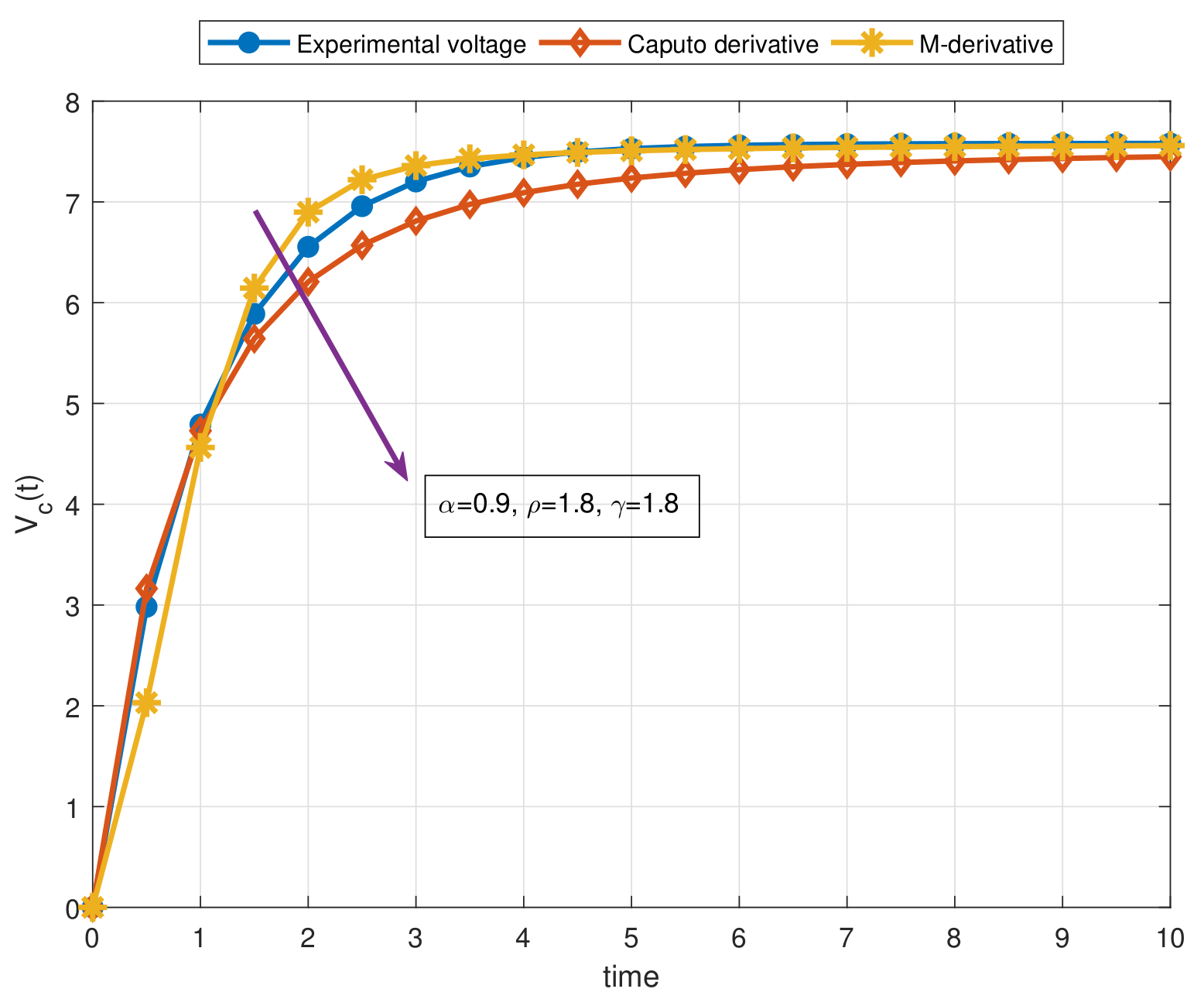
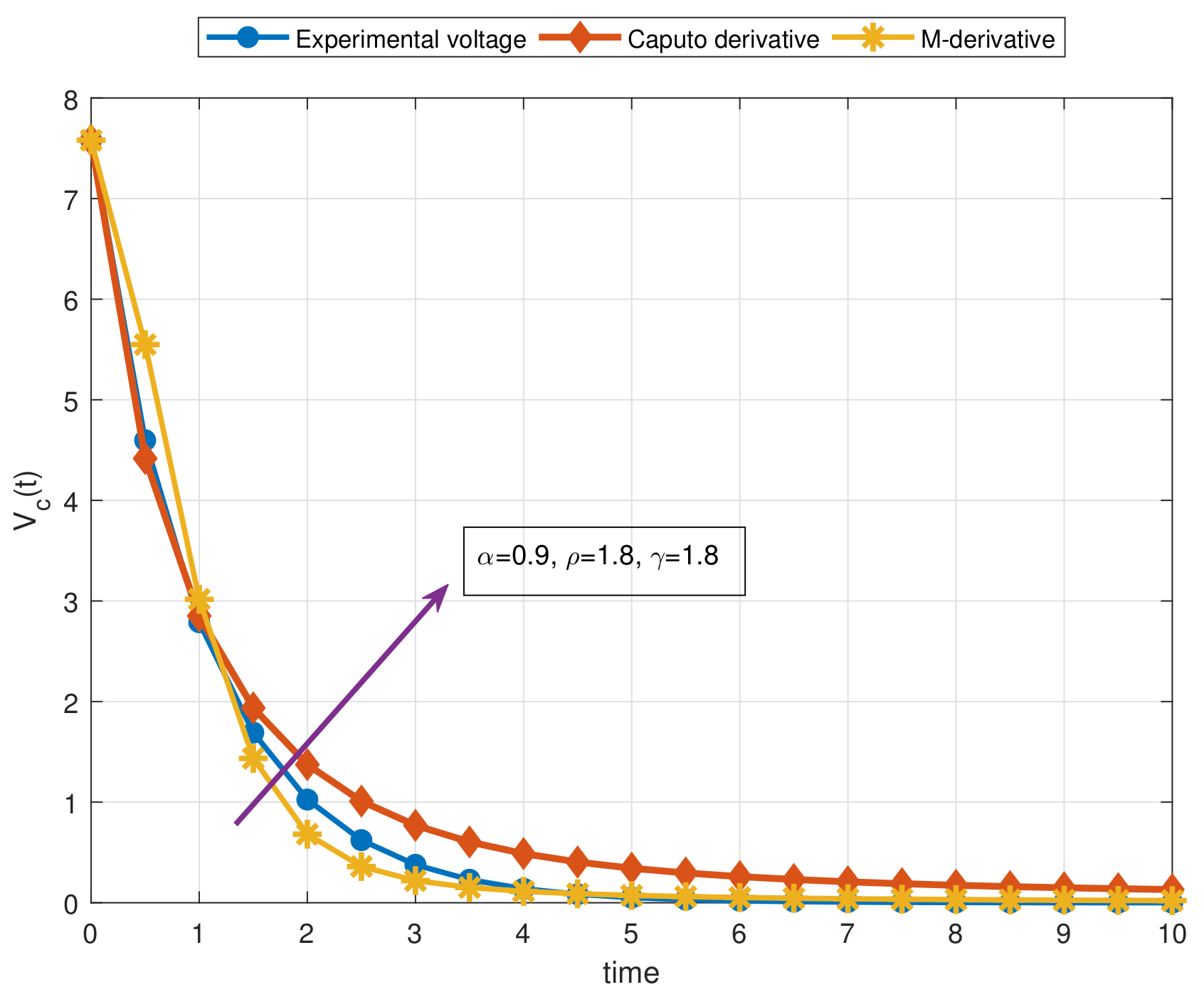
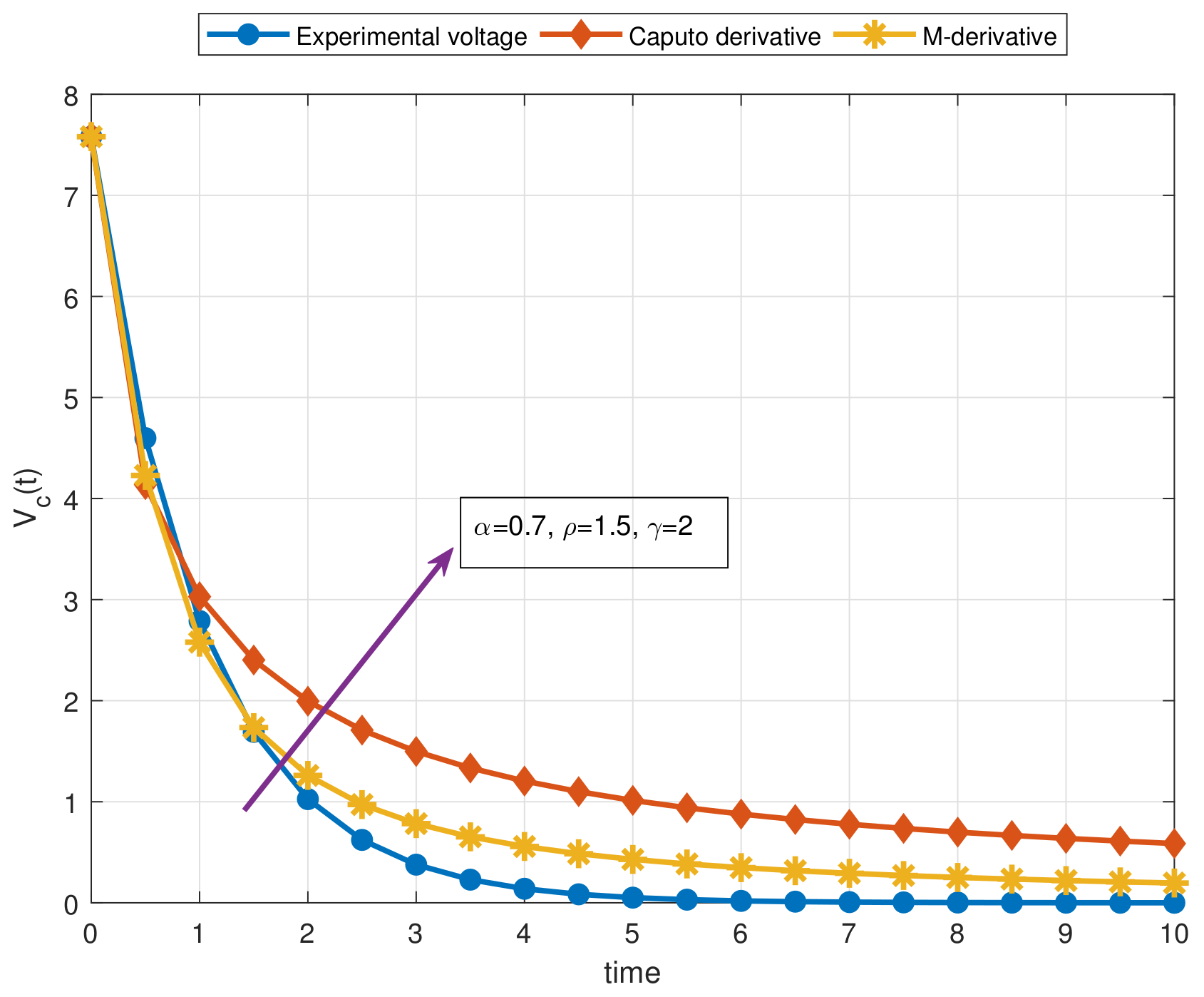
- In order to show the benefits of the non-local M-derivative for the proposed physical problem, a comprehensive comparison has been addressed for the RC circuit with constant source in the light of experimental data;
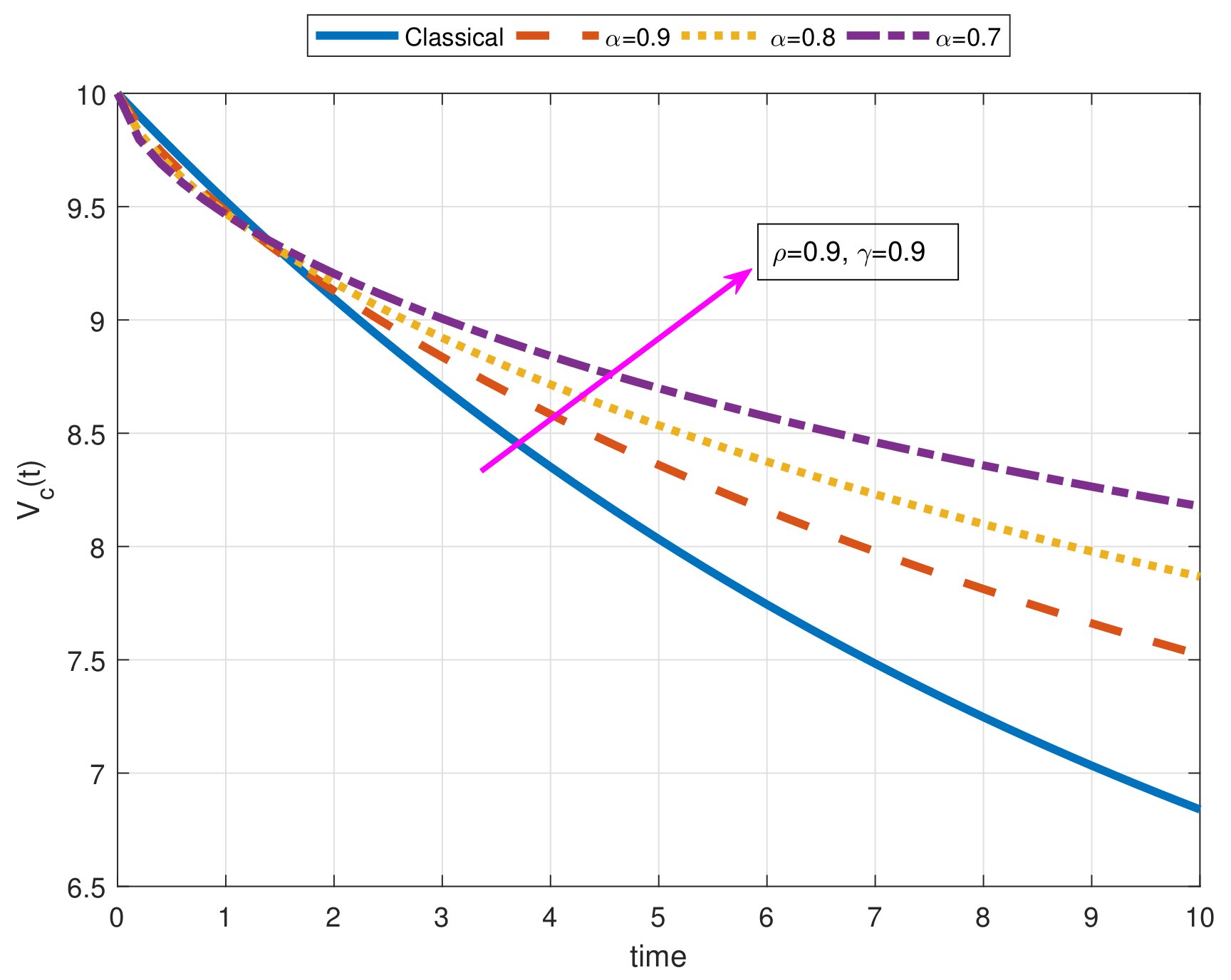
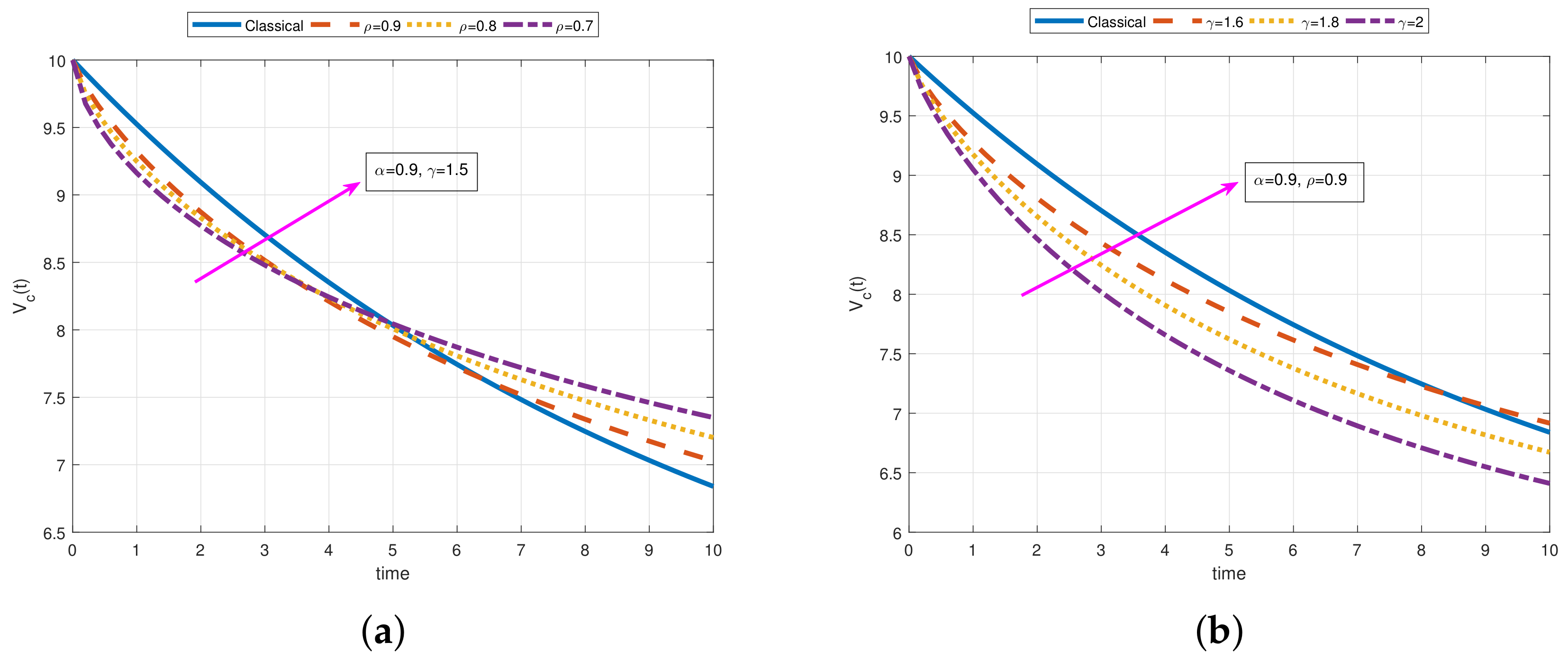
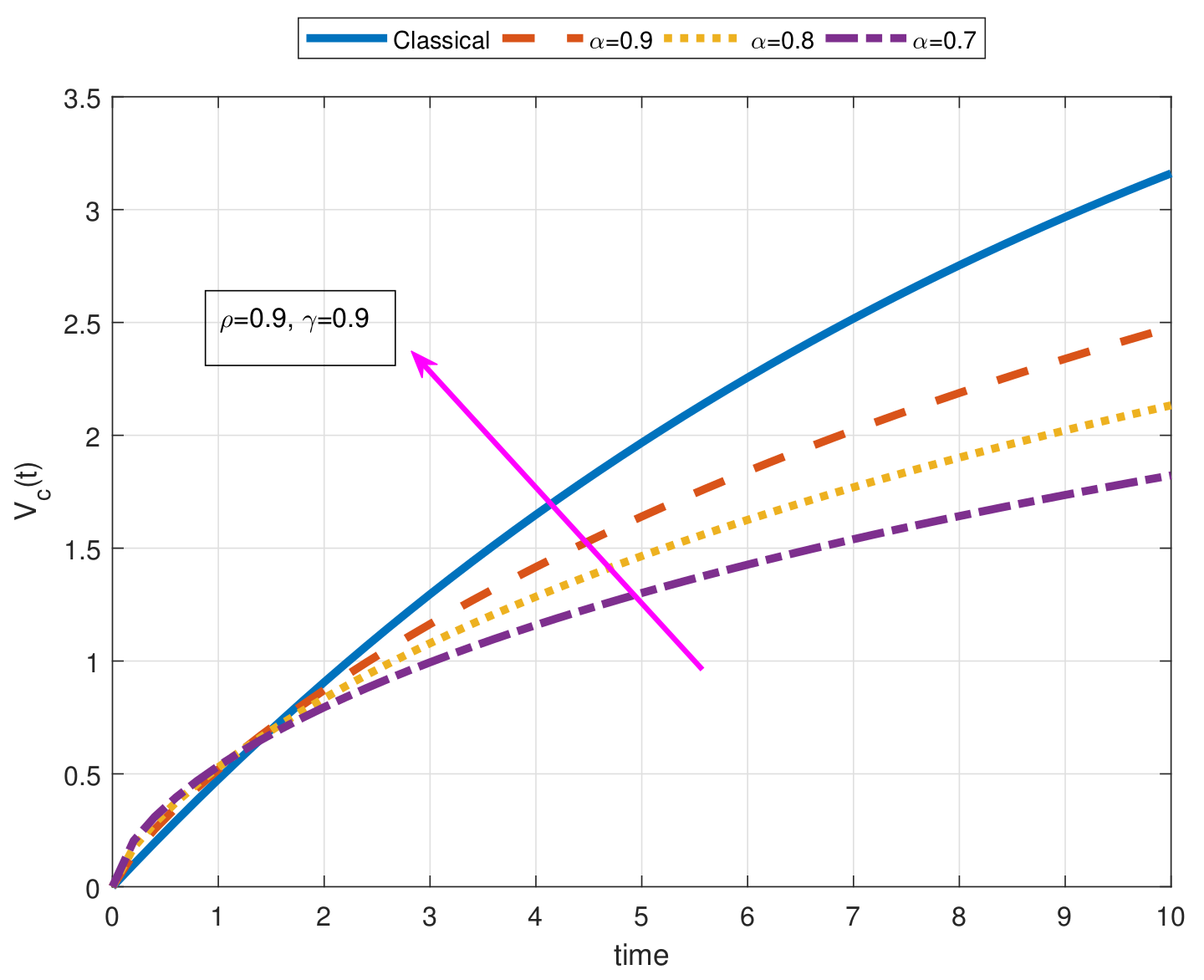
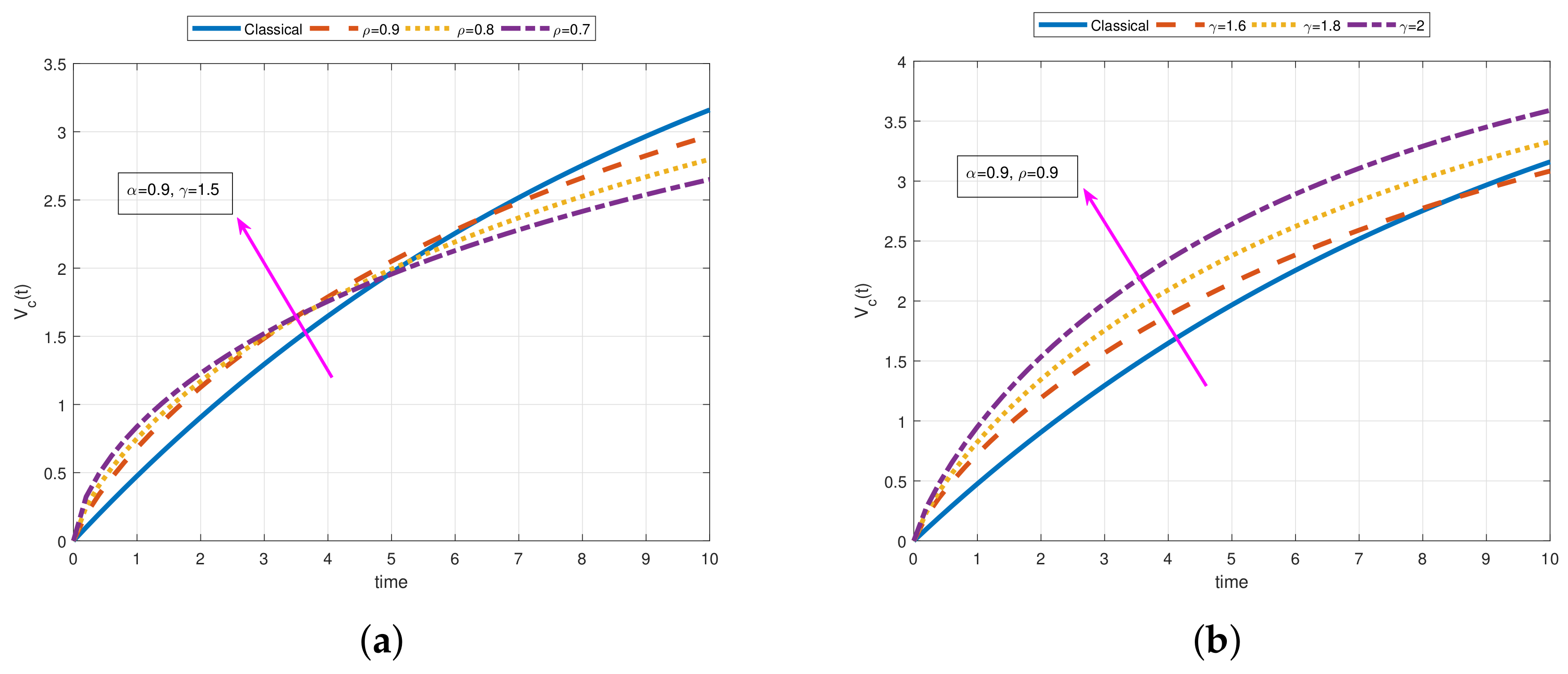
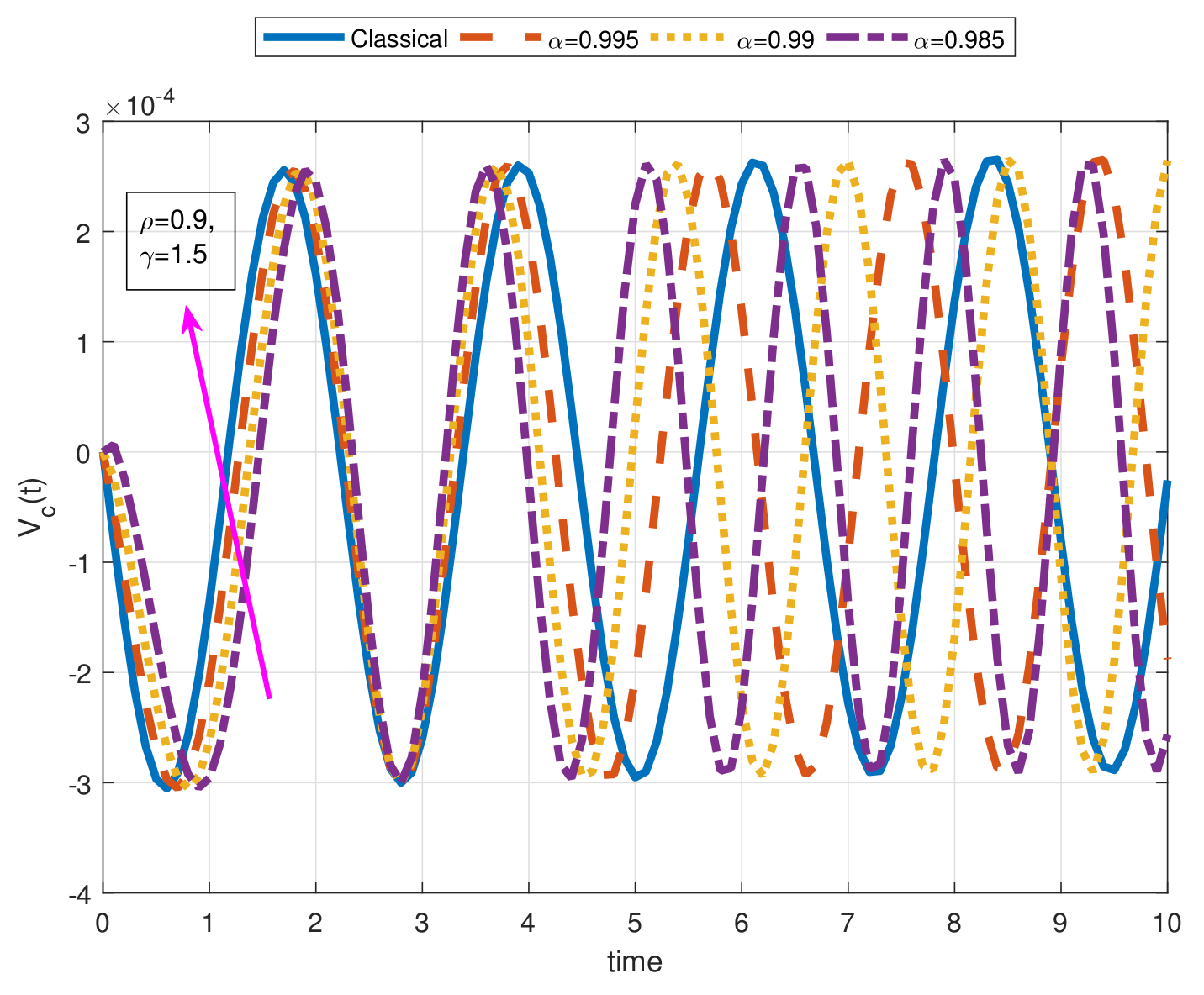
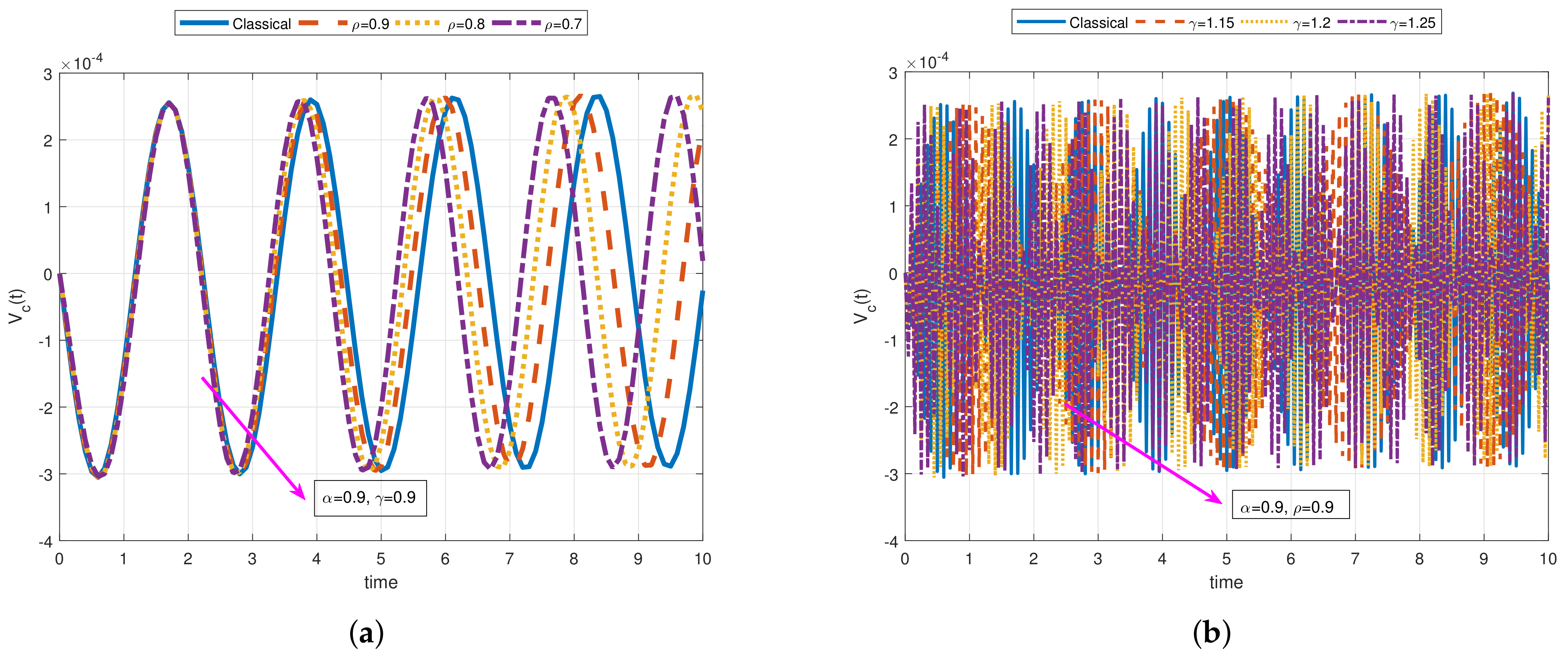
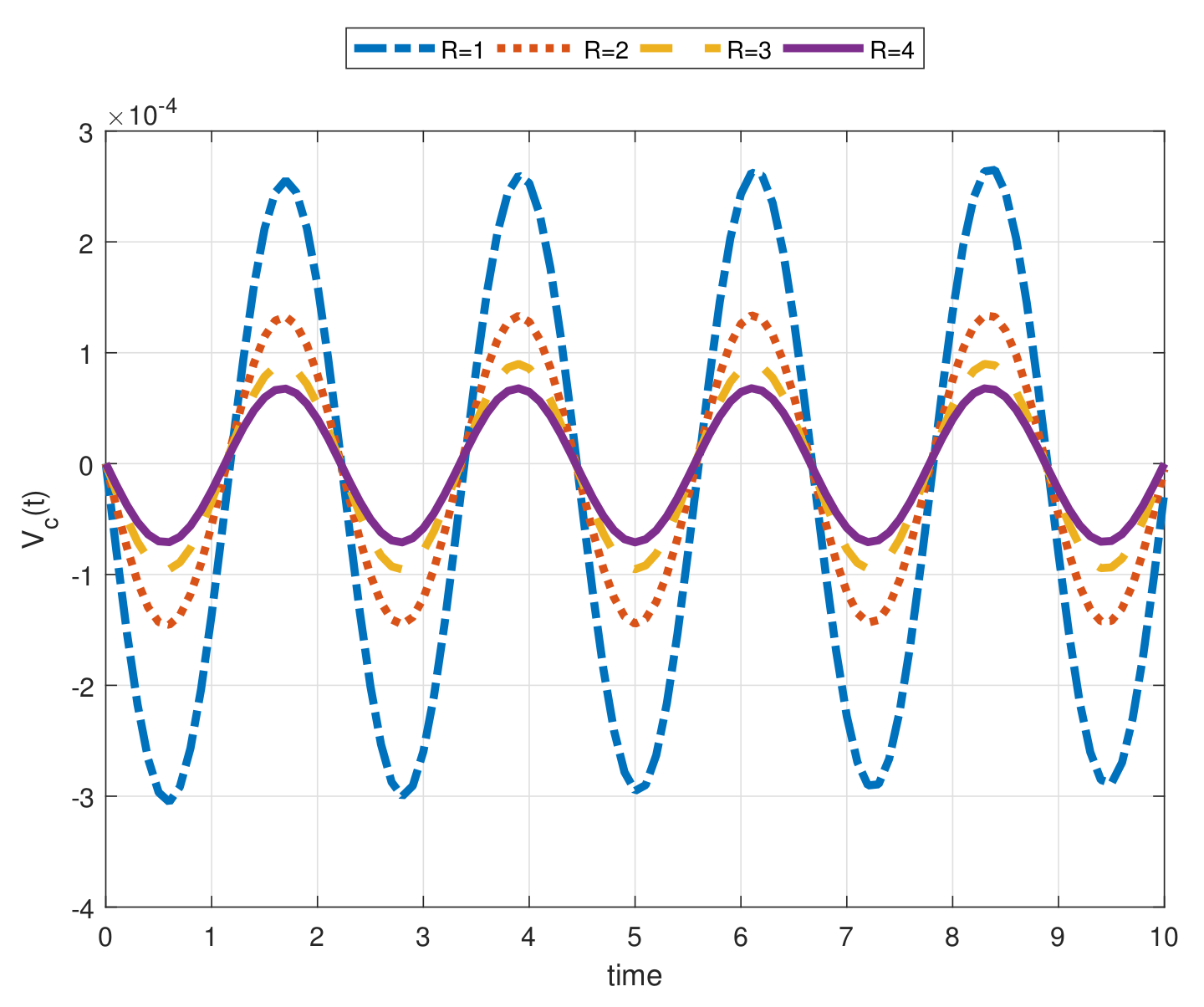
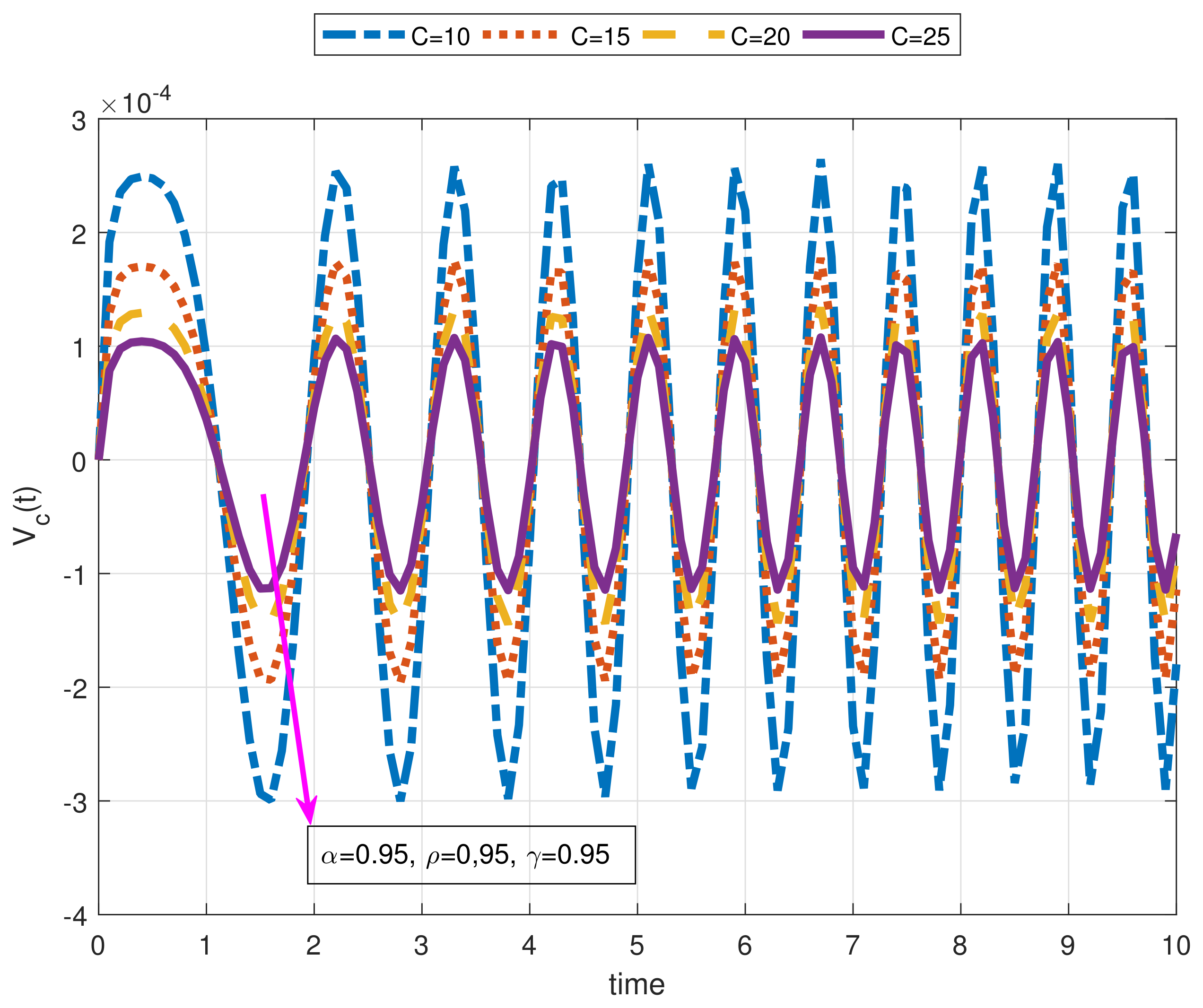
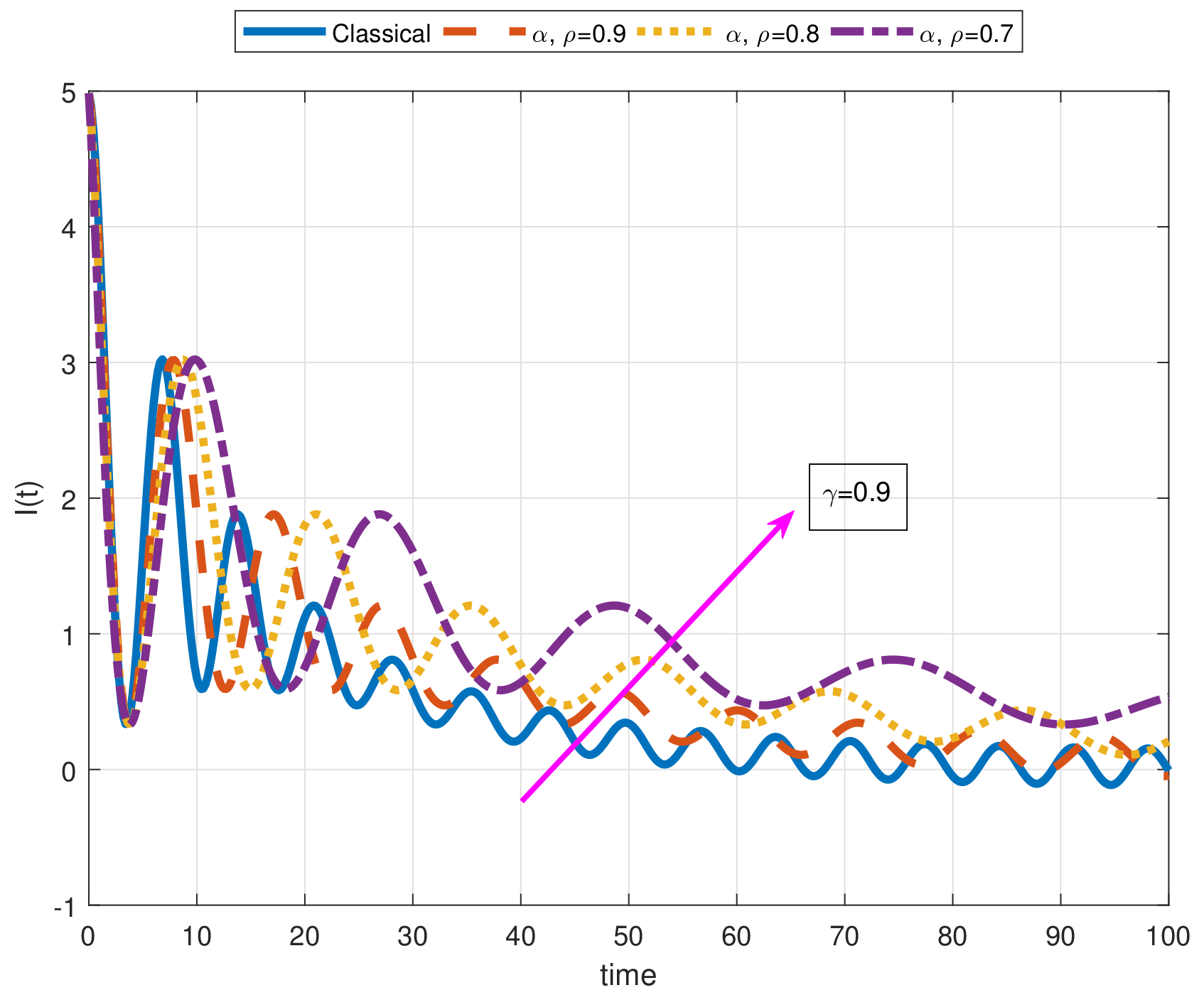
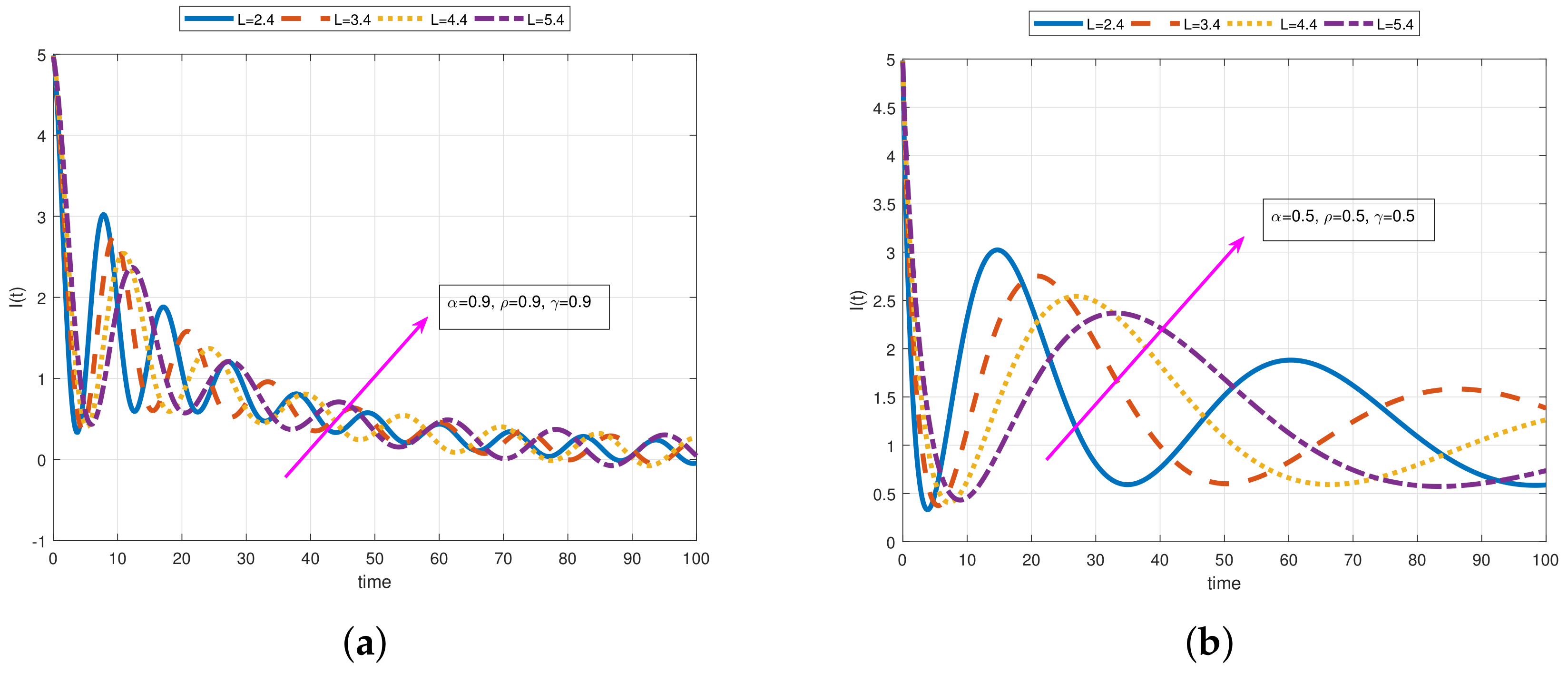
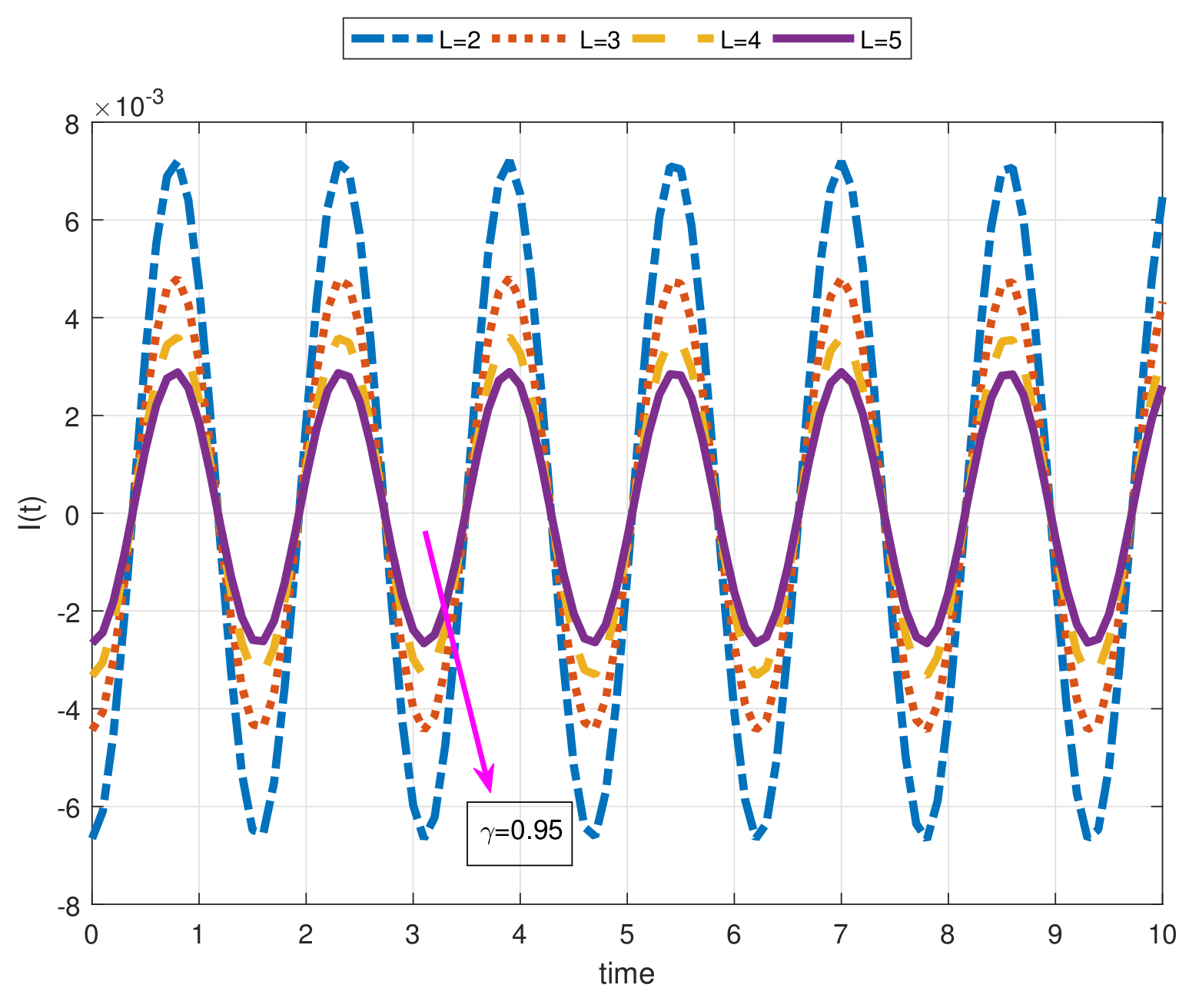
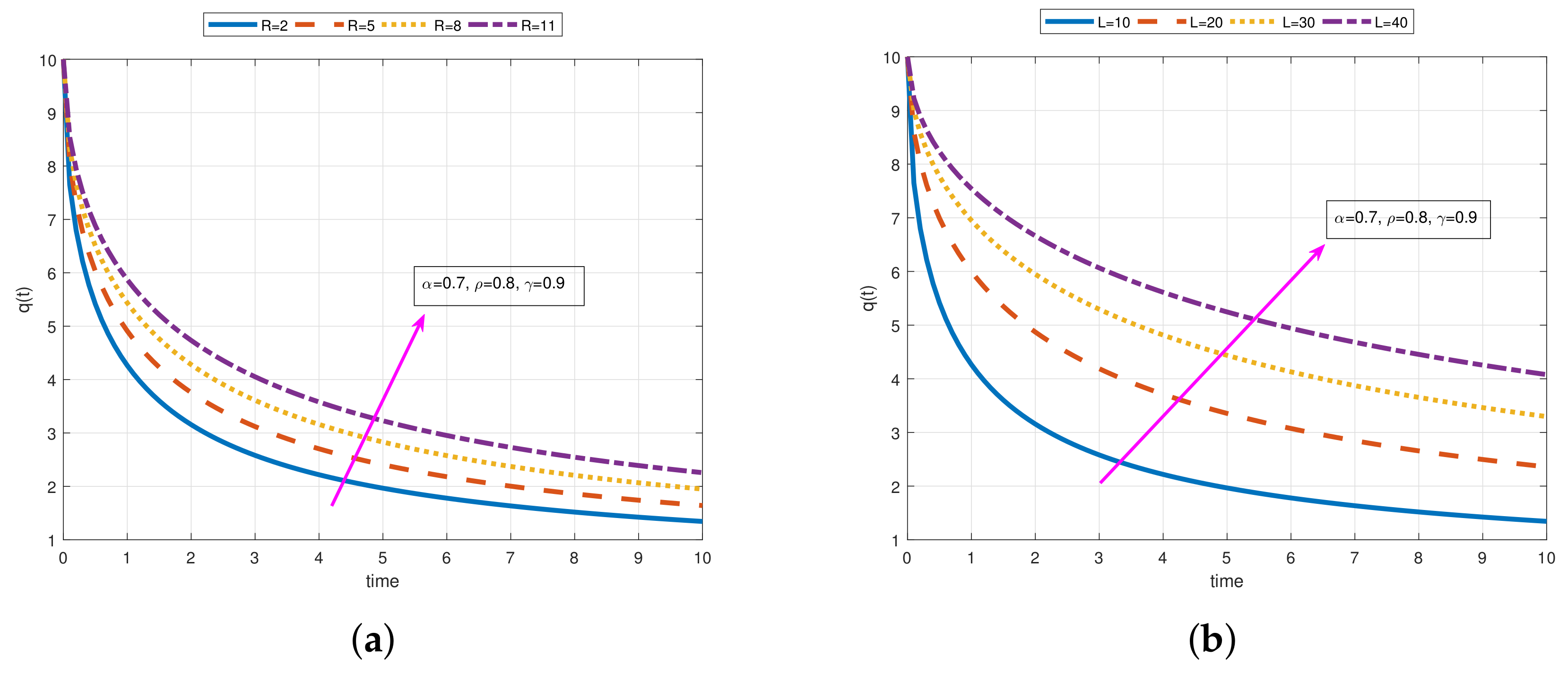
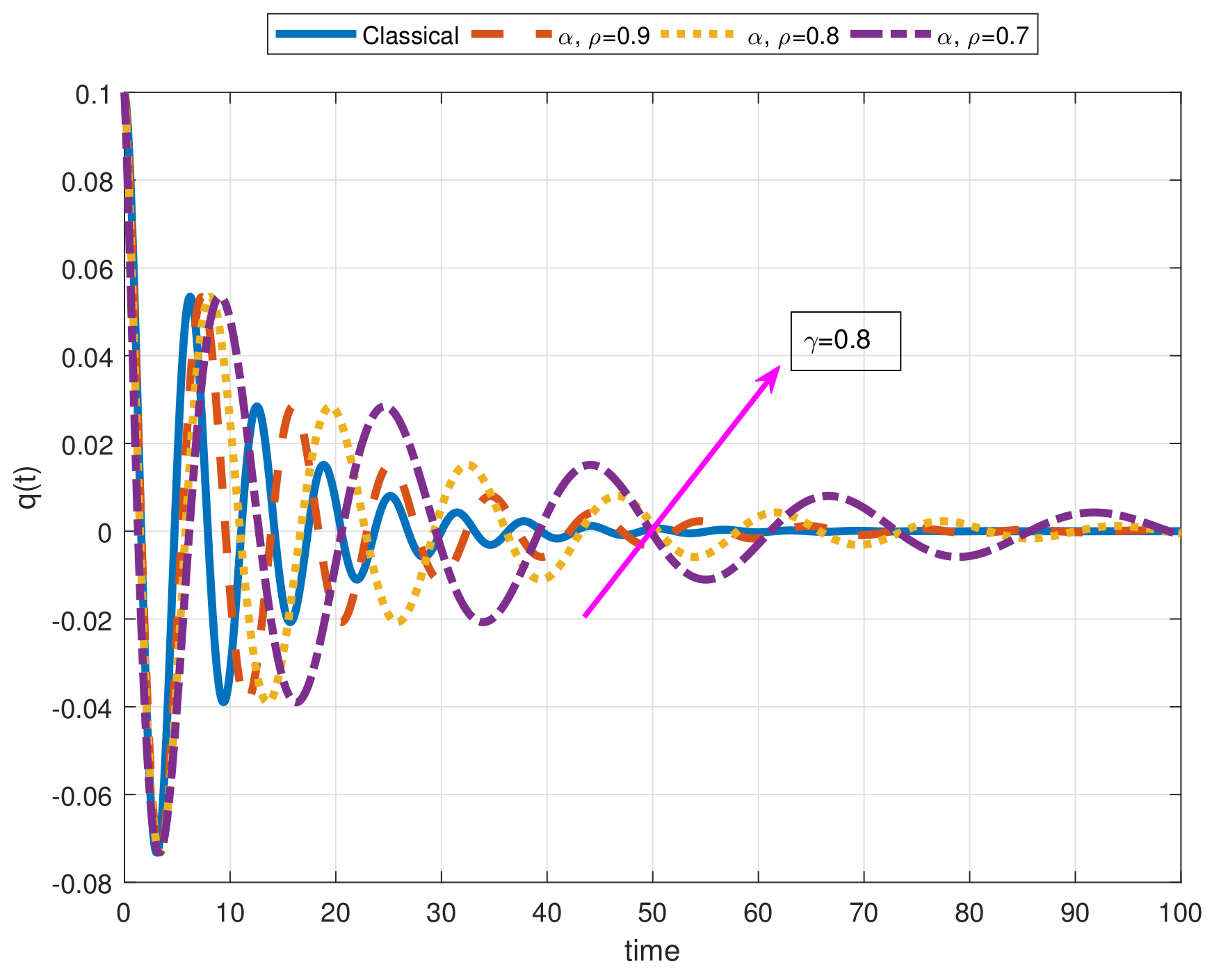
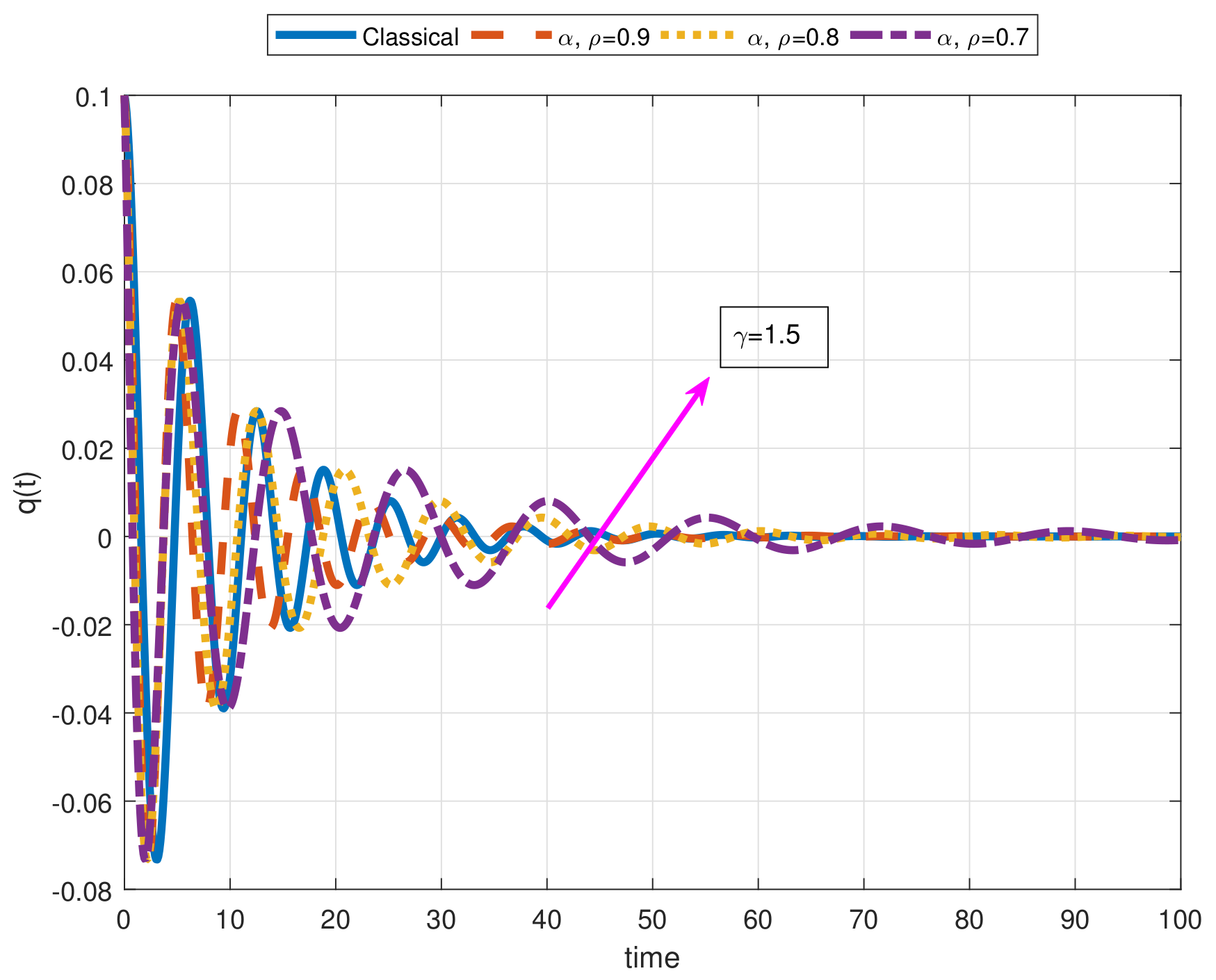
- As a result of our observations on Figure 1, Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12, Figure 13, Figure 14, Figure 15 and Figure 16, we see that the amplitudes get smaller or grow for some increasing or decreasing values of , , and . The waves also displace as , , and change;
- Importantly, the arbitrary parameters , , and allow us to get some crucial information about the intrinsic properties of the problem under investigation.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006; p. 204. [Google Scholar]
- Katugampola, U.N. New approach to a generalized fractional integral. Appl. Math. Comput. 2011, 218, 860–865. [Google Scholar] [CrossRef]
- Acay, B.; Bas, E.; Abdeljawad, T. Non-local fractional calculus from different viewpoint generated by truncated M-derivative. J. Comput. Appl. Math. 2020, 366, 112410. [Google Scholar] [CrossRef]
- Sousa, J.V.D.C.; de Oliveira, E.C. A new truncated M-fractional derivative type unifying some fractional derivative types with classical properties. arXiv 2017, arXiv:1704.08187. [Google Scholar]
- Jarad, F.; Abdeljawad, T.; Alzabut, J. Generalized fractional derivatives generated by a class of local proportional derivatives. Eur. Phys. J. Spec. Top. 2017, 226, 3457–3471. [Google Scholar] [CrossRef]
- Baleanu, D.; Fernandez, A.; Akgül, A. On a Fractional Operator Combining Proportional and Classical Differintegrals. Mathematics 2020, 8, 360. [Google Scholar] [CrossRef]
- Gómez-Aguilar, J.F.; Yépez-Martínez, H.; Escobar-Jiménez, R.F.; Astorga-Zaragoza, C.M.; Reyes-Reyes, J. Analytical and numerical solutions of electrical circuits described by fractional derivatives. Appl. Math. Model. 2016, 40, 9079–9094. [Google Scholar] [CrossRef]
- Gómez-Aguilar, J.F. Fundamental solutions to electrical circuits of non-integer order via fractional derivatives with and without singular kernels. Eur. Phys. J. Plus 2018, 133, 197. [Google Scholar] [CrossRef]
- Gómez-Aguilar, J.F.; Atangana, A.; Morales-Delgado, V.F. Electrical circuits RC, LC, and RL described by Atangana–Baleanu fractional derivatives. Int. J. Circuit Theory Appl. 2017, 45, 1514–1533. [Google Scholar] [CrossRef]
- Abro, K.A.; Memon, A.A.; Uqaili, M.A. A comparative mathematical analysis of RL and RC electrical circuits via Atangana-Baleanu and Caputo-Fabrizio fractional derivatives. Eur. Phys. J. Plus 2018, 133, 1–9. [Google Scholar] [CrossRef]
- Sene, N.; Gómez-Aguilar, J.F. Analytical solutions of electrical circuits considering certain generalized fractional derivatives. Eur. Phys. J. Plus 2019, 134, 1–14. [Google Scholar] [CrossRef]
- Martinez, L.; Rosales, J.J.; Carreño, C.A.; Lozano, J.M. Electrical circuits described by fractional conformable derivative. Int. J. Circuit Theory Appl. 2018, 46, 1091–1100. [Google Scholar] [CrossRef]
- Jarad, F.; Ugurlu, E.; Abdeljawad, T.; Baleanu, D. On a new class of fractional operators. Adv. Differ. Equ. 2017, 2017, 247. [Google Scholar] [CrossRef]
- Baleanu, D.; Fernandez, A. On fractional operators and their classifications. Mathematics 2019, 7, 830. [Google Scholar] [CrossRef]
- Qureshi, S.; Yusuf, A.; Shaikh, A.A.; Inc, M.; Baleanu, D. Fractional modeling of blood ethanol concentration system with real data application. Chaos Interdiscip. J. Nonlinear Sci. 2019, 29, 013143. [Google Scholar] [CrossRef] [PubMed]
- Qureshi, S.; Yusuf, A. Modeling chickenpox disease with fractional derivatives: From caputo to atangana-baleanu. Chaos Solitons Fractals 2019, 122, 111–118. [Google Scholar] [CrossRef]
- Acay, B.; Bas, E.; Abdeljawad, T. Fractional economic models based on market equilibrium in the frame of different type kernels. Chaos Solitons Fractals 2020, 130, 109438. [Google Scholar] [CrossRef]
- Bas, E.; Acay, B.; Ozarslan, R. The price adjustment equation with different types of conformable derivatives in market equilibrium. AIMS Math. 2019, 4, 805–820. [Google Scholar] [CrossRef]
- Acay, B.; Ozarslan, R.; Bas, E. Fractional physical models based on falling body problem. AIMS Math. 2020, 5, 2608. [Google Scholar] [CrossRef]
- Yavuz, M. Novel solution methods for initial boundary value problems of fractional order with conformable differentiation. Int. J. Optim. Control Theor. Appl. IJOCTA 2017, 8, 1–7. [Google Scholar] [CrossRef]
- Yusuf, A.; Inc, M.; Aliyu, A.I. On dark optical solitons of the space time nonlinear Schrödinger equation with fractional complex transform for Kerr and power law nonlinearities. J. Coupled Syst. Multiscale Dyn. 2018, 6, 114–120. [Google Scholar] [CrossRef]
- Ozarslan, R. Microbial survival and growth modeling in frame of nonsingular fractional derivatives. Math. Methods Appl. Sci. 2020, 2020, 1–19. [Google Scholar] [CrossRef]
- Yavuz, M.; Abdeljawad, T. Nonlinear regularized long-wave models with a new integral transformation applied to the fractional derivative with power and Mittag-Leffler kernel. Adv. Differ. Equ. 2020, 2020, 367. [Google Scholar] [CrossRef]
- Yavuz, M.; Sene, N. Stability Analysis and Numerical Computation of the Fractional Predator–Prey Model with the Harvesting Rate. Fractal Fract. 2020, 4, 35. [Google Scholar] [CrossRef]
- Jarad, F.; Abdeljawad, T. Generalized fractional derivatives and Laplace transform. Discret. Contin. Dyn. Syst. S 2020, 13, 709. [Google Scholar] [CrossRef]
- Ozarslan, R.; Bas, E.; Baleanu, D.; Acay, B. Fractional physical problems including wind-influenced projectile motion with Mittag-Leffler kernel. AIMS Math. 2020, 5, 467. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Acay, B.; Inc, M. Electrical Circuits RC, LC, and RLC under Generalized Type Non-Local Singular Fractional Operator. Fractal Fract. 2021, 5, 9. https://doi.org/10.3390/fractalfract5010009
Acay B, Inc M. Electrical Circuits RC, LC, and RLC under Generalized Type Non-Local Singular Fractional Operator. Fractal and Fractional. 2021; 5(1):9. https://doi.org/10.3390/fractalfract5010009
Chicago/Turabian StyleAcay, Bahar, and Mustafa Inc. 2021. "Electrical Circuits RC, LC, and RLC under Generalized Type Non-Local Singular Fractional Operator" Fractal and Fractional 5, no. 1: 9. https://doi.org/10.3390/fractalfract5010009
APA StyleAcay, B., & Inc, M. (2021). Electrical Circuits RC, LC, and RLC under Generalized Type Non-Local Singular Fractional Operator. Fractal and Fractional, 5(1), 9. https://doi.org/10.3390/fractalfract5010009




