Abstract
In this paper, the fractal derivative is introduced into a neural network-based discrete-time fractional-order PID controller in two areas, namely, in the controller’s structure and in the parameter optimization algorithm. The first use of the fractal derivative is to reconstruct the fractional-order PID controller by using the Hausdorff difference and Hausdorff sum derived from the Hausdorff derivative and Hausdorff integral. It can avoid the derivation of the Gamma function for the order updating to realize the parameter and order tuning based on neural networks. The other use is the optimization of order and parameters by using Borges derivative. Borges derivative is a kind of fractal derivative as a local fractional-order derivative. The chain rule of composite function is consistent with the integral-order derivative. It is suitable for updating the parameters and the order of the fractional-order PID controller based on neural networks. This paper improves the neural network-based PID controller in two aspects, which accelerates the response speed and improves the control accuracy. Two illustrative examples are given to verify the effectiveness of the proposed neural network-based discrete-time fractional-order PID control scheme with fractal derivatives.
1. Introduction
Due to the introductions of integral-order and differential-order, the design of fractional-order proportion-integral-derivative (PID) controllers is more flexible compared with that of integral-order PID controllers, allowing better control, which has attracted attention from many scholars [1]. Due to the simple structure of fractional-order PID controllers, as effective fractional-order controllers, they have been widely used in many control systems and achieved satisfactory control performances [2]. Take the examples of power systems [3], TCP networks [4], DC motors [5], supercapacitor energy storage systems [6], and robotic manipulator systems [7]. In addition, a variety of mixed fractional-order PID controllers have been derived from other algorithms, such as the fuzzy PID controller [8] and fractional-order PID sliding mode controllers [9].
The tuning methods of parameters in fractional-order PID controllers mainly include the analytic method and intelligent optimization algorithms. The analytic method can give the optimal parameters of fractional-order PID controllers with the given performance indexes. Generally, the method of analytic method is to design the parameters of the fractional-order controller in the frequency domain [10]. The dominant pole placement was used to tune the parameters of fractional-order PID controller to obtain a satisfactory load disturbance response in [11]. The phase margin and gain crossover frequency were concerned to present a tuning method of fractional-order PID controllers for minimum phase plants [12]. The robustness on the loop gain variations was guaranteed to tune the parameters of fractional-order PID controller in [13]. Although the analytic method can provide the mathematical expression of the parameter tuning, this method depends on the mathematical model of the controlled plant. It is difficult to use for the parameter tuning of fractional-order PID controllers of complex nonlinear controlled plants. Therefore, many scholars have studied the parameter tuning methods of fractional-order PID controllers based on various intelligent optimization methods, such as the genetic algorithm [14], the chaotic atom search optimization algorithm [15], the quantum bacterial foraging algorithm [16], the extremum seeking algorithm [17], and the particle swarm optimization algorithm [18]. Although the above intelligent optimization algorithms can obtain the effective parameter tuning results for the nonlinear controlled plant, the parameter tuning methods are offline calculation methods.
As an intelligent optimization and decision algorithm, the neural network algorithm is also applied in the design of fractional-order PID controllers. In [19], the RBF neural network algorithm was used to tune the parameters of fractional-order PID controllers and applied for a wind turbine. However, it is also an offline parameter tuning method and requires a lot of offline data. The difficulty of online parameter tuning methods of fractional-order PID controllers is mainly the adaptive tuning of fractional-orders, due to the global operators of fractional-order derivatives in the Caputo sense or Riemann–Liouville sense, and the fractional-order difference in the Grünwald–Letnikov (G–L) sense. The fractional-order operators also play a role in neural networks. Many scholars have proposed various fractional-order neural networks defined by fractional-order derivatives [20,21,22,23,24]. There are many research results in the cross research of neural networks and fractional-order calculus. Hence, it is worth studying the application of neural network optimization algorithms to the parameter tuning of fractional-order PID controllers.
In order to emphasize the adaptive adjustments of fractional-orders, the parameters of fractional-order PID controller in this paper include the parameters the proportional coefficient, the integral coefficient, and the differential coefficient; and orders integral order and differential order. The neural network algorithm is also used to adjust the parameters and orders of fractional-order PID controllers. It is necessary to study the discretized method of fractional-order operators to design a discrete-time fractional-order PID controller. There are many discretization methods of fractional-order derivatives [25,26]; the simplest discretization form of a fractional-order derivative is the G–L difference [27]. The discretization method via the G–L difference is simple, but the mathematical expression of the discretization result contains the Gamma function related to the order. If the orders in fractional-order PID controllers are adjusted adaptively by a neural network, the derivatives of the Gamma function with respect to the orders need to be obtained. Unfortunately, the derivative of the Gamma function is not a closed-form mathematical expression [28], and it not easy to calculate directly to hinder the adaptive updating of orders.
As a special fractional-order derivative, the fractal derivative deals with the local characteristics. The fractal derivatives are widely used in the modeling of real physical systems [29], such as anomalous diffusion [30] and viscoelastic materials [31]. Meanwhile, the validity of the fractal derivative for achieving chaotic attractors was discussed in [32] to show that the nonlinear system described by fractal derivative can also produce complex, dynamic behavior. The Hausdorff derivative as one of the fractal derivative definitions does not contain the Gamma function [33]. Therefore, a novel discrete-time fractional-order PID controller can be constructed by using the discretized forms of the Hausdorff derivative and the Hausdorff integral, and the adaptive tuning method of parameters and orders can be realized by using neural networks. Besides, the power-law stability of nonlinear systems via the Hausdorff derivative was investigated in [34]. The fractal derivative mainly generalizes the first-order derivative with many definitions. The Borges derivative is another form of fractal derivative which is given in [35], and it can also describes the dynamic behavior of complex systems.
In this paper, fractal calculus theory is applied to the design of a neural network PID controller in two ways. According to the Hausdorff derivative and the Hausdorff integral, the definitions of the Hausdorff difference and Hausdorff sum are derived. Compared with the fractional-order PID controller via the G–L definition, the derivation of the Gamma function is avoided in parameter updating based on neural networks. In addition, the fractional-order PID controller based on fractal theory has no memory of difference, and the updating of parameters and orders is simpler. Another improvement is to introduce the Borges derivative into the optimization of parameters and orders. The derivation of a composite function based on the Caputo derivative is very complex; hence, the chain rule of the derivative of am integer-order composite function cannot be used directly. However, the chain rule of the Borges derivative of a composite function is consistent with the integral-order derivative, and the effect can also be optimized by adjusting the order. Therefore, this paper applies the Borges derivative to the training of controller parameters and orders, and discusses the problem of order selection in the Borges derivative.
The main contributions of this paper are summarized as follows: (1) The definition and calculation method of Hausdorff difference and Hausdorff sum are proposed, and their introduction into PID controllers is described. (2) A novel type of fractional-order PID controller is proposed to realize the online adjustment of parameters and orders, and the online tuning method of parameters and orders based on the first order gradient information is given. (3) The Borges derivative is introduced into the tuning of parameters and orders, and the influence of the order in the Borges derivative on the optimization performance in regard to parameters and orders is offered. (4) The tuning methods of the parameters and orders of the proposed fractional-order PID controller based on the fractal derivative is proposed, and it improves the optimization speed of the parameters and orders.
The rest of this paper is organized as follows. In Section 2, the definitions of Hausdorff difference and sum derived from Hausdorff derivative and integral are given, and the fractional-order PID controller in the sense of a Riemann–Liouville (R–L) derivative and Caputo derivative with zero-initial-condition is also given. Based on the Hausdorff difference and sum, two kinds of neural network-based tuning methods are proposed for the parameters and fractional-orders of a fractional-order PID controller via the first order and the Borges derivative in Section 3. In Section 4, two illustrative examples are offered to verify the effectiveness of this paper. The conclusion is given in Section 5.
2. Problem Statement
In this paper, a novel type of fractional-order PID controller is constructed based on the difference and sum operators extended by the Hausdorff derivative and Hausdorff integral. The Hausdorff derivative with for is defined in [33] as
where is the set of positive real numbers.
It is not difficult to calculate the Hausdorff derivative if the function is a differentiable function as follows:
The Hausdorff difference for derived from the Hausdorff derivative is given as follows.
Consequently, the Hausdorff sum for derived from the Hausdorff integral is determined by
Thus means that the Hausdorff difference and Hausdorff sum include the first order difference and sum operations. Therefore, the main investigated issue of this paper is the tuning design of parameters and orders in the fractional-order PID control scheme with neural networks based on the Hausdorff difference and Hausdorff sum.
As the fractional-order PID controller has two more important parameters that are the integral-order and the differential-order, the controller design is more flexible compared with the integer-order PID controller. Generally, the basic definitions of fractional-order derivatives are the R–L definition and Caputo definition. In a continuous-time, fractional-order PID controller, the mathematical descriptions under these two definitions are usually used. The definitions are given as follows.
The Caputo derivative [25] is defined by
where is Caputo derivative from 0 to t with the order , and it satisfies with ; is the set of positive integer numbers, and the function is the gamma function.
Accordingly, the R–L derivative [25] is defined by
where is R–L derivative from 0 to t with the order and satisfies with .
If the initial conditions are zero for both the Caputo derivative and the R–L derivative; the Laplace transformation of fractional-order derivative with respect to the function with the fractional-order is with the Laplace operator s, where is the Laplace transformation of . Then, the transfer function of fractional-order PID controller [36] in the frequency domain is offered as follows.
where , , , , and are the proportional coefficient, the integral coefficient, the differential coefficient, the integral order, and the differential order; and is the set of positive real numbers.
The fractional-order operation in the discrete-time fractional-order PID controller is described by G–L definition. The G–L difference is provided as follows.
where the factor is computed by
Generally, the fractional-order operators in the fractional-order controller (8) are discretized by the G–L difference, but the coefficients of the discretized fractional-order operators are all related to the orders, and the relationship between the corresponding coefficient and the order is more complex due to the Gamma function in terms of the order. Therefore, the adaptive adjustments of corresponding orders and are quite difficult via the G–L difference. As the Hausdorff derivative, and its discretization are both local operators, the orders in the discrete-time fractional-order PID controller based on the Hausdorff difference and Hausdorff sum can be adjusted adaptively.
3. Main Results
3.1. A Discrete-Time Fractional-Order PID Controller Based on the Hausdorff Difference and Hausdorff Sum
Since the fractional-order operators in fractional-order PID controller defined by Equation (11) are global operators, the adaptive adjustments of orders are not easy to calculate. Therefore, a fractional order PID controller based on the Hausdorff derivative and Hausdorff integral is proposed in this paper. The corresponding controller in the time domain is offered as follows:
where is the output error.
By using the Hausdorff difference and Hausdorff sum described by Equations (3) and (5), the discrete-time, fractional-order PID controller is given as follows.
where is the sampling value of at with the sampling period T, and
The influences of different orders on the control effect based on Hausdorff difference and the Hausdorff sum in the fractional-order controller (12) are discussed. Then, we define and in respectively, and the curves of and are drawn in Figure 1 and Figure 2 respectively.
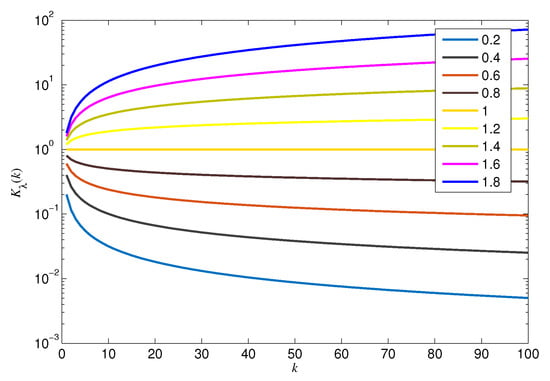
Figure 1.
Curves of with different orders .
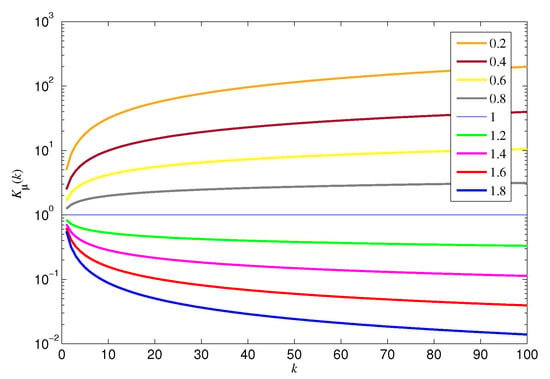
Figure 2.
Curves of with different orders .
It can be seen from the curves described in Figure 1 and Figure 2 that increases and decreases with an increase of fractional-order or . If the order is set as a larger value, the role of the current time is larger, and the role of the historical information of the error is smaller. That is to say, more attention is paid to the error information of the current time in . However, a larger order makes the sum term too large; hence, it is necessary to choose a reasonable order . Correspondingly, the order is set as a smaller value; then the effect of the difference becomes larger. Therefore, the order should be made smaller with the increase of the iteration k.
Next, we give the calculation method of the parameters and orders of the discrete-time fractional-order PID controller (12) trained by the neural network method.
3.2. Tuning Method of Parameters and Orders of Discrete-Time Fractional-Order PID Controllers with Neural Networks
The neural network-based discrete-time fractional-order (NNDTFO) PID controller with the neural network identifier (NNI) is the focus, and its structure is shown in Figure 3.
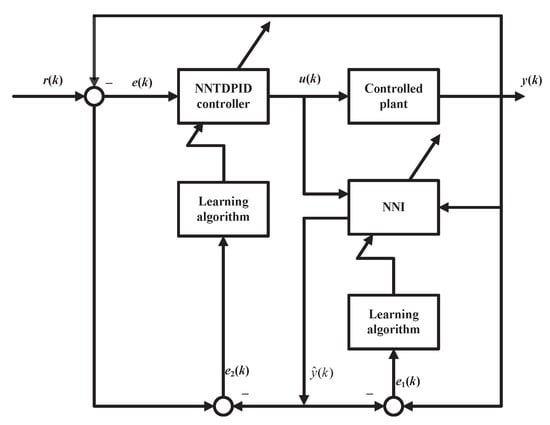
Figure 3.
Structure of the control system with a neural network-based discrete-time fractional-order (NNDTFO) PID controller and a neural network identifier (NNI).
The nonlinear controlled plant is presented by
where is the nonlinear function in terms of the control input and output , , , and is the set of positive integer numbers.
The weight matrices corresponding the connection from the input layer to the hidden layer and the connection from the hidden layer to the output layer are denoted as and , where is the number of the neurons in the input layer.
The input of NNI is ; the output of the output layer is determined by
where is the output of the hidden layer, is activation function of the hidden layer, and and are the biases of the hidden layer and output layer.
Let the cost function with ; then the updating formulas of the weights and biases in NNI are determined by
where is the learning rate of NNI, and and are determined by
and for ; is the entry in corresponding to the ith row and the jth column; and is the jth entry in the input .
A BP neural network with one hidden layer is adopted as the NNI for the controlled plant (13). Let the controller for be
where , is the reference signal, and
Define the cost function as with ; then the tuning formulas of parameters are determined by
where , , and are the learning rates for the parameters , , and .
Consider that
then the tuning formulas of orders are also determined by
where and are the learning rates for the orders and .
There is the function term in the above updating formulas of the parameters and orders; hence, the calculation method of is as follows:
where
Therefore, the updating formulas of parameters and orders of NNDTFO PID controller (19) are determined by
Considering the effective selection intervals of parameters and orders in the controller (19), we restrict the optimization results of parameters and orders as , , , , or if , , , or occurs; and or if or occurs.
3.3. Tuning Method of Parameters and Orders Based on the Borges Derivative
In the updating Formulas (45)–(49), the updating methods of parameters , , and and orders and depend on the information of the first order negative gradient. We investigate the updating method based on the improved Borges gradient to improve the optimizations of parameters and fractional-orders in NNTDFO PID controller (19).
The Borges derivative is provided in [35] as follows.
where with and .
If the function is differentiable, we have
If we set in (31), the Borges derivative is equivalent to the first-order derivative. Therefore, we use the Borges gradient consisting of the Borges derivatives to generalize the updating Equations (45)–(49). In addition, the Borges derivative is a local operator, which satisfies the chain rule; hence, the training of parameters and orders of the controller (19) based on the neural network algorithm can be applied. Let and ; then the Borges derivative of is obtained as
In order to give the adjustment methods of these orders, we take the order of the updating formula of the proportional coefficient as an example, and the relative speed is defined as
The relationship between the index and is shown in Figure 4.
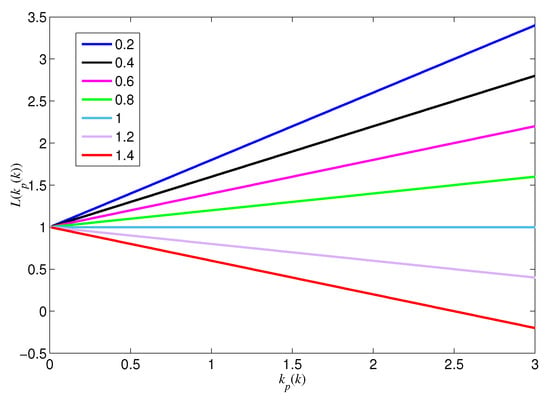
Figure 4.
Curves of with different orders .
It is obvious from Figure 4 that the Borges derivative of with respect to is lager if the order is set to be smaller. If is larger than a certain value, the sign of derivative changes, and this is an undesirable result. With the increase of parameter , the index corresponding to a smaller order becomes larger, while the index corresponding to a larger order becomes smaller, and it may be less than zero.
Let ; then we have , which is the maximum of . Thereby, the range of is . If the indexes corresponding to different parameters are the same as , we have
We hope that the Borges derivative is less than the first-order derivative to accelerate the optimization at the beginning of parameter optimization. Meanwhile, the Borges derivative is greater than the first-order derivative to improve the accuracy of parameter optimization at the end of the optimization. Then, the order is determined by
where and satisfy ; is a random number uniformly distributed between 0 and 1; and M is the number of iterations.
Similarly, the tuning methods of other fractional-orders are offered as follows:
where , , , or is a random number uniformly distributed between 0 and 1; and the conditions , , , and are also required.
4. Illustrative Examples
4.1. Example 1
Consider the following discrete-time nonlinear controlled plant as
The reference signal is chosen as , and the initial value is set. The NNI is used to identified the model of the nonlinear plant and the activation function in the hidden layer of NNI is selected as
In the NNI, the number of the neurons in the hidden layer is , and is obtained with and . To verify the effectiveness of the proposed NNDTFO PID controller, the results were compared with those of a neural network discrete-time (NNDT) PID controller. The learning rates in NNI were both set as for the two types of controller. The learning rates of the parameters in two types of controllers were both set as , , and , and the learning rates of the orders were set as 10,000 and 10,000. The initial value for weights and biases in NNI was chosen as 0.01, and the weight in the NNDTFO PID controller and NNDT PID controller was set as 0.1; was used. Meanwhile, the initial value of the orders and was set as 1 in the NNDTFO PID controller.
The responses of the outputs via two types of controllers, and the responses of two types of controllers , are shown in Figure 5 and Figure 6, respectively.
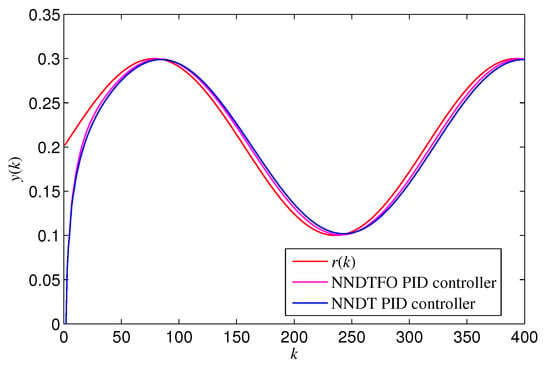
Figure 5.
Responses of outputs for the closed loop system of example 1 via two types of controller.
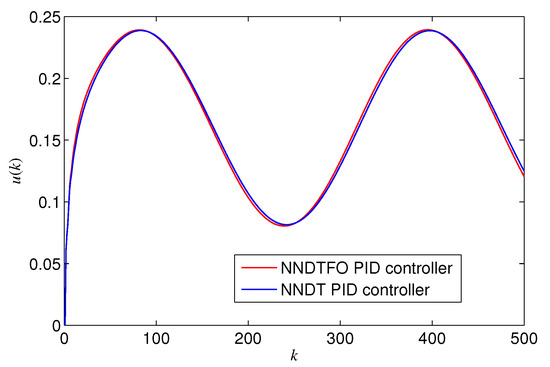
Figure 6.
Responses of controllers for the closed loop system of example 1 with a sinusoidal signal.
It can be seen from the output responses via the different controllers described in Figure 5 that the NNDTFO PID controller with Hausdorff difference and Hausdorff sum can obtain a more accurate response compared with the output response via the NNTD PID controller. From the curves of the two types of PID controllers described in Figure 6, it can be seen that the outputs of the two types of PID controller are bounded with no significant control effects.
In order to show that Hausdorff sum and difference operations can reduce the response error, the index function is defined as
While letting , the parameters were set as with , and with respectively; then the corresponding indexes E are offered in Table 1 and Table 2.

Table 1.
Index E for different parameters with via two types of controller.

Table 2.
Index E for different parameters A with via two types of controller.
It can be seen from the data in Table 1 and Table 2 that the response error of system output can be reduced by introducing the Hausdorff difference and Hausdorff sum for different reference signals. These results show that the proposed NNDTFO PID controller can further improve the accuracy of the output response.
To illustrate the improvement of the proposed controller in regard to the dynamic response of the controlled plant, the reference input signal was changed to with .
From the experimental results in Figure 7, it is obvious that the controller with the Hausdorff sum and difference operations can make the response of the output faster, which is another advantage of the control strategy proposed in this paper. Besides, the parameters and orders in the NNDTFO PID controller are shown in Figure 8 respectively.
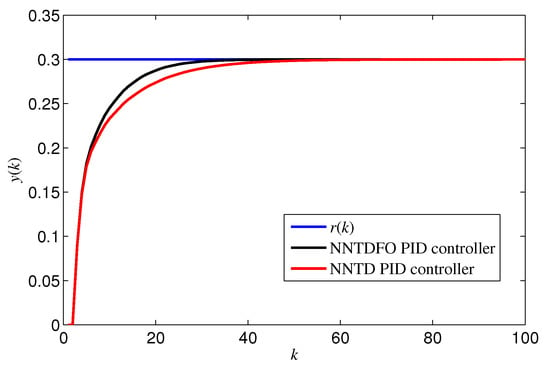
Figure 7.
Responses of outputs closed loop system for example 1 with a constant signal.
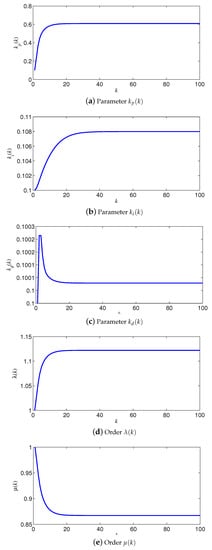
Figure 8.
Parameters and orders.
From the curves of control parameters and orders in Figure 8, it can be seen that parameters , , and , and orders and converge to the fixed values quickly. The orders and in the proposed controller are greater than 1 or less than 1 for the reference signal , and this phenomenon corresponds to the analysis of orders in Section 3.
4.2. Example 2
In this example, the Borges derivative is focused on to improve the control performance based on the NNTD PID controller. The nonlinear controlled plant used was
The parameters of the NNI and NNDTFO PID controller were consistent with the corresponding ones in example 1. Other parameters were set as and , , , , and . In consideration of the existence of random functions with the use of the Borges derivative to optimize the parameters and orders of the controller, the average result of 100 experiments was used for the evaluation in this case. The reference signal was set as with ; then the response of the average value of output via the NNDTFO PID controller with Borges derivative, and the responses of outputs via the NNDTFO PID controller and NNDT PID controller were plotted in Figure 9. The corresponding errors based on (52) via the NNDTFO PID controller via Borges derivative, the NNDTFO PID controller, and the NNDT PID controller were 0.0729 (the average result for 100 times), 0.0892, 0.1296 respectively.
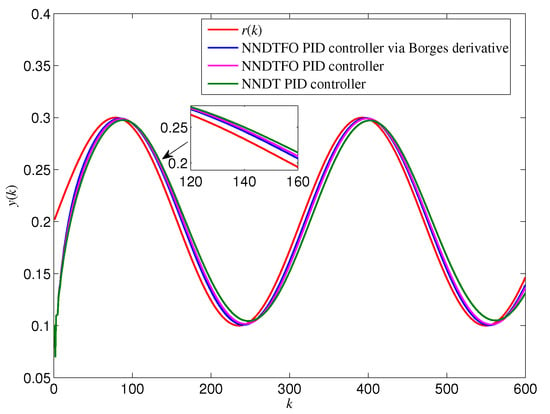
Figure 9.
Responses of outputs via three types of PID controller of a closed loop system for example 2 with a sinusoidal signal.
It can be seen from the experimental results in Figure 9 that the NNDTFO PID controller with Borges derivative achieved the best control effect in three types of PID controller. By using Borges derivative, the output of the system can track the reference signal well; the tracking errors via the three controllers were the smallest. This phenomenon illustrates that the introduction of the Borges derivative can improve the optimization effect of parameters and orders in NNTDFO controller. For this example, we can draw the conclusion that the use of the Hausdorff difference and Hausdorff sum can improve the control accuracy. On this basis, the control accuracy can be further improved by introducing the Borges derivative. It was verified that the control effect of the NNTD controller can be improved by introducing fractal derivatives into two areas, i.e., the controller structure and the optimization strategy.
Figure 10 shows the average values of the relative speeds corresponding to the parameters and orders of the NNTD PID controller with the Borges derivative from 100 experiments.
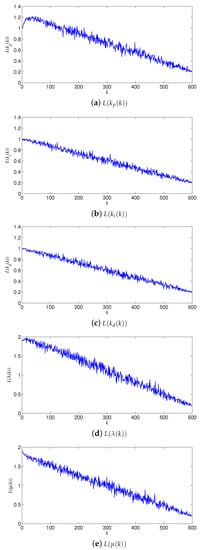
Figure 10.
Relative average speeds of parameters and orders.
It can be seen from the average values of relative speeds corresponding to different parameters and orders described in Figure 10 that all of the average relative speeds can be gradually reduced from a number greater than 1 to a number less than 1, by adopting the order adjustment strategy proposed in this paper. According to this strategy, the optimization speed can be accelerated at the beginning of optimization stage for parameters and orders in the NNTDFO PID controller, and the optimization precision and effect can be improved at the end of the optimization stage.
To compare the robustness of the three types of controllers, the coefficient 0.1 before the nonlinear function term in the model was changed to , and the error indexes for different values of parameter B are shown in Table 3. (The index of the NNDTFO PID controller is the average result of 100 rounds).

Table 3.
Index E for different parameters B via three types of controller.
The experimental results in Table 3 show that the three controllers based on neural networks have robustness and can adapt to disturbances in parameters. In addition, the fractal derivative can reduce the control error E to improve the control accuracy of the closed-loop system even, if parameter 0.1 is disturbed.
In order to investigate the response of the Borges derivative to the convergence speed of the control effect, the reference signal was set to , and was set for this case; other parameters in three types of controllers were not changed. Then, from the average value of output via the NNDTFO PID controller with Borges derivative, the responses of outputs via NNDTFO PID controller and NNDT PID controller are drawn in Figure 11.
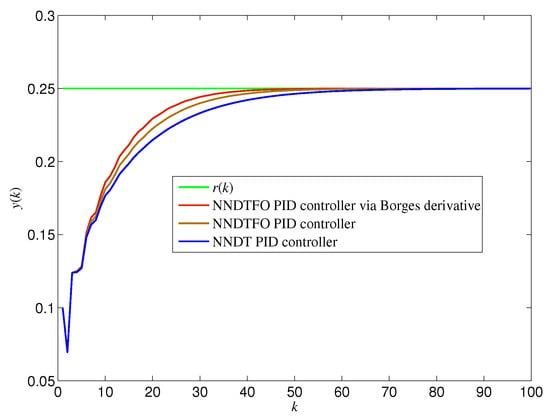
Figure 11.
Responses of outputs via three types of PID controller using the closed loop system of example 2 with a constant signal.
The control effect of the three controllers described in Figure 11 shows that the NNTDFO PID controller with the Borges derivative achieved the fastest convergence speed, followed by the NNTDFO PID controller without the Borges derivative, and the NNTD PID controller without the fractal derivative had the slowest convergence speed. It is shown that the Borges derivative can further accelerate the response of the controlled plant.
Next, we study the error index for a differing constant reference signal, and the results are given in Table 4.

Table 4.
Index E for constant reference signal via three types of controller.
From the experimental results described in Table 4, it can be seen that the rule of the control effect is consistent for constant input signals of different values. In other words, the use of a fractal derivative to optimize controller parameters and the use of fractal difference and fractal sum can improve control effect.
To verify the fact that the designed NNI can identify the system model well based on three kinds of neural network PID controllers, the errors between the output of NNI and the output as for and are shown in Figure 12.
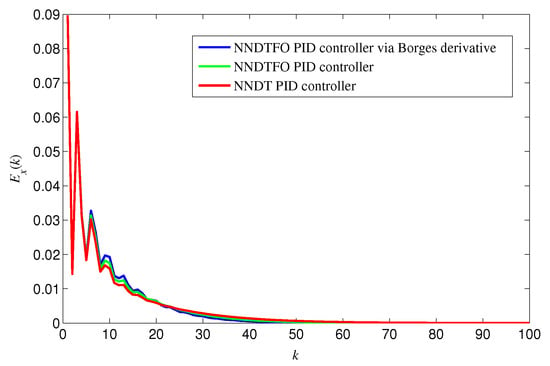
Figure 12.
Errors for three types of neural network PID controller.
It can be seen from the error curves in Figure 12 that NNIs are not affected by the three types of neural network PID controllers, and NNIs can identify the dynamic characteristics of the controlled plant effectively, and the identification error converges to zero quickly.
5. Conclusions
This paper mainly studied the applications of two kinds of fractal derivative in the design of a neural network-based PID controller. Based on the definition of the Hausdorff derivative and Hausdorff integral, the calculation formulas of Hausdorff difference and Hausdorff sum were given to construct NNTDFO PID controllers. By using the local operation characteristics of Hausdorff difference and Hausdorff sum, the tuning method of parameters and orders in the proposed NNTDFO PID controllers were given. The orders corresponding to the Hausdorff difference and Hausdorff sum were introduced to make the controller design more flexible, and the adaptive adjustment algorithm of orders is also provided in this paper.
In addition, the learning rules of parameters and orders were further discussed. The first derivative was replaced by the Borges derivative; then the parameters and orders with the adaptive relative velocity were adjusted to improve the optimization performance. The adaptive tuning rules of the orders in the Borges derivatives were given to gain a more satisfactory control effect via NNTDFO PID controllers. The use of a fractal derivative, like the integer derivative, satisfies the chain rule, which provides the basis for the training parameters of neural networks. The applications of fractal difference and fractal sum derived from the fractal derivative and integral can avoid the derivation of the Gamma function, which is convenient for calculations and can also increase the flexibility of controller design. In this paper, two kinds of fractional-order PID controller based on fractal derivative and derived fractal difference and fractal sum were proposed, which can improve the response speed and accuracy of the closed-loop control system. Compared with the integer-order PID algorithm, the calculation is more complex and the calculation time is longer. However, in view of the fact that many controllers are operated by computers, the calculation burden of the proposed algorithm is not large. In future research, the basic neural network learning and construction method based on fractal derivatives will be extended to a more complex neural network model and neural network control algorithm.
Funding
This research was funded by Liaoning Revitalization Talents Program under grant number XLYC1807229, the Natural Science Foundation of Liaoning Province, China under grant number 20180520009, the China Postdoctoral Science Foundation Funded Project under grant number 2019M651206, and the Scientific Research Fund of Liaoning Provincial Education Department, China under grant LJC202010.
Data Availability Statement
Not applicable.
Conflicts of Interest
The author declares no conflict of interest.
References
- Shah, P.; Agashe, S. Review of fractional PID controller. Mechatronics 2016, 38, 29–41. [Google Scholar] [CrossRef]
- Tejado, T.; Vinagre, B.M.; Traver, J.E.; Prieto-Arranz, J.; Nuevo-Gallardo, C. Back to basics: Meaning of the parameters of fractional order PID controllers. Mathematics 2019, 7, 530. [Google Scholar] [CrossRef]
- Haroun, A.H.G.; Li, Y.Y. A novel optimized fractional-order hybrid fuzzy intelligent PID controller for interconnected realistic power systems. Trans. Inst. Meas. Control 2019, 41, 3065–3080. [Google Scholar] [CrossRef]
- Hamidian, H.; Beheshti, M.T.H. A robust fractional-order PID controller design based on active queue management for TCP network. Int. J. Syst. Sci. 2018, 49, 211–216. [Google Scholar] [CrossRef]
- Viola, J.; Angel, L.; Sebastian, J.M. Design and robust performance evaluation of a fractional order PID controller applied to a DC motor. IEEE-CAA J. Autom. Sin. 2017, 4, 304–314. [Google Scholar] [CrossRef]
- Yang, B.; Wang, J.B.; Wang, J.T.; Shu, H.C.; Li, D.Y.; Zeng, C.Y.; Chen, Y.J.; Zhang, X.S.; Yu, T. Robust fractional-order PID control of supercapacitor energy storage systems for distribution network applications: A perturbation compensation based approach. J. Clean. Prod. 2021, 279, 123362. [Google Scholar] [CrossRef]
- Kumar, J.; Kumar, V.; Rana, K.P.S. Fractional-order self-tuned fuzzy PID controller for three-link robotic manipulator system. Neural Comput. Appl. 2020, 32, 7235–7257. [Google Scholar] [CrossRef]
- Ray, P.K.; Paital, S.R.; Mohanty, A.; Foo, Y.S.E.; Krishnan, A.; Gooi, H.B.; Amaratunga, G.A.J. A hybrid firefly-swarm optimized fractional order interval type-2 fuzzy PID-pss for transient stability improvement. IEEE Trans. Ind. Appl. 2019, 55, 6486–6498. [Google Scholar] [CrossRef]
- Gao, P.; Zhang, G.M.; Ouyang, H.M.; Mei, L. An adaptive super twisting nonlinear fractional order PID sliding mode control of permanent magnet synchronous motor speed regulation system based on extended state observer. IEEE Access 2020, 8, 53498–53510. [Google Scholar] [CrossRef]
- Chevalier, A.; Francis, C.; Copot, C.; Ionescu, C.M.; Keyser, R.D. Fractional-order PID design: Toward stransition from state-of-art to state-of-use. ISA Trans. 2019, 84, 178–186. [Google Scholar] [CrossRef] [PubMed]
- Mandic, P.D.; Sekara, T.B.; Lazarevic, M.P.; Boskovic, M. Dominant pole placement with fractional order PID controllers: D-decomposition approach. ISA Trans. 2017, 67, 76–86. [Google Scholar] [CrossRef]
- Feliu-Batlle, V.; Castillo-Garcia, F.J. On the robust control of stable minimum phase plants with large uncertainty in a time constant. A fractional-order control approach. Automatica 2014, 50, 218–224. [Google Scholar] [CrossRef]
- Luo, Y.; Chen, Y.Q.; Wang, C.Y.; Pi, Y.G. Tuning fractional order proportional integral controllers for fractional order systems. J. Process Control 2010, 20, 823–831. [Google Scholar] [CrossRef]
- Machado, J.A.T. Optimal tuning of fractional controllers using genetic algorithms. Nonlinear Dyn. 2010, 62, 447–452. [Google Scholar]
- Hekimoglu, B. Optimal tuning of fractional order PID controller for DC motor speed control via chaotic atom search optimization algorithm. IEEE Access 2019, 7, 38100–38114. [Google Scholar] [CrossRef]
- Liu, L.; Shan, L.; Dai, Y.W.; Liu, C.L.; Qi, Z.D. Improved quantum bacterial foraging algorithm for tuning parameters of fractional-order PID controller. J. Syst. Eng. Electron. 2018, 29, 166–175. [Google Scholar] [CrossRef]
- Zhao, J.B.; Jing, W.C.; Wang, J.Z. An indirect optimization scheme for tuning a fractional order PI controller using extremum seeking. Mechatronics 2018, 56, 146–156. [Google Scholar] [CrossRef]
- Liu, X.Y. Optimization design on fractional order PID controller based on adaptive particle swarm optimization algorithm. Nonlinear Dyn. 2016, 84, 379–386. [Google Scholar] [CrossRef]
- Asgharnia, A.; Jamali, A.; Shahnazi, R.; Maheri, A. Load mitigation of a class of 5-MW wind turbine with RBF neural network based fractional-order PID controller. ISA Trans. 2020, 96, 272–286. [Google Scholar] [CrossRef]
- Chen, C.Y.; Zhu, S.; Wei, Y.C.; Yang, C.Y. Finite-time stability of delayed memristor-based fractional-order neural networks. IEEE Trans. Cybern. 2020, 50, 1607–1616. [Google Scholar] [CrossRef]
- Lv, Y.J.; Hu, C.; Yu, J.; Jiang, H.J.; Huang, T.W. Edge-based fractional-order adaptive strategies for synchronization of fractional-order coupled networks with reaction–diffusion terms. IEEE Trans. Cybern. 2020, 50, 1582–1594. [Google Scholar] [CrossRef] [PubMed]
- Zhang, F.H.; Zeng, Z.G. Multiple mittag-leffler stability of delayed fractional-order Cohen-Grossberg neural networks via mixed monotone operator pair. IEEE Trans. Cybern. 2020, 31995512. [Google Scholar] [CrossRef]
- Liu, P.; Zeng, Z.G.; Wang, J. Global synchronization of coupled fractional-order recurrent neural networks. IEEE Trans. Neural Netw. Learn. Syst. 2019, 30, 2358–2368. [Google Scholar] [CrossRef] [PubMed]
- Wang, F.X.; Liu, X.G.; Tang, M.L.; Chen, L.F. Further results on stability and synchronization of fractional-order Hopfield neural networks. Neurocomputing 2019, 346, 12–19. [Google Scholar] [CrossRef]
- Krishna, B.T. Studies on fractional order differentiators and integrators: A survey. Signal Process. 2011, 91, 386–426. [Google Scholar] [CrossRef]
- El-Khazali, R. Discretization of fractional-order differentiators and integrators. IFAC Proc. Vol. 2014, 47, 2016–2021. [Google Scholar] [CrossRef]
- Sierociuk, D.; Dzielinski, A. Fractional Kalman filter algorithm for the states, parameters and order of fractional system estimation. Int. J. Appl. Math. Comput. Sci. 2006, 16, 129–140. [Google Scholar]
- Batir, N. On some properties of the Gamma function. Expo. Math. 2008, 26, 187–196. [Google Scholar] [CrossRef]
- Chen, W.; Liang, Y.J. New methodologies in fractional and fractal derivatives modeling. Chaos Solitons Fractals 2017, 102, 72–77. [Google Scholar] [CrossRef]
- Liang, Y.J.; Ye, A.Q.; Chen, W.; Gatto, R.G.; Colon-Perez, L.; Mareci, T.H.; Magin, R.L. A fractal derivative model for the characterization of anomalous diffusion in magnetic resonance imaging. Commun. Nonlinear Sci. Numer. Simul. 2016, 39, 529–537. [Google Scholar] [CrossRef]
- Cai, W.; Chen, W.; Xu, W.X. Characterizing the creep of viscoelastic materials by fractal derivative models. Int. J. Non-Linear Mech. 2016, 87, 58–63. [Google Scholar] [CrossRef]
- Atangana, A.; Khan, M.A. Validity of fractal derivative to capturing chaotic attractors. Chaos Solitons Fractals 2019, 126, 50–59. [Google Scholar] [CrossRef]
- Chen, W. Time-space fabric underlying anomalous diffusion. Chaos Solitons Fractals 2006, 28, 923–929. [Google Scholar] [CrossRef]
- Hu, D.L.; Chen, W.; Sun, H.G. Power-law stability of Hausdorff derivative nonlinear dynamical systems. Int. J. Syst. Sci. 2020, 51, 601–607. [Google Scholar] [CrossRef]
- Borges, E.P. A possible deformed algebra and calculus inspired in nonextensive thermostatistics. Phys. A Stat. Mech. Its Appl. 2004, 340, 95–101. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional-order systems and PIλDμ controllers. IEEE Trans. Autom. Control 1999, 44, 208–214. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).