Stability Analysis and Numerical Computation of the Fractional Predator–Prey Model with the Harvesting Rate
Abstract
1. Introduction
2. Some Preliminaries
3. Fractional Predator–Prey Model with Caputo Derivative
Positivity and Boundedness
4. Qualitative Properties of the P–PM
5. Stability Analysis of the Predator–Prey Model
5.1. Existence of Equilibria
5.2. Stability of Equilibria
6. Numerical Scheme of the Predator–Prey Model
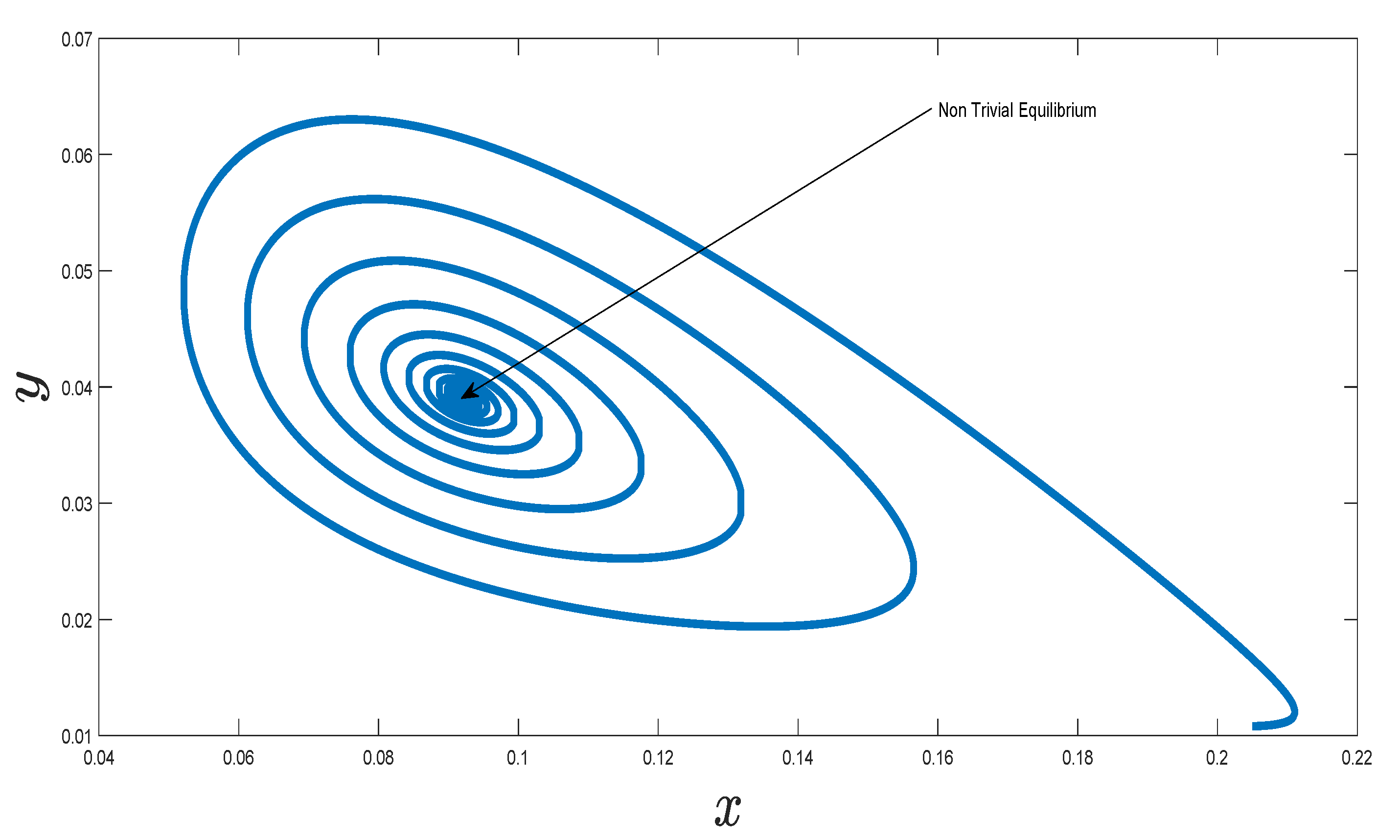
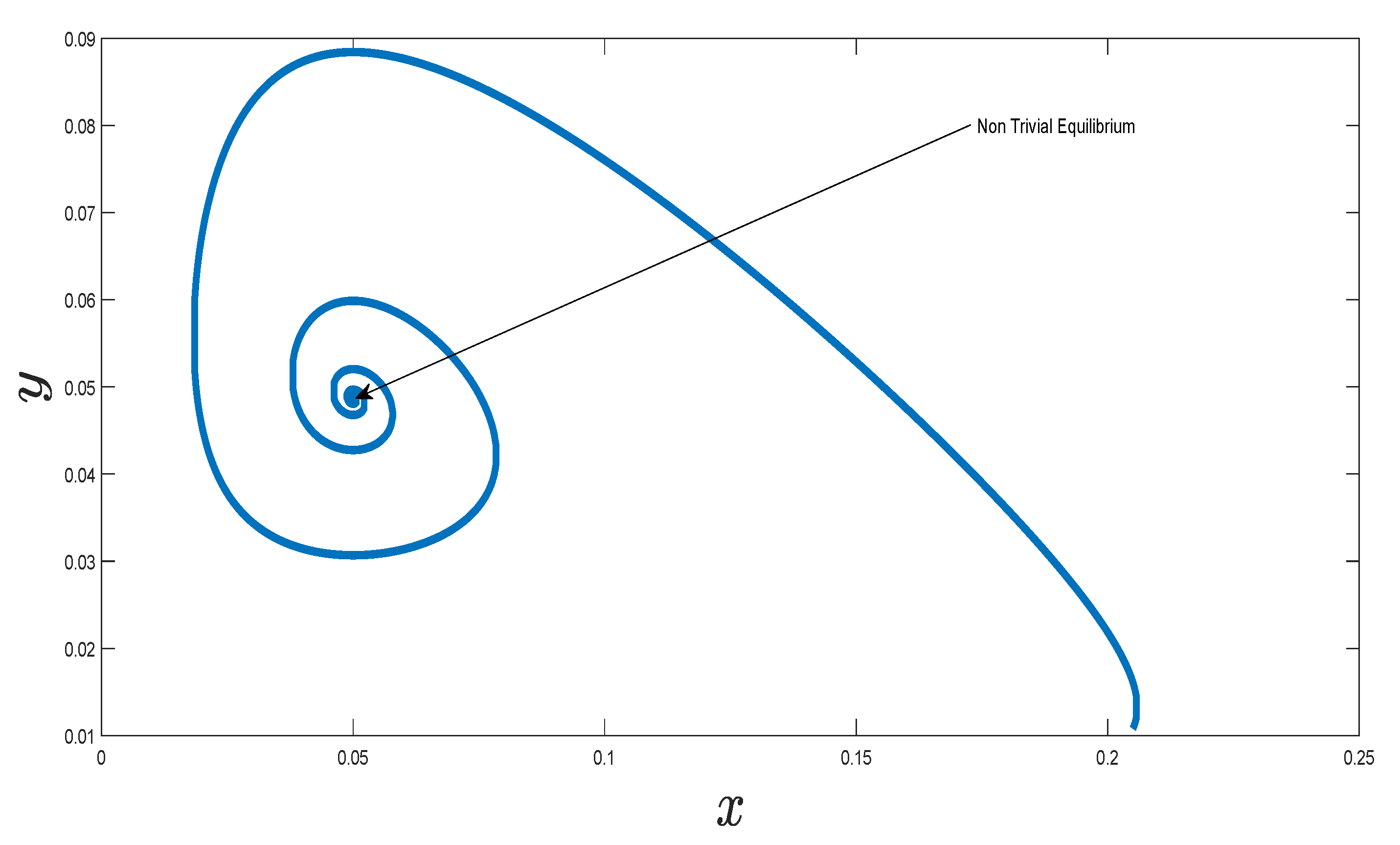
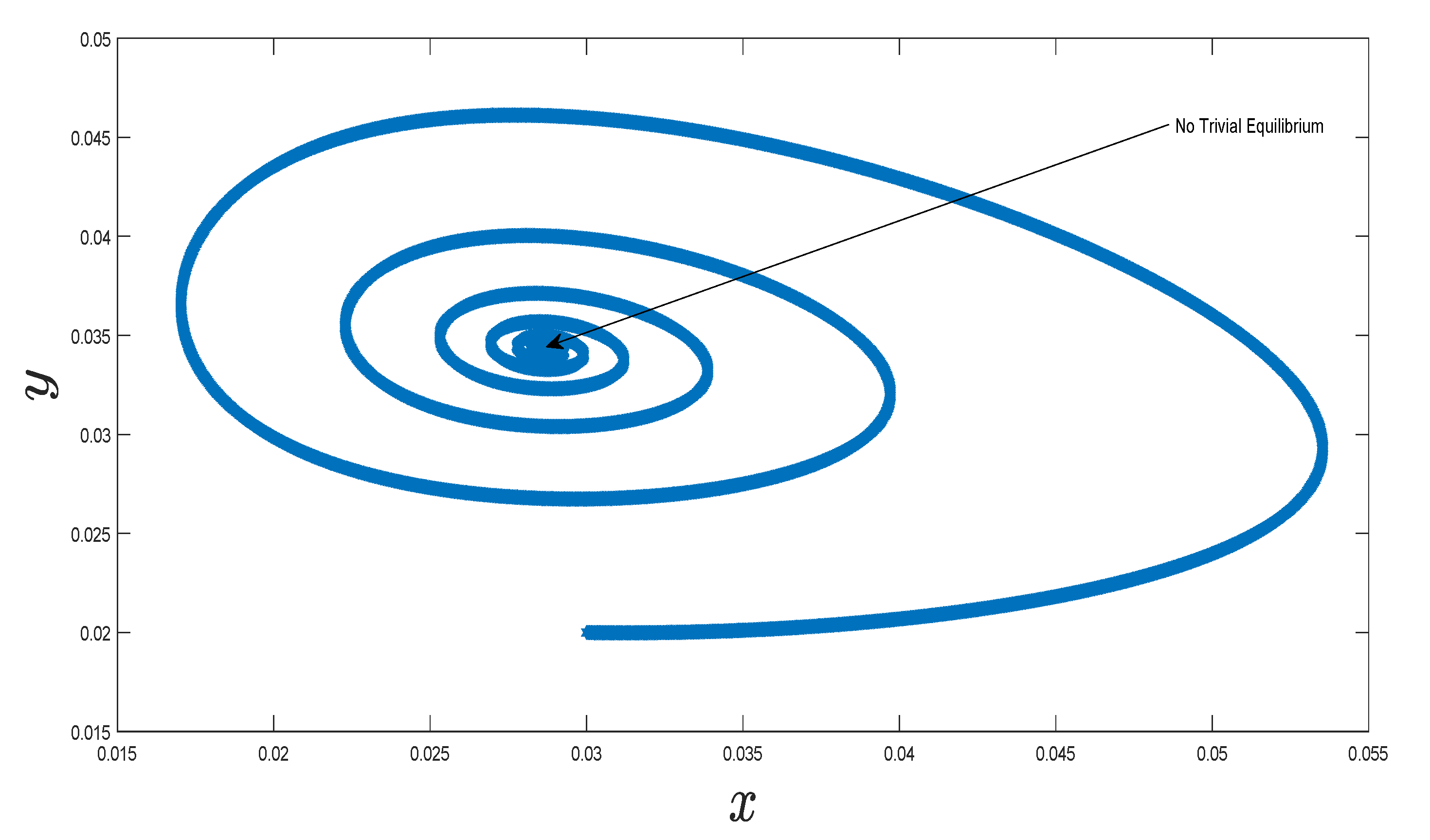
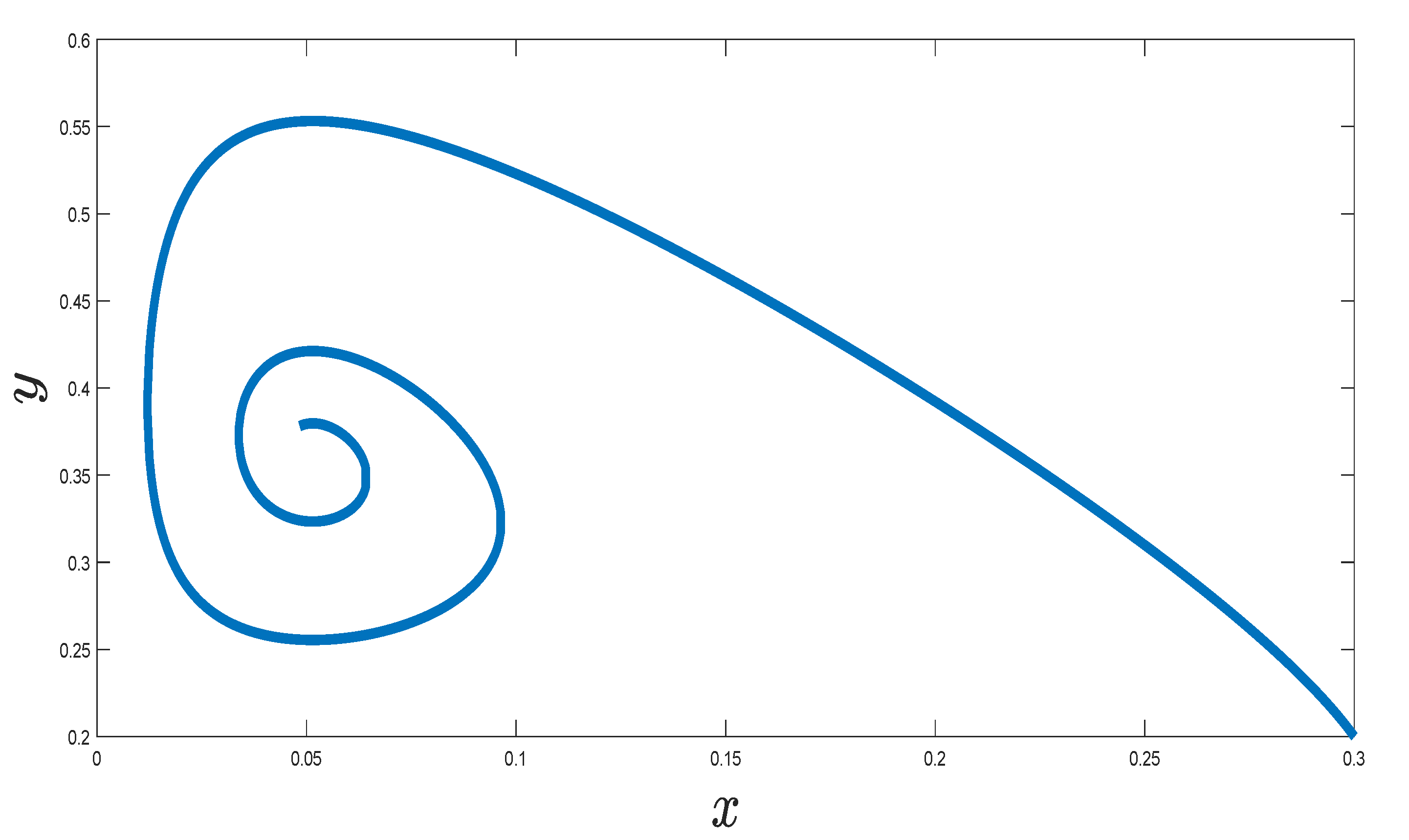
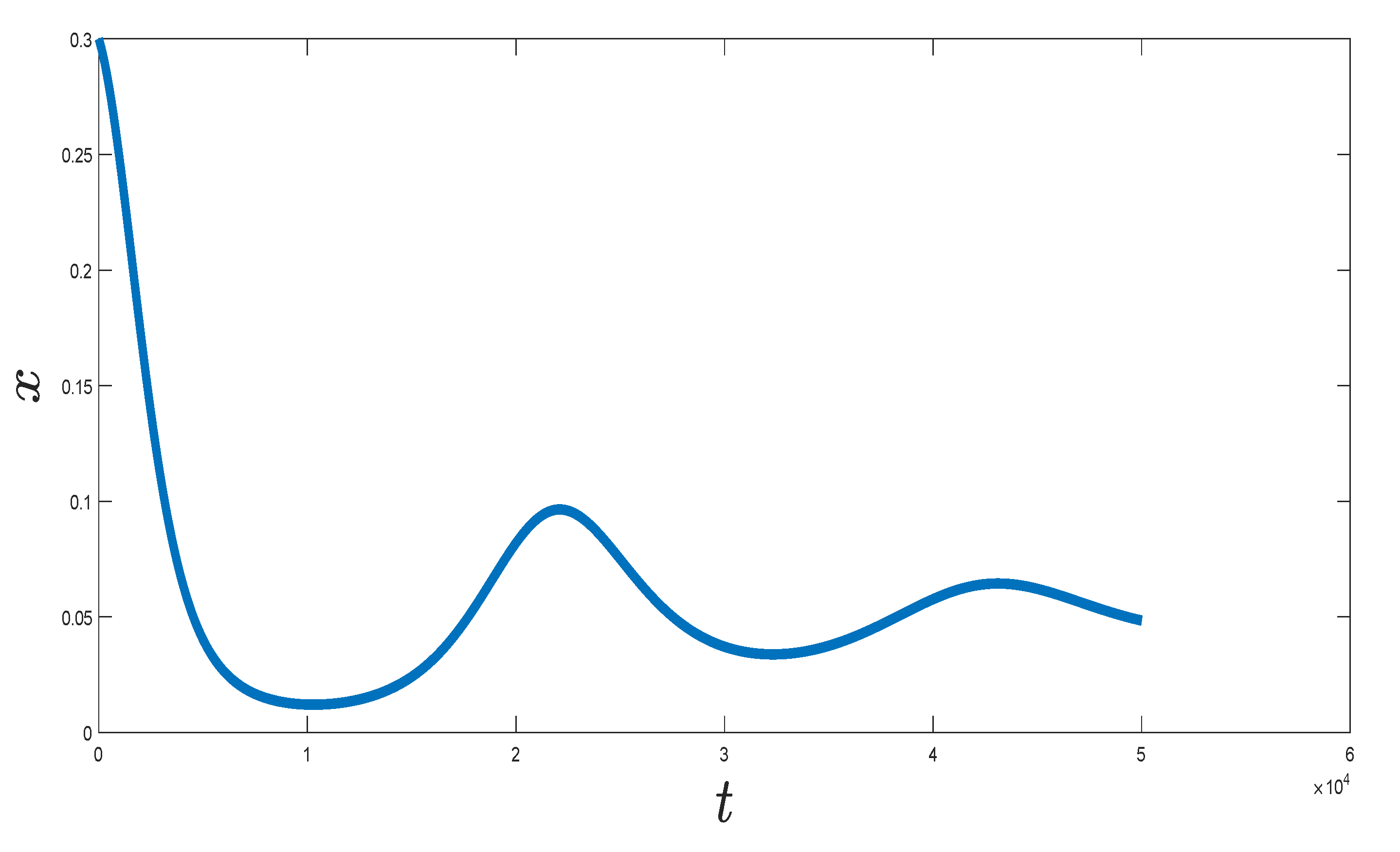
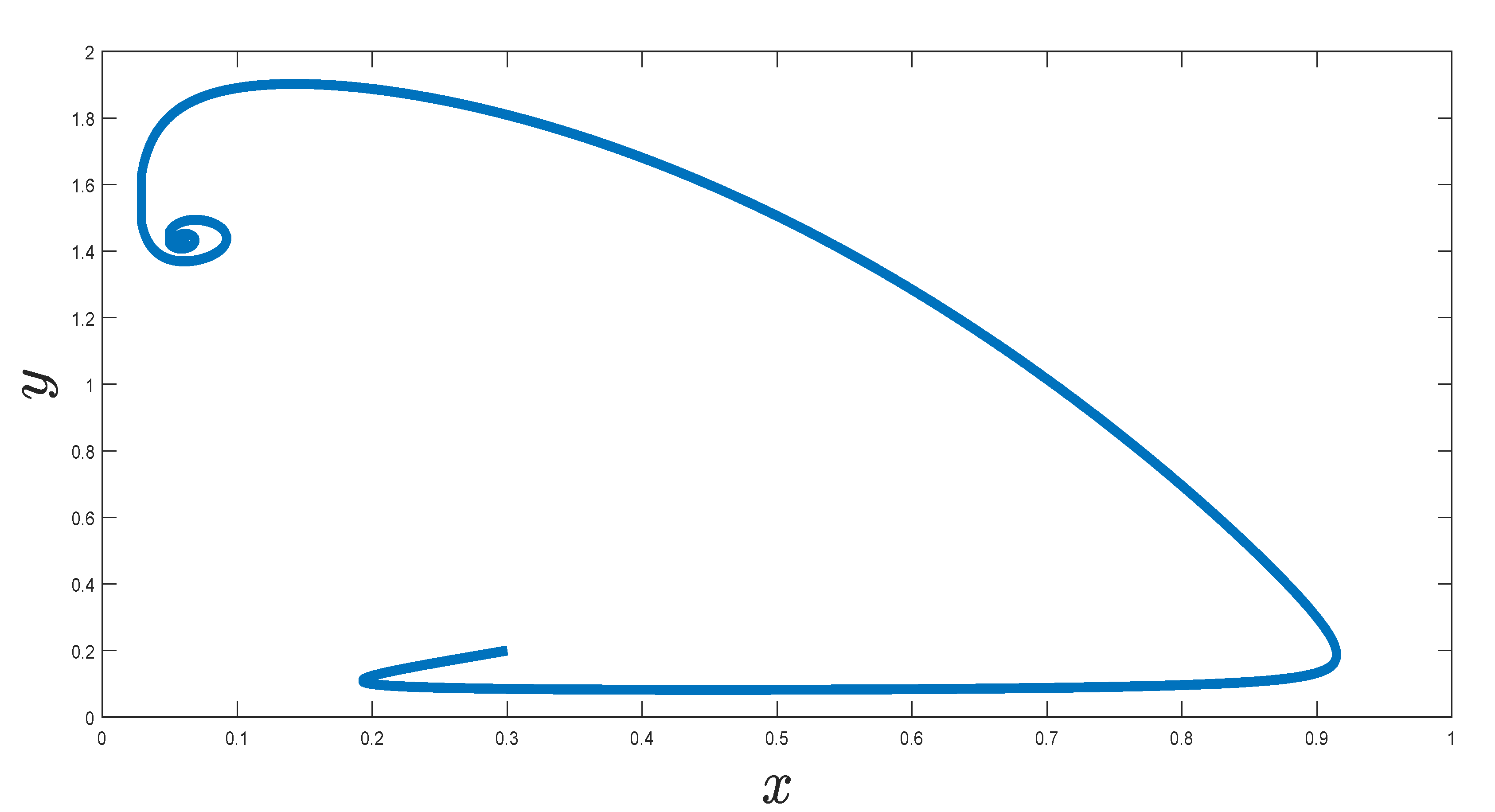
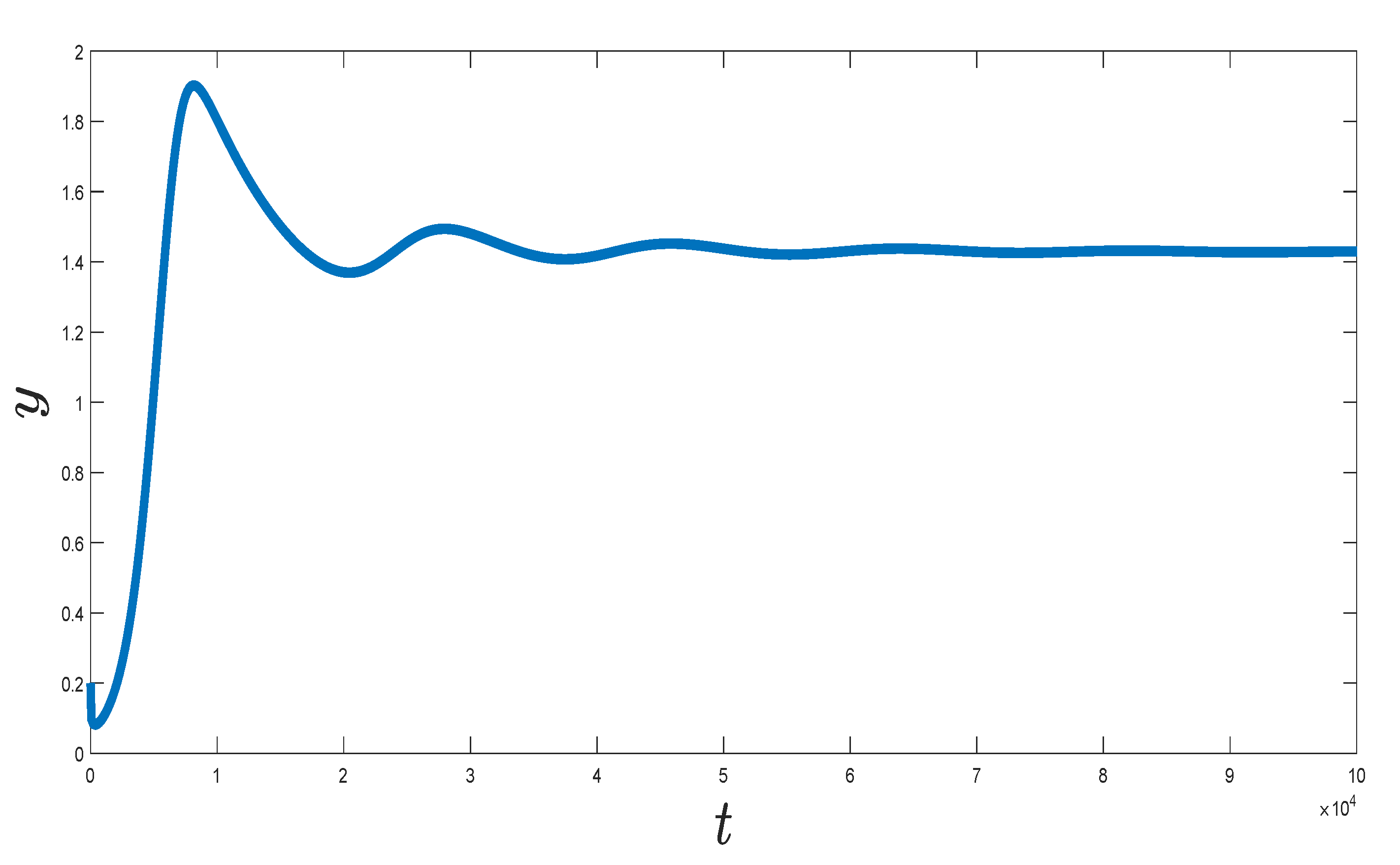
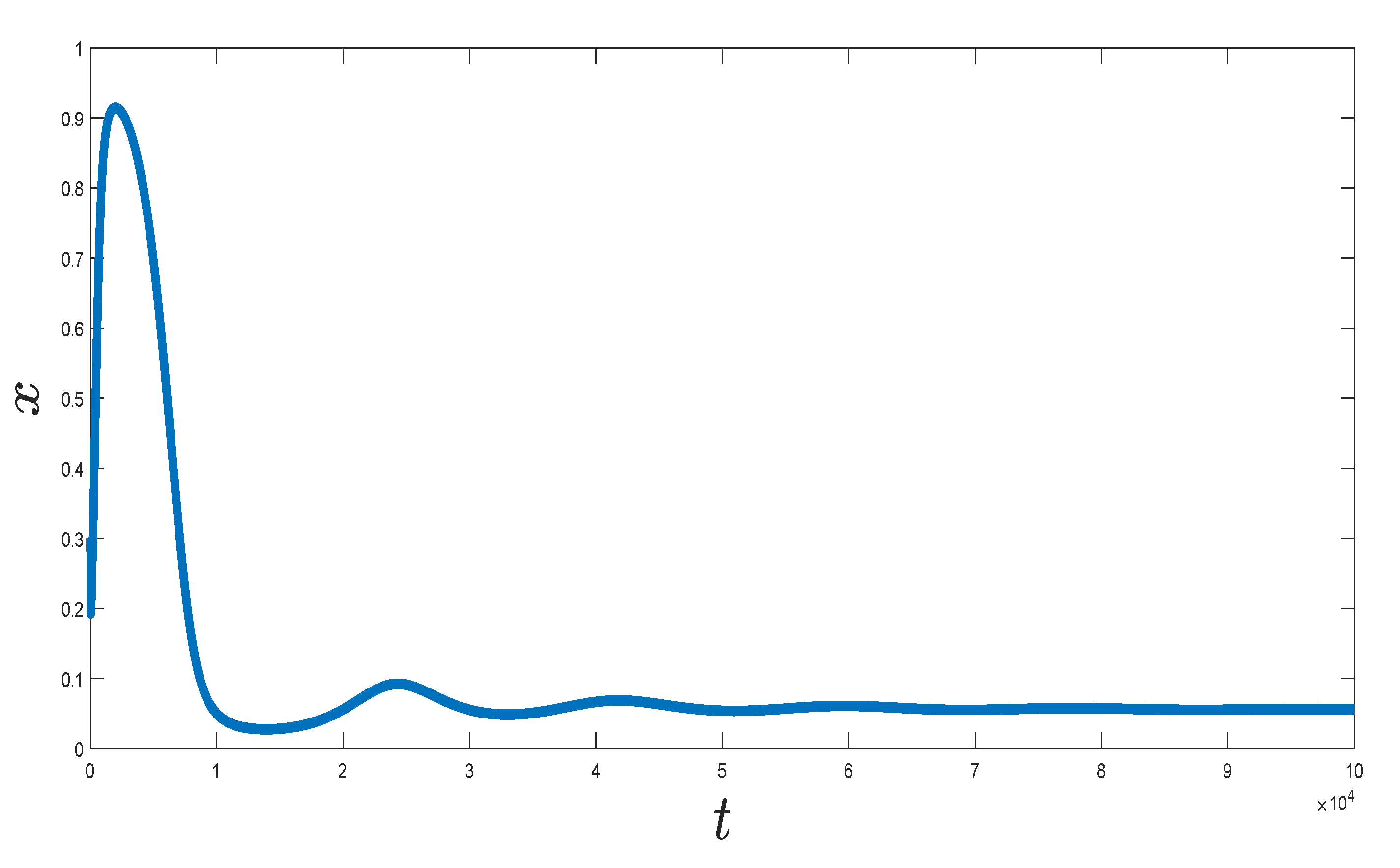
7. Numerical Simulation of the Implicit Scheme
8. Concluding Remarks
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Podlubny, I. Fractional Differential Equations. In Mathematics in Science and Engineering; Academic Press: New York, NY, USA, 1999; Volume 198. [Google Scholar]
- Samko, S.G.; Kilbas, A.A.; Marichev, O.I. Fractional Integrals and Derivatives; Gordon and Breach Science Publishers: Yverdon Yverdon-les-Bains, Switzerland, 1993; Volume 1. [Google Scholar]
- Katugampola, U.N. New approach to a generalized fractional integral. Appl. Math. Comput. 2011, 218, 860–865. [Google Scholar] [CrossRef]
- Caputo, M.; Fabrizio, M. A new definition of fractional derivative without singular kernel. Progr. Fract. Differ. Appl. 2015, 1, 1–15. [Google Scholar]
- Atangana, A.; Baleanu, D. New fractional derivatives with non-local and non-singular kernel theory and application to heat transfer model. arXiv 2016, arXiv:1602.03408. [Google Scholar]
- Wang, X.; Wang, Z. Dynamic Analysis of a Delayed Fractional-Order SIR Model with Saturated Incidence and Treatment Functio. Int. J. Bifurc. Chaos 2018, 28, 1850180. [Google Scholar] [CrossRef]
- Yavuz, M.; Bonyah, E. New approaches to the fractional dynamics of schistosomiasis disease model. Phys. A Stat. Mech. Its Appl. 2019, 525, 373–393. [Google Scholar] [CrossRef]
- Ucar, S.; Ucar, E.; Ozdemir, N.; Hammouch, Z. Mathematical analysis and numerical simulation for a smoking model with Atangana–Baleanu derivative. Chaos Solitons Fractals 2019, 118, 300–306. [Google Scholar] [CrossRef]
- Jajarmi, A.; Ghanbari, B.; Baleanu, D. A new and efficient numerical method for the fractional modelling and optimal control of diabetes and tuberculosis co-existence. Chaos 2019, 29, 093111. [Google Scholar] [CrossRef]
- Naik, P.A.; Yavuz, M.; Zu, J. The Role of Prostitution on HIV Transmission with Memory: A Modeling Approach. Alex. Eng. J. 2020. [Google Scholar] [CrossRef]
- Yavuz, M.; Ozdemir, N. Analysis of an Epidemic Spreading Model with Exponential Decay Law. Math. Sci. Appl. E Notes 2020, 8, 142–154. [Google Scholar] [CrossRef]
- Sene, N. Stokes’ first problem for heated flat plate with Atangana–Baleanu fractional derivative. Chaos Solitons Fractals 2018, 117, 68–75. [Google Scholar] [CrossRef]
- Sene, N. Integral Balance Methods for Stokes’ First, Equation Described by the Left Generalized Fractional Derivative. Physics 2019, 1, 15. [Google Scholar] [CrossRef]
- Sene, N. Second-grade fluid model with Caputo-Liouville generalized fractional derivative. Chaos Solitons Fractals 2020, 133, 109631. [Google Scholar] [CrossRef]
- Ozarslan, R.; Bas, E.; Baleanu, D.; Acay, B. Fractional physical problems including wind-influenced projectile motion with Mittag-Leffler kernel. AIMS Math. 2020, 5, 467. [Google Scholar] [CrossRef]
- Kumar, D.; Singh, J.; Tanwar, K.; Baleanu, D. A new fractional exothermic reactions model having constant heat source in porous media with power, exponential and Mittag-Leffler laws. Int. J. Heat Mass Transf. 2019, 138, 1222–1227. [Google Scholar] [CrossRef]
- Yavuz, M.; Ozdemir, N. European vanilla option pricing model of fractional order without singular kernel. Fractal Fract. 2018, 2, 3. [Google Scholar] [CrossRef]
- Yavuz, M.; Ozdemir, N. A different approach to the European option pricing model with new fractional operator. Math. Model. Nat. Phenom. 2018, 13, 12. [Google Scholar] [CrossRef]
- Sene, N. Analytical solutions and numerical schemes of certain generalized fractional diffusion models. Eur. Phys. J. Plus 2019, 134, 199. [Google Scholar] [CrossRef]
- Qureshi, S.; Yusuf, A.; Ali Shaikh, A.; Inc, M.; Baleanu, D. Mathematical modeling for adsorption process of dye removal nonlinear equation using power law and exponentially decaying kernels. Chaos Interdiscip. J. Nonlinear Sci. 2020, 30, 043106. [Google Scholar] [CrossRef]
- Owolabi, K.M.; Atangana, A. On the formulation of Adams-Bashforth scheme with Atangana-Baleanu-Caputo fractional derivative to model chaotic problems. Chaos 2019, 29, 023111. [Google Scholar] [CrossRef]
- Bhatter, S.; Mathur, A.; Kumar, D.; Nisar, K.S.; Singh, J. Fractional modified Kawahara equation with Mittag-Leffler law. Chaos Solitons Fractals 2020, 131, 109508. [Google Scholar] [CrossRef]
- Usta, F. A conformable calculus of radial basis functions and its applications. Int. J. Optim. Control. Theor. Appl. (IJOCTA) 2018, 8, 176–182. [Google Scholar] [CrossRef]
- Yavuz, M. Characterization of two different fractional operators without singular kernel. Math. Model. Nat. Phenom. 2019, 14, 302. [Google Scholar] [CrossRef]
- Yildiz, T.A.; Jajarmi, A.; Yıldız, B.; Baleanu, D. New aspects of time fractional optimal control problems within operators with nonsingular kernel. Discret. Contin. Dyn. Syst. S 2020, 13, 407–428. [Google Scholar] [CrossRef]
- Budak, H.; Usta, F.; Sarikaya, M.Z.; Ozdemir, M.E. On generalization of midpoint type inequalities with generalized fractional integral operators. Revista de la Real Academia de Ciencias Exactas, Físicas y Naturales. Serie A. Matemáticas 2019, 113, 769–790. [Google Scholar] [CrossRef]
- Yavuz, M.; Sulaiman, T.A.; Usta, F.; Bulut, H. Analysis and numerical computations of the fractional regularized long-wave equation with damping term. Math. Methods Appl. Sci. 2020. [Google Scholar] [CrossRef]
- Özkan, Y.S.; Yaşar, E.; Seadawy, A.R. A third-order nonlinear Schrödinger equation: The exact solutions, group-invariant solutions and conservation laws. J. Taibah Univ. Sci. 2020, 14, 585–597. [Google Scholar] [CrossRef]
- Yavuz, M.; Yaşkıran, B. Conformable Derivative Operator in Modelling Neuronal Dynamics. Appl. Appl. Math. 2018, 13, 803–817. [Google Scholar]
- Jena, R.M.; Chakraverty, S.; Yavuz, M. Two-hybrid techniques coupled with an integral transform for caputo time-fractional Navier-Stokes Equations. Prog. Fract. Differ. Appl. 2020, 6, 201–213. [Google Scholar]
- Ahmad, H.; Seadawy, A.R.; Khan, T.A.; Thounthong, P. Analytic approximate solutions for some nonlinear Parabolic dynamical wave equations. J. Taibah Univ. Sci. 2020, 14, 346–358. [Google Scholar] [CrossRef]
- Yavuz, M. Dynamical behaviors of separated homotopy method defined by conformable operator. Konuralp J. Math. 2019, 7, 1–6. [Google Scholar]
- Avci, D.; Yavuz, M.; Özdemir, N. Fundamental solutions to the Cauchy and Dirichlet problems for a heat conduction equation equipped with the Caputo-Fabrizio differentiation. In Heat Conduction: Methods, Applications and Research; Nova Science Publishers: Hauppauge, NY, USA, 2019; pp. 95–107. [Google Scholar]
- Arnous, A.H.; Seadawy, A.R.; Alqahtani, R.T.; Biswas, A. Optical solitons with complex Ginzburg–Landau equation by modified simple equation method. Optik 2017, 144, 475–480. [Google Scholar] [CrossRef]
- Yavuz, M.; Yokus, A. Analytical and numerical approaches to nerve impulse model of fractional-order. Numer. Methods Partial. Differ. Equ. 2020. [Google Scholar] [CrossRef]
- Selima, E.S.; Seadawy, A.R.; Yao, X. The nonlinear dispersive Davey-Stewartson system for surface waves propagation in shallow water and its stability. Eur. Phys. J. Plus 2016, 131, 1–16. [Google Scholar] [CrossRef]
- Yavuz, M.; Özdemir, N. New numerical techniques for solving fractional partial differential equations in conformable sense. In Non-Integer Order Calculus and Its Applications; Springer: Cham, Switzerland, 2019; pp. 49–62. [Google Scholar]
- Seadawy, A.R.; Jun, W. Mathematical methods and solitary wave solutions of three-dimensional Zakharov-Kuznetsov-Burgers equation in dusty plasma and its applications. Results Phys. 2017, 7, 4269–4277. [Google Scholar]
- Naik, P.A.; Zu, J.; Ghoreishi, M. Estimating the approximate analytical solution of HIV viral dynamic model by using homotopy analysis method. Chaos Solitons Fractals 2020, 131, 109500. [Google Scholar] [CrossRef]
- Yavuz, M. Novel recursive approximation for fractional nonlinear equations within Caputo-Fabrizio operator. In ITM Web of Conferences; EDP Sciences: Jules, France, 2018; Volume 22, p. 01008. [Google Scholar]
- Naik, P.A.; Zu, J.; Owolabi, K.M. Modeling the mechanics of viral kinetics under immune control during primary infection of HIV-1 with treatment in fractional order. Phys. A Stat. Mech. Its Appl. 2020, 545, 123816. [Google Scholar] [CrossRef]
- Avci, D.; Ozdemir, N.; Yavuz, M. Fractional Optimal Control of Diffusive Transport Acting on a Spherical Region. In Methods of Mathematical Modelling: Fractional Differential Equations; CRC Press: Boca Raton, FL, USA, 2019; p. 63. [Google Scholar]
- Seadawy, A.R.; El-Rashidy, K. Dispersive solitary wave solutions of Kadomtsev-Petviashvili and modified Kadomtsev-Petviashvili dynamical equations in unmagnetized dust plasma. Results Phys. 2018, 8, 1216–1222. [Google Scholar] [CrossRef]
- Yavuz, M.; Özdemir, N.; Baskonus, H.M. Solutions of Partial Differential Equations Using the Fractional Operator Involving Mittag-Leffler Kernel. Eur. Phys. J. Plus 2018, 133, 215. [Google Scholar] [CrossRef]
- Tukur, A.S.; Yavuz, M.; Bulut, H.; Baskonus, H.M. Investigation of the Fractional Coupled Viscous Burger’s Equation Involving Mittag-Leffler Kernel. Phys. A Stat. Mech. Its Appl. 2019, 527, 121126. [Google Scholar]
- Iqbal, M.; Seadawy, A.R.; Lu, D. Construction of solitary wave solutions to the nonlinear modified Kortewege-de Vries dynamical equation in unmagnetized plasma via mathematical methods. Mod. Phys. Lett. A 2018, 33, 1850183. [Google Scholar] [CrossRef]
- Keten, A.; Yavuz, M.; Baleanu, D. Nonlocal cauchy problem via a fractional operator involving power kernel in Banach spaces. Fractal Fract. 2019, 3, 27. [Google Scholar] [CrossRef]
- Helal, M.A.; Seadawy, A.R.; Zekry, M.H. Stability analysis of solitary wave solutions for the fourth-order nonlinear Boussinesq water wave equation. Appl. Math. Comput. 2014, 232, 1094–1103. [Google Scholar] [CrossRef]
- Sulaiman, T.A.; Bulut, H.; Yokus, A.; Baskonus, H.M. On the exact and numerical solutions to the coupled Boussinesq equation arising in ocean engineering. Indian J. Phys. 2019, 93, 647–656. [Google Scholar] [CrossRef]
- Evirgen, F.; Yavuz, M. An alternative approach for nonlinear optimization problem with Caputo-Fabrizio derivative. In ITM Web of Conferences; EDP Sciences: Jules, France, 2018; Volume 22, p. 01009. [Google Scholar]
- Fahd, J.; Abdeljawad, T.; Baleanu, D. On the generalized fractional derivatives and their Caputo modification. J. Nonlinear Sci. Appl. 2017, 10, 2607–2619. [Google Scholar]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations. In North-Holland Mathematics Studies; Elsevier: Amsterdam, The Netherlands, 2006; Volume 204. [Google Scholar]
- Li, B.; Liu, S.; Cui, J.; Li, J. A Simple Predator-Prey Population Model with Rich Dynamics. Appl. Sci. 2016, 6, 151. [Google Scholar] [CrossRef]
- Dubey, B. A Prey-Predator Model with a Reserved Area. Nonlinear Anal. Model. Control 2007, 12, 479–494. [Google Scholar] [CrossRef]
- Seo, G.; DeAngelis, D.L. A Predator-Prey Model with a Holling Type I Functional Response Including a Predator Mutual Interference. J. Nonlinear Sci. 2013, 21, 811–833. [Google Scholar] [CrossRef]
- Suryanto, A.; Darti, I.; Panigoro, H.S.; Kilicman, A. A Fractional-Order Predator–Prey Model with Ratio-Dependent Functional Response and Linear Harvesting. Mathematics 2019, 7, 1100. [Google Scholar] [CrossRef]
- Tang, B. Dynamics for a fractional-order predator-prey model with group defense. Sci. Rep. 2020, 10, 4906. [Google Scholar] [CrossRef]
- Elettreby, M.F.; Al-Raezah, A.A.; Nabil, T. Fractional-Order Model of Two-Prey One-Predator System. Math. Probl. Eng. 2017, 2017, 6714538. [Google Scholar] [CrossRef]
- Liu, Y.; Xin, B. Numerical Solutions of a Fractional Predator-Prey System. Adv. Differ. Equ. 2011, 2011, 1–11. [Google Scholar] [CrossRef]
- Lv, Y.; Yuan, R.; Pei, Y. A prey-predator model with harvesting for fishery resource with reserve area. Appl. Math. Model. 2013, 37, 3048–3062. [Google Scholar] [CrossRef]
- Heggeru, C.M.; Lan, K. Local stability analysis of ratio-dependent predator–prey models with predator harvesting rates. Appl. Math. Comput. 2015, 270, 349–357. [Google Scholar]
- Kar, T.K. Selective harvesting in a predator-prey fishery with time delay. Math. Comput. Model. 2003, 38, 449–458. [Google Scholar] [CrossRef]
- Javidi, M.; Nyamoradi, N. Dynamic analysis of a fractional order prey-predator interaction with harvesting. Appl. Math. Model. 2013, 37, 8946–8956. [Google Scholar] [CrossRef]
- Huanga, J.; Ruan, S.; Song, J. Bifurcations in a predator-prey system of Leslie type with generalized Holling typeIII functional response. J. Differ. Equ. 2014, 257, 1721–1752. [Google Scholar] [CrossRef]
- Rebaza, J. Dynamics of prey threshold harvesting and refuge. J. Comput. Appl. Math. 2012, 236, 1743–1752. [Google Scholar] [CrossRef]
- Bulai, I.M.; Hilker, F.M. Eco-epidemiological interactions with predator interference and infection. Theor. Popul. Biol. 2019, 130, 191–202. [Google Scholar] [CrossRef]
- Laurie, H.; Venturino, E.; Bulai, I.M. Herding induced by encounter rate, with predator pressure influencing prey response. In Current Trends in Dynamical Systems in Biology and Natural Sciences; Springer: Cham, Switzerland, 2020; pp. 63–93. [Google Scholar]
- Matignon, D. Stability results on fractional differential equations to control processing. In Proceedings of the Computational Engineering in Syatems and Application Multiconference, Lille, France, 9–12 July 1996; IMACS, IEEE-SMC: Lille, France, 1996; Volume 2, pp. 963–968. [Google Scholar]
- Sene, N. Stability analysis of the generalized fractional differential equations with and without exogenous inputs. J. Nonlinear Sci. Appl. 2019, 12, 562–572. [Google Scholar] [CrossRef]
- Seo, G.; Kot, M. A comparison of two predator–prey models with Holling’s type I functional response. Math. Biosci. 2008, 212, 161–179. [Google Scholar] [CrossRef]
- Murdoch, W.W.; Briggs, C.J.; Nisbet, R.M. Consumer-Resource Dynamics; Princeton University Press: Princeton, NJ, USA, 2003; Volume 36. [Google Scholar]
- Lin, W. Global existence theory and chaos control of fractional differential equations. J. Math. Anal. Appl. 2007, 332, 709–726. [Google Scholar] [CrossRef]
- Garrappa, R. Numerical solution of fractional differential equations: A survey and a software tutorial. Mathematics 2018, 6, 16. [Google Scholar] [CrossRef]


© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yavuz, M.; Sene, N. Stability Analysis and Numerical Computation of the Fractional Predator–Prey Model with the Harvesting Rate. Fractal Fract. 2020, 4, 35. https://doi.org/10.3390/fractalfract4030035
Yavuz M, Sene N. Stability Analysis and Numerical Computation of the Fractional Predator–Prey Model with the Harvesting Rate. Fractal and Fractional. 2020; 4(3):35. https://doi.org/10.3390/fractalfract4030035
Chicago/Turabian StyleYavuz, Mehmet, and Ndolane Sene. 2020. "Stability Analysis and Numerical Computation of the Fractional Predator–Prey Model with the Harvesting Rate" Fractal and Fractional 4, no. 3: 35. https://doi.org/10.3390/fractalfract4030035
APA StyleYavuz, M., & Sene, N. (2020). Stability Analysis and Numerical Computation of the Fractional Predator–Prey Model with the Harvesting Rate. Fractal and Fractional, 4(3), 35. https://doi.org/10.3390/fractalfract4030035





