Solving Helmholtz Equation with Local Fractional Derivative Operators
Abstract
:1. Introduction
2. Basic Definitions of Local Fractional Calculus
3. Analysis of the Method
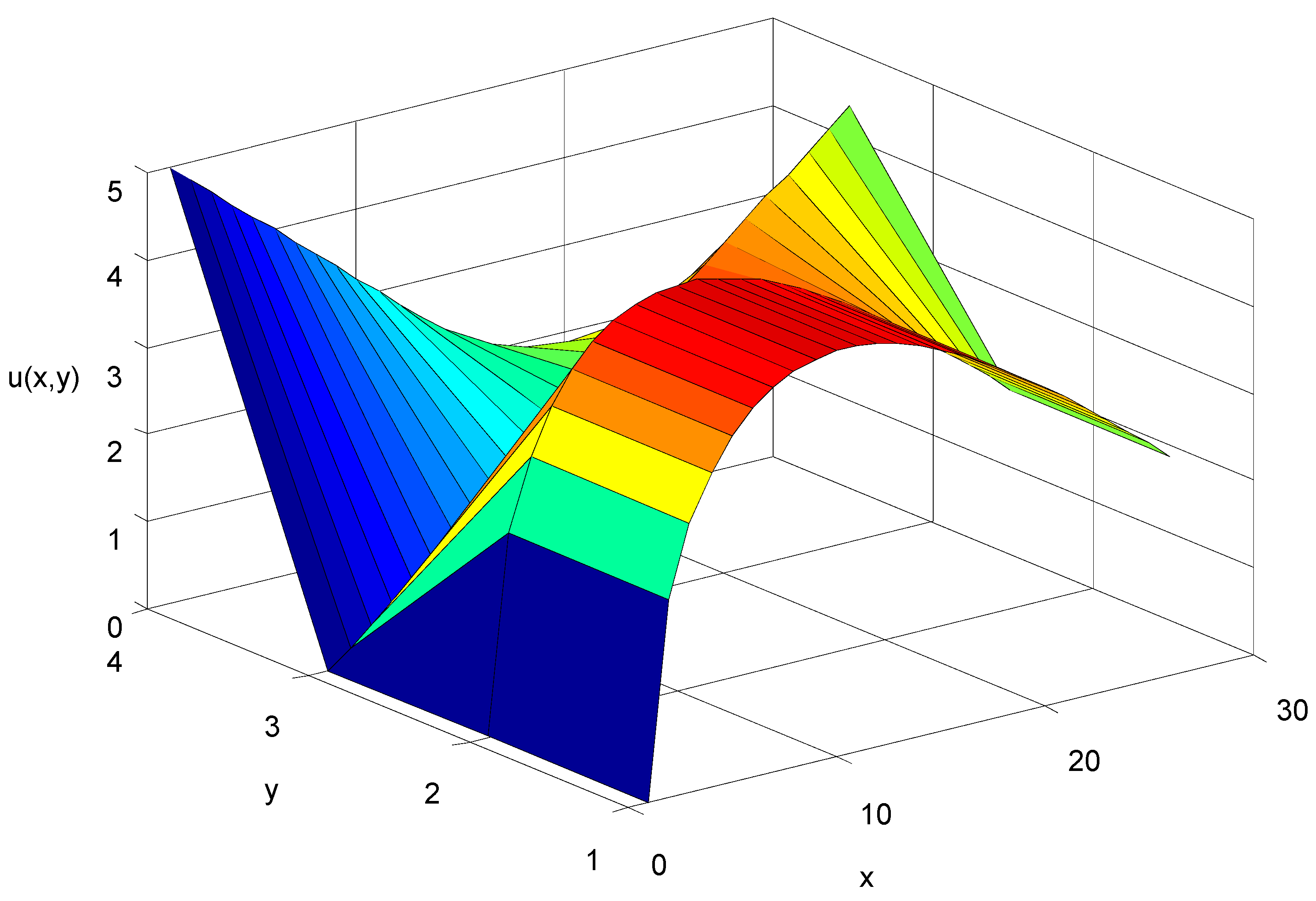
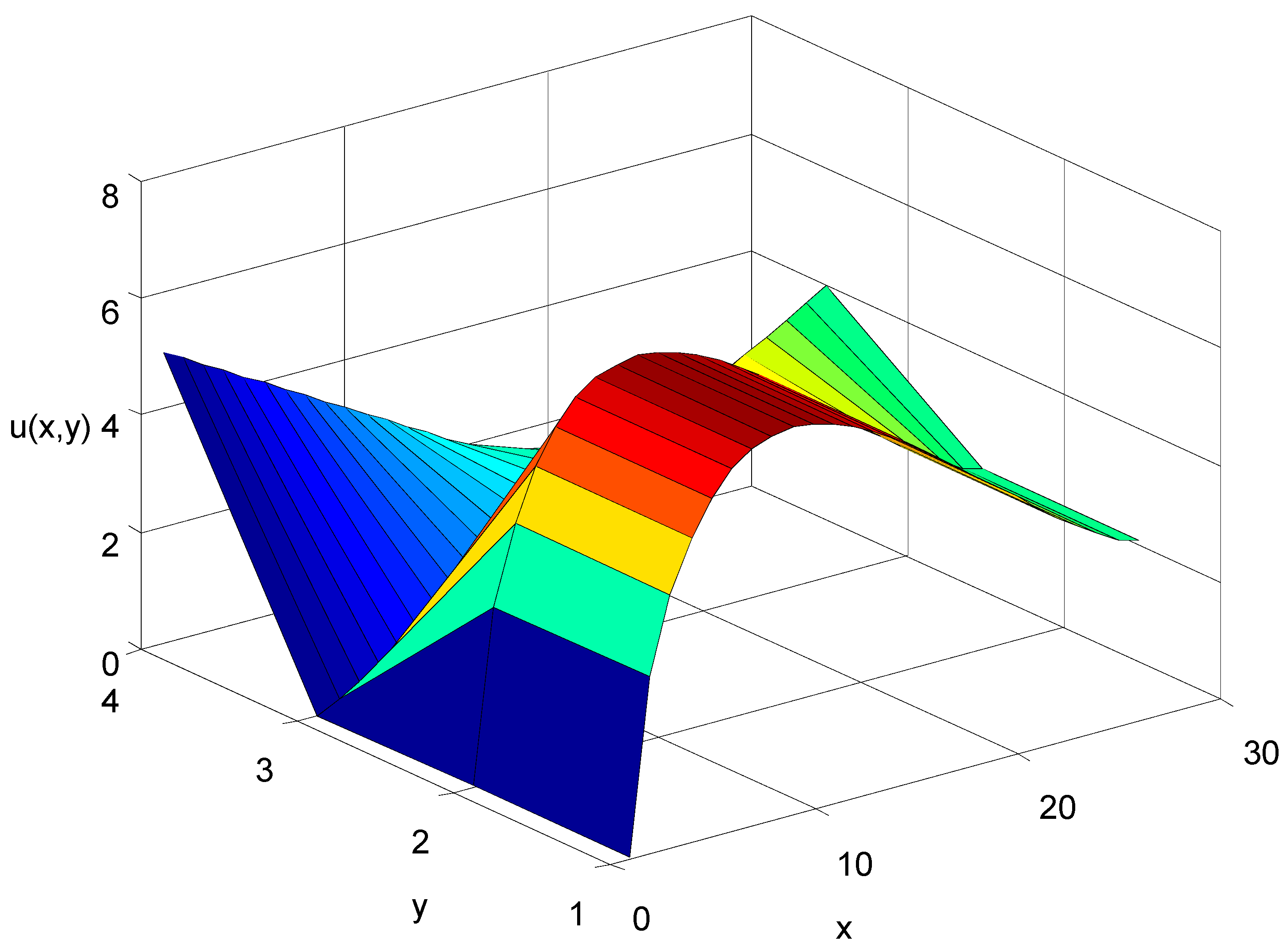
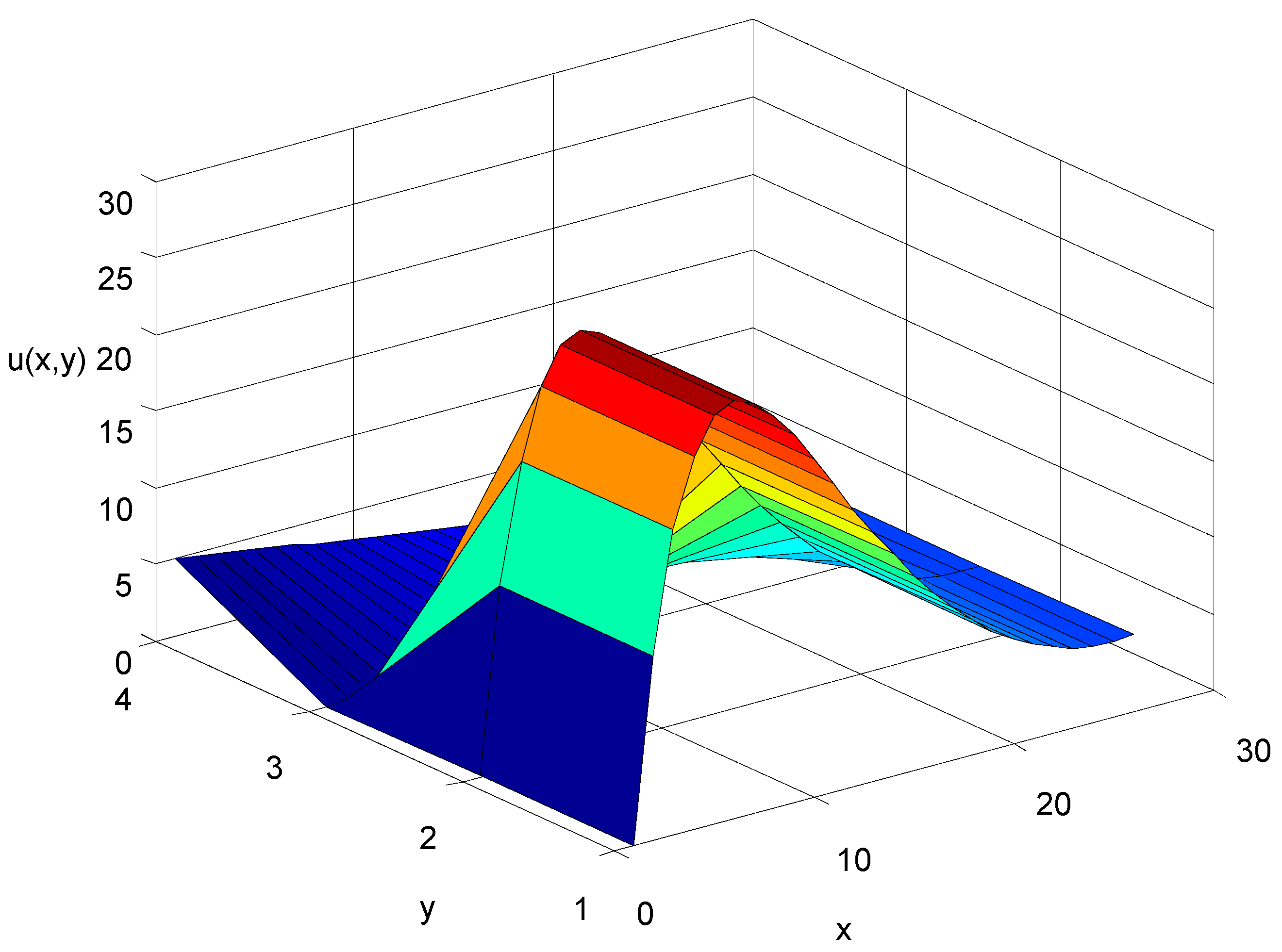
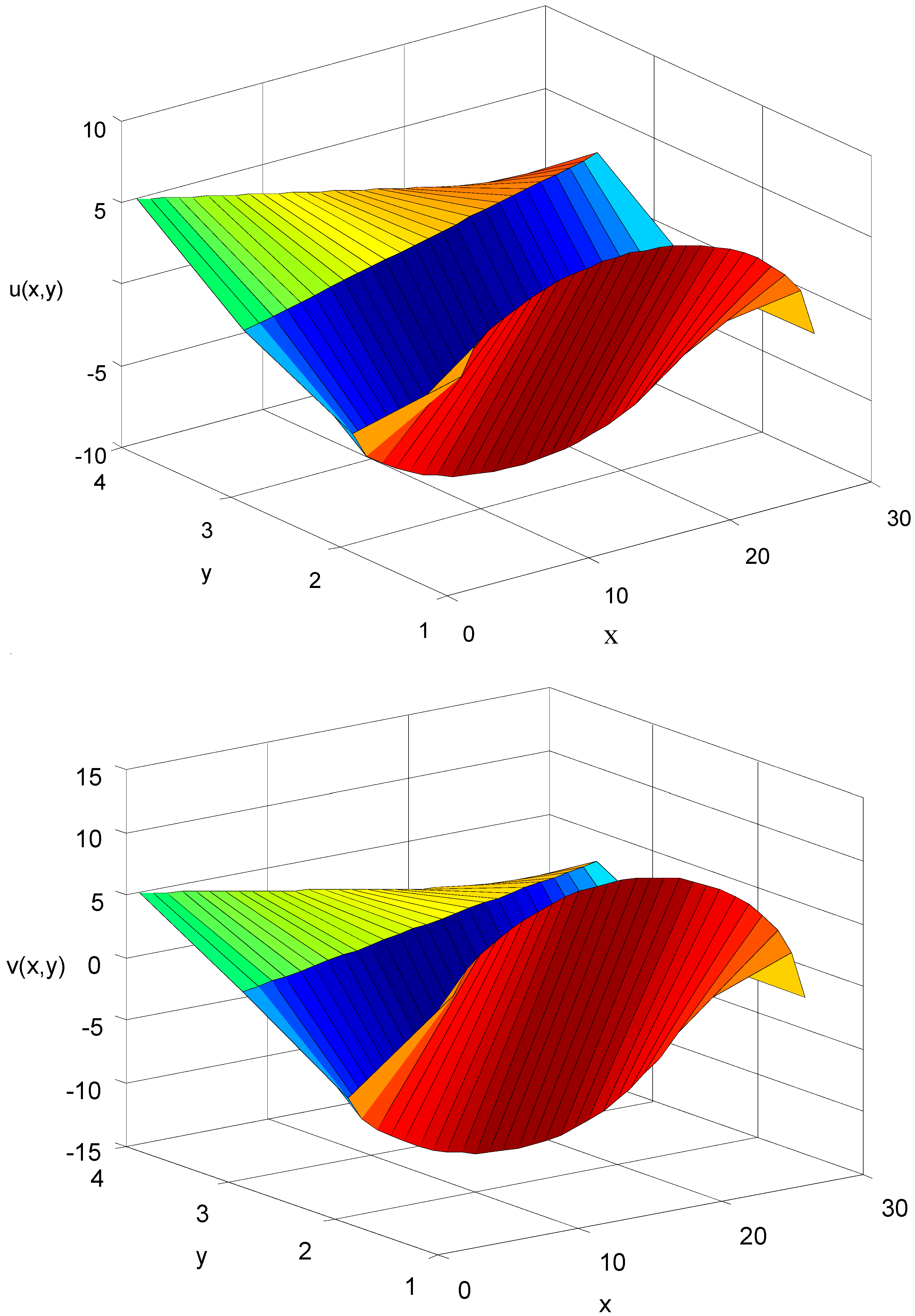
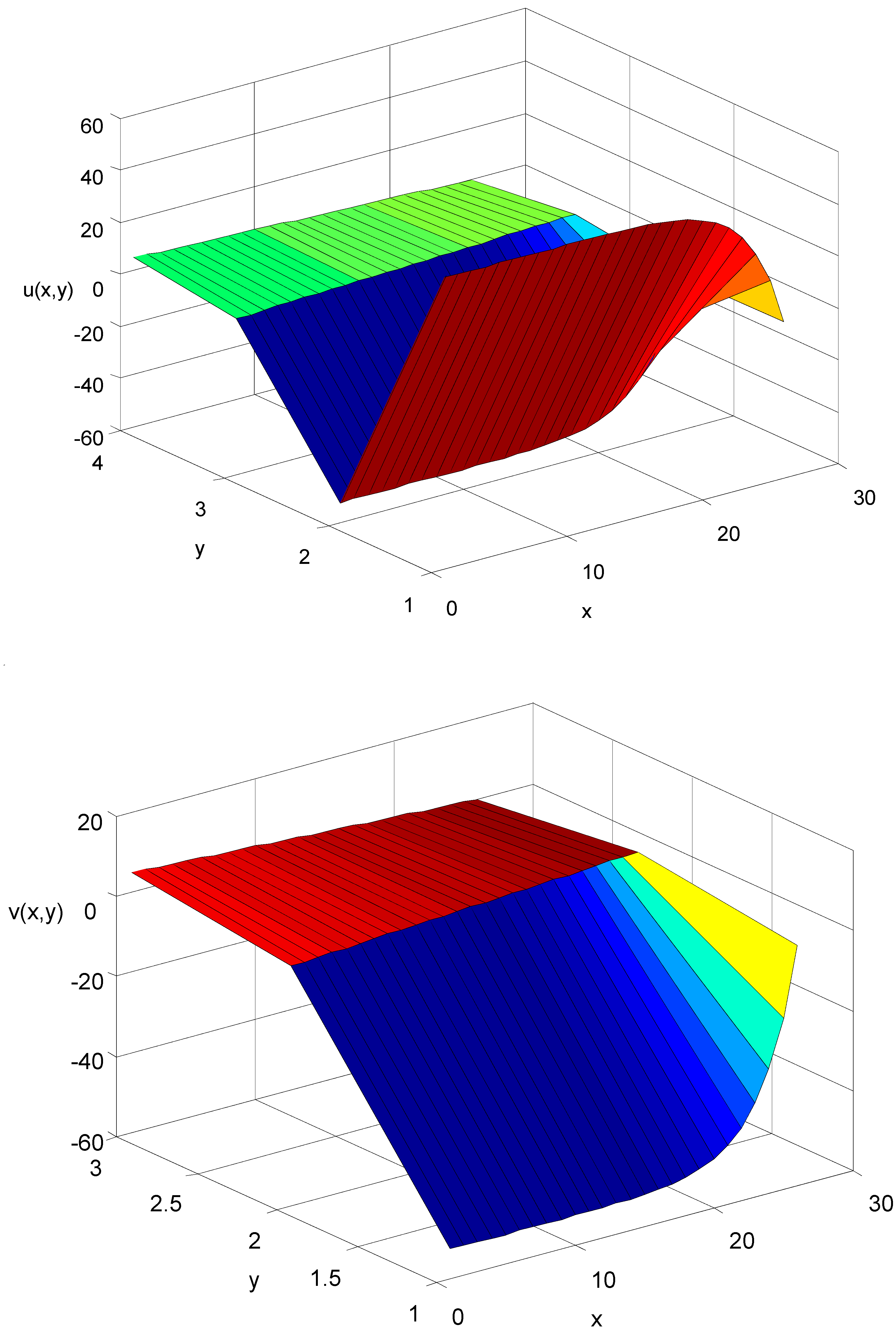
4. Illustrated Examples
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hao, Y.; Srivastava, H.M.; Jafari, H.; Yang, X.J. Helmholtz and diffusion equations associated with local fractional derivative operators involving the Cantorian and Cantor-type cylindrical coordinates. Adv. Math. Phys. 2013, 2013, 754248. [Google Scholar] [CrossRef]
- Jassim, H.K. The approximate solutions of helmholtz and coupled helmholtz equations on cantor sets within local fractional operator. J. Zankoy Sulaimani Part A 2015, 17, 19–25. [Google Scholar] [CrossRef]
- Baleanu, D.; Jassim, H.K.; Qurashi, M.A. Approximate analytical solutions of goursat problem within local fractional operators. J. Nonlinear Sci. Appl. 2016, 9, 4829–4837. [Google Scholar] [CrossRef]
- Fan, Z.P.; Jassim, H.K.; Raina, R.K.; Yang, X.-J. Adomian decomposition method for three-dimensional diffusion model in fractal heat transfer involving local fractional derivatives. Therm. Sci. 2015, 19, S137–S141. [Google Scholar] [CrossRef]
- Jafari, H.; Jassim, H.K. Local fractional adomian decomposition method for solving two dimensional heat conduction equations within local fractional operators. J. Adv. Math. 2014, 9, 2574–2582. [Google Scholar]
- Baleanu, D.; Jassim, H.K.; Khan, H. A modification fractional variational iteration method for solving nonlinear gas dynamic and coupled KdV equations involving local fractional operators. Therm. Sci. 2018, 19, S165–S175. [Google Scholar] [CrossRef]
- Baleanu, D.; Jassim, H.K. Approximate solutions of the damped wave equation and dissipative wave equation in fractal strings. Fractal Fract. 2019, 3, 26. [Google Scholar] [CrossRef]
- Jafari, H.; Jassim, H.K. Local fractional variational iteration method for nonlinear partial differential equations within local fractional operators. Appl. Appl. Math. 2015, 10, 1055–1065. [Google Scholar]
- Xu, S.; Ling, X.; Zhao, Y.; Jassim, H.K. A novel schedule for solving the two-dimensional diffusion in fractal heat transfer. Therm. Sci. 2015, 19, S99–S103. [Google Scholar] [CrossRef]
- Jafari, H.; Jassim, H.K.; Vahidi, J. Reduced differential transform and variational iteration methods for 3D diffusion model in fractal heat transfer within local fractional operators. Therm. Sci. 2018, 22, S301–S307. [Google Scholar] [CrossRef]
- Jassim, H.K.; Shahab, W.A. Fractional variational iteration method to solve one dimensional second order hyperbolic telegraph equations. J. Phys. Conf. Ser. 2018, 1032, 1–9. [Google Scholar] [CrossRef]
- Yang, X.J.; Machad, J.A.; Srivastava, H.M. A new numerical technique for solving the local fractional diffusion equation: Two-dimensional extended differential transform approach. Appl. Math. Comput. 2016, 274, 143–151. [Google Scholar] [CrossRef]
- Jafari, H.; Jassim, H.K.; Tchier, F.; Baleanu, D. On the approximate solutions of local fractional differential equations with local fractional operator. Entropy 2016, 18, 150. [Google Scholar] [CrossRef]
- Baleanu, D.; Jassim, H.K. A novel approach for Korteweg-de Vries equation of fractional order. J. Appl. Comput. Mech. 2019, 5, 192–198. [Google Scholar]
- Yang, A.-M.; Yang, X.-J.; Li, Z.-B. Local fractional series expansion method for solving wave and diffusion equations Cantor sets. Abstr. Appl. Anal. 2013, 2013, 351057. [Google Scholar] [CrossRef]
- Jassim, H.K. On approximate methods for fractal vehicular traffic flow. TWMS J. Appl. Eng. Math. 2017, 7, 58–65. [Google Scholar]
- Srivastava, H.M.; Golmankhaneh, A.K.; Baleanu, D. Local fractional sumudu transform with application to IVPs on Cantor Set. Abstr. Appl. Anal. 2014, 2014, 620529. [Google Scholar] [CrossRef]
- Hu, M.-S.; Agarwal, R.P.; Yang, X.-J. Local fractional fourier series with application to wave equation in fractal vibrating. Abstr. Appl. Anal. 2012, 2012, 567401. [Google Scholar] [CrossRef]
- Wang, S.Q.; Yang, Y.J.; Jassim, H.K. Local fractional function decomposition method for solving inhomogeneous wave equations with local fractional derivative. Abstr. Appl. Anal. 2014, 2014, 176395. [Google Scholar] [CrossRef]
- Yan, S.P.; Jafari, H.; Jassim, H.K. Local fractional adomian decomposition and function decomposition methods for solving laplace equation within local fractional operators. Adv. Math. Phys. 2014, 2014, 161580. [Google Scholar] [CrossRef]
- Jassim, H.K. The analytical solutions for volterra integro-differential equations involving local fractional operators by yang-laplace transform. Sahand Commun. Math. Anal. 2017, 6, 69–76. [Google Scholar]
- Zhao, C.G.; Yang, A.-M.; Jafari, H.; Haghbin, A. The Yang-Laplace transform for solving the IVPs with local fractional derivative. Abstr. Appl. Anal. 2014, 2014, 386459. [Google Scholar] [CrossRef]
- Jafari, H.; Jassim, H.K.; Moshokoa, S.P.; Ariyan, V.M.; Tchier, F. Reduced differential transform method for partial differential equations within local fractional derivative operators. Adv. Mech. Eng. 2016, 8, 1–6. [Google Scholar] [CrossRef]
- Jassim, H.K. An efficient technique for solving linear and nonlinear wave equation within local fractional operators. J. Hyperstruct. 2017, 6, 136–146. [Google Scholar]
- Ait, T.; Hammouch, Z.; Mekkaoui, T.; Belgacem, F.B.M. Implementation and convergence analysis of homotopy perturbation coupled with sumudu transform to construct solutions of local-fractional PDEs. Fractal Fract. 2018, 2, 1–22. [Google Scholar]
- Jafari, H.; Jassim, H.K.; Qurashi, M.A.; Baleanu, D. On the existence and uniqueness of solutions for local differential equations. Entropy 2016, 18, 420. [Google Scholar] [CrossRef]
- Bayour, B.; Torres, D.F.M. Existence of solution to a local fractional nonlinear differential equation. J. Comput. Appl. Math. 2017, 312, 127–133. [Google Scholar] [CrossRef] [Green Version]
- Yang, X.J. Local Fractional Functional Analysis and Its Applications; Asian Academic Publisher: Hong Kong, China, 2011. [Google Scholar]
- Baleanu, D.; Jassim, H.K. A modification fractional homotopy perturbation method for solving helmholtz and coupled helmholtz equations on cantor sets. Fractal Fract. 2019, 3, 30. [Google Scholar] [CrossRef]
- He, J.-H.; Liu, H. Local fractional variational iteration method for fractal heat transfer in silk cocoon hierarchy. Nonlinear Sci. Lett. A 2013, 4, 15–20. [Google Scholar]
- Wu, G. Applications of the variational iteration method to fractional diffusion equations: Local versus nonlocal Ones. Int. Rev. Chem. Eng. 2012, 4, 505–510. [Google Scholar]
- Yang, X.J. Advanced Local Fractional Calculus and Its Applications; World Science: New York, NY, USA, 2012. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Baleanu, D.; Jassim, H.K.; Al Qurashi, M. Solving Helmholtz Equation with Local Fractional Derivative Operators. Fractal Fract. 2019, 3, 43. https://doi.org/10.3390/fractalfract3030043
Baleanu D, Jassim HK, Al Qurashi M. Solving Helmholtz Equation with Local Fractional Derivative Operators. Fractal and Fractional. 2019; 3(3):43. https://doi.org/10.3390/fractalfract3030043
Chicago/Turabian StyleBaleanu, Dumitru, Hassan Kamil Jassim, and Maysaa Al Qurashi. 2019. "Solving Helmholtz Equation with Local Fractional Derivative Operators" Fractal and Fractional 3, no. 3: 43. https://doi.org/10.3390/fractalfract3030043
APA StyleBaleanu, D., Jassim, H. K., & Al Qurashi, M. (2019). Solving Helmholtz Equation with Local Fractional Derivative Operators. Fractal and Fractional, 3(3), 43. https://doi.org/10.3390/fractalfract3030043





