Fractal Logistic Equation
Abstract
:1. Introduction
2. Basic Tools
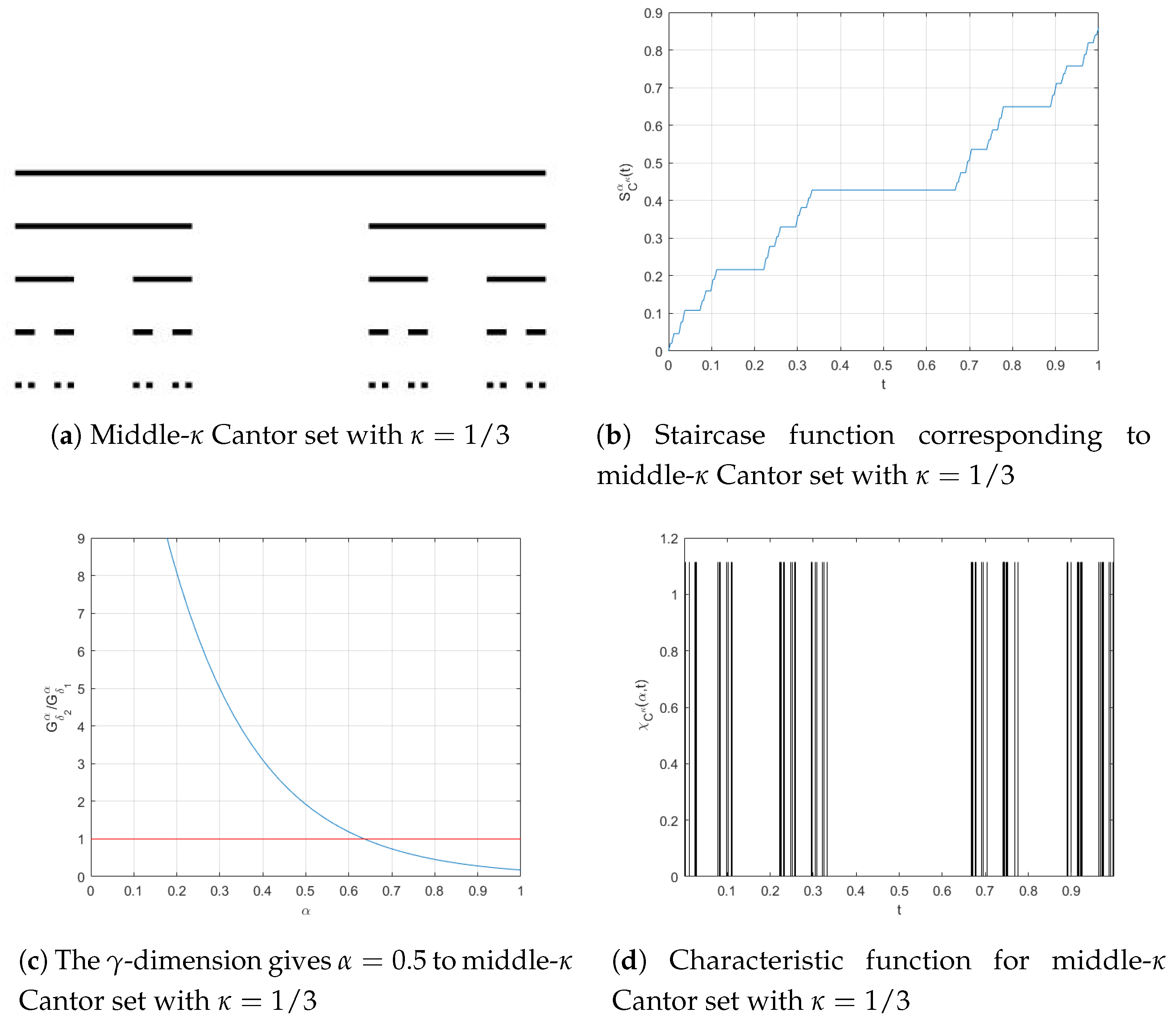
2.1. Middle- Cantor Set
- 1-Step 1.
- Pick up an open interval of length from the middle of the .
- 2-Step 2.
- Delete disjoint open intervals of length from the middle of the remaining closed intervals of step 1.
- 3-Step m.
- Remove disjoint open intervals of length from the middle of the remaining closed intervals of step m-1.
2.2. Local Fractal Calculus
3. Fractal Finite Difference and Fractal Derivative
4. Fractal Difference and Differential Equations
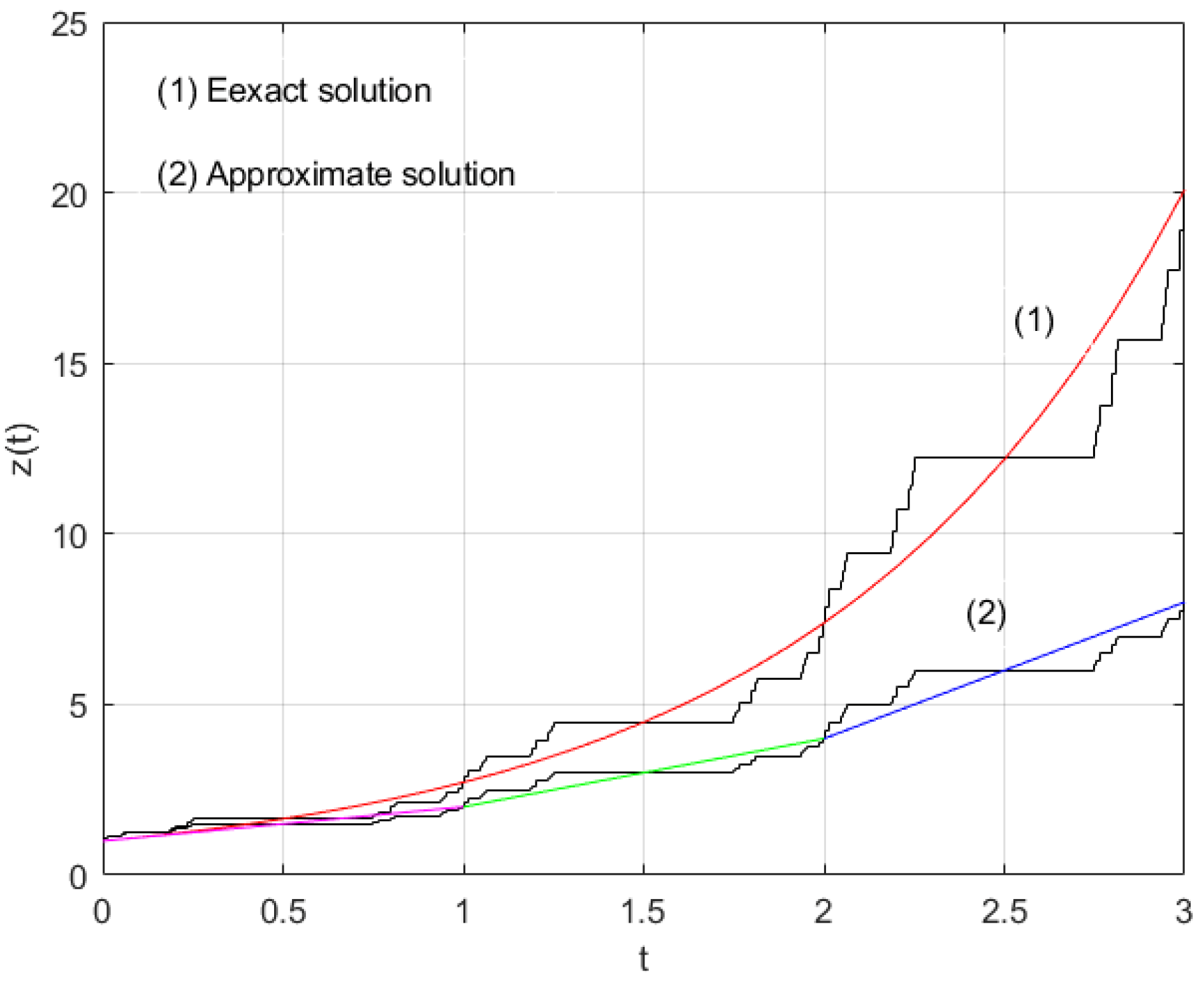
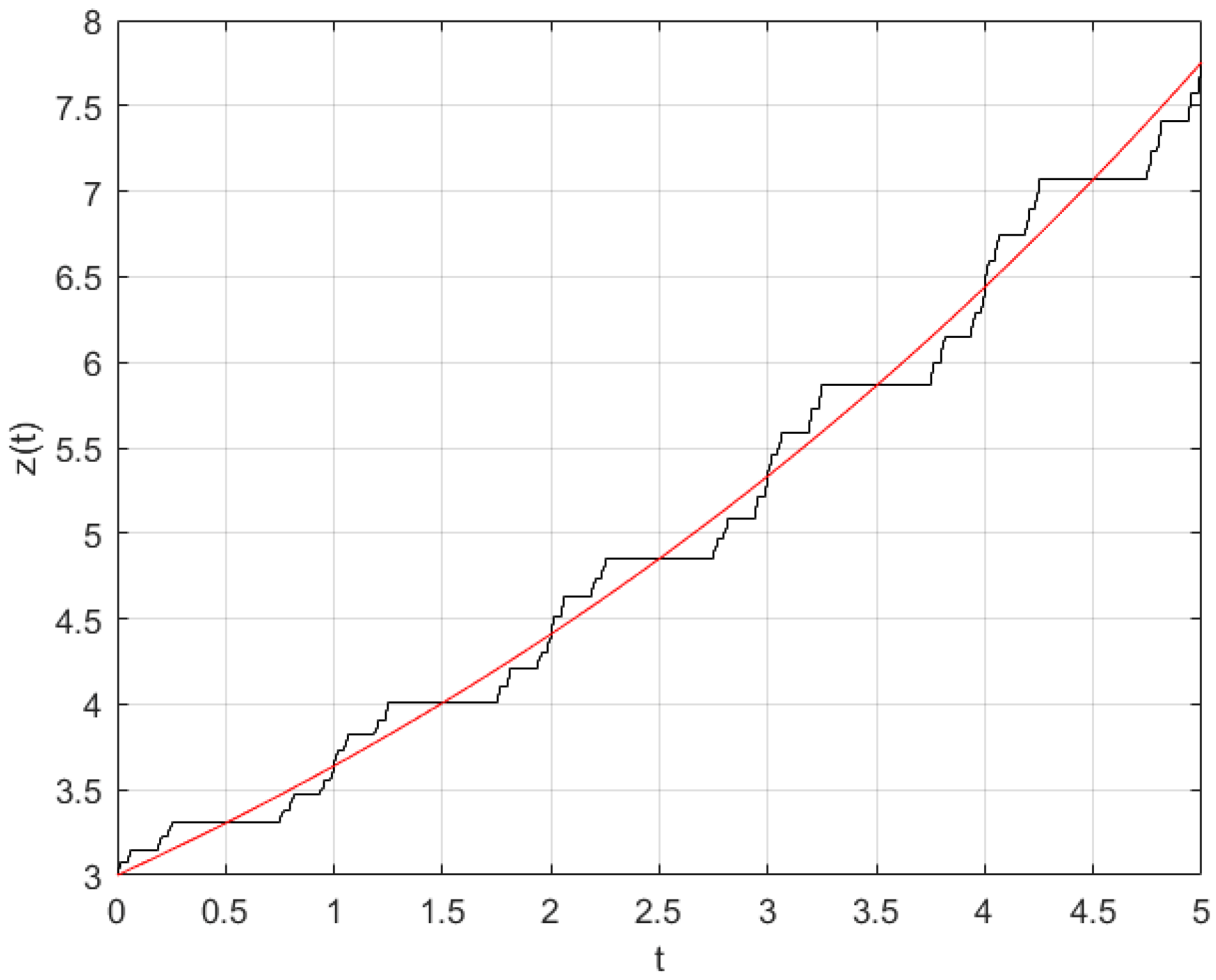
5. Numerical Method for Solving Fractal Differential Equation
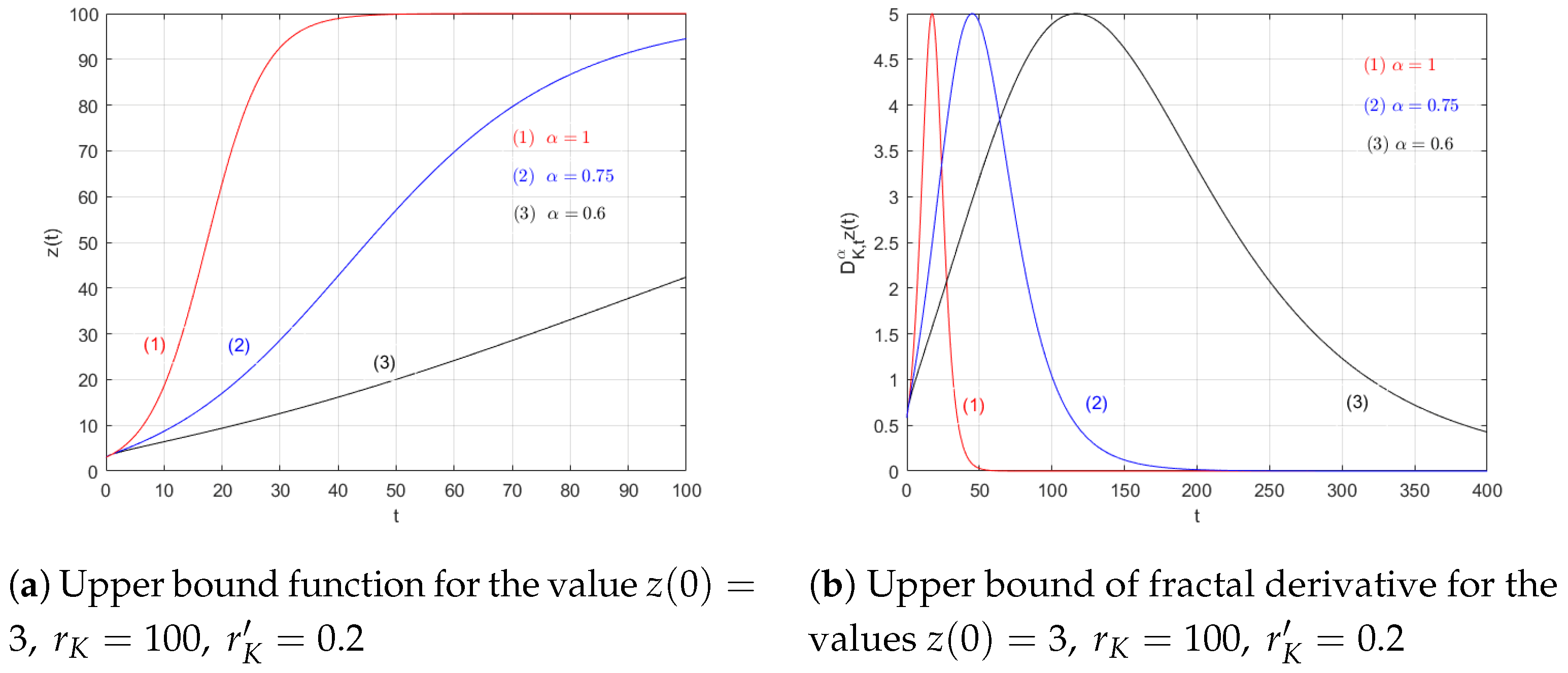
6. Fractal Logistic Equation
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Mandelbrot, B.B. The Fractal Geometry of Nature; WH Freeman: New York, NY, USA, 1983; Volume 173. [Google Scholar]
- Barnsley, M.F. Fractals Everywhere; Academic Press: Cambridge, MA, USA, 2014. [Google Scholar]
- Cattani, C.; Pierro, G. On the fractal geometry of DNA by the binary image analysis. Bull. Math. Biol. 2013, 75, 1544–1570. [Google Scholar] [CrossRef] [PubMed]
- Heydari, M.H.; Hooshmandasl, M.R.; Ghaini, F.M.; Cattani, C. Wavelets method for solving fractional optimal control problems. Appl. Math. Comput. 2016, 286, 139–154. [Google Scholar] [CrossRef]
- Badiali, J.P. Fractal behavior in quantum statistical physics. Phys. Rev. E 1999, 60, 2533. [Google Scholar] [CrossRef]
- Demmie, P.N.; Ostoja-Starzewski, M. Waves in fractal media. J. Elast. 2011, 104, 187–204. [Google Scholar] [CrossRef]
- Tarasov, V.E. Fractional hydrodynamic equations for fractal media. Ann. Phys. 2005, 318, 286–307. [Google Scholar] [CrossRef] [Green Version]
- Lapidus, M.; Lu, H.; van Frankenhuijsen, M. Minkowski dimension and explicit tube formulas for p-adic fractal strings. Fractal Fract. 2018, 2, 26. [Google Scholar] [CrossRef]
- Wang, Z.S.; Lu, B.W. The scattering of electromagnetic waves in fractal media. Wave Random Media 1994, 4, 97. [Google Scholar] [CrossRef]
- Baish, J.W.; Jain, R.K. Fractals and cancer. Cancer Res. 2000, 60, 3683–3688. [Google Scholar]
- Jorgensen, P.E. Analysis and Probability: Wavelets, Signals, Fractals; Springer Science Business Media: Berlin, Germany, 2006; Volume 234. [Google Scholar]
- Hinz, M.; Lancia, M.R.; Teplyaev, A.; Vernole, P. Fractal snowflake domain diffusion with boundary and interior drifts. J. Math. Anal. Appl. 2018, 457, 672–693. [Google Scholar] [CrossRef] [Green Version]
- Czachor, M. Waves along fractal coastlines: From fractal arithmetic to wave equations. Acta Phys. Pol. 2019, 50, 813–831. [Google Scholar] [CrossRef]
- Riane, N.; David, C. The finite difference method for the heat equation on Sierpinski simplices. Int. J. Comput. Math. 2019, 96, 1477–1501. [Google Scholar] [CrossRef]
- Joumaa, H.; Ostoja-Starzewski, M. On the dilatational wave motion in anisotropic fractal solids. Math. Comput. Simul. 2016, 127, 114–130. [Google Scholar] [CrossRef] [Green Version]
- Jayasinghe, J.; Andújar, A.; Anguera, J. On the properties of Sierpinski gasket fractal microstrip antennas. Microw. Opt. Technol. Lett. 2019, 61, 772–776. [Google Scholar] [CrossRef]
- Djida, J.D.; Nieto, J.J.; Area, I. Nonlocal time porous medium equation with fractional time derivative. Rev. Mat. Complut. 2019, 32, 273–304. [Google Scholar] [CrossRef]
- Kigami, J. Analysis on Fractals; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Freiberg, U.; Zahle, M. Harmonic calculus on fractals-a measure geometric approach I. Potential Anal. 2002, 16, 265–277. [Google Scholar] [CrossRef]
- Strichartz, R.S. Differential Equations on Fractals: A Tutorial; Princeton University Press: Princeton, NJ, USA, 2006. [Google Scholar]
- Falconer, K. Techniques in Fractal Geometry; John Wiley and Sons: Hoboken, NJ, USA, 1997. [Google Scholar]
- Barlow, M.T.; Perkins, E.A. Brownian motion on the Sierpinski gasket. Probab. Theory Relat. Fields 1988, 79, 543–623. [Google Scholar] [CrossRef]
- Stillinger, F.H. Axiomatic basis for spaces with noninteger dimension. J. Math. Phys. 1977, 18, 1224–1234. [Google Scholar] [CrossRef]
- Balankin, A.S. A continuum framework for mechanics of fractal materials I: From fractional space to continuum with fractal metric. Eur. Phys. J. B 2015, 88, 90. [Google Scholar] [CrossRef]
- Zubair, M.; Mughal, M.J.; Naqvi, Q.A. Electromagnetic Fields and Waves in Fractional Dimensional Space; Springer: New York, NY, USA, 2012. [Google Scholar]
- Liang, W.C.Y. New methodologies in fractional and fractal derivatives modeling. Chaos Soliton Fract. 2017, 102, 72–77. [Google Scholar]
- Liang, Y.; Ye, A.Q.; Chen, W.; Gatto, R.G.; Colon-Perez, L.; Mareci, T.H.; Magin, R.L. A fractal derivative model for the characterization of anomalous diffusion in magnetic resonance imaging. Commun. Nonlinear Sci. Numer. Simul. 2016, 39, 529–537. [Google Scholar] [CrossRef]
- Nottale, L.; Schneider, J. Fractals and nonstandard analysis. J. Math. Phys. 1998, 25, 1296–1300. [Google Scholar] [CrossRef]
- Célérier, M.N.; Nottale, L. Quantum-classical transition in scale relativity. J. Phys. A Math. Gen. 2004, 37, 931–955. [Google Scholar] [CrossRef]
- Kolwankar, K.M.; Gangal, A.D. Local fractional Fokker-Planck equation. Phys. Rev. Lett. 1998, 80, 214. [Google Scholar] [CrossRef]
- El-Nabulsi, R.A. Classical string field mechanics with non-standard Lagrangians. Math. Sci. 2015, 9, 173–179. [Google Scholar] [CrossRef] [Green Version]
- Yang, H.; Sun, J.; Fu, C. Time-fractional Benjamin-Ono equation for algebraic gravity solitary waves in baroclinic atmosphere and exact multi-soliton solution as well as interaction. Commun. Nonlinear Sci. 2019, 71, 187–201. [Google Scholar] [CrossRef]
- Wu, G.C.; Baleanu, D.; Luo, W.H. Lyapunov functions for Riemann–Liouville-like fractional difference equations. Appl. Math. Comput. 2017, 314, 228–236. [Google Scholar] [CrossRef]
- Wu, G.C.; Baleanu, D.; Xie, H.P. Riesz Riemann-Liouville difference on discrete domains. Chaos 2016, 26, 084308. [Google Scholar] [CrossRef]
- Das, S. Functional Fractional Calculus; Springer Science Business Media: Berlin, Germany, 2011. [Google Scholar]
- Verhulst, P.F. Notice sur la loi que la population suit dans son accriossement. Corresp. Math. Phys. 1838, 10, 113–121. [Google Scholar]
- Blumberg, A.A. Logistic growth rate functions. J. Theor. Biol. 1968, 21, 42–44. [Google Scholar] [CrossRef]
- Cohen, J.E. Population growth and earth’s human carrying capacity. Science 1995, 269, 341–346. [Google Scholar] [CrossRef]
- Cameron, A.C.; Trivedi, P.K. Regression Analysis of Count Data; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- Brenner, J.R. Data analysis made easy with Data Fit. Educ. Chem. Eng. 2006, 40, 60–65. [Google Scholar]
- El-Sayed, A.M.A.; El-Mesiry, A.E.M.; El-Saka, H.A.A. On the fractional-order logistic equation. Appl. Math. Lett. 2007, 20, 817–823. [Google Scholar] [CrossRef] [Green Version]
- Sweilam, N.H.; Nagy, A.M.; Elfahri, L.E. Nonstandard Finite Difference Scheme For The Fractional Order Salmonella Transmission Model. J. Fract. Calc. Appl. 2019, 10, 197–212. [Google Scholar]
- Area, I.; Losada, J.; Nieto, J.J. A note on the fractional logistic equation. Physica A Stat. Mech. Appl. 2016, 444, 182–187. [Google Scholar] [CrossRef] [Green Version]
- Ausloos, M.; Dirickx, M. (Eds.) The Logistic Map and the Route to Chaos: From the Beginnings to Modern Applications; Springer Science Business Media: Berlin, Germany, 2006. [Google Scholar]
- Strogatz, S.H. Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry, and Engineering; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Atici, F.M.; Sengul, S. Modeling with fractional difference equations. J. Math. Anal. Appl. 2010, 369, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Zhang, B.G.; Zhou, Y. Oscillations of difference equations with several delays. Comput. Math. Appl. 2002, 44, 817–821. [Google Scholar] [CrossRef] [Green Version]
- Siegmund, S. Normal forms for nonautonomous difference equations. Comput. Math. Appl. 2003, 45, 1059–1073. [Google Scholar] [CrossRef] [Green Version]
- Chen, F.; Luo, X.; Zhou, Y. Existence results for nonlinear fractional difference equation. Adv. Differ. Equ. 2011, 2011, 713201. [Google Scholar] [CrossRef]
- Miller, K.S.; Ross, B. Fractional difference calculus. In Proceedings of the International Symposium on Univalent Functions, Fractional Calculus and Their Applications, Koriyama, Japan, May 1988; pp. 139–152. [Google Scholar]
- Ferreira, R.A.C.; Torres, D.F. Fractional h-difference equations arising from the calculus of variations. Appl. Anal. Discrete Math. 2011, 5, 110–121. [Google Scholar] [CrossRef] [Green Version]
- Atici, F.M.; Eloe, P.W. A transform method in discrete fractional calculus. Int. J. Differ. Equ. 2007, 2, 165–176. [Google Scholar]
- Abdeljawad, T.; Al-Mdallal, Q.M.; Jarad, F. Fractional logistic models in the frame of fractional operators generated by conformable derivatives. Chaos Soliton Fract. 2019, 119, 94–101. [Google Scholar] [CrossRef]
- Abdeljawad, T.; Al-Mdallal, Q.M. Discrete Mittag-Leffler kernel type fractional difference initial value problems and Gronwall’s inequality. J. Comput. Appl. Math. 2018, 339, 218–230. [Google Scholar] [CrossRef]
- Singh, J. A new analysis for fractional rumor spreading dynamical model in a social network with Mittag-Leffler law. Chaos 2019, 29, 013137. [Google Scholar] [CrossRef] [PubMed]
- Singh, J.; Kumar, D.; Hammouch, Z.; Atangana, A. A fractional epidemiological model for computer viruses pertaining to a new fractional derivative. Appl. Math. Comput. 2018, 316, 504–515. [Google Scholar] [CrossRef]
- Parvate, A.; Gangal, A.D. Calculus on fractal subsets of real-line I: Formulation. Fractals 2009, 17, 53–148. [Google Scholar] [CrossRef]
- Parvate, A.; Gangal, A.D. Calculus on fractal subsets of real line II: Conjugacy with ordinary calculus. Fractals 2011, 19, 271–290. [Google Scholar] [CrossRef]
- Golmankhaneh, A.K.; Baleanu, D. Diffraction from fractal grating Cantor sets. J. Mod. Opt. 2016, 63, 1364–1369. [Google Scholar] [CrossRef]
- Golmankhaneh, A.K.; Fernandez, A.; Golmankhaneh, A.K.; Baleanu, D. Diffusion on middle-ξ Cantor sets. Entropy 2018, 20, 504. [Google Scholar] [CrossRef]
- Golmankhaneh, A.K.; Balankin, A.S. Sub-and super-diffusion on Cantor sets: Beyond the paradox. Phys. Lett. A 2018, 382, 960–967. [Google Scholar] [CrossRef]
- Golmankhaneh, A.K.; Tunç, C. Sumudu transform in fractal calculus. Appl. Math. Comput. 2019, 350, 386–401. [Google Scholar] [CrossRef]
- Golmankhaneh, A.K.; Fernandez, A. Random Variables and Stable Distributions on Fractal Cantor Sets. Fractal Fract. 2019, 3, 31. [Google Scholar] [CrossRef]
- DiMartino, R.; Urbina, W. On Cantor-like sets and Cantor-Lebesgue singular functions. arXiv 2014, arXiv:1403.6554. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khalili Golmankhaneh, A.; Cattani, C. Fractal Logistic Equation. Fractal Fract. 2019, 3, 41. https://doi.org/10.3390/fractalfract3030041
Khalili Golmankhaneh A, Cattani C. Fractal Logistic Equation. Fractal and Fractional. 2019; 3(3):41. https://doi.org/10.3390/fractalfract3030041
Chicago/Turabian StyleKhalili Golmankhaneh, Alireza, and Carlo Cattani. 2019. "Fractal Logistic Equation" Fractal and Fractional 3, no. 3: 41. https://doi.org/10.3390/fractalfract3030041
APA StyleKhalili Golmankhaneh, A., & Cattani, C. (2019). Fractal Logistic Equation. Fractal and Fractional, 3(3), 41. https://doi.org/10.3390/fractalfract3030041





