A Novel Method for Solutions of Fourth-Order Fractional Boundary Value Problems
Abstract
:1. Introduction
2. Preliminaries and Notations
3. Reproducing Kernel Hilbert Space Method
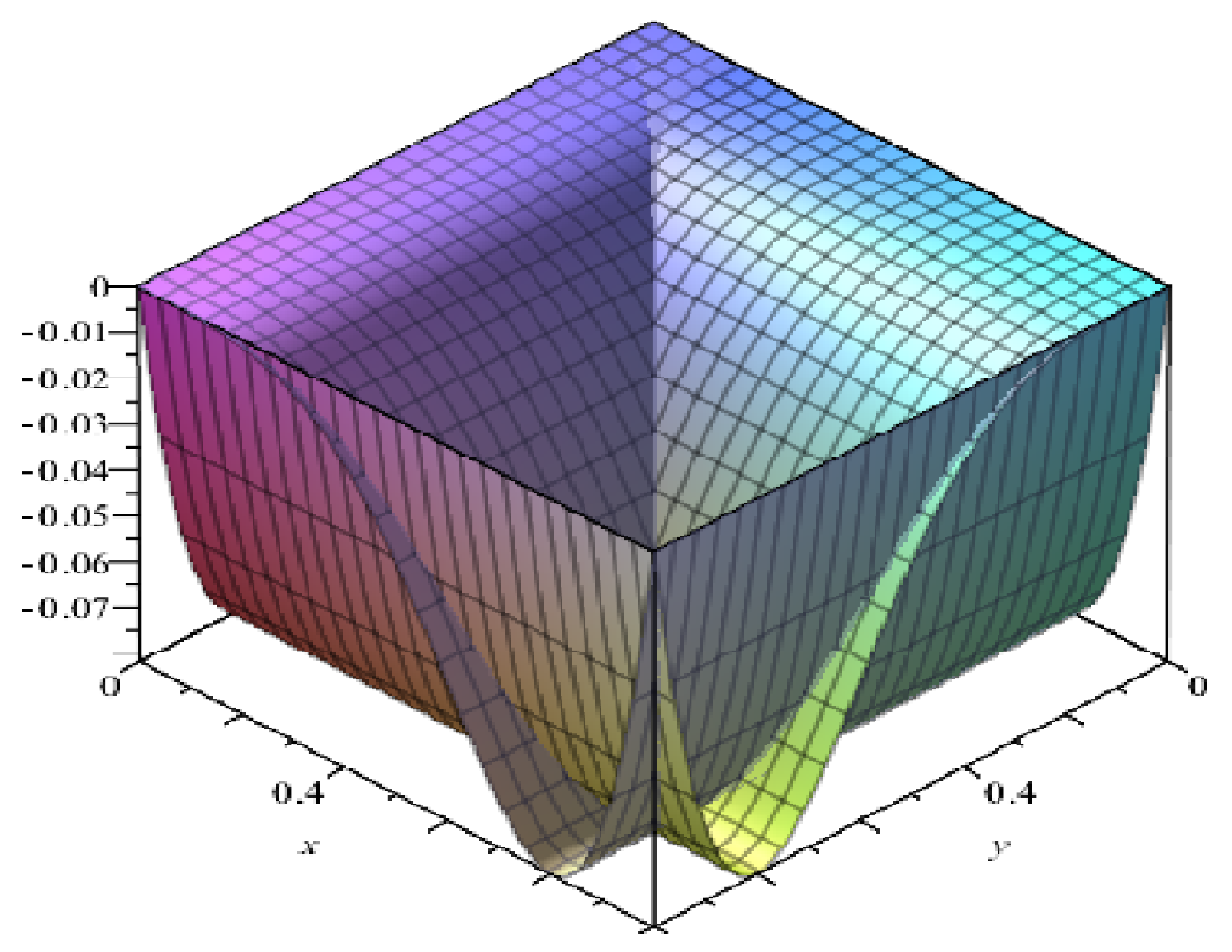
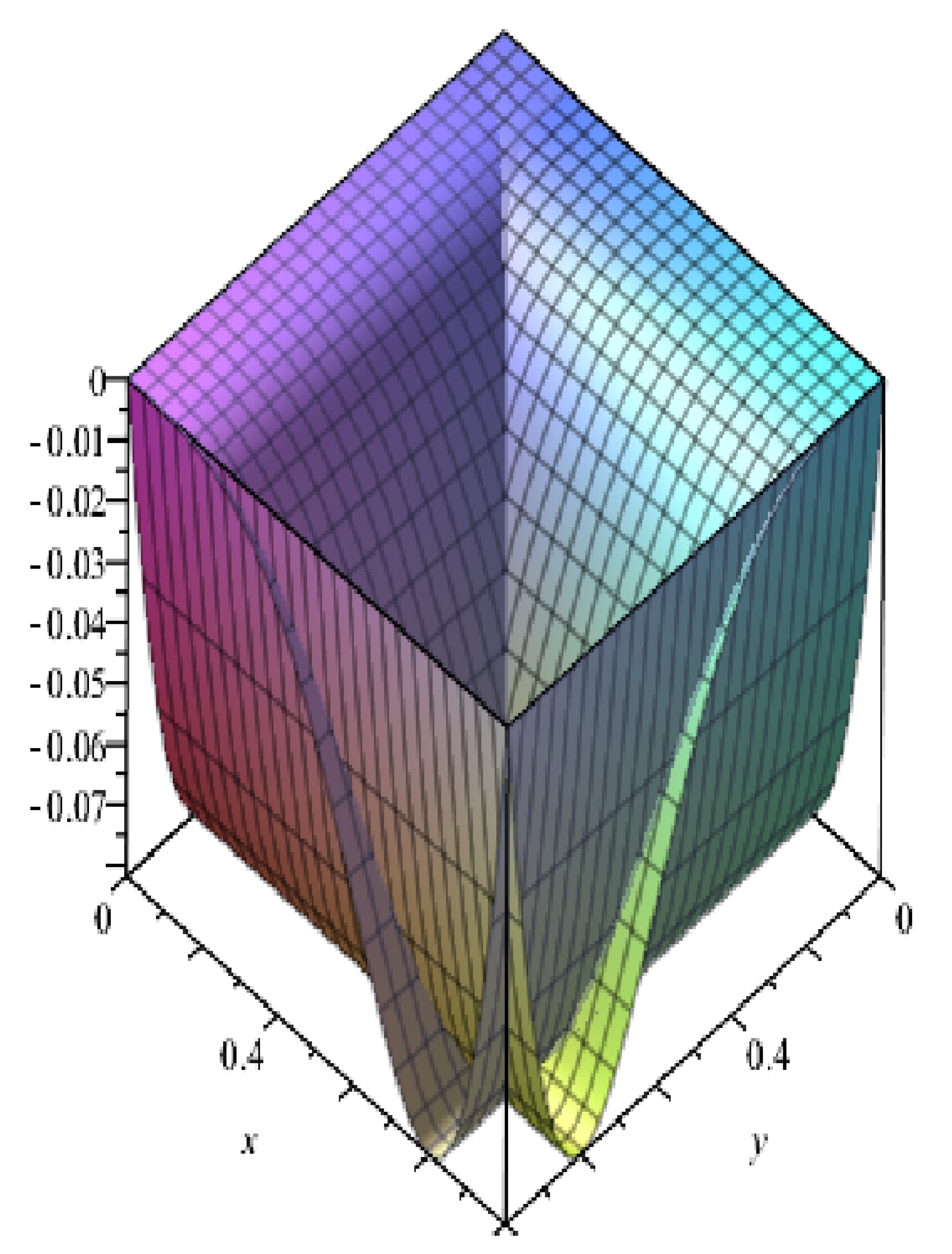
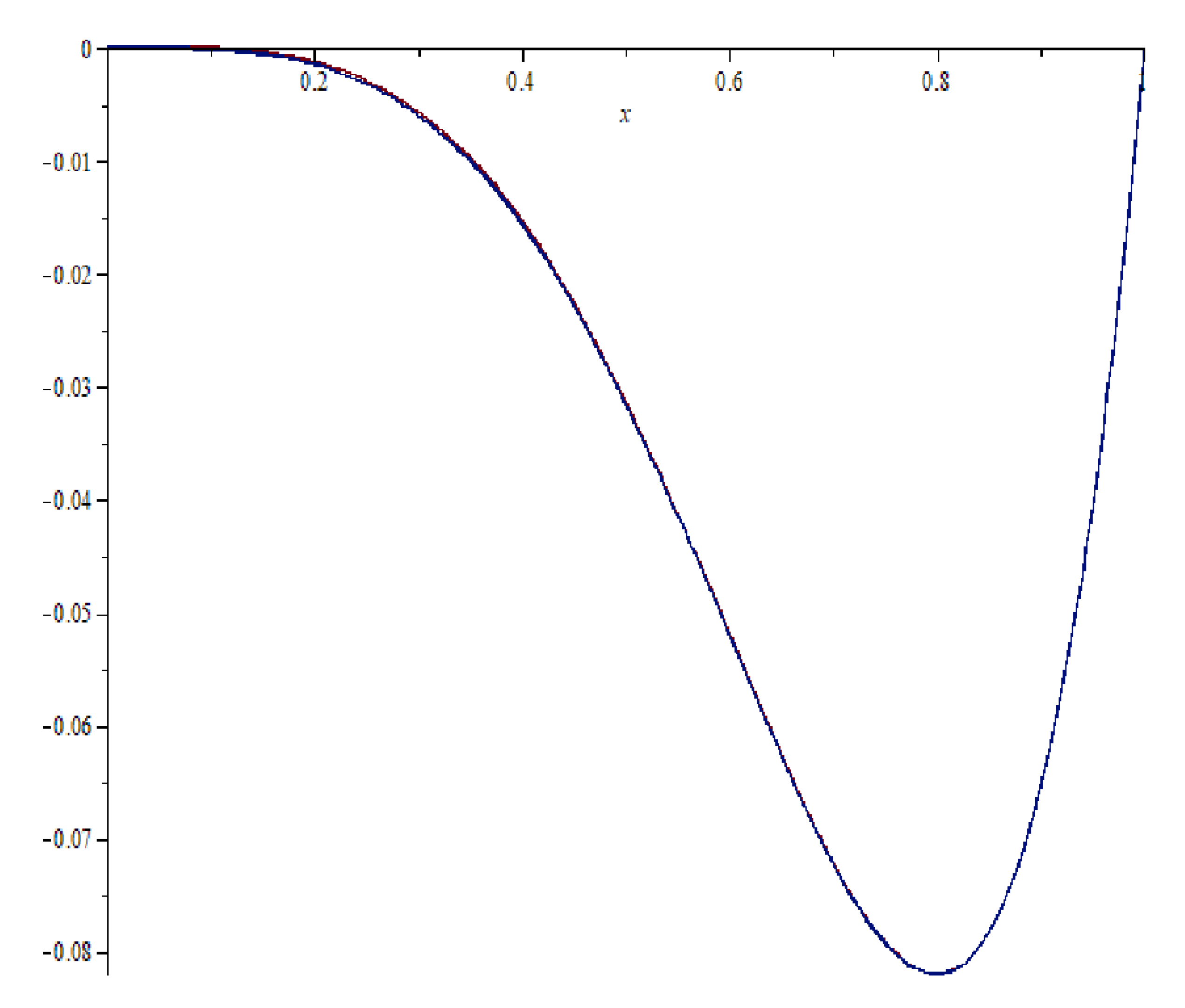
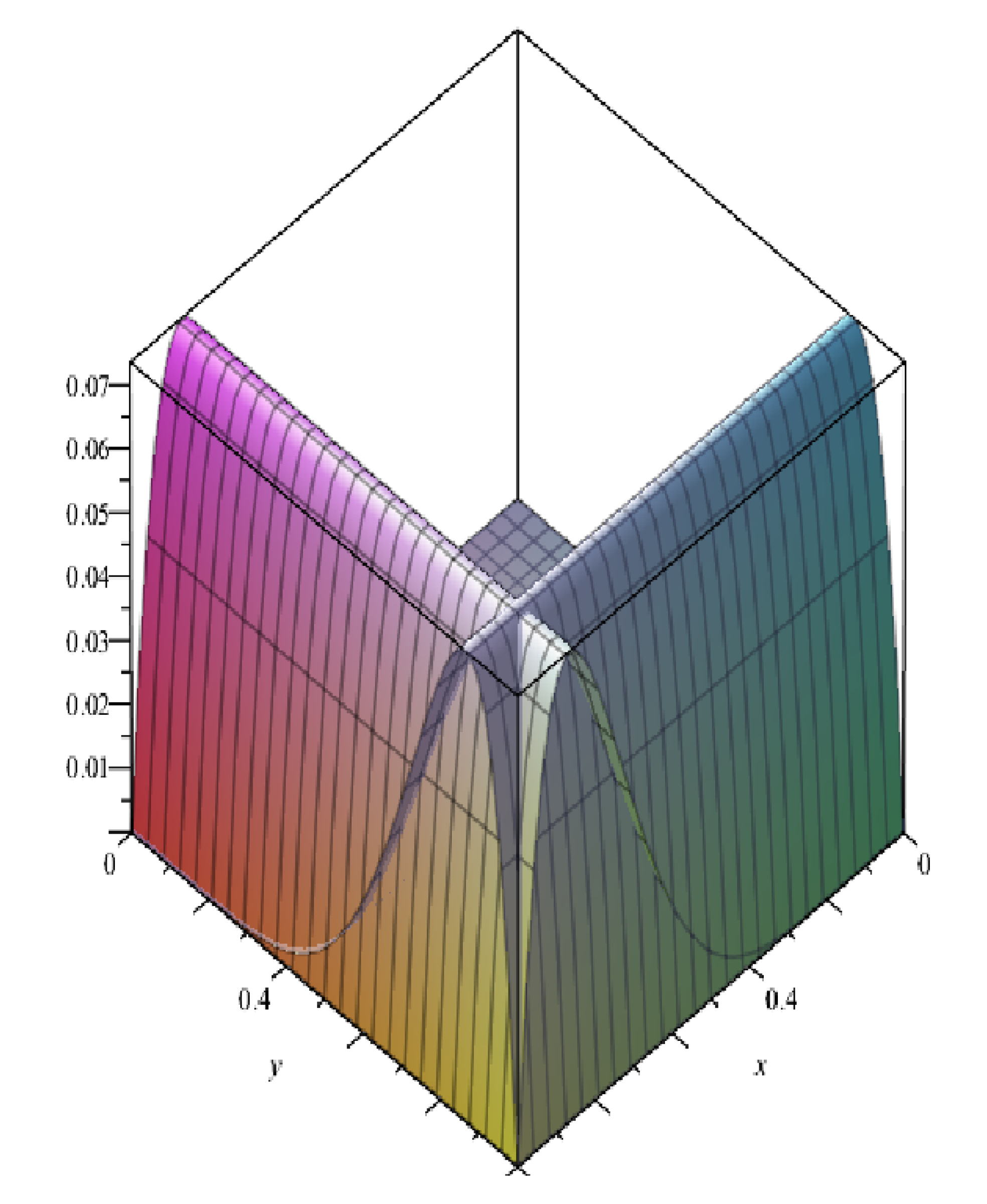
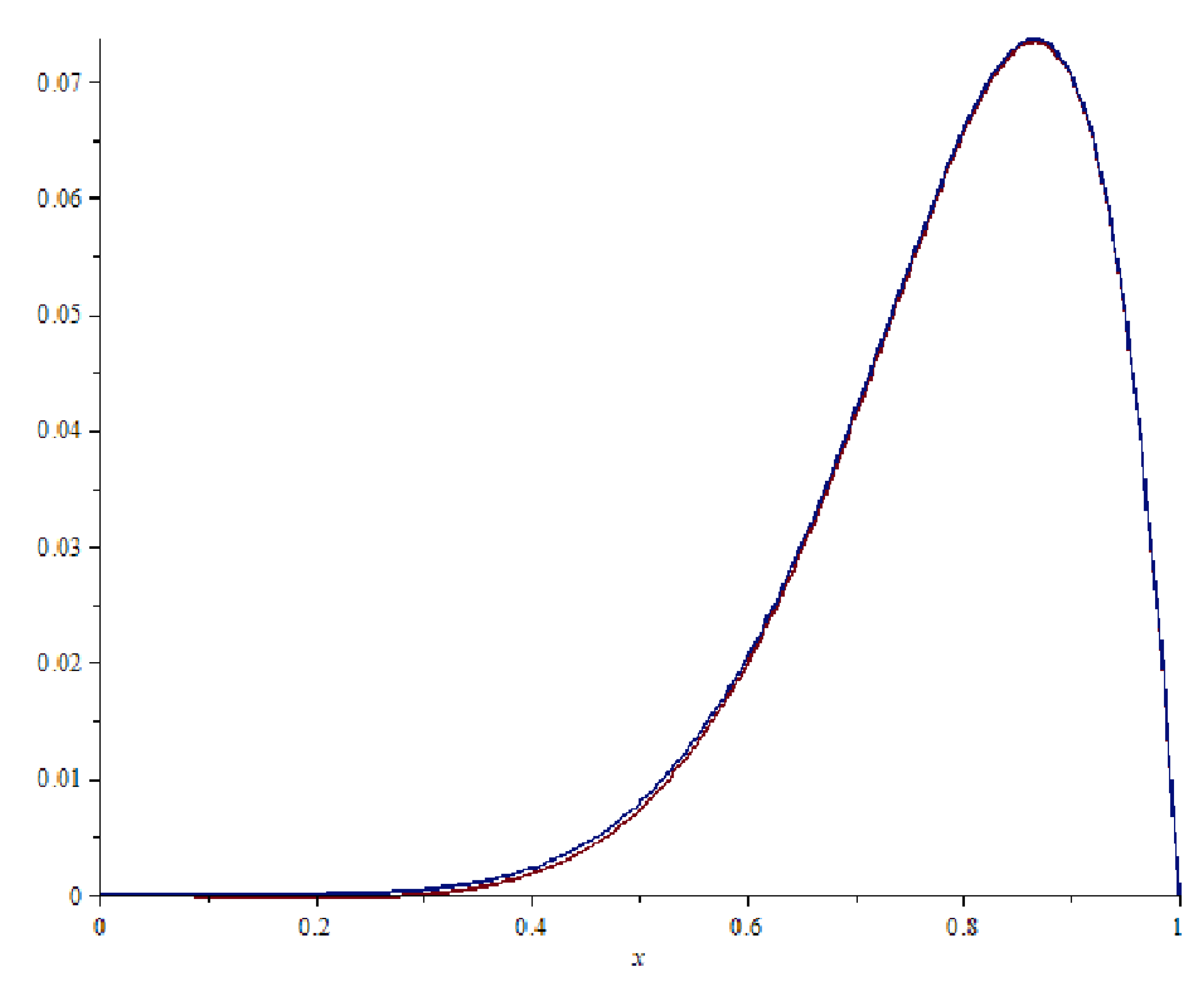
4. Numerical Experiments
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Hajji, M.A.; Al-Khaled, K. Numerical methods for nonlinear fourth-order boundary value problems with applications. Int. J. Comput. Math. 2008, 85, 83–104. [Google Scholar] [CrossRef]
- Dehghan, M.; Lakestani, M. Numerical solution of nonlinear system of second-order boundary value problems using cubic B-spline scaling functions. Int. J. Comput. Math. 2008, 85, 1455–1461. [Google Scholar] [CrossRef]
- Wazwaz, A.M. The numerical solution of special fourth-order boundary value problems by the modified decomposition method. Int. J. Comput. Math. 2002, 79, 345–356. [Google Scholar] [CrossRef]
- Momani, S.; Moadi, K. A reliable algorithm for solving fourth-order boundary value problems. J. Appl. Math. Comput. 2006, 22, 185–197. [Google Scholar] [CrossRef]
- Ertürk, V.S.; Momani, S. Comparing numerical methods for solving fourth-order boundary value problems. Appl. Math. Comput. 2007, 188, 1963–1968. [Google Scholar] [CrossRef]
- Ramadan, M.; Lashien, I.; Zahra, W. Quintic nonpolynomial spline solutions for fourth order two-point boundary value problem. Commun. Nonlinear Sci. Numer. Simul. 2009, 14, 1105–1114. [Google Scholar] [CrossRef]
- Srivastava, P.K.; Kumar, M.; Mohapatra, R. Solution of fourth order boundary value problems by numerical algorithms based on nonpolynomial quintic splines. J. Numer. Math. Stoch. 2012, 4, 13–25. [Google Scholar]
- Lodhi, R.K.; Mishra, H.K. Solution of a class of fourth order singular singularly perturbed boundary value problems by quintic b-spline method. J. Niger. Math. Soc. 2016, 35, 257–265. [Google Scholar] [CrossRef]
- Lodhi, R.K.; Mishra, H.K. Computational approach for fourth-order self-adjoint singularly perturbed boundary value problems via non-polynomial quintic spline. Iran. J. Sci. Technol. Trans. A Sci. 2016, 42, 1–8. [Google Scholar] [CrossRef]
- Akram, G.; Amin, N. Solution of a fourth order singularly perturbed boundary value problem using quintic spline. Proc. Int. Math. Forum 2012, 7, 2179–2190. [Google Scholar]
- Khalid, N.; Abbas, M.; Iqbal, M.K. Non-polynomial quintic spline for solving fourth-order fractional boundary value problems involving product terms. Appl. Math. Comput. 2019, 349, 393–407. [Google Scholar] [CrossRef]
- Aronszajn, N. Theory of reproducing kernels. Trans. Am. Math. Soc. 1950, 68, 337–404. [Google Scholar] [CrossRef]
- Sababe, S.H.; Ebadian, A. Some Properties of Reproducing Kernel Banach and Hilbert Spaces. SCMA 2018, 12, 167–177. [Google Scholar]
- Arqub, O.A. Approximate solutions of DASs with nonclassical boundary conditions using novel reproducing kernel algorithm. Fundamenta Informaticae 2016, 146, 231–254. [Google Scholar] [CrossRef]
- Arqub, O.A. The reproducing kernel algorithm for handling differential algebraic systems of ordinary differential equations. Math. Methods Appl. Sci. 2016, 39, 4549–4562. [Google Scholar] [CrossRef]
- Arqub, O.A. Fitted reproducing kernel Hilbert space method for the solutions of some certain classes of time-fractional partial differential equations subject to initial and Neumann boundary conditions. Comput. Math. Appl. 2017, 73, 1243–1261. [Google Scholar] [CrossRef]
- Azarnavid, B.; Parvaneh, F.; Abbasbandy, S. Picard-reproducing Kernel Hilbert space method for solving generalized singular nonlinear Lane–Emden type equations. Math. Model. Anal. 2015, 20, 754–767. [Google Scholar] [CrossRef]
- Azarnavid, B.; Shivanian, E.; Parand, K.; Soudabeh, N. Multiplicity results by shooting reproducing kernel Hilbert space method for the catalytic reaction in a flat particle. J. Theor. Comput. Chem. 2018, 17, 1850020. [Google Scholar] [CrossRef]
- Azarnavid, B.; Parand, K.; Abbasbandy, S. An iterative kernel based method for fourth order nonlinear equation with nonlinear boundary condition. Commun. Nonlinear Sci. Numer. Simul. 2018, 59, 544–552. [Google Scholar] [CrossRef]
| x | ||
|---|---|---|
| x | |
|---|---|
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Akgül, A.; Karatas Akgül, E. A Novel Method for Solutions of Fourth-Order Fractional Boundary Value Problems. Fractal Fract. 2019, 3, 33. https://doi.org/10.3390/fractalfract3020033
Akgül A, Karatas Akgül E. A Novel Method for Solutions of Fourth-Order Fractional Boundary Value Problems. Fractal and Fractional. 2019; 3(2):33. https://doi.org/10.3390/fractalfract3020033
Chicago/Turabian StyleAkgül, Ali, and Esra Karatas Akgül. 2019. "A Novel Method for Solutions of Fourth-Order Fractional Boundary Value Problems" Fractal and Fractional 3, no. 2: 33. https://doi.org/10.3390/fractalfract3020033
APA StyleAkgül, A., & Karatas Akgül, E. (2019). A Novel Method for Solutions of Fourth-Order Fractional Boundary Value Problems. Fractal and Fractional, 3(2), 33. https://doi.org/10.3390/fractalfract3020033






