Statistical Mechanics Involving Fractal Temperature
Abstract
1. Introduction
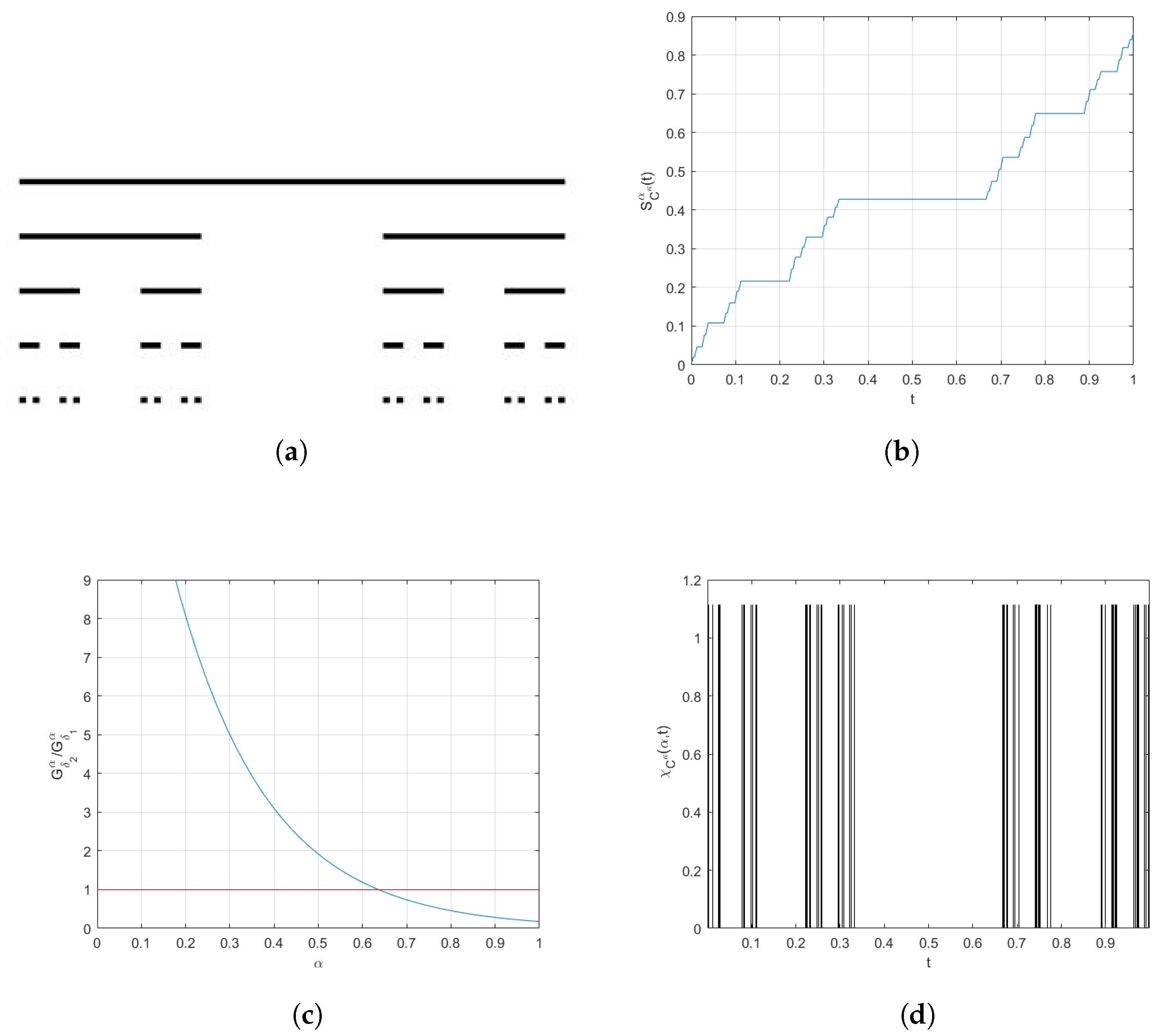
2. Basic Tools
Local Fractal Calculus
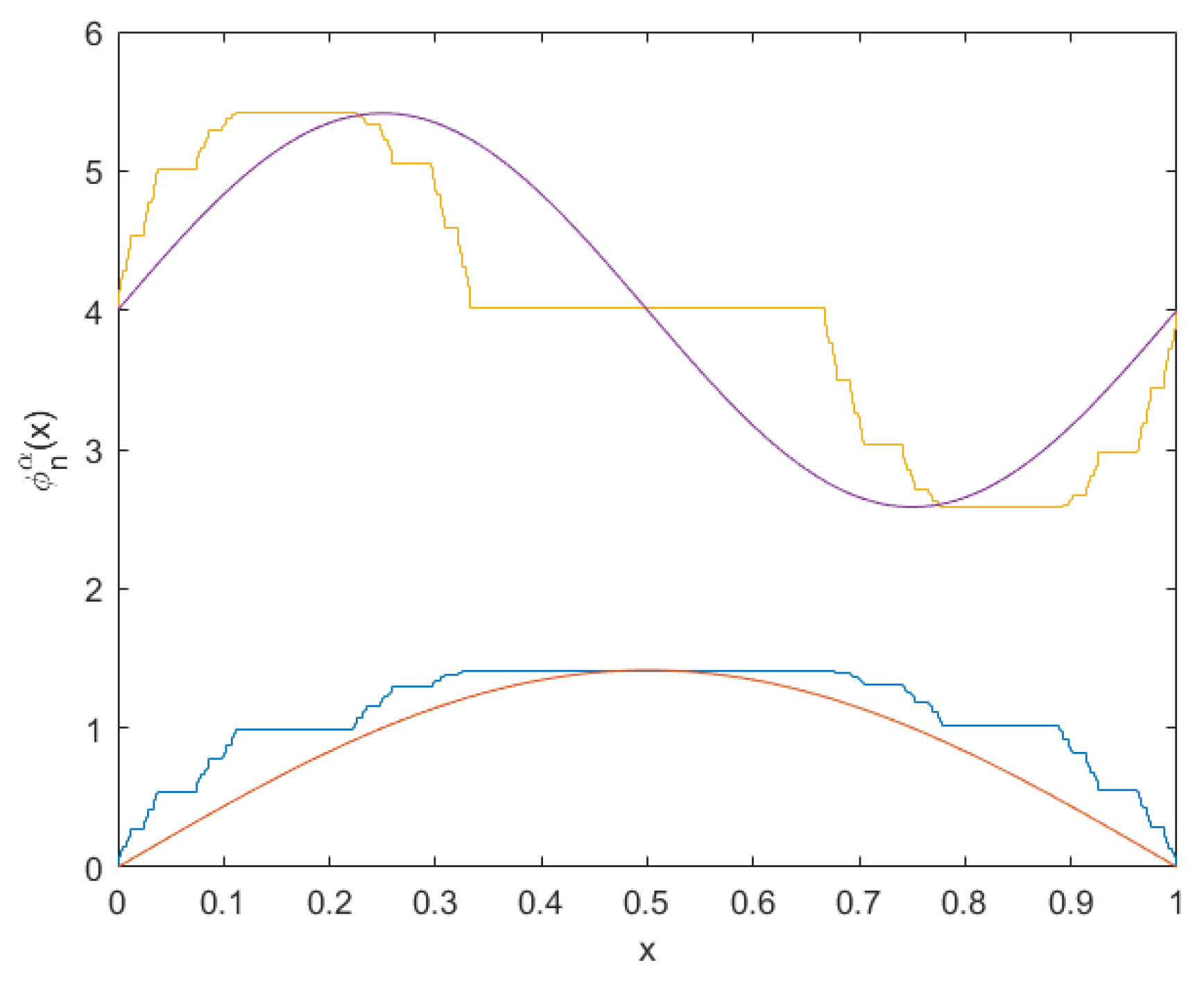
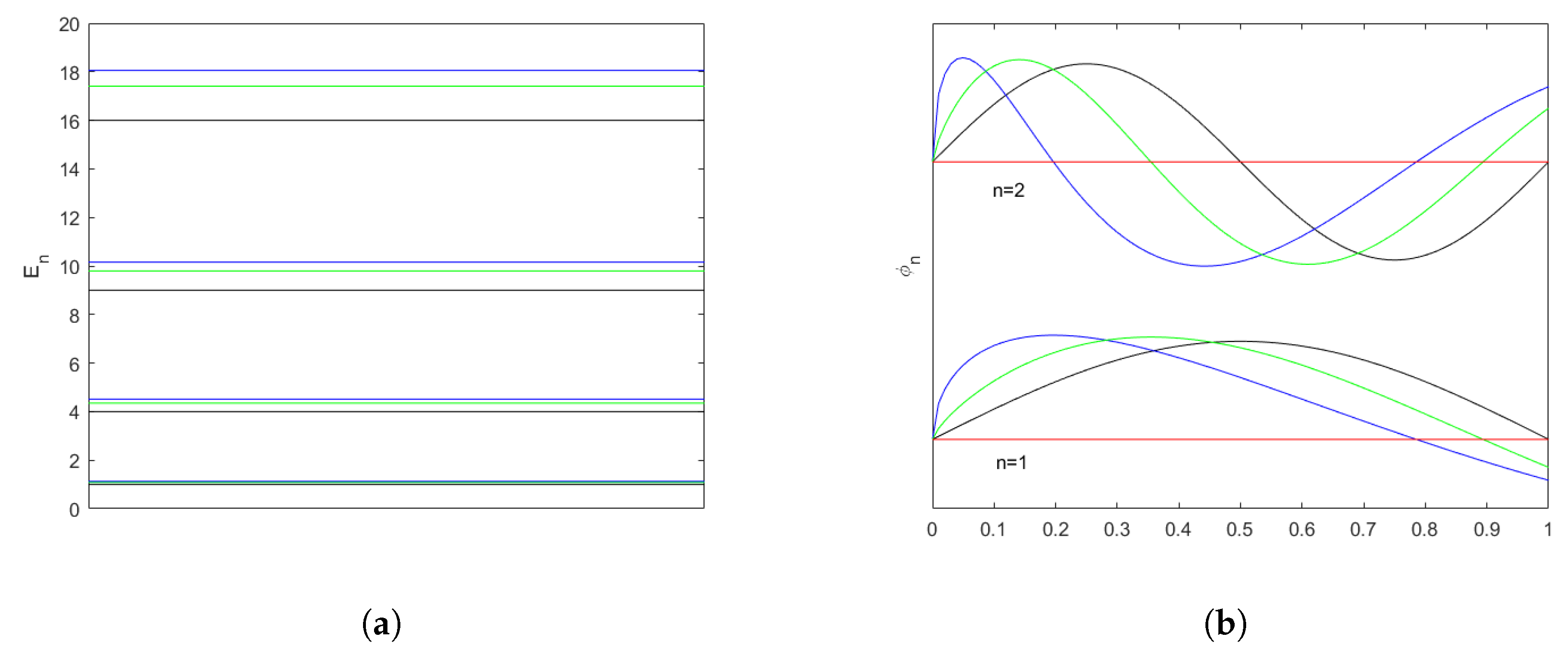
3. Shrödinger Equation on Thin Cantor Sets
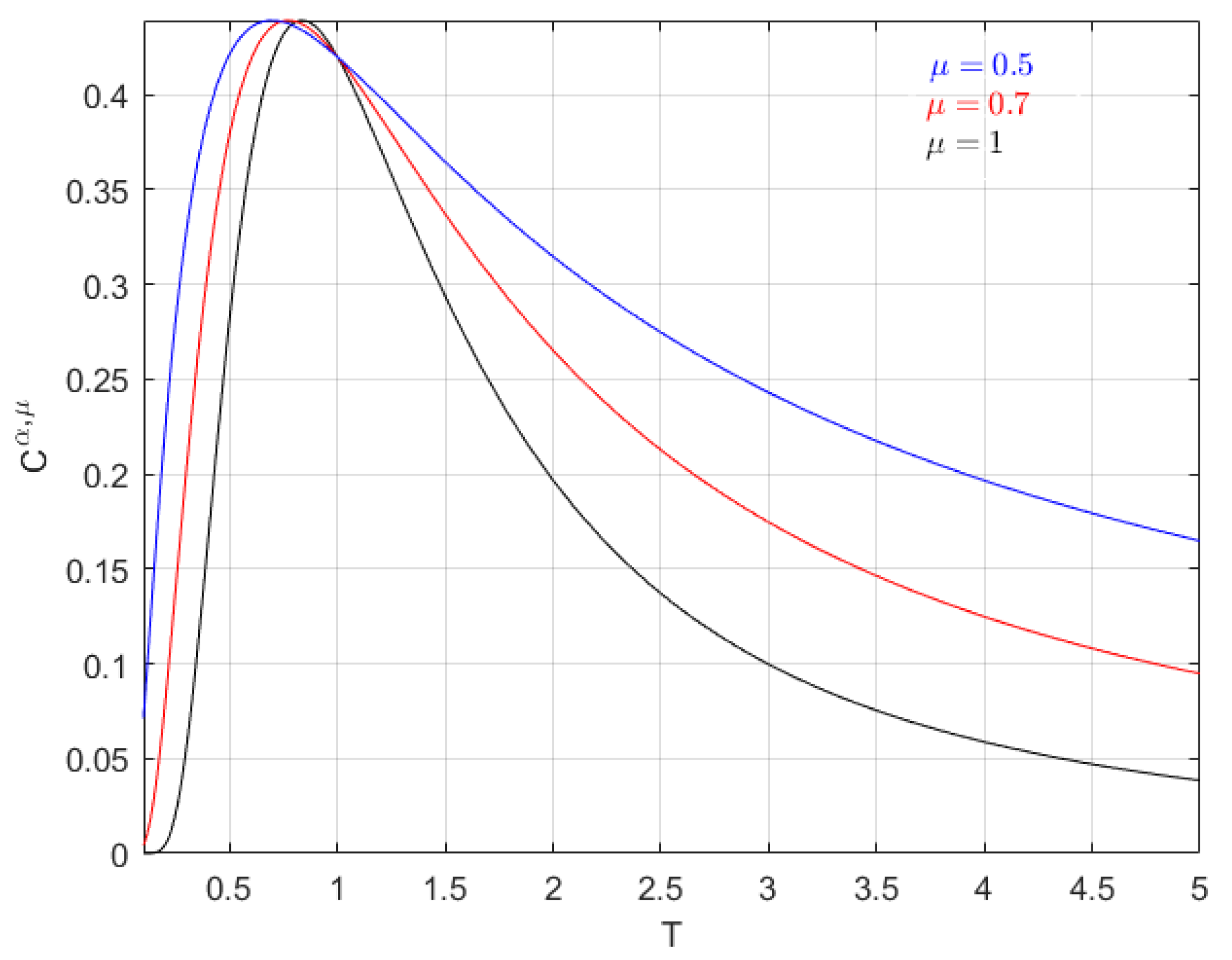
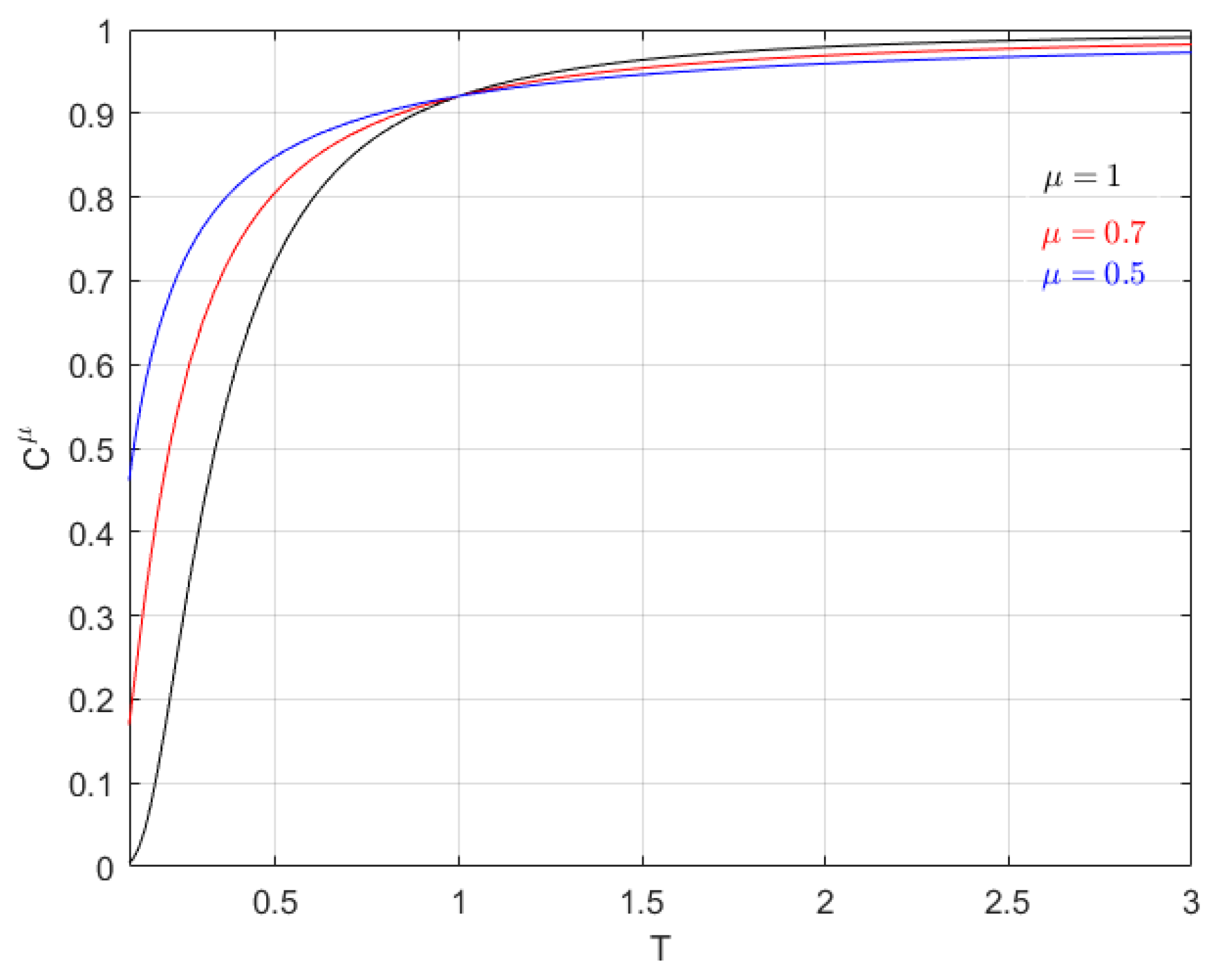
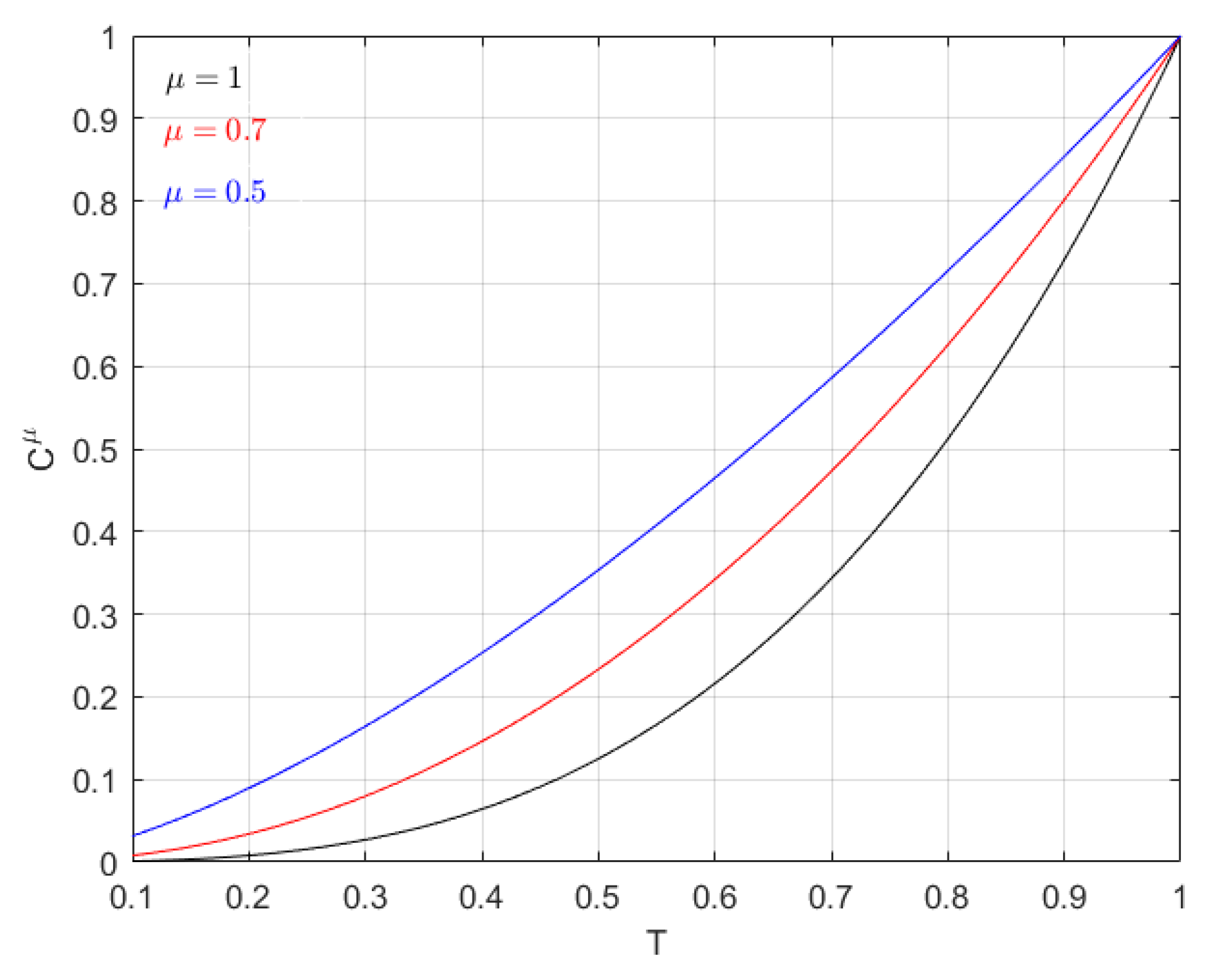
4. Partition Function on Thin Cantor-Like Sets
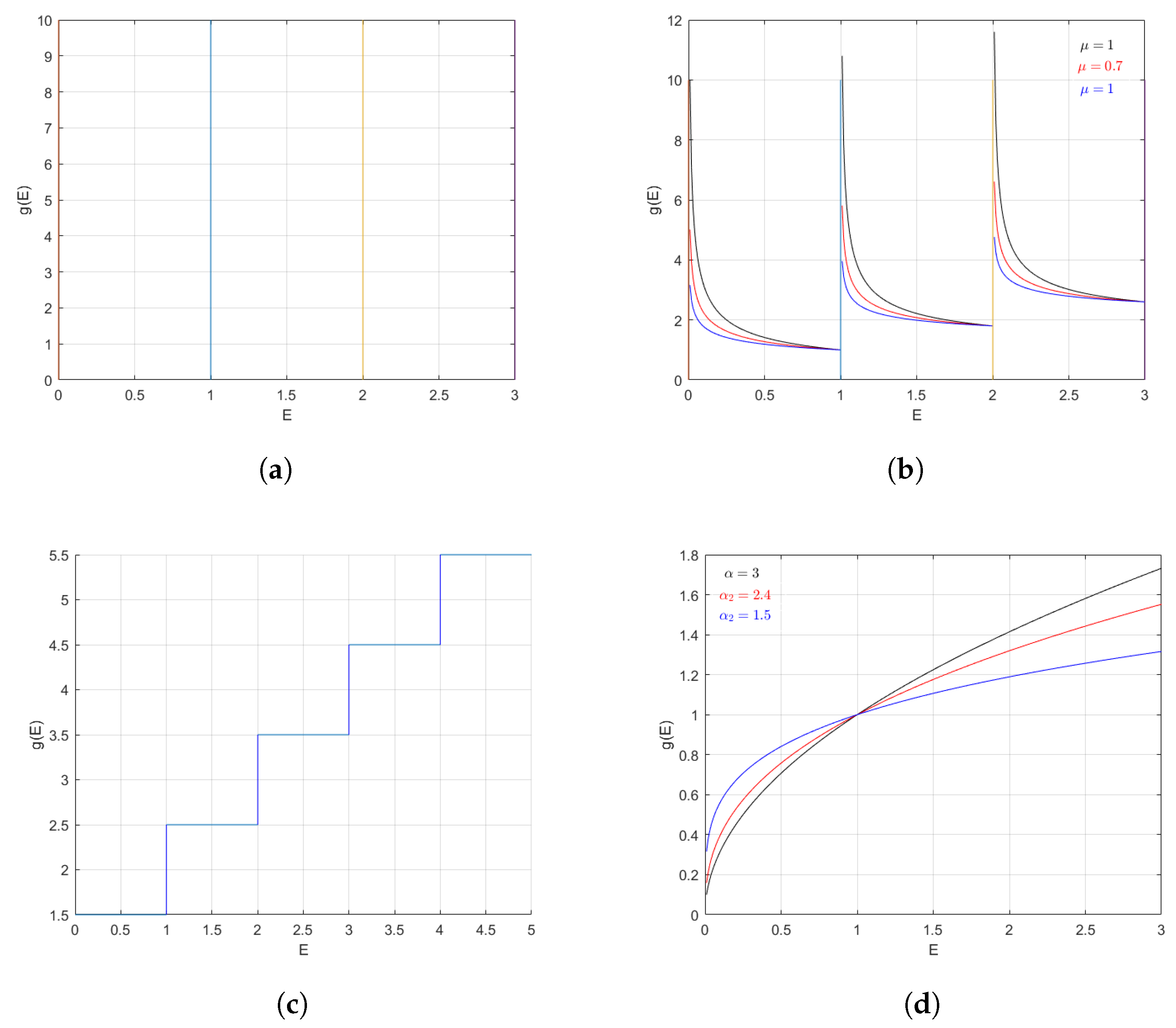
5. Density of States in Fractal Spaces
6. Conclusions
Acknowledgments
Conflicts of Interest
References
- Mandelbrot, B.B. The Fractal Geometry of Nature; WH Freeman: New York, NY, USA, 1983; Volume 173. [Google Scholar]
- Barnsley, M.F. Fractals Everywhere; Academic Press: Cambridge, MA, USA, 2014. [Google Scholar]
- Dewey, T.G. Fractals in Molecular Biophysics; Oxford University Press: Oxford, UK, 1998. [Google Scholar]
- Pietronero, L.; Tosatti, E. Fractals in Physics; Elsevier Science: Amsterdam, The Netherlands, 2012. [Google Scholar]
- Freiberg, U.; Zahle, M. Harmonic calculus on fractals-a measure geometric approach I. Potential Anal. 2002, 16, 265–277. [Google Scholar] [CrossRef]
- Kigami, J. Analysis on Fractals; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Jiang, H.; Su, W. Some fundamental results of calculus on fractal sets. Commun. Nonlinear Sci. Numer. Simul. 1998, 3, 22–26. [Google Scholar] [CrossRef]
- Strichartz, R.S. Differential Equations on Fractals: A Tutorial; Princeton University Press: Princeton, NJ, USA, 2006. [Google Scholar]
- Falconer, K. Techniques in Fractal Geometry; John Wiley & Sons: Hoboken, NJ, USA, 1997. [Google Scholar]
- Barlow, M.T.; Perkins, E.A. Brownian motion on the Sierpinski gasket. Probab. Theory Relat. Fields 1988, 79, 543–623. [Google Scholar] [CrossRef]
- Stillinger, F.H. Axiomatic basis for spaces with noninteger dimension. J. Math. Phys. 1977, 18, 1224–1234. [Google Scholar] [CrossRef]
- Balankin, A.S. A continuum framework for mechanics of fractal materials I: From fractional space to continuum with fractal metric. Eur. Phys. J. B 2015, 88, 90. [Google Scholar] [CrossRef]
- Zubair, M.; Mughal, M.J.; Naqvi, Q.A. Electromagnetic Fields and Waves in Fractional Dimensional Space; Springer: New York, NY, USA, 2012. [Google Scholar]
- Podlubny, I. Fractional Differential Equations; Academic Press: New York, NY, USA, 1999. [Google Scholar]
- Das, S. Functional Fractional Calculus; Springer Science Business Media: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Tarasov, V.E. Fractional Dynamics: Applications of Fractional Calculus to Dynamics of Particles, Fields and Media; Springer Science Business Media: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Tatom, F.B. The relationship between fractional calculus and fractals. Fractals 1995, 3, 217–229. [Google Scholar] [CrossRef]
- Nigmatullin, R.R.; Le Mehaute, A. Is there geometrical/physical meaning of the fractional integral with complex exponent? J. Non-Cryst. Solids 2005, 351, 2888–2899. [Google Scholar] [CrossRef]
- Sumelka, W.; Voyiadjis, G.Z. A hyperelastic fractional damage material model with memory. Int. J. Solids Struct. 2017, 124, 151–160. [Google Scholar] [CrossRef]
- Dos Santos, M.A. Fractional Prabhakar Derivative in Diffusion Equation with Non-Static Stochastic Resetting. Physics 2019, 1, 58. [Google Scholar] [CrossRef]
- Sokolov, I. Fractals: A possible new path to diagnose and cure cancer? Future Oncol. 2015, 11, 3049–3051. [Google Scholar] [CrossRef]
- Baish, J.W.; Jain, R.K. Fractals and cancer. Cancer Res. 2000, 60, 3683–3688. [Google Scholar]
- Koh, K.J.; Park, H.N.; Kim, K.A. Prediction of age-related osteoporosis using fractal analysis on panoramic radiographs. Imaging Sci. Dent. 2012, 42, 231–235. [Google Scholar] [CrossRef]
- Ord, G.N. Fractal space-time: A geometric analogue of relativistic quantum mechanics. J. Phys. A Math. Gen. 1983, 16, 1869. [Google Scholar] [CrossRef]
- Célérier, M.N.; Nottale, L. Quantum-classical transition in scale relativity. J. Phys. A Math. Gen. 2004, 37, 931–955. [Google Scholar] [CrossRef]
- Wjcik, D.; Białynicki-Birula, I.; Życzkowski, K. Time evolution of quantum fractals. Phys. Rev. Lett. 2000, 85, 5022. [Google Scholar] [CrossRef]
- Coletta, K.; Dias, K.; Strichartz, R.S. Numerical analysis on the Sierpinski gasket, with application to Schrodinder equations, wave equation, and Gibbs’ phenomenon. Fractals 2004, 12, 413–449. [Google Scholar] [CrossRef]
- El-Nabulsi, R.A. Path integral formulation of fractionally perturbed Lagrangian oscillators on fractal. J. Stat. Phys. 2018, 172, 1617–1640. [Google Scholar] [CrossRef]
- Parvate, A.; Gangal, A.D. Calculus on fractal subsets of real-line I: Formulation. Fractals 2009, 17, 53–148. [Google Scholar] [CrossRef]
- Parvate, A.; Gangal, A.D. Calculus on fractal subsets of real line II: Conjugacy with ordinary calculus. Fractals 2011, 19, 271–290. [Google Scholar] [CrossRef]
- Golmankhaneh, A.K.; Fernandez, A.; Golmankhaneh, A.K.; Baleanu, D. Diffusion on middle-ξ Cantor sets. Entropy 2018, 20, 504. [Google Scholar] [CrossRef]
- Golmankhaneh, A.K.; Fernandez, A. Fractal Calculus of Functions on Cantor Tartan Spaces. Fractal Fract. 2018, 2, 30. [Google Scholar] [CrossRef]
- Jafari, F.K.; Asgari, M.S.; Pishkoo, A. The Fractal Calculus for Fractal Materials. Fractal Fract. 2019, 3, 8. [Google Scholar] [CrossRef]
- Golmankhaneh, A.K.; Baleanu, D. Diffraction from fractal grating Cantor sets. J. Mod. Opt. 2016, 63, 1364–1369. [Google Scholar] [CrossRef]
- Golmankhaneh, A.K.; Balankin, A.S. Sub- and super-diffusion on Cantor sets: Beyond the paradox. Phys. Lett. A 2018, 382, 960–967. [Google Scholar] [CrossRef]
- Golmankhaneh, A.K. On the Fractal Langevin Equation. Fractal Fract. 2019, 3, 11. [Google Scholar] [CrossRef]
- Bodri, L. Fractal analysis of climatic data: Mean annual temperature records in Hungary. Theor. Appl. Climatol. 1994, 49, 53–57. [Google Scholar] [CrossRef]
- Rammal, R. Spectrum of harmonic excitations on fractals. J. Phys. 1984, 45, 191–206. [Google Scholar] [CrossRef][Green Version]
- Iliasov, A.A.; Katsnelson, M.I.; Yuan, S. Power-law energy level spacing distributions in fractals. Phys. Rev. B 2019, 99, 075402. [Google Scholar] [CrossRef]
- Katomeris, G.N.; Evangelou, S.N. Level statistics for electronic states in a disordered fractal. J. Phys. A Math. Gen. 1996, 29, 2379. [Google Scholar] [CrossRef]
- Wang, X.R. Localization in fractal spaces: Exact results on the Sierpinski gasket. Phys. Rev. B 1995, 51, 9310. [Google Scholar] [CrossRef]
- Domany, E.; Alexander, S.; Bensimon, D.; Kadanoff, L.P. Solutions to the Schrödinger equation on some fractal lattices. Phys. Rev. B 1983, 28, 3110. [Google Scholar] [CrossRef]
- Tanese, D.; Gurevich, E.; Baboux, F.; Jacqmin, T.; Lemaître, A.; Galopin, E.; Sagnes, I.; Amo, A.; Bloch, J.; Akkermans, E. Fractal energy spectrum of a polariton gas in a Fibonacci quasiperiodic potential. Phys. Rev. Lett. 2014, 112, 146404. [Google Scholar] [CrossRef] [PubMed]
- Robert, D.; Urbina, W. On Cantor-like sets and Cantor-Lebesgue singular functions. arXiv, 2014; arXiv:1403.6554. [Google Scholar]
- Sakurai, J.J.; Napolitano, J. Modern Quantum Mechanics; Pearson: Harlow, UK, 2014. [Google Scholar]
- Dirac, P.A.M. The Principles of Quantum Mechanics (No. 27); Oxford University Press: Oxford, UK, 1981. [Google Scholar]
- Zettili, N. Quantum Mechanics: Concepts and Applications; Wiley: Yew York, NY, USA, 2001. [Google Scholar]
- Griffiths, D.J.; Schroeter, D.F. Introduction to Quantum Mechanics; Cambridge University Press: Cambridge, UK, 2018. [Google Scholar]
- Kittel, C. Introduction to Solid State Physics; Wiley: New York, NY, USA, 1976; Volume 8. [Google Scholar]
- Hofmann, P. Solid State Physics: An Introduction; John Wiley Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Srivastava, R.K.; Ashok, J. Statistical Mechanics; PHI Learning Pvt. Ltd.: Delhi, India, 2005. [Google Scholar]
- Ruelle, D. Thermodynamic Formalism: The Mathematical Structure of Equilibrium Statistical Mechanics; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khalili Golmankhaneh, A. Statistical Mechanics Involving Fractal Temperature. Fractal Fract. 2019, 3, 20. https://doi.org/10.3390/fractalfract3020020
Khalili Golmankhaneh A. Statistical Mechanics Involving Fractal Temperature. Fractal and Fractional. 2019; 3(2):20. https://doi.org/10.3390/fractalfract3020020
Chicago/Turabian StyleKhalili Golmankhaneh, Alireza. 2019. "Statistical Mechanics Involving Fractal Temperature" Fractal and Fractional 3, no. 2: 20. https://doi.org/10.3390/fractalfract3020020
APA StyleKhalili Golmankhaneh, A. (2019). Statistical Mechanics Involving Fractal Temperature. Fractal and Fractional, 3(2), 20. https://doi.org/10.3390/fractalfract3020020




