A Fractional Complex Permittivity Model of Media with Dielectric Relaxation
Abstract
:1. Introduction
2. Fractional Generalized Debye’s Equation
3. The Fractional Model
4. Numerical Results
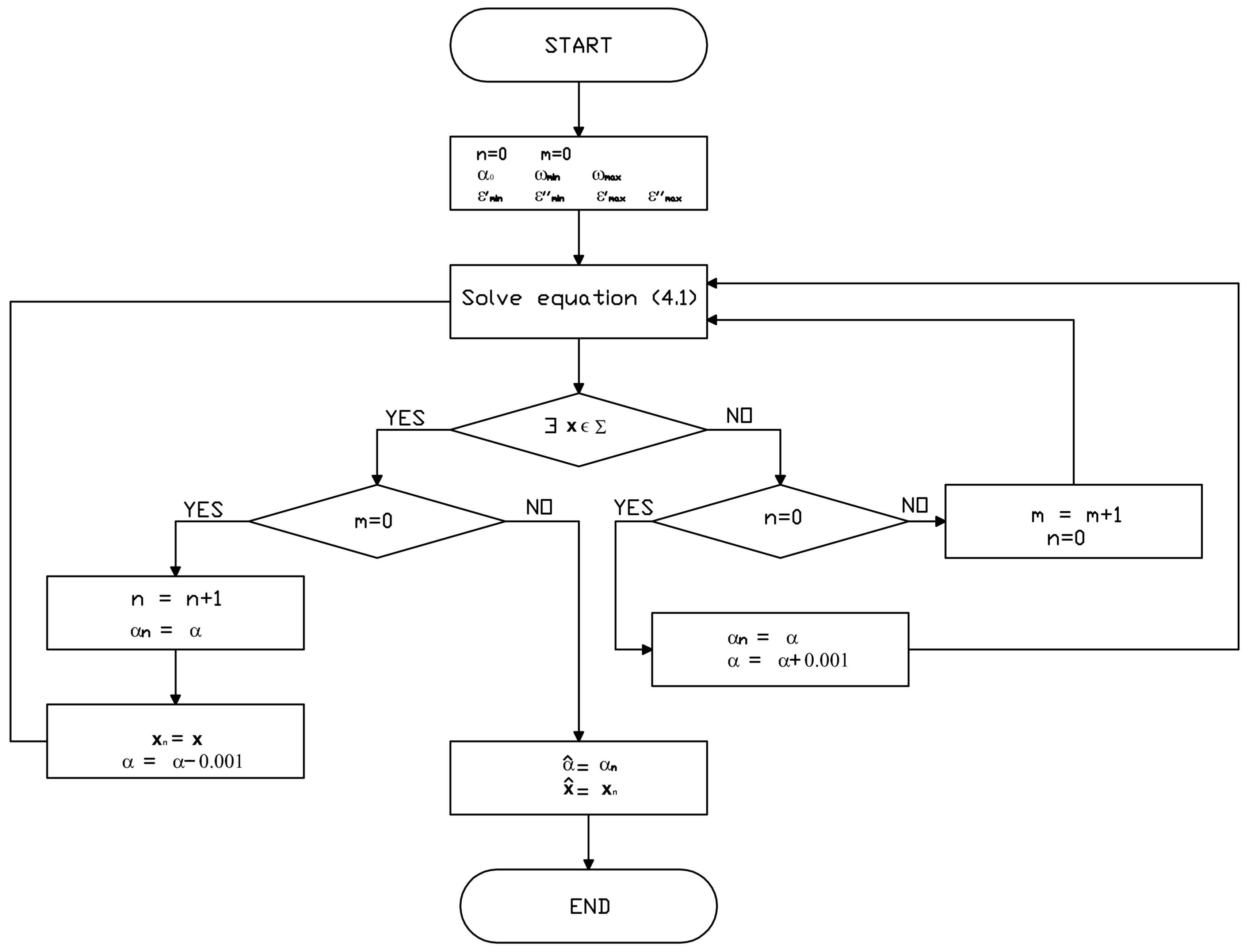
- Step 1
- one chooses a frequency range () and a test value for ;one read the correspondent permittivity experimental values:, , , ;one initializes and .
- Step 2
- one resolves the system at frequencies and .
- Step 3
- If there is a real and positive solution, then if m is not null go to end; otherwise, one puts:; ; ; ; ; ; ;it reduces = - 0.001 and go back to step 2.
- Step 4
- If n is null, one puts and = + 0.001 and go back to step 2; otherwise, one puts , and goes back to step 2.
- End
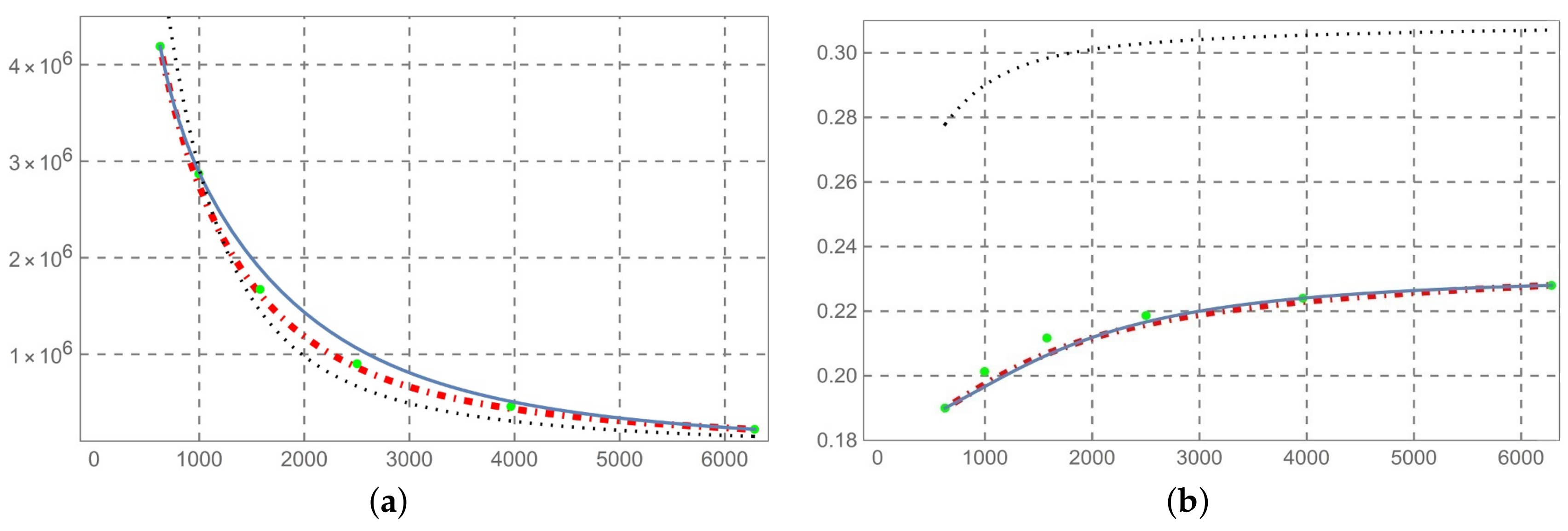
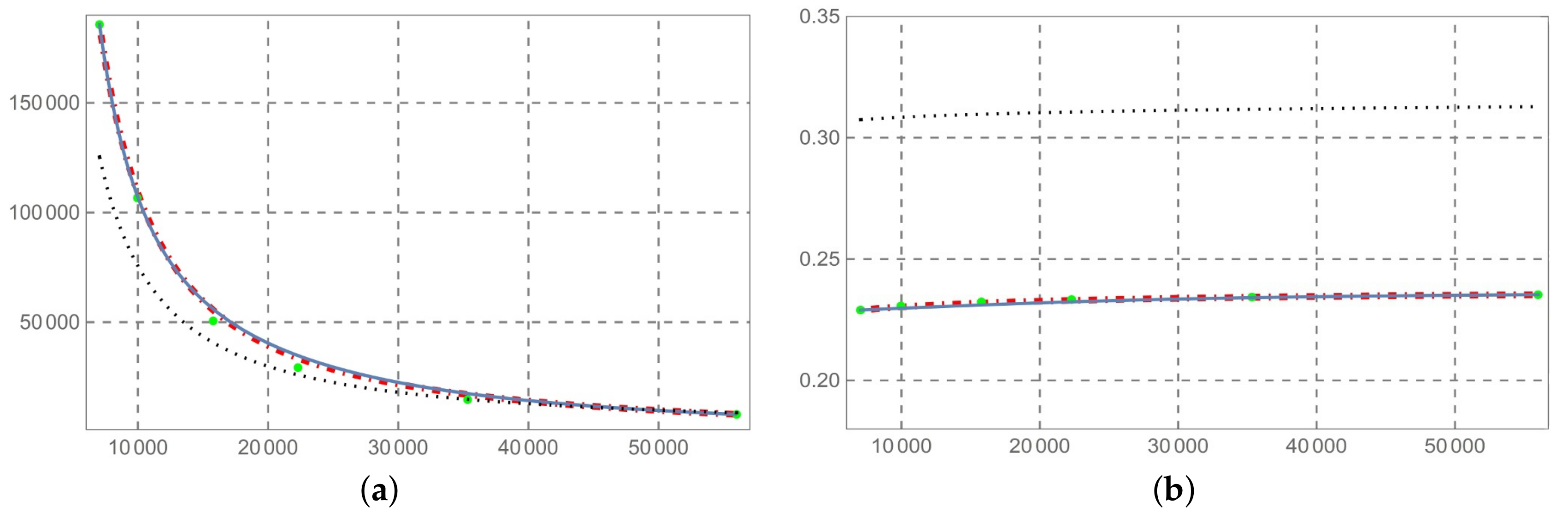
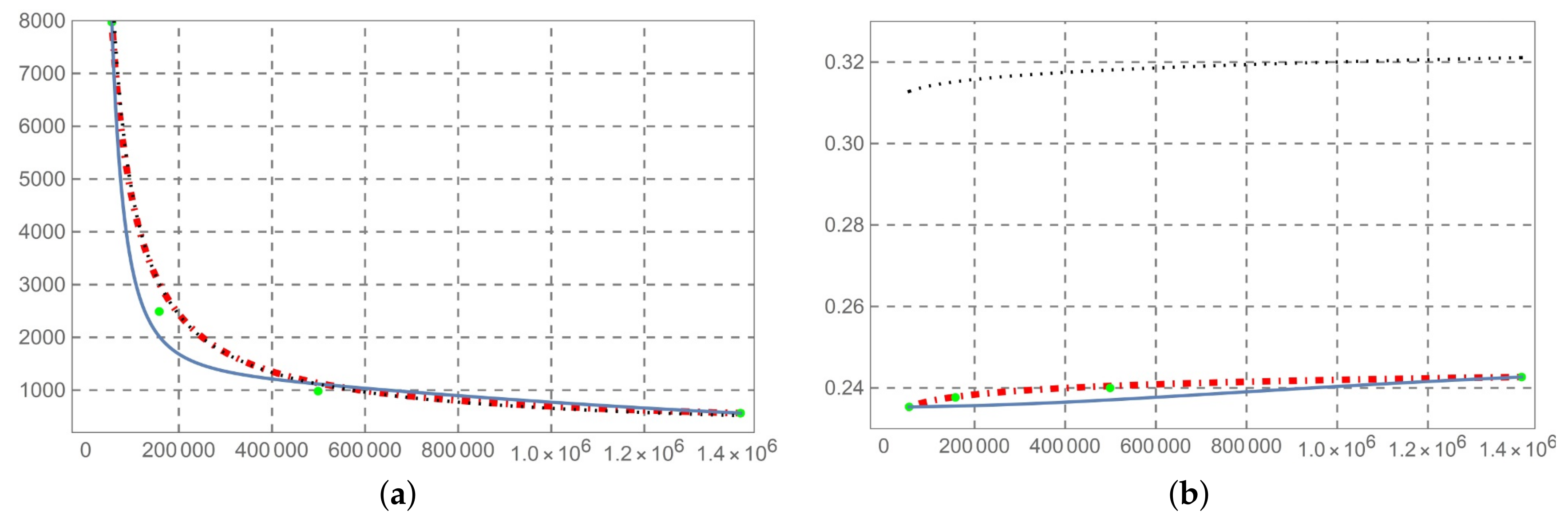
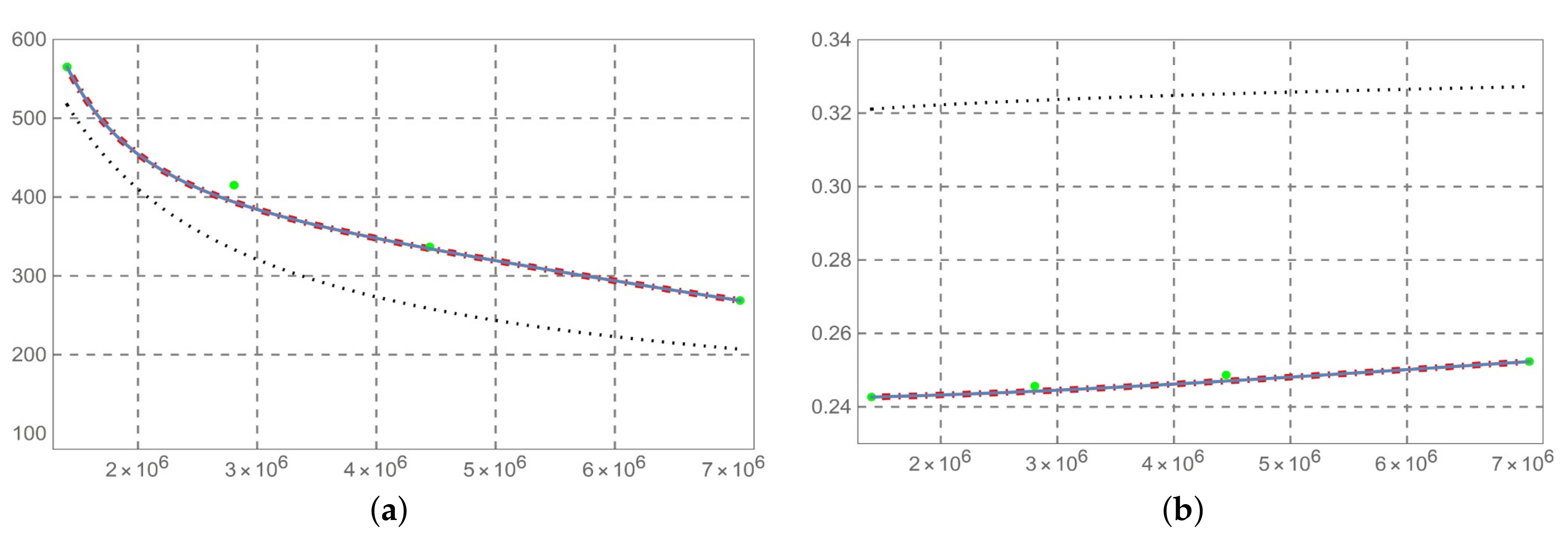
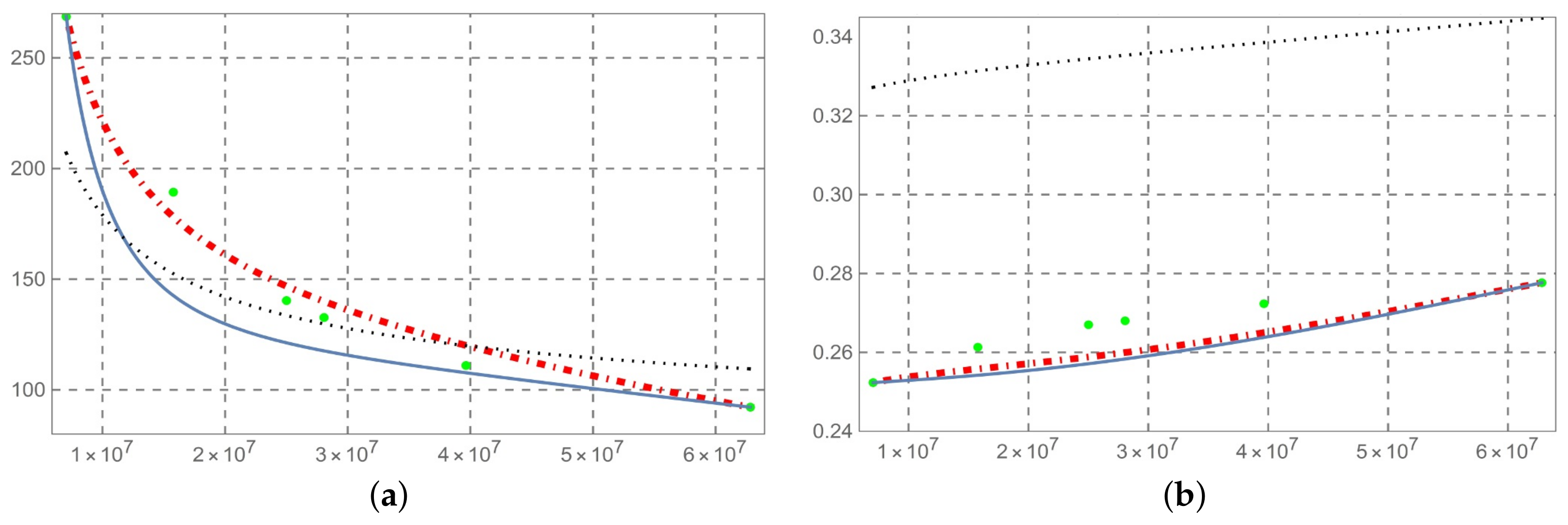
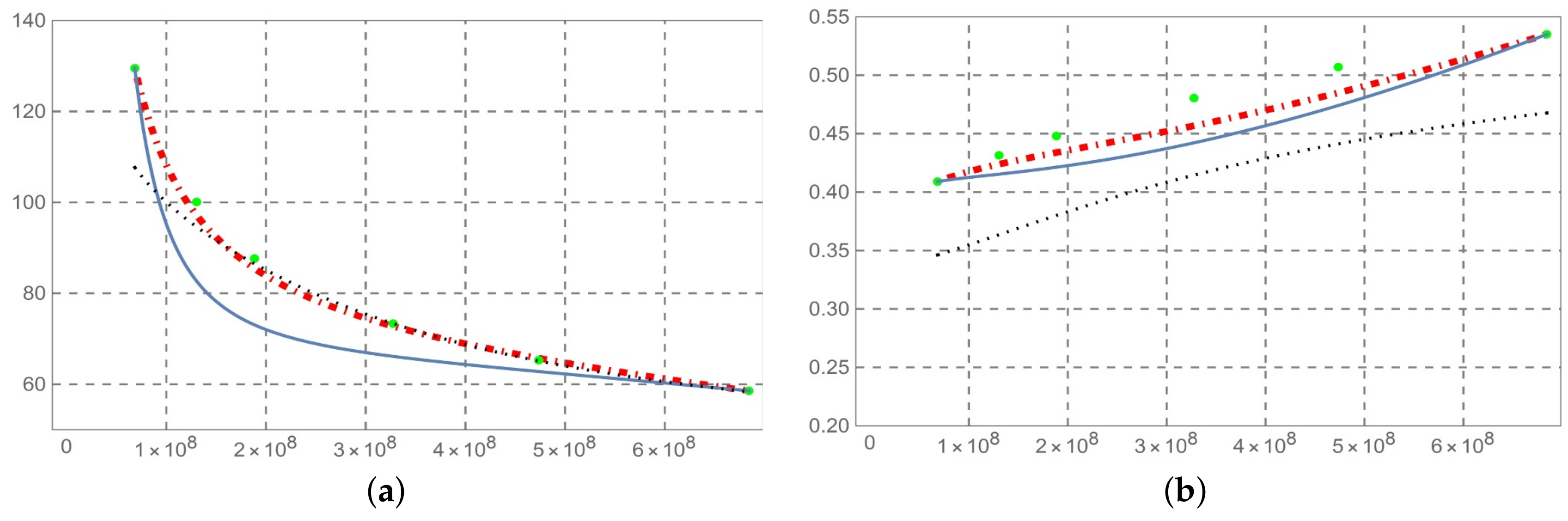
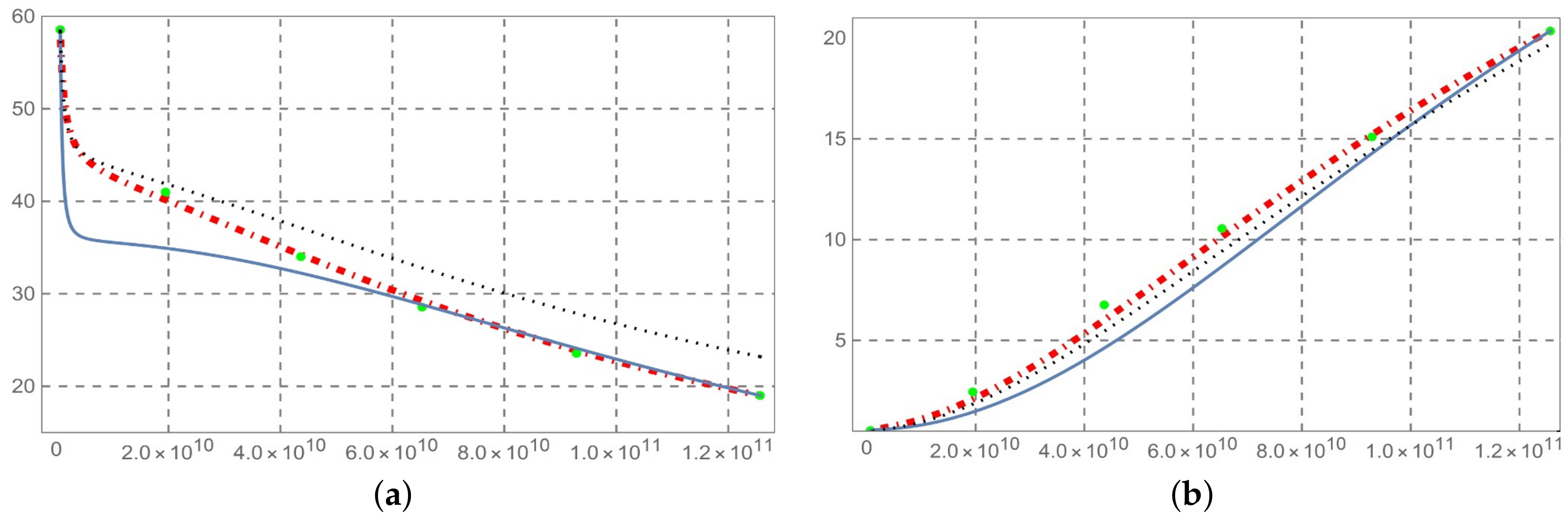
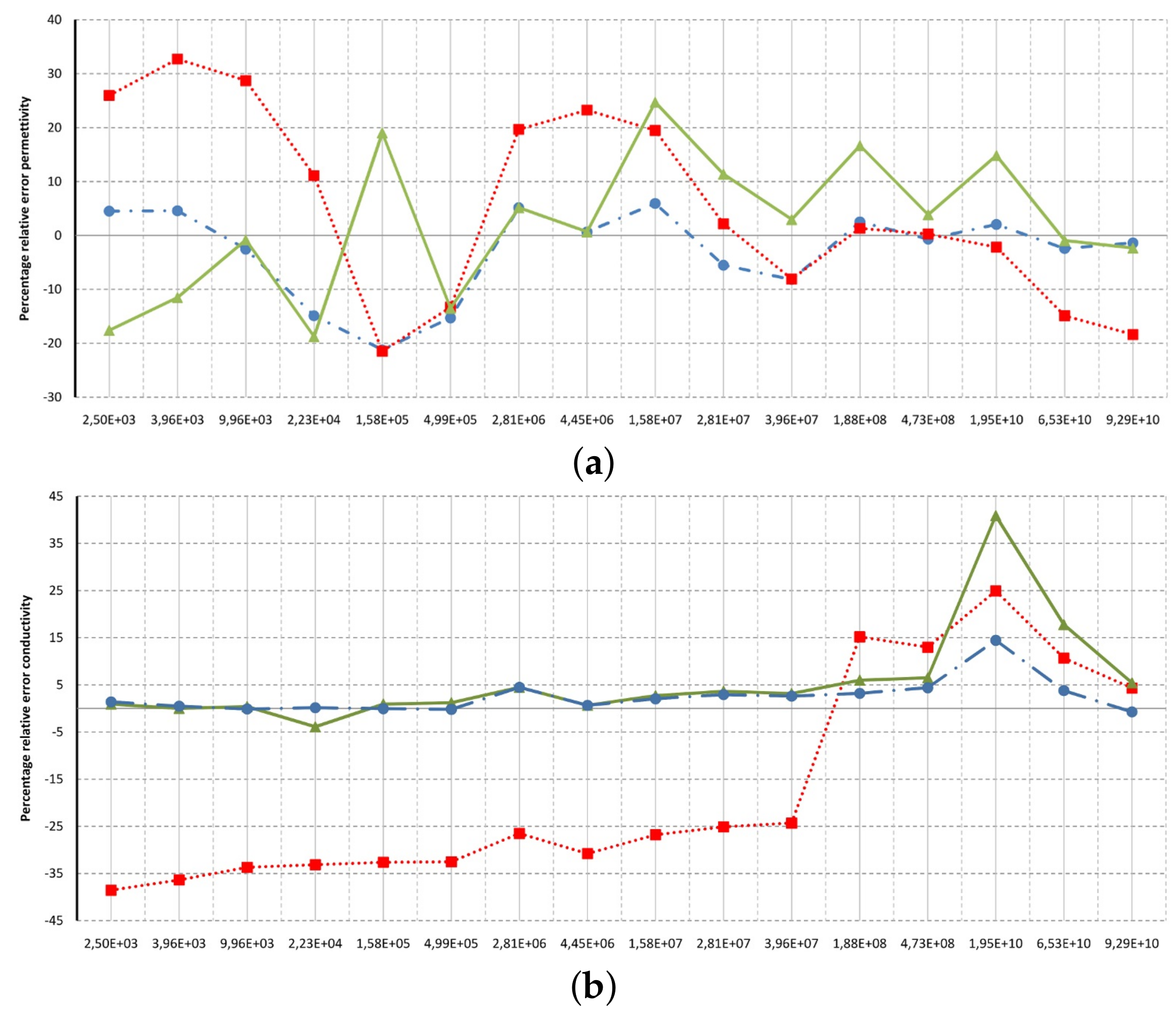
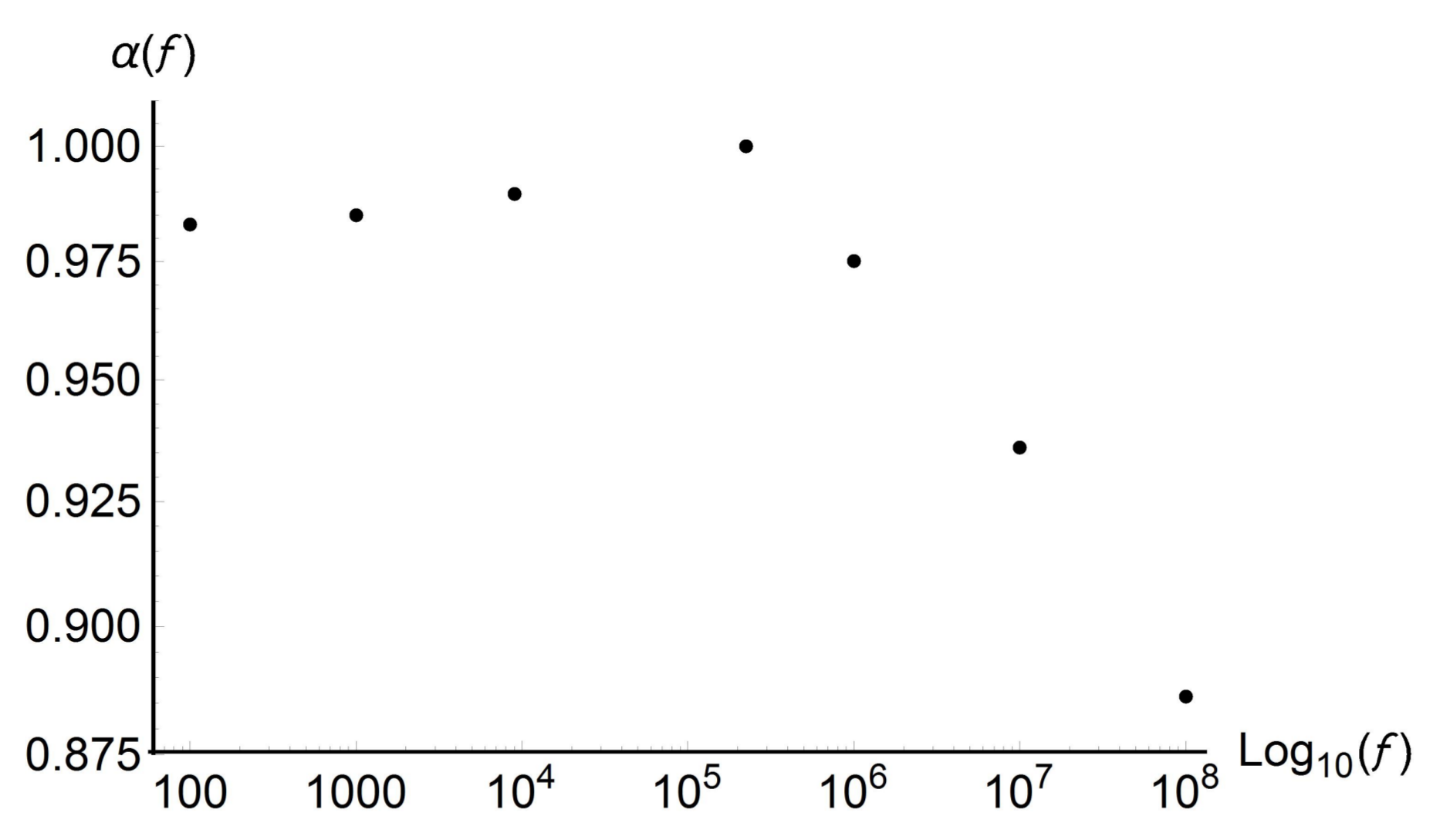
- The solution so determined is compared with the predictive permittivity model in [10], at a temperature of 37 °C with reference to the human aorta. This method is equally applicable to biological tissues. From Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8 (horizontal axis rad/s), we observe that a predictive fractional model of the complex permittivity is in accordance with experimental data with good approximation. The experimental data are those relating to measure campaign published in [10]. In particular from Figure 9, we see that percentage error relative permittivity and conductivity to experimental data is, respectively, almost always lower and thorough than that of the Ciancio–Kluitenberg model and Cole–Cole extended model [7,8,9,10]. In the frequency range 2.5 × 10 @ 9.29 × 10, the maximum relative error to experimental data of permittivity fractional model is −21% at 1.58 × 10 rad/s; of Ciancio–Kluitenberg’s model is +25% at 1.58 × 10 rad/s and extended of Cole–Cole’s model is +35% at 1.58 × 10 rad/s; in the same frequency range, the maximum relative error to experimental data of conductivity fractional model is +15% at 1.95 × 10 rad/s; of Ciancio–Kluitenberg’s model is +41% at 1.95 × 10 rad/s and extended of Cole–Cole’s model is −37% at 2.5 × 10 rad/s. In Figure 10, we show the trend of fractional order with respect to the frequency.
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Artis, F.; Chen, T.; Chretiennot, T.; Fournie, J.-J.; Poupot, M.; Dubuc, D.; Grenier, K. Microwaving biological cells. IEEE Microw. Mag. 2015, 16, 87–96. [Google Scholar] [CrossRef]
- Debye, P. Zur theorie der spezifischen Wärme. Ann. Phys. 1912, 39, 789–839. [Google Scholar] [CrossRef]
- Cole, K.S.; Cole, R.H. Dispersion and absorption in dielectrics I. Alternating current characteristics. J. Chem. Phys. 1941, 9, 341–349. [Google Scholar] [CrossRef]
- Cole, K.S.; Cole, R.H. Dispersion and absorption in dielectrics II. Direct current characteristics. J. Chem. Phys. 1942, 10, 98–105. [Google Scholar] [CrossRef]
- Davidson, D.W.; Cole, R.H. Dielectric relaxation in glycerol, propylene glycol, and n-propanol. J. Chem. Phys. 1951, 19, 1484–1490. [Google Scholar] [CrossRef]
- Havriliak, S.; Negami, S. A complex plane representation of dielectric and mechanical relaxation processes in some polymers. Polymer 1967, 8, 161–210. [Google Scholar] [CrossRef]
- Gabriel, S.; Lau, R.W.; Gabriel, C. The dielectric properties of biological tissues: I. Literature survey. Phys. Med. Biol. 1996, 41, 2231–2250. [Google Scholar] [CrossRef] [PubMed]
- Gabriel, S.; Lau, R.W.; Gabriel, C. The dielectric properties of biological tissues: II. Measurements in the frequency range 10 Hz to 20 GHz. Phys. Med. Biol. 1996, 41, 2251–2270. [Google Scholar] [CrossRef] [PubMed]
- Gabriel, S.; Lau, R.W.; Gabriel, C. The dielectric properties of biological tissues: III. Parametric models for the dielectric spectrum of tissues. Phys. Med. Biol. 1996, 41, 2271–2294. [Google Scholar] [CrossRef] [PubMed]
- Gabriel, C. Compilation of the Dielectric Properties of Body Tissues at RF and Microwave Frequencies; Amstrong Laboratory, Ed.; AFOSR/NL Bolling AFB DC 20332-0001; Report: N.AL/OE-TR-1996-0037; Brooks Air Force Base: San Antonio, TX, USA, 1996; pp. 1–272. [Google Scholar]
- Ciancio, V.; Kluitenberg, G.A. On electromagnetic waves in isotropic media with dielectric relaxation. Acta Phys. Hung. 1989, 66, 251–276. [Google Scholar] [CrossRef]
- Ciancio, V.; Farsaci, F.; Di Marco, G. A method for experimental evalutation of phenomenological coefficients in media with dielectric relaxation. Phys. B Condens. Matter 2007, 387, 130–135. [Google Scholar] [CrossRef]
- Ciancio, V.; Farsaci, F.; Rogolino, P. On a thermodynamical model for dielectric relaxation phenomena. Phys. B Condens. Matter 2010, 405, 175–179. [Google Scholar] [CrossRef]
- Kluitenberg, G.A. On vectorial internal variables and dielectric and magnetic relaxation phenomena. Phys. A Stat. Mech. Appl. 1981, 109, 91–122. [Google Scholar] [CrossRef]
- Caputo, M. Distributed order differential equations modelling dielectric induction and diffusion. Fract. Calc. Appl. Anal. 2001, 4, 421–442. [Google Scholar]
- Garrappa, R.; Mainardi, F.; Maione, G. Models of dielectric relaxation based on completely monotone functions. Fract. Calc. Appl. Anal. 2016, 19, 1105–1160. [Google Scholar] [CrossRef]
- Kiryakova, V. A brief story about the operators of generalized fractional calculus. Fract. Calc. Appl. Anal. 2008, 11, 201–218. [Google Scholar]
- Caputo, M.; Fabrizio, M. Applications of New Time and Spatial Fractional Derivatives with Exponential Kernels. PFDA 2016, 2, 1–11. [Google Scholar] [CrossRef]
- Caputo, M.; Fabrizio, M. A new definition of fractional derivative without singular kernel. PFDA 2015, 1, 73–85. [Google Scholar] [CrossRef]
- Ciancio, V.; Flora, B.F.F. Technical Note on a New Definition of Fractional Derivative. PFDA 2017, 3, 1–4. [Google Scholar] [CrossRef]
- Caputo, M.; Fabrizio, M. Admissible frequency domain response functions of dielectrics. Math. Meth. Appl. Sci. 2015, 38, 930–936. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ciancio, A.; Flora, B.F.F. A Fractional Complex Permittivity Model of Media with Dielectric Relaxation. Fractal Fract. 2017, 1, 4. https://doi.org/10.3390/fractalfract1010004
Ciancio A, Flora BFF. A Fractional Complex Permittivity Model of Media with Dielectric Relaxation. Fractal and Fractional. 2017; 1(1):4. https://doi.org/10.3390/fractalfract1010004
Chicago/Turabian StyleCiancio, Armando, and Bruno Felice Filippo Flora. 2017. "A Fractional Complex Permittivity Model of Media with Dielectric Relaxation" Fractal and Fractional 1, no. 1: 4. https://doi.org/10.3390/fractalfract1010004
APA StyleCiancio, A., & Flora, B. F. F. (2017). A Fractional Complex Permittivity Model of Media with Dielectric Relaxation. Fractal and Fractional, 1(1), 4. https://doi.org/10.3390/fractalfract1010004





