Fractal Simulation of Flocculation Processes Using a Diffusion-Limited Aggregation Model
Abstract
:1. Introduction
2. Model
3. Results and Discussion
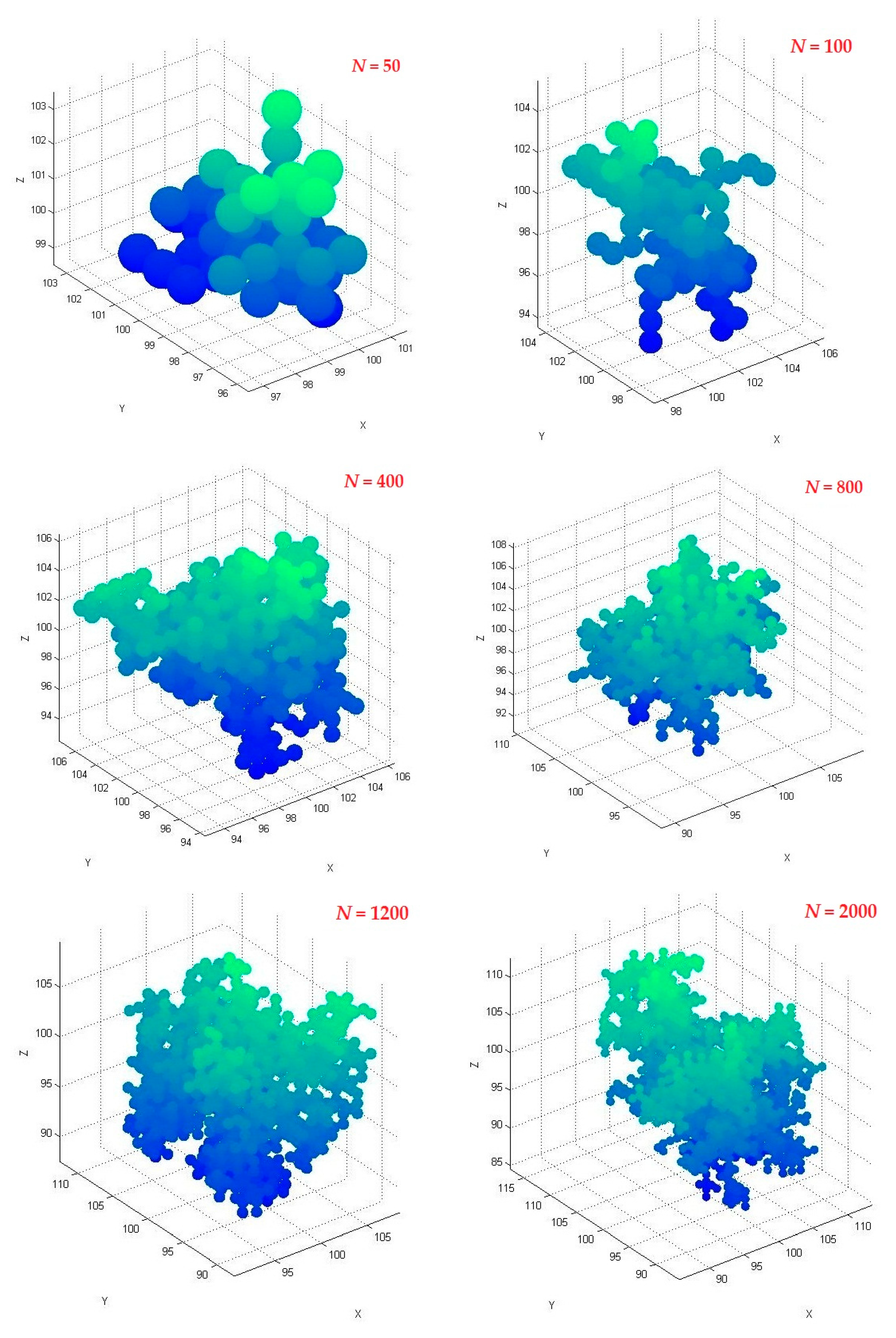
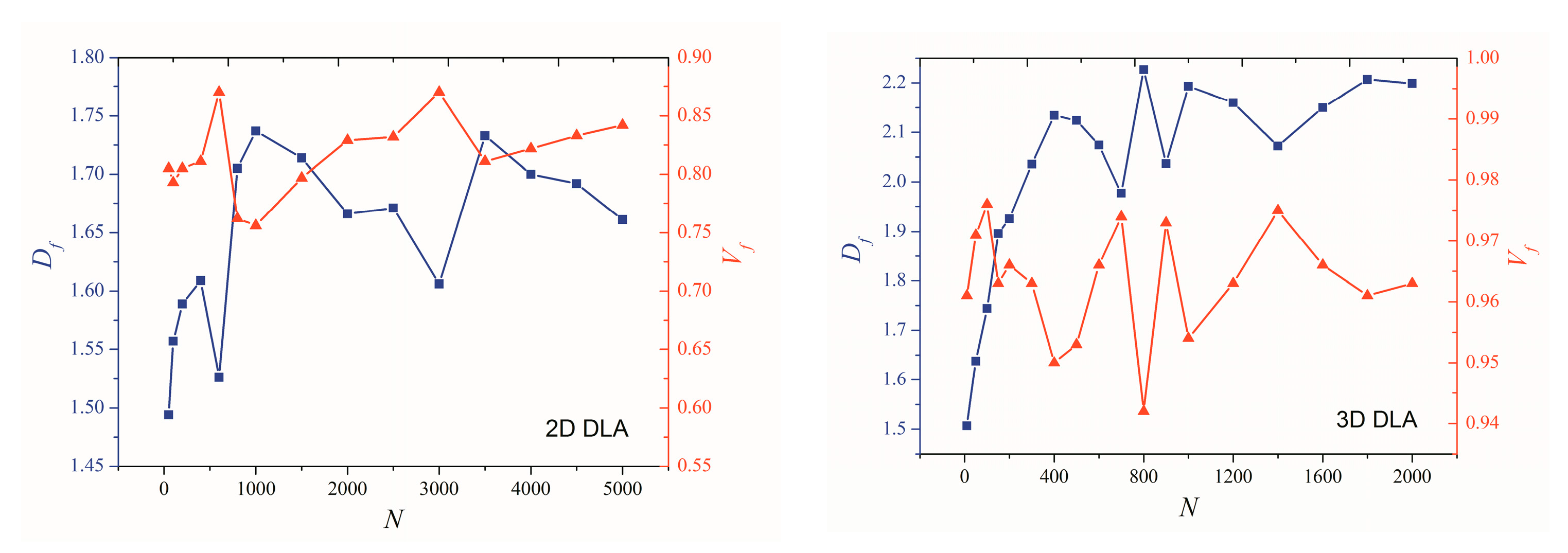
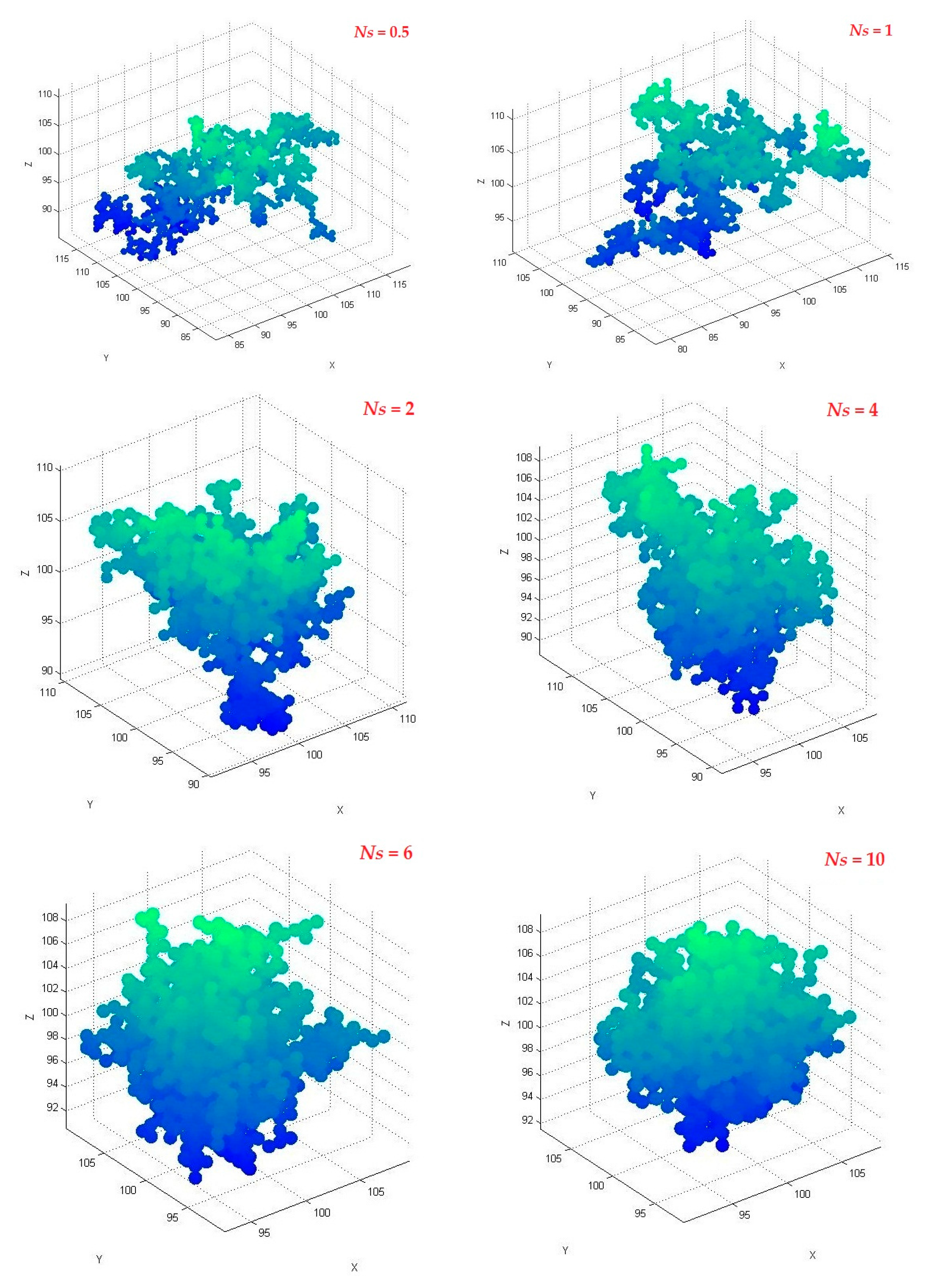
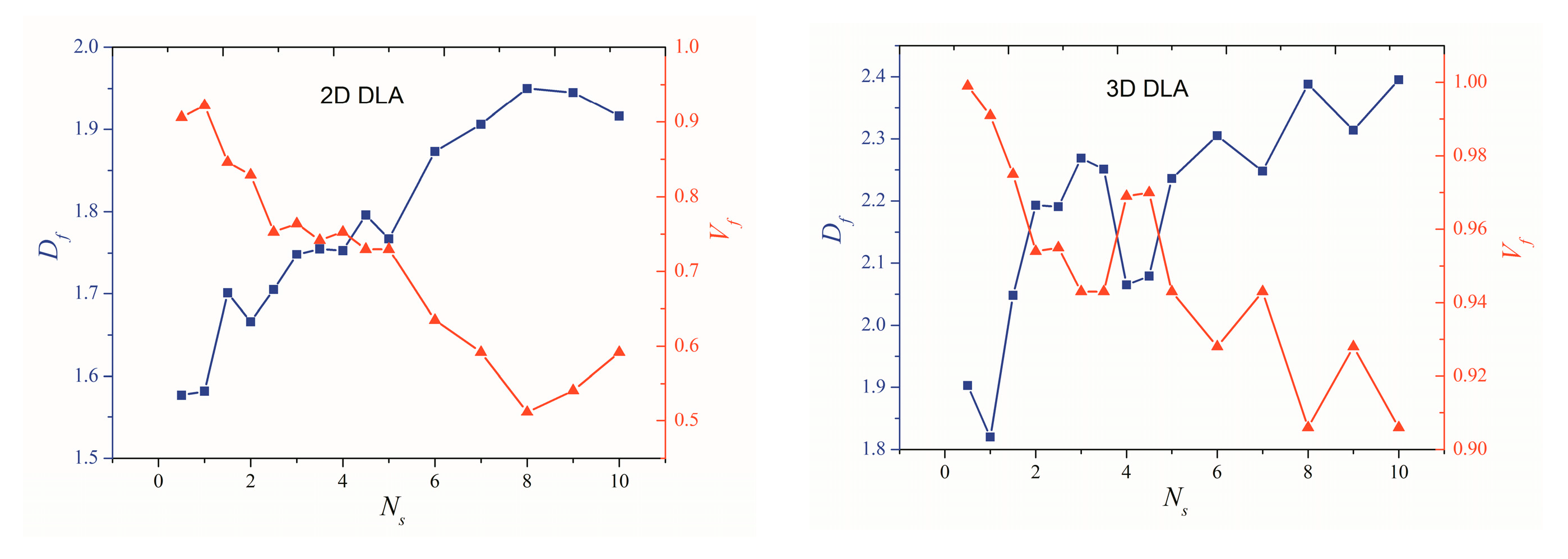
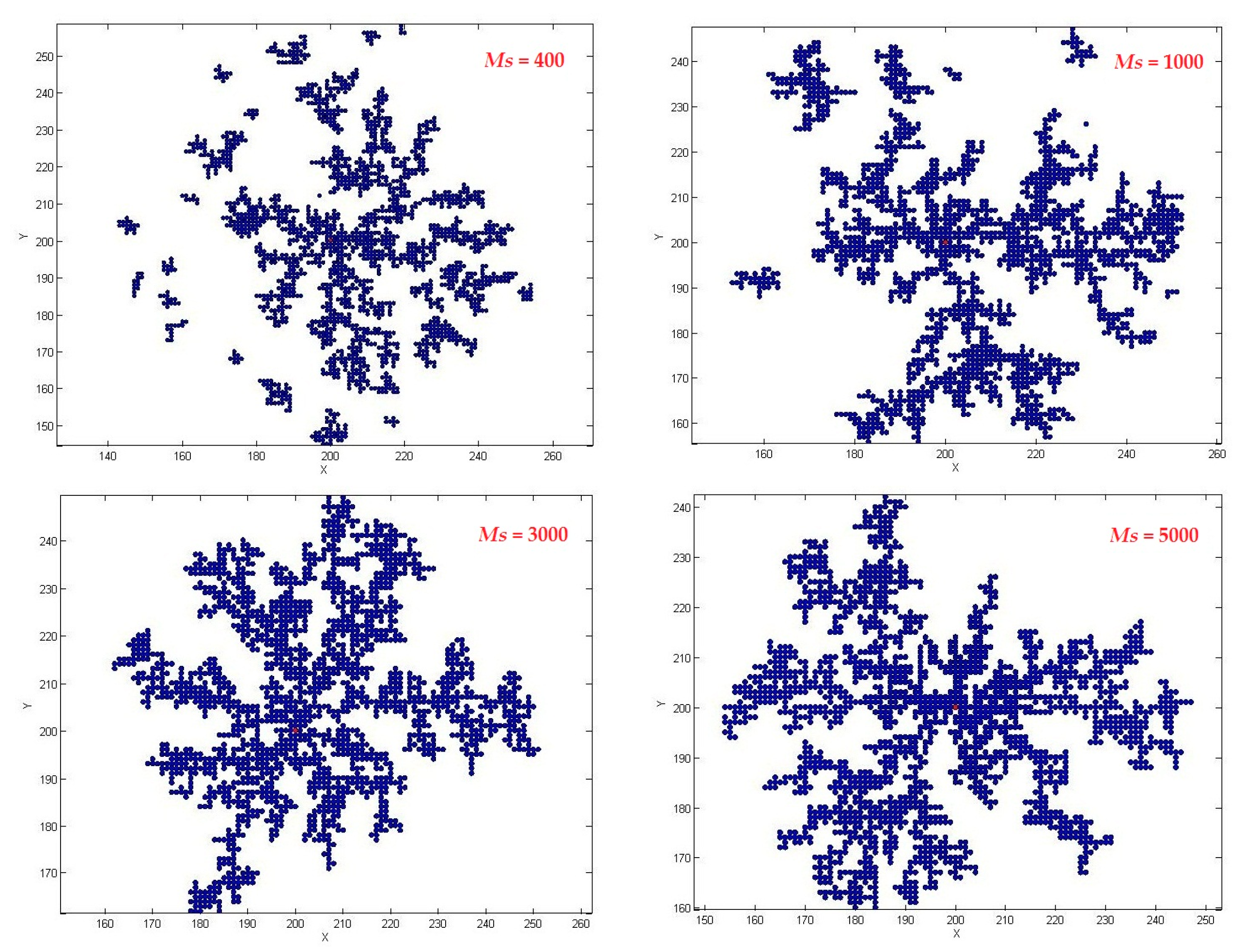
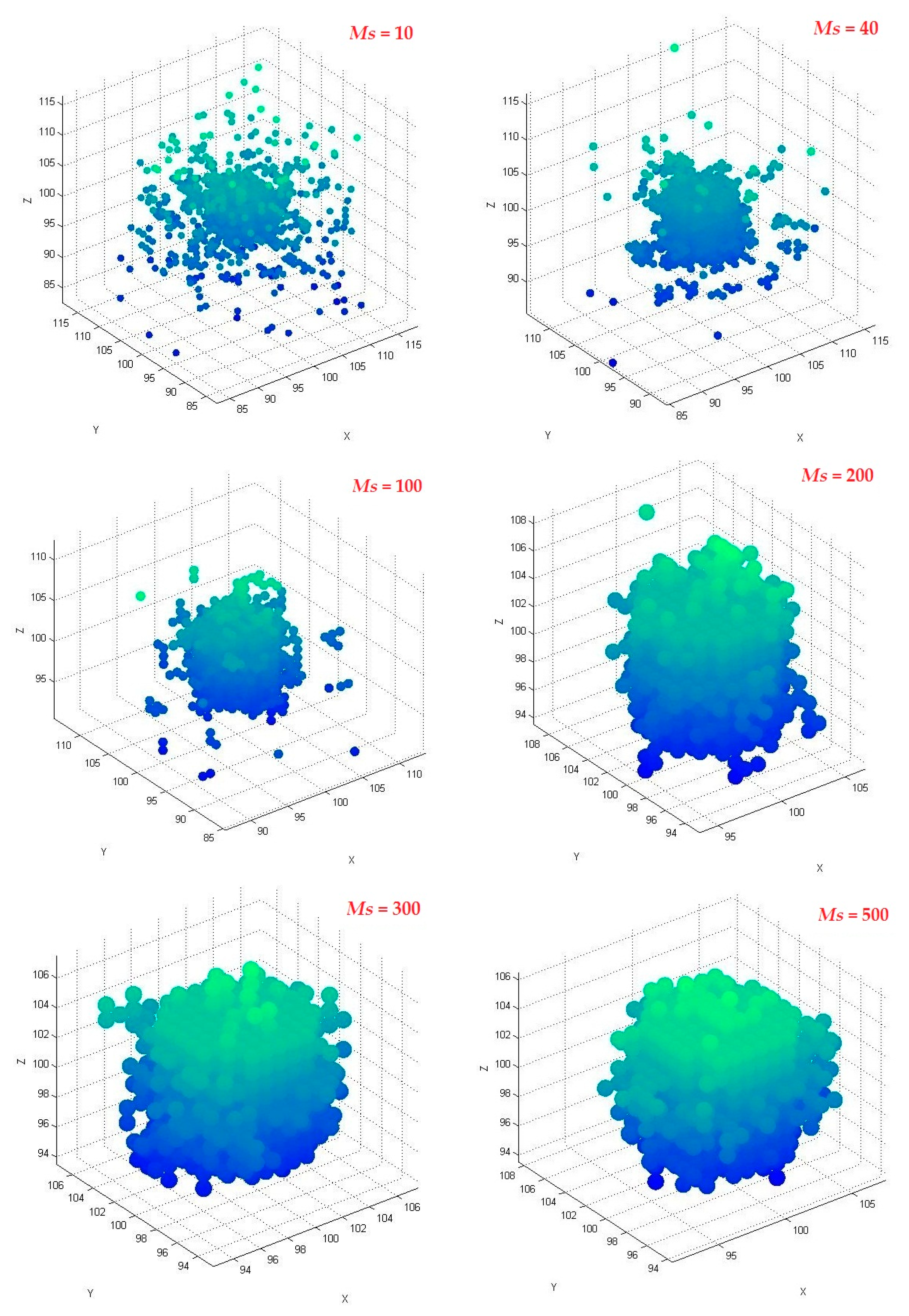
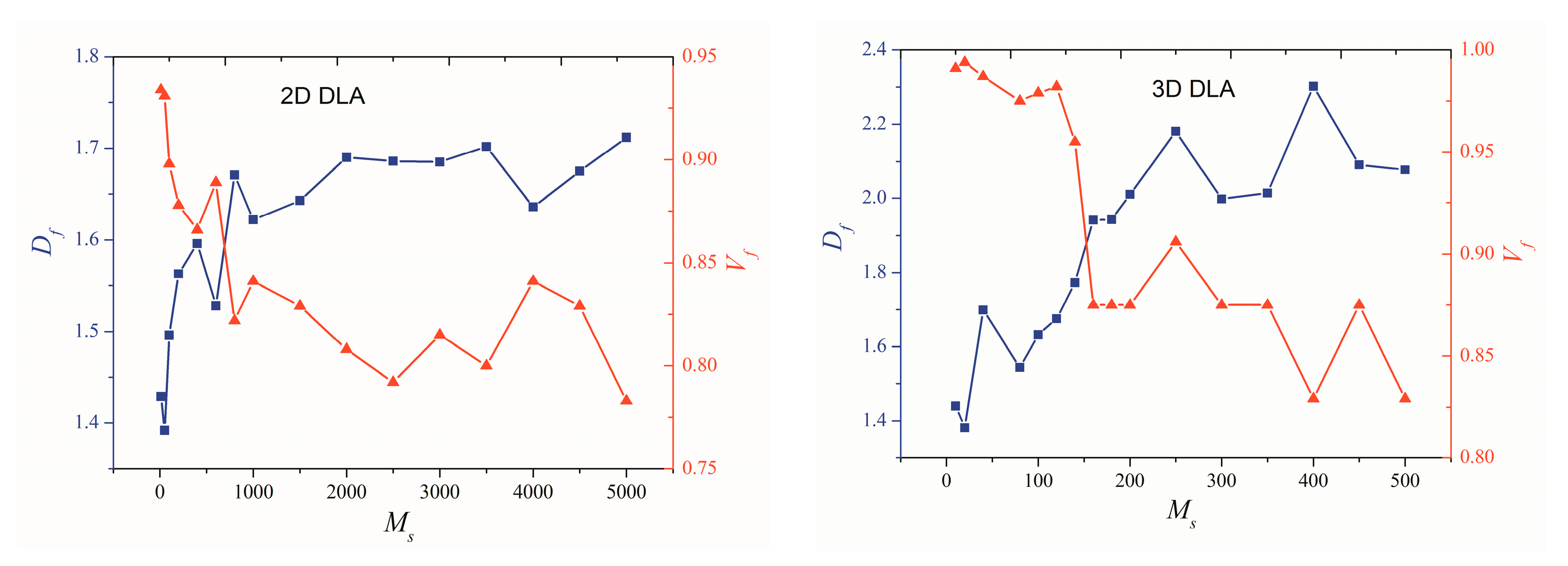
3.1. Effect of Particle Number
3.2. Effect of Motion Step Length
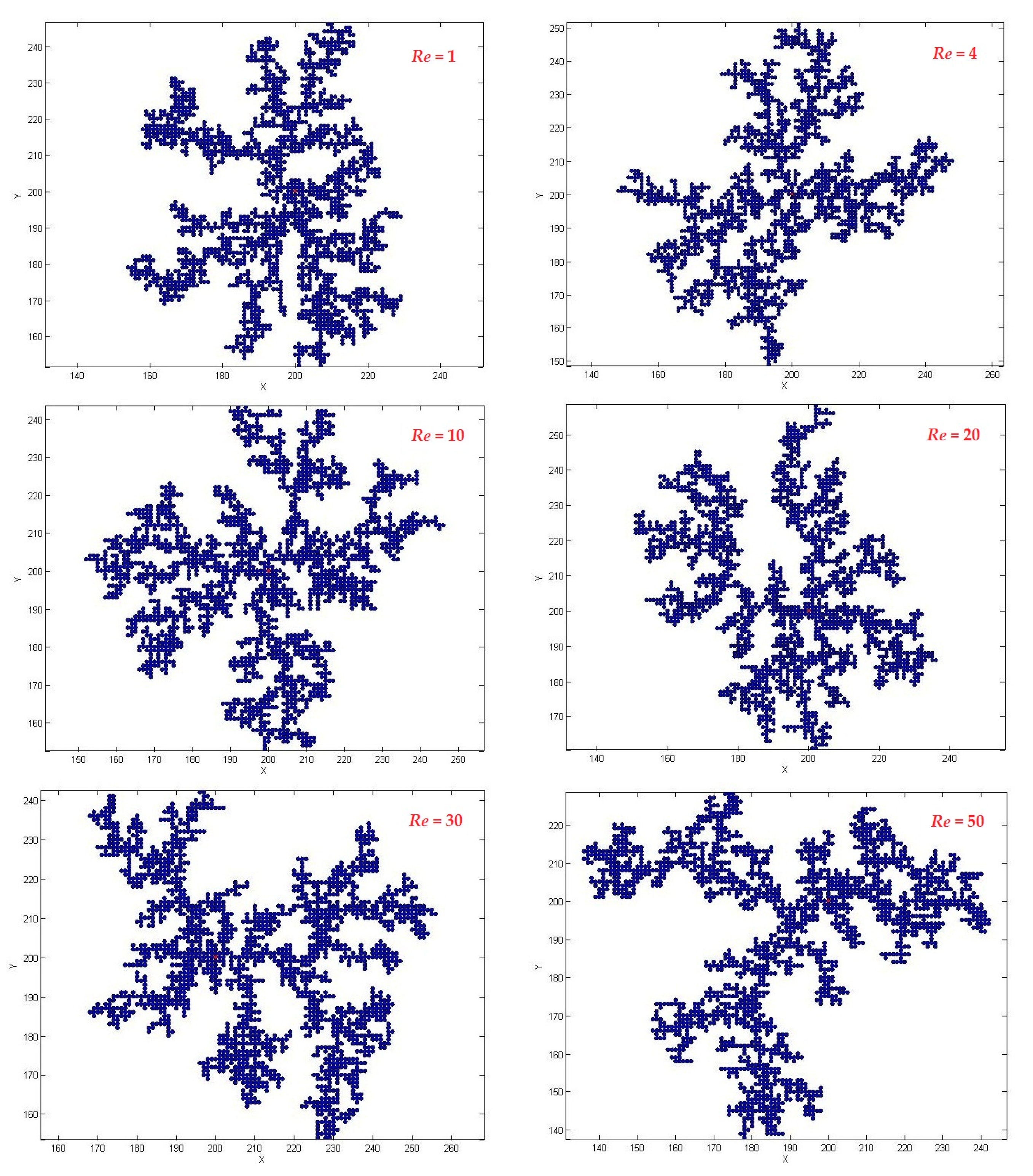
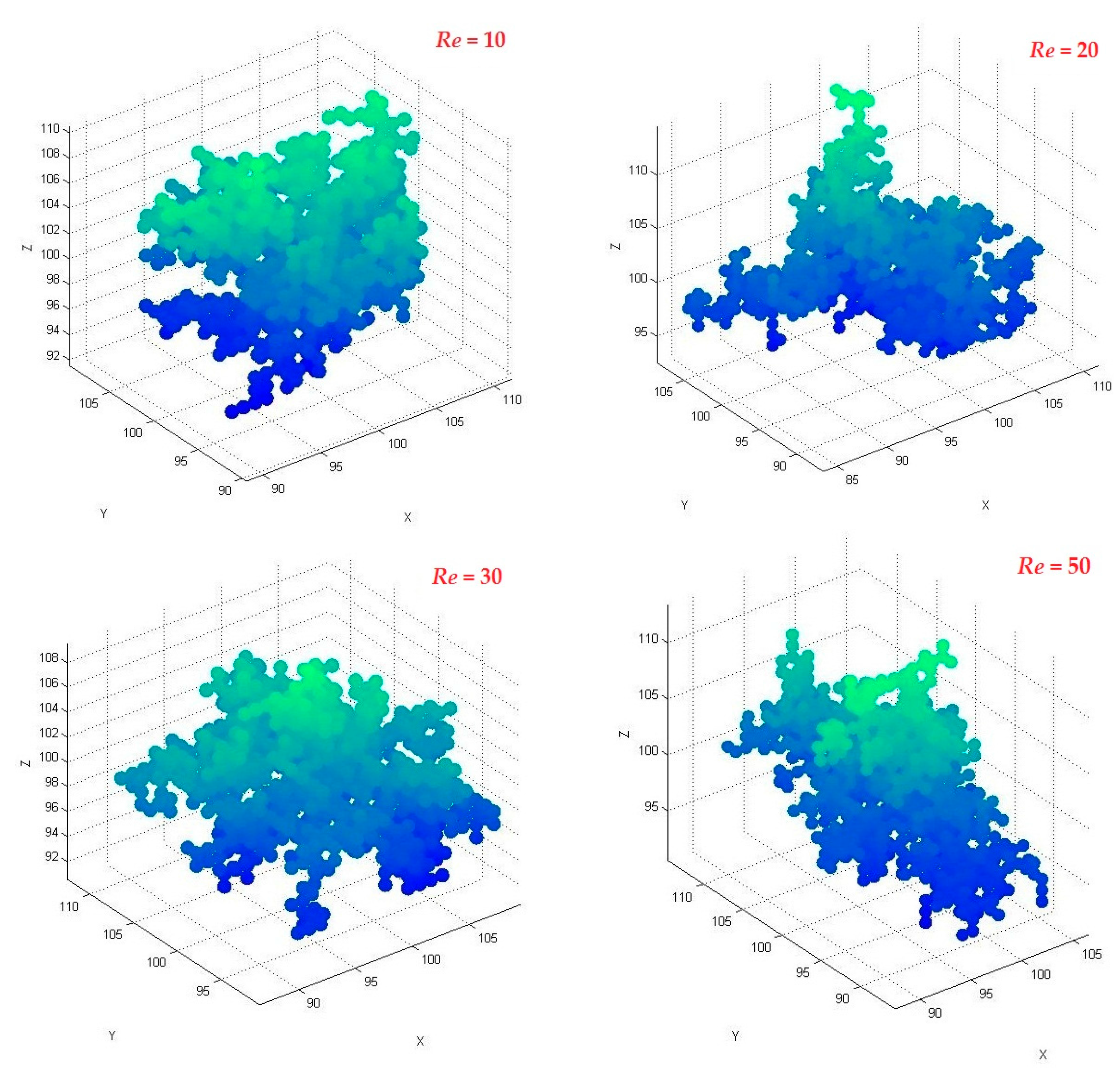
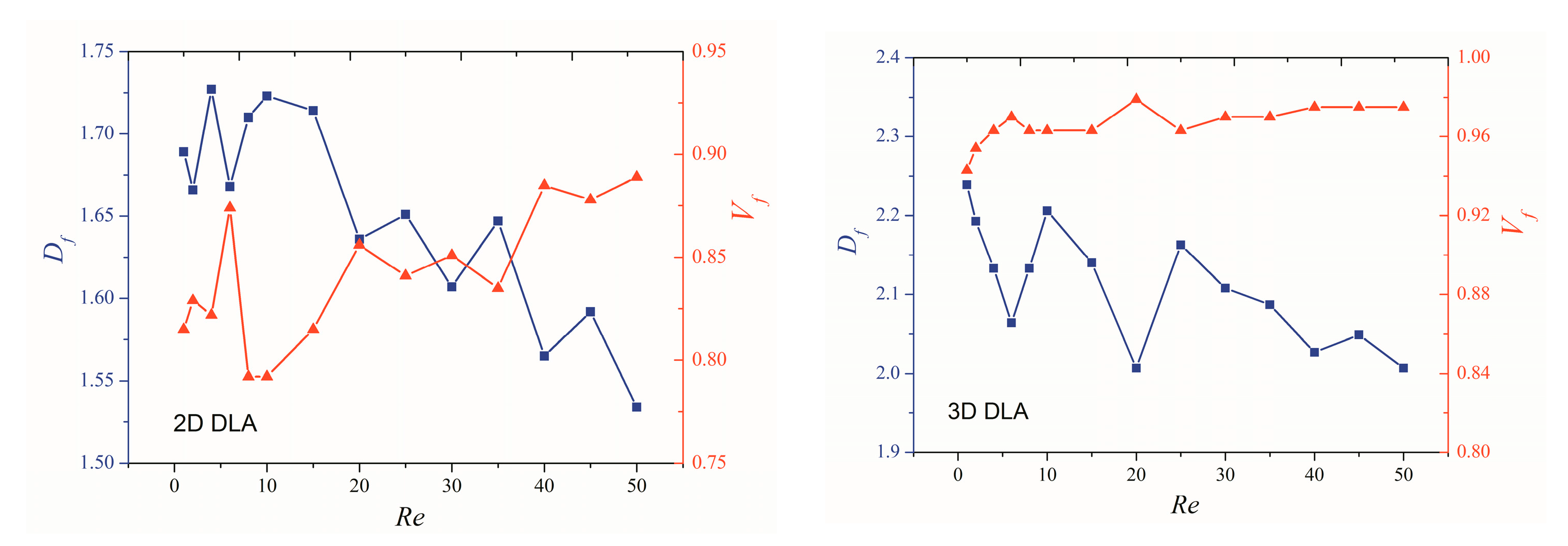
3.3. Effect of Launch Radius
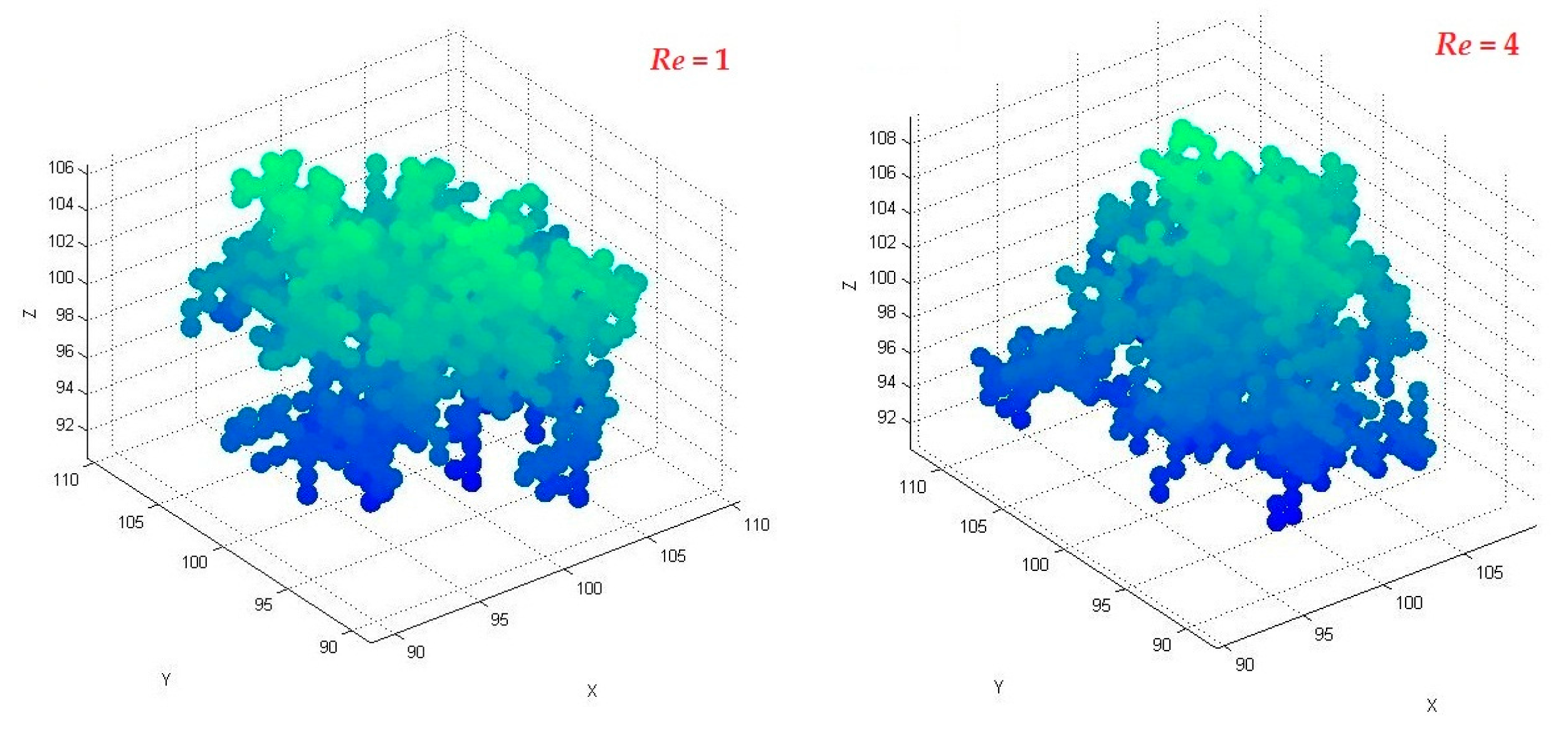
3.4. Effect of Finite Motion Step
4. Conclusions
Author Contributions
Conflicts of Interest
References
- Moghaddam, S.S.; Moghaddam, M.R.A.; Arami, M. Coagulation/flocculation process for dye removal using sludge from water treatment plant: Optimization through response surface methodology. J. Hazard. Mater. 2010, 175, 651–657. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.F.; Liu, W.; Gao, N.Y.; Tao, T. A study of titanium sulfate flocculation for water treatment. Water Res. 2011, 45, 3704–3711. [Google Scholar] [CrossRef] [PubMed]
- Gan, L.M.; Yeoh, K.W.; Chew, C.H.; Koh, L.L.; Tan, T.L. Poly(sodium acrylamidoalkanoate) s: Syntheses and solution properties in relation to flocculation study in water treatment. J. Appl. Polym. Sci. 2010, 42, 225–232. [Google Scholar] [CrossRef]
- Jiang, Q.; Logan, B.E. Fractal dimensions of aggregates from shear devices. J. Am. Water Works Assoc. 1996, 88, 100–113. [Google Scholar]
- Oles, V. Shear-induced aggregation and breakup of polystyrene latex particles. J. Colloid Interface Sci. 1992, 154, 351–358. [Google Scholar] [CrossRef]
- Adachi, Y.; Kobayashi, A.; Kobayashi, M. Structure of colloidal flocs in relation to the dynamic properties of unstable suspension. Int. J. Polym. Sci. 2012, 2012, 1–14. [Google Scholar] [CrossRef]
- Adachi, Y.; Kobayashi, M.; Ooi, S. Applicability of fractals to the analysis of the projection of small flocs. J. Colloid Interface Sci. 1998, 208, 353–355. [Google Scholar] [CrossRef] [PubMed]
- Matsumoto, T.; Adachi, Y. Effect of ionic strength on the initial dynamics of flocculation of polystyrene latex with polyelectrolyte. J. Colloid Interface Sci. 1998, 204, 328–335. [Google Scholar] [CrossRef] [PubMed]
- Kobayashi, M.; Adachi, Y.; Ooi, S. On the steady shear viscosity of coagulated suspensions. J. Soc. Rheol. Jpn. 2000, 28, 143–144. [Google Scholar] [CrossRef]
- Sato, D.; Kobayashi, M.; Adachi, Y. Effect of floc structure on the rate of shear coagulation. J. Colloid Interface Sci. 2004, 272, 345–351. [Google Scholar] [CrossRef] [PubMed]
- Adachi, Y.; Aoki, K. Restructuring of small flocs of polystyrene latex with polyelectrolyte. Colloids Surf. A Physicochem. Eng. Asp. 2009, 342, 24–29. [Google Scholar] [CrossRef]
- Witten, T.A.; Sander, L.M. Diffusion-limited aggregation. Phys. Rev. B Condens. Matter 1983, 27, 5686–5697. [Google Scholar] [CrossRef]
- Meakin, P. Formation of fractal clusters and networks by irreversible diffusion-limited aggregation. Phys. Rev. Lett. 1983, 51, 1119–1122. [Google Scholar] [CrossRef]
- Meakin, P. The structure of two-dimensional Witten-Sander aggregates. J. Phys. A Gen. Phys. 1985, 18, L661–L666. [Google Scholar] [CrossRef]
- Meakin, P.; Vicsek, T. Diffusion-limited aggregation with radial bias. J. Phys. A Gen. Phys. 1987, 20, L171–L175. [Google Scholar] [CrossRef]
- Sander, L.M.; Cheng, Z.M.; Richter, R. Diffusion-limited aggregation in three dimensions. Phys. Rev. B 1983, 27, 5686–5697. [Google Scholar] [CrossRef]
- Paterson, L. Diffusion-limited aggregation and two-fluid displacements in porous media. Phys. Rev. Lett. 1984, 52, 1621–1624. [Google Scholar] [CrossRef]
- Rangel, R.; Rojas, S. Montecarlo DLA-type simulations of wetting effects in fluid displacement in porous media. Comput. Geosci. 2009, 13, 215–225. [Google Scholar] [CrossRef]
- Gentile, F.; Coluccio, M.L.; Toma, A.; Rondanina, E.; Leoncini, M.; Angelis, F.D.; Das, G.; Dorigoni, C.; Candeloro, P.; Fabrizio, E.D. Electroless deposition dynamics of silver nanoparticles clusters: A diffusion limited aggregation (DLA) approach. Microelectron. Eng. 2012, 98, 359–362. [Google Scholar] [CrossRef]
- Sun, W.; Wang, W.; Gu, Y.; Xu, X.; Gong, J. Study on the wax/asphaltene aggregation with diffusion limited aggregation model. Fuel 2017, 191, 106–113. [Google Scholar] [CrossRef]
- Novotny, M.A.; Tao, R.; Landau, D.P. Relaxation in DLA with surface tension. J. Phys. A Gen. Phys. 1990, 23, 3271–3278. [Google Scholar] [CrossRef]
- Tan, Z.J.; Zou, X.W.; Zhang, W.B.; Jin, Z.Z. Influence of particle size on diffusion-limited aggregation. Phys. Rev. E Stat. Phys. Plasmas Fluid. Relat. Interdiscip. Top. 1999, 60, 6202–6205. [Google Scholar] [CrossRef]
- Braga, F.L.; Mattos, O.A.; Amorin, V.S.; Souza, A.B. Diffusion limited aggregation of particles with different sizes: Fractal dimension change by anisotropic growth. Phys. A Stat. Mech. Appl. 2015, 429, 28–34. [Google Scholar] [CrossRef]
- Deng, L.; Wang, Y.; Ouyang, Z. Diffusion-limited aggregation with polygon particles. Commun. Theor. Phys. 2012, 58, 895–901. [Google Scholar] [CrossRef]
- Xu, C. A flocculation simulation method based on two-dimensional DLA model. J. Simul. 2014, 2, 19–22. [Google Scholar]
- Qiu, Z.; Liu, D.; Zhang, R. Simulation of two-dimensional floc growth using improved DLA model. In Proceedings of the 2011 IEEE 2nd International Conference on Computing, Control and Industrial Engineering, Wuhan, China, 20–21 August 2011; pp. 246–249. [Google Scholar]
- Qiu, Z.; Liu, D.; He, Z.; Wu, Y. Simulation of three-dimensional floc growth using improved DLA model. In Proceedings of the 2011 IEEE 2nd International Conference on Computing, Control and Industrial Engineering, Wuhan, China, 20–21 August 2011; pp. 250–253. [Google Scholar]
- Scarnato, B.V.; Vahidinia, S.; Richard, D.T.; Kirchstetter, T.W. Effects of internal mixing and aggregate morphology on optical properties of black carbon using a discrete dipole approximation method. Atmos. Chem. Phys. 2013, 13, 5089–5101. [Google Scholar] [CrossRef]
- Radney, J.G.; You, R.; Ma, X.; Conny, S.M.; Zachariah, M.R.; Hodges, J.T.; Zangmeister, C.D. Dependence of soot optical properties on particle morphology: Measurements and model comparisons. Environ. Sci. Technol. 2014, 48, 3169–3176. [Google Scholar] [CrossRef] [PubMed]
- Serra, T.; Casamitjana, X. Structure of the aggregates during the process of aggregation and breakup under a shear flow. J. Colloid Interface Sci. 1998, 206, 505–511. [Google Scholar] [CrossRef] [PubMed]
- Wu, H.; Lattuada, M.; Morbidelli, M. Dependence of fractal dimension of dlca clusters on size of primary particles. Adv. Colloid Interface Sci. 2013, 195–196, 41–49. [Google Scholar] [CrossRef] [PubMed]
- Heinson, W.R.; Sorensen, C.M.; Chakrabarti, A. Does shape anisotropy control the fractal dimension in diffusion-limited cluster-cluster aggregation? Aerosol Sci. Technol. 2010, 44, 1–4. [Google Scholar] [CrossRef]
- Heinson, W.R.; Chakrabarti, A.; Sorensen, C.M. Divine proportion shape invariance of diffusion limited cluster–cluster aggregates. Aerosol Sci. Technol. 2015, 49, 786–792. [Google Scholar] [CrossRef]


© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, D.; Zhou, W.; Song, X.; Qiu, Z. Fractal Simulation of Flocculation Processes Using a Diffusion-Limited Aggregation Model. Fractal Fract. 2017, 1, 12. https://doi.org/10.3390/fractalfract1010012
Liu D, Zhou W, Song X, Qiu Z. Fractal Simulation of Flocculation Processes Using a Diffusion-Limited Aggregation Model. Fractal and Fractional. 2017; 1(1):12. https://doi.org/10.3390/fractalfract1010012
Chicago/Turabian StyleLiu, Dongjing, Weiguo Zhou, Xu Song, and Zumin Qiu. 2017. "Fractal Simulation of Flocculation Processes Using a Diffusion-Limited Aggregation Model" Fractal and Fractional 1, no. 1: 12. https://doi.org/10.3390/fractalfract1010012
APA StyleLiu, D., Zhou, W., Song, X., & Qiu, Z. (2017). Fractal Simulation of Flocculation Processes Using a Diffusion-Limited Aggregation Model. Fractal and Fractional, 1(1), 12. https://doi.org/10.3390/fractalfract1010012




