Fractal and Fractional are two words referring to some characteristics and fundamental problems which arise in all fields of science and technology. These problems are characterized by having some non-integer order features. Fractals are geometrical objects with non-integer dimension, while fractional is the non-integer order of differential operators. Fractals and fractional calculus have been deeply studied since the beginning of calculus, however non-integer order objects were mainly considered as singular objects or outstanding topics and they were usually approached as geometrical or analytical oddities. Indeed, in the last century, it became more and more evident that when dealing with real problems we have to face the complexity with sophisticated mathematical models. As a consequence, scholars became more familiar with fractal objects and found that the real world is more like a fractal object than they initially thought.
Fractals are geometric objects, usually defined by a recursive law, which are characterized by some peculiar properties such as self-similarity and scale. According to self-similarity, a small part of a fractal looks like the whole. The scale property can be explained, in short, by the fact that by increasing the unit length by an integer factor, the measure of the fractal increases by a non-integer factor. In the last Century, due to developing technologies and growing interest, many fractal-like objects were discovered nearly everywhere, at the micro- and nano-scale of matter as well as at the cosmological scale. The most striking result was the observation of self-similarity and scale dependence in almost all fields of investigation, from biology and medicine to geography and astronomy. Moreover, the human morphology of organs, e.g., of the brain, lungs, vessels, and the activity of heart, neurons, and cells, are fractals. Fractals and fractal-like objects were investigated in almost all fields of science and technology, e.g., in mathematics, computer science, image analysis, communications, medicine, seismology, structural mechanics, nano-composites, nano-fluidics, and fracture analysis.
New findings about the fractal nature in some specific topics led to unexpected new results and progress in research. As a consequence, we became more and more aware both of the fractal nature of the world and of the importance of the fractal models to describe the evolution of the world around us. We have gone from the original idea that fractals were some picturesque singularities to the modern point of view that sees them at the core of knowledge. It has been a tortuous path, at each step of which new discoveries appear in different unexpected fields.
In recent years, there has also been increasing interest in the analytical properties of geometrical fractal-like objects. However, when dealing with fractals, the fundamental characteristic of being differentiable is missing, therefore it is a challenging problem to define operators on fractal sets.
Smoothness and differentiability are the two fundamental pillars of any analytical structure. Moreover, the integer order of derivatives was considered the necessary condition for building differential operators. Nevertheless, since the origin of differential calculus, Cauchy was proposing a definition of fractional order repeated integrals, thus opening new perspectives in differential calculus. Since then, there has been increasing interest in such a kind of operators and differential problems with fractional order operators. The main idea in fractional calculus is to define a suitable differential operator which depends on a fractional order parameter. The fundamental properties of these operators are the following: when the parameter is integer, then each fractional operator must reduce to the ordinary differential operators, moreover, the basic rules of calculus, e.g., linearity, should hold true. However, the fractional differential operator defined on the Cauchy fractional order integral, does not vanish when applied to a constant value. There have been many efforts to overcome this problem and one solution was found in the so-called Caputo fractional derivative. As a consequence, we became aware that the definition of fractal derivative is not unique and since then many other kinds of fractional differential operators have been proposed and studied, such as the classical Grünwald–Letnikov, Riemann–Liouville, Hadamard definitions. In recent years, many other new definitions of fractional operators (local and non-local, with singular and non-singular kernel), all with interesting properties, have been given and deeply investigated, thus opening new perspectives in the analysis of differential problems. It is still an open question why we have so many different definitions, even though it was possible to explore almost all fields of science and technology within each model. Therefore, even if no unique definition of fractional operator exists and even if some of these fractional operators do not satisfy some basic rules of calculus, such as the Leibnitz rule or the vanishing of the fractional derivative of a constant value, their application to the analysis of theoretical or applied problems has opened new horizons in research.
At the moment, there is much interest in the application of these fractional operators in all branches of science, therefore many papers are dealing with fractional dynamical systems, fractional differential equations, fractional partial differential equations, and fractional integro-differential equations with specific application to the solution of concrete problems in almost all branches of physics, chemistry, biology, medicine, computer science, and in all fields of engineering applications from structural models to energetic, nano-structures, electrodynamics and fluidics. Some authors also found many interesting new results by solving fractional order problems in psychiatry, social science and economics.
What are the reasons behind this increasing interest in fractional order operators? On one hand, the real order derivatives give a wider range of solutions, therefore it is possible to better fit the theoretical model with data collected from observations and experiments. On the other hand, it should be noticed that this generalization of differential operators is more suitable for dealing with nonlinear and complex problems. The major step forward in science and research, during the last century, was to handle nonlinear problems and their complexity, which is based on a large number of parameters. Nowadays, the most challenging goal that scholars face is to investigate such challenging problems and one possibility is offered by generalized operators such as the fractional ones.
Finally, the recent striking discoveries in the modern topics of fractional order operators on fractal sets should be briefly mentioned. This is a completely new field in which fractional operators are defined on fractals and more in general on some special set which are piecewise continuous, scale-dependent and self-similar. These fractional operators on fractal sets, e.g., the Cantor set, are opening new frontiers in research for the investigation of real word problems.
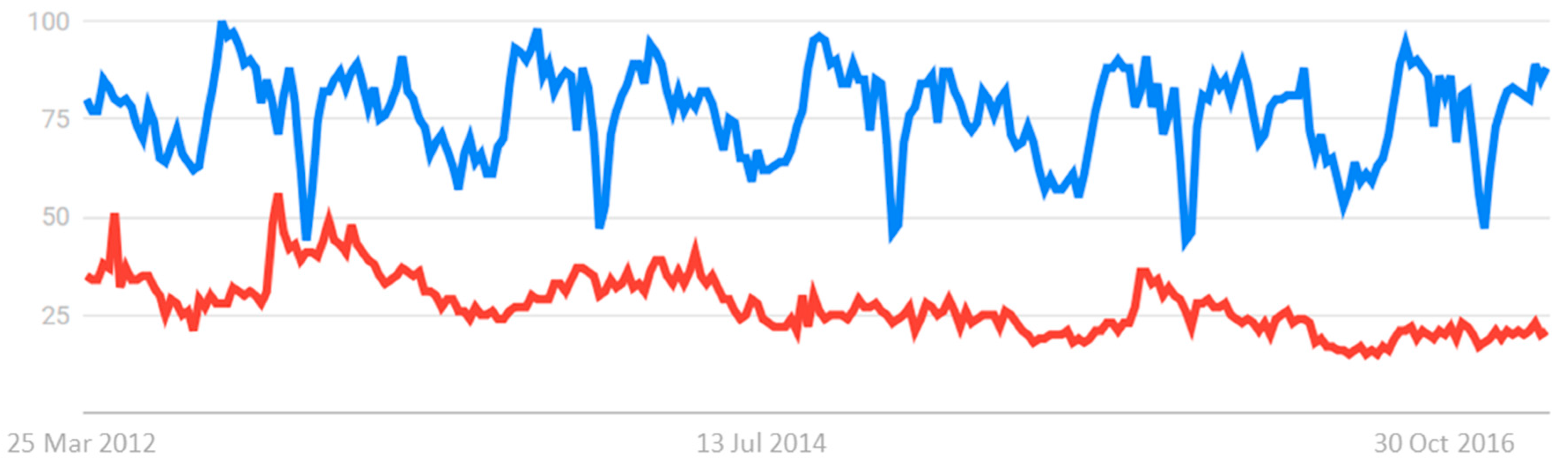
Since there is a huge bibliography on fractals and fractional calculus, in this editorial, I have intentionally not mentioned the main significant contributions given by these authors who are leading these fields. In some future review papers, these contributions will be reported and discussed in detail. I would only like to note the correlation between fractals and fractional calculus and the impact that these concepts have had on science and technology in the last 4 years (2012–2016). It can be seen, from
Figure 1, that by analysing the google queries, there has been a continuous high frequency of searches for the terms fractals and fractional, with respect to the highest values (100). This demonstrates the intensity of the interest in these two topics and in the influence that they have on modern knowledge.