QiGSAN: A Novel Probability-Informed Approach for Small Object Segmentation in the Case of Limited Image Datasets

Abstract

The paper presents a novel probability-informed approach to improving the accuracy of small object semantic segmentation in high-resolution imagery datasets with imbalanced classes and a limited volume of samples. Small objects imply having a small pixel footprint on the input image, for example, ships in the ocean. Informing in this context means using mathematical models to represent data in the layers of deep neural networks. Thus, the ensemble Quadtree-informed Graph Self-Attention Networks (QiGSANs) are proposed. New architectural blocks, informed by types of Markov random fields such as quadtrees, have been introduced to capture the interconnections between features in images at different spatial resolutions during the graph convolution of superpixel subregions. It has been analytically proven that quadtree-informed graph convolutional neural networks, a part of QiGSAN, tend to achieve faster loss reduction compared to convolutional architectures. This justifies the effectiveness of probability-informed modifications based on quadtrees. To empirically demonstrate the processing of real small data with imbalanced object classes using QiGSAN, two open datasets of synthetic aperture radar (SAR) imagery (up to $0.5$ m per pixel) are used: the High Resolution SAR Images Dataset (HRSID) and the SAR Ship Detection Dataset (SSDD). The results of QiGSAN are compared to those of the transformers SegFormer and LWGANet, which constitute a new state-of-the-art model for UAV (Unmanned Aerial Vehicles) and SAR image processing. They are also compared to convolutional neural networks and several ensemble implementations using other graph neural networks. QiGSAN significantly increases the $F_1$-score values by up to $63.93\%$, $48.57\%$, and $9.84\%$ compared to transformers, convolutional neural networks, and other ensemble architectures, respectively. QiGSAN outperformed the base segmentors with the mIOU (mean intersection-over-union) metric too: the highest increase was $35.79\%$. Therefore, our approach to knowledge extraction using mathematical models allows us to significantly improve modern computer vision techniques for imbalanced data.

1. Introduction

Semantic segmentation is a relevant approach used in various applied fields, such as autonomous driving [1], navigation [2], or Earth monitoring [3]. However, there is often a class imbalance in real data. One of the most significant examples is the segmentation of small or background objects in an image [4]. The number of elements in the training data for such objects is typically much lower than for other categories. This leads to greater intra-class variation than inter-class one, resulting in poor generalization of neural network (NN) architectures.

Modern large neural network architectures that deal with high-resolution images, such as visual transformers, demonstrate great performance in processing large datasets [5]. However, when the dataset is highly unbalanced, for instance, when some classes correspond to $1\%$ of all training examples, these NNs demonstrate lower performance. Various modifications to NN architecture, the training process, and augmentation techniques are still being investigated to improve the efficiency of handling imbalanced image datasets [6,7,8]. For imbalanced semantic segmentation, specific (usually weighted) loss functions such as weighted cross entropy, dual cross entropy, or focal loss and their modifications [8,9,10,11] can be used. Another approach consists of NN architecture modifications such as attention modules [12] or special hierarchical decoders [13,14,15,16], which are designed to capture the details of small objects. Finally, the features from another modalities [17] can be used to improve the segmentation accuracy.

However, such approaches often face difficulties when dealing with real-world problems, where the training datasets are limited [18,19,20,21,22]. For example, in the small data case, the amount of data available is often limited to 1000 or fewer elements. In this case, NNs tend to just remember small objects [23,24]. The decrease in training sample size and intra-class variance can lead to the overfitting. Therefore, more complex and deep NN architectures, even with custom loss functions, are less effective. A solution can be found in ensemble approaches and mathematical models.

This paper introduces a novel probability-informed approach to improving the accuracy of neural network processing for small datasets with imbalanced classes. Our methodology is based on the possibility of obtaining additional information in the case of a limited volume of data using their mathematical (probability) models [25]. It is inspired by the principles of physics-informed machine learning [26]. Previously, this approach was shown to be effective for the segmentation problems with a small receptive field ($32\times 32$ pixels) [27,28]. This paper extends the basic idea to high-resolution image processing.

The aim of this paper is to develop a novel ensemble graph convolution neural network (GCN) architecture, informed by the Markov random field model, namely the quadtrees [29], for the effective segmentation of small objects on high-resolution images with limited training data volumes. Therefore, Quadtree-informed Graph Self-Attention Network (QiGSAN) is proposed. It consists of novel quadtree-informed self-attention and compression blocks as well as graph convolutional layers to take into account the complex spatial and hierarchical interconnections between image pixels. Convolutional and transformer encoders are also tested in QiGSAN to extract image pixel features.

As an example of a real imbalanced segmentation problem, ship segmentation on high-resolution synthetic aperture radar (SAR) imagery is used. There are two imbalanced classes in this task: the target, which is the ship, and the background, which includes other surfaces. The target label can occupy only a few pixels or be barely distinguishable from noise. At the same time, real SAR image datasets are usually small, as the variability and uniqueness of the images makes them difficult to label [30,31], so they fit the definition of a small imbalanced dataset well.

The main contributions of the paper are as follows:

• A novel probability-informed ensemble architecture QiGSAN was developed to improve the accuracy of small object semantic segmentation in high-resolution imagery datasets with imbalanced classes and a limited volume of samples;
• New quadtree-informed architectural blocks have been introduced to capture the interconnections between features in images at different spatial resolutions during the graph convolution of superpixel subregions [32];
• The theorem concerning faster loss reduction in the quadtree-informed graph convolutional neural networks was proved;
• Using QiGSAN, the ship segmentation accuracy ($F_1$-score) on high resolution SAR images (HRSID [33] and SSDD [34] datasets) increased up to $63.93\%$ compared SegFormer [35] and LWGANet, a new state-of-the-art transformer for UAV (Unmanned Aerial Vehicles) and SAR image processing [36]. It also improves the results of non-informed convolutional architectures, such as ENet [37] and DeepLabV3 [38] (up to $48.57\%$ in $F_1$-score), and other ensemble implementations with the various graph NNs (up to $9.84\%$ in $F_1$-score).

The rest of the paper is organized as follows. Section 2 discusses known approaches to the construction of graph architectures and the division of images into superpixels for small sample learning cases. Section 3 presents details of our approach to small object segmentation based on QiGSAN architecture, including a proof of the theorem concerning faster loss reduction in the quadtree-informed graph convolutional neural networks. Section 4 is devoted to the results obtained by QiGSANs on the open datasets HRSID and SSDD. Section 5 presents a comprehensive ablation study. Section 6 summarizes the results achieved and discusses future research directions.

2. Related Works

In this section, we will briefly review some previous research on the subject area that is relevant to our research.

2.1. Small Data in Image Processing

Small datasets consist of a small number of observations. They are often used in practical data processing applications, including SAR objects segmentation. The high variability in the data, which is typical of high resolution images, and the difficulty in labeling SAR images limit the number of available images for training. Traditional machine learning approaches, such as modern transformer architectures or Faster R-CNN-based methods [39], demonstrate a weak generalization ability and a tendency towards overfitting when processing small datasets [19]. The most popular methods for improving the efficiency of small data processing are augmentation, regularization [40], and transfer learning [41]. However, in SAR image processing, these methods often face difficulties due to differences in the subject areas or the insufficient diversity in the augmented data [42]. Indeed, augmentations are constructed on a limited part of data, so they cannot reproduce the variability found in real data. Architectural modifications allowing for more efficient identification of the distinctive features of objects seem to be a promising approach. Such solutions may lie in finding the most important regions of an image for the correct identification of an object [20,43] or in methods for comparing global and local features of objects [44].

Small object processing relates to class imbalance problems. The core issue is the lack of data to distinguish between rare small objects and the background. Weighted loss functions [45] can be used for small objects. Modifications to the training process include range training data for segmentation [13]. Architecture modifications, such as the use of attention blocks and hierarchical encoder features [14], and small object activation branches [46] are also implemented.

2.2. Graph Neural Network Image Analysis

GCNs [47] are used for the analysis of data whose internal structure can be described by a graph. Modern graph architectures used for practical tasks are often modifications of graph neural networks with attention (GAT) [48] or simple GCN [49]. For example, GraphSAGE [50] differs from simple GCN only in that it aggregates node features using a predefined number of neighbours. There are also GCN modifications that implement the self-attention mechanisms. For example, they can be used for preprocessing concatenated node features [51,52] or to detect global node attributes [53].

Typically, graph processing architectures consist of the following parts: a feature encoder and a graph block that performs convolution using a two-dimensional grid. The grid represents pixel features at a single spatial resolution and does not consider their hierarchical properties. Methods that suggest using features at different resolutions are uncommon, and these features are not integrated into a single (trainable) structure like quadtrees. Therefore, implementing a quadtree into an NN architecture can significantly improve the efficiency of convolution on graphs. However, a quadtree has more nodes than a comparable grid graph, making it necessary to optimise it, particularly to process high resolution images.

Existing quadtree implementations are only used in specific problems, such as image tokenization [54], or the implementation of multi-scale attention [55,56]. In addition, convolutions rather than graphs are usually used to represent spatial relationships [57].

A well-known method for optimizing graph convolution is to reduce the number of nodes in the graph being processed from the total number of pixels in an image to a fixed number N. The structure of sub-areas may be irregular, when pixels are grouped according to their brightness properties [58]. It may also be regular if the superpixels have a predetermined size and shape.

The reduction in graph node numbers often leads to a decrease in the accuracy of data processing, which is similar to reducing the number of NN weights. In order to prevent this decrease in accuracy, especially in small sample learning, various modifications to GCNs have been proposed. Specifically, an effective method is related to different attention mechanisms, such as those based on the concatenation of feature vectors [48] or the dot product [53].

GCNs are also used for SAR image segmentation [59] or object detection [60]. High resolution images processed by GCNs are divided into superpixels, which are image regions consisting of spatially adjacent pixels with similar brightness properties. The division into superpixels with different sizes takes into account the similarity between neighbouring pixels. However, this requires time-intensive preprocessing of images using specific algorithms such as Bayesian adaptive superpixel segmentation [61]. Using superpixels of the same size does not require the graph to adapt to each new image. However, it does not take into account the similarities in the reflective properties of the pixels. A solution to this problem is to use a hierarchical graph that aggregates node information at various spatial resolutions.

2.3. Probability-Informed Neural Networks

Probability informing is used to solve a wide range of tasks related to analyzing data with stochastic properties. It was demonstrated in papers [62,63,64] that using probabilistic characteristics as additional NN features or constructing the NN architecture based on probability models (for example, deep Gaussian mixture one [25]) can improve the NN predictions for time-series analysis. Promising results were also obtained for SAR image analysis [28]. Probability informing can be used to estimate the uncertainty in NN predictions [65], reliability of engineering systems, and model risk functions using NN [66]. It can also be utilized to refine cost function estimates [67] or to improve the interpretability of spiking NN predictions [68]. In particular, these studies demonstrate that using probability models improves the accuracy of the processing with a limited number of training examples. This approach has previously been used to analyze turbulent plasma data [69,70] and information flows [71], but there are no published studies in the literature on SAR images based on these principles.

2.4. Summary

This paper develops a methodology for using GCNs with attention to process small objects in datasets of high-resolution images with a limited volume of training samples. A probability-informed approach has been proposed to improve GCN’s accuracy. Division into regular superpixels organized into a quadtree structure has been introduced in order to improve the computational efficiency of NNs, while taking account of the similarity between neighbouring pixels. Our model requires less training data and computational resources than other types of neural networks, which makes it applicable to small sample learning problems. Therefore, this approach can also be applied in cases where commonly used NN models do not produce good results.

3. Methodology

This section is devoted to the mathematical formulation of the research problem and a description of our methodology for solving it.

3.1. Problem Statement

Let $\mathbb{X}={\left\{X^k\right\}}_{k=1,\dots ,K}$ be a set of images that needs to be segmented. That is, for each image, we need to determine for each pixel $X_{ij}^k$, $i=1,\dots ,H_X$, $j=1,\dots ,W_X$, where $H_X,W_X$ are height and width of images, the most probable class label $y_{ij}^k$ from two variants (t denotes the target or background class number, the target class corresponds to index 0):

$$y_{ij}^s=\underset{t=0,\dots ,1}{arg\; max}\mathbb{P}(X_{ij}^k\mid t).$$

(1)

Let $F(·)$ be a function of some neural encoder, and let the set $\mathbb{X}$ correspond to small data, that is, $K\sim 1000$. The research problem is to improve the accuracy of the small target segmentation obtained by $F(·)$ and avoid overfitting.

The suggested solution is based the construction of an ensemble of $F(·)$ with the another neural network $G(·)$ to model the spatial connections between pixels using a quadtree adjacency matrix A (that is, a quadtree-informed model):

$$G:{\mathbb{R}}^{ch+2}\times A\to {\mathbb{R}}^2,$$

(2)

where $ch$ is the number of image channels. $G(·)$ takes a vector $X_{cat}^k=(F\left(X^k\right),X^k)\in {\mathbb{R}}^{ch+2}$ as input data, where $F\left(X^k\right)\in {\mathbb{R}}^2$ (there are two classes: target and background). $G(·)$ has to improve the segmentation of the target class with respect to the probability of the correct class label choosing, as follows:

$$\mathbb{P}(G{(X^k,F\left(X^k\right),A)}_0=Y_0^k)⩾\mathbb{P}(F{\left(X^k\right)}_0=Y_0^k),$$

(3)

where $Y^k$ is the real class label for $X^k$ pixels, and index 0 corresponds to small objects.

3.2. Quadtree-Informed Graph Self-Attention Networks

The section presents a methodology for SAR image segmentation using QiGSAN. Figure 1 presents the corresponding NN architecture.

This is an ensemble neural network consisting of a pre-trained encoder $F(·)$, which can be implemented by a convolutional or transformer network, and a quadtree-informed GCN $G(·)$. $F(·)$ and $G(·)$ are trained separately. A graph self-attention mechanism is used in $G(·)$ that is based on the dot product. This architecture consists of 5 blocks. Quadtree-informed stages, see blocks “2” and “5” on Figure 1, are placed within the dashed borders.

3.3. Pre-Processing of Image Features by Convolutional Layers

Image features obtained from the output and preceding n-channel layers of the $F(·)$ are used as additional input data to the graph neural network $G(·)$, which takes the composition of the source image and the encoder features as inputs. First, these features are consistently processed in the first architectural block by three two-dimensional convolutional layers $c_{1-3}(·)$, with a kernel size $3\times 3$, and a GeLU (Gaussian Error Linear Units) activation function [72,73,74]. In the first and second layer, the number of output channels increases by two times compared to input ones. In the third layer, it decreases to one. Convolutional layers compress the information about the pixel features before dividing the image into superpixels and creating the quadtree.

3.4. Superpixels

Before performing the graph convolution operation, the outputs of the three convolutional layers and the constructed quadtree layers on their basis ${\left\{X_{Q_i}^k\right\}}_{Q_i=1,\dots ,h}$ (see Section 3.5) are divided into superpixels of size $M\times M$, where M is a hyperparameter.

In the block “3” (see Figure 1), pixels from different quadtree layers with sizes $H_X^{Q_i}\times W_X^{Q_i}$, $Q_i=1,\dots ,h$ are concatenated to form a vector ${\mathbf{x}}_{\mathbf{Q}}$ and then combined to create a superpixel vector ${\mathbf{x}}_{\mathbf{Q}}^{\left(\mathbf{sp}\right)}$ in the $\mathcal{C}(·)$ procedure, which is equivalent to the PyTorch unfold operation that creates a vector of vectors of image segments with size $M\times M$:

$$\mathcal{C}:{\mathbb{R}}^{H_X^{Q_i}\times W_X^{Q_i}}\to {\mathbb{R}}^{{\displaystyle \frac{H_X^{Q_i}·W_X^{Q_i}}{M^2}}\times M^{*}},$$

(4)

where $M^{*}=M^2$ is the size of the pixel features in a superpixel. The superpixel vector is obtained by applying $C(·)$ to each of the h of quadtree layers of ${\mathbf{x}}_{\mathbf{Q}}$. Obtained vector ${\mathbf{x}}_{\mathbf{Q}}^{\left(\mathbf{sp}\right)}$ is a quadtree node vector that is used in the graph convolution operation.

3.5. Quadtree Informing

The quadtree informing of QiGSAN is implemented in the second and fifth blocks of $G(·)$ called “Quadtree layers compression” and “Quadtree structure forming” (see Figure 1), which precede superpixel formation.

A quadtree of height h is a hierarchical structure, where elements are organized into $h>1$ layers, with each element on the $k-1$-th layer being connected to four elements (children) on the $k^{th}$ layer and no more than one of the elements on the $k-2$-th layer. In the $S_k$ layer, elements are often organized as $\left\{s_{i,j}^k\right\}$, $i,j=1,\dots ,L_k$ and $L_k=2·L_{k-1}$. Figure 2 presents an example of a quadtree with height $h=2$ constructed from an image of size $L\times L$, which is divided into superpixels. A source image is placed in the $h^{th}$ layer of the quadtree. Features of other quadtree layers are usually [75] constructed with average pooling with a kernel size of $2^{h-i}$, $i=1,\dots ,h-1$. The input of the “Quadtree structure forming” block is processed through $h-1$ pooling layers, and these results are concatenated to form a vector of quadtree layers divided into superpixels.

The neighboring elements of the $S_k$ layer are also connected to each other. Then, the quadtree becomes a spatial-hierarchical one [29]. An approach to establishing interconnections within the layer is using a two-dimensional grid, as shown in Figure 3. Such a graph structure does not have hierarchical interconnections and its elements, $\left\{s_{i,j}^k\right\}$, are connected to their nearest neighbors horizontally, vertically, and along diagonals. This quadtree model has the Markov property [29] because the state of an element depends only on its nearest neighbors.

The modern graph convolutional neural networks for image analysis use two-dimensional grids and their variations as image representations. Let us demonstrate that that the use of quadtrees improves the training of neural networks. Let $X\in {\mathbb{R}}^{N\times N}$, $X\in \mathbb{X}$, be a processed image. Denote the pixels of X as $X_{i,j}$, $i,j=1,\dots ,N$ and the vector of these pixels as $\mathbf{x}\in {\mathbb{R}}^{N^2\times 1}$. The elements of the vector $\mathbf{x}$ are obtained from X by the rule $x_{i·N+j}=X_{i,j}$. Let ${\mathbf{x}}^{\left(sp\right)}\in {\mathbb{R}}^{{\displaystyle \frac{N^2}{M^2}}\times M^2}$ be a vector of superpixels of size M, obtained from the image X. Denote ${\mathbf{x}}_Q$ as a vector that contains all the elements in a quadtree with h layers. Vector ${\mathbf{x}}_Q$ is constructed in the block Quadtree structure forming, see Figure 1. Features for the $h-1$ quadtree layers are constructed from the output of the previous convolutional layer $c_{1-3}(concat(X,F\left(X\right))$ using several average pooling with a kernel of size $2^{h-i}$, $i=1,\dots ,h-1$. Vector ${\mathbf{x}}_Q^{\left(sp\right)}$ is the quadtree one divided into superpixels: ${\mathbf{x}}_Q^{\left(sp\right)}=C\left({\mathbf{x}}_Q\right)$, see Section 3.4.

Linear graph convolution network (GCN) $G(·)$ can be defined as a network of the following form [76]:

$$G\left({\mathbf{x}}^{\left(sp\right)}\right)=A·{\mathbf{x}}^{\left(sp\right)}·B,$$

(5)

where $A\in {\mathbb{R}}^{{\displaystyle \frac{N^2}{M^2}}\times {\displaystyle \frac{N^2}{M^2}}}$ is an adjacency matrix, and B is a linear transformation matrix, for which we propose that ${\mathbf{x}}^{\left(sp\right)}·B\in {\mathbb{R}}^{{\displaystyle \frac{N^2}{M^2}}\times M^2}$. Let $G_{skip}(·)$ be the linear GCN with the skip connections [76], that is

$$G_{skip}\left({\mathbf{x}}^{\left(sp\right)}\right)=\sum _{l=0}^H{W}_{\left(l\right)}·X_{\left(l\right)},$$

(6)

where $X_{\left(l\right)}=A·B_{\left(l\right)}·X_{(l-1)}$, $X_{\left(0\right)}={\mathbf{x}}^{\left(sp\right)}$, and H is the number of graph convolution layers. According to the Formula (6), when $H=1$, we have $G_{skip}\left({\mathbf{x}}^{\left(sp\right)}\right)=W_{\left(0\right)}·{\mathbf{x}}^{\left(sp\right)}+W_{\left(1\right)}·G\left({\mathbf{x}}^{\left(sp\right)}\right)$.

Theorem 1.

Let $G(·)$ and $G_Q(·)$ be one-layer linear GCNs. If the graph convolution of $G(·)$ is a two-dimensional grid and the graph convolution of $G_Q(·)$ is a spatial-hierarchical quadtree with h layers, then

$${\displaystyle \frac{d}{dt}}\left(L_t(G\left({\mathbf{x}}^{\left(sp\right)}\right),Y)\right)<{\displaystyle \frac{d}{dt}}\left(L_t(G_Q\left({\mathbf{x}}_Q^{\left(sp\right)}\right),Y)\right),$$

(7)

where $L_t(·,y)$ is an arbitrary differentiable loss function, Y are the labels, and t is the number of training epoch. This implies that the loss function decreases faster in the quadtree-informed GCNs.

Proof. 

It is well known [76] that

$${\displaystyle \frac{d}{dt}}\left(L_t(G(·),y)\right)<{\displaystyle \frac{d}{dt}}\left(L_t(G_{skip}(·),y)\right)$$

(8)

for an arbitrary differentiable loss function $L_t(·,y)$ in the case of linear models. So, to prove theorem’s claim, it suffices to show that the $G_Q(·)$ is a NN with skip connections.

For a vector ${\mathbf{x}}_Q$, constructed using average pooling, the following representation holds:

$${\mathbf{x}}_Q=U·\mathbf{x},$$

(9)

where U is the block matrix composed from h blocks ${\left(U_{2^{h-1}},\dots ,U_2,I\right)}^T$, I is the identity matrix, and $U_p\in {\mathbb{R}}^{{\displaystyle \frac{N^2}{p^2}}\times N^2}$ is a matrix, in which rows contain p sequences of units of the length p, $p=1,\dots ,h-1$, separated by $N-1$ zeros. $U_p$ is a pooling matrix, and p represents the size of a pooling area. Multiplication at $U_p$ means that each element in the result vector is obtained as the mean of the elements in the $p\times p$ field from the image X. When X is represented as a vector $\mathbf{x}$, $p\times p$, field is placed in $\mathbf{x}$ row by row with each row consisting of p units and the end and beginning of each row separated by $N-1$ zeros. All elements after the final row are zeros. One can calculate directly that $av{g}_p\left(x\right)=avg\_pool(x,2^p\times 2^p)$ is equal to the $U_p·x$. Therefore, ${\mathbf{x}}_Q=\left(avg\left(x\right),x\right)$ where $avg\left(x\right)=\left(av{g}_{h-1}\left(x\right)\dots ,av{g}_2\left(x\right)\right)$ can be obtained by multiplying the block matrix U and the vector x.

Next, denote ${\mathbf{x}}_{flat}$ as the vector ${\mathbf{x}}^{\left(sp\right)}$ resized to $N^2\times 1$ , preserving the ordering of pixels in the superpixel structure. The difference between the image X and vectors ${\mathbf{x}}_{flat}$, $\mathbf{x}$, and ${\mathbf{x}}^{\left(sp\right)}$ is shown in Figure 4.

Figure 4 shows that each consecutive $M^2$ element of ${\mathbf{x}}_{flat}$ belongs to a single image superpixel. The unfolding operation is carried out on the vector ${\mathbf{x}}^{\left(sp\right)}$ from left to right and from top to down. Then, by performing direct multiplication, one can verify that ${\mathbf{x}}_{flat}$ can be obtained by matrix multiplication from $\mathbf{x}$: ${\mathbf{x}}_{flat}=D·x$ where $D={\left(D_1,\dots ,D_{{\displaystyle \frac{N^2}{M^2}}}\right)}^T$ and $D_i\in {\mathbb{R}}^{M^2\times N^2}$ and have the following form:

$$D_i=\left(\begin{array}{c}{0}_{M\times M·i},I_{M\times M},0_{M\times (N^2-M·(i+1))}\\ 0_{M\times (N+M·i)},I_{M\times M},0_{M\times (N^2-M·(i+1)-N)}\\ \dots \\ 0_{M\times (N+i)·M},I_{M\times M},0_{M\times N^2-(N+i+1)·M}\end{array}\right),$$

(10)

Matrix D reorders the elements of $\mathbf{x}$, forming the flattened vector of superpixels ${\mathbf{x}}^{\left(sp\right)}$. The multiplication $D_i·x$ forms the vector of a length $M^2$ of pixels from the $i^{th}$ superpixel. This is constructed using the fact that superpixel elements are placed into M consecutive rows, with each element located one after another in the vector $\mathbf{x}$. $D_i$ is a block diagonal matrix containing M identical matrices $I_{M\times M}$, shifted left by $N·j+i·M$ where j is a number of identical matrix in $D_i$. The jth identical matrix extracts the j-th row of the i-th superpixel, preserving the order of the elements in the resulting vector. The shift of the next identical matrix in $D_i$ is equal to the shift of the $j+1$ superpixel row in the vector $\mathbf{x}$.

The vector ${\mathbf{x}}_{flat}$ was defined to show that the vector of superpixels ${\mathbf{x}}^{\left(sp\right)}$ can be represented as a linear transformation of the vector $\mathbf{x}$, as follows:

$${\mathbf{x}}^{\left(sp\right)}=\sum _{i=1}^{{\displaystyle \frac{N^2}{M^2}}}\sum _{j=1}^{M^2}{\left(e_i^1\right)}^T·e_{(i-1)·M^2+j}^2·{\mathbf{x}}_{flat}·e_j^{\left(3\right)},$$

(11)

where $e_i^k$, $k=1,\dots ,3$ are the basis vectors, and $e_i^1\in {\mathbb{R}}^{1\times {\displaystyle \frac{N^2}{M^2}}}$, $e_i^2\in {\mathbb{R}}^{1\times N^2}$ and $e_i^3\in {\mathbb{R}}^{1\times M^2}$.

For the vector ${\mathbf{x}}^{\left(sp\right)}$ and the matrices $A=\left\{a_{kl}\right\}\in {\mathbb{R}}^{{\displaystyle \frac{N^2}{M^2}}\times {\displaystyle \frac{N^2}{M^2}}},B=\left\{b_{kl}\right\}\in {\mathbb{R}}^{M^2\times M^2}$, the following equations hold:

$$\begin{array}{c}A·{\mathbf{x}}^{\left(sp\right)}·B=\sum _{i=1}^{{\displaystyle \frac{N^2}{M^2}}}\sum _{j=1}^{M^2}{\left(e_i^1\right)}^T·e_{(i-1)·M^2+j}^2·A^{flat}{B}^{flat}·D·\mathbf{x}·e_j^3,\end{array}$$

(12)

where $A^{flat}=\left\{A_k^{flat}\right\},B^{flat}=\left\{B_k^{flat}\right\},B_k^{flat}\in {\mathbb{R}}^{{\displaystyle \frac{N^2}{M^2}}\times N^2},A_k^{flat}\in {\mathbb{R}}^{{\displaystyle \frac{N^2}{M^2}}\times N^2}$, $k=1,\dots ,J$, and $J={\displaystyle \frac{N^2}{M^2}}$:

$$\begin{array}{c}{A}_k^{flat}=\left(\begin{array}{c}{a}_{k1},\underset{M^2-1}{\underbrace{0..0}},a_{k2},..,a_{kJ},0..0\\ 0,a_{k1},\underset{M^2-1}{\underbrace{0..0}},a_{k2},..,a_{kJ},0..0\\ \dots \\ \underset{M^2-1}{\underbrace{0..0}},a_{k1},\underset{M^2-1}{\underbrace{0..0}},a_{k2},\dots a_{kJ}\end{array}\right),B_k^{flat}=\left(\begin{array}{c}\underset{k·M^2}{\underbrace{0..0}},b_{11}..b_{M1},b_{M+1,1}..b_{M^2,1},..0\\ \dots \\ \underset{k·M^2}{\underbrace{0..0}},b_{1M}..b_{MM},b_{M+1,M}..b_{M^2,M},..0\end{array}\right).\end{array}$$

(13)

Multiplication $A_k^{flat}·D·\mathbf{x}$ presents the results of multiplying the kth row of matrix A and ${\mathbf{x}}^{\left(sp\right)}$. The offsets $M^2-1$ in $A_k^{flat}$ are used to perform the multiplication of the kth row with the column containing the elements in the same positions from different superpixels. Multiplication $B_k^{flat}·D·\mathbf{x}$ presents the results of multiplying each kth superpixel elements and the matrix B. Each row of $B_k^{flat}$ contains the elements from each column of B. Direct multiplication leads to the Equation (12), which shows that linear modifications of ${\mathbf{x}}^{\left(sp\right)}$ can be represented by a linear transformation of $\mathbf{x}$.

Let A be the adjacency matrix for a two-dimensional grid graph convolution and $A_Q$ be the adjacency matrix of the spatial-hierarchical quadtree. A describes the spatial connections between the elements in the h-layers quadtree, and $A_Q$ can be represented as follows: $A_Q=A_q+\left(\begin{array}{cc}0& 0\\ 0& A\end{array}\right)$. For the vector of quadtree’s features divided into superpixels ${\mathbf{x}}_Q^{\left(sp\right)}$, Formula (9) implies that ${\mathbf{x}}_Q^{\left(sp\right)}=U·{\mathbf{x}}^{\left(sp\right)}$. Then, the $G_Q\left({\mathbf{x}}_Q^{\left(sp\right)}\right)$ can be represented as follows:

$$\begin{array}{c}{G}_Q\left({\mathbf{x}}_Q^{\left(sp\right)}\right)=A_Q·{\mathbf{x}}_Q^{\left(sp\right)}·B=A_q·{\mathbf{x}}_Q^{\left(sp\right)}·B+\left(\begin{array}{cc}0& 0\\ 0& A\end{array}\right)·{\mathbf{x}}_Q^{\left(sp\right)}·B.\end{array}$$

(14)

In this formula

$$\left(\begin{array}{cc}0& 0\\ 0& A\end{array}\right)·{\mathbf{x}}_Q^{\left(sp\right)}=\left(\begin{array}{cc}0& 0\\ 0& A\end{array}\right)·\left(\begin{array}{c}0\\ {\mathbf{x}}^{\left(sp\right)}\end{array}\right)=\left(\begin{array}{c}0\\ I_{{\displaystyle \frac{N^2}{M^2}}\times {\displaystyle \frac{N^2}{M^2}}}\end{array}\right)·A·{\mathbf{x}}^{\left(sp\right)}.$$

(15)

Moreover, $A_q·{\mathbf{x}}_Q^{\left(sp\right)}·B=A_q·U·{\mathbf{x}}^{\left(sp\right)}·B=A_{qU}·{\mathbf{x}}^{\left(sp\right)}·B$. Then

$$\begin{array}{c}{G}_Q\left({\mathbf{x}}_Q^{\left(sp\right)}\right)=(A_{qU}·{\mathbf{x}}^{\left(sp\right)}+\left(\begin{array}{c}0\\ I_{{\displaystyle \frac{N^2}{M^2}}\times {\displaystyle \frac{N^2}{M^2}}}\end{array}\right)·A·{\mathbf{x}}^{\left(sp\right)})·B=\\ =A_{qU}·{\mathbf{x}}^{\left(sp\right)}·B+\left(\begin{array}{c}0\\ I_{{\displaystyle \frac{N^2}{M^2}}\times {\displaystyle \frac{N^2}{M^2}}}\end{array}\right)·G\left({\mathbf{x}}^{\left(sp\right)}\right).\end{array}$$

(16)

According to the Formula (6) for the case of $H=1$ and Formula (12), which proposes that $A_{qU}·{\mathbf{x}}^{\left(sp\right)}·B$ can be denoted by $W_{\left(0\right)}·{\mathbf{x}}^{\left(sp\right)}$), $G_Q(·)$ is a graph convolutional network with a skip connection and an adjacency matrix A.  □

The theorem presented above demonstrates that using quadtrees to describe spatial interconnections between pixels improves the training process of graph neural networks. This is seen as a theoretical justification for the results of testing QiGSAN and comparing it to other types of graph.

In the block “Quadtree layers compression”, the graph convolution output is divided into h subvectors (Figure 1 presents the case where $h=5$), where each of them corresponds to one of the quadtree layers. An image is formed from each subvector. Starting with $k=1$, each $k^{th}$ layer is scaled by bilinear interpolation to match the size of of $k+1$-th layer and then concatenated with it. The resulting multi-channel image is processed using two-dimensional convolutions. This method allows you to consistently take into account the influence of elements from the upper layers of the quadtree on the final image segmentation result.

3.6. Graph Self-Attention Operation

The graph convolution operation in block “4” (see Figure 1) is performed on a self-attention graph layer (the corresponding NN can be called “GSAN”), incorporating the self-attention mechanism into the graph network [53]. We use a graph self-attention based on the dot product (see, for example, [53]) instead of a standard GAT’s variant, which is based on concatenation (see [77]):

$${\mathbf{x}}_i^{(att-sp)}=\sum _{j=1}^{N}softmax(A·LeakyReLU(a^T·{\mathbf{x}}_i^{\left(sp\right)}·{\mathbf{x}}_j^{\left(sp\right)}))·{\mathbf{x}}_j^{\left(sp\right)}·W.$$

(17)

where $X_i$ is a feature vector for the $i^{th}$ node, $X_i^{*}$ is a vector of updated node features, A is the adjacency matrix, and W and a are the trainable weights. The use of GSAN allows us for a better understanding of the relationships between the features of a quadtree.

4. Experiments

This section contains details about testing QiGSAN using open SAR datasets.

4.1. Datasets

QiGSAN is tested on SAR images of ships from HRSID [33] and SSDD [34] datasets. To simulate a lack of training data for HRSID, only images from the testing part are used.

Table 1. Characteristics of datasets.

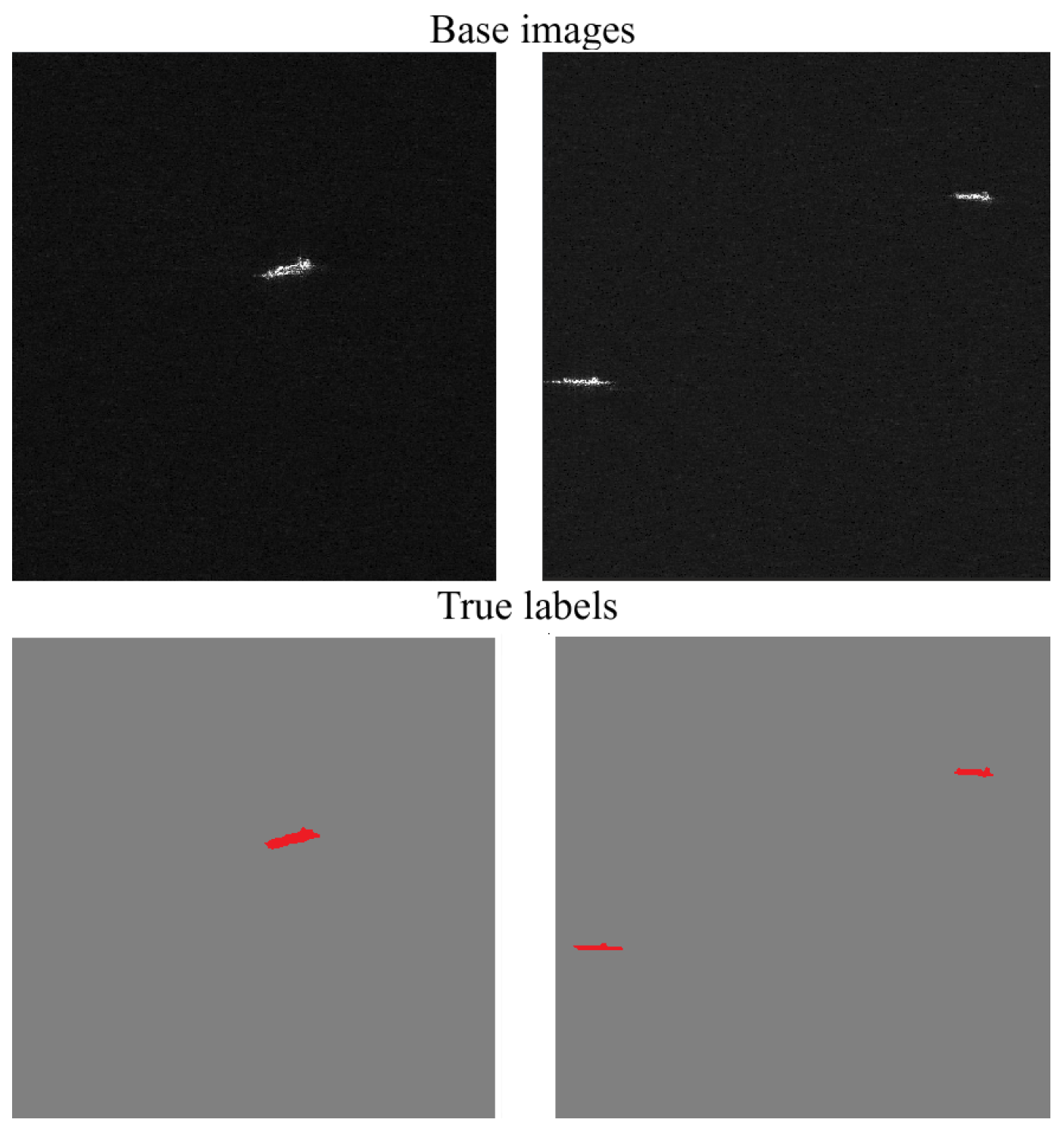
Dataset	Number of Images	Image Size	Resolution (m)	Small Objects	Middle Objects	Large Objects
SSDD	1160	190–668	1–10	1529	935	76
HRSID (test)	1962	800	0.5–3	5176	619	127

presents descriptions of the datasets, including the sizes and resolutions of the images processed as well as the size of objects within them. Following a structure proposed by the creators of HRSID [33], the objects were split into three categories: small (the object area is less than $32\times 32$ pixels), middle (less than $64\times 64$), and large (greater than $64\times 64$) objects. Examples of the segmented images are presented in Figure 5 and Figure 6.

4.2. Training, Metrics, and Hyperparameters

To estimate the efficiency of the proposed approach, a five-fold cross-validation was conducted. Overall, $70\%$ of the four folds were used for training, and the last $30\%$ was used as the validation set. So, the training sample volume is about $56\%$ of the full data. All source images were processed using patches of size $256\times 256$ pixels.

An augmentation used for training increases the diversity of the dataset. Each image patch is rotated at a random angle (from 0 to 180 degrees) and is shifted by a random value less than 128 pixels. In the case of the HRSID dataset, objects are mostly small. Patches containing ships were enhanced by applying the Gaussian blur transform [78] to them.

The $F_1$-score calculated using the Precision and Recall values is a metric for estimating segmentation accuracy, as follows:

$$\begin{array}{c}{F}_1={\displaystyle \frac{2·Recall·Precision}{Recall+Precision}},Precision={\displaystyle \frac{TP}{TP+FP}},Recall={\displaystyle \frac{TP}{TP+FN}},\end{array}$$

(18)

where True Positive (TP) are pixels, correctly classified as the chosen class, False Positive (FP) are pixels, incorrectly determined to be the chosen class, and False Negative (FN) are pixels of the chosen class that are classified incorrectly.

The batch size is 32. Adam [79] is used as an optimizer. This demonstrates better convergence compared to AdamW [80] and RMSProp [81]. The cross-entropy $H(p,q)$ is the loss function, as follows:

$$H(p,q)=D_{KL}(p\mid q)-\sum _{x}p\left(x\right)ln\left(q\left(x\right)\right),$$

(19)

where $p\left(x\right)$ and $q\left(x\right)$ are the target and estimated distributions, and $D_{KL}(p\mid q)$ is a Kullback–Leibler divergence [82].

The description of the hyperparameters and their possible values are presented in

Table 2. The description and range of change for the NNs hyperparameters.

Hyperparameter	Description	Values
Encoder	Architecture of the basic segmenter	ENet, Fully-Conv. Network (FCN) based on ResNet50 [83], DeepLabV3 (DLv3), SegFormer, LWGANet
Pre-train	Pre-trained weights for base networks	None; PyTorch’s weights for DeepLabV3 and FCN; Imagenet, ADE20K
Epochs	Number of training epochs of base segmenter	100–300
lr_decay	Learning rate decay	None; 0.5; 0.8
h	Quadtree height	4; 5
M	Superpixel size	4; 8; 16

.

For graph network $G(·)$ processing, all images are divided into superpixels. The best results for both datasets were obtained when the superpixel size was $8\times 8$ ($M=8$) and the quadtree height was $h=5$. Most HRSID and SSDD objects are very small (less than $32\times 32$ pixels), and using larger superpixels results in losing object details. In addition, using smaller ones increases computational complexity and introduces noise distortion.

4.3. Variants of the $G(·)$ Network

QiGSAN is compared with several graph architectures that can be used as alternatives to $G(·)$ although they are all based on the same encoders (ENet, FCN, DeepLabV3, SegFormer, and LWGANet). These networks form two groups: quadtree-informed networks and NNs (see Figure 7). The acronyms for these architectures also depend on the implementation of graph block.

Quadtree-informed architectures (see the orange dashed block at the bottom left corner of Figure 7) are similar to QiGSAN (see Figure 1), except for the graph block:

• QiGSAN uses self-attention graph layers;
• GCN-QT and GAT-QT are based on vanilla GCN and GAT, respectively.

The NNs from the second group use a two-dimensional grid graph for image processing. These networks do not process the multi-scale features from quadtree layers. So, these architectures consist of only blocks “1”, “3”, and “4” (see Figure 1). Uninformed alternatives of QiGSAN are called GCN, GSAN, and GAT by the acronyms of the chosen layer in the graph block.

4.4. Main Results on SAR Images

This section compares the results of QiGSAN with those of NNs using alternative implementations of $G(·)$, as well as various convolutional and transformer architectures. Some of these, such as LWGANet and DeepLabV3 and U-Net++ with across feature map attention (AFMA) [14], were designed to improve the accuracy of small object recognition.

Table 3. Mean and median Recall, Precision, and $F_1$-score values ($\times 100\%$) for 5-fold HRSID and SSDD cross-validation. The best metric values for dataset are highlighted in bold.

NN		HRSID			SSDD
	Recall	Precision	${\mathit{F}}_{\mathbf{1}}$-Score	Recall	Precision	${\mathit{F}}_{\mathbf{1}}$-Score
ENet	79.70 ± 10.02 (82.12)	68.87 ± 10.46 (70.87)	73.77 ± 9.59 (77.74)	74.54 ± 7.45 (75.02)	23.51 ± 18.66 (17.96)	33.04 ± 19.4 (29.28)
DeepLabV3	74.68 ± 15.25 (80.1)	62.84 ± 5.65 (62.75)	60.45 ± 18.67 (69.97)	66.93 ± 11.68 (68.72)	52.76 ± 5.26 (53.58)	58.35 ± 4.47 (57.81)
FCN	77.82 ± 8.25 (81.06)	69.55 ± 6.83 (66.99)	59.87 ± 32.15 (74.13)	80.54 ± 4.15 (80.55)	12.70 ± 3.48 (12.71)	21.87 ± 5.35 (21.86)
SegFormer	73.98 ± 12.84 (78.56)	76.50 ± 20.42 (85.85)	74.98 ± 16.59 (82.61)	57.22 ± 26.57 (68.68)	38.15 ± 8.43 (39.83)	44.64 ± 16.05 (50.36)
LWGANet	78.74 ± 12.35 (80.74)	69.28 ± 16.14 (73.36)	73.36 ± 13.58 (78.34)	72.72 ± 9.39 (74.46)	10.41 ± 2.43 (9.94)	17.68 ± 3.29 (16.82)
Small object-oriented models
AFMA DeepLabV3	86.02 ± 11.42 (89.33)	51.61 ± 15.19 (55.06)	64.05 ± 14.92 (69.14)	72.85 ± 8.87 (73.01)	16.48 ± 5.08 (16.48)	26.47 ± 6.49 (27.22)
AFMA U-Net++	88.72 ± 8.39 (91.51)	47.56 ± 9.47 (51.54)	62.06 ± 10.43 (66.12)	63.37 ± 11.59 (64.22)	33.23 ± 11.42 (31.19)	40.04 ± 6.31 (39.29)
Ensembles specified by type of the $G(·)$ network (on the left column)
GCN	73.89 ± 11.72 (76.72)	74.50 ± 8.39 (75.79)	73.84 ± 9.56 (76.92)	74.22 ± 4.64 (72.93)	78.14 ± 3.21 (79.28)	76.09 ± 3.48 (75.55)
GAT	33.68 ± 29.03 (34.44)	54.17 ± 39.36 (65.43)	68.08 ± 9.02 (71.54)	72.41 ± 5.64 (71.62)	78.48 ± 9.99 (80.03)	74.87 ± 4.01 (76.58)
GSAN	74.77 ± 16.32 (80.1)	67.03 ± 8.18 (65.79)	69.38 ± 13.55 (72.22)	81.87 ± 2.21 (82.11)	75.95 ± 4.97 (76.74)	78.71 ± 2.36 (78.38)
GCN-QT	68.58 ± 13.36 (74.12)	74.78 ± 18.42 (82.91)	75.27 ± 10.00 (78.72)	78.01 ± 6.46 (78.92)	79.66 ± 5.67 (80.98)	78.64 ± 4.27 (77.98)
GAT-QT	72.57 ± 18.00 (78.38)	75.95 ± 20.98 (86.11)	76.53 ± 10.86 (80.36)	78.14 ± 4.42 (77.92)	82.52 ± 4.21 (83.89)	80.46 ± 3.78 (80.27)
QiGSAN	73.44 ± 12.71 (77.90)	77.84 ± 21.31 (87.55)	78.60 ± 11.38 (82.87)	78.27 ± 4.12 (78.72)	84.79 ± 4.59 (86.29)	81.61 ± 3.6 (81.76)

presents the best Recall, Precision, and $F_1$-score values for ship segmentation accuracy obtained in five-fold cross-validation on HRSID and SSDD datasets (the best metric values for each dataset are highlighted in bold). It contains the results of convolutional NNs (ENet, DeepLabV3 and FCN), transformers (SegFormer, LWGANet), and proposed graph ensemble architecture with different implementations of the $G(·)$ network, such as GCN-QT, QiGSAN, GAT-QT, GCN, GSAN, and GAT. A more detailed analysis of the ensemble results, including the accuracy estimates obtained for each encoder, is provided in Section 5.

QiGSAN improves the accuracy of ship segmentation, compared to the results of all tested configurations. The increase in the mean $F_1$ values is $0.33$–$63.93\%$ compared to the transformer results ($0.33$–$36.97\%$ for the best ones). For the convolutional NNs, the mean increase in $F_1$ is $9.91$–$48.57\%$ ($9.91$–$23.81\%$ for the best ones).

QiGSAN achieves the highest accuracy results among all ensemble modifications. The mean $F_1$ increase for informed (GCN-QT and GAT-QT) networks is $1.15$–$4.45\%$, whereas for non-informed networks, it is $2.95$–$9.84\%$. QiGSAN also outperformed AFMA DeepLabV3, AFMA U-Net++, and LWGANet with an increase in $F_1$-score of $5.24\%$ to $63.93\%$.

QiGSAN achieves the best Precision values for both datasets. The increase is 1.34–70.38%, compared to the baseline convolution networks and transformers. According to Table 3, QiGSAN’s Recall value is often lower than that of other networks, but this difference is offset by the significant increase in precision, resulting in an increase in $F1$-score and improved image segmentation quality. Examples of HRSID and SSDD image segmentation are shown in Figure 8 and Figure 9.

The results obtained by QiGSAN and the base segmentors (FCN, ENet, SegFormer, LWGANet, and DeepLabV3) were also compared using the mIoU (mean Intersection-over-Union) metric. For HRSID, the QiGSAN’s mIoU was $82.76\%$, while the mIoUs of the base segmentor models ranged from $73.66\%$ to $80.87\%$. This represents an increase of 1.88–9.09%. For SSDD, QiGSAN had an mIoU score of $83.94\%$, and the mIoUs of the other models ranged from $48.14\%$ to $66.85\%$. This represents a range of increases from $17.08\%$ to $35.79\%$.

5. Ablation Study

Within the ablation study, several issues related to the influence of architectural elements on results are considered.

5.1. HRSID

The estimations of the ship segmentation accuracy obtained in five-fold cross-validation on HRSID images are presented in

Table 4. Mean and Median $F_1$-score values ($\times 100\%$) for five-fold HRSID cross-validation. The best metric values for each $F(·)$ encoder are highlighted in bold.

Encoder $\mathit{F}(·)$	VanillaValues	Graph NN $\mathit{G}(·)$
		GCN-QT	QiGSAN	GAT-QT	GCN	GSAN	GAT
ENet	73.77 ± 9.59 (77.74)	71.97 ± 9.01 (75.38)	75.66 ± 14.6 (79.62)	72.68±6.79 (74.81)	61.57 ± 17.39 (64.86)	56.40 ± 5.1 (58.40)	11.77 ± 10.29 (9.65)
DeepLabV3	60.45 ± 18.67 (69.97)	67.23 ± 14.69 (75.32)	70.03 ± 14.1 (76.97)	44.18 ± 28.9 (51.15)	66.28 ± 13.9 (74.44)	50.91 ± 19.68 (63.00)	31.46 ± 19.62 (38.41)
FCN	59.87 ± 32.15 (74.13)	72.77 ± 8.16 (76.02)	74.94 ± 7.9 (78.47)	72.64 ± 4.95 (74.45)	50.65 ± 34.05 (65.58)	58.15 ± 6.47 (60.09)	23.65 ± 21.7 (22.49)
SegFormer	74.98 ± 16.59 (82.61)	71.48 ± 15.74 (78.82)	75.31 ± 16.89 (82.59)	71.67 ± 17.70 (78.75)	65.51 ± 15.19 (66.83)	41.06 ± 33.14 (44.86)	51.75 ± 34.72 (66.55)
LWGANet	73.36 ± 13.58 (78.34)	75.27 ± 10.00 (78.72)	78.60 ± 11.38 (82.87)	76.53 ± 10.86 (80.36)	73.84 ± 9.56 (76.92)	69.38 ± 13.55 (72.22)	68.08 ± 9.02 (71.54)

. The column “Vanilla values” contains the $F_1$-score values obtained by the pre-trained convolutional NNs and transformers used in the ensembles as an $F(·)$ encoders, which are mentioned in the first column. Each cell in other columns contains a mean $F_1$ value and its standard deviation, as well as the median (in brackets) for the graph ensemble NNs. The ensemble configuration is defined by the cell location: $F(·)$ and $G(·)$ are defined by row and column name, respectively. The best metric values for each $F(·)$ encoder are highlighted in bold.

QiGSAN improves the accuracy of ship segmentation according to the results from all convolutional and transformer encoders. The increase in mean $F_1$ values is $0.33$–$5.24\%$ for transformer encoders and $1.89$–$15.07\%$ for convolutional ones. For median values, the increase is $0.47$–$6.92\%$ for both encoder type. QiGSAN also outperforms simpler graph block implementations, such as GCN-QT and GAT-QT in terms of accuracy. The advantage is between $2.8\%$ and $25.85\%$ for the networks with the same encoders. Furthermore, the quadtree-informed networks significantly outperforms GSAN, GAT, and GCN using a graph-grid. The difference in mean $F_1$ value is between $2.53$ and $24.25\%$. Applying networks without informing images from HRSID in two out of the three cases does not improve the segmentation accuracy compared to the basic convolutional encoder.

5.2. SSDD

The estimations of the ship segmentation accuracy obtained in five-fold cross-validation on SSDD images are presented in

Table 5. Mean and Median $F_1$-score values ($\times 100\%$) for 5-fold SSDD cross-validation. The best metric values for each $F(·)$ encoder are highlighted in bold.

Encoder $\mathit{F}(·)$	VanillaValues	Graph NN $\mathit{G}(·)$
		GCN-QT	QiGSAN	GAT-QT	GCN	GSAN	GAT
ENet	33.04 ± 19.4 (29.28)	72.63 ± 5.78 (74.56)	$\mathbf{81.18}\mathbf{\pm }\mathbf{2.15}$ $\mathbf{\left(}\mathbf{81.41}\mathbf{\right)}$	75.54 ± 8.5 (80.07)	76.09 ± 3.48 (75.55)	78.71 ± 2.36 (78.38)	74.87 ± 4.01 (76.58)
DeepLabV3	58.35 ± 4.47 (57.81)	68.20 ± 7.51 (70.23)	$\mathbf{68.65}\mathbf{\pm }\mathbf{5.9}$ $\mathbf{\left(}\mathbf{70.28}\mathbf{\right)}$	67.81 ± 3.24 (68.51)	65.84 ± 7.25 (65.73)	50.92 ± 34.4 (65.25)	52.72 ± 5.98 (55.80)
FCN	21.87 ± 5.35 (21.86)	78.64 ± 4.27 (77.98)	$\mathbf{78.35}\mathbf{\pm }\mathbf{6.0}$ $\mathbf{\left(}\mathbf{78.09}\mathbf{\right)}$	72.71 ± 10.8 (76.82)	74.61 ± 5.62 (74.56)	74.96 ± 3.92 (73.86)	71.98 ± 7.63 (73.83)
SegFormer	44.64 ± 16.05 (50.36)	55.89 ± 19.80 (63.64)	$\mathbf{72.00}\mathbf{\pm }\mathbf{3.85}$ $\mathbf{\left(}\mathbf{73.18}\mathbf{\right)}$	58.33 ± 20.75 (65.43)	50.73 ± 20.4 (56.58)	59.37 ± 13.14 (60.93)	54.35 ± 15.10 (59.02)
LWGANet	17.68 ± 3.29 (16.82)	65.59 ± 21.89 (74.16)	$\mathbf{81.61}\mathbf{\pm }\mathbf{3.6}$ $\mathbf{\left(}\mathbf{81.76}\mathbf{\right)}$	80.46 ± 3.78 (80.27)	73.19 ± 1.44 (73.16)	69.93 ± 17.53 (78.08)	72.11 ± 8.99 (75.58)

. The best metric values for each $F(·)$ encoder are highlighted in bold.

For all base convolutional and transformer encoders, the graph neural network processing improves the ship segmentation results. The best accuracy metric values are achieved using QiGSAN. The increase in mean $F_1$ values is 10.3–56.48% for convolutional encoders and 27.36–63.93% for transformer ones. For median values, the increase is $12.47$–$64.94\%$. QiGSAN outperforms the results of GCN-QT and GAT-QT. An advantage in $F_1$-score is up to $16.11\%$ for the networks with the same encoders. The quadtree-informed networks significantly outperform GSAN, GAT, and GCN: the difference in the mean $F_1$ value is between $2.47\%$ and $17.73\%$.

The presented results are independent of the fold splitting in cross-validation. Additional experiments for three-fold cross-validation on SSDD are shown in

Table 6. Mean and median $F_1$-score values ($\times 100\%$), 3-fold cross-validation (SSDD). The best metric values for each $F(·)$ encoder are highlighted in bold.

Encoder $\mathit{F}(·)$	VanillaValues	Graph NN $\mathit{G}(·)$
		GCN-QT	QiGSAN	GAT-QT	GCN	GSAN	GAT
ENet	25.08 ± 3.83 (25.98)	75.05 ± 3.08 (75.05)	$\mathbf{80.47}\mathbf{\pm }\mathbf{3.9}$ $\mathbf{\left(}\mathbf{80.87}\mathbf{\right)}$	77.14 ± 0.41 (77.94)	73.32 ± 0.88 (73.32)	78.90 ± 4.53 (78.92)	71.02 ± 4.3 (73.12)
DeepLabV3	51.32 ± 5.80 (50.59)	63.26 ± 7.54 (63.09)	$\mathbf{68.34}\mathbf{\pm }\mathbf{4.1}$ $\mathbf{\left(}\mathbf{66.19}\mathbf{\right)}$	66.11 ± 3.75 (63.74)	62.47 ± 4.80 (60.51)	55.82 ± 19.73 (62.84)	50.32 ± 12.56 (51.52)
FCN	25.69 ± 13.06 (25.37)	$\mathbf{74.39}\mathbf{\pm }\mathbf{0.2}$ $\mathbf{\left(}\mathbf{74.39}\mathbf{\right)}$	69.78 ± 5.68 (69.38)	68.24 ± 9.13 (68.14)	71.06 ± 2.09 (71.16)	67.35 ± 10.53 (67.75)	70.41 ±  2.51 (70.85)
SegFormer	45.32 ± 5.12 (44.47)	67.19 ± 2.49 (68.09)	$\mathbf{74.0}\mathbf{\pm }\mathbf{1.84}$ $\mathbf{\left(}\mathbf{74.22}\mathbf{\right)}$	72.95 ± 1.17 (72.75)	67.28 ± 0.81 (65.18)	65.04 ± 1.94 (63.74)	66.2 ± 0.28 (65.9)
LWGANet	20.34 ± 8.82 (20.34)	80.41 ± 1.47 (81.91)	$\mathbf{83.7}\mathbf{\pm }\mathbf{0.38}$ $\mathbf{\left(}\mathbf{84.2}\mathbf{\right)}$	82.83 ± 0.78 (82.22)	79.61 ± 1.97 (78.06)	80.01 ± 2.63 (79.11)	78.16 ± 3.39 (76.55)

. The best metric values for each $F(·)$ encoder are highlighted in bold. In all cases, quadtree-informed networks demonstrate the best accuracy metrics. The increase in $F_1$ values is $17.02$–$63.36\%$, while GSAN, GAT, and GCN accuracies increase by $11.15$–$59.27\%$.

5.3. Comparison of QiGSAN with Other Configurations of Graph Networks

Theorem 1 implies a faster loss function reduction in quadtree-informed neural networks. This theoretical result was confirmed by experiments, as shown in the curves for informed and non-informed graph neural network with the LWGANet encoder, presented in Figure 10, for both datasets.

According to the results of the experiments presented in Section 5.1 and Section 5.2, quadtree-informed architectures are able to segment ships more accurately than the networks without informing processes, see Figure 11 and Figure 12.

They present the differences in ship segmentation accuracy averaged over five-fold cross-validation between the ensemble graph network and vanilla encoders. Proposed architectures learn effectively with a small number of training samples: both HRSID and SSDD contain no more than 1962 images. In all cases, QiGSAN demonstrates the best results in accuracy metric values. In addition, this architecture shows superior results on HRSID, in which $87.4\%$ of objects are small (see Section 4.1) and comparable to the superpixel size. The ensemble architectures based on the FCN (see Figure 11) and LWGANet (see Figure 12) encoders demonstrate the maximum differences in $F_1$ value. While LWGANet shows the lowest accuracy in ship segmentation, QiGSAN based on LWGANet achieves the best accuracy for data segmentation.

The results obtained by vanilla FCN and LWGANet show the lowest accuracy in ship segmentation for both datasets. These are the NNs with the largest number of parameters among other base segmentors, as shown in

Table 7. The number of parameters (in thousands) and the computing performance (in GFLOPS) of base segmentors $F(·)$ and graph networks $G(·)$.

	ENet	DeepLabV3	FCN	LWGANet	Segformer	GCN	GAT	GSAN	QiGCN	QiGAT	QiGSAN
GFLOPs	46.6	157.74	2360	196	88.7	168.16	168.08	168.08	174.84	174.72	174.76
Params	358.7	11029	35322	12583	3755	49.8	48.5	48.5	370.3	370.1	370.1

, so these NNs are prone to overfitting if the training dataset is small. Ensemble with graph networks combine the information from networks with large numbers of parameters to produce more accurate predictions.

Table 7 shows that the graph NN $G(·)$ from QGISAN contains about 370,000 parameters. This small network combined with convolution or transformer NNs can improve segmentation accuracy by up to $59.27\%$. For SSDD, the ensemble NN that achieves one of the highest segmentation accuracies (based on the ENet encoder) has much fewer parameters compared to the best baseline network (DeeplabV3). Table 7 also demonstrates that quadtree-informed NNs have more parameters compared to non-informed ones. However, the majority of these extra parameters correspond to normalization layers in block “5” in the QiGSAN architecture, see Figure 1. Therefore, increasing the number of parameters does not necessarily lead to decreased performance: the increase in FLOPS is up to $3.57\%$.

6. Conclusions and Discussion

6.1. Discussion

QiGSAN leads to more accurate results for small object segmentation than all other architectures, including transformers, and can also be used on large datasets with imbalanced or heterogeneous classes, which is common in real-world datasets. The main limitation of neural network architectures that QiGSAN compares with is the low training efficiency on small and imbalanced datasets. Another limitation of QiGSAN is the correlation between the accuracy values obtained from the base encoder network and the graph part of the architecture. Accurate predictions from the base encoder generally improve the results of QiGSAN.

In a few aspects, QiGSAN can be described as a trustworthy graph neural network [84]. The first aspect is explainability, as QiGSAN has a graph block based on a quadtree model. This is an effective method for describing the connections between features in images with different spatial resolutions. Second, fairness is important, as QiGSAN helps improve the segmentation of smaller objects. Third, environmental well-being is also important, since the graph network used in QiGSAN has only a few thousand parameters, significantly increasing segmentation accuracy even with small and weak encoder models. However, robustness and privacy issues are not addressed in this paper.

6.2. Summary

The paper proposes a novel ensemble graph neural network QiGSAN to perform semantic segmentation of imbalanced small datasets of high-resolution images. It is composed of a convolutional or transformer encoder and a graph network with a special self-attention block and block of multi-resolution feature compression informed by a quadtree. To process high resolution images, QiGSAN contains a special module for dividing images into superpixels of a fixed size incorporated into NN architecture, which reduces the number of graph nodes. Different well-known implementations of graph convolution, GCN and GAT, were tested. Comparison is also made to the traditional approach, which uses a two-dimensional grid to represent connections between pixels as a graph.

QiGSAN was applied to segment ships on real SAR images from two open datasets. Experiments showed that quadtree-informed networks are more efficient for small objects than transformer or convolutional NNs. Using QiGSAN, the increase in $F_1$-score values compared to convolutional NNs is up to $48.57\%$ and for transformers is up to $63.93\%$. QiGSAN also demonstrates the best accuracy values compared to other variations in graph ensemble networks: the increase in $F_1$-score values is up to $9.84\%$. QiGSAN showed the greatest efficiency when processing objects comparable in size with superpixels. NNs without informing processes, when processing the HRSID dataset, where $87.4\%$ of the objects are small, could not improve the results of the convolutional and transformer networks used as encoders in most cases.

6.3. Furher Research Directions

First of all, architectural modifications can be made to effectively process both global and local superpixels features to detect objects of various sizes. The analytical results for new architectures are also required. Second, the types of analyzed data should be extended, for example, by using images and videos from unmanned vehicles. Third, interconnection scaling is another research direction, and QiGSAN is able to handle this challenge, as it successfully deals with hierarchical structures. Finally, detection problems can also be solved using QiGSAN-segmented images and standard OpenCV [85] tools, as well as by incorporating a quadtree-informed approach into the architectures of widely used neural networks detectors for the development of smart systems, such as those used in ports [86].