Evidential K-Nearest Neighbors with Cognitive-Inspired Feature Selection for High-Dimensional Data
Abstract
1. Introduction
2. Preliminaries
2.1. Genetic Algorithm
- Selection: Genetic operators are used to create the next generation. Elite individuals are selected as parents based on their fitness values, and offspring are generated through crossover and mutation. Individuals with higher fitness are more likely to be selected, mimicking the principle of survival of the fittest in natural selection. To ensure consistent generation size, Equation (3) must be satisfied:BS is the number of individuals selected as the best, RS is the number of randomly selected individuals, children is the number of offspring produced by each pair of parents, and the initial population size is the size of the initial population.
- Crossover: A pair of individuals is selected from the previously selected parents, and a crossover operation is performed to generate new individuals. This study employed the single-point crossover technique.
- Mutation: After crossover, individuals in the current population are replaced. The new individuals undergo mutation to introduce genetic variations.
- Stopping Criteria: Common stopping criteria in Genetic Algorithms include reaching a set number of iterations or observing no improvement in the fitness function over consecutive generations. In this experiment, the criterion of a fixed number of iterations is applied.
2.2. Evidential K-NN
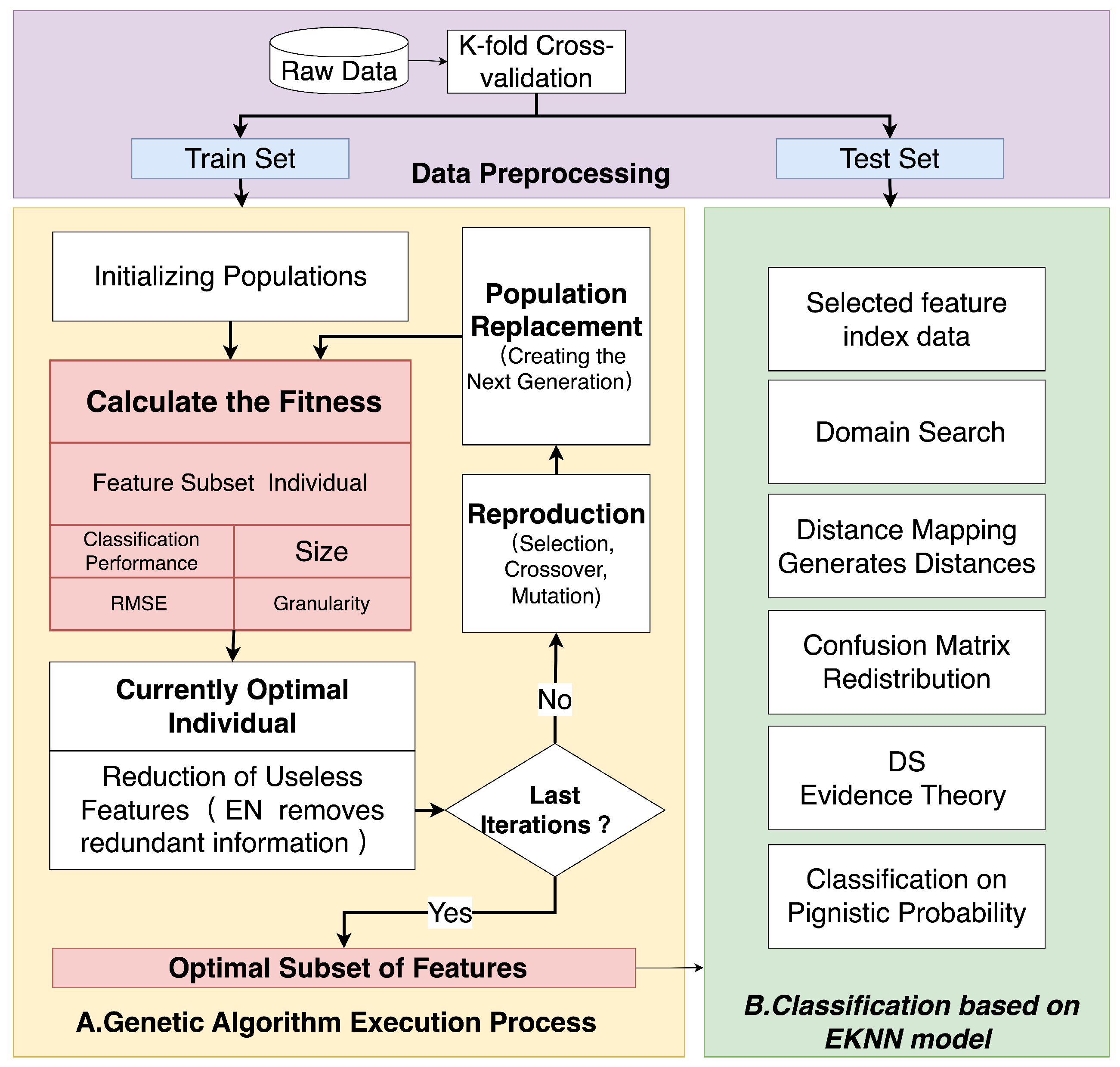
3. GEK-NN Implementation Method
3.1. Genetic Algorithm Execution Process
3.2. Classification Based on EK-NN Model
3.3. GEK-NN Classification Procedure and Time Complexity
4. Experimental Results
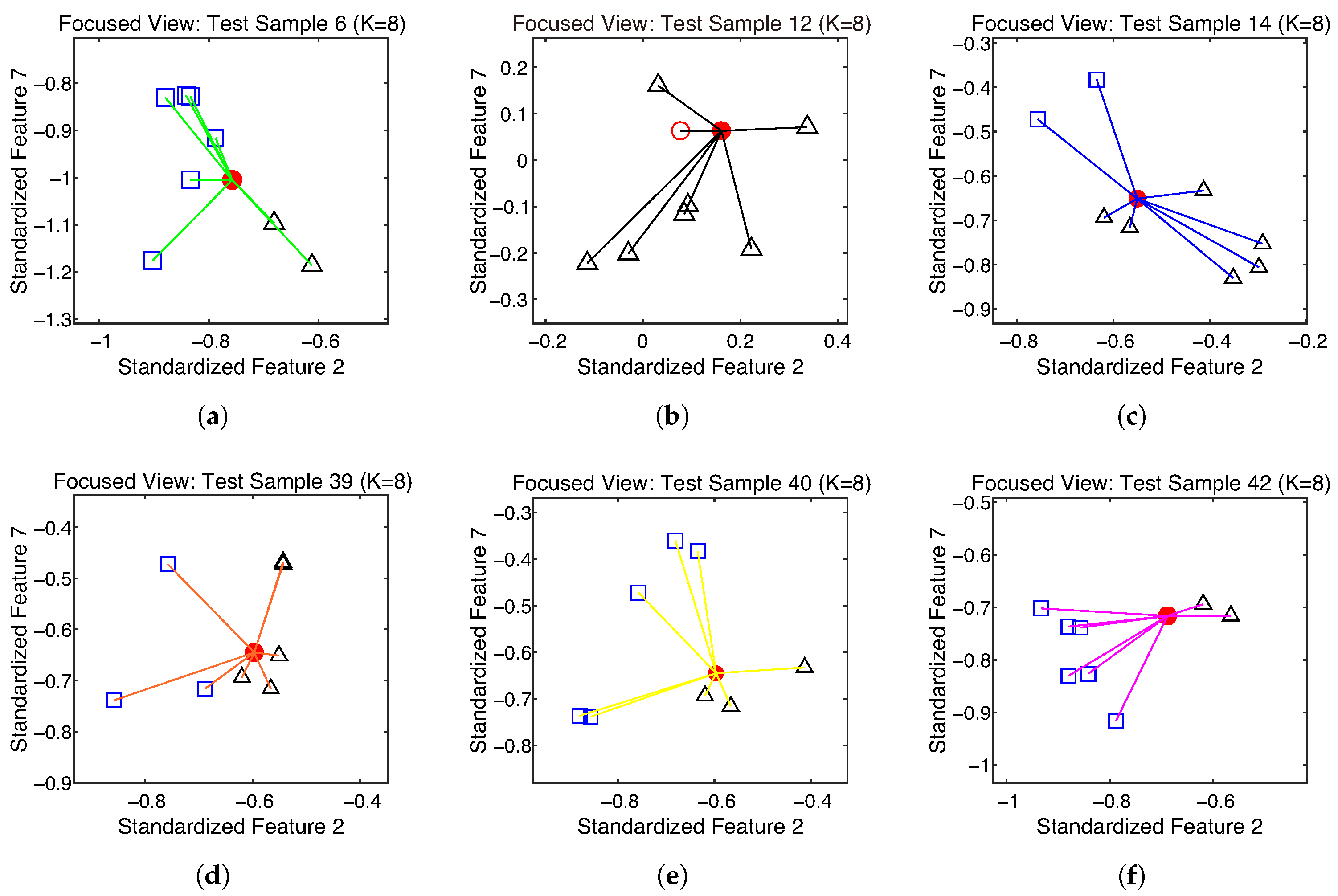
4.1. An Illustrative Example (Seeds)
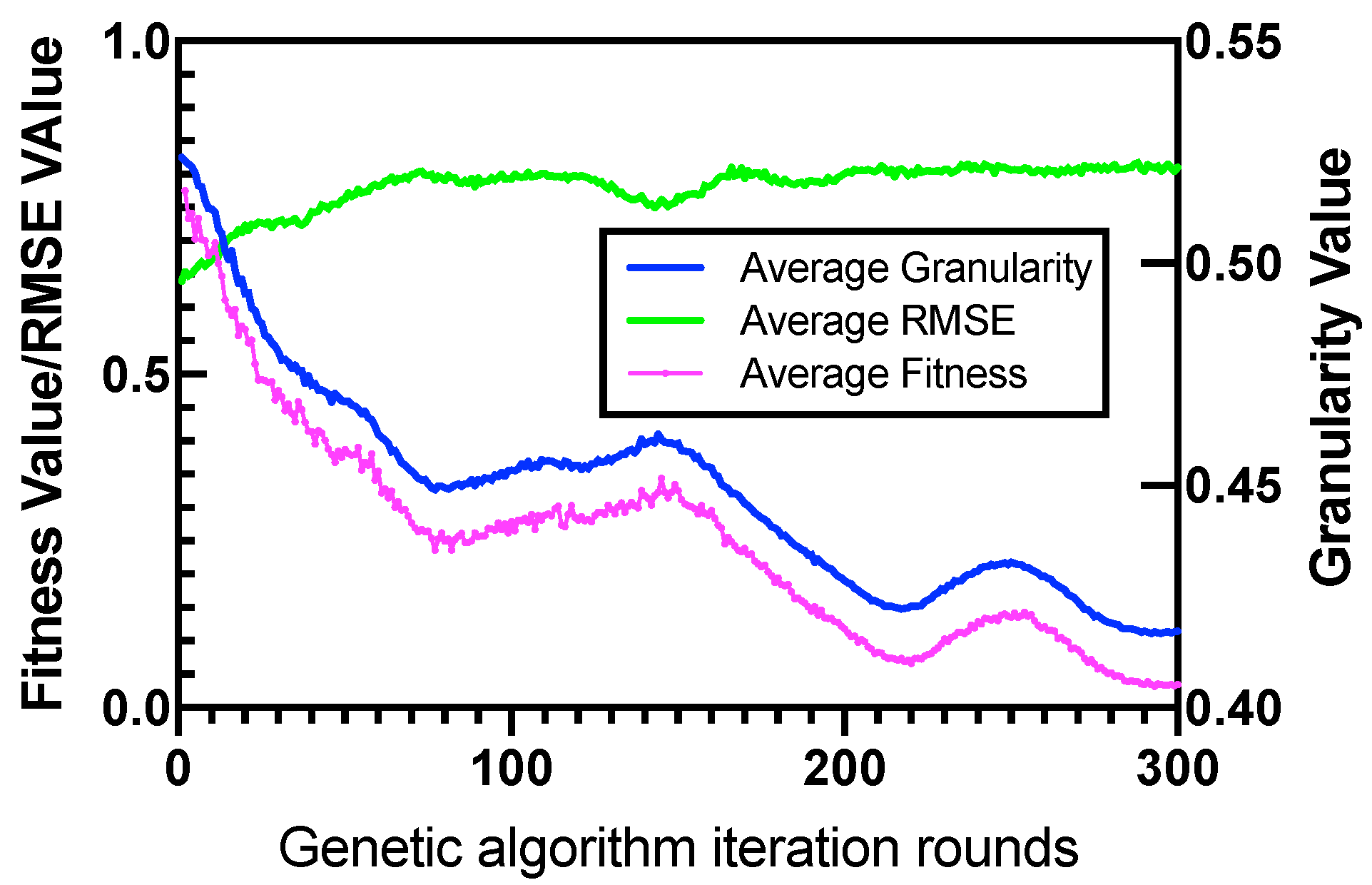
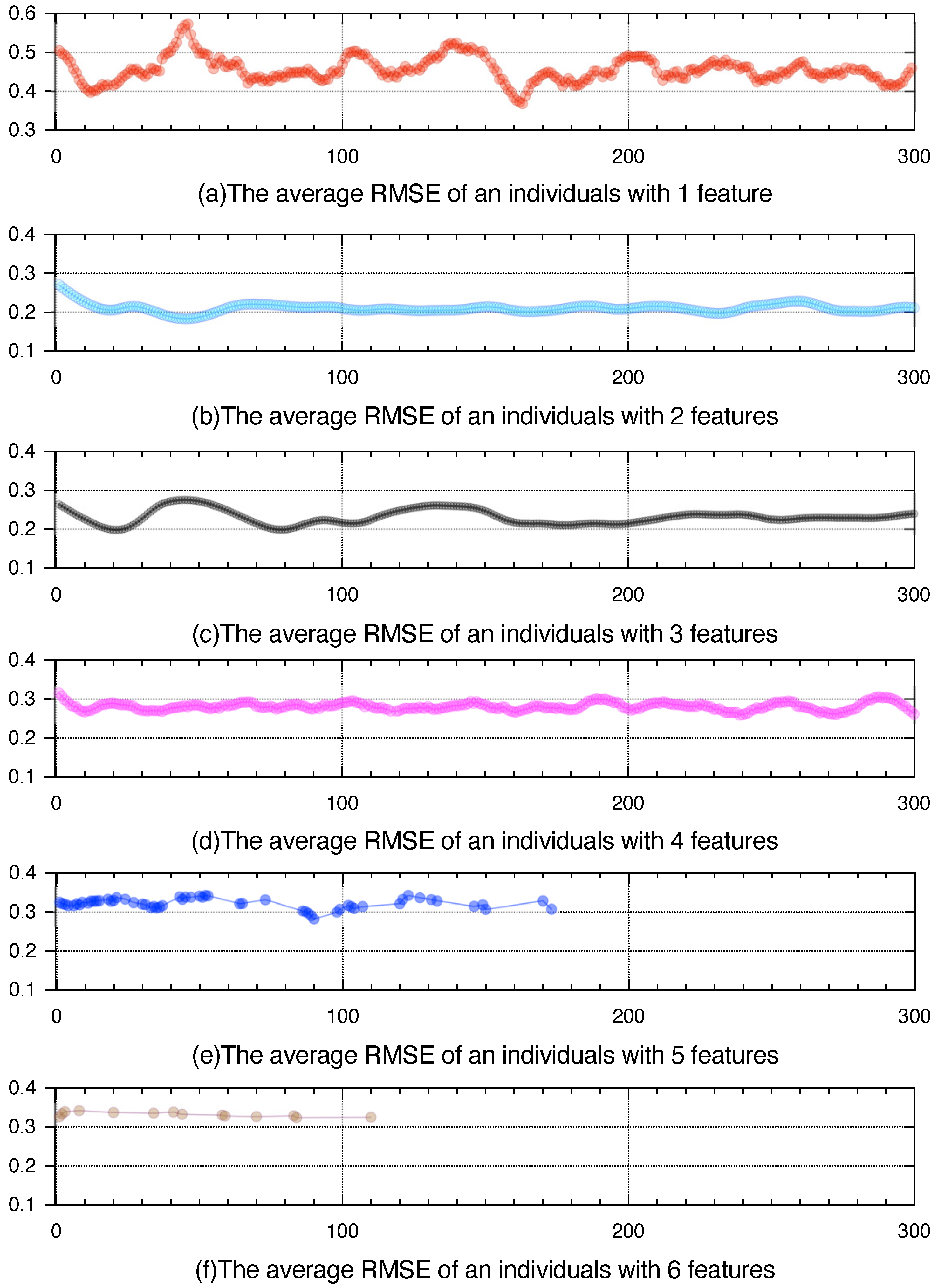
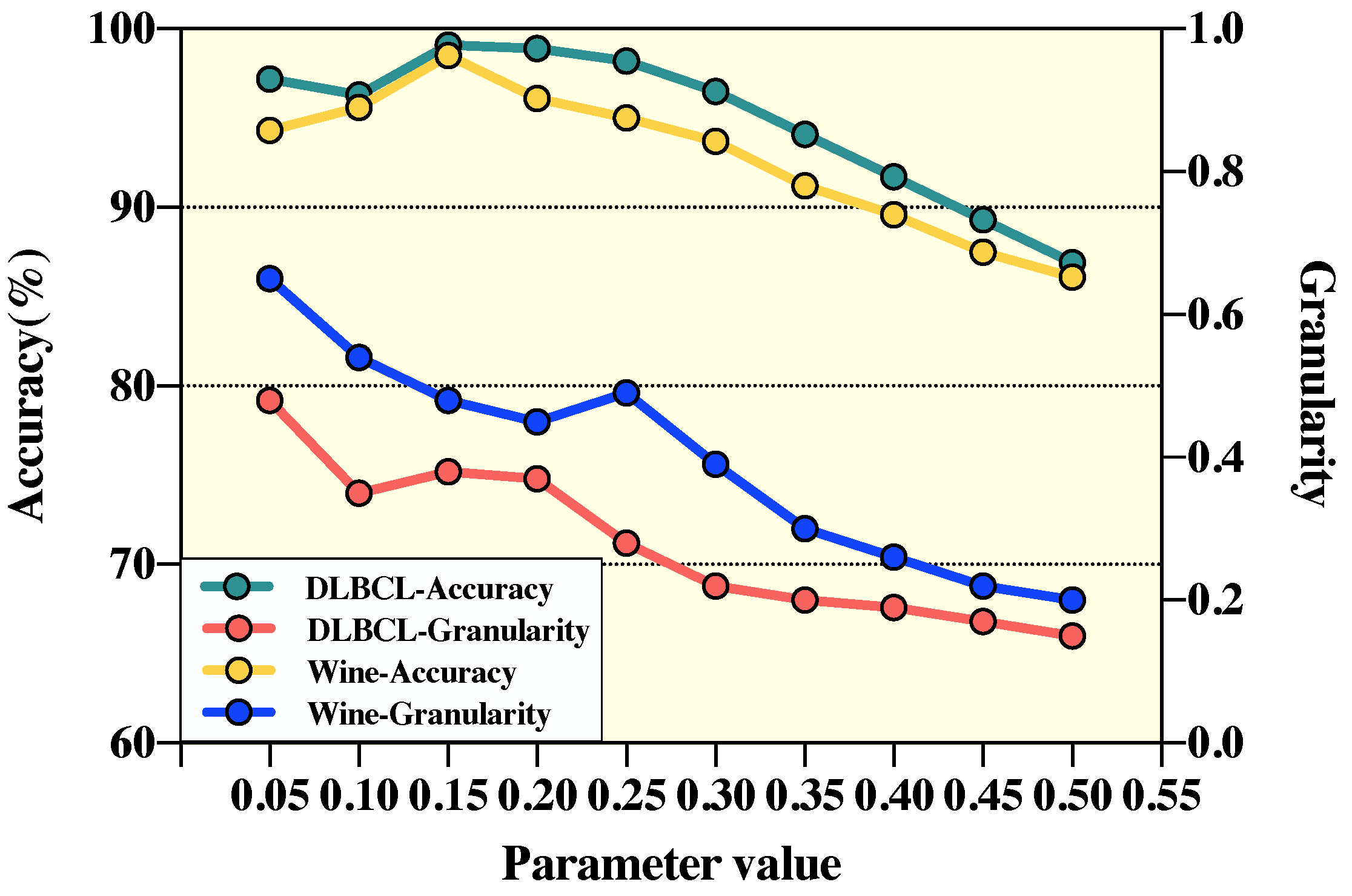
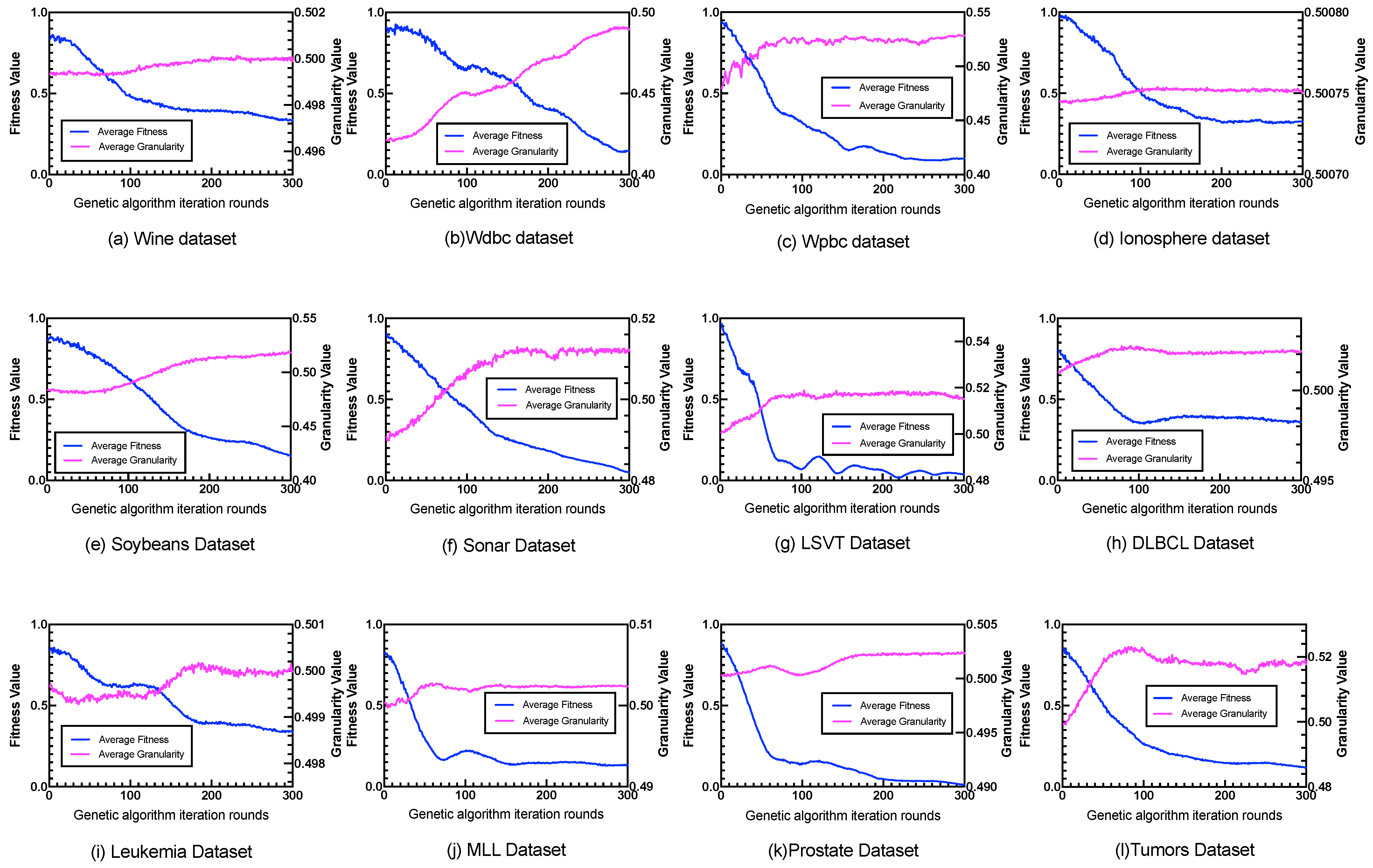
4.2. Parameter Sensitivity Analysis
4.3. Performance of GEK-NN
4.4. Performance Evaluation
- (1)
- Original EK-NN method.
- (2)
- Feature-selection methods based on Genetic Algorithms with embedded machine learning models (KNN, SVM, and logistic regression) applied to EK-NN models.
- (3)
- Feature-selection method using fuzzy mathematics and domain knowledge for EK-NN models [25,39,40,41]. The cited algorithms NDD, NMI, FINEN, and REK-NN all belong to a class of algorithms for feature selection, and in the paper [25] these algorithms are used for comparison by applying them to the EK-NN model.
4.5. Limitations and Discussions on Model Complexity
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Cover, T.; Hart, P. Nearest neighbor pattern classification. IEEE Trans. Inf. Theory 1967, 13, 21–27. [Google Scholar] [CrossRef]
- Denoeux, T. A k-nearest neighbor classification rule based on Dempster-Shafer theory. IEEE Trans. Syst. Man, Cybern. 1995, 25, 804–813. [Google Scholar] [CrossRef]
- Dempster, A.P. Upper and Lower Probabilities Induced by a Multivalued Mapping; Springer: Berlin/Heidelberg, Germany, 2008; pp. 57–72. [Google Scholar]
- Denœux, T. 40 years of Dempster-Shafer theory. Int. J. Approx. Reason. 2016, 79, 1–6. [Google Scholar] [CrossRef]
- Shafer, G. A Mathematical Theory of Evidence; Princeton University Press: Princeton, NJ, USA, 1976; Volume 42. [Google Scholar]
- Kanjanatarakul, O.; Kuson, S.; Denoeux, T. An evidential K-nearest neighbor classifier based on contextual discounting and likelihood maximization. In Belief Functions: Theory and Applications, Proceedings of the 5th International Conference (BELIEF 2018), Compiègne, France, 17–21 September 2018; Proceedings 5; Springer: Cham, Switzerland, 2018; pp. 155–162. [Google Scholar]
- Huang, L.; Fan, J.; Zhao, W.; You, Y. A new multi-source transfer learning method based on two-stage weighted fusion. Knowl.-Based Syst. 2023, 262, 110233. [Google Scholar] [CrossRef]
- Toman, P.; Ravishanker, N.; Rajasekaran, S.; Lally, N. Online Evidential Nearest Neighbour Classification for Internet of Things Time Series. Int. Stat. Rev. 2023, 91, 395–426. [Google Scholar] [CrossRef]
- Trabelsi, A.; Elouedi, Z.; Lefevre, E. An ensemble classifier through rough set reducts for handling data with evidential attributes. Inf. Sci. 2023, 635, 414–429. [Google Scholar] [CrossRef]
- Zouhal, L.M.; Denoeux, T. An evidence-theoretic k-NN rule with parameter optimization. IEEE Trans. Syst. Man Cybern. Part C (Appl. Rev.) 1998, 28, 263–271. [Google Scholar] [CrossRef]
- Su, Z.-G.; Wang, P.-H.; Yu, X.-J. Immune genetic algorithm-based adaptive evidential model for estimating unmeasured parameter: Estimating levels of coal powder filling in ball mill. Expert Syst. Appl. 2010, 37, 5246–5258. [Google Scholar] [CrossRef]
- Gong, C.-Y.; Su, Z.-G.; Zhang, X.-Y.; Yang, Y. Adaptive evidential K-NN classification: Integrating neighborhood search and feature weighting. Inf. Sci. 2023, 648, 119620. [Google Scholar] [CrossRef]
- Liu, Z.-G.; Pan, Q.; Dezert, J.; Mercier, G. Hybrid classification system for uncertain data. IEEE Trans. Syst. Man, Cybern. Syst. 2016, 47, 2783–2790. [Google Scholar] [CrossRef]
- Gong, C.; Su, Z.-G.; Wang, P.-H.; Wang, Q.; You, Y. Evidential instance selection for K-nearest neighbor classification of big data. Int. J. Approx. Reason. 2021, 138, 123–144. [Google Scholar] [CrossRef]
- Altınçay, H. Ensembling evidential k-nearest neighbor classifiers through multi-modal perturbation. Appl. Soft Comput. 2007, 7, 1072–1083. [Google Scholar] [CrossRef]
- Trabelsi, A.; Elouedi, Z.; Lefevre, E. Ensemble enhanced evidential k-NN classifier through random subspaces. In Symbolic and Quantitative Approaches to Reasoning with Uncertainty, Proceedings of the 14th European Conference (ECSQARU 2017), Lugano, Switzerland, 10–14 July 2017; Springer: Cham, Switzerland, 2017; pp. 212–221. [Google Scholar]
- Denoeux, T.; Kanjanatarakul, O.; Sriboonchitta, S. A new evidential k-nearest neighbor rule based on contextual discounting with partially supervised learning. Int. J. Approx. Reason. 2019, 113, 287–302. [Google Scholar] [CrossRef]
- Vommi, A.M.; Battula, T.K. A hybrid filter-wrapper feature selection using Fuzzy KNN based on Bonferroni mean for medical datasets classification: A COVID-19 case study. Expert Syst. Appl. 2023, 218, 119612. [Google Scholar] [CrossRef]
- Zhang, X.; Xiao, H.; Gao, R.; Zhang, H.; Wang, Y. K-nearest neighbors rule combining prototype selection and local feature weighting for classification. Knowl.-Based Syst. 2022, 243, 108451. [Google Scholar] [CrossRef]
- Guyon, I.; Elisseeff, A. An introduction to variable and feature selection. J. Mach. Learn. Res. 2003, 3, 1157–1182. [Google Scholar]
- Li, Y.; Chen, C.-Y.; Wasserman, W.W. Deep feature selection: Theory and application to identify enhancers and promoters. J. Comput. Biol. 2016, 23, 322–336. [Google Scholar] [CrossRef]
- Molchanov, D.; Ashukha, A.; Vetrov, D. Variational dropout sparsifies deep neural networks. In Proceedings of the 34th International Conference on Machine Learning (ICML), Sydney, Australia, 6–11 August 2017; pp. 2498–2507. [Google Scholar]
- Gaudel, R.; Sebag, M. Feature selection as a one-player game. In Proceedings of the 27th International Conference on Machine Learning (ICML), Haifa, Israel, 21–24 June 2010; pp. 359–366. [Google Scholar]
- Lian, C.; Ruan, S.; Denœux, T. An evidential classifier based on feature selection and two-step classification strategy. Pattern Recognit. 2015, 48, 2318–2327. [Google Scholar] [CrossRef]
- Su, Z.-G.; Hu, Q.; Denoeux, T. A distributed rough evidential K-NN classifier: Integrating feature reduction and classification. IEEE Trans. Fuzzy Syst. 2020, 29, 2322–2335. [Google Scholar] [CrossRef]
- Holland, J.H. Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control, and Artificial Intelligence; MIT Press: Cambridge, MA, USA, 1992. [Google Scholar]
- Katoch, S.; Chauhan, S.S.; Kumar, V. A review on genetic algorithm: Past, present, and future. Multimed. Tools Appl. 2021, 80, 8091–8126. [Google Scholar] [CrossRef]
- Jiao, R.; Nguyen, B.H.; Xue, B.; Zhang, M. A survey on evolutionary multiobjective feature selection in classification: Approaches, applications, and challenges. IEEE Trans. Evol. Comput. 2023, 28, 1156–1176. [Google Scholar] [CrossRef]
- Oh, I.-S.; Lee, J.-S.; Moon, B.-R. Hybrid genetic algorithms for feature selection. IEEE Trans. Pattern Anal. Mach. Intell. 2004, 26, 1424–1437. [Google Scholar] [CrossRef]
- Fukushima, A.; Sugimoto, M.; Hiwa, S.; Hiroyasu, T. Elastic net-based prediction of IFN-β treatment response of patients with multiple sclerosis using time series microarray gene expression profiles. Sci. Rep. 2019, 9, 1822. [Google Scholar] [CrossRef]
- Park, I.W.; Mazer, S.J. Overlooked climate parameters best predict flowering onset: Assessing phenological models using the elastic net. Glob. Change Biol. 2018, 24, 5972–5984. [Google Scholar] [CrossRef]
- Zou, H.; Hastie, T. Regularization and variable selection via the elastic net. J. R. Stat. Soc. Ser. Stat. Methodol. 2005, 67, 301–320. [Google Scholar] [CrossRef]
- Amini, F.; Hu, G. A two-layer feature selection method using genetic algorithm and elastic net. Expert Syst. Appl. 2021, 166, 114072. [Google Scholar] [CrossRef]
- Zhang, Z.; Lai, Z.; Xu, Y.; Shao, L.; Wu, J.; Xie, G.-S. Discriminative elastic-net regularized linear regression. IEEE Trans. Image Process. 2017, 26, 1466–1481. [Google Scholar] [CrossRef]
- Dong, H.; Li, T.; Ding, R.; Sun, J. A novel hybrid genetic algorithm with granular information for feature selection and optimization. Appl. Soft Comput. 2018, 65, 33–46. [Google Scholar] [CrossRef]
- Blake, C.L.; Merz, C.J. UCI Repository of Machine Learning. 1998. Available online: http://www.ics.uci.edu/mlearn/MLRepository (accessed on 1 January 2024).
- Kent Ridge Bio-Medical Dataset. 2015. Available online: http://datam.i2r.atar.edu.sg/datasets/krbd/index.html (accessed on 1 January 2024).
- Derrac, J.; Garcia, S.; Sanchez, L.; Herrera, F. Keel data-mining software tool: Data set repository, integration of algorithms and experimental analysis framework. J.-Mult.-Valued Log. Soft Comput. 2015, 17, 255–287. [Google Scholar]
- Hu, Q.; Yu, D.; Liu, J.; Wu, C. Neighborhood rough set based heterogeneous feature subset selection. Inf. Sci. 2008, 178, 3577–3594. [Google Scholar] [CrossRef]
- Hu, Q.; Zhang, L.; Zhang, D.; Pan, W.; An, S.; Pedrycz, W. Measuring relevance between discrete and continuous features based on neighborhood mutual information. Expert Syst. Appl. 2011, 38, 10737–10750. [Google Scholar] [CrossRef]
- Hu, Q.; Yu, D.; Xie, Z.; Liu, J. Fuzzy probabilistic approximation spaces and their information measures. IEEE Trans. Fuzzy Syst. 2006, 14, 191–201. [Google Scholar] [CrossRef]


| Parameter Name | Parameter Setting | Specific Value |
|---|---|---|
| Population size | Determines how many chromosomes will initialize | 50 |
| Chromosome length | The number of genes contained in the chromosome | equal to the number of features |
| Crossover mode | The mode of crossover of the chromosome | Single point (crossover at one site only) |
| Probability of mutation | Probability of chromosome mutation | 0.05 |
| Number of iterations T | Total number of iterations performed | 300 |
| ID | Dataset | Samples | Attributes | Classes |
|---|---|---|---|---|
| 1 | Seeds | 210 | 7 | 3 |
| 2 | Wine | 178 | 13 | 3 |
| 3 | Wdbc | 569 | 30 | 2 |
| 4 | Wpbc | 198 | 33 | 2 |
| 5 | Ionosphere | 351 | 34 | 2 |
| 6 | Soybean | 47 | 35 | 4 |
| 7 | Sonar | 208 | 60 | 2 |
| 8 | LSVT | 126 | 309 | 2 |
| ID | Dataset | Samples | Attributes | Classes |
|---|---|---|---|---|
| 9 | DLBCL | 77 | 5469 | 2 |
| 10 | Leukemia | 72 | 11,225 | 3 |
| 11 | MLL | 72 | 11,225 | 3 |
| 12 | Prostate | 136 | 12,600 | 2 |
| 13 | Tumors | 327 | 12,588 | 7 |
| Wine | DLBCL | |||
|---|---|---|---|---|
| Accuracy (%) | Granularity | Accuracy (%) | Granularity | |
| 0.05 | 94.3 | 0.65 | 97.2 | 0.48 |
| 0.10 | 95.6 | 0.54 | 96.3 | 0.35 |
| 0.15 | 98.5 | 0.48 | 99.1 | 0.38 |
| 0.20 | 96.1 | 0.45 | 98.9 | 0.37 |
| 0.25 | 95.0 | 0.49 | 98.2 | 0.28 |
| 0.30 | 93.7 | 0.39 | 96.5 | 0.22 |
| 0.35 | 91.2 | 0.30 | 94.1 | 0.20 |
| 0.40 | 89.6 | 0.26 | 91.7 | 0.19 |
| 0.45 | 87.5 | 0.22 | 89.3 | 0.17 |
| 0.50 | 86.1 | 0.20 | 86.9 | 0.15 |
| Datasets | Original EK-NN | NDD Based EK-NN | NMI Based EK-NN | FINEN Based EK-NN | REK-NN | GA-KNN Based EK-NN | GA-SVM Based EK-NN | GA-LG Based EK-NN | GEK-NN |
|---|---|---|---|---|---|---|---|---|---|
| Wine | |||||||||
| Wdbc | |||||||||
| Wpbc | |||||||||
| Ion. | |||||||||
| Soybean | |||||||||
| Sonar | |||||||||
| LSVT |
| Datasets | Original EK-NN | NDD Based EK-NN | NMI Based EK-NN | FINEN Based EK-NN | REK-NN | GA-KNN Based EK-NN | GA-SVM Based EK-NN | GA-LG Based EK-NN | GEK-NN |
|---|---|---|---|---|---|---|---|---|---|
| DLBCL | |||||||||
| Leu. | |||||||||
| MLL | |||||||||
| Prostate | |||||||||
| Tumors |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Zhang, Y.; Wang, X.; Qu, X. Evidential K-Nearest Neighbors with Cognitive-Inspired Feature Selection for High-Dimensional Data. Big Data Cogn. Comput. 2025, 9, 202. https://doi.org/10.3390/bdcc9080202
Liu Y, Zhang Y, Wang X, Qu X. Evidential K-Nearest Neighbors with Cognitive-Inspired Feature Selection for High-Dimensional Data. Big Data and Cognitive Computing. 2025; 9(8):202. https://doi.org/10.3390/bdcc9080202
Chicago/Turabian StyleLiu, Yawen, Yang Zhang, Xudong Wang, and Xinyuan Qu. 2025. "Evidential K-Nearest Neighbors with Cognitive-Inspired Feature Selection for High-Dimensional Data" Big Data and Cognitive Computing 9, no. 8: 202. https://doi.org/10.3390/bdcc9080202
APA StyleLiu, Y., Zhang, Y., Wang, X., & Qu, X. (2025). Evidential K-Nearest Neighbors with Cognitive-Inspired Feature Selection for High-Dimensional Data. Big Data and Cognitive Computing, 9(8), 202. https://doi.org/10.3390/bdcc9080202






