A Quantum Key Distribution Routing Scheme for a Zero-Trust QKD Network System: A Moving Target Defense Approach

Abstract

Quantum key distribution (QKD), a key application of quantum information technology and “one-time pad” (OTP) encryption, enables secure key exchange with information-theoretic security, meaning its security is grounded in the laws of physics rather than computational assumptions. However, in QKD networks, achieving long-distance communication often requires trusted relays to mitigate channel losses. This reliance introduces significant challenges, including vulnerabilities to compromised relays and the high costs of infrastructure, which hinder widespread deployment. To address these limitations, we propose a zero-trust spatiotemporal diversification framework for multipath–multi-key distribution. The proposed approach enhances the security of end-to-end key distribution by dynamically shuffling key exchange routes, enabling secure multipath key distribution. Furthermore, it incorporates a dynamic adaptive path recovery mechanism that leverages a recursive penalty model to identify and exclude suspicious or compromised relay nodes. To validate this framework, we conducted extensive simulations and compared its performance against established multipath QKD methods. The results demonstrate that the proposed approach achieves a 97.22% lower attack success rate with 20% attacker pervasiveness and a 91.42% reduction in the attack success rate for single key transmission. The total security percentage improves by 35% under 20% attacker pervasiveness, and security enhancement reaches 79.6% when increasing QKD pairs. Additionally, the proposed scheme exhibits an 86.04% improvement in defense against interception and nearly doubles the key distribution success rate compared to traditional methods. The results demonstrate that the proposed approach significantly improves both security robustness and efficiency, underscoring its potential to advance the practical deployment of QKD networks.

1. Introduction

In today’s digital era, information security is of crucial importance. Traditional cryptography, such as the Rivest–Shamir–Adleman (RSA) algorithm, has long been relied upon for secure network communications through robust key agreements and authentication protocols. However, the security of these systems largely relies on the computational difficulty of factoring large integers and solving discrete logarithm problems. These are vulnerable to attacks by quantum computers, notably through the Shor algorithm [1,2].

The quantum key distribution (QKD) represents a pivotal advancement in countering these new threats. It secures key exchanges by utilizing the principles of quantum mechanics, such as the no-cloning theorem, which prevents the undetected replication of quantum states [3]. Qubits, employed in QKD, are typically transmitted by photons across distances of up to 833 km using protocols like BB84 and BBM92 through optical fibers or free space [4,5].

Despite QKD’s theoretical security, it encounters practical challenges, especially over long distances. Photon loss and decoherence limit its effective range. To address these limitations, technologies such as quantum repeaters, trusted relays, and satellite-based solutions have been developed [6,7]. Quantum repeaters improve communication distances by segmenting the channel into shorter links, facilitating entanglement swapping and purification [8]. Trusted relays, using one-time pad (OTP) encryption, extend QKD’s reach by enhancing its scalability and flexibility [5,9,10]. Alternatively, satellite-based QKD circumvents terrestrial limitations by enabling global key distribution.

However, these advancements come with their own set of vulnerabilities. For example, photon sources and detector imperfections can be exploited through side-channel and Trojan horse attacks [11], while satellite-based systems are particularly vulnerable to signal jamming and denial-of-service attacks [12]. Advanced quantum hacking techniques, such as photon number splitting (PNS) attacks, exploit multiphoton emissions to extract information without detection [13]. Moreover, the assumption that relays are secure poses risks in real-world applications, as classical components of QKD networks remain susceptible to data tampering and replay attacks [14].

Therefore, enhanced security measures are necessary to protect QKD networks. Solutions such as measurement-device-independent QKD (MDI-QKD) and multipath key distribution offer improvements by removing traditional vulnerabilities and distributing keys across multiple paths, respectively [15,16,17]. However, these techniques introduce new challenges, such as increased system complexity and the need for precise knowledge of the locations of measurement nodes, which can be problematic near untrusted relays [18,19].

Given these considerations, developing robust and adaptive security mechanisms is crucial. An effective strategy is moving target defense (MTD), which dynamically alters key distribution paths to complicate potential attacks. This paper proposes a systematic approach for secure and efficient key distribution in networks with untrusted relays, adopting a zero-trust model in which all nodes are potential threats. The model incorporates a behavior inspection module that dynamically evaluates and adjusts node behavior based on trust variations, further strengthening network security. Therefore, to improve network security and efficiency, we propose a novel spatiotemporal diversification scheme that alternates key distribution paths. An adaptive model optimizes key reconstruction, incorporating a penalty mechanism to detect and exclude suspicious relays. This approach provides a resilient framework for secure quantum communication that addresses the challenges of untrusted relay environments.

The main contributions of our work are summarized as follows:

• To address the security challenges in QKD networks with untrusted relays, we propose a spatiotemporal diversification-based key distribution method. This method dynamically distributes multiple keys across various paths, ensuring high security in end-to-end key distribution while meeting diverse security requirements. The proposed approach effectively overcomes the limitations of the existing methods.
• To meet the diverse security needs of applications, an adaptive path recovery process is introduced. The system employs a penalty-based strategy to detect and exclude suspicious relay nodes from path selection. It dynamically tests compromised routes, imposes penalties, and monitors node behavior to ensure compromised nodes are excluded from participation.
• Extensive simulations were conducted under various scenarios to evaluate the performance of the proposed method. The results demonstrate that our method significantly outperforms traditional multipath methods in terms of both security and efficiency.

The remainder of this paper is organized as follows: Section 2 provides the background research on QKD, covering key concepts such as point-to-point QKD, long-distance QKD, and multipath QKD. Section 3 presents the proposed zero-trust QKD system model, including network architecture, classification of trusted and untrusted relays, adversary model, and problem statement. Section 4 details the proposed spatiotemporal diversification-based multipath–multi-key distribution framework and its algorithmic components, including path selection criteria, routing procedures, execution phases, and an inspection/testing phase. Section 5 introduces the mathematical transmission model for multipath QKD networks based on zero-trust relays, incorporating probabilistic security analysis and a behavior inspection module. Section 6 presents the evaluation of the system through simulations, comparing the proposed approach with traditional multipath QKD methods without MTD. Finally, Section 7 concludes the paper and discusses potential future research directions. All notations used are defined in

Table 1. Notations table.

Variable	Definition
$R_i$	The ith routing path selected for key distribution
K	Global key reconstructed at the destination
$p_j$	Security probability of relay node j
$S_i$	Security state of the path i, $S_i\in \{0,1\}$ (1: secure, 0: insecure)
${\delta }_j\left(t\right)$	Temporal penalty imposed on node j at time t
$W_j$	Penalty weight assigned to relay node j
$P\left(S_i\right)$	Adjusted security probability of path $R_i$
$PT(A,B)$	Combined security fraction between source node A and destination node B
$P_{\min }$	Minimum acceptable security threshold
$ϵ$	Multiplicative security probability metric for path evaluation
${\mathrm{Cor}}_{S\left(P\right)}$	Path correlation metric for evaluating path diversity
${\mathrm{TH}}_{\mathrm{Corr}}$	Dynamically adjusted correlation threshold for path security evaluation
${\lambda }_{\mathrm{Cor}}$	Scaling factor used in path correlation threshold calculation
$W_j$	Penalty weight assigned to node j based on historical compromise data
$\Delta W$	Incremental penalty adjustment for nodes detected as compromised
$R\left(t\right)$	Reward function for network adjustments considering node security states
$\alpha ,\beta$	Weights assigned in the reward function to compromised and secure nodes, respectively
$d_i$	Transmission delay associated with path $R_i$
$E(A,B)$	Performance metrics balancing security and efficiency between nodes A and B
$\gamma ,\eta$	Scaling coefficients balance security and efficiency in the metric $E(A,B)$
$d_{\max }$	Maximum radius for penalizing nodes near compromised links
${\delta }_j\left(t\right)$	Temporal penalty imposed on node j at time t based on proximity to compromised links

.

2. Background and Related Works

Quantum key distribution (QKD) protocols leverage the principles of quantum mechanics to enable secure communication. Notable protocols include the Bennett–Brassard 1984 (BB84) protocol, the Ekert-91 (E91) protocol [9], and the measurement device-independent QKD (MDI-QKD) protocol [20].

As an illustrative example, we consider the BB84 protocol—a prepare-and-measure scheme—to outline the specific implementation procedure of QKD. This example elucidates how the key distribution operates over long distances and across multiple paths.

2.1. Point-to-Point QKD

In classical QKD communication, two parties, Alice and Bob, exchange secret keys via quantum and classical channels, as depicted in Figure 1. Alice sends “Qubits” to Bob, each determined by two random classical bits: one for the encoding basis and another for the bit to be sent (0 or 1) [9]. Bob measures the received “Qubits” using a randomly chosen basis and informs Alice of his measurement choices over a public channel. They then compare their chosen bases over a classical channel and retain only the measurement results where their bases match—a process known as sifting. In particular, during sifting, Alice and Bob agree on a subset of raw data for subsequent post-processing, which typically involves error correction, verification, and privacy amplification to establish a secret key [20]. If an eavesdropper, Eve, intercepts the quantum states during transmission, the no-cloning theorem ensures that any measurement by Eve will disturb the quantum states, introducing detectable errors. Consequently, any potential eavesdropping on QKD can be detected.

However, the practical implementation of point-to-point QKD is limited by factors such as photon loss and decoherence, which constrain the effective communication distance. To overcome these limitations, various methods, including the use of trusted relays and quantum repeaters, have been proposed to extend the range of QKD systems [21].

2.2. Long-Distance QKD

Extending QKD over long distances can be achieved using a hop-by-hop approach, employing trusted relays between distant nodes to mitigate distance limitations [21]. In this scenario, intermediate nodes establish secure keys with their adjacent nodes, effectively creating a chain of secure links that spans the desired distance.

For instance, consider a network where nodes B and C act as relays between nodes A and D, as illustrated in Figure 1. Node A establishes a secret key $K_1$ with node B, and node B establishes another key $K_2$ with node C. Through a process of key forwarding and re-encryption, node C eventually shares a key with node D, allowing A and D to share a global key.

This method relies on the assumption that all intermediate nodes are fully trusted. However, the security of such networks is highly dependent on the integrity of each relay node. If an adversary compromises any relay, the overall security of the key distribution process is jeopardized. To address this risk, alternative approaches, such as QKD networks with partially trusted relays and the development of quantum repeaters, have been proposed to enhance security and extend communication distances without relying solely on trusted nodes [22].

2.3. Multipath QKD

Multipath QKD has emerged as a critical strategy for improving security in networks containing partially trusted relays. The fundamental principle involves dividing the global key into multiple segments, each transmitted over distinct paths. Techniques such as secret sharing and error correction ensure secure key reconstruction at the destination. As depicted in Figure 1, for example, if Alice and Bob share $K_1$ on the first path (nodes A, B, and C) and $K_5$ on the second path (nodes D and E), the final key shared by Alice and Bob is $K=K_1\oplus K_5$. Even if one path is compromised, overall security can still be preserved, as Eve would need to intercept all key segments to reconstruct the final key.

Chen et al. [23] presented a hybrid-trusted QKD network using semi-trusted nodes and multipath transmission, significantly improving efficiency and load balancing. However, their static trust assumptions limit adaptability against dynamically compromised nodes. Similarly, Li et al. [24] proposed a progressive recovery scheme employing deep reinforcement learning (DRL) for rapid restoration of the network after failure. Although this model is effective for recovery, it lacks proactive defensive measures for ongoing threats. Moreover, Sharma et al. [25] developed a DRL-based routing strategy that reduces blocking probabilities in optical QKD networks. Although efficient, their method assumes an inherently secure infrastructure and does not address dynamic compromises. Kong et al. [22] optimized routing by minimizing the number of activated trusted nodes, significantly reducing vulnerabilities but remaining static in trust management. Yu et al. [26] introduced a collaborative routing algorithm, improving key distribution rates but employing static strategies without real-time adaptability. In [27], the authors explored joint optimization for routing and photon source provisioning, enhancing resource efficiency. However, their framework does not dynamically adapt to real-time node compromise.

Wen et al. [17] investigated a probabilistic multipath routing model, improving security through stochastic selections but lacking dynamic penalty mechanisms for suspicious nodes. The authors in [28] studied multipath routing for entanglement distribution, significantly increasing distribution rates yet failing to explicitly manage security threats from untrusted relays. In [29], the authors proposed routing strategies that minimize node compromise vulnerabilities using multiple non-overlapping paths but lacked dynamic threat detection. Lin et al. [30] and Wang et al. [19] introduced partially trusted routing algorithms in ring networks and segment-based multipath methods, respectively, achieving security enhancements but restricted by static segmentation and topology limitations.

The reviewed studies highlight several unresolved challenges: (1) Limited dynamic mechanisms for identifying and managing compromised nodes in real time; (2) static or semi-static assumptions about node trust, hindering adaptability and resilience; (3) insufficient integration of proactive and reactive security strategies to actively mitigate attack scenarios. Addressing these gaps, this paper proposes a zero-trust, adaptive QKD routing framework employing an MTD-based approach. Our model dynamically diversifies routing paths, incorporates recursive penalty mechanisms to isolate compromised nodes, and utilizes adaptive key transmission strategies based on real-time security assessments. This comprehensive strategy significantly improves network security and resilience, directly overcoming limitations identified in the previous literature.

3. System Model

3.1. Network Model

In this paper, we investigate a zero-trust QKD relay network where no relay is fully trusted. The adoption of a zero-trust architecture, traditionally used in cybersecurity, assumes that threats could exist on both internal and external networks and that no actors or systems should be automatically trusted [31]. This philosophy is particularly powerful in QKD, where trust assumptions can be critical vulnerabilities [32].

The proposed system comprises a central key management server (KMS) that functions as the control plane (CP), responsible for overseeing network operations and managing key distribution to the data plane (DP). Each quantum node is equipped with quantum devices, a classical information processing unit for encryption and decryption, and a quantum key pool (QKP) to manage local keys with neighboring nodes. This architecture reflects the principles of software-defined networking (SDN), which separates network control from data forwarding, facilitating flexible network management—a concept increasingly applied in QKD networks to enhance scalability and adaptability [33,34].

In the proposed model, the controller dynamically selects route combinations based on the involved relays, while the QKD nodes temporarily transmit key pairs. Implementing an adaptive MTD approach, the model aims to confuse potential attackers by altering multidimensional parameters. This strategy, discussed in more detail in Section 4.1, leverages the unpredictable nature of quantum processes to enhance security dynamically.

To outline security challenges, this paper introduces general relay types and the adversary model within the network in subsequent sections.

3.1.1. Trusted/Untrusted Relays

Relay nodes are categorized into two groups, namely, trusted and untrusted. Trusted relays implement stringent security measures, including robust cybersecurity defenses, such as advanced quantum-resistant firewalls and access control mechanisms (i.e., memory encryption), to prevent illegal access and unauthorized use of sensitive resources. They are typically deployed in highly secure environments to ensure network integrity.

In contrast, untrusted relays have lower security guarantees, making them susceptible to interception by eavesdroppers. Their security measures are less robust, potentially rendering them vulnerable to unauthorized access and compromise. Recent studies have explored varying trust levels in QKD networks, introducing classifications such as full access trust (FAT), partial access trust (PAT), and no access trust (NAT), each defining the degree of trust required for relays within the key management system [35].

For example, the trusted QKD relay network includes quantum nodes and quantum links, which continuously generate quantum keys for neighboring nodes. Multi-hop technology is employed for secure end-to-end key relays when remote communication is needed. The SDN controller assumes a central role in QKD decision-making, effectively separating network control from QKD equipment and facilitating flexible network management [23,36]. The architecture is organized into four layers, as illustrated in Figure 2.

Application Layer

This layer is composed of applications running on user terminals and ensures secure communication between applications using the keys provided by the key management layer. The control center formulates suitable strategies based on varying application key requests.

Controller Layer

This layer—considered the core of the QKD network architecture—is primarily responsible for the unified scheduling of resources and the coordination of communication between layers.

Key Management Layer

This layer receives keys generated by QKD links in the quantum layer and manages the life cycle of keys, including key generation, destruction, and storage in QKP. The key management layer serves the crucial role of providing keys to the application layer while actively participating in information interactions with the application layer, the control layer, and the quantum layer. It is noteworthy that in our model, we have consolidated the control and key management layers, allocating them collectively as CP.

Quantum Layer

It functions as the infrastructure layer, establishing connections with physical QKD hardware devices. These devices carry out the generation of unconditionally secure quantum keys, guided by CP instructions. The quantum layer is responsible for processing both quantum and classical information and performing critical functions, such as qubit exchange, key screening, and key extraction. In our model, this layer is denoted as DP.

3.1.2. Adversary Model

In end-to-end key distribution, secret keys are converted from ciphertext to plaintext at relay nodes, making these points attractive targets for eavesdroppers. Each untrusted relay node has a security probability indicating the likelihood that it has not been compromised. Attackers can only access key information from successfully compromised relays.

The security of a single-path key distribution depends on all uncompromised relay nodes on the path. In contrast, multipath key distribution security relies on at least one path remaining secure.

Implementing an MTD strategy, which involves dynamically changing network parameters to confuse potential attackers, can further enhance security. This approach complicates the attack process and requires adversaries to adapt to changing network configurations. Therefore, in our proposed model, illustrated in Figure 3, the attacker faces the challenge of deciphering multidimensional parameters, such as ensuring the security of at least one path and the generated key pairs at the correct time, to successfully decrypt the transmitted key. Moreover, the attack process in our model is further complicated by the adaptive penalty-based approach. This means that even if the attacker succeeds in compromising a particular node, this node will face penalties in subsequent transmissions, requiring the attacker to adapt and change the targeted relay to achieve further success.

3.1.3. Problem Statement

While many QKD networks currently rely on trusted relay techniques, the security risks posed by partially trusted or untrusted relay nodes in large networks cannot be ignored. Addressing these risks requires a shift from the assumption that all relay nodes are fully trusted, prompting the development of zero-trust relay approaches.

Existing solutions, such as multipath QKD strategies, aim to protect key distribution in networks with partially trusted relays. These approaches can be categorized into network connectivity schemes, which tolerate a specified number of compromised nodes [16], and probabilistic approaches, which analyze key distribution security based on the security probability of untrusted relays and paths [17,19]. However, these studies often overlook the impact of key distribution path selection, diverse user security requirements, and compromised node detection. To address these limitations and improve key distribution security while balancing efficiency, a multipath-based spatiotemporal diversification approach is introduced.

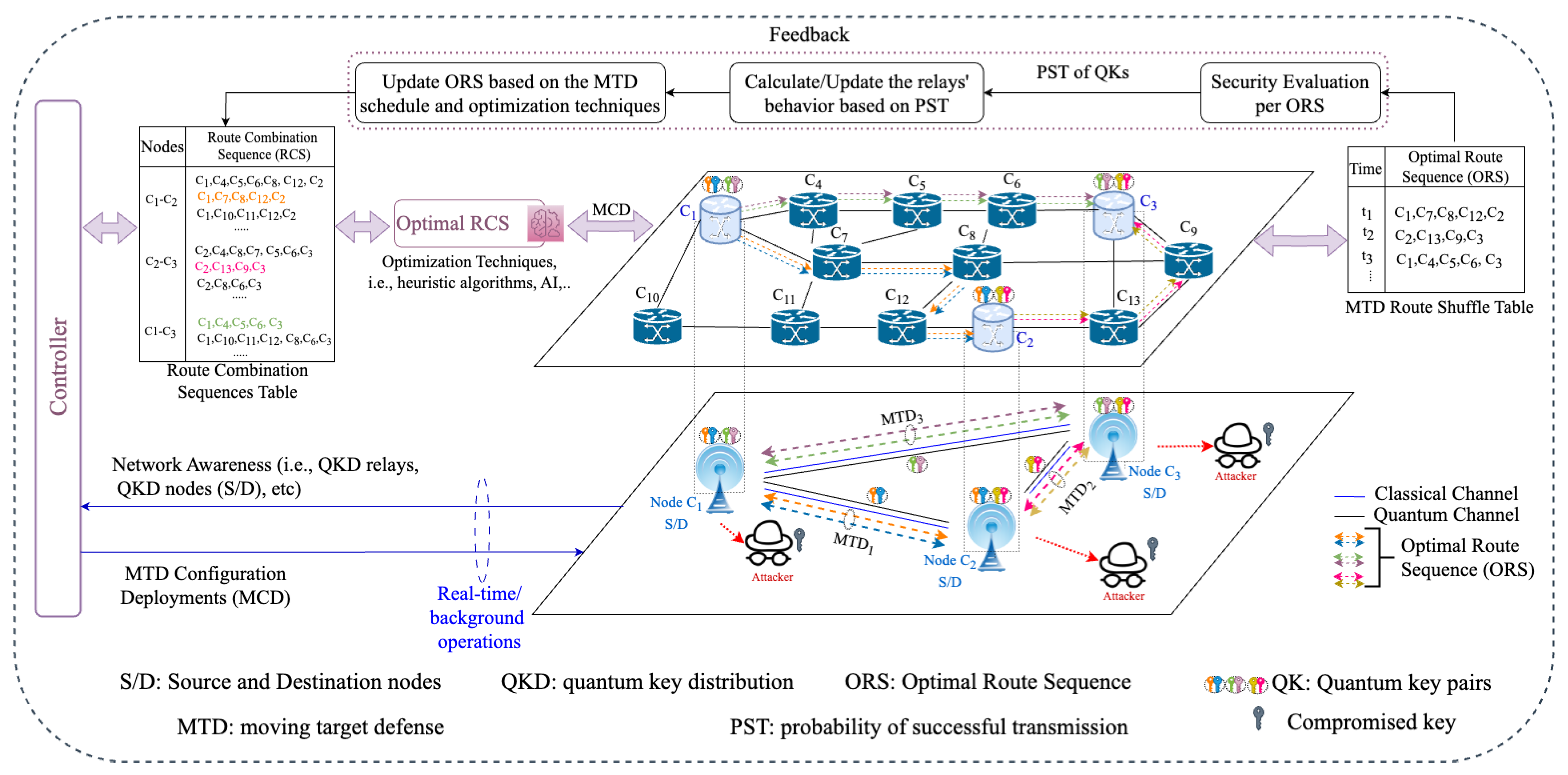
4. The Proposed Key Distribution Framework

4.1. A Spatiotemporal Diversification-Based Multipath–Multi-Key Distribution

The proposed framework operates in three primary stages: selection and execution phases for multi-key distribution on different routes, and the testing phase to detect compromised nodes. The basic representation of the proposed model is shown in Figure 4.

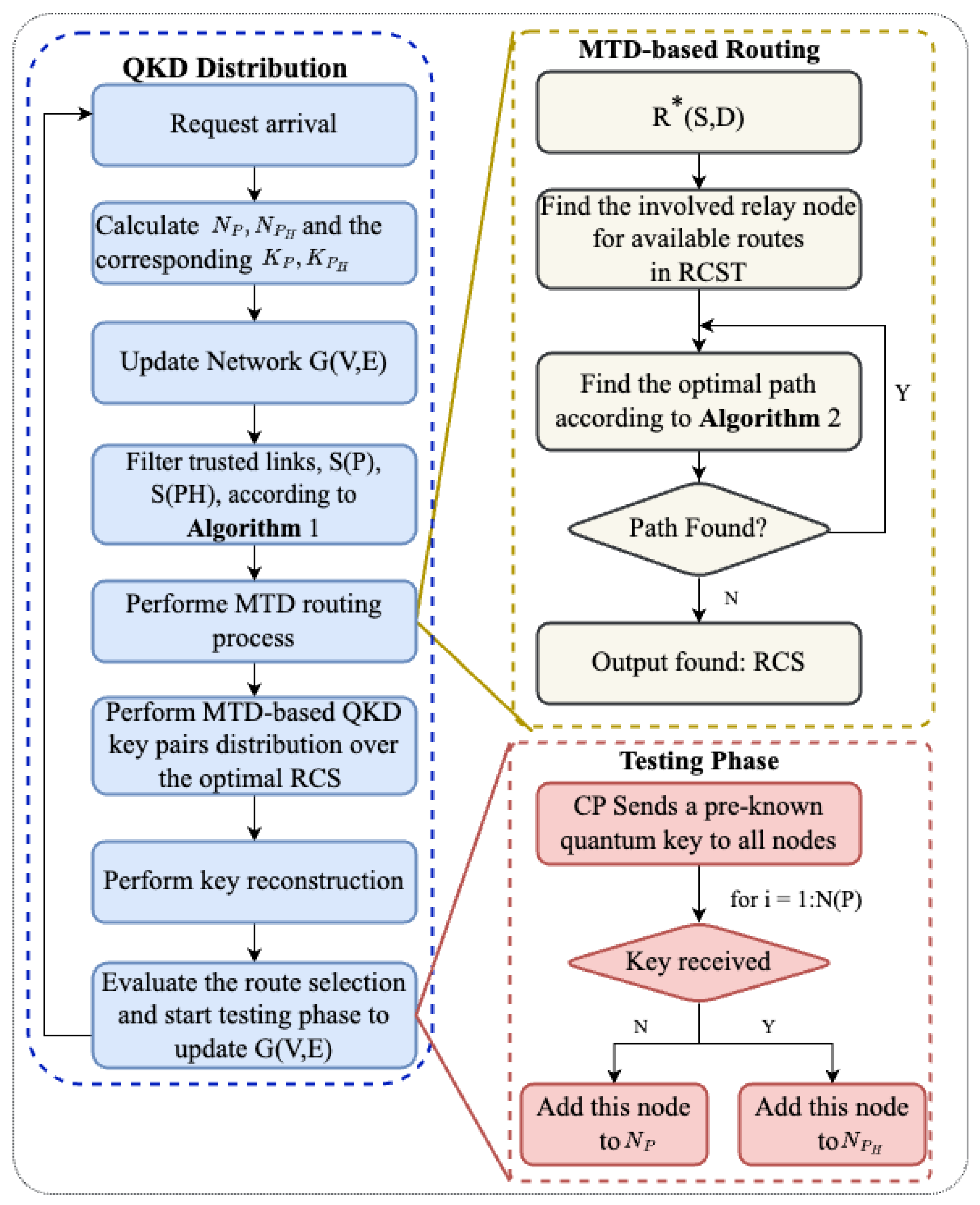
4.1.1. Selection Phase

Upon receiving a key distribution request, the central server of the CP determines optimal routing paths and key reconstruction strategies based on the current state of the network and predefined security requirements, as detailed in Section 4.2.1. This phase involves selecting paths that minimize the risk of interception and ensure efficient key distribution. Algorithms such as the K-shortest path (KSP) and enhanced versions of Yen’s algorithm are utilized to identify candidate paths with minimal correlation, thereby reducing the likelihood of common vulnerabilities across these paths [37]. After path selection, the server sends the MTD configuration deployment pattern (MTD-CDP) to the network relays.

4.1.2. Execution Phase

Keys are distributed across the selected paths with spatiotemporal diversification, as described in Section 4.2.2. In this phase, multiple key pairs are generated and transmitted through different routes at each time step. A flexible key reconstruction scheme is used to optimize the security and efficiency of the end-to-end key distribution, allowing for dynamic adjustments based on varying security requirements. This approach is analogous to multipath-based quasi-real-time QKD schemes in SDNs, enhancing the resilience of the key distribution process against potential eavesdropping.

4.1.3. Testing Phase

The core concept of this phase is that, in the event of a successful interception of a relay node, the key can be rerouted to alternative paths during the same time step. Unlike conventional multipath distribution methods, where the process stops after a key compromise, the proposed model activates an inspection/testing phase to identify and evaluate the compromised nodes. This phase introduces a mechanism to assess all nodes involved in the key distribution process, assigning rewards or penalties based on their behavior. Compromised nodes are identified and penalized, and if a node consistently fails to improve its behavior, it is excluded from the network. This proactive approach not only addresses vulnerabilities as they occur but also adapts to potential threats dynamically, maintaining robust security over time.

4.2. A Multipath–Multi-Key Distribution Algorithm

4.2.1. Path Selection Criteria

The algorithm for selecting trusted paths addresses the K max–min problem through a two-phase approach, employing the KSP algorithm, specifically Yen’s algorithm, to initially identify a diverse set of candidate paths that minimize common security threats. The second phase uses a modified greedy algorithm to finalize the selection, prioritizing path isolation to reduce simultaneous compromises. This method leverages dynamic link weighting based on real-time network data and historical security incidents to adjust path classifications [23,38,39].

Assuming that the source node is S, the destination node is D, and there are k paths that need to be selected, the specific steps are outlined in Algorithm 1.

Algorithm 1: Path selection algorithm.

In particular, correlation (Cor) measures the overlap of risk factors between paths, such as shared physical infrastructure or geographical proximity, which could expose paths to common vulnerabilities. In our model, we consider the correlation among all involved paths to ensure a comprehensive evaluation of path suitability. This consideration helps maintain a balance between path diversity and network resource utilization. Balancing these factors is essential for efficient and secure key distribution [29]. The correlation of a set of paths is defined as follows:

$${\mathrm{Cor}}_{S\left(P\right)}={\displaystyle \frac{{\sum }_{L\in S\left(L_{\mathrm{comm}}\right)}({\mathrm{freq}}_L-1)}{{\sum }_{P_i\in S\left(P\right)}\mathrm{card}\left(S{\left(L\right)}_{P_i}\right)}}$$

(1)

where $S\left(P\right)$ represents the set of paths, ${\mathrm{freq}}_L$ represents the number of paths containing the link L, and $\mathrm{card}\left(S{\left(L\right)}_{P_i}\right)$ represents the number of links on the path i. In addition, the correlation threshold ($T{H}_{\mathrm{Corr}}$) is a dynamically adjusted threshold that helps to determine acceptable risk levels for path correlations, allowing the system to adapt to varying security needs and external conditions [40]. This threshold is determined using a scaling factor (${\lambda }_{\mathrm{Cor}}$), with a value range between $(0,1)$, applied to the average correlation, $\overline{\mathrm{Cor}}$, and can be formulated as follows:

$$T{H}_{\mathrm{Corr}}={\lambda }_{\mathrm{Cor}}·\overline{\mathrm{Cor}}$$

(2)

4.2.2. Routing Procedure

The search for optimal routing combination paths (RCS) is a critical step in the proposed QKD network. In traditional networks, routing algorithms such as Dijkstra prioritize the shortest path based on additive metrics such as distance or time. However, QKD networks require a focus on security due to the quantum nature of the key distribution [19]. The proposed multiplicative security probability metric is defined as follows:

$$ϵ=\prod _{j=1}^{m_i}{p}_j$$

(3)

where $p_j$ represents the security probability of node j and $m_i$ is the total number of nodes on the path $R_i$, effectively capturing the compounded security risks associated with each relay. This approach ensures that paths with higher overall security are preferred, aligning with the need for secure key distribution in QKD networks [39]. This multiplicative metric contrasts with the additive metrics used in classical algorithms such as Dijkstra, necessitating a modified approach for path-finding. Therefore, the proposed model adapts the classical Dijkstra algorithm into what might be termed ‘ExDijkstra’, which optimizes paths based on a non-additive, monotonically decreasing function of path security, reflecting a more holistic approach to secure communications in quantum networks. This modification allows the algorithm to prioritize paths that offer a balance between length and security, which is crucial for the efficient operation of QKD networks [41].

Addressing time constraints through proactive key generation at the source node is a practical solution. By generating QKD key pairs in advance, the network can select faster routes without altering the physical path, thereby enhancing both efficiency and security [42]. This strategy aligns with the need for timely key distribution in QKD systems.

Finally, in the proposed model, the implementation of a test mode to detect and analyze the node’s suspicious behavior adds an essential layer of security. This feature enables the network to identify and respond to potential threats promptly while maintaining the integrity of the key distribution process. Although node-disjoint paths prevent untrusted nodes from accessing multiple keys, they can lead to longer paths and increased resource consumption [19,28]. The reliance of the proposed model on behavioral evaluations over time rather than predefined trust values offers a more adaptable solution suitable for zero-trust environments, as illustrated in Figure 5.

4.2.3. Selection Phase

CP plays a pivotal role in determining the most secure and efficient routes for QKD between the source and destination nodes. The process begins with an initially empty route combination sequence table (RCST), which is then populated based on a comprehensive analysis of current network conditions, historical data, and potential security threats.

Process Overview

• Data collection: The CP collects and analyzes real-time and historical network data, including traffic patterns, previous security breaches, and ongoing threats. The data help to predict potential vulnerabilities and optimize route selections.
• Path enumeration: Utilizing algorithms like those described in Section 4.2.1, the CP enumerates all possible paths that could potentially connect S and D. This enumeration considers not only the shortest paths but also alternative routes that may offer greater security against potential eavesdropping or quantum attacks. Techniques such as the tandem queue decomposition (TQD) policy are utilized to achieve secure and efficient packet routing by considering time-varying key availability and link capacities [41].
• Optimization and selection: Each potential route combination is evaluated as presented in Algorithm 1, which assesses routes based on their security probability and operational efficiency. The algorithm prioritizes routes with the highest security metrics, ensuring compliance with quantum security standards. To provide a more comprehensive assessment of route security, metrics such as the quantum bit error rate (QBER) and key generation rates (KGR) could be incorporated into the optimization process [43].
• Threshold evaluation: The security probability of each proposed distribution is compared against a predefined threshold ${\Delta }_{\mathrm{Sec}}$, which represents the minimum acceptable security level, typically set above the standard achieved by classical Dijkstra-based routing methods. This threshold should be set according to the specific security requirements of the network and can be dynamically adjusted to respond to evolving threats [44].
• Iterative improvement: If the selected route combination (RCS, R) meets the security and efficiency criteria, it serves as a baseline for further optimization in subsequent iterations. This iterative process continues until no significant improvements in the route combinations are found, ensuring that the network adapts dynamically to changing conditions and requirements [45].

MTD-Based Multi-Pathfinding

Following the selection of an optimal RCS, the CP configures multiple paths to distribute quantum keys. This process involves:

• Path optimization: For each pair of keys, the CP utilizes feedback from previous distributions and current network data to select the most secure and efficient paths. This step is vital to maintaining high security, especially in environments with dynamic threat landscapes. To enhance this process, an adaptive routing strategy that considers key consumption and link state information is implemented [46].
• Dynamic adaptation: The optimization algorithm continuously adjusts the selected paths based on real-time feedback and network conditions. This dynamic adaptation mitigates new or evolving threats, ensuring that the key distribution remains secure [45].
• Termination: The algorithm terminates when all possible secure paths have been optimized or when all key pairs have been successfully assigned secure paths for distribution. Establishing clear termination criteria based on network performance metrics ensures efficient resource utilization.

4.2.4. Execution Phase

Since different applications have varying security requirements, implementing a flexible key reconstruction method that allows dynamic adaptation of the number of keys needed for reconstruction can significantly improve key distribution efficiency. This adaptability ensures that the system can meet different security requirements without unnecessary resource expenditure.

4.2.5. Inspection/Test Phase

After selecting optimal paths with key distribution, the CP initiates a testing phase to identify compromised nodes, as follows:

Penalty Assignment Mechanism

Assigning penalties $\pm W$, where W is adjusted based on node behavior, to nodes based on their proximity to potential attacks is a strategic method to mitigate risks [47]. Recognizing that attackers can move in space, making a compromised link more likely than a compromised node, the system assigns a smaller penalty (W) to nodes close to compromised nodes [22]. By imposing higher penalties on nodes closer to detected threats, the system can dynamically adjust routing decisions to avoid compromised areas. Implementing such a penalty system can improve the resilience of the QKD network against attacks [38].

Node and Link Compromise Detection

In QKD networks, the security of intermediate nodes often referred to as trusted nodes, is paramount. If a node is compromised, it can undermine the entire key distribution process. Therefore, detecting compromised nodes or links is essential. The proposed method involves sending pre-known quantum keys to all nodes and monitoring their responses to identify any anomalies that may indicate a compromise. This approach is consistent with strategies discussed in recent studies, which emphasize the importance of monitoring node behavior to detect potential security breaches [7,48].

Time as a Correction Factor

Incorporating time as a correction factor where the absence of attacks detected over a significant period suggests the correctness of CP selections [49].

4.3. A Multipath–Multi-Key Distribution Algorithm Complexity Analysis

The complexity of the proposed spatiotemporal diversification-based multipath–multi-key distribution framework is analyzed in its core components: path selection, routing, and security evaluation mechanisms.

(1)

The path selection process uses an improved KSP algorithm, specifically an optimized version of Yen’s algorithm, to identify secure and disjoint paths for key distribution. The computational complexity of Yen’s algorithm for finding K shortest paths in a graph G(V,E) with $m=\left|V\right|$ nodes and $n=\left|E\right|$ edges is $O(K·(n+mlogm\left)\right)$ [23]. In addition, a correlation-based path optimization step is introduced to minimize redundancy and reduce attack surfaces, adding an overhead of $O\left(K^2\right)$. Therefore, the overall complexity of the path selection phase is $O(K·(n+mlogm)+K^2)$.

(2)

The routing procedure employs an adaptive security-aware ExDijkstra algorithm, which evaluates paths based on a multiplicative security probability metric instead of an additive shortest-path criterion. The traditional Dijkstra algorithm has a complexity of $O(mlogm+n)$, but with additional security computations, the proposed model introduces an overhead P for security evaluations, leading to a worst-case complexity of $O(mlogm+n+P)$. Furthermore, the inspection module dynamically evaluates the trustworthiness of the nodes and enforces penalties for compromised relays. This phase consists of compromised node detection ($O(K·M)$, where M is the number of monitored relays). Combining these components, the total complexity of the proposed model is given by $O(K·(n+mlogm)+K^2+mlogm+n+K·M)$. Since the number of selected paths (K) and monitored nodes (M) is significantly smaller than the total number of network nodes (m) and edges (n), the proposed algorithm remains computationally efficient and scalable.

5. Transmission Model of Multipath QKD Network-Based Zero-Trust Relays

In [50], the authors proposed a formula to quantify the security rate in multipath networks for QKD. The QKD network topology is generally designed to reflect real-world conditions, prioritizing adaptability to various scenarios. As illustrated in Figure 5, node A performs a multipath key distribution to node B, utilizing various path combinations over time. The optimal paths are dynamically selected using an optimization algorithm that considers network conditions and pre-defined security metrics. These paths facilitate the distribution of multiple keys while enhancing overall security through redundancy and spatiotemporal diversification.

5.1. Selection Phase: Mathematical Representation

According to the illustrated model in Figure 5, in a zero-trust QKD relay network, the key negotiation between node A and node B occurs via multiple paths $\{R_1,R_2,\dots ,R_n\}$. The network comprises n paths, each containing $m_i$ nodes. Let b denote the number of public nodes in the paths.

For a given path $R_i$, the security state is represented by $S_i\in \{0,1\}$, where $S_i=1$ indicates the path is secure and $S_i=0$ indicates the path is insecure. In the proposed algorithm, the paths dynamically change over time, ensuring improved security. The total probability of security of a given path $R_i$ depends on the number of nodes $m_i$ on that path $R_i$, the trust levels $p_j$ of the node j on that path, and the temporary penalties $\delta \left(t\right)$ imposed for suspected compromise. Therefore, the adjusted security probability for the $R_i$ path is defined as follows:

$$P\left(S_i\right)=\prod _{j=1}^{m}max\{0,\left(p_j-{\delta }_j\left(t\right)\right)\},0\le {\delta }_j\left(t\right)<p_j$$

(4)

where ${\delta }_j\left(t\right)$ is the temporal penalty, defined as ${\delta }_j\left(t\right)={\displaystyle \frac{W_j}{t^k}},0\le {\delta }_j\left(t\right)<p_j,k>0$, where $W_j$ is the penalty weight based on historical observations of the node compromise, and t is the time. This time-dependent penalty reduces trust in the suspected nodes over time.

In this paper, the combined security fraction is defined as $P_T(A,B)$, where it describes the probability that a transmission with multipath key distribution is secure. The combined security fraction $P_T(A,B)$ on the n paths is defined as follows:

$$\begin{array}{c}\hfill P_T(A,B)=\left\{\begin{array}{cc}1-{\prod }_{i=1}^n(1-P\left(S_i\right))\hfill & \mathrm{if}\mathrm{at}\mathrm{least}\mathrm{one}\mathrm{path}\mathrm{is}\sec \mathrm{ure}\hfill \\ {\prod }_{i=1}^n(1-P\left(S_i\right))\hfill & \mathrm{if}\mathrm{all}\mathrm{paths}\mathrm{are}\mathrm{insecure}\hfill \end{array}\right.\end{array}$$

(5)

If $P_T(A,B)\ge P_{\min }$, where $P_{\min }$ is the minimum acceptable security threshold, the transmission is deemed secure. Consequently, the distribution function of the transmission security state $S\left(T\right)$ is defined as follows:

$$S\left(T\right)=\left\{\begin{array}{cc}1\hfill & P_T(A,B)\ge P_{\min }\hfill \\ 0\hfill & P_T(A,B)<P_{\min }\hfill \end{array}\right.$$

(6)

5.2. Execution Phase: Probabilistic Model

Integrating public nodes modifies the security fraction by accounting for their behaviors. The adjusted security fraction for n paths considering b public nodes is calculated as follows.

$$P_T(A,B)=\prod _{u=1}^b{p}_u\left(t\right)·\left[1-\prod _{i=1}^n\left(1-\prod _{j=1}^{m-b}P\left(S_i\right)\right)\right]$$

(7)

where $p_u\left(t\right)$ is the security probability of the public nodes over time. In addition, ${\prod }_{j=1}^{m_i-b}$ is used to exclude the influence of the public nodes. The proposed model adjusts security metrics to account for public node behavior.

5.3. Behavior Inspection Module

In QKD environments, particularly under zero-trust conditions, network nodes cannot be implicitly considered secure. Hence, a Manhattan distance metric is adopted to quantify the proximity of the nodes in a two-dimensional mesh topology, where each node is represented as coordinates $(x,y)$, where $x,y\in \{0,1,\dots ,m-1\}$. The distance between two nodes is measured as the Manhattan distance: $L[(x_1,y_1);(x_2,y_2)]=|x_2-x_1|+|y_2-y_1|$ [17]. When a link $R_i$ between the nodes $(x_1,y_1)$ and $(x_2,y_2)$ is compromised, penalties are assigned to the nearby nodes to prevent further security breaches. Specifically, any node located within a threshold $d_{\max }$ from either endpoint of the compromised link is penalized. Therefore, node $(x,y)$ receives an increase in penalty if $L_j=min\{L[(x,y);(x_1,y_1)],L[(x,y);(x_2,y_2)]\}\le d_{\max }$. To detect compromised nodes, the inspection module iteratively adjusts node penalties $W_j$ based on their behavior. The proposed model incorporates periodic testing and adaptive penalty mechanisms to improve network resilience.

5.3.1. Penalty Assignment

$$\begin{array}{c}\hfill W_j=\left\{\begin{array}{c}{W}_j^{\left(0\right)}+\Delta W,\mathrm{if}{L}_j\le d_{\max }\hfill \\ W_j^{\left(0\right)},\mathrm{O}.\mathrm{W}\hfill \end{array}\right.\end{array}$$

(8)

where $W_j^{\left(0\right)}$ is the initial penalty and $\Delta W$ is an increment factor. The system dynamically penalizes suspected nodes and reallocates keys, ensuring the security fraction $P_T(A,B)$ remains above $P_{\min }$.

5.3.2. Reward Function for Network Adjustments

$$\begin{array}{c}\hfill R\left(t\right)=\beta \sum _{j\in M_S}{p}_j\left(t\right)-\alpha \sum _{k\in M_C}{\displaystyle \frac{1}{L_k}}\end{array}$$

(9)

where $\alpha$ is the weight used to penalize compromised nodes and $M_C$ is the set of compromised nodes. Moreover, $\beta$ is the weight used to reward secure nodes and $M_S$ is the set of currently secure nodes considered in the routing at time t. It should be mentioned that the reward calculation excludes the zero-distance scenario, that is, $d_k\ne 0$.

5.4. Efficiency and Security Trade-Off

To balance security and efficiency, the performance metric $E(A,B)$ jointly integrates security probability and the delay as follows:

$$E(A,B)=\gamma ·P_T(A,B)-\eta ·D(A,B)$$

(10)

where $\gamma$ and $\eta$ are the security and efficiency scaling coefficients, respectively. Moreover, $D(A,B)$ represents the average transmission delay. The delay $D(A,B)$ accounts for both path length and network load and can be calculated as follows:

$$\begin{array}{c}\hfill D(A,B)={\displaystyle \frac{{\sum }_{i=1}^n{d}_i·\left(P\left(S_i\right)\right)}{{\sum }_{i=1}^{n}P\left(S_i\right)}}\end{array}$$

(11)

where the numerator ${\sum }_{i=1}^n{d}_i·\left(P\left(S_i\right)\right)$ represents the expected delay, considering the security probability as a weighting factor. Secure paths (higher $P\left(S_i\right)$) have more influence on the average delay calculation, reflecting realistic path utilization.

This approach ensures a balance between delay and security that reflects real operational conditions. The paths used more frequently (secure paths) accurately dominate the average delay calculation, and this logically aligns with the standard QKD network optimization practices.

6. Performance Evaluation

In this section, we conduct experiments to assess the performances of our proposed algorithm for the QKD network based on multipath–multi-key spatiotemporal diversification in a zero-trust environment. We denote our proposed MTD-based framework as the “proposed method”. To establish a baseline for comparison, we refer to benchmark schemes that do not involve untrusted relay nodes or incorporate adaptive algorithms to avoid compromised relay [51]. In particular, this benchmark relies on multipath selection in a zero-trust environment. This benchmark scheme is denoted as the “traditional method”.

Figure 6 illustrates the time required to execute multipath QKD using both the proposed and traditional methods. As the number of nodes increases, the delay also increases in both frameworks. It is important to note that the proposed method employs more delay due to additional steps needed to determine the best path and transmit multiple QKD pairs simultaneously. Observing Figure 6, we can see that both methods initially achieve similar results, but the gap between them increases as the number of nodes increases.

In Figure 7, the plot illustrates the success rate of the attack versus the pervasiveness of the attacker, which refers to the extent or degree of the presence or influence of the attacker within the system. Attacker pervasiveness represents how extensively an attacker can penetrate or impact the system’s security. In this context, it reflects the percentage or proportion of the network compromised or controlled by the attacker. As the attacker’s pervasiveness increases, there is a greater likelihood for the attacker to exploit system vulnerabilities and intercept QKD transmissions. However, increasing the number of transmission paths reduces the attack success rate by enhancing system complexity and making it more challenging for the attacker to compromise the system. The proposed method consistently achieves a lower attack success rate compared to traditional methods, even with a lower number of active transmission paths. Specifically, at a 20% attacker pervasiveness level, the proposed spatiotemporal diversification algorithm with two active paths demonstrates a 97.22% lower success rate compared to the traditional method.

In Figure 8, the total security percentage versus the attacker’s pervasiveness is depicted as a function of different multipath selections ($n=2,4,6$) for both the proposed and traditional methods. The total security percentage of the system increases as the number of active paths increases and decreases as the attacker’s pervasiveness increases. Notably, the proposed method enhances overall security by nearly 35% when the attacker’s pervasiveness is 20%. Remarkably, even in the worst-case scenario with 80% attacker pervasiveness, the proposed spatiotemporal diversification algorithm achieves a substantial 90% overall security percentage. In conclusion, as we can see from Figure 7 and Figure 8, leveraging additional transmission paths enhances the system’s dimensionality, thereby mitigating the impact of pervasive attackers.

In Figure 9, the attack success rate versus multipath selections as a function of the QKD pairs (number of QKD = 1, 3, 5) for both the proposed and traditional methods is illustrated. Remarkably, the attack success rate decreases as the number of QKD pairs increases. It’s noteworthy that the proposed method achieves a significant improvement over the traditional method, with a reduction of 91.42% in the attack success rate for single key transmission and 75% for multiple QKD pairs.

In Figure 10, the total security percentage versus multipath selections is depicted as a function of the QKD pairs (number of QKD = 1, 3, 5) for both the proposed and traditional methods. Notably, as the number of QKD pairs increases, the proposed model demonstrates a security enhancement of 79.6% compared to the traditional approach. Even in a worst-case scenario, such as single-key transmission typical in traditional approaches, the proposed method achieves a significantly higher security percentage, exceeding the traditional method by almost 71.15%.

The analysis of multiple figures, including Figure 7, Figure 8, Figure 9 and Figure 10, reveals that the proposed algorithms outperform traditional methods in terms of total success rate and attack success rate. Notably, leveraging advanced techniques like multipath selection and transmitting multiple keys enhances system security and resilience. As the number of transmitted keys and exploited paths increases, the proposed methods consistently achieve higher security percentages and success rates, underscoring their effectiveness. Increasing the number of transmitted keys has a more significant impact on system performance than exploited paths. The proposed method exhibits versatility and can be applied in various scenarios, including real-time applications, demonstrating its potential for practical implementation in real-world QKD systems. Overall, the findings emphasize the effectiveness of innovative algorithms in mitigating security risks and improving system performance, paving the way for more secure communication infrastructures in the face of evolving threats.

In summary,

Table 2. Comparison of overall results between the proposed and traditional methods.

Metric	Description	Proposed vs. Traditional Method
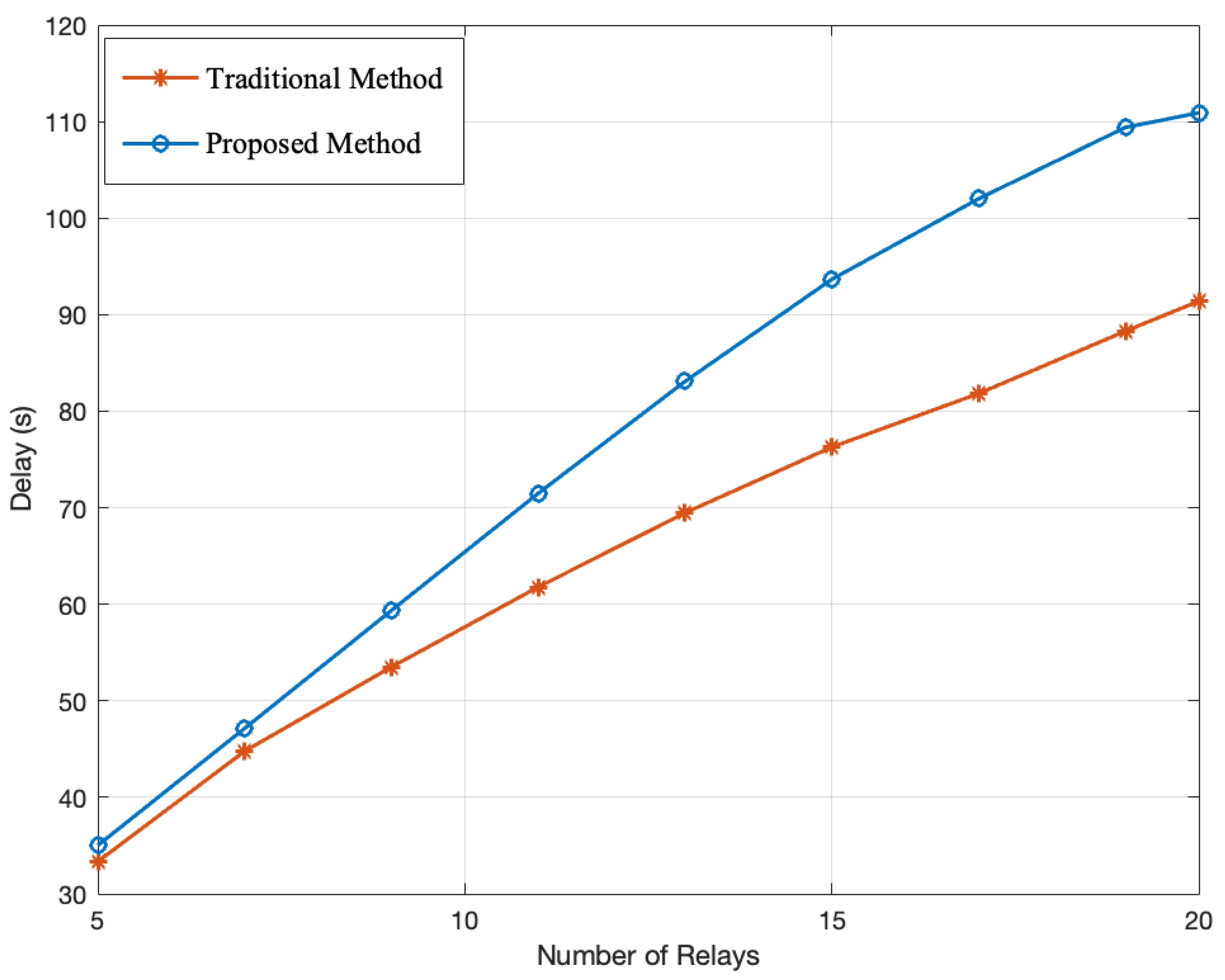
Execution time	Multipath QKD	Higher due to additional security processes, while traditional methods have lower execution time but lack adaptive security mechanisms.
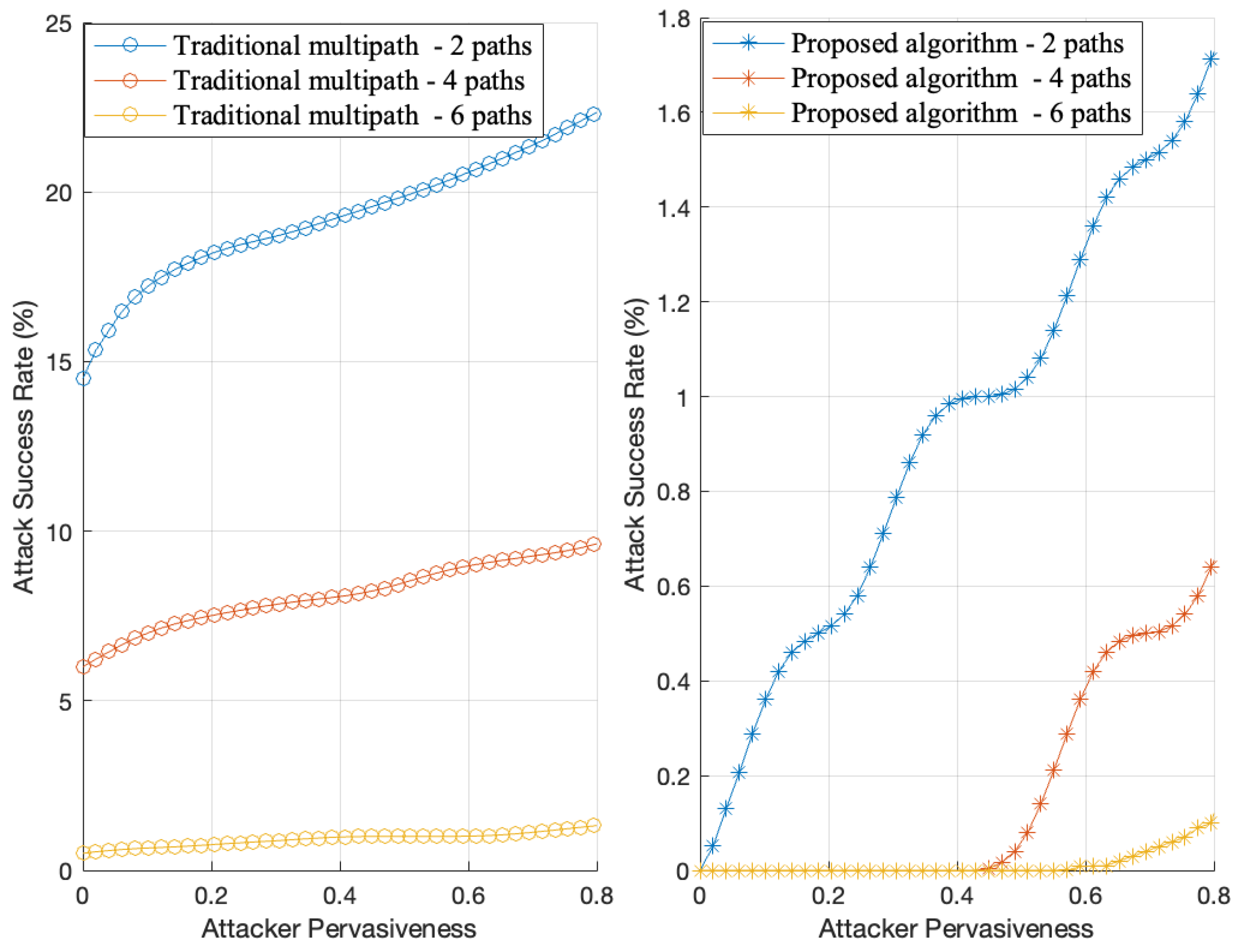
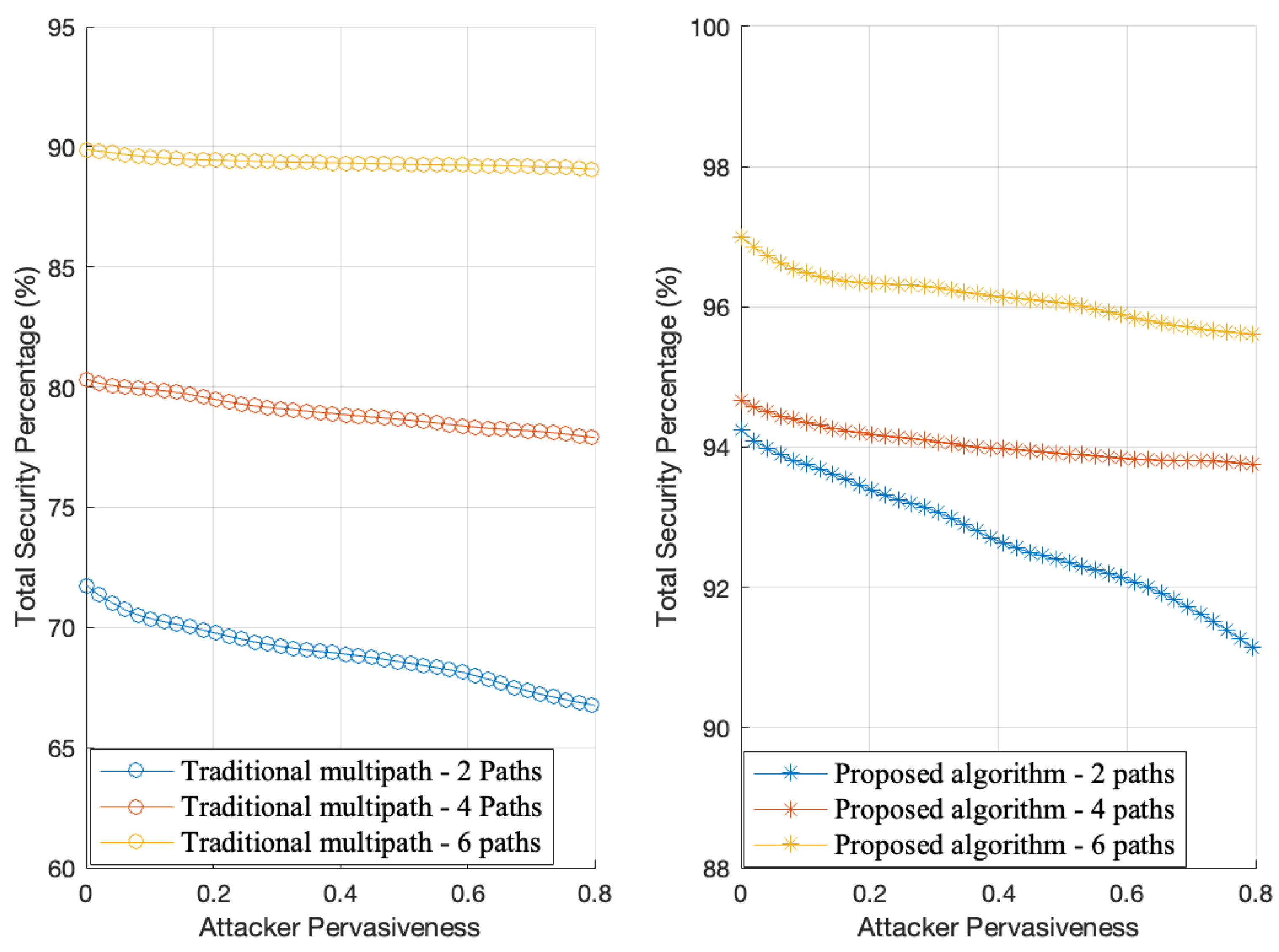
Attack success rate	20% attacker pervasiveness	97.22% lower than traditional methods;
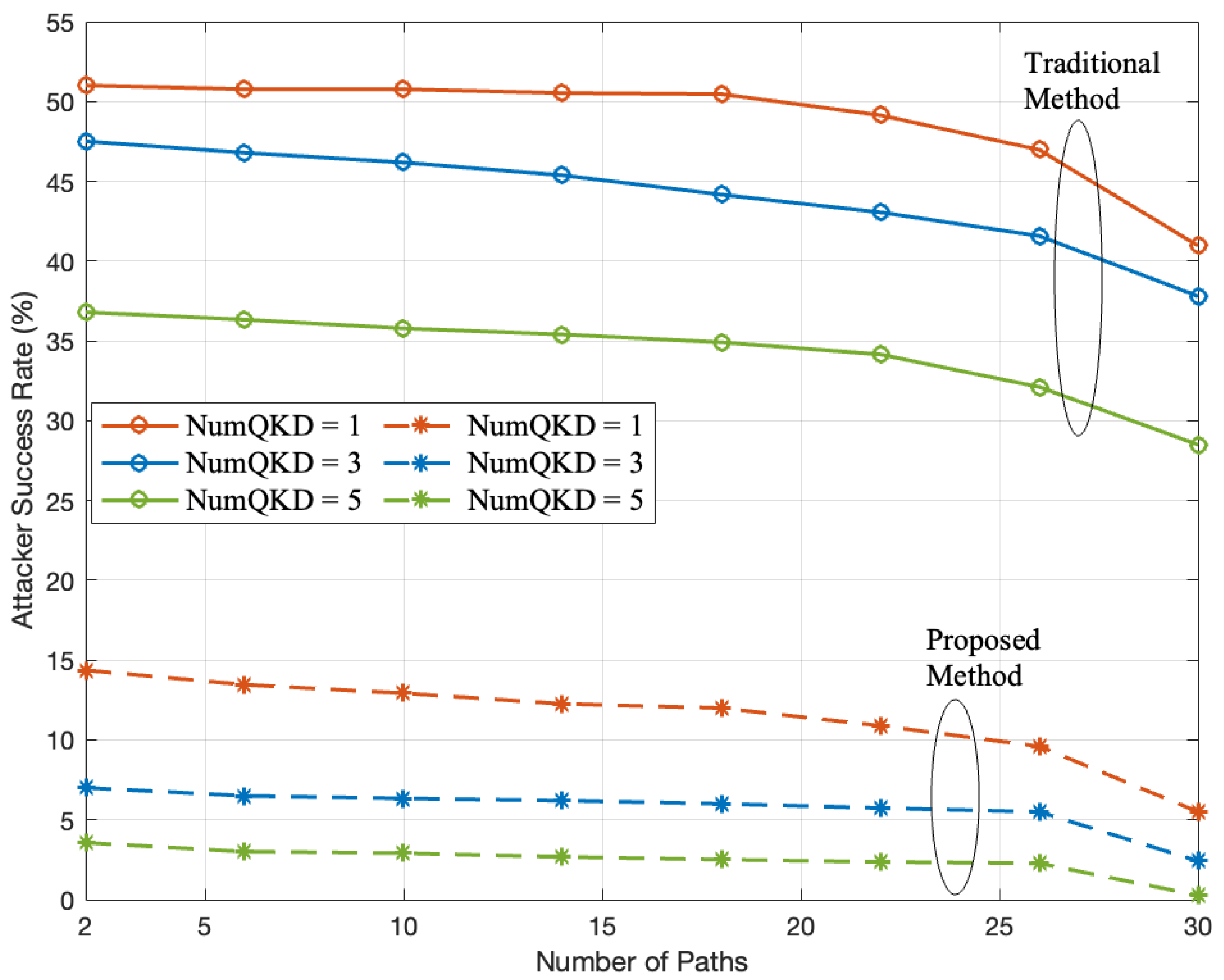
	Single key transmission	91.42% lower than traditional methods;
	Multiple QKD pairs	75% lower than traditional methods.
Total security percentage	20% attacker pervasiveness	35% higher than traditional methods;
	80% attacker pervasiveness	90% overall security retained, while traditional methods experience a significant security drop.
Security enhancement	Increasing QKD pairs	79.6% improvement over traditional methods;
	Single key transmission	71.15% higher than traditional methods, which are less resilient to attacks.
Impact of multipath selection on attack resilience	Adaptive path selection	Higher resilience in the proposed method as the number of paths increases, whereas traditional methods remain more susceptible to attacks.
Effectiveness against interception	Multipath routing strategy	86.04% stronger defense against interception compared to traditional methods.
Success rate improvement	Adaptive multipath strategy	Nearly double the success rate compared to traditional methods.

presents a comparative analysis of the proposed QKD network based on multipath–multi-key spatiotemporal diversification in a zero-trust environment, and the traditional benchmark that relies on multipath selection in a zero-trust environment.

7. Conclusions

In this study, we introduced a novel spatiotemporal diversification scheme to enhance the security of end-to-end key distribution in quantum key distribution (QKD) networks. The proposed strategy dynamically alternates key distribution paths and incorporates an adaptive path recovery process. By employing a penalty-based mechanism, the system detects and excludes suspicious relay nodes, ensuring the integrity of the key distribution process while maintaining high efficiency. Our results demonstrate that the proposed method significantly improves system performance by leveraging multipath key distribution and dynamic path recovery. Diversifying transmission routes reduces the risk of attacks by lowering the adversary’s success rate while transmitting multiple keys simultaneously introduces randomness that further strengthens the system’s security. These findings underscore the importance of integrating dynamic path selection and penalty-based node evaluation in designing secure QKD systems. The proposed approach offers a promising solution for improving the security and robustness of QKD networks, paving the way for practical and reliable implementation across diverse environments.