From Rating Predictions to Reliable Recommendations in Collaborative Filtering: The Concept of Recommendation Reliability Classes
Abstract
1. Introduction
2. Related Work
3. Foundations
3.1. CF Recommendation Generation Procedure
- For each user, the CF RecSys selects the set of users (the NNs) who will act as the user recommenders. The NNs are typically the users who have the largest vicinity values with the user. The most commonly adopted techniques for selecting NNs are the top-K method (users with the K-highest vicinity metrics with target user U are selected as U’s NNs) and the correlation threshold method (users whose vicinity with target user U surpasses a threshold T are selected as U’s NNs) [5,6], as described in the Introduction Section;
- For each user, the CF RecSys tries to formulate predictions for every item the user has not rated yet. It does so by using a prediction formula that fuses the user NNs’ ratings of the same item into a single prediction value;
- Typically, for each user, the item(s) receiving the top rating prediction arithmetic score(s) is/are presented (suggested) to them.
3.2. CF Rating Prediction Accuracy Factors
- The cardinality of NNs contributing to the prediction computation for the specific item (termed as FNN). Note that, out of all the NNs of a user U, only the NNs that have rated an item i contribute to the computation of the prediction of the rating that U would assign to i. For sparse datasets, if FNN ≥ 2, then the prediction is considered “accurate” and if FNN ≥ 4, then the prediction is considered “very accurate”. The respective boundaries for dense datasets are 6% (“accurate”) and 15% (“very accurate”);
- The user’s average value of ratings (termed as FU_AVG). For both dense and sparse datasets, when using a five-star evaluation scale, as happens in the majority of the CF RecSys datasets, if (FU_AVG ≤ 2.0 OR FU_AVG ≥ 4.0), then the prediction is considered “accurate”, and if (FU_AVG ≤ 1.5 OR FU_AVG ≥ 4.5), then the prediction is considered “very accurate”;
- The item’s average value of ratings (termed as FI_AVG). The boundaries are exactly the same with the FU_AVG factor, i.e., (FI_AVG ≤ 2.0 OR FI_AVG ≥ 4.0) for the “accurate” predictions and (FI_AVG ≤ 1.5 OR FI_AVG ≥ 4.5) for the “very accurate” predictions.
4. Experimental Settings and Evaluation Results of the Study on Rating Prediction Confidence Factors in CF
4.1. Experimental Settings and Procedure
| Name | Attributes |
|---|---|
| Amazon CDs_and_Vinyl [34] | 112 K Users, 73.7 K items, 1.44 M ratings (range 1–5), 5-core, density 0.017% (sparse) |
| Amazon Musical Instruments [34] | 27.5 K Users, 10.6 K items, 231 K ratings (range 1–5), 5-core, density 0.08% (sparse) |
| Amazon Videogames [34] | 17.5 K users, 55 K items, 473 K ratings (range 1–5), 5-core, 0.05% density (sparse) |
| Amazon Digital Music [34] | 12 K users, 17 K items, 145 K ratings (range 1–5), 5-core, 0.07% density (sparse) |
| CiaoDVD [35] | 17.6 K users, 16 K items, 73 K ratings (range 1–5), 0.026% density (sparse) |
| Epinions [36] | 22 K users, 296 K items, 922 K ratings (range 1–5), 0.014% density (sparse) |
| MovieLens 100K old [37] | 1 K users, 1.7 K items, 100 K ratings (range 1–5), 5.88% density (dense) |
| MovieLens 1M [37] | 6 K users, 3.7 items, 1 M ratings (range 1–5), 4.5% density (dense) |
- The precision of the recommendations;
- The average actual arithmetic rating values of the items that have been recommended.
4.2. Evaluation Results of the Study on Rating Prediction Confidence Factors in CF
- If the rating prediction fulfils the strict criterion for the specific factor (and is considered “very accurate”), we assign a factor-specific confidence score of 1.0 to the particular prediction;
- Otherwise, if the rating fulfills the loose criterion for the specific factor (and is thus considered “accurate”), we assign a factor-specific confidence score of 0.5 to the prediction;
- Otherwise, the rating does not fulfill either the strict or the loose criterion for the specific factor; thus we assign a factor-specific confidence score of 0.0 to the prediction.
5. The Concept of Recommendation Reliability Classes and the Proposed Algorithm
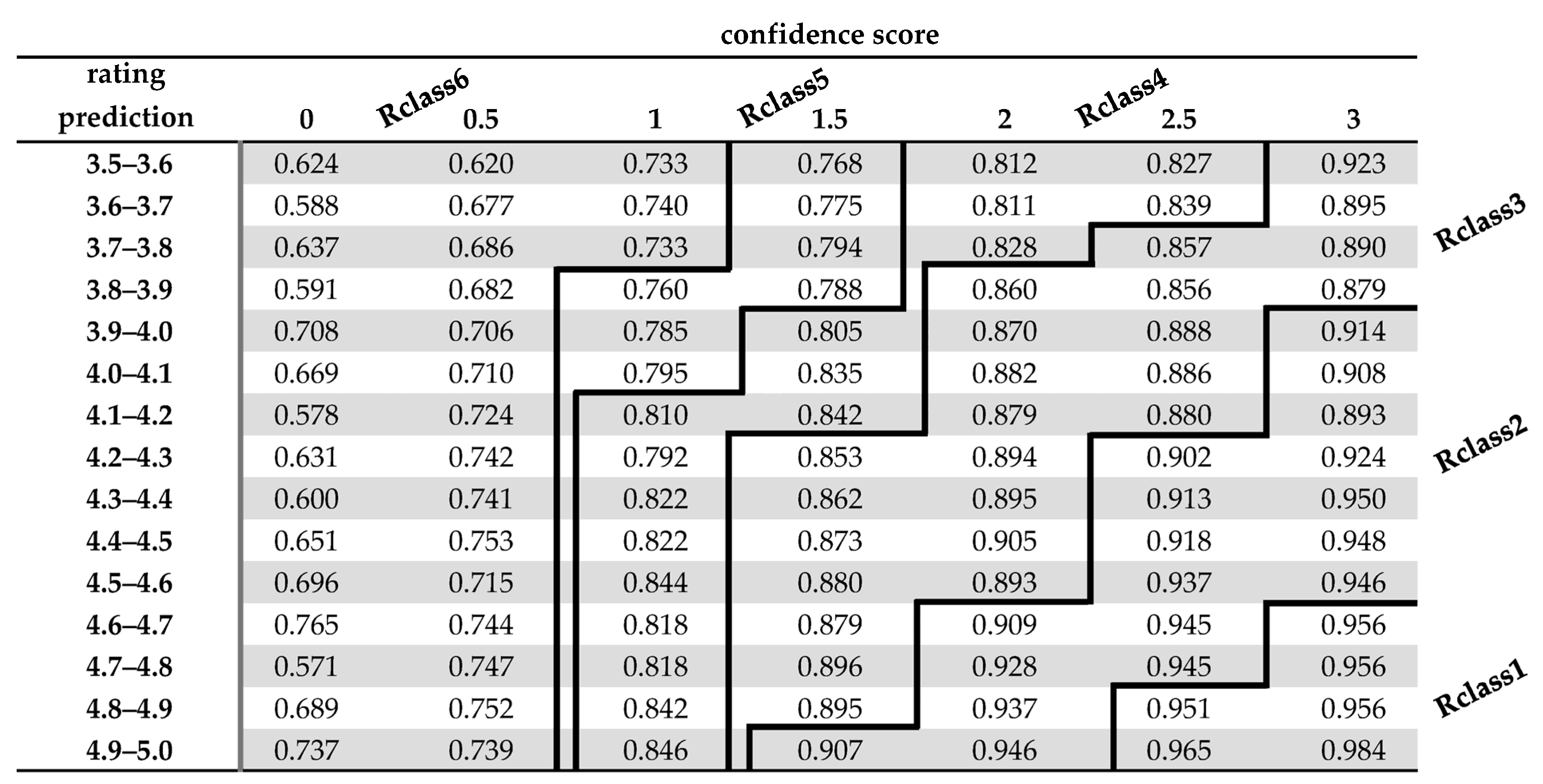
5.1. The Concept of Recommendation Reliability Classes in CF
- Reliability Class 1 (Rclass1): it contains the rating predictions where (CSC = 3.0 AND RPV ≥ 4.6) OR (CSC = 2.5 AND RPV ≥ 4.8);
- Reliability Class 2 (Rclass2): it contains the rating predictions which do not already belong to RClass1 and where (CSC = 3.0 AND RPV ≥ 3.9) OR (CSC = 2.5 AND RPV ≥ 4.2) OR (CSC = 2.0 AND RPV ≥ 4.6) OR (CSC = 1.5 AND RPV ≥ 4.9);
- Reliability Class 3 (Rclass3): it contains the rating predictions which do not already belong to RClass1 or RClass2 and where (CSC = 3.0 AND RPV ≥ 3.5) OR (CSC = 2.5 AND RPV ≥ 3.7) OR (CSC = 2.0 AND RPV ≥ 3.8) OR (CSC = 1.5 AND RPV ≥ 4.2);
- Reliability Class 4 (Rclass4): it contains the rating predictions which do not already belong to RClass1, RClass2, or RClass3 and where (CSC = 2.5 AND RPV ≥ 3.5) OR (CSC = 2.0 AND RPV ≥ 3.5) OR (CSC = 1.5 AND RPV ≥ 3.9) OR (CSC = 1.0 AND RPV ≥ 4.1);
- Reliability Class 5 (Rclass5): it contains the rating predictions which do not already belong to RClass1, RClass2, RClass3, or RClass4 and where (CSC = 1.5 AND RPV ≥ 3.5) OR (CSC = 1.0 AND RPV ≥ 3.8);
- Reliability Class 6 (Rclass6): the rest of the rating predictions with RPV ≥ 3.5 (which is the typical threshold used by CF RecSys algorithms for a prediction to be considered in the recommendation formulation phase).
5.2. The Proposed Algorithm
- The algorithm computes the RPV and CSC for every item prediction;
- The rating predictions with RPV ≥ 3.5 are classified into one of the six reliability classes, as defined above;
- For each user, the proposed algorithm begins to select items with predictions that belong to Rclass1. If they do not suffice, the items with predictions that belong to Rclass2 are selected for recommendation, and so on. If more than one item exists in the same class, based on the results shown in the previous subsection, firstly the CSC and secondly the RPV are used as tie-breakers.
6. Experimental Evaluation
7. Discussion
- The methodology presented in this paper for recommendation formulation can be used in conjunction with rating prediction approaches that consider additional factors, such as user demographics, item categories and characteristics, contextual information, social network graphs, etc. This applies both to memory-based and user-based techniques;
- The confidence factor computation procedure can itself be augmented to consider the abovementioned additional factors and/or to use different weights for the contributing features.
8. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Amazon Videogames | Amazon Digital Music | CiaoDVD | Epinions | MovieLens 100 K | MovieLens 1 M | |
|---|---|---|---|---|---|---|
| PC, K = 200 | ||||||
| Rclass1 | 98% | 99% | 96% | 96% | 97% | 93% |
| Rclass2 | 93% | 97% | 92% | 92% | 92% | 92% |
| Rclass3 | 84% | 90% | 86% | 84% | 87% | 89% |
| Rclass4 | 81% | 87% | 79% | 81% | 84% | 87% |
| Rclass5 | 76% | 82% | 76% | 74% | 76% | 82% |
| Rclass6 | 67% | 74% | 66% | 68% | 65% | 68% |
| PC, K = 500 | ||||||
| Rclass1 | 97% | 99% | 97% | 96% | 97% | 95% |
| Rclass2 | 93% | 98% | 90% | 90% | 92% | 93% |
| Rclass3 | 85% | 90% | 84% | 85% | 86% | 89% |
| Rclass4 | 81% | 86% | 79% | 80% | 81% | 88% |
| Rclass5 | 75% | 82% | 74% | 74% | 74% | 81% |
| Rclass6 | 68% | 75% | 65% | 69% | 64% | 70% |
| PC, CT = 0.0 | ||||||
| Rclass1 | 97% | 99% | 97% | 96% | 96% | 96% |
| Rclass2 | 93% | 98% | 92% | 91% | 93% | 93% |
| Rclass3 | 85% | 91% | 86% | 84% | 87% | 85% |
| Rclass4 | 80% | 87% | 80% | 80% | 81% | 77% |
| Rclass5 | 74% | 82% | 74% | 72% | 73% | 72% |
| Rclass6 | 68% | 74% | 68% | 70% | 64% | 61% |
| PC, CT = 0.5 | ||||||
| Rclass1 | 97% | 99% | 97% | 96% | 93% | 96% |
| Rclass2 | 93% | 97% | 92% | 92% | 94% | 93% |
| Rclass3 | 85% | 92% | 85% | 84% | 88% | 86% |
| Rclass4 | 81% | 87% | 81% | 80% | 86% | 82% |
| Rclass5 | 75% | 82% | 76% | 72% | 77% | 74% |
| Rclass6 | 68% | 74% | 68% | 70% | 67% | 66% |
| CS, K = 200 | ||||||
| Rclass1 | 97% | 99% | 96% | 96% | 94% | 93% |
| Rclass2 | 93% | 98% | 91% | 91% | 94% | 93% |
| Rclass3 | 85% | 91% | 85% | 84% | 88% | 89% |
| Rclass4 | 81% | 86% | 80% | 81% | 86% | 87% |
| Rclass5 | 76% | 83% | 76% | 74% | 79% | 83% |
| Rclass6 | 67% | 73% | 70% | 69% | 66% | 69% |
| CS, K = 500 | ||||||
| Rclass1 | 97% | 99% | 96% | 96% | 96% | 94% |
| Rclass2 | 93% | 98% | 91% | 91% | 93% | 92% |
| Rclass3 | 84% | 91% | 84% | 84% | 85% | 90% |
| Rclass4 | 80% | 86% | 81% | 80% | 83% | 88% |
| Rclass5 | 75% | 82% | 75% | 73% | 75% | 83% |
| Rclass6 | 67% | 74% | 68% | 69% | 65% | 70% |
| CS, CT = 0.0 | ||||||
| Rclass1 | 97% | 99% | 96% | 96% | 96% | 96% |
| Rclass2 | 92% | 98% | 91% | 91% | 91% | 91% |
| Rclass3 | 84% | 91% | 85% | 84% | 84% | 84% |
| Rclass4 | 79% | 85% | 79% | 79% | 79% | 78% |
| Rclass5 | 73% | 81% | 73% | 72% | 72% | 72% |
| Rclass6 | 67% | 73% | 68% | 71% | 63% | 61% |
| CS, CT = 0.5 | ||||||
| Rclass1 | 97% | 99% | 96% | 96% | 95% | 96% |
| Rclass2 | 93% | 97% | 90% | 91% | 92% | 92% |
| Rclass3 | 84% | 90% | 85% | 84% | 84% | 84% |
| Rclass4 | 79% | 85% | 79% | 79% | 79% | 78% |
| Rclass5 | 73% | 81% | 73% | 72% | 73% | 72% |
| Rclass6 | 67% | 73% | 68% | 71% | 67% | 61% |
| Amazon Videogames | Amazon Digital Music | CiaoDVD | Epinions | MovieLens 100 K | MovieLens 1 M | |
|---|---|---|---|---|---|---|
| PC, K = 200 | ||||||
| Rclass1 | 4.87 | 4.94 | 4.75 | 4.75 | 4.72 | 4.67 |
| Rclass2 | 4.69 | 4.85 | 4.51 | 4.55 | 4.58 | 4.59 |
| Rclass3 | 4.39 | 4.48 | 4.30 | 4.32 | 4.37 | 4.43 |
| Rclass4 | 4.26 | 4.28 | 4.14 | 4.18 | 4.25 | 4.37 |
| Rclass5 | 4.1 | 4.13 | 4.04 | 3.98 | 4.01 | 4.21 |
| Rclass6 | 3.81 | 3.97 | 3.79 | 3.77 | 3.77 | 3.85 |
| PC, K = 500 | ||||||
| Rclass1 | 4.87 | 4.93 | 4.76 | 4.75 | 4.67 | 4.71 |
| Rclass2 | 4.67 | 4.82 | 4.47 | 4.53 | 4.57 | 4.61 |
| Rclass3 | 4.38 | 4.45 | 4.27 | 4.29 | 4.31 | 4.45 |
| Rclass4 | 4.25 | 4.25 | 4.11 | 4.15 | 4.17 | 4.38 |
| Rclass5 | 4.06 | 4.12 | 3.99 | 3.95 | 3.96 | 4.17 |
| Rclass6 | 3.83 | 3.97 | 3.76 | 3.80 | 3.74 | 3.88 |
| PC, CT = 0.0 | ||||||
| Rclass1 | 4.87 | 4.94 | 4.77 | 4.75 | 4.65 | 4.72 |
| Rclass2 | 4.69 | 4.84 | 4.54 | 4.52 | 4.58 | 4.53 |
| Rclass3 | 4.39 | 4.46 | 4.29 | 4.28 | 4.31 | 4.31 |
| Rclass4 | 4.22 | 4.26 | 4.12 | 4.11 | 4.14 | 4.05 |
| Rclass5 | 4.04 | 4.15 | 3.98 | 3.90 | 3.94 | 3.92 |
| Rclass6 | 3.84 | 3.96 | 3.80 | 3.84 | 3.72 | 3.67 |
| PC, CT = 0.5 | ||||||
| Rclass1 | 4.87 | 4.94 | 4.77 | 4.75 | 4.59 | 4.74 |
| Rclass2 | 4.71 | 4.83 | 4.55 | 4.53 | 4.56 | 4.55 |
| Rclass3 | 4.40 | 4.48 | 4.31 | 4.29 | 4.37 | 4.34 |
| Rclass4 | 4.24 | 4.27 | 4.16 | 4.12 | 4.31 | 4.17 |
| Rclass5 | 4.06 | 4.14 | 4.02 | 3.90 | 4.02 | 3.97 |
| Rclass6 | 3.84 | 3.95 | 3.81 | 3.83 | 3.82 | 3.78 |
| CS, K = 200 | ||||||
| Rclass1 | 4.87 | 4.94 | 4.73 | 4.74 | 4.61 | 4.68 |
| Rclass2 | 4.71 | 4.85 | 4.52 | 4.54 | 4.60 | 4.56 |
| Rclass3 | 4.39 | 4.47 | 4.29 | 4.31 | 4.38 | 4.44 |
| Rclass4 | 4.24 | 4.26 | 4.16 | 4.18 | 4.32 | 4.36 |
| Rclass5 | 4.08 | 4.15 | 4.04 | 3.97 | 4.08 | 4.25 |
| Rclass6 | 3.8 | 3.96 | 3.84 | 3.8 | 3.8 | 3.86 |
| CS, K = 500 | ||||||
| Rclass1 | 4.87 | 4.93 | 4.73 | 4.74 | 4.63 | 4.69 |
| Rclass2 | 4.68 | 4.84 | 4.52 | 4.53 | 4.57 | 4.60 |
| Rclass3 | 4.39 | 4.44 | 4.29 | 4.29 | 4.33 | 4.46 |
| Rclass4 | 4.21 | 4.24 | 4.15 | 4.15 | 4.21 | 4.38 |
| Rclass5 | 4.06 | 4.14 | 4 | 3.95 | 3.99 | 4.24 |
| Rclass6 | 3.81 | 3.99 | 3.81 | 3.8 | 3.76 | 3.87 |
| CS, CT = 0.0 | ||||||
| Rclass1 | 4.86 | 4.93 | 4.74 | 4.74 | 4.66 | 4.72 |
| Rclass2 | 4.67 | 4.83 | 4.50 | 4.53 | 4.54 | 4.49 |
| Rclass3 | 4.35 | 4.42 | 4.29 | 4.28 | 4.28 | 4.28 |
| Rclass4 | 4.18 | 4.24 | 4.11 | 4.11 | 4.12 | 4.07 |
| Rclass5 | 4.01 | 4.14 | 3.95 | 3.90 | 3.92 | 3.91 |
| Rclass6 | 3.83 | 3.97 | 3.80 | 3.85 | 3.70 | 3.66 |
| CS, CT = 0.5 | ||||||
| Rclass1 | 4.86 | 4.93 | 4.74 | 4.74 | 4.63 | 4.71 |
| Rclass2 | 4.66 | 4.83 | 4.51 | 4.53 | 4.52 | 4.51 |
| Rclass3 | 4.36 | 4.44 | 4.28 | 4.28 | 4.27 | 4.26 |
| Rclass4 | 4.18 | 4.24 | 4.11 | 4.11 | 4.08 | 4.06 |
| Rclass5 | 4.01 | 4.14 | 3.95 | 3.90 | 3.91 | 3.90 |
| Rclass6 | 3.83 | 3.97 | 3.80 | 3.85 | 3.66 | 3.66 |
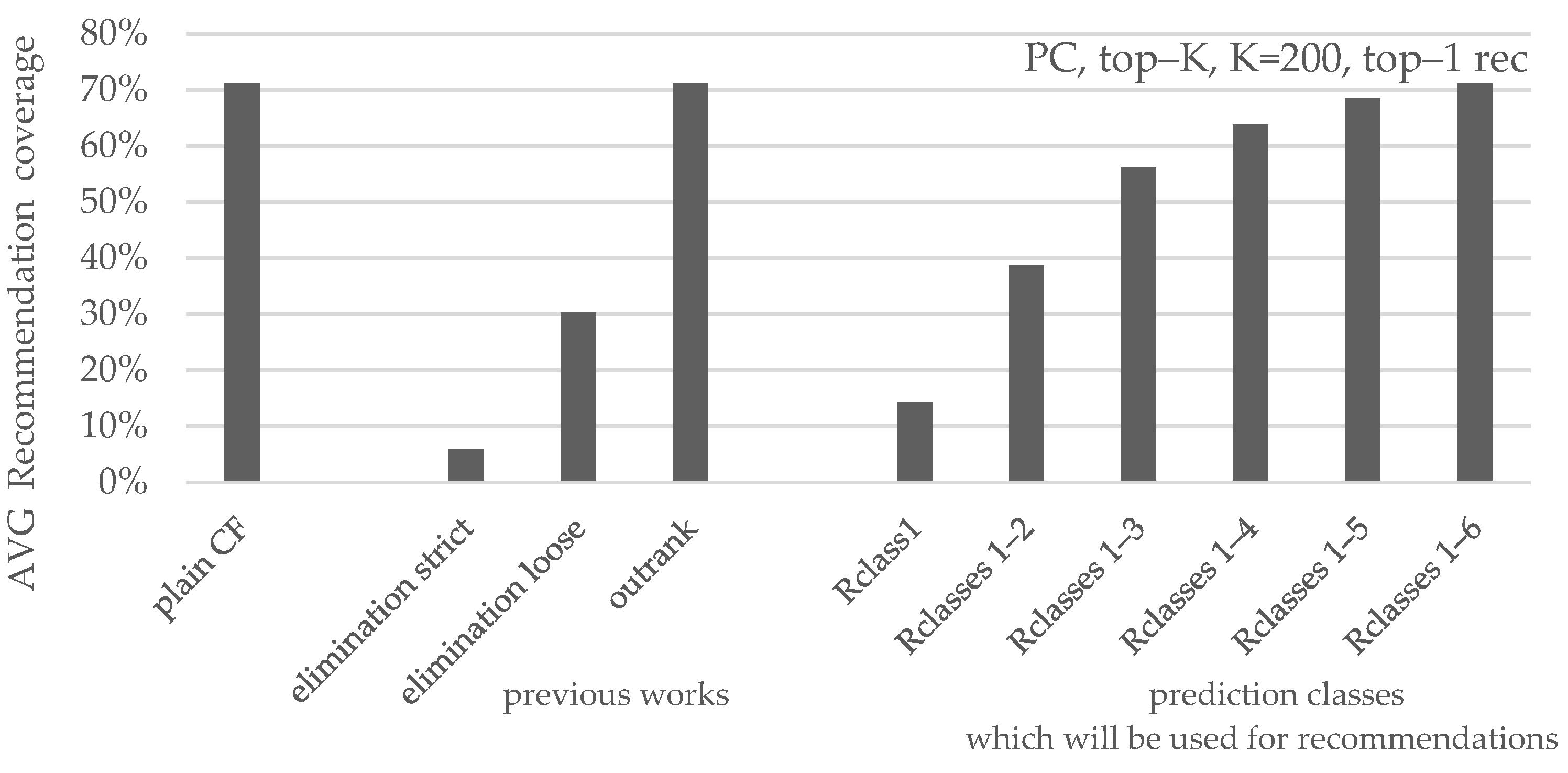
| Setting/Metric | Rclass1 | Rclasses1–2 | Rclasses1–3 | Rclasses1–4 | Rclasses1–5 | Rclasses1–6 |
|---|---|---|---|---|---|---|
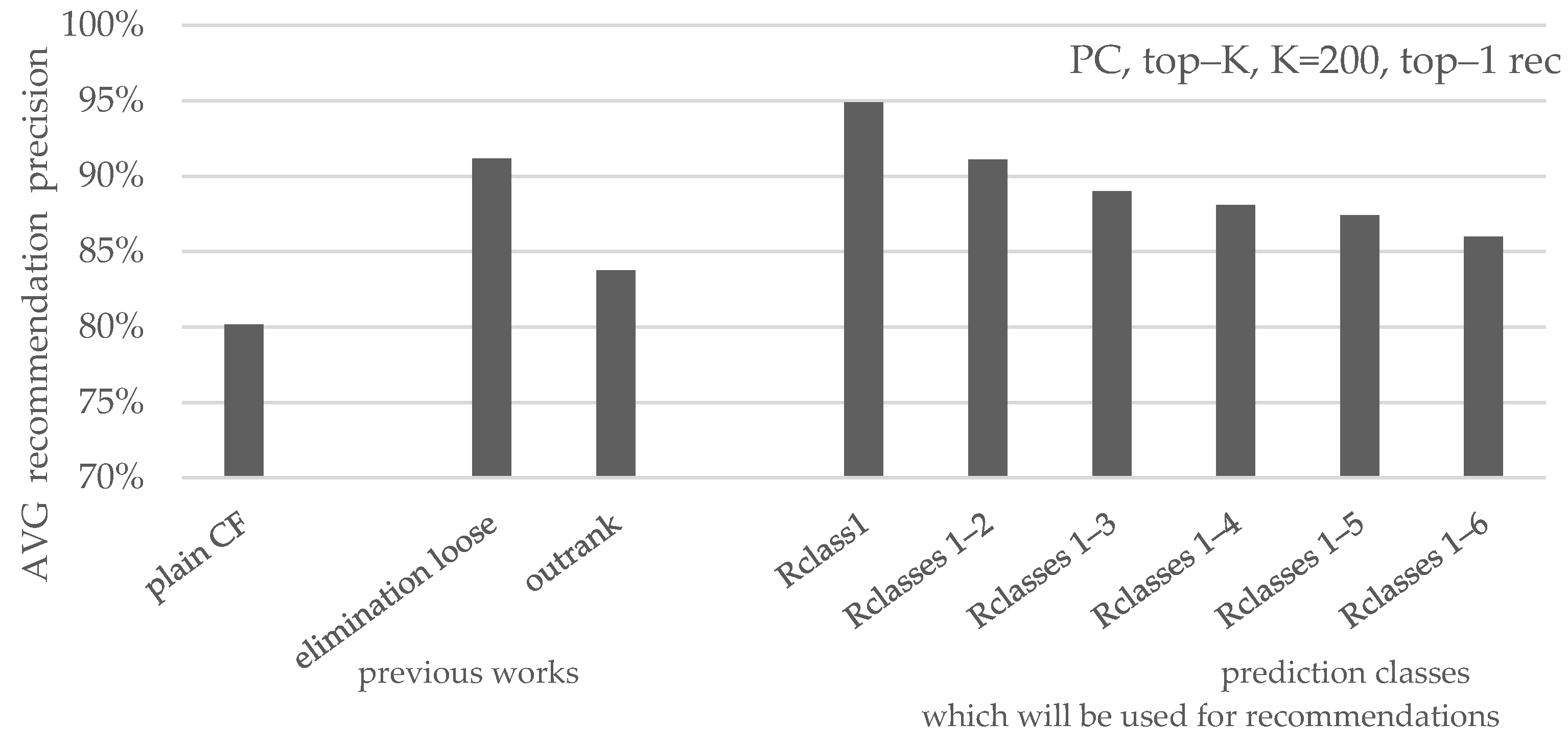
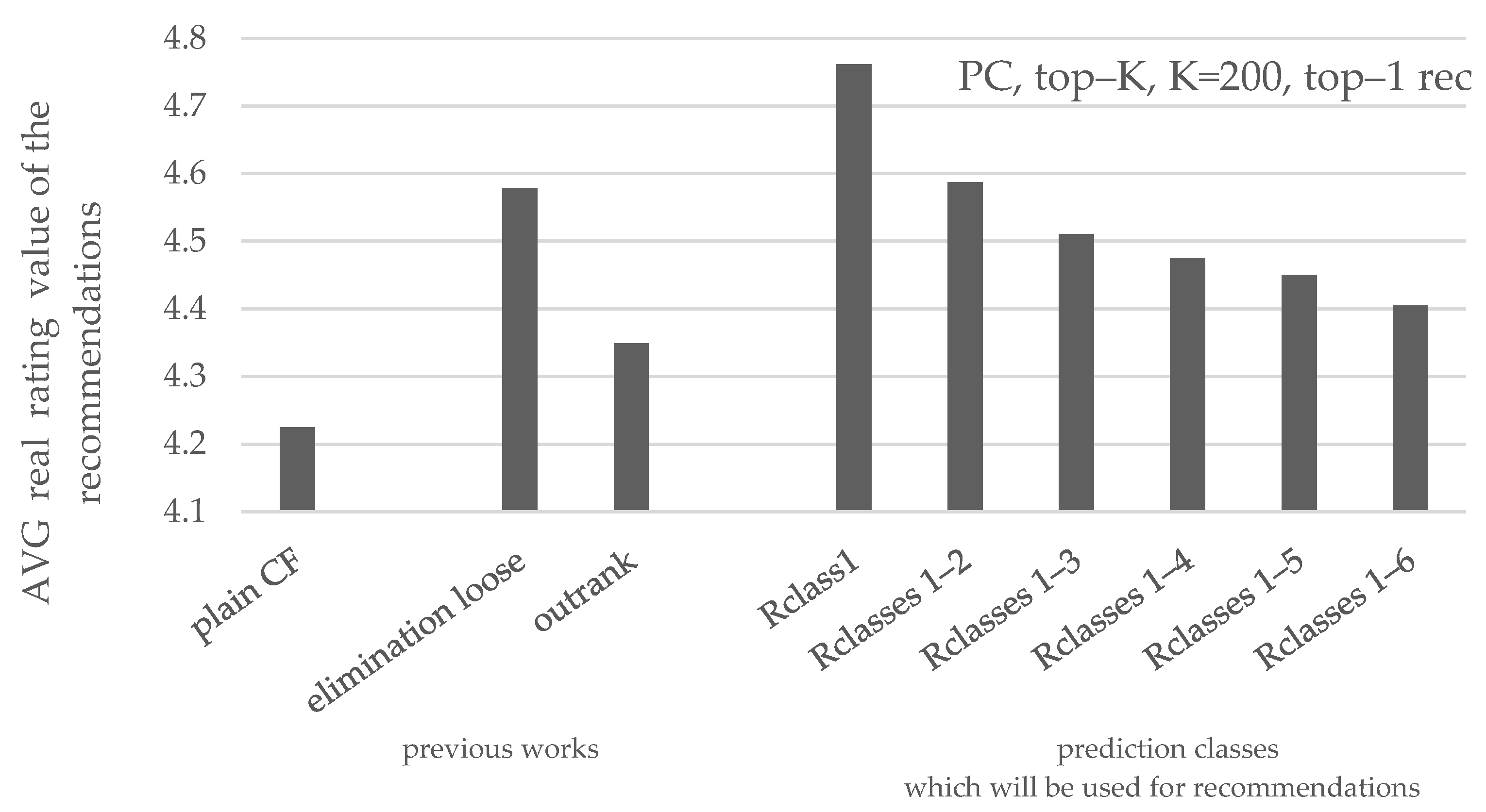
| PC, K = 200, top-1 | ||||||
| avg. coverage | 14.2% | 38.8% | 56.2% | 63.8% | 68.5% | 71.1% |
| avg. precision | 94.9% | 91.0% | 89.0% | 88.1% | 87.4% | 86.0% |
| avg. real rating | 4.76/5 | 4.60/5 | 4.50/5 | 4.48/5 | 4.45/5 | 4.41/5 |
| PC, K = 500, top-1 | ||||||
| avg. coverage | 16.2% | 40.7% | 58.2% | 64.7% | 68.8% | 71.4% |
| avg. precision | 95.4% | 91.3% | 89.6% | 88.4% | 87.6% | 86.5% |
| avg. real rating | 4.77/5 | 4.59/5 | 4.51/5 | 4.48/5 | 4.46/5 | 4.42/5 |
| PC, CT = 0.0, top-1 | ||||||
| avg. coverage | 18.2% | 43.7% | 60.5% | 66.5% | 69.8% | 72.1% |
| avg. precision | 95.6% | 92.1% | 90.1% | 89.1% | 88.4% | 87.4% |
| avg. real rating | 4.78/5 | 4.62/5 | 4.54/5 | 4.51/5 | 4.48/5 | 4.45/5 |
| PC, CT = 0.5, top-1 | ||||||
| avg. coverage | 17.7% | 43.5% | 60.5% | 65.2% | 69.5% | 71.9% |
| avg. precision | 95.4% | 92.1% | 90.2% | 88.4% | 87.5% | 86.2% |
| avg. real rating | 4.76/5 | 4.62/5 | 4.52/5 | 4.49/5 | 4.46/5 | 4.42/5 |
| CS, K = 200, top-1 | ||||||
| avg. coverage | 17.8% | 42.7% | 60.4% | 69.0% | 74.8% | 78.2% |
| avg. precision | 94.1% | 90.7% | 88.6% | 87.5% | 86.6% | 84.9% |
| avg. real rating | 4.72/5 | 4.58/5 | 4.48/5 | 4.46/5 | 4.43/5 | 4.38/5 |
| CS, K = 500, top-1 | ||||||
| avg. coverage | 19.9% | 44.8% | 63.4% | 70.8% | 75.6% | 78.3% |
| avg. precision | 94.6% | 91.1% | 89.1% | 88.0% | 87.2% | 85.9% |
| avg. real rating | 4.75/5 | 4.61/5 | 4.49/5 | 4.47/5 | 4.45/5 | 4.41/5 |
| CS, CT = 0.0, top-1 | ||||||
| avg. coverage | 22.9% | 49.1% | 66.7% | 72.7% | 76.2% | 77.9% |
| avg. precision | 95.1% | 90.7% | 88.9% | 87.8% | 87.0% | 86.2% |
| avg. real rating | 4.74/5 | 4.58/5 | 4.49/5 | 4.47/5 | 4.44/5 | 4.42/5 |
| CS, CT = 0.5, top-1 | ||||||
| avg. coverage | 22.9% | 49.3% | 66.7% | 72.7% | 76.2% | 77.9% |
| avg. precision | 95.1% | 90.8% | 88.9% | 87.7% | 86.9% | 86.1% |
| avg. real rating | 4.75/5 | 4.62/5 | 4.49/5 | 4.47/5 | 4.44/5 | 4.41/5 |
| Setting/Metric | Rclass1 | Rclasses1–2 | Rclasses1–3 | Rclasses1–4 | Rclasses1–5 | Rclasses1–6 |
|---|---|---|---|---|---|---|
| PC, K = 200, top-3 | ||||||
| avg. coverage | 5.8% | 23.1% | 37.9% | 47.5% | 55.6% | 60.7% |
| avg. precision | 95.6% | 92.3% | 90.3% | 89.1% | 87.9% | 86.2% |
| avg. real rating | 4.77/5 | 4.62/5 | 4.52/5 | 4.50/5 | 4.47/5 | 4.41/5 |
| PC, K = 500, top-3 | ||||||
| avg. coverage | 7.5% | 25.5% | 41.6% | 49.7% | 56.3% | 60.3% |
| avg. precision | 95.6% | 92.0% | 90.2% | 89.2% | 88.1% | 86.7% |
| avg. real rating | 4.75/5 | 4.64/5 | 4.52/5 | 4.51/5 | 4.48/5 | 4.43/5 |
| PC, CT = 0.0, top-3 | ||||||
| avg. coverage | 9.0% | 29.1% | 46.3% | 53.6% | 59.1% | 62.2% |
| avg. precision | 95.8% | 92.9% | 91.1% | 89.9% | 88.8% | 87.7% |
| avg. real rating | 4.76/5 | 4.67/5 | 4.57/5 | 4.53/5 | 4.50/5 | 4.46/5 |
| PC, CT = 0.5, top-3 | ||||||
| avg. coverage | 8.5% | 27.2% | 42.4% | 51.3% | 57.9% | 62.4% |
| avg. precision | 95.5% | 92.9% | 90.8% | 89.5% | 88.3% | 86.8% |
| avg. real rating | 4.74/5 | 4.66/5 | 4.54/5 | 4.52/5 | 4.48/5 | 4.44/5 |
| CS, K = 200, top-3 | ||||||
| avg. coverage | 7.2% | 26.6% | 40.9% | 51.5% | 61.0% | 67.7% |
| avg. precision | 94.8% | 92.1% | 90.1% | 88.8% | 87.4% | 85.3% |
| avg. real rating | 4.74/5 | 4.64/5 | 4.54/5 | 4.50/5 | 4.45/5 | 4.39/5 |
| CS, K = 500, top-3 | ||||||
| avg. coverage | 9.4% | 29.3% | 45.4% | 55.0% | 63.2% | 67.8% |
| avg. precision | 95.2% | 92.3% | 90.3% | 89.3% | 88.0% | 86.5% |
| avg. real rating | 4.74/5 | 4.63/5 | 4.54/5 | 4.51/5 | 4.47/5 | 4.42/5 |
| CS, CT = 0.0, top-3 | ||||||
| avg. coverage | 11.5% | 33.2% | 51.4% | 59.1% | 64.9% | 67.7% |
| avg. precision | 95.7% | 92.1% | 90.2% | 89.0% | 88.0% | 87.1% |
| avg. real rating | 4.75/5 | 4.65/5 | 4.52/5 | 4.50/5 | 4.47/5 | 4.44/5 |
| CS, CT = 0.5, top-3 | ||||||
| avg. coverage | 11.5% | 33.1% | 51.5% | 59.1% | 65.0% | 67.7% |
| avg. precision | 95.7% | 92.1% | 90.1% | 89.0% | 87.9% | 87.1% |
| avg. real rating | 4.75/5 | 4.64/5 | 4.52/5 | 4.50/5 | 4.47/5 | 4.44/5 |
References
- Wang, D.; Yih, Y.; Ventresca, M. Improving Neighbor-Based Collaborative Filtering by Using a Hybrid Similarity Measurement. Expert Syst. Appl. 2020, 160, 113651. [Google Scholar] [CrossRef]
- Rosa, R.E.; Guimarães, F.A.; da Silva Mendonça, R.; de Lucena, V.F. Improving Prediction Accuracy in Neighborhood-Based Collaborative Filtering by Using Local Similarity. IEEE Access 2020, 8, 142795–142809. [Google Scholar] [CrossRef]
- Jain, G.; Mahara, T.; Tripathi, K.N. A Survey of Similarity Measures for Collaborative Filtering-Based Recommender System. In Soft Computing: Theories and Applications; Pant, M., Sharma, T.K., Verma, O.P., Singla, R., Sikander, A., Eds.; Advances in Intelligent Systems and Computing; Springer: Singapore, 2020; Volume 1053, pp. 343–352. ISBN 978-981-15-0750-2. [Google Scholar]
- Khojamli, H.; Razmara, J. Survey of Similarity Functions on Neighborhood-Based Collaborative Filtering. Expert Syst. Appl. 2021, 185, 115482. [Google Scholar] [CrossRef]
- Nguyen, L.V.; Vo, Q.-T.; Nguyen, T.-H. Adaptive KNN-Based Extended Collaborative Filtering Recommendation Services. Big Data Cogn. Comput. 2023, 7, 106. [Google Scholar] [CrossRef]
- Fkih, F. Similarity Measures for Collaborative Filtering-Based Recommender Systems: Review and Experimental Comparison. J. King Saud Univ. Comput. Inf. Sci. 2022, 34, 7645–7669. [Google Scholar] [CrossRef]
- Koren, Y.; Rendle, S.; Bell, R. Advances in Collaborative Filtering. In Recommender Systems Handbook; Ricci, F., Rokach, L., Shapira, B., Eds.; Springer: New York, NY, USA, 2022; pp. 91–142. ISBN 978-1-0716-2196-7. [Google Scholar]
- Wu, L.; He, X.; Wang, X.; Zhang, K.; Wang, M. A Survey on Accuracy-Oriented Neural Recommendation: From Collaborative Filtering to Information-Rich Recommendation. IEEE Trans. Knowl. Data Eng. 2022, 35, 4425–4445. [Google Scholar] [CrossRef]
- Margaris, D.; Vassilakis, C.; Spiliotopoulos, D. On Producing Accurate Rating Predictions in Sparse Collaborative Filtering Datasets. Information 2022, 13, 302. [Google Scholar] [CrossRef]
- Spiliotopoulos, D.; Margaris, D.; Vassilakis, C. On Exploiting Rating Prediction Accuracy Features in Dense Collaborative Filtering Datasets. Information 2022, 13, 428. [Google Scholar] [CrossRef]
- Liao, C.-L.; Lee, S.-J. A Clustering Based Approach to Improving the Efficiency of Collaborative Filtering Recommendation. Electron. Commer. Res. Appl. 2016, 18, 1–9. [Google Scholar] [CrossRef]
- Valdiviezo-Diaz, P.; Ortega, F.; Cobos, E.; Lara-Cabrera, R. A Collaborative Filtering Approach Based on Naïve Bayes Classifier. IEEE Access 2019, 7, 108581–108592. [Google Scholar] [CrossRef]
- Margaris, D.; Vassilakis, C. Improving Collaborative Filtering’s Rating Prediction Quality in Dense Datasets, by Pruning Old Ratings. In Proceedings of the 2017 IEEE Symposium on Computers and Communications (ISCC), Heraklion, Greece, 3–6 July 2017; IEEE: Heraklion, Greece, 2017; pp. 1168–1174. [Google Scholar]
- Neysiani, B.S.; Soltani, N.; Mofidi, R.; Nadimi-Shahraki, M.H. Improve Performance of Association Rule-Based Collaborative Filtering Recommendation Systems Using Genetic Algorithm. Int. J. Inf. Technol. Comput. Sci. 2019, 11, 48–55. [Google Scholar] [CrossRef]
- Thakkar, P.; Varma, K.; Ukani, V.; Mankad, S.; Tanwar, S. Combining User-Based and Item-Based Collaborative Filtering Using Machine Learning. In Information and Communication Technology for Intelligent Systems; Satapathy, S.C., Joshi, A., Eds.; Smart Innovation, Systems and Technologies; Springer: Singapore, 2019; Volume 107, pp. 173–180. ISBN 978-981-13-1746-0. [Google Scholar]
- He, X.; Deng, K.; Wang, X.; Li, Y.; Zhang, Y.; Wang, M. LightGCN: Simplifying and Powering Graph Convolution Network for Recommendation. In Proceedings of the 43rd International ACM SIGIR Conference on Research and Development in Information Retrieval, Virtual Event, China, 25–30 July 2020; ACM: New York, NY, USA, 2020; pp. 639–648. [Google Scholar]
- Li, A.; Cheng, Z.; Liu, F.; Gao, Z.; Guan, W.; Peng, Y. Disentangled Graph Neural Networks for Session-Based Recommendation. IEEE Trans. Knowl. Data Eng. 2023, 35, 7870–7882. [Google Scholar] [CrossRef]
- Wei, Y.; Wang, X.; Li, Q.; Nie, L.; Li, Y.; Li, X.; Chua, T.-S. Contrastive Learning for Cold-Start Recommendation. In Proceedings of the 29th ACM International Conference on Multimedia, Virtual Event, China, 20–24 October 2021; ACM: New York, NY, USA, 2021; pp. 5382–5390. [Google Scholar]
- Yang, B.; Lei, Y.; Liu, J.; Li, W. Social Collaborative Filtering by Trust. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 1633–1647. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Deng, J.; Gao, J.; Zhang, P. A Hybrid User Similarity Model for Collaborative Filtering. Inf. Sci. 2017, 418–419, 102–118. [Google Scholar] [CrossRef]
- Islam, R.; Keya, K.N.; Zeng, Z.; Pan, S.; Foulds, J. Debiasing Career Recommendations with Neural Fair Collaborative Filtering. In Proceedings of the Web Conference 2021, Ljubljana, Slovenia, 19–23 April 2021; ACM: New York, NY, USA, 2021; pp. 3779–3790. [Google Scholar]
- Iwendi, C.; Ibeke, E.; Eggoni, H.; Velagala, S.; Srivastava, G. Pointer-Based Item-to-Item Collaborative Filtering Recommendation System Using a Machine Learning Model. Int. J. Inf. Technol. Decis. Mak. 2022, 21, 463–484. [Google Scholar] [CrossRef]
- Chen, G.; Zeng, F.; Zhang, J.; Lu, T.; Shen, J.; Shu, W. An Adaptive Trust Model Based on Recommendation Filtering Algorithm for the Internet of Things Systems. Comput. Netw. 2021, 190, 107952. [Google Scholar] [CrossRef]
- Chang, J.-L.; Li, H.; Bi, J.-W. Personalized Travel Recommendation: A Hybrid Method with Collaborative Filtering and Social Network Analysis. Curr. Issues Tour. 2022, 25, 2338–2356. [Google Scholar] [CrossRef]
- Vuong Nguyen, L.; Nguyen, T.; Jung, J.J.; Camacho, D. Extending Collaborative Filtering Recommendation Using Word Embedding: A Hybrid Approach. Concurr. Comput. Pract. Exp. 2023, 35, e6232. [Google Scholar] [CrossRef]
- Rohit; Sabitha, S.; Choudhury, T. Proposed Approach for Book Recommendation Based on User K-NN. In Advances in Computer and Computational Sciences; Bhatia, S.K., Mishra, K.K., Tiwari, S., Singh, V.K., Eds.; Advances in Intelligent Systems and Computing; Springer: Singapore, 2018; Volume 554, pp. 543–558. ISBN 978-981-10-3772-6. [Google Scholar]
- Shambour, Q. A Deep Learning Based Algorithm for Multi-Criteria Recommender Systems. Knowl. Based Syst. 2021, 211, 106545. [Google Scholar] [CrossRef]
- Margaris, D.; Sgardelis, K.; Spiliotopoulos, D.; Vassilakis, C. Exploiting Rating Prediction Certainty for Recommendation Formulation in Collaborative Filtering. Big Data Cogn. Comput. 2024, 8, 53. [Google Scholar] [CrossRef]
- Sgardelis, K.; Margaris, D.; Spiliotopoulos, D.; Vassilakis, C.; Ougiaroglou, S. Improving Recommendation Quality in Collaborative Filtering by Including Prediction Confidence Factors. In Proceedings of the 20th International Conference on Web Information Systems and Technologies, Porto, Portugal, 17–19 November 2024; SCITEPRESS—Science and Technology Publications: Setúbal, Portugal, 2024; pp. 372–379. [Google Scholar]
- Pugoy, R.A.; Kao, H.-Y. NEAR: Non-Supervised Explainability Architecture for Accurate Review-Based Collaborative Filtering. IEEE Trans. Knowl. Data Eng. 2022, 36, 750–765. [Google Scholar] [CrossRef]
- Ghasemi, N.; Momtazi, S. Neural Text Similarity of User Reviews for Improving Collaborative Filtering Recommender Systems. Electron. Commer. Res. Appl. 2021, 45, 101019. [Google Scholar] [CrossRef]
- Chen, Y.; Xie, T.; Chen, H.; Huang, X.; Cui, N.; Li, J. KGCF: Social Relationship-Aware Graph Collaborative Filtering for Recommendation. Inf. Sci. 2024, 680, 121102. [Google Scholar] [CrossRef]
- Lee, Y.-C. Application of Support Vector Machines to Corporate Credit Rating Prediction. Expert Syst. Appl. 2007, 33, 67–74. [Google Scholar] [CrossRef]
- Ni, J.; Li, J.; McAuley, J. Justifying Recommendations Using Distantly-Labeled Reviews and Fine-Grained Aspects. In Proceedings of the 2019 Conference on Empirical Methods in Natural Language Processing and the 9th International Joint Conference on Natural Language Processing (EMNLP-IJCNLP), Hong Kong, China, 3–7 November 2019; Association for Computational Linguistics: Stroudsburg, PA, USA, 2019; pp. 188–197. [Google Scholar]
- Guo, G.; Zhang, J.; Thalmann, D.; Yorke-Smith, N. ETAF: An Extended Trust Antecedents Framework for Trust Prediction. In Proceedings of the 2014 IEEE/ACM International Conference on Advances in Social Networks Analysis and Mining (ASONAM 2014), Beijing, China, 17–20 August 2014; IEEE: Beijing, China, 2014; pp. 540–547. [Google Scholar]
- Richardson, M.; Agrawal, R.; Domingos, P. Trust Management for the Semantic Web. In The Semantic Web—ISWC 2003; Fensel, D., Sycara, K., Mylopoulos, J., Eds.; Lecture Notes in Computer Science; Springer: Berlin, Heidelberg, 2003; Volume 2870, pp. 351–368. ISBN 978-3-540-20362-9. [Google Scholar]
- Harper, F.M.; Konstan, J.A. The MovieLens Datasets: History and Context. ACM Trans. Interact. Intell. Syst. 2016, 5, 1–19. [Google Scholar] [CrossRef]
- Krichene, W.; Rendle, S. On Sampled Metrics for Item Recommendation. In Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Virtual Event, CA, USA, 6–10 July 2020; ACM: New York, NY, USA, 2020; pp. 1748–1757. [Google Scholar]
- Chin, J.Y.; Chen, Y.; Cong, G. The Datasets Dilemma: How Much Do We Really Know About Recommendation Datasets? In Proceedings of the Fifteenth ACM International Conference on Web Search and Data Mining, Virtual Event, AZ, USA, 21–25 February 2022; ACM: New York, NY, USA, 2022; pp. 141–149. [Google Scholar]
- Margaris, D.; Vassilakis, C.; Spiliotopoulos, D. What Makes a Review a Reliable Rating in Recommender Systems? Inf. Process. Manag. 2020, 57, 102304. [Google Scholar] [CrossRef]
- Trattner, C.; Said, A.; Boratto, L.; Felfernig, A. Evaluating Group Recommender Systems. In Group Recommender Systems; Felfernig, A., Boratto, L., Stettinger, M., Tkalčič, M., Eds.; Signals and Communication Technology; Springer Nature: Cham, Switzerland, 2024; pp. 63–75. ISBN 978-3-031-44942-0. [Google Scholar]
- Felfernig, A.; Boratto, L.; Stettinger, M.; Tkalčič, M. Evaluating Group Recommender Systems. In Group Recommender Systems; Springer Briefs in Electrical and Computer Engineering; Springer: Cham, Switzerland, 2018; pp. 59–71. [Google Scholar]
- Ackermann, M.R.; Blömer, J.; Kuntze, D.; Sohler, C. Analysis of Agglomerative Clustering. Algorithmica 2014, 69, 184–215. [Google Scholar] [CrossRef]
- Tokuda, E.K.; Comin, C.H.; Costa, L.D.F. Revisiting Agglomerative Clustering. Phys. A Stat. Mech. Appl. 2022, 585, 126433. [Google Scholar] [CrossRef]
- Xiao, J.; Lu, J.; Li, X. Davies Bouldin Index Based Hierarchical Initialization K-Means. Intell. Data Anal. 2017, 21, 1327–1338. [Google Scholar] [CrossRef]
- Bobadilla, J.; Gutiérrez, A.; Alonso, S.; González-Prieto, Á. Neural Collaborative Filtering Classification Model to Obtain Prediction Reliabilities. Int. J. Interact. Multimed. Artif. Intell. 2022, 7, 18. [Google Scholar] [CrossRef]
- He, X.; Liao, L.; Zhang, H.; Nie, L.; Hu, X.; Chua, T.-S. Neural Collaborative Filtering. In Proceedings of the 26th International Conference on World Wide Web, Perth, Australia, 3–7 April 2017; International World Wide Web Conferences Steering Committee: Geneva, Switzerland, 2017; pp. 173–182. [Google Scholar]
- Nesmaoui, R.; Louhichi, M.; Lazaar, M. A Collaborative Filtering Movies Recommendation System Based on Graph Neural Network. Procedia Comput. Sci. 2023, 220, 456–461. [Google Scholar] [CrossRef]
- Forouzandeh, S.; Berahmand, K.; Rostami, M. Presentation of a Recommender System with Ensemble Learning and Graph Embedding: A Case on MovieLens. Multimed. Tools Appl. 2021, 80, 7805–7832. [Google Scholar] [CrossRef]
- Ho, T.-L.; Le, A.-C.; Vu, D.-H. Multiview Fusion Using Transformer Model for Recommender Systems: Integrating the Utility Matrix and Textual Sources. Appl. Sci. 2023, 13, 6324. [Google Scholar] [CrossRef]
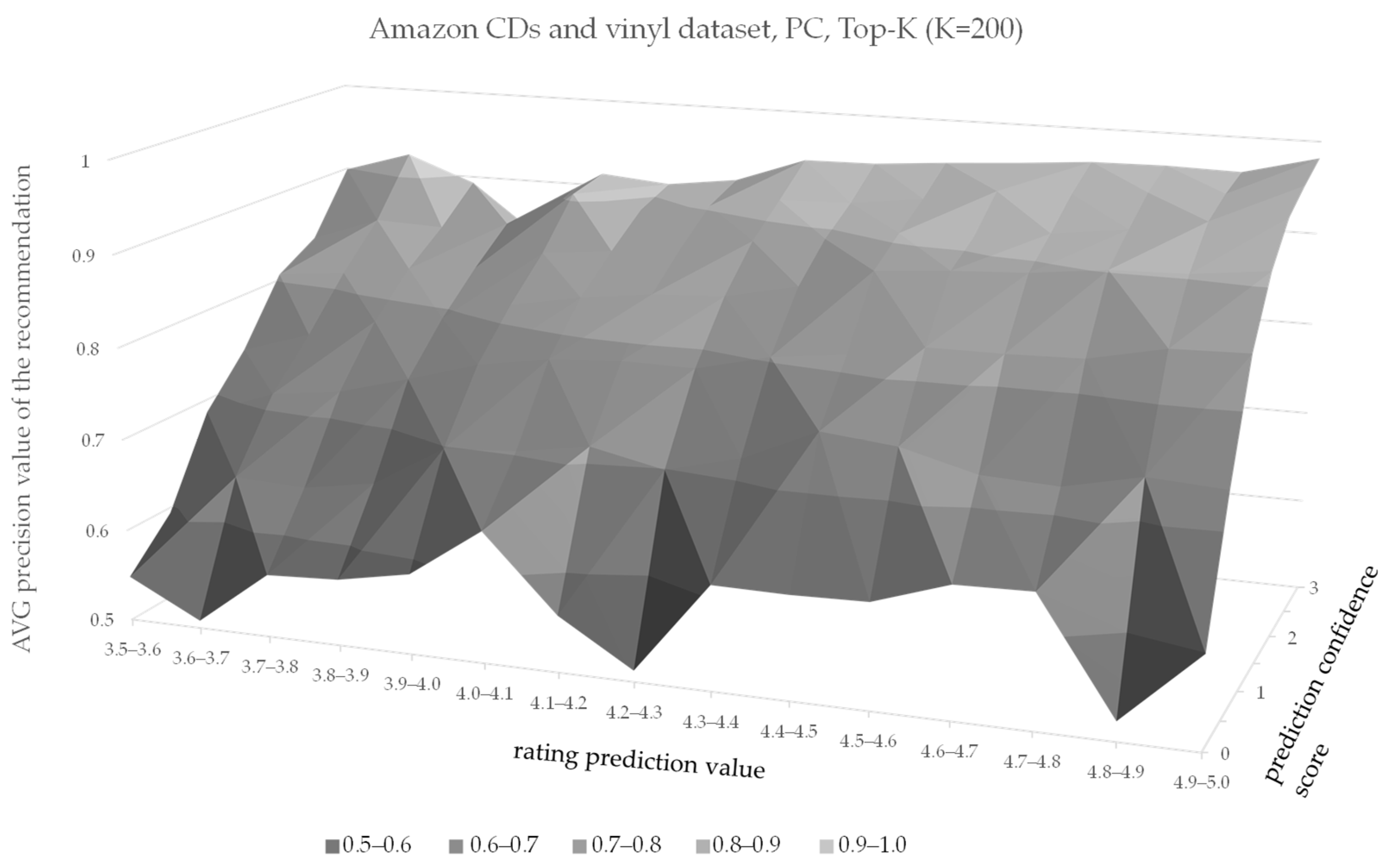
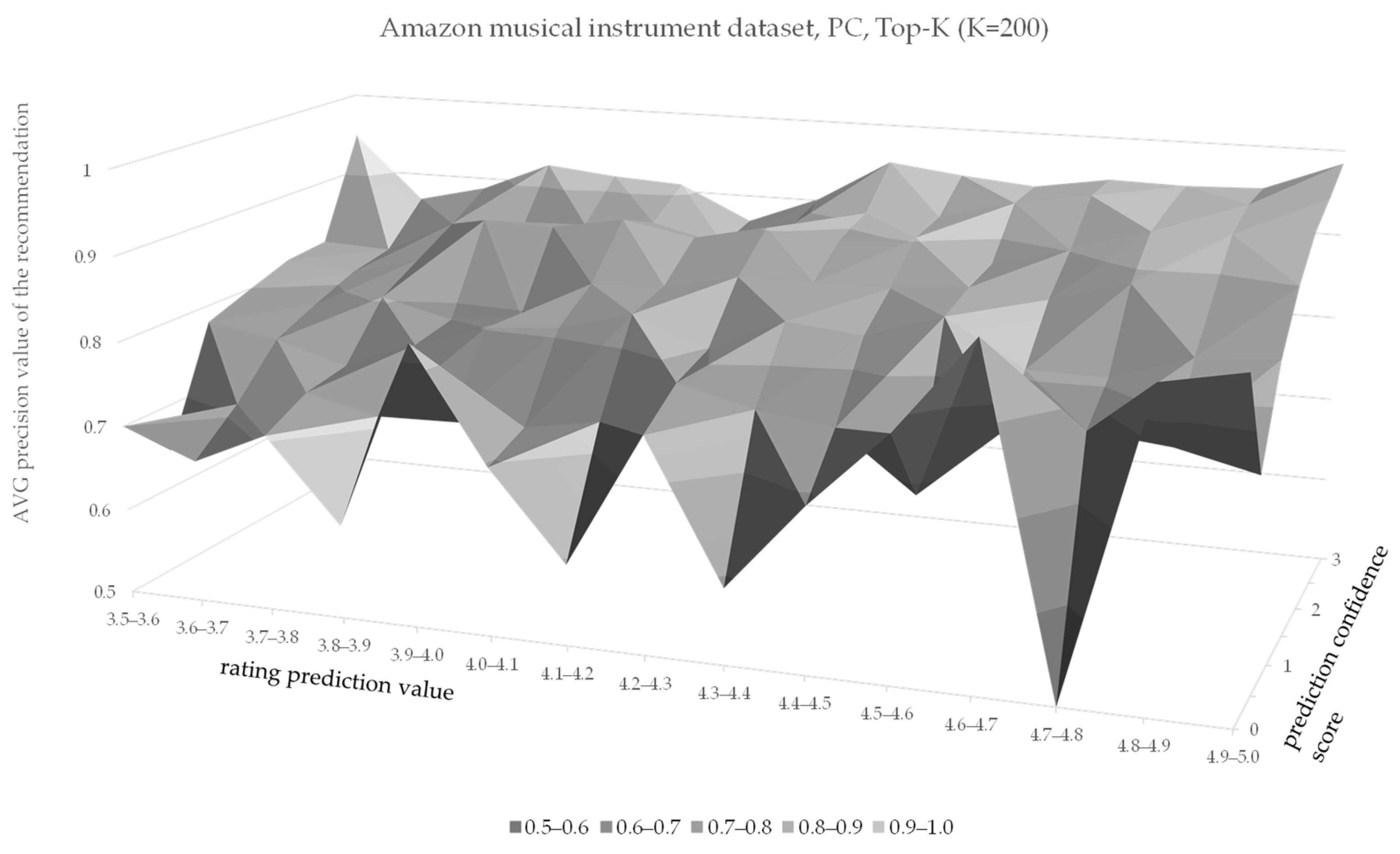

| Rating Prediction Value | Rating Prediction Confidence Score | ||||||
|---|---|---|---|---|---|---|---|
| 0 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | |
| 3.5–3.6 | 0.548 | 0.594 | 0.686 | 0.737 | 0.806 | 0.832 | 0.899 |
| 3.6–3.7 | 0.508 | 0.643 | 0.714 | 0.761 | 0.814 | 0.859 | 0.922 |
| 3.7–3.8 | 0.568 | 0.639 | 0.724 | 0.783 | 0.825 | 0.856 | 0.893 |
| 3.8–3.9 | 0.572 | 0.652 | 0.745 | 0.793 | 0.832 | 0.866 | 0.835 |
| 3.9–4.0 | 0.587 | 0.698 | 0.768 | 0.815 | 0.855 | 0.906 | 0.914 |
| 4.0–4.1 | 0.642 | 0.703 | 0.781 | 0.829 | 0.863 | 0.893 | 0.907 |
| 4.1–4.2 | 0.561 | 0.716 | 0.786 | 0.839 | 0.873 | 0.903 | 0.917 |
| 4.2–4.3 | 0.512 | 0.699 | 0.785 | 0.843 | 0.886 | 0.915 | 0.945 |
| 4.3–4.4 | 0.612 | 0.719 | 0.804 | 0.86 | 0.894 | 0.917 | 0.946 |
| 4.4–4.5 | 0.611 | 0.755 | 0.814 | 0.883 | 0.906 | 0.927 | 0.952 |
| 4.5–4.6 | 0.613 | 0.747 | 0.828 | 0.889 | 0.908 | 0.941 | 0.957 |
| 4.6–4.7 | 0.64 | 0.726 | 0.828 | 0.893 | 0.917 | 0.943 | 0.963 |
| 4.7–4.8 | 0.642 | 0.722 | 0.83 | 0.902 | 0.927 | 0.95 | 0.964 |
| 4.8–4.9 | 0.521 | 0.74 | 0.847 | 0.904 | 0.941 | 0.954 | 0.962 |
| 4.9–5.0 | 0.599 | 0.735 | 0.849 | 0.913 | 0.951 | 0.968 | 0.982 |
| Rating Prediction Value | Rating Prediction Confidence Score | ||||||
|---|---|---|---|---|---|---|---|
| 0 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | |
| 3.5–3.6 | 3.48 | 3.577 | 3.865 | 4.01 | 4.184 | 4.199 | 4.42 |
| 3.6–3.7 | 3.339 | 3.695 | 3.934 | 4.071 | 4.201 | 4.273 | 4.461 |
| 3.7–3.8 | 3.474 | 3.726 | 3.956 | 4.12 | 4.261 | 4.309 | 4.385 |
| 3.8–3.9 | 3.478 | 3.758 | 4.029 | 4.154 | 4.282 | 4.352 | 4.21 |
| 3.9–4.0 | 3.499 | 3.84 | 4.065 | 4.261 | 4.354 | 4.47 | 4.348 |
| 4.0–4.1 | 3.649 | 3.908 | 4.134 | 4.249 | 4.386 | 4.468 | 4.515 |
| 4.1–4.2 | 3.473 | 3.913 | 4.144 | 4.293 | 4.426 | 4.52 | 4.514 |
| 4.2–4.3 | 3.366 | 3.886 | 4.136 | 4.313 | 4.461 | 4.576 | 4.635 |
| 4.3–4.4 | 3.562 | 3.921 | 4.197 | 4.386 | 4.484 | 4.59 | 4.704 |
| 4.4–4.5 | 3.58 | 4.022 | 4.224 | 4.444 | 4.532 | 4.629 | 4.704 |
| 4.5–4.6 | 3.559 | 3.969 | 4.256 | 4.474 | 4.562 | 4.676 | 4.759 |
| 4.6–4.7 | 3.584 | 3.959 | 4.291 | 4.496 | 4.61 | 4.708 | 4.777 |
| 4.7–4.8 | 3.642 | 3.923 | 4.316 | 4.524 | 4.646 | 4.735 | 4.791 |
| 4.8–4.9 | 3.408 | 4.033 | 4.318 | 4.533 | 4.696 | 4.766 | 4.813 |
| 4.9–5.0 | 3.534 | 3.966 | 4.339 | 4.588 | 4.755 | 4.825 | 4.898 |
| Class | Amazon Videogames | Amazon Digital Music | CiaoDVD | Epinions | MovieLens 100 K | MovieLens 1 M | AVG |
|---|---|---|---|---|---|---|---|
| Rclass1 | 98% | 99% | 96% | 96% | 97% | 93% | 97% |
| Rclass2 | 93% | 97% | 91% | 91% | 92% | 92% | 93% |
| Rclass3 | 85% | 91% | 86% | 85% | 88% | 89% | 87% |
| Rclass4 | 81% | 87% | 79% | 81% | 84% | 87% | 83% |
| Rclass5 | 76% | 82% | 74% | 74% | 76% | 82% | 78% |
| Rclass6 | 67% | 74% | 68% | 68% | 65% | 68% | 68% |
| Class | Amazon Videogames | Amazon Digital Music | CiaoDVD | Epinions | MovieLens 100 K | MovieLens 1 M | AVG |
|---|---|---|---|---|---|---|---|
| Rclass1 | 4.87 | 4.94 | 4.75 | 4.75 | 4.72 | 4.67 | 4.78 |
| Rclass2 | 4.69 | 4.84 | 4.51 | 4.54 | 4.58 | 4.57 | 4.62 |
| Rclass3 | 4.40 | 4.48 | 4.31 | 4.33 | 4.38 | 4.45 | 4.39 |
| Rclass4 | 4.26 | 4.28 | 4.14 | 4.18 | 4.25 | 4.37 | 4.25 |
| Rclass5 | 4.10 | 4.13 | 4.04 | 3.98 | 4.01 | 4.21 | 4.08 |
| Rclass6 | 3.81 | 3.97 | 3.79 | 3.77 | 3.77 | 3.85 | 3.83 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Margaris, D.; Vassilakis, C.; Spiliotopoulos, D. From Rating Predictions to Reliable Recommendations in Collaborative Filtering: The Concept of Recommendation Reliability Classes. Big Data Cogn. Comput. 2025, 9, 106. https://doi.org/10.3390/bdcc9040106
Margaris D, Vassilakis C, Spiliotopoulos D. From Rating Predictions to Reliable Recommendations in Collaborative Filtering: The Concept of Recommendation Reliability Classes. Big Data and Cognitive Computing. 2025; 9(4):106. https://doi.org/10.3390/bdcc9040106
Chicago/Turabian StyleMargaris, Dionisis, Costas Vassilakis, and Dimitris Spiliotopoulos. 2025. "From Rating Predictions to Reliable Recommendations in Collaborative Filtering: The Concept of Recommendation Reliability Classes" Big Data and Cognitive Computing 9, no. 4: 106. https://doi.org/10.3390/bdcc9040106
APA StyleMargaris, D., Vassilakis, C., & Spiliotopoulos, D. (2025). From Rating Predictions to Reliable Recommendations in Collaborative Filtering: The Concept of Recommendation Reliability Classes. Big Data and Cognitive Computing, 9(4), 106. https://doi.org/10.3390/bdcc9040106








