1. Introduction
Because of privacy guidelines—the likes of HIPAA and GDPR—medical imaging data are usually kept in individual institutional silos that make collaboration model development impossible. Through Federated Learning (FL), integrated training of AI models can occur at different sites but keep patient data locally. Within MRI, FL provides generalized reconstruction models with the ability to work with troubled heterogeneous and cross-institutional data taken from the magnetic resonance. In recent studies, FL has been configured to solve problems of domain heterogeneity and stability in medical imaging in an adaptive aggregation and transformer framework. The early medical imaging techniques involved the application of radioactive tracers and gamma cameras, which captured the functional distribution of isotopes in a body. Although they gave physiologic information, it had limited anatomical detail and thus led to further development of improved imaging techniques like computed tomography (CT) and Magnetic Resonance Imaging (MRI) [
1,
2,
3].
Recent technological developments in imaging—from X-ray computed tomography (CT) to Magnetic Resonance Imaging (MRI)—have greatly improved visualization of anatomy and delineation of tumors. The principles of tracer kinetics used in iodine-based CT examinations have passed on to MRI, allowing for high-resolution anatomical imaging with better contrast sensitivity [
4,
5].
Thus, MRI has evolved into a very potent non-invasive tool for assessment of tissue perfusion and organ functional characteristics in various organs like the brain, heart, liver, and breast [
6,
7].
Information is acquired on the imaging signal from MRI in the frequency domain (k-space), which stores spatial-frequency information reconstructed into pixel-domain images [
8,
9,
10]. The quality and speed of the MRI process have been improved more and more with the learning-based reconstruction techniques ever since artificial intelligence and deep learning came into existence [
11,
12]. The research mentioned above lays the groundwork for our proposed federated learning framework aimed at reconstruction to enhance image fidelity while preserving patient privacy across decentralized institutions.
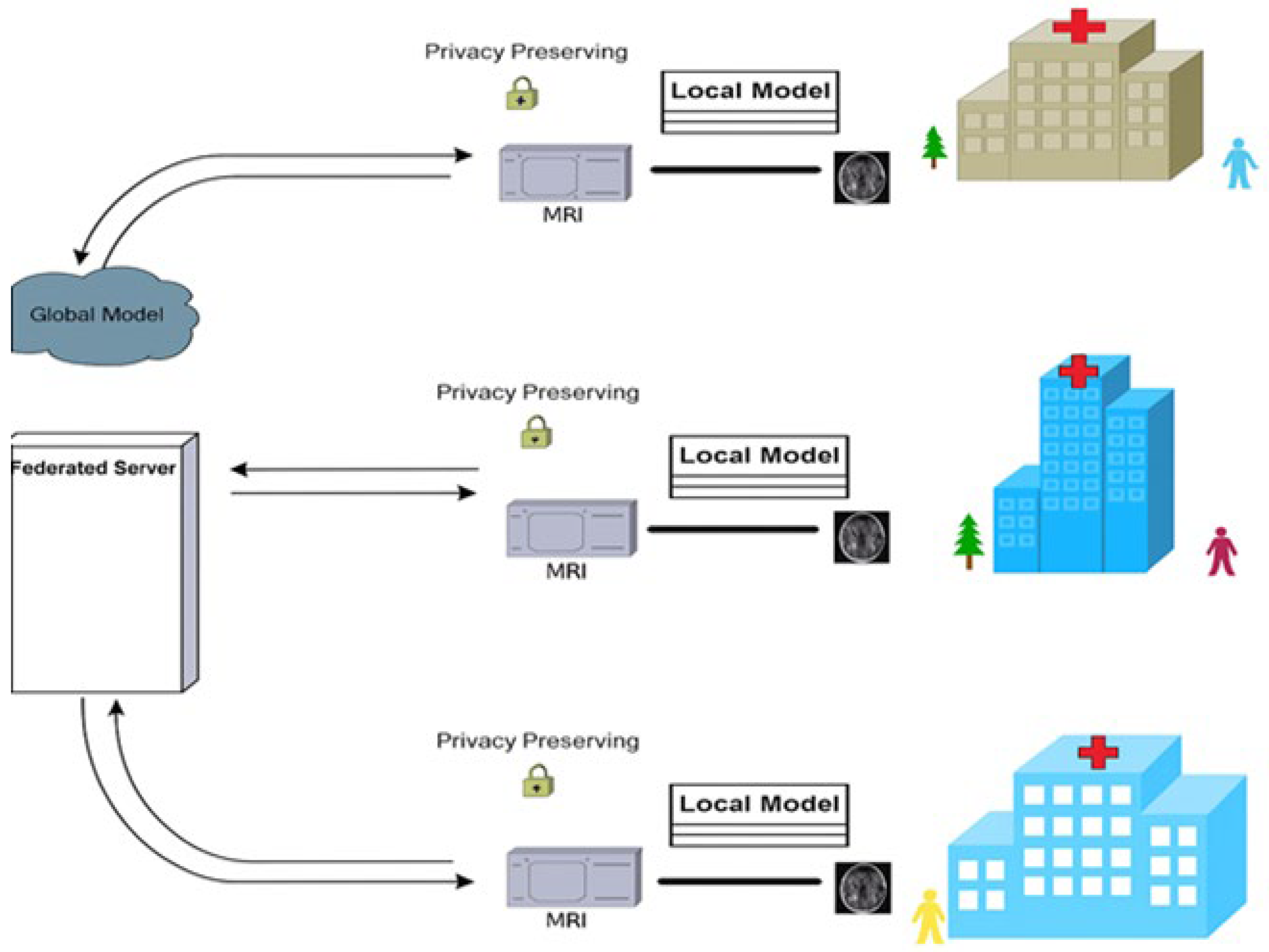
Machine learning methods utilize mathematical models which are fed image input data and are trained to produce outputs. These models are trained for ‘n’ number of epochs which represent the experiences and are adjusted to generate predictions for the training dataset with the help of an optimization algorithm [
13]. The implementation of deep learning techniques in MR image acquisition and reconstruction needs to be assessed carefully to avoid false positives for both present and non-present pathologies. Further, maintaining a centralized database at any institution representing diverse clinical conditions is a challenging task and can be addressed with decentralization of the image database. To keep the confidentiality of data, we implemented a federated learning approach. Federated learning is a distributed machine learning model that allows training of shared models over decentralized data sources without needing the data to be centralized by allowing clients to train models locally and sending only aggregated model updates to the central server. Federated learning, often called ‘collaborative learning’, is a specialized form of machine learning [
14]. In the decentralized FL setting, each collaborating site represents a node which collaborates with a central global server to train a global model [
15]. The mathematical model and its objective function are represented by Equation (1).
In the MRI context this equation defines Federated Averaging (FedAvg), where represents local model parameters for MRI reconstruction from hospital i, K is the number of participating hospitals, and is the ground truth MR image.
To further improve the image quality and reduce error, we propose a novel MR image reconstruction technique which harnessed the FL with dynamic regularization along with lasso regression to reduce the loss. Structured cross entropy was used to provide better classification results along with generative adversarial networks which were employed to further reduce loss and increase the overall performance of the reconstructed MR image. The normal cross-entropy considers each pixel/class as an independent entity, while structured cross-entropy sees the spatial relationship between neighboring pixels. This property is essential in MR image reconstruction, where anatomical plausibility must be maintained (e.g., tumor margins).
Prior works related to our problem can be grouped into three categories: (i) FL-MRCM (2022): It couples re-construction as part of federated averaging without addressing the problem of clients drifting under non-IID partitions and depends on fixed hyper-parameters, which can destabilize adversarial training. (ii) FedGIMP (2023): It adds personalization/aggregation but does not incorporate adversarial optimization for reconstruction quality nor client-side hyper-parameter search. (iii) GAN-PSO models: These optimize GANs via swarm strategies in centralization and do not have a federated objective that jointly deals with privacy, non-IID heterogeneity, and communication-round stability. Our approach is conceptually different by incorporating FedDyn-based dynamic regularization to control the client drift, client-side PSO that online adapts the GAN hyper-parameters per site, and a structure-aware loss guiding the entire thing into one federated objective while maintaining anatomical consistency. This distinct combination explicitly couples local adversarial training with global dynamic aggregation and formally defined total loss, allowing reproducible optimization boundaries and resilient non-IID performance across multi-center MRI data.
Unified federated objective with explicit total loss for reproducible optimization boundaries.
Dynamic aggregation based on FedDyn to limit client drift and enhance stability when criterion data are not the same.
Client-based PSO for adapting the hyper-parameters of the online GAN against site heterogeneity.
Structure-aware regularization in order to maintain anatomical fidelity under adversarial training.
Multi-site validation results on fastMRI, BraTS, and OASIS with consistent mean±SD improvements over FL baselines.
2. Related Work
The k-space stores the acquired digitized MR signals. Reconstruction of the MR images from the k-space is an inverse problem and computationally heavy task. To solve this problem, compressed sensing improved image reconstruction with fewer k-space samples [
16]. Some of the deep learning techniques have produced far better results on the MR reconstruction process where the k-space data was reduced using sub-Nyquist sampling techniques which made the MR image reconstruction faster [
17]. However, these centralized deep learning methodologies are based on pooled datasets compromising the medical data privacy constraints, and in addition, they usually generalize poorly between institutions. This limitation unavoidably leads to motivation in exploring federated alternatives for learning from pooled, distributed data without central aggregation. Few DL techniques utilized k-space data which are undersampled to accomplish accelerated scan times [
18].
There are several implementation strategies for federated learning including FedAvg [
2], FedProx [
19], FedSGD [
20], and FedDyn [
21]. The FedAvg technique harnessed the data dispersed across two or more devices to acquire the classification tasks collaboratively without the need to share the data. It was introduced in 2017 and focused on solving the optimization of the local device [
22]. This is the most widely used framework of federated learning.
FedDyn uses dynamic regularization with the intent of minimizing the communications, thereby increasing the processing and the optimizations on the local devices, thus reducing the energy consumptions. Despite its efficacy, FedDyn does not directly address any instability issues arising during adversarial training or how hyper-parameters are tailored on the non-IID MRI data. Hence, in pursuit of improved convergence and reconstruction quality, it becomes imperative to integrate dynamic regularization within an adaptive optimization mechanism. This algorithm dynamically regularizes the loss function of each, and every device and the total accumulated loss converges to the actual global loss.
In [
23] proposed multi-institutional fMRI classification and examined the use of federated models and the privacy preserving techniques. The MR image reconstruction with the collaboration of multiple institutions with the FL was proposed [
5]. In contrast, ref. [
24] proposed a federated learning-based framework for MRI reconstruction that balances performance with privacy and employs lightweight CNN models. However, this approach does not consider issues of domain shift or adversarial optimization, both of which are central to our proposed FL-SwarmGAN MRCM framework. Recently, some authors have focused on addressing client heterogeneity and privacy issues in federated healthcare scenarios. Ref. [
25] uses an FL framework that is lightweight and privacy-preserving for the skin cancer diagnosis using client-adaptive knowledge distillation across institutions to alleviate non-IID issues. This means that it becomes even more essential to design FL models that can withstand variability across clients, a consideration we also bear in mind within the MR image reconstruction context for our proposed FL-SwarmGAN MRCM framework. Indeed, the earlier works justify the potential of FL for collaborative medical imaging; however, most frameworks remain limited to fixed local optimization and do not add any generative adversarial refinement mechanism. We build on this foundation by integrating an adversarial reconstruction with a swarm-based hyperparameter tuning for attaining stable learning under clients’ heterogeneity. FL framework paved way for a secure multi-site and cross-site analysis of data which enhanced the performances and helped in diagnosing the diseased biomarkers quickly. The overall performance of the image reconstruction methods used earlier mostly employed L1 regularization and reduced loss using lasso regression techniques.
Even if the proposed federated learning pipeline is focused on MRI, we remain architecture agnostic, and thus it can be extended to any other biomedical imaging modality. For example, SwarmGAN could be trained on compressed ECG or CT data in a decentralized setup; as in prior works, extensions are feasible because of the modular framework of the encoder–decoder and federated optimization strategies [
26].
Other state-of-the-art biomedical image reconstruction techniques are being integrated into federated learning (FL) frameworks including CycleGAN, Federated learning of Generative IMage Priors (FedGIMP), and auxiliary Variational Autoencoder (VAE) [
27]. This research lacks in different sections, including CycleGAN’s propensity for introducing artifacts and mode collapse and FedGIMP’s potential for localized information loss, impacting reconstruction quality. Furthermore, generative models like VAEs and CycleGANs face challenges in handling data heterogeneity, including variations in annotations and image distortions, during harmonization within FL frameworks.
A careful examination of existing recent FL-based reconstruction systems indicates some clear weaknesses in adaptability, stability, and loss formulation, as summarized below. Standard FedAvg was employed by FL-MR; hence, it did not account for the issues caused by domain shifts. FL-MRCM, on the other hand, is based on adversarial domain alignment, yet depends on FedAvg, which is sensitive to data heterogeneity. Our model FL-SwarmGAN MRCM integrates FedDyn, which mitigates client drift through dynamic regularization. It uses SwarmGAN with Particle Swarm Optimization to adaptively tune generator/discriminator parameters. It also applies structured cross-entropy loss, enhancing reconstruction fidelity across diverse domains. FL-SwarmGAN MRCM addresses, with a combined objective, optimizing adversarial learning while regularizing clients and tuning the parameters dynamically, which also includes addressing certain data imbalances due to non-IID and the reproducibility gaps that still remain from previous works.
The contributions made by this paper are summarized below:
Federated Learning with Dynamic Regularization (FedDyn) is employed, enabling multi-institutional collaborations for the reconstruction of MRI images.
This paper exploits the FL-MRCM (MR with cross-site modeling) to approach the domain shift problem.
To reconstruct faster MR images, this paper puts into service the SwarmGAN algorithm.
This paper employs the L1 regularization to minimize the loss at each institutional local model.
This paper conducts trials on various GAN losses to check the overall performance of the reconstructed image.
This paper incorporates the structured cross entropy which provides better classification results.
A comparison of prior lines of research and the conceptual differences of the proposed framework is summarized in
Table 1.
To evaluate the cross-site generalization ability of the proposed framework, we compared the reconstruction performance across multiple institutions using standard quantitative metrics. This analysis highlights how well the model adapts to heterogeneous data distributions while preserving image fidelity across different domains.
3. Materials and Methods
In this paper, the proposed technique addresses the inverse and ill-posed MRI reconstruction problems arising due to discretization of MR data and under-sampling by mapping the k-space data to fully sampled data. The reconstruction of the MR images can be obtained using Equation (2). Let denote the MRI data sample for client , and represent the local generator and discriminator, and and are the local and global model parameters, respectively. The losses , , and refer to the reconstruction, adversarial, and structure-aware components of the total objective function.
Let x denote undersampled image data, y is fully sampled image data,
is noise, F and F
−1 denote the Fourier Transform, and
undersampled Fourier encoded matrix
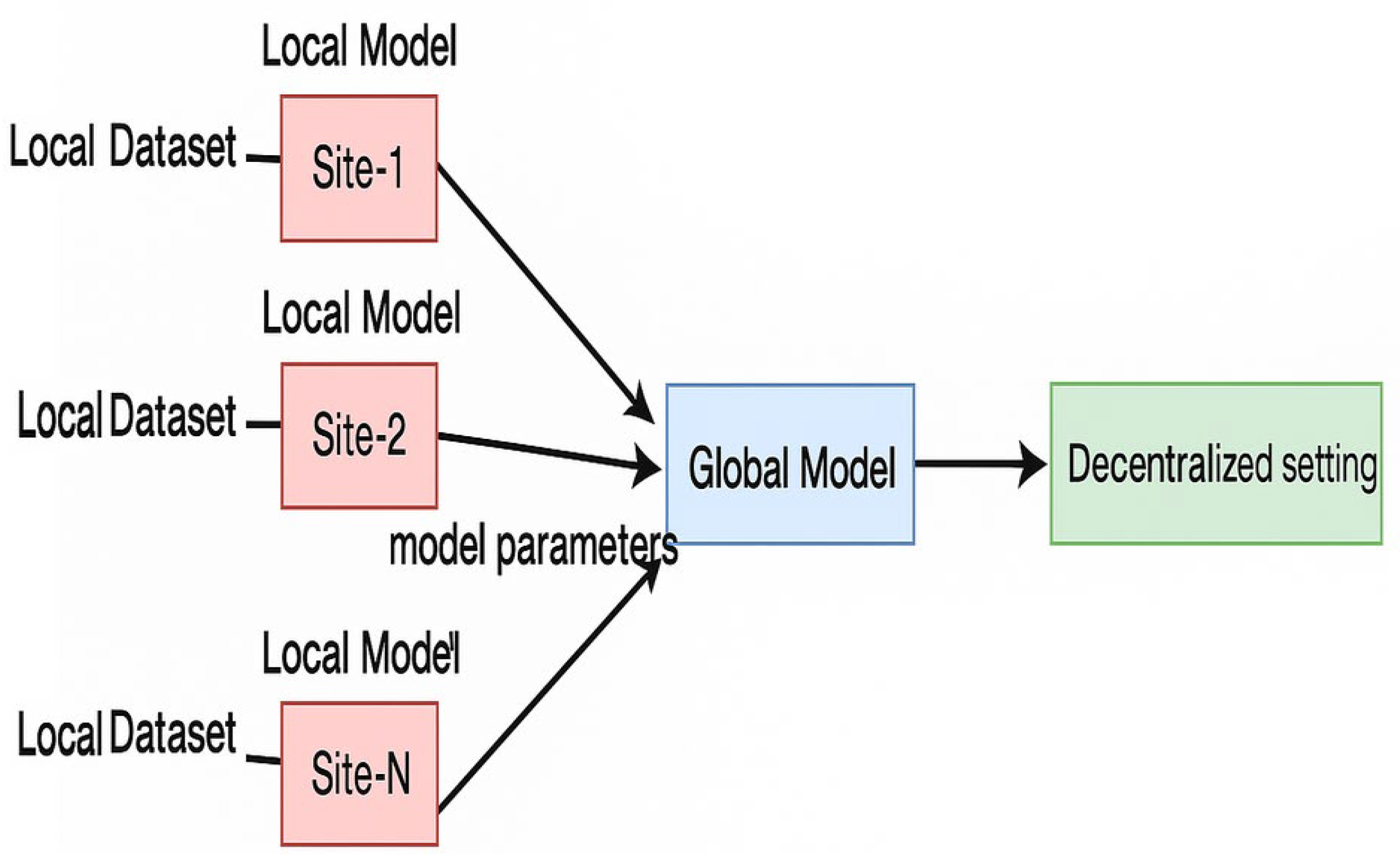
Federated learning, often called ‘collaborative learning’, is a sub-division of machine learning as shown in
Figure 1.
The multiple clients within FL collaborate to train a model and at the same time ensure the data is decentralized. The training process within the FL consists of the following steps: (1) Every institution is responsible to estimate its gradients and then sublimate the trained network parameters computed locally to the server. (2) The server accumulates the uploaded parameters from all the ‘K’ institutions. (3) Now the server begins to broadcast the accumulated parameters to all the ‘K’ institutions. (4) Every institution then updates its local model with the aggregated parameters and begins testing the performance of their respective models as shown in
Figure 2. Collectively the institutions learn a ML model with the help of the cloud server [
15]. A global optimum model is obtained after an umpteen number of training exercises and exchanges between the institutions and the server have taken place.
Generally, FedDyn’s work is to stabilize the convergence of client models when operating in non-iid environments. On the other hand, SwarmGAN works by optimizing the GAN’s generator and discriminator parameters with particle swarm optimization (PSO), thereby improving the feature realism of each local client’s generated outputs. In other terms, updates from FedDyn are on the server, but then SwarmGAN basically does its parts at each of the local clients, which altogether makes the entire training even more stable and adaptive [
28].
The proposed FL-Swarm MRCM becomes a self-contained end-to-end framework that incorporates client adversarial training along with PSO-based parameter optimization and server-side dynamic aggregation. Each of the local clients trains its GAN-based reconstructor on MRI data and runs a Particle Swarm Optimization (PSO) routine to tune the generator and discriminator hyper-parameters for minimum reconstruction error and adversarial loss. After each global communication round t, local model weights
are sent to the central server, which updates the global model according to the FedDyn rule using those local models.
Moreover, they penalize client drift and stabilize convergence. The structured cross-entropy loss encourages the maintenance of spatial continuity among neighboring pixels to produce anatomically consistent reconstructed images. Together, these stages create a unified optimization loop that combines dynamic regularization, adversarial learning, and swarm-based hyper-parameter tuning in a federated environment.
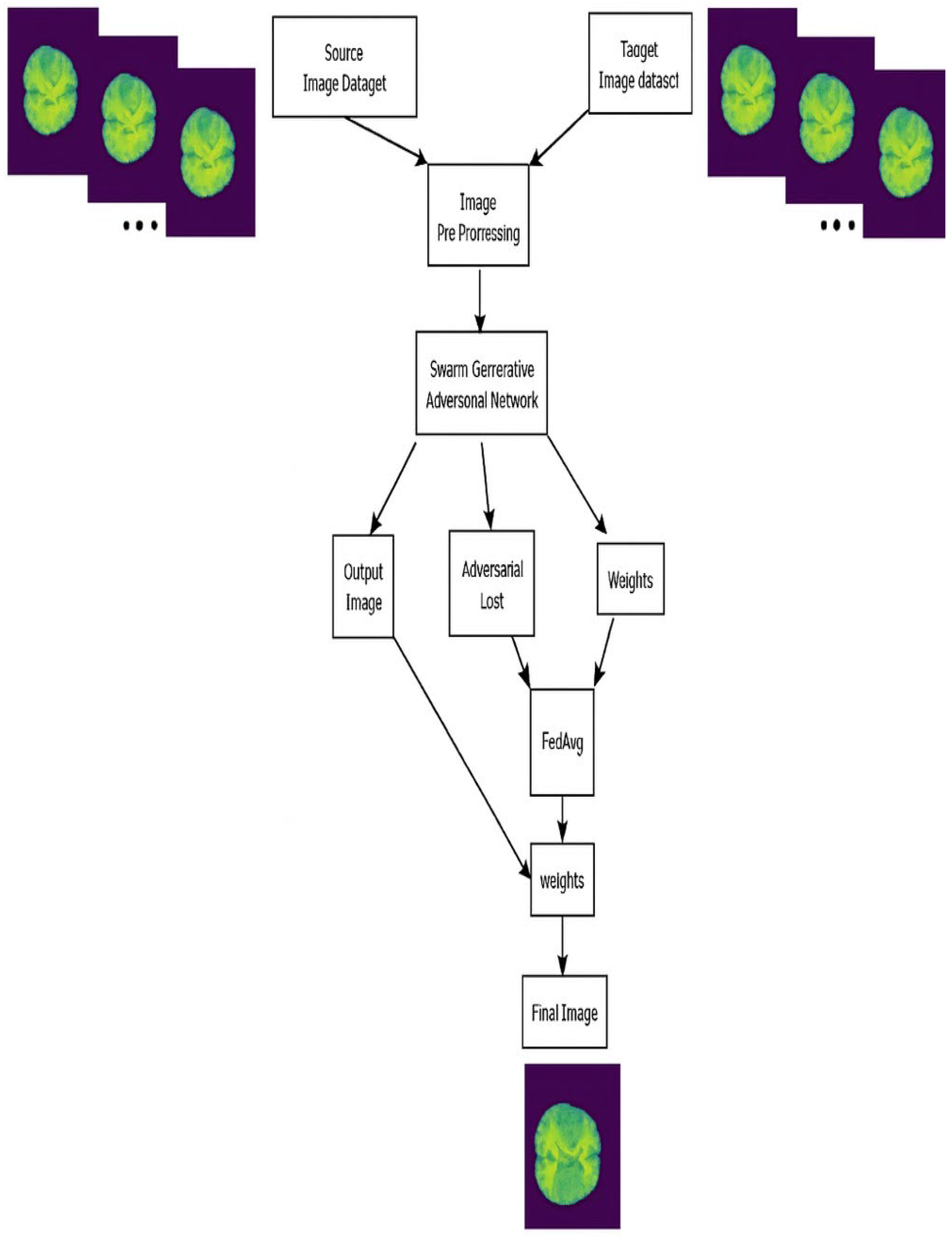
The overall workflow of the proposed FL-SwarmGAN MRCM pipeline is illustrated in
Figure 1. This figure provides a high-level overview of the model structure and data processing stages.
The key components of the reconstruction framework are visually detailed in
Figure 2. This summarizes the core modules used during training and inferenceMR image reconstruction using Federated Learning is discussed in three sections, namely (1) FL-MR, (2) FL-MR with cross-site modeling (FL-MRCM), and (3) FL-SwarmGAN MRCM. Arrows denote the directional flow of data and model updates. Colored boxes/arrows represent distinct components of the framework.
3.1. FL-Based MRI Reconstruction
The FL-MR image reconstruction technique is shown in
Figure 3.
An overview of the FL-MR framework is shown in
Figure 4.
The local models maintained with each institution are trained with their own data. Lasso regression is computed on each local model to reduce the loss by using Equation (3).
Pairs of undersampled and fully sampled images
Gk Local model at the site k
Gk(x) Reconstructed image
The global model is run for several epochs, i.e., P epochs to optimize the parameters within the global model defined by the following equation:
Each institution or hospital is equipped with Magnetic Resonance Imaging technology which scans the human body to capture image data. It followed some acquisition protocols to capture the diseased tissue and accumulates the same in
database [
29].
Every local database is unique and has certain features. So, when a local model gets trained, it inserts bias and will not extrapolate with other datasets from different institutions [
2]. To overcome this problem, we can train the network with a combination of all datasets from K institutions as D = {
. This is not feasible in the medical domain as there are privacy regulations of the medical body to be followed, as distributing and disclosing the patient data with public is prohibited. Each institution works on its local dataset, and no data is exchanged amongst the other institutions for any kind of testing.
The federated learning setup across participating institutions is depicted in
Figure 3. It highlights the collaborative process between local clients and the central server.
The PSO-based optimization procedure is outlined in
Figure 4. This diagram helps clarify the role of swarm dynamics in parameter adjustment.
3.2. MRCM-Based MRI Reconstruction
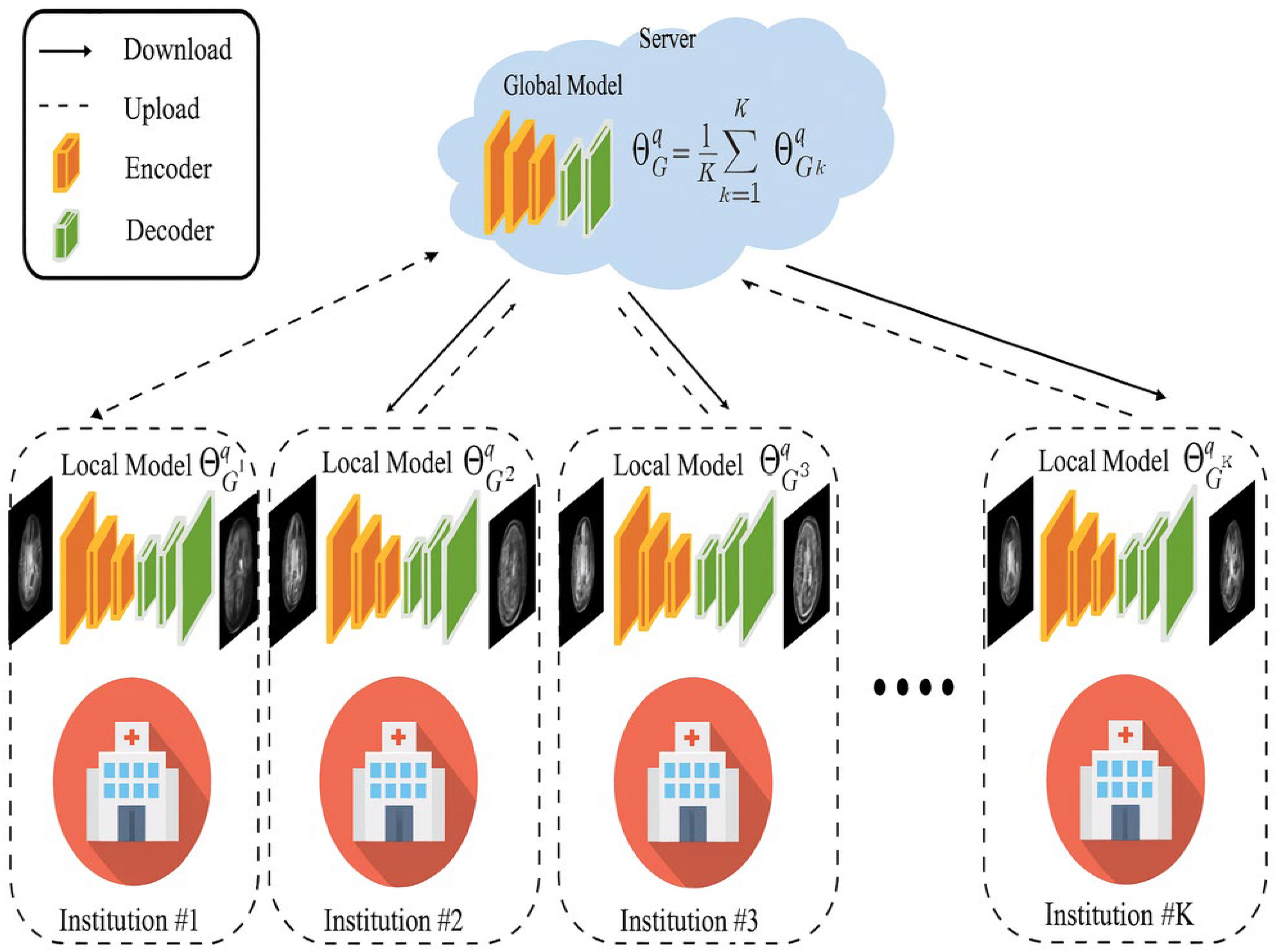
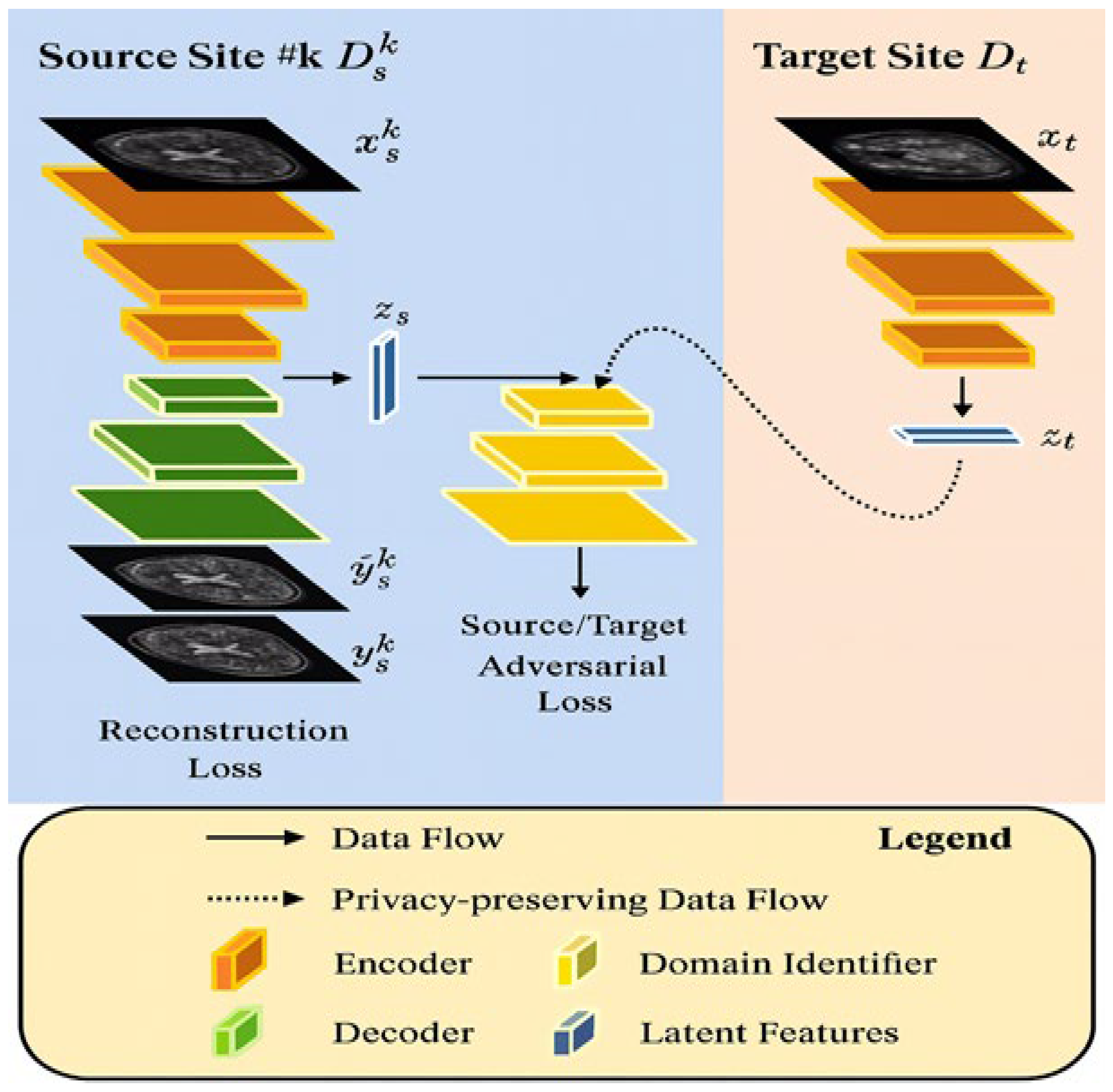
Federated learning framework with cross-site modeling (FL-MRCM) reconstructs MR images where the arbitrable learned latent features from different source sites are adjusted with the features of target site. This uses a two-step optimization technique, and an adversarial domain identifier was trained to train the probability distribution of source and target domains. This minimized the loss of the adversarial domain identifiers, which resulted in the network weights being adjusted to the target domain.
Figure 5 shows that the varied institutions with a central server in a cross-site modeling technique reconstruct the MR images quickly.
The FL-MRCM image reconstruction technique is shown in
Figure 6. The FL-MRCM technique addresses the domain shift issues found in reconstruction of MR images. As there are many source domains each representing an institution, the data is stored locally in the institution itself. This methodology employed FedAvg algorithm which summed all the local model updates together.
Federated Averaging (FedAvg) is an abstraction of FedSGD. The local nodes or edge devices are allowed to perform more than one batch on the local dataset and the weights are updated. Here the central server aggregated the model by averaging the model parameters from all the local models emanating from different sites.
The architectural design of the discriminator and generator networks is shown in
Figure 6. This figure highlights the structural components used in adversarial training.
In this methodology, the adversarial latent codes for source site
were mapped across target site
These are supplemented by reconstruction networks
to project the data onto latent space
. The latent space
is obtained for the target site
. An adversarial domain identifier
is introduced for source–target domain pair (
). This identifier aligns and distributes the latent space between the source and the target domains. This is trained in an adversarial fashion.
is first trained to recognize from which source site the latent features arise. Next the encoder is trained to confuse the
; this has access to output latent features from source reconstruction network
to target reconstruction network
. The loss function for
, given source–target domain pair (
) is as follows:
where
and
.
The loss function for the encoders is defined by the following equation.
The total loss function for training
consists of computing the adversarial and reconstruction losses. They are defined as follows:
where
is a constant controlling the contributions of the adversarial losses.
3.3. FL-SwarmGAN MRCM MRI Reconstruction
Existing work showcased that the FL-based MRCM technique produced superior results for MR image reconstructions by supplementing the training. The proposed technique harnessed the hyper-parameters of the adversarial training to tune the model towards minimal loss. This was ascertained by employing the SwarmGAN technique in MRCM environment as shown in
Figure 7, instead of choosing manually or hardcoding the parameters for each learning session. The SwarmGAN presents a network which trains the GAN. A swarm technique is used to initialize the parameters of the GAN. Swarm intelligence depends on mutual communication and cooperation amongst the individuals of a group of living organisms. In this paper, particle swarm optimization (PSO) is used to steer both the generator and the discriminator blocks of the GAN.
PSO is a metaheuristic algorithm, which was introduced by Kennedy, Eberhart, and Shi [
30]. This is an AI methodology which is used to compute the maximum or minimum of an objective function. This algorithm is based on the swarm behavior of fishes, birds, etc. The objective function of the PSO algorithm is designed so that the Adam optimizer computes and selects the parameters for optimization instead of manually selecting the hyper-parameter. This algorithm stabilizes the weights during training [
31].
The block diagram of the SwarmGAN-MRCM methodology is presented in
Figure 7. It summarizes the interactions between the SwarmGAN model and the reconstruction process.
To provide a clear overview of the PSO-driven optimization routine, we detail the complete process in Algorithm 1.
| Algorithm 1: FL-Novel MRI Reconstruction—PSO |
Step 1: Initialize the swarm population of N particles
x_i = 1 … Q |
Step 2: Choose c1 cognitive coefficient and c2 social coefficient
Choose w inertia weight |
| Step 3: Choose an objective function and evaluate the position of the particle |
Step 4:
for j = 1, … epochs
for i = 1, … Q
Evaluate the following
Compute pBest and gBest
|
|
|
| Update all the velocities |
|
| Update the positions |
|
|
To illustrate the interactions between local and global models during reconstruction, the full federated learning procedure is outlined in Algorithm 2.
| Algorithm 2: FL-Novel MRI Reconstruction |
Input: D = {D1, D2 ….Dk} are datasets from
K institutions |
P → number of epochs
Q → number of global epochs
γ → Learning rate
G1, G2 ….Gk → Local models
θG1, θG2 … θGk → Parameters of Local models
G → Global Model parameterized by θG
Output: well-trained Global model G
Parameters Initialization using PSO for Discriminator
for q = 0 to Q do
for k = 0 to K in parallel do
distribute model weights to local model
for p = 0 to P do
FL-MRCM:
Compute GAN losses
SwarmGAN Modeling:
end
Upload weights to server
end
Update global model with FedDyn
end
|
3.4. Datasets
In this paper, three different datasets were used to evaluate the effectiveness of the proposed methodology. The three different datasets are fastMRI, BraTS2020, and OASIS. The details of each dataset are discussed in the following paragraphs.
3.4.1. BraTS [33]
(Data B for short). BraTS stands for Multimodal Brain Tumor Image Segmentation Benchmark. This dataset is primarily focused on the segmentation of the inherent heterogenous gliomas. T1- and T2-weighted images from 494 subjects were used, of which 369 were used for training and the remaining 125 were used for testing purposes. The brain tissues of 120 axial cross-sectional images for both the MR sequences for each subject are provided.
3.4.2. fastMRI [11]
(Data F for short). T1-weighted images corresponding to 3443 subjects were used, of which 2583 were used for training and the remaining 860 were used for testing purposes. Another set of T2-weighted images was used to conduct the experiments. A total of 3832 subjects were used, of which 2874 were used for training and the remaining 958 were used for testing purposes. The brain tissues of 15 axial cross-sectional images for each subject are provided.
3.4.3. OASIS [34]
(Data O for short). OASIS stands for Open Access Series of Imaging Studies. This dataset is primarily focused on the neuroimaging of the brain. This dataset contains T1 weighted images of 414 subjects with a voxel spacing of 1 × 1 × 1 and an image size of 256 × 256 × 256, of which 331 were used for training and the remaining 83 were used for testing purposes.
3.5. Training and Implementation
In this paper, the proposed technique utilized SwarmGAN encoder–decoder architecture for MR reconstruction purposes. The acceleration factor is set to 3 and the network is trained using Adam Optimizer with a learning rate of 0.0001 for a total of 50 global epochs with a batch size of 16.
3.6. Performance Metrics
The performance metrics that are used to evaluate the proposed methodology are SSIM [
35] and PSNR [
36].
SSIM: Structural Similarity (SSIM) is a metric used to estimate the similarity between two or more images. At its core the metric is a product of components like luminance, structure, and contrast. The below equation defines the SSIM metric,
PSNR: This metric measures the peak signal-to-noise ratio between two or more images. This ratio measures the image compression quality. The below equation defines the PSNR metric,
The metrics deployed to check the performance of the algorithms are Structural Similarity Index (SSIM), peak signal-to-noise ratio (PSNR), and MSE loss. The combination of PSNR and SSIM, two conventional quantitative indices for medical image reconstruction, can assess numerical fidelity and perceptual quality. PSNR measures the ratio between the image intensity maximum and the reconstruction error that indicates how accurately anatomical structures are preserved. SSIM models human perceptual vision comparing luminance, contrast, and structure, which are critical in MRI because small differences may indicate pathology. Clinically, higher SSIM values imply better conservation of tissue boundaries and lesions from noise, whereas higher PSNR values suggest less noise, which would improve diagnostic reliability. This is why these metrics together are clinically informative for depicting reconstruction accuracy and visual realism. All experiments were run in a federated framework with five clients handling non-IID MRI data, modeling the real-world heterogeneity. Each client receives 20% of the data, while class imbalance is preserved. Fed-Dyn aggregation was used to proceed with the training of the models for 36 communication rounds with a PSO-based GAN optimization on an NVIDIA RTX 3090 GPU (24 GB VRAM), Intel i9 CPU, and 64 GB RAM under PyTorch 2.1.
4. Results and Discussions
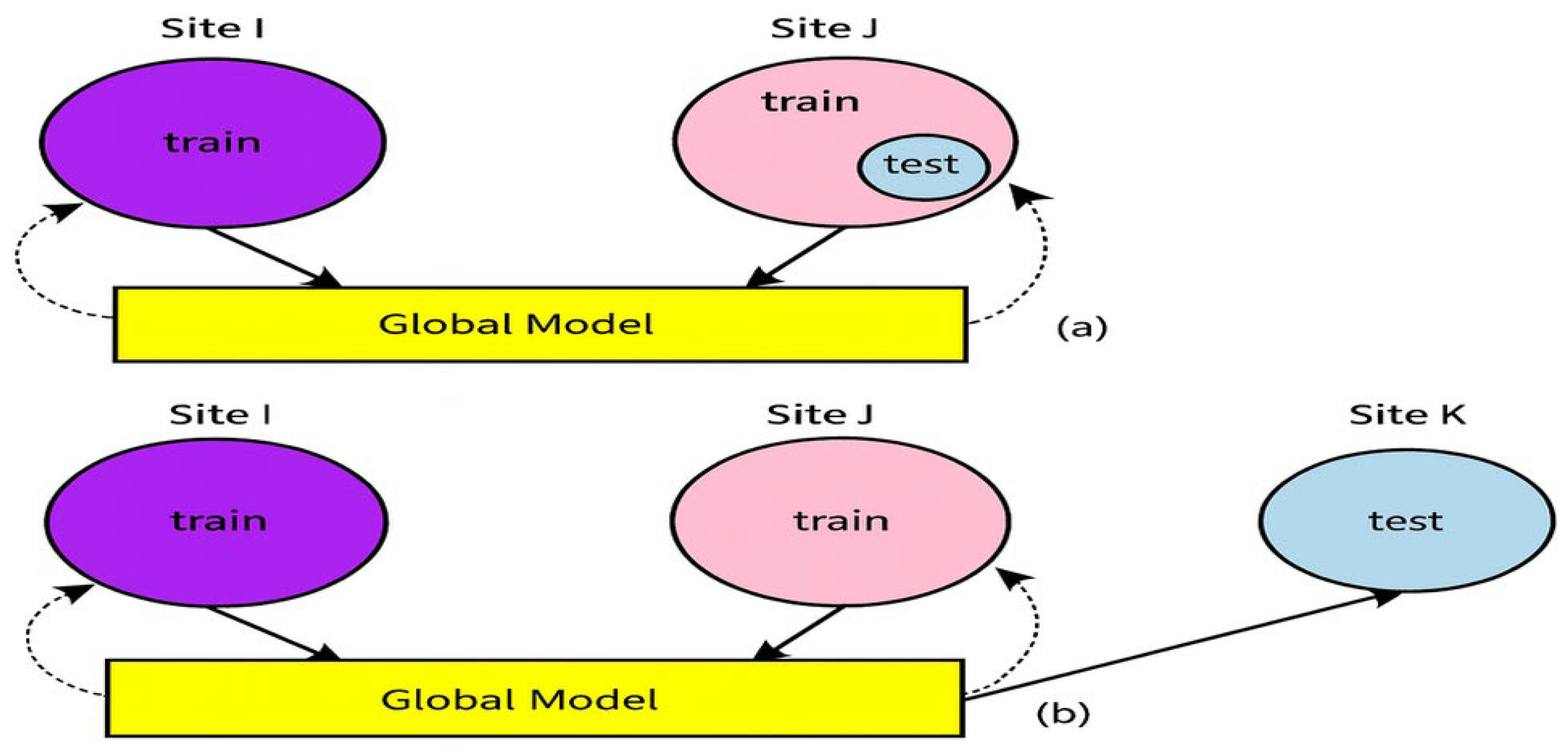
The research carried out and the experiments conducted exhibit the efficacy of the proposed methodology. The experiments were conducted using two different scenarios. In scenario 1, the effectiveness of the proposed technique was analyzed by improving the applicability and portability of the trained models and thus improving its usage compared against the previously used methodologies. The performance of the trained model is determined after subjecting it to a dataset which is not used directly during training process. Incidentally, a dataset emulates an institution, and the datasets from other sites are chosen for training purposes which are commonly seen in clinical practices. The user institutions do not have access to complete and fully sampled image databases for all training purposes in scenario 2 as shown in
Figure 9. The proposed methodology is evaluated by first training the dataset which is made available from all the institutions to exhibit the benefits of collaboration of the datasets via the federated learning technique.
4.1. Evaluation of the Generalizability
In the first category, the model is tested to evaluate its generalization to data from other sites and than the quality of the reconstructed images is compared after testing with different methods on three different datasets. The metrics deployed to check the performance of the algorithms are Structural Similarity Index (SSIM), peak signal-to-noise ratio (PSNR), and MSE loss. The performance of the proposed framework and its models is trained with the dataset available in a single data center. Here, the trained model is obtained from one amongst all institutions, and the performance is evaluated on another data center. This is termed as ‘Cross Modeling’. Multiple trained models are obtained from different institutions. The outputs or reconstructed images from different institutions can be fused together by computing the averages. In addition, a model can be generated which is trained with the datasets made available from all institutions; this is also tabulated.
The proposed FL-MRCM with SwarmGAN is better performing in comparison to FL-MR and FL-MRCM. This algorithm displays generalization and preserves the privacy of the data of the patients. SwarmGAN with FL-MRCM settings improves the reconstructed image quality. T1- and T2-weighted images were taken for all three datasets. The SSIM of the SwarmGAN reveals that the reconstructed images of the outputs are visually similar to the reference images. They produce better results in comparison to other FL techniques discussed in this paper. The higher the PSNR, the lower the error, so the PSNR of the SwarmGAN also showcases a reconstructed image quality that is better than the other FL alternatives. Moreover, other baselines grounded in federated learning like FedProx and FedGAN exhibit lower performance with about 28 dB PSNR and 0.90 SSIM in similar experimental setups. This reflects the superior reconstruction fidelity and perceptual consistency attained by the proposed FL-MRCM SwarmGAN framework. Improvements in PSNR and SSIM indicate that the proposed framework not only reduces the reconstruction error but also enhances perceptual image quality with reference to the radiological interpretative process.
Table 2 shows that FL-MRCM with SwarmGAN is superior to FL-MR, FL-MRCM by itself, and FL-MRCM with other improvements. In statistical measures, each experiment was performed five times with a random initialization. The mean ± standard deviation of PSNR and SSIM for each dataset and method were calculated to ensure that differences in the performance observed can be demonstrated to be statistically significant (
p < 0.05, paired
t-test). This increases the credibility of this measure and enhances reproducibility when different runs and datasets are used.
The distribution of training data across participating institutions for the federated learning experiments is illustrated in
Figure 10. This figure summarizes the number of samples available at each site, highlighting the inherent data imbalance across centers. The quantitative results for this single-site evaluation are summarized in
Table 3.
To improve the understanding of the generalizability of FL-SwarmGAN MRCM across imaging contexts, the interpretation was performed at a subset level according to the dataset and MR modality. PSNR and SSIM measures for T1 and T2 sequences separately across fastMRI, BraTS, and OASIS datasets are indicated in
Table 4. The results confirm that the proposed method outperforms baselines across the board for all subsets, providing groundwork for robustness across clinical modalities and institutions.
The ablation analysis emphasizes well each component’s complementary role in the proposed FL-SwarmGAN MRCM framework. Integrating FedDyn promotes convergence stability and robustness to diversified non-IID data distributions, while SwarmGAN fills perceptual realism and reconstruction of fine details, and the structured cross-entropy loss maintains images with spatial constraints on distortion while preserving anatomical consistency. Altogether, these modules create a unified optimization process with competing interests for global learning stability and local image fidelity, leading to superior performance in terms of PSNR and SSIM as compared to baseline methods.
4.2. Evaluation of FL-Based Collaborations
In the second category of experiments, we tested the efficiency of the proposed methodology by evaluating its performance with models that are trained with data from a single institution and tested on its own data. This is termed as ‘Single’ and tabulated in
Table 5. Next, a model is obtained which is trained with data from all institutions. It is clear that the SwarmGAN-based FL-MRCM outperforms the FL-MR and FL-MRCM in terms of metrics SSIM and PSNR.
4.3. Ablation Study
The SwarmGAN-based cross-site modeling algorithm demonstrated the effectiveness of multi-institutional FL-based classification and showed improved performance when compared to FL-MR and FL-MRCM methodologies.
Detailed ablation studies were conducted to analyze the efficiency of the proposed methodology. Here, a trained model was obtained from one of the sites (institutions) and evaluated against data from another institution. The performance metrics obtained after executing the FL algorithms are tabulated in
Table 5. It is clear from
Table 5 that the proposed FL-SwarmGAN MRCM outperforms, exhibiting better collaborations and generalizability. It clearly improves the reconstruction image quality in every dataset as shown in
Figure 11 and
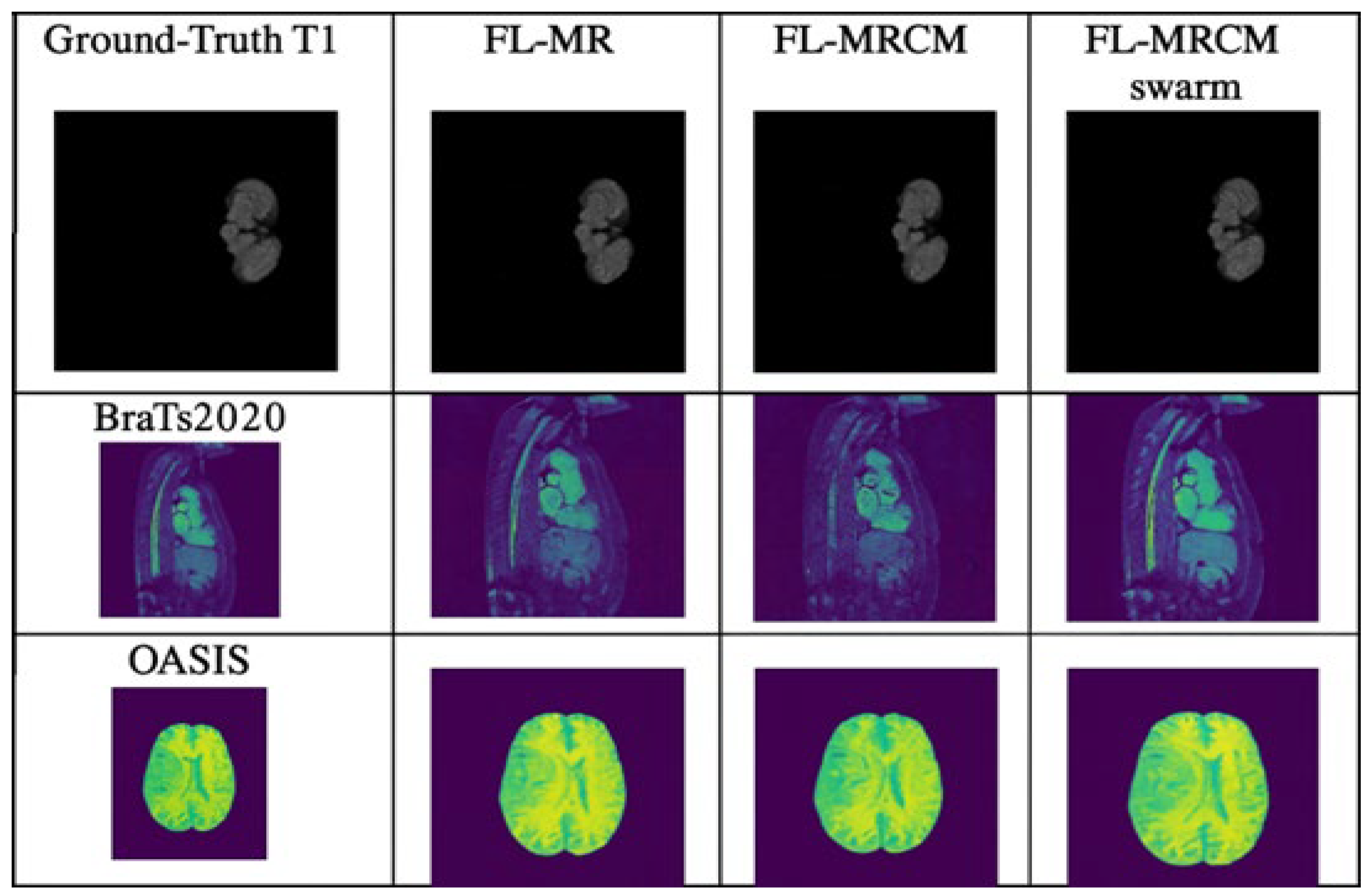
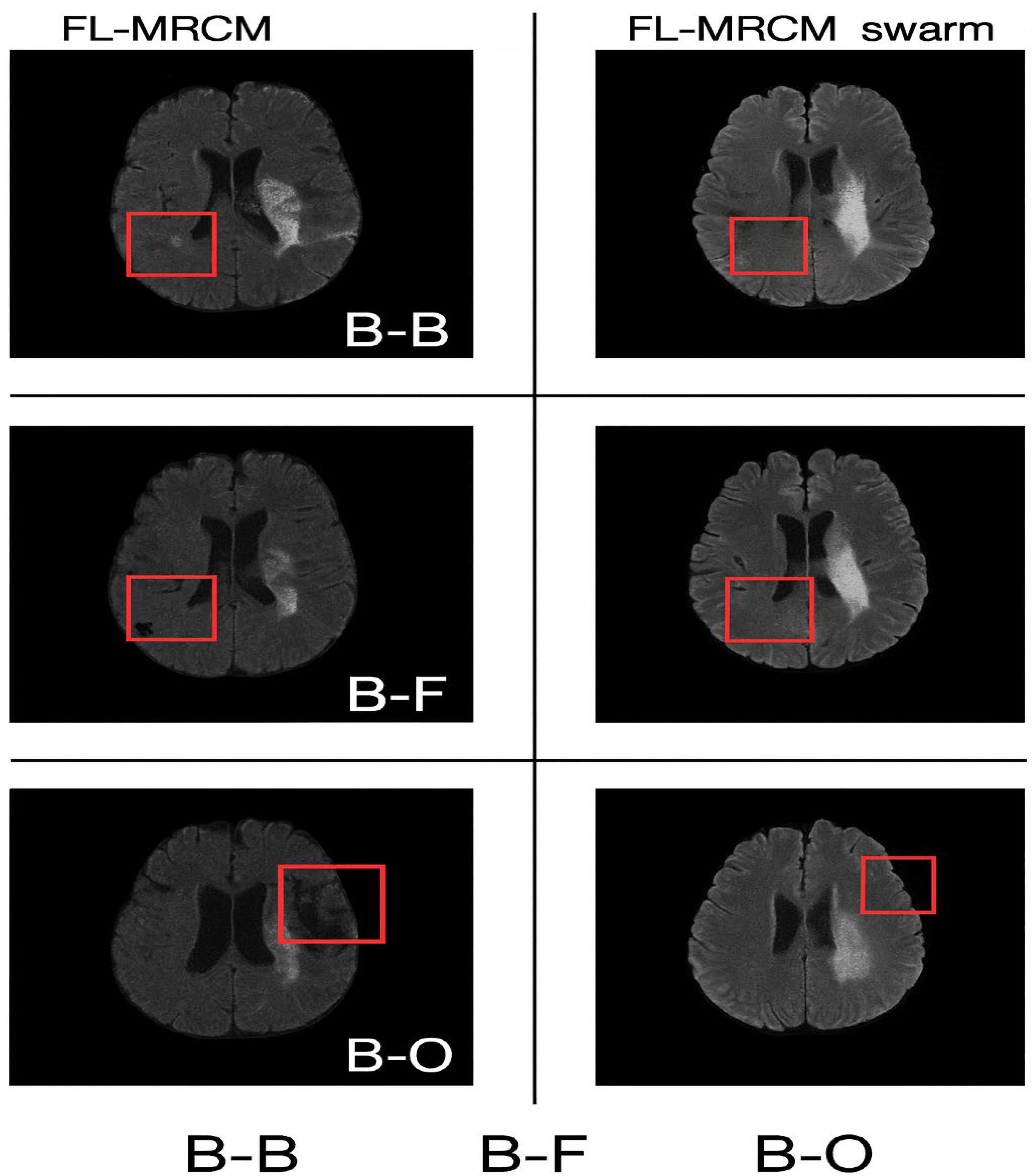
Figure 12. The qualitative reconstruction comparisons for cross-site scenarios (B-B, B-F, and B-O) are presented in
Figure 11. This figure illustrates the visual differences between FL-MRCM and FL-MRCM-Swarm across varying institutional configurations. The red boxes highlight the regions of interest used to visually assess reconstruction differences between the methods.
The qualitative reconstruction results for cross-site scenarios B–B, B–F, and B–O generated using FL-MRCM and FL-MRCM-swarm are shown in
Figure 12. These visual examples highlight method-specific differences in anatomical preservation and artifact suppression.
4.4. Computational Time
The proposed SwarmGAN based MRCM methodology demonstrates competitive computational efficiency, completing image reconstruction in an average time of 59,212 s executed for 50 epochs. For 1 epoch FL-MRCM takes around 42.8 s, while FL-MRCM Swarm takes around 34.6 s to reconstruct the MR image. Compared to FL-MRCM method, our approach achieves faster processing as tabulated in
Table 6 while maintaining high image quality, making it suitable for real-time clinical applications.
5. Conclusions
In this paper, the proposed SwarmGAN in a MRCM environment was analyzed and compared against the other FL alternatives. Cross-site modeling along with SwarmGAN and FedDyn was introduced to overcome the domain shift problems faced during collaborations and improve the quality of the reconstructed images. Without sharing data, the local models are tested to generate global models. Three datasets were used to test the diverse characteristics of the proposed methodology and showcased that the novel technique performed better than its alternatives. This paper also displayed that the FL alternatives and the multi-institutional collaborations can be used for MR image reconstruction without the need to share the data amongst the other sites.
Conceptual Advancement of FL-MRCM/FedGIMP/GAN-PSO: We advance former art by tying together these three mechanisms under one federated objective: (1) server-side FedDyn aims to regularize aggregation and suppress client drift under non-IID partitions; (2) client-side PSO aims to adapt GAN hyper-parameters online to each site’s distribution; and (3) structure-aware loss retains anatomical consistency during adversarial refinement. Unlike FL-MRCM (static and drift-prone) and FedGIMP (personalization without adversarial/PSO coupling), our design binds adversarial learning to dynamic aggregation with formalized, weighted loss, thereby clarifying the learning boundary, thus allowing stable and reproducible optimization. Unlike centralized GAN-PSO, our approach guarantees privacy and shows multi-center robustness with improved mean ± SD PSNR/SSIM across fastMRI, BraTS, and OASIS for the same non-IID splits. A major limitation of GAN-based reconstructions is the ability to generate hallucinated image features that can be diagnostically relevant. Our approach employs structured cross-entropy loss and dynamic regularization to help anchor the generated output to the actual data distribution across multiple institutions. Furthermore, all models were ranked by quantitative (PSNR, SSIM) and by qualitative (visual) assessments by imaging experts for anatomical plausibility. In the future, uncertainty quantification and expert-based validation will be further investigated.
Even though FL-SwarmGAN MRCM has vastly outperformed other methods across modalities and institutions, future works will include the following measures:
Reduced artifacts that could be attributed to GAN;
More diverse datasets such as PET and CT would be integrated;
Uncertainty-aware reconstruction will be further explored;
Validation in a real-world clinical setting with radiologists.