Abstract
Forecasting high-volume, univariate, and multivariate longitudinal data streams is a critical challenge in Big Data systems, especially with constrained computational resources and pronounced data variability. However, existing approaches often neglect multivariate statistical complexity (e.g., covariance, skewness, kurtosis) of multivariate time series or rely on recency-only windowing that discards informative historical fluctuation patterns, limiting robustness under strict resource budgets. This work makes two core contributions to big data forecasting. First, we establish a formal, multi-dimensional framework for quantifying “data bigness” across statistical, computational, and algorithmic complexities, providing a rigorous foundation for analyzing resource-constrained problems. Second, guided by this framework, we extend and validate the Adaptive High-Fluctuation Recursive Segmentation (AHFRS) algorithm for multivariate time series. By incorporating higher-order statistics such as covariance, skewness, and kurtosis, AHFRS improves predictive accuracy under strict computational budgets. We validate the approach in two stages. First, a real-world case study on a univariate Bitcoin time series provides a practical stress test using a Long Short-Term Memory (LSTM) network as a robust baseline. This validation reveals a significant increase in forecasting robustness, with our method reducing the Root Mean Squared Error (RMSE) by more than 76% in a challenging scenario. Second, its generalizability is established on synthetic multivariate data sets in Finance, Retail, and Healthcare using standard statistical models. Across domains, AHFRS consistently outperforms baselines; in our multivariate Finance simulation, RMSE decreases by up to 62.5% in Finance and Mean Absolute Percentage Error (MAPE) drops by more than 10 percentage points in Healthcare. These results demonstrate that the proposed framework and AHFRS advances the theoretical modeling of data complexity and the design of adaptive, resource-efficient forecasting pipelines for real-world, high-volume data ecosystems.
1. Introduction
The rapid increase in multivariate longitudinal data across industries has created a new era of big data analytics that present both vast opportunities and significant challenges. As data continuously expand in volume, velocity, and variety, traditional analytical frameworks often fail to address the complexities of dynamic real-world data sets [1,2]. The need for scalable, context-aware solutions to extract meaningful insights and improve predictive accuracy has become paramount, particularly in domains such as finance, healthcare, and retail where forecasting accuracy directly impacts critical decision-making [3].
The central research problem addressed in this paper is designing forecasting methods that remain computationally feasible while preserving the statistical richness of multivariate data. Previous research advanced big data analytics by proposing quantitative definitions of “data bigness” and the “3Vs” framework (volume, velocity, variety) [4]. However, these approaches often overlook critical multivariate statistical properties such as covariance, skewness, and kurtosis [5,6]. Furthermore, segmentation algorithms developed primarily for univariate scenarios struggle to adapt to the intricate interdependencies present in multivariate longitudinal data sets [7]. These limitations highlight the need for methodologies that capture nuanced statistical variability while adhering to resource constraints [3,8].
To address this gap, this paper builds on these foundations by introducing an enhanced adaptive segmentation framework that integrates statistical variability with traditional attributes of big data. Specifically, we refine the quantitative definition of “data bigness” introduced in [7] to include multivariate statistical measures. This enables dynamic computation of window sizes tailored to individual data set characteristics [3,9]. The proposed Adaptive High-Fluctuation Recursive Segmentation (AHFRS) framework dynamically identifies and preserves information-dense historical segments, optimally combining high-fluctuation data with recent trends to form robust predictive inputs under computational constraints [7,10].
The core contribution of this paper lies in the application of advanced multivariate statistical analysis to dynamically adjust segmentation processes. By incorporating measures such as mean vectors, covariance matrices, skewness, and kurtosis, the proposed methodology precisely models temporal and structural patterns across industries [5,6,11]. These higher-order moments are particularly relevant in volatile domains: skewness captures asymmetry in fluctuations, which is critical for distinguishing directionally sensitive risks (e.g., in finance and healthcare), while kurtosis reflects the prevalence of extreme events or shocks. Their inclusion allows AHFRS to identify historically significant periods of abnormal variability, thereby strengthening forecasting robustness under high volatility. Empirical evaluations in finance, retail, and healthcare demonstrate significant improvements in forecasting accuracy. For example, in Finance RMSE decreased by up to 62.5%, in Healthcare MAPE dropped by more than 10 percentage points, and in the Bitcoin case study RMSE was considerably reduced. These results underscore the scalability and effectiveness of the approach [12,13,14].
This work not only advances the theoretical understanding of data bigness but also provides a practical framework for Big Data analytics that bridges the gap between research and real-world applications. By offering scalable and context-aware solutions for multivariate longitudinal data challenges, this paper enables more informed decision-making and innovation across sectors [15]. Although the focus here is multivariate forecasting, the foundational segmentation framework is designed to operate on both univariate and multivariate longitudinal data. In prior work [7], we demonstrated that the AHFRS approach significantly improved forecasting performance for univariate financial time series (Bitcoin), even under strict processing constraints. This study generalizes that work, extending the methodology to multivariate contexts with domain-specific temporal characteristics and interdependencies. The primary contributions of this work are threefold:
- A novel framework for quantifying “Data Bigness”: Moving beyond the conventional “3Vs”, we propose a rigorous, operational definition of data bigness grounded in measurable statistical variability, computational resource demands, and algorithmic hardness. This provides a formal lens through which to analyze and address resource-constrained analytical problems.
- A statistically-driven segmentation algorithm for both univariate and multivariate data: We generalize our AHFRS algorithm to effectively handle the complex inter-dependencies in multivariate data. The algorithm dynamically identifies and preserves statistically significant historical segments by incorporating covariance structures, skewness, and kurtosis, offering a robust alternative to standard recency-based windowing methods.
- Comprehensive empirical validation across diverse domains: We provide empirical evidence of AHFRS’s effectiveness through experiments on real-world financial data and synthetic data sets engineered to mimic finance, retail, and healthcare dynamics. Our results confirm that AHFRS delivers significant, model-agnostic improvements in forecasting accuracy while adhering to strict processing budgets.
The remainder of this paper is organized as follows. Section 2 reviews the existing literature on the definition of Big Data. Section 3 introduces our multi-dimensional framework for quantifying “data bigness”. Section 4 outlines the primary challenges in Big Data analytics. Section 5 details the proposed AHFRS methodology. Section 6 presents the empirical evaluation of our framework, and Section 7 concludes with a discussion of limitations and future work.
2. Setting the Stage for Complexity-Aware Forecasting: A Critique of Big Data Definitions
Discussions of “Big Data” often begin with the well-known “3Vs” framework—volume, velocity, and variety—which has served as a useful starting point for describing large-scale data environments [4]. Although this perspective has been influential, it does not fully capture the challenges faced in applied forecasting domains such as finance, healthcare, and retail. In these areas, the main difficulty is not only the scale of the data, but also the need to handle complex statistical dependencies within predefined computational limits. Consequently, conventional definitions are increasingly insufficient, and there is a need for a foundation that explicitly incorporates complexity into the way we think about modern forecasting problems.
2.1. Foundational Frameworks: The “3Vs” Model
Doug Laney’s “3Vs” model (volume, variety, and velocity) was one of the earliest attempts to frame the idea of Big Data [4]. By emphasizing issues of scale and speed, it drew attention to the technological challenges of managing increasingly massive data sets and quickly became a reference point in both research and industry practice [4,16]. However, over time, this framework has been criticized as too narrow. More recent work has pointed out that defining Big Data solely in terms of size overlooks other important dimensions, such as the computational resources required and the algorithmic strategies needed to process it effectively [9,16]. These critiques underscore the need for definitions that better reflect the complexity of today’s data ecosystems.
2.2. Expanded Definitions: Moving Beyond the “3Vs”
Researchers have tried to move beyond the “3Vs” by proposing more comprehensive definitions. De Mauro et al. (2016), for instance, focused on processing challenges, defining Big Data as anything “too large, too complex, and too fast” for conventional tools to handle effectively [1]. This thinking was instrumental in driving the development of scalable platforms such as Hadoop and Spark [8]. Yet, one unresolved issue remains: the lack of standardized thresholds for what qualifies as “big”. Many definitions fall back on arbitrary metrics like terabytes or petabytes, which are heavily dependent on context or application [1,16], and ultimately fail to provide a universal benchmark.
2.3. Industry-Specific Definitions: Real-Time Analytics and Decision-Making
In practice, definitions of Big Data are often tailored to specific industry needs. Ajah and Nweke (2019) emphasized its role in enabling real-time analytics, which allows businesses to react swiftly to market shifts and customer behavior [2]. Gandomi and Haider (2015) pointed to the rising challenge of unstructured data—social media posts, images, and videos—which now represents the bulk of Big Data [10]. Analyzing and extracting value from this type of data requires advanced algorithms, reinforcing the need for industry-specific definitions that align with these evolving data types [2,10].
2.4. Critical Challenges and the Need for Standardization
Despite these advancements, the field continues to struggle with key challenges. The lack of standardized thresholds remains a significant issue, as system-specific constraints often stand in for universal metrics [1,8]. As technology evolves and data complexity grows, frameworks must also adapt. Researchers like De Mauro et al. (2016) and others have stressed that definitions must be refined to address emerging concerns like data quality, accessibility, and ethics [1,5]. This landscape is further complicated by the rise of artificial intelligence and machine learning, which introduce new requirements around privacy, governance, and ethical considerations [2,8].
2.5. Toward a Quantitative and Contextual Understanding
This review of the literature reveals a field in constant evolution. While the “3Vs” remain a useful starting point, they are insufficient for the complex, resource-constrained environments where modern forecasting takes place. By overlooking higher-order statistical variability and concrete computational limits, these definitions risk obscuring the true design needs of adaptive forecasting systems. This critique highlights the gaps in current thinking and sets the stage for the multidimensional framework we introduce in Section 3, which explicitly incorporates statistical, computational, and algorithmic complexity into the definition of “data bigness”.
3. Data Bigness: A Statistical Variability-Based Framework
In response to the gaps identified in the existing literature, this paper proposes a more comprehensive framework. Building on prior definitions (Section 2), this section enhances the definition of data bigness introduced by D. Fomo and A.-H. Sato in [17] by proposing a multi-dimensional framework to characterize “Big Data” more rigorously and quantitatively. Traditional definitions, often focused on the “3Vs” (volume, velocity, and variety), lack the nuance to capture the full range of modern data analysis challenges, particularly those encountered in forecasting. Grounded in principles from complexity theory, this framework extends these concepts by integrating three crucial dimensions of complexity: statistical, computational, and algorithmic (NP-Hard). Thus, “bigness” is evaluated not just by data scale (volume, velocity) or diversity (variety), but more holistically by its inherent statistical properties, required computational resources, and the intrinsic difficulty of analytical tasks. This comprehensive view provides a more operationally relevant and analytically insightful definition, especially for navigating forecasting challenges in data-intensive domains like finance, retail, and healthcare.
3.1. Multidimensional Quantitative Definition of Big Data
We propose that a data set , in the context of a specific analytical task implemented via algorithm , qualifies as Big Data if it meets or exceeds predefined context-dependent thresholds () in at least one of the following complexity dimensions ():
Each dimension is defined more formally as follows:
3.1.1. Statistical Complexity ()
This dimension quantifies complexity from the data set’s intrinsic statistical characteristics, particularly deviations from simplifying assumptions (like normality or independence) or the presence of high variability, heterogeneity, or instability. Such characteristics often necessitate more sophisticated or robust analytical methods. A composite measure, , is proposed in [17], integrating key multivariate statistical properties:
where
- : The norm of the estimated mean vector. Significant magnitude or temporal drift in can complicate modeling, especially in non-stationary contexts [5].
- : The norm of the estimated covariance matrix, representing the overall magnitude of pairwise linear dependencies and individual variances. High values indicate strong correlations or high variance, often increasing model complexity or requiring regularization [5,18].
- : Absolute multivariate skewness, defined by K.V. Mardia in [6], quantifying the degree of asymmetry in the multivariate distribution. High skewness violates normality assumptions common in classical methods and may require data transformations or distribution-agnostic techniques [19].
- : Absolute multivariate kurtosis, defined by K.V. Mardia in [6], assessing the characteristics of its distributional tails and peakedness relative to a multivariate normal distribution. High kurtosis indicates heavy tails (leptokurtosis), suggesting a higher propensity for outliers or extreme events that can destabilize standard estimators and necessitate robust statistical approaches [20].
- Tr(): The trace of the covariance matrix, equivalent to the sum of the variances of individual variables . It provides a simple scalar summary of the total variance or dispersion within the data set [21]. High total variance can be indicative of complexity, particularly in high-dimensional settings.
The non-negative weights () allow for domain-specific calibration, emphasizing the most relevant statistical complexities for an application (e.g., prioritizing kurtosis for financial risk [14,19,22] or skewness for population heterogeneity in healthcare [11]).
3.1.2. Computational Complexity ()
This dimension quantifies the practical resource requirements associated with executing algorithm on data set , specifically processing time and memory (space). It directly reflects the computational burden and scalability challenges.
where
- : A numerical representation of the algorithm’s asymptotic time complexity (e.g., mapping , , , to a monotonically increasing numerical scale). High time complexity signifies that execution time grows rapidly with data size n, potentially exceeding acceptable latency or processing windows [16,20,23].
- : A numerical representation of the algorithm’s asymptotic space complexity. High space complexity indicates substantial memory needs (e.g., linear, quadratic, exponential), which can be a critical bottleneck for large data sets, especially for in-memory computations [16,20,23].
The weights and permit balancing the relative importance of time versus memory constraints based on specific system limitations or application requirements.
3.1.3. Algorithmic (NP-Hard) Complexity ()
This dimension addresses the intrinsic computational difficulty of the analytical problem algorithm aims to solve, especially if the problem is in a computationally hard complexity class (e.g., NP-hard [24,25]). For such problems, finding an exact optimal solution is generally considered intractable for large input sizes within feasible time, necessitating heuristic or approximation strategies. Many core tasks in Big Data analytics including certain types of clustering, feature selection, graph partitioning, network analysis, and combinatorial optimization fall into this category.
where
- : An indicator reflecting the complexity class of the problem solved by A. For instance, could be assigned a high value (e.g., 1) if the problem is NP-hard and typically requires non-exact methods for large instances encountered in Big Data, and a low value (e.g., 0) if the problem admits efficient polynomial-time algorithms.
This dimension highlights scenarios where the primary challenge stems from the combinatorial nature of the problem itself, demanding specialized algorithmic techniques beyond just scalable infrastructure.
3.1.4. Operational Calculation of the “Data Bigness” Classification
The classification of a data set as “Big Data” is determined through a clear three-step process:
- Score each dimension: A score is determined for each of the three dimensions individually: statistical complexity () is calculated quantitatively using Equation (2); computational complexity () is assessed based on the algorithm’s resource needs (Equation (8)); and algorithmic complexity () is determined by the problem’s known intractability (Equation (9)).
- Compare with thresholds: Each score is compared against its predefined, context-specific threshold (, , ), which represents the operational limit for a given analytical environment.
- Apply logical condition: A data set is classified as “Big Data” if any one of these scores exceeds its respective threshold, per the logical OR condition in Equation (1). For example, a data set could be classified as “Big Data” not because of its statistical properties (), but because the required algorithm is too heavy and slow for the available system ().
3.2. Establishing Domain-Specific Thresholds () and Implication
It is essential to recognize that the thresholds (, , ) that delineate “Big Data” within this framework are not universal constants. Instead, they are context-dependent benchmarks established relative to domain norms, analytical objectives, available infrastructure, and current algorithmic advancements.
- Finance: Statistical thresholds () for high kurtosis might be benchmarked against historical crisis data [14,22]. Computational thresholds () could be dictated by latency requirements (e.g., algorithms slower than deemed too slow). NP-hard complexity () could be triggered by tasks like complex portfolio optimization [19,21,26].
- Retail: Statistical thresholds () might relate to identifying significant deviations in customer behavior [27]. Computational limits () could be set by the feasibility of daily analyses on massive transaction volumes (e.g., infeasible). NP-hard challenges arise in vehicle routing or large-scale clustering [28].
- Healthcare: Statistical thresholds () for kurtosis might link to detecting rare clinical events [11]. Computational complexity () becomes paramount with potentially exponential-time algorithms in genomics. NP-hard problems are common in sequence assembly or treatment planning [29].
Defining appropriate thresholds requires careful consideration, empirical analysis, and domain expertise. This multi-dimensional framework practically guides the selection of appropriate analytical strategies. Diagnosing the dominant complexity source(s) leads to targeted interventions:
- High Statistical Complexity (): Signals the need for robust statistical methods, non-parametric approaches, data transformations, or adaptive methods like the segmentation strategy explored in this paper [7,22,30].
- High Computational Complexity (): Necessitates computationally efficient algorithms, parallelization, distributed computing platforms (e.g., Spark, Hadoop), hardware acceleration, or data reduction techniques [16,20].
- High Algorithmic Complexity (): Requires shifting from exact methods to well-justified heuristics, approximation algorithms, randomized algorithms, or specialized solvers [31].
3.3. Contextualizing Statistical Complexity: Positioning Within Existing Frameworks
Efforts to formalize complexity have yielded a wide variety of measures across disciplines, each grounded in specific theoretical frameworks and optimized for different modeling goals. Some aim to quantify the balance between order and randomness, others assess memory or predictability, and others reflect the difficulty of learning or compressing data. These perspectives have driven fundamental progress in physics, information theory, computational mechanics, and neuroscience.
This section situates the proposed measure within this broader methodological landscape. It does not attempt to generalize, replace, or outperform these well-established frameworks. Instead, it addresses a growing operational need to quantify statistical heterogeneity in large multivariate data sets in a computable, interpretable, and useful way for adaptive data handling under resource constraints.
Each of these frameworks depicted in Table 1 formalizes complexity within its respective theoretical domain. Some focus on intrinsic system structure, others on descriptive efficiency, and some on the hardness of learning or predicting under uncertainty. In contrast to these system-oriented or task-oriented metrics, is defined specifically to characterize segments of multivariate data that exhibit properties that challenge conventional modeling assumptions. These include:
- Elevated variance (trace or norm of the covariance matrix)
- Non-Gaussian behavior (skewness and kurtosis)
- Strong inter-variable correlation (covariance structure)
- Shifting distributional centers (mean norm)

Table 1.
Representative statistical complexity measures and contribution of AHFRS.
Table 1.
Representative statistical complexity measures and contribution of AHFRS.
| Measure | Purpose | Contribution of AHFRS |
|---|---|---|
| López-Ruiz-Mancini-Calbet (CLMC) [32] | Balance between entropy and disequilibrium | Captures intermediate complexity via high-fluctuation segments. |
| Excess Entropy [33] | Quantify mutual information across time | Preserves temporal dependence through selective windowing. |
| Statistical Complexity () [34] | Minimal memory for optimal prediction | Retains only segments essential for predictive sufficiency. |
| Kolmogorov Complexity (KC) [35,36] | Shortest description length/compressibility | Compresses adaptively while maintaining diversity. |
| Decision-Estimation Coefficient (DEC) [37] | Sample complexity of decision tasks | Reduces sample size by emphasizing fluctuation-rich subsets. |
| Neural/Integrated Complexity () [38] | Causal integration and differentiation | Highlights fluctuation-driven interdependencies. |
Each component is a standard multivariate statistic, making transparent, scalable, and compatible with existing data preprocessing pipelines. Moreover, its weighted form enables domain customization, where weights can reflect analytic priorities (e.g., tail risk in finance or asymmetry in population health data). Rather than framing as a general-purpose statistical complexity measure, we position it as a task-aware diagnostic designed to flag data segments that are statistically complex in ways that impede efficient modeling. Key distinctions include:
- Objective: Classical complexity measures aim to understand system behavior; aims to support model selection and window adaptation.
- Granularity: Other measures operate at the level of entire systems or sequences; is local and segment-level.
- Actionability: Its values directly inform whether a data set slice warrants specialized modeling strategies or resource allocation.
This makes particularly valuable in data-intensive applications such as real-time forecasting, anomaly detection, and adaptive sampling, where decisions must be informed by local statistical characteristics under strict processing budgets.
The concept of statistical complexity is not monolithic. It must be understood in relation to what is being modeled, the constraints under which the modeling occurs, and the outcomes being sought. While Kolmogorov complexity addresses informational minimalism, Excess Entropy captures the presence of structure, and Decision Entropy Complexity (DEC) formalizes the difficulty of decision-making, is designed to address a different but complementary question, namely, to evaluate whether a given segment of data shows enough statistical regularity for standard modeling, or if it instead requires adaptive methods. In doing so, does not redefine the notion of statistical complexity; it preserves its essence while making it practical for large-scale data analysis.
3.4. Advantages of Our Proposed Multi-Dimensional Framework
This framework offers several significant advantages over traditional, often underspecified, “Big Data” definitions:
- Theoretical Rigor and Comprehensiveness: Provides a more complete, multifaceted, and conceptually sound basis for characterizing the challenges posed by modern data sets, grounded in statistics and computer science principles.
- Enhanced Interpretability: It clearly separates distinct sources of difficulty (statistical properties, resource demands, intrinsic problem hardness), allowing a more precise diagnosis of analytical bottlenecks.
- Actionable Analytical Guidance: It directly informs strategic decisions on selecting appropriate statistical methods, computational infrastructure, and algorithmic techniques tailored to the specific complexities encountered.
- Contextual Adaptability: It formalizes the context-dependent nature of “bigness,” allowing calibration to specific domains, analytical objectives, and technological capabilities. This offers greater flexibility and practical relevance than fixed, universal definitions [1,8].
Adopting this multi-dimensional perspective can help the field develop a more standardized, insightful, and operationally useful understanding of “Big Data”. This facilitates the development and application of more effective strategies for data analysis and robust data-driven decision-making in an increasingly complex data landscape.
In summary, the practical relevance of this multi-dimensional framework extends far beyond a simple academic redefinition of “Big Data.” By enabling a precise diagnosis of whether a challenge is the result of statistical, computational, or algorithmic complexity, it empowers analysts to move beyond managing mere data volume and instead select targeted and resource-efficient strategies. This complexity-aware perspective is the foundation for the adaptive and context-aware forecasting approach detailed later in this paper, highlighting how a robust definition of the problem is the first step toward a more effective solution.
3.5. Scope and Applicability of the Framework
It is important to clarify the intended scope of the proposed multidimensional definition of data bigness. Because the statistical component relies on measures such as variance, covariance, skewness, and kurtosis, the framework is directly applicable to numerical multivariate data sets and time series. For categorical or unstructured data types such as text, images, or video, the current framework can only be applied once the data have been transformed into quantitative vector representations (for example, through feature extraction or embeddings). While this transformation step makes the framework usable for a broader range of domains, its most natural and direct applicability remains within structured numerical data. Extending the framework to operate directly on unstructured data is an important direction for future research.
4. Review of Big Data Analytics Challenges
Having established our multi-dimensional “data bigness” framework in the preceding section, we now use it as a lens to analyze the specific, interconnected challenges in Big Data analytics. These obstacles, which often stem from the inherent characteristics of Big Data, can be better understood when categorized by their primary source of complexity: statistical (), computational (), or algorithmic ().
While the potential for deriving valuable insights from vast data sets is immense [39], realizing this potential is frequently hindered by obstacles stemming directly from the inherent characteristics of Big Data often summarized by the Vs: volume, velocity, variety, and increasingly, veracity and value [40,41]. As highlighted, efficiently managing, processing, and extracting insights from massive, diverse, and rapidly generated data sets is a primary hurdle for organizations using big data for forecasting and strategic decisions. These challenges necessitate sophisticated analytical strategies and robust computational infrastructure.
4.1. Challenges Stemming from Statistical Complexity () and Data Veracity
A primary set of challenges arises from the intrinsic statistical properties and quality issues within Big Data. Common in many industries, multivariate longitudinal data sets often show significant non-stationarity, heterogeneity, and high statistical variability (including complex correlations, skewness, and kurtosis), which complicates using traditional models. Identifying and modeling these underlying structures requires advanced analytical approaches adaptable to local data characteristics.
Compounding this statistical complexity is the challenge of Data Veracity, ensuring the quality, accuracy, consistency, and trustworthiness of the data [40,41]. Big Data, often aggregated from diverse sources, is frequently messy, with issues like incompleteness, noise, errors, inconsistencies, and duplication [41,42,43,44]. Poor data quality is a critical bottleneck, as it can lead to flawed analysis, unreliable conclusions, and poor decision-making [39,43,45]. Studies suggest a significant percentage of Big Data projects fail due to data quality management issues [45]. Addressing this requires robust data governance, rigorous (and potentially computationally intensive) data cleaning and preprocessing, and validation procedures [39,40,41,42,45]. However, automated cleaning techniques often struggle with the diversity and complexity of real-world data sets [42], necessitating human intervention and domain expertise [42].
Moreover, our prior work highlighted a challenge: balancing the capture of relevant historical patterns (e.g., high fluctuations or seasonality in older data) with an emphasis on recent trends, especially under strict data volume constraints. Naively discarding older data, a common approach to manage volume, can lead to a significant loss of information about long-term cycles or rare events crucial for accurate forecasting.
4.2. Challenges Stemming from Computational Complexity (), Volume, and Velocity
The defining characteristics of Volume and Velocity translate directly into significant computational hurdles. Organizations now grapple with petabytes or exabytes of data, rendering traditional storage solutions inadequate and requiring scalable infrastructure like cloud storage (e.g., Amazon S3, Google Cloud Storage, Microsoft Azure), data lakes, compression, and deduplication techniques [41,44,46]. The sheer volume strains processing capacity, impacting both time complexity () and space complexity (). Many standard algorithms, particularly traditional Machine Learning algorithms, scale poorly and become computationally prohibitive as data size grows [42,47].
The rapid rate at which data is generated (e.g., from IoT devices, social media) and needs processing demands real-time or near-real-time analytical capabilities [39,41]. This often necessitates stream processing frameworks (e.g., Apache Kafka, Apache Flink) over traditional batch processing, adding complexity and cost [39,41]. Efficiently collecting, processing (transforming, extracting), and analyzing these large, fast-moving data sets is a significant challenge [39,40]. Achieving true scalability requires efficient distributed computing techniques, parallel processing, data partitioning, and fault tolerance, which present their own implementation challenges [42,47]. System limitations, like maximum processable data volume (discussed in prior work), necessitate intelligent data reduction or selection to preserve information within computational budgets.
4.3. Challenges Stemming from Algorithmic Complexity ()
Beyond resource constraints, some Big Data analytics tasks, such as specific types of clustering, feature selection, optimization, or network analysis, are intrinsically difficult due to their underlying Algorithmic Complexity. Many such problems are NP-hard, meaning exact optimal solutions are generally intractable for large inputs within feasible timeframes. This necessitates the use of approximation algorithms, heuristics, or randomized methods, which trade optimality for computational feasibility. Recognizing and appropriately addressing this intrinsic hardness is crucial for selecting suitable analytical techniques.
4.4. Interrelated Challenges: Variety, Integration, Security, Value Extraction, and Skills
The aforementioned challenges are often compounded by other factors:
- Variety and Integration: Big Data encompasses diverse types (structured, unstructured, semi-structured) from multiple sources. Integrating these heterogeneous sources for analysis is challenging, sometimes requiring specialized tools (e.g., NoSQL databases [48]) and potentially leading to data silos that hinder comprehensive analysis [41,43,44,46].
- Security and Privacy: Protecting vast amounts of potentially sensitive data is paramount [39,40]. Concerns include data breaches, compliance with regulations (e.g., GDPR, CCPA), unauthorized access, and ensuring privacy throughout the data lifecycle [41,43,44,49]. Big Data environments, including IoT initiatives, increase the potential attack surface by introducing more endpoints [49]. Robust security measures like comprehensive data protection strategies, encryption, authentication, authorization, and strict, granular access control are essential but challenging to implement at scale [40,41,44,49,50].
- Value Extraction and Skills Gap: Extracting meaningful, actionable insights and generating tangible value from Big Data is the ultimate goal, yet it remains a significant challenge [40,50]. Furthermore, surveys indicate a lack of skilled personnel (e.g., data scientists) with the expertise to manage the infrastructure, apply advanced analytical techniques, and correctly interpret results is a major barrier to adoption [44,49]. Selecting the right tools and platforms is also crucial but complex, as no single solution fits all Big Data needs [39,43].
Addressing this complex web of challenges requires multifaceted solutions. Methodologies must be statistically robust, computationally scalable, algorithmically sophisticated, secure, and flexible. The adaptive segmentation framework proposed later contributes a strategy to navigate trade-offs between incorporating rich historical information (including fluctuations) and adhering to processing constraints. This enhances forecasting model effectiveness for complex multivariate Big Data.
5. Proposed Methodology: Adaptive High-Fluctuation Recursive Segmentation
5.1. Introduction and Context
To address the big data analytics challenges from Section 4, computational constraints () limiting processable data, statistical complexity () of multivariate longitudinal data and balancing recent trends with historical fluctuations, advanced data selection strategies are required for effective forecasting. A key issue is how to select the most informative subset of data, as depicted in Figure 1. Naive methods often rely solely on the most recent data points, discarding older but potentially important patterns [7]. This can lead to missed signals from significant past fluctuations. While data segmentation plays an important role, existing techniques have notable limitations in this context. To overcome these, we introduce a new method: the Adaptive High-Fluctuation Recursive Segmentation algorithm (AHFRS). This approach dynamically combines statistical variability analysis with likelihood-based segmentation to construct a highly optimized forecasting data set.
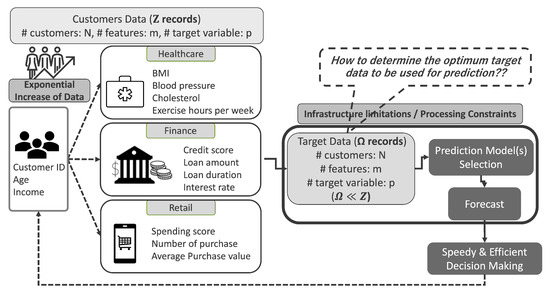
Figure 1.
General scenario depicting processing limitation during forecasting. (Given a data set of size records, features, and targets, with a physical processing constraint of ).
5.2. Review of Baseline Segmentation Approaches and Their Limitations
To contextualize our method’s contributions, we review two common baseline approaches for processing time series data streams (Fixed-Size Sliding Windows and ADWIN). We then evaluate their limitations regarding our objective: optimizing data sets for multivariate longitudinal forecasting under processing constraints while preserving historical context.
5.2.1. Fixed-Size Sliding Windows
Overview: This approach, arguably the most conventional and straightforward, applies a sliding window of fixed length over the time series. As new observations arrive, the window advances by one step, and forecasting models are trained or updated using only the data within the current window.
Relevance and Limitations in Multivariate Longitudinal Big Data: Fixed-size windows naturally extend to multivariate settings by including the most recent multivariate observations. However, their main limitation is their non-adaptive nature. Multivariate longitudinal data sets, particularly in domains such as finance, retail, and healthcare, are typically non-stationary, exhibiting dynamic trends, evolving volatility, and varying seasonality [8,11,14,27]. A static window size cannot accommodate these fluctuations effectively. Short windows may fail to capture long-term dependencies or seasonal cycles present in the historical data. While long windows, conversely, risk smoothing over recent changes, reducing responsiveness and adaptability. Most importantly, this approach discards all observations older than , thereby neglecting potentially valuable historical segments. This omission is problematic when earlier fluctuations contain significant predictive value; an insight our method leverages [7].
5.2.2. ADWIN (Adaptive Windowing)
Overview: ADWIN [51] is a parameter-free, adaptive algorithm developed to detect concept drift in data streams by monitoring changes in the mean or distribution. It maintains a dynamic window of recent data and reduces its size when a statistically significant difference is observed between sub-windows. For multivariate data, ADWIN typically requires modification, such as monitoring a univariate proxy derived from the multivariate input (e.g., Mahalanobis distance, model prediction error, or combined variance metrics).
Relevance and limitations in multivariate longitudinal Big Data: Compared to fixed-size windows, ADWIN introduces adaptivity by reacting to changes in data distribution and is thus a more sophisticated baseline. However, its design and objectives are not fully aligned with the requirements of our task, for the following reasons:
- ADWIN is optimized for detecting recent changes and retaining data from the current distribution. In contrast, our approach identifies historically significant segments with pronounced statistical fluctuation and integrates them with recent observations to form a forecasting-optimized data set.
- Upon detecting change, ADWIN discards the older portion of its window to maintain adaptability. In contrast, our method explicitly retrieves and reuses historical segments, selecting those with statistically significant fluctuation for inclusion in the forecasting data set. Thus, where ADWIN forgets, our approach selectively remembers.
- ADWIN primarily bases its adaptation on changes in means or simple distributional statistics. Our method incorporates a richer multivariate statistical characterization, leveraging higher-order moments such as skewness and kurtosis. This design allows our method to adapt to complex features like volatility, asymmetry, and heavy-tailed behavior, which are important in real-world, high-dimensional forecasting across diverse industries [6,22,52].
In summary, while both fixed-size sliding windows and ADWIN serve as important baselines, they are not fully equipped to address the dual challenges of statistical adaptivity and historical context utilization under constrained conditions. Our method overcomes these limitations by using likelihood-ratio segmentation to identify significant past fluctuations. It also utilizes higher-order statistical adaptation for window sizing and segment replacement, and explicitly constructs an optimized forecasting data set by selectively combining historical and recent data.
5.3. Foundational Recursive Segmentation (Likelihood Ratio)
The core segmentation technique employed in our proposed architecture (Figure 2) for identifying high-fluctuation segments is a likelihood-based recursive segmentation algorithm, originally proposed by Sato [53] and used in our prior work [7]. This method builds on principles from change point detection [54,55], aiming to detect time points where the statistical properties of a time series exhibit abrupt shifts.
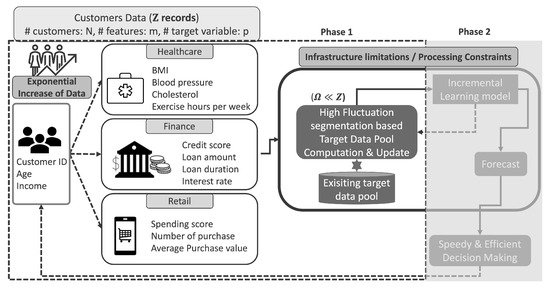
Figure 2.
Solution architecture of the proposal framework, where Phase 1 represents the scope of this paper and Phase 2 outlines the next phase of development.
Let us consider a multivariate time series segment of length (Here denotes the length of the sequence being segmented), represented by its -dimentional fractional changes , where and (with ). For each candidate split point , where denotes the minimum segment length, the algorithm computes a likelihood ratio . This statistic compares the likelihood under a two-segment model (with a split at time t) against a single-segment model.
Assuming approximate multivariate normality within segments, the statistic is computed via the determinants of the estimated covariance matrices for the entire segment (), the left segment (), and the right segment (), as described in references [7,17]:
The covariance matrices are estimated from as:
The optimal split point is identified as the value of t that maximizes :
A larger value indicates a more statistically significant deviation between sub-segments, suggesting a high fluctuation change point. This binary splitting is applied recursively to the resulting segments. The process terminates when for a potential split falls below a predefined statistical significance threshold, typically based on the distribution [7]. The result is a partition of the series into statistically homogeneous segments, denoted by the set of boundaries .
5.4. Adaptive Window Size Determination
A central innovation introduced in [17] is the adaptive replacement of the fixed window percentage used in [7] with a dynamically computed window size, denoted as . This addresses the limitation that a fixed percentage () may not adequately capture the statistical stability or variability of the recent segment (length ).
The method identifies the largest, most recent, contiguous sub-segment within that shows high internal statistical similarity. The segment is assumed to be relatively stable and less informative compared to high-fluctuation historical periods.
For all possible partitions of into left (, from start to time t) and right (, from to end), two similarity metrics are computed:
- Preliminary Similarity () which captures differences in central tendency and overall variance:where and represent the norm of the mean vector and the trace of the covariance matrix for data segment respectively, and , are a non-negative weights. and represent the same for data segment .
- Detailed Similarity () which measures difference in higher-order moments using the composite variability metric defined in [17], which includes skewness and kurtosis and ensures that the two segments are also aligned in their distributional characteristics, such as shape, asymmetry, and tail behavior [6,22,53]:where and represent the weighted aggregation composite metrics (defined in [17]) for data segment and respectively, and is a non-negative weight.
The partition that minimizes the combined similarity score constitutes the final window size () which is computed as follows:
The argmin operation identifies the specific data subset within the Top Subsets that yields the minimum combined similarity score. In this context, Top Subsets represents a set of candidate data segments derived from that have the lowest preliminary similarity (), suggesting high internal statistical stability. The function returns the length (number of observations) of the data subset.
The adaptive percentage is then defined as:
which reflects the fraction of considered statistically stable and subject to replacement.
5.5. High-Fluctuation Segment Selection and Optimal Dataset Construction
With the adaptive percentage computed, the algorithm constructs the optimized data set by incorporating relevant historical context as depicted in Figure 3.
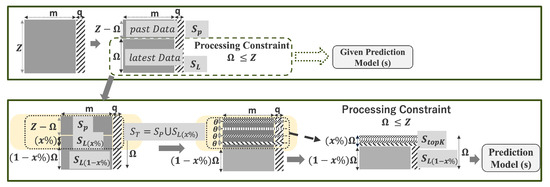
Figure 3.
Segmentation framework for constructing the optimized training dataset under the processing constraint , for a data set of size records with features and targets.
- Target Set for Segmentation (): Constructed by combining the full past segment of size with the earliest portion of the recent segment of length :
- Recursive Segmentation: Apply the likelihood-ratio segmentation algorithm (Section 5.3) on , yielding a set of statistically significant boundaries:
- Top-k Segment Selection: Rank boundaries by descending and select the top k. For each , extract a segment around it. The value of k and chunk sizes are chosen such that:
- Optimal Data set Construction:
This ensures retains the original window size while integrating statistically significant historical fluctuations.
5.6. Advantages and Scalability
The adaptive window segmentation algorithm presented here, summarized in Figure 4 and Algorithm 1, is designed with scalability as a key consideration, making it suitable for large, high-dimensional data sets typical in big data scenarios. To clarify the motivation for distributed implementations, it is useful to analyze the computational complexity of the AHFRS segmentation process. For a given iteration on a data segment of length Z with M features, the algorithm evaluates potential split points by computing two covariance matrices (one per sub-segment) and their determinants. Constructing an covariance matrix has complexity , while computing its determinant requires . Since this procedure is repeated across candidate split points, the total complexity of one segmentation iteration is approximately . This implies that runtime scales quadratically with the segment length and cubically with dimensionality, making naive single-machine execution inefficient for large-scale data sets. In practice, incremental updates of summary statistics can reduce overhead in streaming contexts, but the polynomial dependence on M remains a key factor for high-dimensional data. These complexity considerations provide the rationale for employing distributed frameworks such as Spark and Hadoop, where covariance and determinant computations can be parallelized across partitions, ensuring tractability for real-world applications in finance, healthcare, and retail. These computationally intensive aspects can significantly benefit from parallel execution across multiple processing cores or nodes within a cluster.
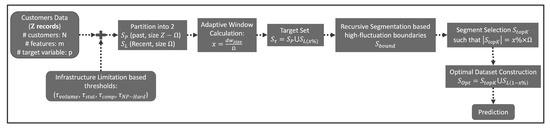
Figure 4.
Segmentation-based proposal process flow.
For potential real-time or near-real-time applications, the methodology can be further optimized by leveraging distributed computing frameworks like Apache Spark or Hadoop [20,46]. These platforms enable efficient data partitioning, allowing independent processing of data segments before merging the final segmentation results. This parallelization capability is particularly advantageous in data-intensive domains such as finance and healthcare, where rapid data ingestion and timely analysis are often critical. Further investigation into implementing and benchmarking the algorithm within these distributed frameworks is warranted to empirically validate its scalability across diverse, large-scale data sets [17].
It is important to clarify the intended application of AHFRS in streaming or near-real-time contexts. Given the computational complexity of the full segmentation process, the framework is not designed to re-calculate the optimal data set () upon the arrival of every new data point. Instead, the update frequency would be a key operational parameter, with the full AHFRS process being triggered periodically (e.g., hourly or daily) in a batch-processing manner to generate a new, optimized training window. The latency of this update task would depend on the data set size, dimensionality, and the scale of the distributed computing environment. During the intervals between these updates, a trained forecasting model can still perform real-time inference on new incoming data. This approach allows the system to benefit from a periodically refreshed, statistically robust training data set without incurring the segmentation overhead on a per-observation basis. A full implementation and empirical benchmark of this hybrid approach within a true, low-latency streaming architecture is an important direction for future work.
| Algorithm 1 Adaptive High-Fluctuation Recursive Segmentation (AHFRS) |
|
6. Evaluation Across Univariate and Multivariate Forecasting
This section presents the empirical validation of the AHFRS framework across both univariate and multivariate longitudinal time series scenarios. We begin by evaluating performance on a real-world univariate financial data set, followed by assessments on synthetically generated multivariate data sets simulating domain-specific temporal patterns in Finance, Retail, and Healthcare.
The data sets for this study were carefully selected to ensure both domain relevance and statistical diversity. Finance, Healthcare, and Retail are representative domains where forecasting accuracy has direct and significant practical implications, from managing market risk and monitoring patient health to optimizing supply chains. At the same time, these domains present distinct statistical challenges. The financial series (Bitcoin) is characterized by high volatility and heavy-tailed distributions, the healthcare data exhibits irregular fluctuations and structural shifts, while the retail data combines strong seasonal patterns with abrupt changes in demand. By evaluating the AHFRS framework against this spectrum of behaviors, we provide strong evidence of its robustness and ability to generalize across varied statistical environments.
6.1. Univariate Forecasting: Bitcoin Case Study
This experiment evaluates the performance of AHFRS in a univariate forecasting context using hourly Bitcoin price data. The goal is to assess the impact of statistically guided segmentation on forecasting accuracy under memory constraints.
6.1.1. Data set and Forecast Objective
The data set contains 37,196 hourly Bitcoin Weighted Price values (USD) covering the period from 1 January 2017 to 30 March 2021. The time series exhibits complex non-stationarity, volatility clusters, and seasonal structures common in high-frequency financial data. The forecasting target is the most recent 10% to 15%. To simulate operational constraints, the training data set size is limited to of the full history for univariate evaluations.
6.1.2. Experimental and Environment Setup
The Adaptive High-Fluctuation Recursive Segmentation (AHFRS) algorithm identifies segments with high statistical complexity from earlier history and combines them with a proportion of the most recent data. This composite training set is constructed such that its size remains within the constraint.
Suppose that univariate time series . For univariate time series, the statistical complexity metrics Equation (2) are simplified as:
- Mean norm becomes scalar mean .
- Covariance matrix norm is reduced to sample variance .
- Skewness and kurtosis are, respectively, reduced to their standard univariate forms as and .
- Trace of covariance matrix is equivalent to the sample variance .
The weights for this univariate Bitcoin case study were determined through empirical simulations on prior data. We set , , , and . This weighting scheme emphasizes the higher-order moments, skewness and kurtosis. This is crucial for financial time series like Bitcoin, which are characterized by significant non-Gaussian behavior, fat tails, and abrupt, extreme price fluctuations that often hold key predictive information for market volatility. By contrast, lower weights for the mean and variance acknowledge that their contribution to identifying critical high-fluctuation periods is less pronounced in highly non-stationary and volatile financial contexts, enabling the algorithm to focus on segments with genuinely significant deviations.
As our proposed algorithm, segments are identified using a recursive likelihood-ratio test defined in Equations (10)–(12), which for univariate data set are simplified as follow:
The variances are estimated from as:
Here, , , and are the sample means of the entire data set, the left segment, and the right segment, respectively. The optimal split point is still identified as the value of t that maximizes , as per Equation (12). This adaptation allows the recursive segmentation process to accurately identify statistically significant change points in univariate data streams. The top-K historical segments are selected and combined with the dynamically computed latest of data to form the final training window.
For the baseline model, we implemented a Long Short-Term Memory (LSTM) network, widely recognized for time series forecasting tasks. The network was trained using the same hourly Bitcoin Weighted Price series, with identical preprocessing and look-back windows as AHFRS to ensure a fair comparison. The architecture consisted of two stacked LSTM layers with 50 hidden units each, interleaved with dropout regularization (rate = 0.2) to prevent overfitting. The output layer was a fully connected dense layer producing a one-step-ahead forecast. We used the Adam optimizer with a learning rate of 0.001. Training was run for 25 epochs with a batch size of 32. To evaluate the contribution of AHFRS, we compared the below two settings:
- Full-data LSTM baseline, trained on the entire training sequence
- AHFRS ( = 60% of total data), where only the most informative historical segments selected by AHFRS were used to train the LSTM.
Both approaches were tested under two chronological splits: 70% training/15% validation/15% test (Scenario 1) and 80% training/10% validation/10% test (Scenario 2). This consistent setup ensured that performance differences were attributable solely to the -based AHFRS segmentation rather than model or preprocessing discrepancies.
6.1.3. Forecasting Results
- A.
- AHFRS Data Composition and comparative setupTwo experimental conditions were compared: (i) a Full-data LSTM baseline, trained on the entire available training set, and (ii) the proposed AHFRS ( = 60% of total data) approach, where only the most informative historical segments are used for training. This design ensures a fair comparison where both methods rely on the same LSTM architecture and preprocessing pipeline, with the only distinction being the training data selection mechanism.To comply with the system-imposed memory constraint of = 60% of the entire time steps, the AHFRS framework constructs a training data set by combining two complementary segments:
- for scenario 1 (and for scenario 2): the most recent observations, representing (1 – 26.19%) for scenario 1 (and (1 – 24.71%) for scenario 2) of the memory budget , and
- : a set of non-contiguous high-fluctuation historical segments, accounting for the remaining 26.19% for scenario 1 (and 24.71% for scenario 2).
These high-fluctuation segments are identified using the likelihood ratio–based recursive segmentation method developed in our earlier work. This approach partitions the time series into statistically homogeneous intervals by computing likelihood ratios between adjacent windows and selecting breakpoints where a significant statistical shift is detected. The segments are then ranked by their fluctuation intensity, and the top-K segments are chosen based on their relative contribution to the total variability, all while respecting the global memory constraint .Figure 5 illustrates a segmentation layout for the univariate Bitcoin data set for a window . At the end of the series, the contiguous recent segment provides short-term contextual information. Interleaved across the earlier timeline are the selected high-variability segments , which capture historically significant behavioral shifts. The combination ensures that the training data set contains both up-to-date signals and long-range fluctuation patterns that might otherwise be excluded under recency-based schemes. This segmentation strategy distinguishes AHFRS from conventional sliding window methods. Instead of discarding older data outright, AHFRS selectively incorporates historically significant segments based on structural changes in the series. This dynamic windowing capability allows the framework to construct a statistically optimized and computationally feasible training data set that retains both short-term trends and long-term variability patterns critical to accurate forecasting.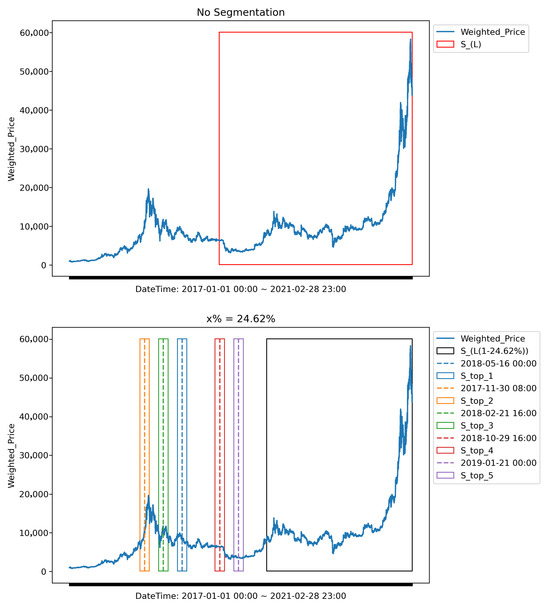 Figure 5. Illustration of the baseline (recency-only) and AHFRS data selection strategies for the Bitcoin time series (1 January 2017 to 28 February 2021). (Top) The time series illustrating the ’No Segmentation’ baseline approach, which utilizes only the most recent data segment (red box) within the constraint. (Bottom) The time series showing the dynamically constructed optimal data set using the Adaptive High-Fluctuation Recursive Segmentation (AHFRS) framework. This data set is composed of the recent, statistically stable segment (black box) and the k = 5 high-fluctuation historical segments (colored boxes) selected via likelihood-ratio-based recursive segmentation. These segments account for the dynamically computed of the training data.
Figure 5. Illustration of the baseline (recency-only) and AHFRS data selection strategies for the Bitcoin time series (1 January 2017 to 28 February 2021). (Top) The time series illustrating the ’No Segmentation’ baseline approach, which utilizes only the most recent data segment (red box) within the constraint. (Bottom) The time series showing the dynamically constructed optimal data set using the Adaptive High-Fluctuation Recursive Segmentation (AHFRS) framework. This data set is composed of the recent, statistically stable segment (black box) and the k = 5 high-fluctuation historical segments (colored boxes) selected via likelihood-ratio-based recursive segmentation. These segments account for the dynamically computed of the training data. - B.
- Forecasting Generation and Evaluation MetricsThe forecasting process involves training a Long Short-Term Memory (LSTM) network (configured as detailed in Section 6.1.2) on the respective training data sets: either the Full-data LSTM baseline (entire training set) or the AHFRS-enhanced data set ( = 60% of total data). Once trained, the LSTM generates multi-step-ahead predictions over the designated test horizon, which corresponds to 15% of the entire data set in Scenario 1 and 10% of the entire data set in Scenario 2. The predicted values are compared with the actual test data.To quantitatively assess and compare the accuracy of these generated forecasts, we utilize three well-established metrics:
- Root Mean Squared Error (RMSE):
- Mean Absolute Error (MAE):
- Mean Absolute Percentage Error (MAPE):
where h is the number of predictions in the forecast horizon, is the actual value for the i-th prediction, and is the predicted value for the i-th prediction.The selection of these three metrics provides a comprehensive and balanced assessment of forecasting performance. RMSE is particularly sensitive to large errors due to its squaring term, making it highly relevant for volatile domains where significant misses must be penalized. MAE provides a more direct and interpretable measure of the average error magnitude in the original units of the data. Finally, MAPE expresses error on a percentage scale, making it independent of the data’s scale and useful for comparing relative performance across different data sets. Using this combination ensures a robust evaluation of the model’s accuracy, its propensity for large errors, and its relative performance. - C.
- Performance SummaryThe univariate forecasting results provide strong empirical evidence of the AHFRS framework’s effectiveness when paired with a recurrent neural architecture. By combining recent data with historically significant, high-fluctuation segments, the AHFRS-enhanced training data set achieves superior statistical diversity and predictive robustness compared to a Full-data LSTM baseline.As shown in Table 2, the improvements are evident across both experimental scenarios:
- In Scenario 1 (70/15/15 split), AHFRS yielded modest yet consistent gains: RMSE decreased from 3376.1 to 3273.1 (a 3.1% reduction), MAE dropped from 1968.7 to 1912.9 (2.8% reduction), and MAPE fell from 4.57% to 4.33% (5.3% relative reduction).
- In Scenario 2 (80/10/10 split), the impact was far more pronounced. The Full-data LSTM baseline struggled under regime shifts, producing RMSE = 5168.3, MAE = 3862.7, and MAPE = 8.98%. By contrast, AHFRS achieved RMSE = 1209.4, MAE = 781.1, and MAPE = 1.81%, corresponding to a 76.6% reduction in RMSE and nearly 80% reductions in both MAE and MAPE.
These results highlight the forecasting benefits of retaining select, high-fluctuation historical segments rather than relying solely on full chronological recency. Crucially, the robustness achieved by AHFRS arises not from increased model complexity but from its principled data segmentation. This underscores the framework’s ability to build resilient models under volatile conditions, even with reduced training set size.

Table 2.
Forecasting performance of proposed AHFRS ( = 60% of total data) in comparison to Full-data LSTM baseline.
Table 2.
Forecasting performance of proposed AHFRS ( = 60% of total data) in comparison to Full-data LSTM baseline.
| Dataset | Model | Scenario | RMSE | MAE | MAPE (%) |
|---|---|---|---|---|---|
| Hourly Bitcoin Price (USD) | LSTM | Scenario 1: Baseline | 3376.1 | 1968.7 | 4.57 |
| Scenario 1: AHFRS | 3273.1 | 1912.9 | 4.33 | ||
| Scenario 2: Baseline | 5168.3 | 3862.7 | 8.98 | ||
| Scenario 2: AHFRS | 1209.4 | 781.1 | 1.81 |
6.2. Multivariate Forecasting
We now evaluate AHFRS in multivariate contexts using synthetic data sets that simulate real-world dynamics in three domains: Finance, Retail, and Healthcare. The empirical evaluation of the AHFRS framework (Section 5) is designed to test its ability to enhance multivariate forecasting in resource-constrained environments. While the “data bigness” framework (Section 3) models statistical (), Computational (), and Algorithmic () complexity, this evaluation isolates as the primary constraint. We assess how effectively AHFRS extracts forecasting value when limited by strict computational constraints on data volume and processing throughput.
6.2.1. System Constraint and Forecasting Objective
Modern data-driven systems in finance, retail, and healthcare often face architectural limits in memory, computation, and latency. These limitations impose practical upper bounds on the historical data available for model training and inference. We define this constraint through a fixed, per-entity training window , representing the maximum allowable volume of past observations that may be processed for forecasting.
To ensure comparability with the univariate case, we apply the same training data constraint of of full historical observations. While multivariate series contain additional variables per time step, the constraint reflects a system-level limitation on the number of observations (rows) that can be stored or processed, rather than the total number of data values. This design choice allows consistent evaluation of AHFRS performance across both data modalities, isolating the effect of segmentation strategy rather than varying memory budgets.
Each of the three domain-specific data sets (Finance, Retail, and Healthcare) used in this paper contains 100 customers, with 2282 daily multivariate records per customer. To simulate -bounded environments, we cap the training data per customer at records, precisely 40% of their historical timeline. The forecasting target representing the next 46 observations (5% of ), a horizon aligned with typical operational lead times in most predictive systems.
The core hypothesis tested in this setting is that not all historical data within are equally informative. The AHFRS algorithm constructs an optimized training subset by identifying segments with high informational density based on multivariate feature space fluctuations. AHFRS aims to outperform naive recency-based strategies under identical volume constraints, thus demonstrating better use of the same data budget.
6.2.2. Principled Data Simulation and Validation Methodology
To create a controlled and reproducible testbed for the AHFRS framework, we employed a principled data simulation methodology. The use of structured simulation is an established practice in machine learning research, providing an environment to isolate algorithmic performance and ensure reproducibility without the confounding variables of real-world data [56]. Our simulation was governed by a framework of explicit constraints designed to ground the synthetic data in empirically observed realities.
- A.
- Simulation Framework:A consistent cohort of 100 customer profiles was simulated across three domains (Finance, Retail, and Healthcare). This design choice controls for population-level variance, allowing for a direct comparison of domain-specific dynamics [57]. Longitudinal attributes were modeled to reflect real-world trends; for instance, individual income trajectories were adjusted annually based on historical U.S. nominal wage growth data published by the U.S. Bureau of Labor Statistics [58]. To embed domain-specific realism, intra-domain variables were simulated based on established causal and correlational structures.
- In the Finance data set, key lending variables (age, income, credit_score, loan_amount, loan_duration_months, interest_rate, default_risk_index) were modeled as co-dependent, with a correlational structure informed by stylized facts from consumer credit markets as documented in Federal Reserve economic reports [59] to simulate financial volatility, abrupt credit score shifts, and latent risk cycles.
- In the Retail data set, customer behavior (spending_score, number_of_purchases, average_purchase_value, churn_likelihood) was simulated by embedding correlations between purchasing frequency and monetary value, consistent with established frameworks in marketing analytics like RFM (Recency, Frequency, Monetary) analysis [60].
- In the Healthcare data set, physiological variables (bmi, blood_pressure, cholesterol_level, exercise_hours_per_week, disease_risk_score) were bounded by clinical norms. For example, Body Mass Index (BMI) and blood pressure fluctuations were simulated within ranges defined by the Centers for Disease Control and Prevention (CDC) [61] and the American Heart Association (AHA) [62].
- B.
- Validation Process:Following the simulation, the data sets underwent a multi-stage validation process. First, we conducted statistical plausibility checks by comparing the distributional properties and temporal patterns of the simulated data against the benchmarks used during generation. Second, to confirm that the data sets presented a forecasting challenge of realistic difficulty, we performed a functional validation. This approach, where synthetic data quality is evaluated on a downstream machine learning task, is an emerging best practice in generative modeling [63]. Baseline models (Random Forest and Gradient Boosting) were trained to predict key target variables, and simulation parameters were calibrated until the models achieved a Mean Absolute Percentage Error (MAPE) within a pre-specified range of 10–20%. This ensures the data contains a non-trivial and plausible balance of signal and noise.
While this principled simulation and validation process provides a rigorous foundation for our study, we concur that validation on authentic multivariate data sets remains a critical next step to confirm the framework’s operational generalization.
6.2.3. Experimental and Environment Setup
- A.
- Comparative method: Latest- baselineThe Latest- strategy represents a common industry practice where the model is trained on the most recent observations. This method assumes that recent data contains the most relevant patterns, but it discards older segments that may contain valuable structural information.
- B.
- Evaluation metrics and model selection rationaleForecasting performance is evaluated using RMSE, MAE, and MAPE. These metrics are first computed for each individual customer i and then averaged across all customers to derive consolidated performance measures (Mean_RMSE, Mean_MAE, and Mean_MAPE).where is the number of predictions in the forecast horizon for customer i, is the actual value, is the predicted value, and N is the total number of customers.We conducted experiments using two tree-based ensemble learning methods: Random Forest Regressor (RF) and Gradient Boosting Regressor (GB). These non-parametric models are robust to non-linearity and heterogeneity, common in real-world data [64,65]. Their effectiveness is well-documented in finance [66,67], healthcare [68,69], and retail [70,71]. They are also computationally tractable and compatible with distributed frameworks like Spark and Hadoop [64,72], making them suitable for -constrained pipelines.
6.2.4. Results and Discussion
- A.
- Industry-Specific Dynamic window computationFigure 6 illustrates the average proportion of the dynamic window selected by AHFRS across the three industries. The variation (Finance: 18.06%, Retail: 25.07%, Healthcare: 24.1%) highlights AHFRS’s dynamic adjustment based on statistical variability. This aligns with the data bigness model, where statistical complexity () interacts with resource constraints (). In industries like Finance, with abrupt shifts, the model selects concise, fluctuation-rich segments. Conversely, domains like Retail and Healthcare, with more gradual shifts, warrant longer segments.
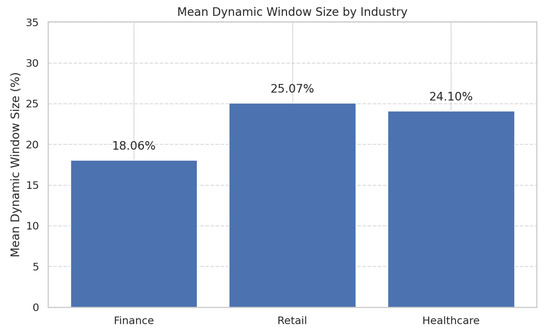 Figure 6. Mean dynamic window size as a percentage of the constrained historical buffer across industries.
Figure 6. Mean dynamic window size as a percentage of the constrained historical buffer across industries. - B.
- Comparative Forecasting PerformanceTable 3 presents the comparative forecasting performance of RF and GB models under baseline and AHFRS-enhanced regimes. Key observations:
- Substantial accuracy gains with AHFRS: Across all industries and metrics, models trained using AHFRS-selected windows consistently outperform their baseline counterparts. For example, in the Finance industry, the RF model’s Mean_RMSE decreases from 0.72 (baseline) to 0.27 with AHFRS—a relative reduction of over 62.5%.
- Retail domain sensitivity: Despite already low error values in the retail baseline, AHFRS delivers notable improvements, emphasizing its efficacy even in domains with high-frequency and potentially noisy data.
- Robustness in Healthcare: The Healthcare data set benefits markedly from AHFRS segmentation. RF’s Mean_MAPE improves from 15.83% to 5.96%, enhancing reliability in critical health forecasting.
- Model-agnostic benefits: Both RF and GB models benefit from AHFRS, suggesting the strategy enhances predictive capacity through upstream data selection, independent of the downstream model architecture.
As summarized in Table 3, the AHFRS-enhanced data sets (Proposal) outperform the recency-based Baseline across all three domains. To provide clearer visualization, Figure 7, Figure 8 and Figure 9 present domain-specific results. Each figure displays RMSE, MAE, and MAPE as percentages for both Random Forest and Gradient Boosting models, enabling direct comparison of Baseline versus Proposal performance.

Table 3.
Summary of Models Performance: Baseline vs. AHFRS-Enhanced data set.
Table 3.
Summary of Models Performance: Baseline vs. AHFRS-Enhanced data set.
| Industry | Model | Scenario | Mean_RMSE | Mean_MAE | Mean_MAPE (%) |
|---|---|---|---|---|---|
| Finance | RF | Baseline | 0.72 | 0.58 | 21.79 |
| Proposal | 0.27 | 0.21 | 8.05 | ||
| GB | Baseline | 0.70 | 0.56 | 21.20 | |
| Proposal | 0.55 | 0.44 | 16.80 | ||
| Retail | RF | Baseline | 0.03 | 0.03 | 18.34 |
| Proposal | 0.01 | 0.01 | 6.84 | ||
| GB | Baseline | 0.03 | 0.03 | 17.94 | |
| Proposal | 0.02 | 0.02 | 14.47 | ||
| Healthcare | RF | Baseline | 4.48 | 3.59 | 15.83 |
| Proposal | 1.70 | 1.35 | 5.96 | ||
| GB | Baseline | 4.25 | 3.42 | 15.16 | |
| Proposal | 3.41 | 2.73 | 12.05 |
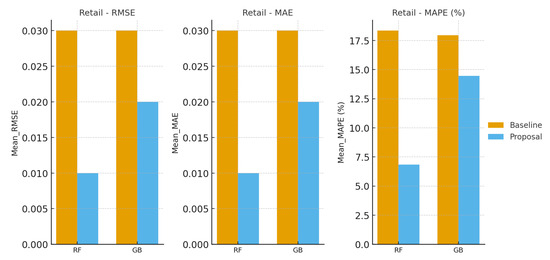
Figure 7.
Retail domain: Baseline vs. Proposal forecasting errors (RMSE, MAE, MAPE, all as percentages) for Random Forest and Gradient Boosting. Proposal consistently reduces error relative to the Baseline.
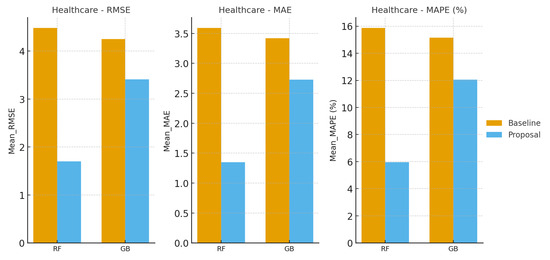
Figure 8.
Healthcare domain: Baseline vs. Proposal forecasting errors (RMSE, MAE, MAPE, all as percentages) for Random Forest and Gradient Boosting. Proposal outperforms Baseline across all metrics.
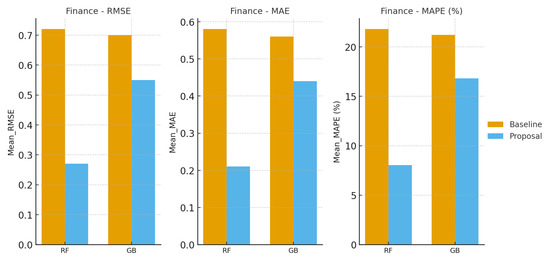
Figure 9.
Finance domain: Baseline vs. Proposal forecasting errors (RMSE, MAE, MAPE, all as percentages) for Random Forest and Gradient Boosting. The largest relative gains appear in Finance, reflecting AHFRS benefits under high volatility.
6.2.5. Summary of Evaluation
This evaluation strongly supports our core hypothesis: intelligent, statistically guided segmentation under volume-based computational constraints can significantly enhance multivariate longitudinal forecasting. The AHFRS framework demonstrates:
- Dynamic Adaptability: Selection of optimal historical windows varies by industry, highlighting that effective forecasting under constrained resources requires context-sensitive segmentation.
- Consistent Predictive Improvements: Across all industries, AHFRS-enhanced training sets yield lower forecasting errors.
- Model-Independent Gains: The segmentation benefits are robust across both RF and GB models, affirming the general applicability of AHFRS.
These findings underscore the practical utility of the AHFRS framework in Big Data environments where processing volume must be minimized while preserving predictive performance.
7. Conclusions
This study introduced the Adaptive High-Fluctuation Recursive Segmentation (AHFRS) framework as a principled solution to forecasting high-volume, multivariate longitudinal data under strict resource constraints. The work makes three contributions. First, it formalizes a quantitative, multi-dimensional definition of “data bigness,” grounded in statistical, computational, and algorithmic complexity. Second, it extends AHFRS from univariate to multivariate settings by incorporating covariance structures, skewness, and kurtosis into the segmentation process. Third, it validates the approach empirically through two complementary streams: a real-world univariate series (Bitcoin) evaluated against a Long Short-Term Memory (LSTM) baseline, and rigorously constructed multivariate simulations for finance, retail, and healthcare.
Beyond qualitative trends, the gains are substantial in numerical terms. In the univariate Bitcoin experiments, AHFRS ( = 60% of total data) achieved consistent improvements under stable conditions and dramatic robustness under stress. In Scenario 1 (70/15/15 split), RMSE dropped from 3376.1 to 3273.1 (3.1% reduction), with comparable improvements in MAE and MAPE. In Scenario 2 (80/10/10 split), the Full-data LSTM baseline failed under regime shifts (RMSE = 5168.3; MAPE = 8.98%), while AHFRS reduced RMSE to 1209.4 and MAPE to 1.81%, corresponding to a 76.6% and nearly 80% improvement, respectively. These results decisively demonstrate that compact, information-dense training sets generated by AHFRS can enable neural models to generalize more robustly in volatile domains.
Across the three synthetic multivariate domains, AHFRS significantly reduced forecasting error, with Random Forest Models showing the most substantial improvement, often exceeding (Table 3). Representative cases include Finance–RF, where Mean_RMSE drops from 0.72 (Baseline) to 0.27 (Proposal), a ∼62.5% reduction; Healthcare–RF, where Mean_RMSE falls from 4.48 to 1.70 (∼62.1%); and consistent MAPE reductions near ∼62–63% in Finance and Healthcare. Retail exhibits the largest point improvement in RMSE for RF (0.03 to 0.01; ∼66.7%), despite small absolute magnitudes. While improvements with Gradient Boosting are more modest (e.g., Finance–GB RMSE: 0.70 to 0.55; ∼21.4%), they remain directionally consistent. Taken together, these results show that upstream, statistically informed data selection confers tangible accuracy gains under fixed processing budgets.
Despite these advances, several limitations should be acknowledged. The multivariate evaluation relied on synthetic data sets that, although carefully constrained and validated against real-world properties, may not capture the full diversity and noise characteristics of operational data. This raises potential concerns about biases in data generation and generalization to domains beyond those modeled. In addition, while the univariate evaluation incorporated a contemporary neural baseline (LSTM), the multivariate evaluation used classical forecasters to isolate segmentation effects. The interaction of AHFRS with more advanced deep learning architectures in multivariate contexts merits further study.
These limitations point directly to future work. We will (i) validate AHFRS on large-scale, authentic multivariate data sets across additional industries; (ii) evaluate its integration with state-of-the-art deep learning architectures (e.g., recurrent and transformer-based sequence models); and (iii) quantify the computational efficiency of AHFRS by implementing the framework in distributed environments such as Apache Spark to benchmark runtime performance and memory usage, complementing the theoretical complexity analysis presented in this paper.
Author Contributions
Conceptualization, D.F. and A.-H.S.; methodology, D.F. and A.-H.S.; software, D.F.; validation, D.F.; formal analysis, D.F.; investigation, D.F.; resources, D.F.; data curation, D.F.; writing—original draft preparation, D.F.; writing—review and editing, D.F. and A.-H.S.; visualization, D.F.; supervision, A.-H.S.; project administration, A.-H.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by JSPS KAKENHI, Grant Number JP24K14859.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- De Mauro, A.; Greco, M.; Grimaldi, M. A Formal Definition of Big Data Based on its Essential Features. Libr. Rev. 2016, 65, 122–135. [Google Scholar] [CrossRef]
- Ajah, I.A.; Nweke, H.F. Big Data and Business Analytics: Trends, Platforms, Success Factors and Applications. Big Data Cogn. Comput. 2019, 3, 32. [Google Scholar] [CrossRef]
- Lee, I. Big Data: Dimensions, evolution, impacts, and challenges. Bus. Horiz. 2017, 60, 293–303. [Google Scholar] [CrossRef]
- Laney, D. 3D Data Management: Controlling Data Volume, Velocity, and Variety; META Group, Inc.: Stamford, CT, USA, 2001. [Google Scholar]
- Wang, X.; Liu, J.; Zhu, Y.; Li, J.; He, X. Mean Vector and Covariance Matrix Estimation for Big Data. IEEE Trans. Big Data 2017, 3, 75–86. [Google Scholar]
- Mardia, K.V. Measures of Multivariate Skewness and Kurtosis with Applications. Biometrika 1970, 57, 519–530. [Google Scholar] [CrossRef]
- Fomo, D.; Sato, A.-H. High Fluctuation Based Recursive Segmentation for Big Data. In Proceedings of the 2024 9th International Conference on Big Data Analytics (ICBDA), Tokyo, Japan, 8–10 March 2024; pp. 358–363. [Google Scholar]
- De Mauro, A.; Greco, M.; Grimaldi, M. What is Big Data? A Consensual Definition and a Review of Key Research Topics. In Proceedings of the 4th International Conference on Integrated Information, Madrid, Spain, 1–4 September 2014. [Google Scholar]
- Editorial: Rethinking Big Data: From 3Vs to Operational Complexity. Front. Big Data 2024, 7, 1371329.
- Gandomi, A.; Haider, M. Beyond the hype: Big Data concepts, methods, and analytics. Int. J. Inf. Manag. 2015, 35, 137–144. [Google Scholar] [CrossRef]
- Schüssler-Fiorenza Rose, S.M.; Contrepois, K.; Moneghetti, K.J.; Zhou, W.; Mishra, T.; Mataraso, S.; Dagan-Rosenfeld, O.; Ganz, A.B.; Dunn, J.; Hornburg, D. A Longitudinal Big Data Approach for Precision Health. Nat. Med. 2019, 25, 792–804. [Google Scholar] [CrossRef]
- Seyedan, M.; Mafakheri, F. Predictive Big Data analytics for supply chain demand forecasting: Methods, applications, and research opportunities. J. Big Data 2020, 7, 53. [Google Scholar] [CrossRef]
- Torrence, C.; Compo, G.P. A Practical Guide to Wavelet Analysis. Bull. Am. Meteorol. Soc. 1998, 79, 61–78. [Google Scholar] [CrossRef]
- Bollerslev, T. Generalized Autoregressive Conditional Heteroskedasticity. J. Econom. 1986, 31, 307–327. [Google Scholar] [CrossRef]
- Bhandari, A.; Rahman, S. Big Data in Financial Markets: Algorithms, Analytics, and Applications; Springer Nature: Cham, Switzerland, 2021. [Google Scholar]
- Bhosale, H.S.; Gadekar, D.P. A Review Paper on Big Data and Hadoop. Int. J. Sci. Res. Publ. 2014, 4, 1–8. [Google Scholar]
- Fomo, D.; Sato, A.-H. Enhancing Big Data Analysis: A Recursive Window Segmentation Strategy for Multivariate Longitudinal Data. In Proceedings of the 2024 IEEE International Conference on Big Data (BigData), Washington, DC, USA, 15–18 July 2024; pp. 870–879. [Google Scholar]
- Jolliffe, I.T. Principal Component Analysis, 2nd ed.; Springer: New York, NY, USA, 2002. [Google Scholar]
- Markowitz, H. Portfolio selection. J. Financ. 1952, 7, 77–91. [Google Scholar] [CrossRef]
- Hashem, I.A.T.; Yaqoob, I.; Anuar, N.B.; Mokhtar, S.; Gani, A.; Khan, S.U. The rise of Big Data on cloud computing: Review and open research issues. Inf. Syst. 2015, 47, 98–115. [Google Scholar] [CrossRef]
- Hirsa, A. Computational Methods in Finance, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Kim, T.H.; White, H. On more robust estimation of skewness and kurtosis: Simulation and application to the S&P 500 index. Financ. Res. Lett. 2004, 1, 56–73. [Google Scholar] [CrossRef]
- Cormen, T.H.; Leiserson, C.E.; Rivest, R.L.; Stein, C. Introduction to Algorithms, 3rd ed.; MIT Press: Cambridge, MA, USA, 2009. [Google Scholar]
- Garey, M.R.; Johnson, D.S. Computers and Intractability: A Guide to the Theory of NP-Completeness; W. H. Freeman: San Francisco, CA, USA, 1979. [Google Scholar]
- Sipser, M. Introduction to the Theory of Computation, 3rd ed.; Cengage Learning: Boston, MA, USA, 2012. [Google Scholar]
- Bienstock, D. Computational complexity of analyzing credit risk. J. Bank. Financ. 1996, 20, 1233–1249. [Google Scholar]
- Sabbirul, H. Retail Demand Forecasting: A Comparative Study for Multivariate Time Series. arXiv 2023, arXiv:2308.11939. [Google Scholar] [CrossRef]
- Hillier, F.S.; Lieberman, G.J. Introduction to Operations Research, 10th ed.; McGraw-Hill: New York, NY, USA, 2014. [Google Scholar]
- Gusfield, D. Algorithms on Strings, Trees, and Sequences: Computer Science and Computational Biology; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Brys, G.; Hubert, M.; Struyf, A. A robust measure of skewness. J. Comput. Graph. Stat. 2004, 13, 996–1017. [Google Scholar] [CrossRef]
- Vazirani, V.V. Approximation Algorithms; Springer: New York, NY, USA, 2001. [Google Scholar]
- López-Ruiz, R.; Mancini, H.L.; Calbet, X. A statistical measure of complexity. Phys. Lett. A 1995, 209, 321–326. [Google Scholar] [CrossRef]
- Feldman, D.P.; Crutchfield, J.P. Measures of statistical complexity: Why? Phys. Lett. A 1998, 238, 244–252. [Google Scholar] [CrossRef]
- Crutchfield, J.P.; Young, K. Inferring statistical complexity. Phys. Rev. Lett. 1989, 63, 105–108. [Google Scholar] [CrossRef] [PubMed]
- Kolmogorov, A.N. Three approaches to the quantitative definition of information. Probl. Inf. Transm. 1965, 1, 1–7. [Google Scholar] [CrossRef]
- Lempel, A.; Ziv, J. On the complexity of finite sequences. IEEE Trans. Inf. Theory 1976, 22, 75–81. [Google Scholar] [CrossRef]
- Foster, D.J.; Kakade, S.M.; Qian, R.; Rakhlin, A. The Statistical Complexity of Interactive Decision Making. J. Mach. Learn. Res. 2023, 24, 1–78. [Google Scholar]
- Tononi, G.; Sporns, O.; Edelman, G.M. A measure for brain complexity: Relating functional segregation and integration in the nervous system. Proc. Natl. Acad. Sci. USA 1994, 91, 5033–5037. [Google Scholar] [CrossRef]
- Tableau. Big Data Analytics: What it is, How it Works, Benefits, and Challenges. Available online: https://www.tableau.com/learn/articles/big-data-analytics (accessed on 31 January 2023).
- Simplilearn. Challenges of Big Data: Basic Concepts, Case Study, and More. Available online: https://www.simplilearn.com/challenges-of-big-data-article (accessed on 17 July 2023).
- GeeksforGeeks. Big Challenges with Big Data. Available online: https://www.geeksforgeeks.org/big-challenges-with-big-data/ (accessed on 17 July 2023).
- Al-Turjman, F.; Hasan, M.Z.; Al-Oqaily, M. Exploring the Intersection of Machine Learning and Big Data: A Survey. Sensors 2024, 7, 13. [Google Scholar]
- ADA Asia. Big Data Analytics: Challenges and Opportunities. Available online: https://www.adaglobal.com/resources/insights/big-data-analytics-challenges-and-opportunities (accessed on 19 January 2024).
- Datamation. Top 7 Challenges of Big Data and Solutions. Available online: https://www.datamation.com/big-data/big-data-challenges/ (accessed on 31 January 2024).
- Yusuf, I.; Adams, C.; Abdullah, N.A. Current Challenges of Big Data Quality Management in Big Data Governance: A Literature Review. In Proceedings of the Future Technologies Conference (FTC) 2024, Vancouver, BC, Canada, 19–20 October 2024; Springer: Cham, Switzerland, 2024; Volume 2. [Google Scholar]
- Kumar, A.; Singh, S.; Singh, P. Big Data Analytics: Challenges, Tools. Int. J. Innov. Res. Comput. Sci. Technol. 2015, 3, 1–5. [Google Scholar]
- Rathore, M.M.; Paul, A.; Ahmad, A.; Chen, B.; Huang, B.; Ji, W. A Survey on Big Data Analytics: Challenges, Open Research Issues and Tools. Int. J. Adv. Comput. Sci. Appl. 2016, 7, 421–437. [Google Scholar] [CrossRef]
- Cattell, R. Operational NoSQL Systems: What’s New and What’s Next? Computer 2016, 49, 23–30. [Google Scholar] [CrossRef]
- 3Pillar Global. Current Issues and Challenges in Big Data Analytics. Available online: https://www.3pillarglobal.com/insights/current-issues-and-challenges-in-big-data-analytics/ (accessed on 19 January 2024).
- Sharma, S.; Gupta, R.; Dwivedi, A. A Challenging Tool for Research Questions in Big Data Analytics. Int. J. Res. Publ. Semin. 2022, 3, 1–7. [Google Scholar]
- Bifet, A.; Gavaldà, R. Learning from Time-Changing Data with Adaptive Windowing. In Proceedings of the SIAM International Conference on Data Mining, Minneapolis, MN, USA, 26–28 April 2007. [Google Scholar]
- Bai, J.; Ng, S. Tests for Skewness, Kurtosis, and Normality for Time Series Data. J. Bus. Econ. Stat. 2005, 23, 49–60. [Google Scholar] [CrossRef]
- Sato, A.-H. Segmentation Study of Foreign Exchange Market. In Applied Data-Centric Social Sciences; Springer: Tokyo, Japan, 2014; pp. 105–119. [Google Scholar] [CrossRef]
- JMP Statistical Discovery LLC. Statistical Details for Change Point Detection. Available online: https://www.jmp.com/support/help/en/17.2/index.shtml#page/jmp/change-point-detection.shtml (accessed on 24 July 2024).
- Aminikhanghahi, M.; Cook, D.J. A Survey of Methods for Time Series Change Point Detection. Knowl. Inf. Syst. 2017, 51, 339–367. [Google Scholar] [CrossRef]
- Jordon, J.; Szpruch, L.; Horel, F.; Wiese, M. Synthetic Data—What, Why and How? The Alan Turing Institute: London, UK, 2022. [Google Scholar]
- Shadish, W.R.; Cook, T.D.; Campbell, D.T. Experimental and Quasi-Experimental Designs for Generalized Causal Inference; Houghton Mifflin: Boston, MA, USA, 2002. [Google Scholar]
- U.S. Bureau of Labor Statistics. Employment Cost Index Historical Data; U.S. Bureau of Labor Statistics: Washington, DC, USA, 2025. Available online: https://www.bls.gov/ncs/ect/ (accessed on 23 March 2025).
- Board of Governors of the Federal Reserve System. Consumer Credit—G.19. Monthly Statistical Release. Available online: https://www.federalreserve.gov/releases/g19/ (accessed on 23 March 2025).
- Fader, P.S.; Hardie, B.G.S.; Lee, K.L. RFM and CLV: Using Iso-Value Curves for Customer Base Analysis. J. Mark. Res. 2005, 42, 415–430. [Google Scholar] [CrossRef]
- Centers for Disease Control and Prevention. About Adult BMI. Healthy Weight, Nutrition, and Physical Activity. Available online: https://www.cdc.gov/bmi/adult-calculator/bmi-categories.html (accessed on 19 March 2025).
- Whelton, P.K.; Carey, R.M.; Aronow, W.S.; Casey, D.E., Jr.; Collins, K.J.; Dennison Himmelfarb, C.; DePalma, S.M.; Gidding, S.; Jamerson, K.A.; Jones, D.W. 2017 ACC/AHA/AAPA/ABC/ACPM/AGS/APhA/ASH/ASPC/NMA/PCNA Guideline for the Prevention, Detection, Evaluation, and Management of High Blood Pressure in Adults. J. Am. Coll. Cardiol. 2018, 71, e127–e248. [Google Scholar] [CrossRef] [PubMed]
- Xu, L.; Skoularidou, M.; Cuesta-Infante, A.; Veeramachaneni, K. Modeling Tabular Data using Conditional GAN. In Proceedings of the 33rd Conference on Neural Information Processing Systems (NeurIPS 2019), Vancouver, WA, Canada, 8–14 December 2019; pp. 7335–7345. [Google Scholar]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Sirignano, R.; Cont, A. Universal features of price formation in financial markets. Quant. Financ. 2019, 19, 1449–1459. [Google Scholar] [CrossRef]
- Heaton, J.B.; Polson, N.G.; Witte, J.H. Deep learning in finance. Appl. Stoch. Model. Bus. Ind. 2017, 33, 3–12. [Google Scholar] [CrossRef]
- Alaa, A.; van der Schaar, M. Forecasting individualized disease trajectories. Nat. Commun. 2018, 9, 276. [Google Scholar]
- Rajkomar, A.; Oren, E.; Chen, K.; Dai, A.M.; Hajaj, N.; Hardt, M.; Liu, P.J.; Liu, X.; Marcus, J.; Sun, M. Scalable and accurate deep learning with electronic health records. NPJ Digit. Med. 2018, 1, 18. [Google Scholar] [CrossRef]
- Zheng, Y.; Liu, Q.; Chen, E.; Ge, Y.; Zhao, J.L. Time Series Classification Using Multi-Channels Deep Convolutional Neural Networks. In Proceedings of the International Conference on Web-Age Information Management, Macau, China, 16–18 June 2014; pp. 298–310. [Google Scholar]
- Chu, W.; Park, S. Personalized recommendation on dynamic content. In Proceedings of the 18th International Conference on World Wide Web, Madrid, Spain, 20–24 April 2009; pp. 691–700. [Google Scholar]
- Zaharia, M.; Xin, R.S.; Wendell, P.; Das, T.; Armbrust, M.; Dave, A.; Meng, X.; Rosen, J.; Venkataraman, S.; Franklin, M.J. Apache Spark: A Unified Engine for Big Data Processing. Commun. ACM 2016, 59, 56–65. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).