Importance of Data Preprocessing for Accurate and Effective Prediction of Breast Cancer: Evaluation of Model Performance in Novel Data
Abstract
1. Introduction
2. Related Works
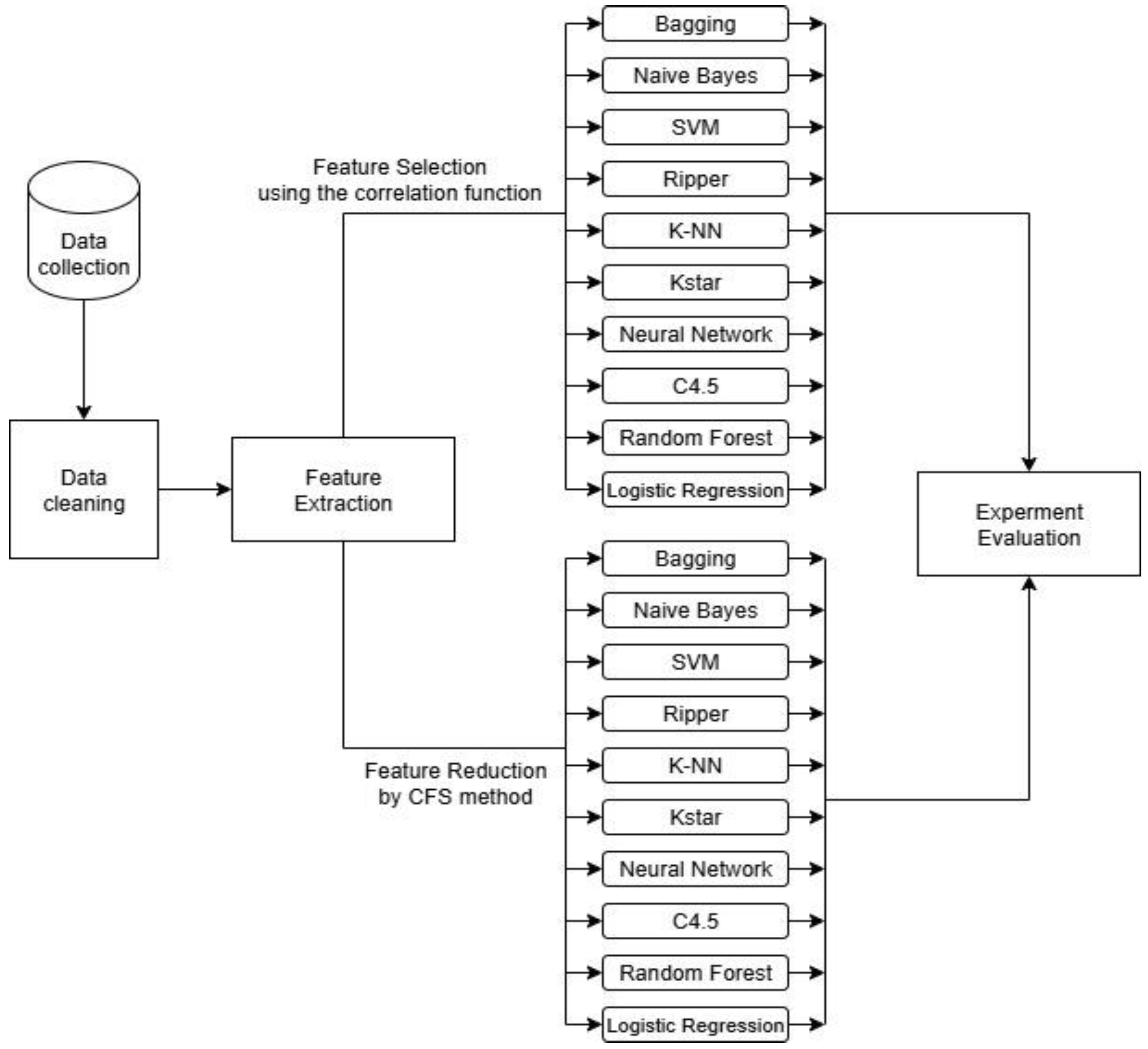
3. Methodology
3.1. Data Collection and Feature Explanation
- Core-needle breast biopsies not performed under ultrasound guidance.
- Fine-needle aspiration (FNA).
- Stereotactic core-needle breast biopsy.
- Axillary lymph node biopsy.
- Size: The maximum dimension of the lesion as measured on ultrasound.
- Number of tissue samples: The total count of tissue samples obtained from the lesion during the biopsy.
- Needle size: The gauge of the needle used for the biopsy procedure.
- Imaging modality: Whether the lesion was assessed using both mammography and ultrasound, or ultrasound only.
- BI-RADS category: The assigned Breast Imaging Reporting and Data System classification.
- Tissue sample adequacy: A clear indication of whether the obtained tissue sample was sufficient for a definitive histological diagnosis.
- Histological diagnosis: The final pathological diagnosis of the biopsied tissue.
3.2. Data Preprocessing
3.2.1. Handling Missing Values
3.2.2. Encoding Categorical Variables
3.3. Correlation-Based Feature Subset Selection Method
| Algorithm 1: A Representative Car Based on Cluster Center (RC) | |
| Input: A dataset D consists of n features with class label C; | |
| Output: An optimal subset of features; | |
| 1. | Initialization: , ; |
| 2. | Define. The merit function is defined as follows: Where k is the number of features in subset S, is the average correlation between features and the class and is the average inter-correlation between features; |
| 3. | Perform Best First Search:
|
| 4. | Stop search: If no improvement in Merit(S) for a predefined number of steps is identified; |
| 5. | Return: The best subset with the highest merit |
3.4. Classification Models
4. Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| CFS | Correlation-based Feature Selection |
| MRI | Magnetic Resonance Imaging |
| ML | Machine Learning |
| DL | Deep Learning |
| AC | Associative Classification |
| SVM | Support Vector Machine |
| CNN | Convolutional Neural Network |
| KNN | K-Nearest Neighbor |
| NB | Naïve Bayes |
| mRMR | Minimum Redundancy Maximum Relevance |
| CAD | Computer-Aided Diagnosis |
| US | Ultrasound |
| BC | Breast Cancer |
| ROI | Region of Interest |
| DDSM | Digital Database for Screening Mammography |
| MLO | Mediolateral Oblique |
| VGG | Visual Geometry Group |
| ANN | Artificial Neural Networks |
| PCA | Principal Component Analysis |
| RF | Random Forest |
| WBSD | Wisconsin Breast Cancer Database |
| RBF | Radial Basis Function |
| LR | Logistic Regression |
| LDA | Linear Discriminant Analysis |
| MLP | Multilayer Perceptron |
| FNA | Fine-Needle Aspiration |
| BI-RADS | Breast Imaging Reporting and Data System |
| OCR | Optical Character Recognition |
| LLM | Large Language Model |
| GLCM | Gray-Level Co-occurrence Matrix |
| GLRLM | Gray-Level Run-Length Matrix |
| GLDM | Gray-Level Dependence Matrix |
References
- Ferlay, J.; Colombet, M.; Soerjomataram, I.; Parkin, D.M.; Piñeros, M.; Znaor, A.; Bray, F. Cancer statistics for the year 2020: An overview. Int. J. Cancer 2021, 149, 778–789. [Google Scholar] [CrossRef]
- Lei, S.; Zheng, R.; Zhang, S.; Wang, S.; Chen, R.; Sun, K.; Zeng, H.; Zhou, J.; Wei, W. Global patterns of breast cancer incidence and mortality: A population-based cancer registry data analysis from 2000 to 2020. Cancer Commun. 2021, 41, 1183–1194. [Google Scholar] [CrossRef]
- Marks, J.S.; Lee, N.C.; Lawson, H.W.; Henson, R.; Bobo, J.K.; Kaeser, M.K. Implementing recommendations for the early detection of breast and cervical cancer among low-income women. Morb. Mortal. Wkly. Rep. Recomm. Rep. 2000, 49, 35–55. [Google Scholar]
- Du-Crow, E. Computer-Aided Detection in Mammography. Ph.D. Thesis, The University of Manchester, Manchester, UK, 1 August 2022. [Google Scholar]
- Evans, A.; Trimboli, R.M.; Athanasiou, A.; Balleyguier, C.; Baltzer, P.A.; Bick, U.; Herrero, J.C.; Clauser, P.; Colin, C.; Cornford, E.; et al. Breast ultrasound: Recommendations for information to women and referring physicians by the European Society of Breast Imaging. Insights Imaging 2018, 9, 449–461. [Google Scholar] [CrossRef]
- Schueller, G.; Schueller-Weidekamm, C.; Helbich, T.H. Accuracy of ultrasound-guided, large-core needle breast biopsy. Eur. Radiol. 2008, 18, 1761–1773. [Google Scholar] [CrossRef]
- Shi, X.; Liang, C.; Wang, H. Multiview robust graph-based clustering for cancer subtype identification. IEEE/ACM Trans. Comput. Biol. Bioinform. 2022, 20, 544–556. [Google Scholar]
- Wang, H.; Jiang, G.; Peng, J.; Deng, R.; Fu, X. Towards Adaptive Consensus Graph: Multi-view Clustering via Graph Collaboration. IEEE Trans. Multimed. 2022, 25, 6629–6641. [Google Scholar] [CrossRef]
- Wang, H.; Wang, Y.; Zhang, Z.; Fu, X.; Zhuo, L.; Xu, M.; Wang, M. Kernelized multiview subspace analysis by self-weighted learning. IEEE Trans. Multimed. 2020, 23, 3828–3840. [Google Scholar] [CrossRef]
- Wang, H.; Yao, M.; Jiang, G.; Mi, Z.; Fu, X. Graph-Collaborated Auto-Encoder Hashing for Multi-view Binary Clustering. arXiv 2023, arXiv:2301.02484. [Google Scholar]
- Bai, J.; Posner, R.; Wang, T.; Yang, C.; Nabavi, S. Applying deep learning in digital breast tomosynthesis for automatic breast cancer detection: A review. Med. Image Anal. 2021, 71, 102049. [Google Scholar] [CrossRef]
- Li, Z.; Liu, F.; Yang, W.; Peng, S.; Zhou, J. A survey of convolutional neural networks: Analysis, applications, and prospects. IEEE Trans. Neural Netw. Learn. Syst. 2022, 33, 6999–7019. [Google Scholar] [CrossRef]
- Zuluaga-Gomez, J.; Al Masry, Z.; Benaggoune, K.; Meraghni, S.; Zerhouni, N. A CNN-based methodology for breast cancer diagnosis using thermal images. Comput. Methods Biomech. Biomed. Eng. Imaging Vis. 2021, 9, 131–145. [Google Scholar] [CrossRef]
- Eroğlu, Y.; Yildirim, M.; Çinar, A. Convolutional Neural Networks based classification of breast ultrasonography images by hybrid method with respect to benign, malignant, and normal using mRMR. Comput. Biol. Med. 2021, 133, 104407. [Google Scholar] [CrossRef]
- Huang, Q.; Yang, F.; Liu, L.; Li, X. Automatic segmentation of breast lesions for interaction in ultrasonic computer-aided diagnosis. Inf. Sci. 2015, 314, 293–310. [Google Scholar] [CrossRef]
- Huang, Q.; Huang, Y.; Luo, Y.; Yuan, F.; Li, X. Segmentation of breast ultrasound image with semantic classification of superpixels. Med. Image Anal. 2020, 61, 101657. [Google Scholar] [CrossRef]
- Mattiev, J.; Kavšek, B. Simple and Accurate Classification Method Based on Class Association Rules Performs Well on Well-Known Datasets. In Machine Learning, Optimization, and Data Science, Proceedings of the 5th International Conference, LOD 2019, Siena, Italy, 10–13 September 2019; Springer: Berlin/Heidelberg, Germany, 2019; pp. 192–204. [Google Scholar]
- Mattiev, J.; Kavšek, B. CMAC: Clustering Class Association Rules to Form a Compact and Meaningful Associative Classifier. In Machine Learning, Optimization, and Data Science, Proceedings of the 6th International Conference, LOD 2020, Siena, Italy, 19–23 July 2020; Springer: Berlin/Heidelberg, Germany, 2020; pp. 372–384. [Google Scholar]
- Mattiev, J.; Davityan, M.; Kavsek, B. ACMKC: A Compact Associative Classification Model Using K-Modes Clustering with Rule Representations by Coverage. Mathematics 2023, 11, 3978. [Google Scholar] [CrossRef]
- Mattiev, J.; Kavsek, B. Distance based clustering of class association rules to build a compact, accurate and descriptive classifier. Comput. Sci. Inf. Syst. 2021, 18, 791–811. [Google Scholar] [CrossRef]
- Mattiev, J.; Sajovic, J.; Drevenšek, G.; Rogelj, P. Assessment of Model Accuracy in Eyes Open and Closed EEG Data: Effect of Data Pre-Processing and Validation Methods. Bioengineering 2023, 10, 42. [Google Scholar] [CrossRef]
- Hall, M.A. Correlation-Based Feature Subset Selection for Machine Learning. Ph.D. Thesis, The University of Waikato, Hamilton, New Zealand, April 1998. [Google Scholar]
- Jessica, E.O.; Hamada, M.; Yusuf, S.I.; Hassan, M. The Role of Linear Discriminant Analysis for Accurate Prediction of Breast Cancer. In Proceedings of the 2021 IEEE 14th International Symposium of Embedded Multicore/Many-Core Systems-on-Chip (MCSoc), Singapore, 20–23 December 2021; pp. 340–344. [Google Scholar]
- Wang, H.; Yoon, S.W. Breast Cancer Prediction Using Data Mining Method. In Proceedings of the IIE Annual Conference, Institute of Industrial and System Engineers (IISE), New Orleans, LA, USA, 30 May–2 June 2015; p. 818. [Google Scholar]
- Boeri, C.; Chiappa, C.; Galli, F.; de Berardinis, V.; Bardelli, L.; Carcano, G.; Rovera, F. Machine learning techniques in breast cancer prognosis prediction: A primary evaluation. Cancer Med. 2020, 9, 3234–3243. [Google Scholar] [CrossRef]
- Khourdifi, Y. Applying Best Machine Learning Algorithms for Breast Cancer Prediction and Classification. In Proceedings of the 2018 International Conference on Electronics, Control, Optimization and Computer Science (ICECOCS), Kenitra, Morocco, 5–6 December 2018; pp. 1–5. [Google Scholar]
- Chaurasia, V.; Pal, S.; Tiwari, B.B. Prediction of benign and malignant breast cancer using data mining techniques. J. Algorithms Comput. Technol. 2018, 12, 119–126. [Google Scholar] [CrossRef]
- Kumar Mandal, S. Performance Analysis of Data Mining Algorithms for Breast Cancer Cell Detection Using Naïve Bayes, Logistic Regression and Decision Tree. Int. J. Eng. Comput. Sci. 2017, 6, 2319–7242. [Google Scholar]
- Asri, H.; Mousannnif, H.; al Moatassime, H.; Noel, T. Using machine learning algorithms for breast cancer risk prediction and diagnosis. Procedia Comput. Sci. 2016, 83, 1064–1069. [Google Scholar] [CrossRef]
- Ricciardi, C.; Valente, S.A.; Edmund, K.; Cantoni, V.; Green, R.; Fiorillo, A.; Picone, I.; Santini, S.; Cesarelli, M. Linear discriminant analysis and principal component analysis to predict coronary artery disease. Health Inform. J. 2020, 26, 2181–2192. [Google Scholar] [CrossRef]
- Kumar, V.; Misha, B.K.; Mazzara, M.; Thanh, D.N.; Verma, A. Prediction of malignant and benign breast cancer: A data mining approach in healthcare applications. In Advances in Data Science and Management; Springer: Berlin/Heidelberg, Germany, 2019; pp. 435–442. [Google Scholar]
- Gupta, S.; Gupta, M.K. A Comparative Study of Breast Cancer Diagnosis Using Supervised Machine Learning Techniques. In Proceedings of the 2nd International Conference on Computing Methodologies and Communication (ICCMC 2018), Erode, India, 15–16 February 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 997–1002. [Google Scholar]
- Zheng, B.; Yoon, S.W.; Lam, S.S. Breast cancer diagnosis based on feature extraction using a hybrid of k-mean and support vector machine algorithms. Experts Syst. Appl. 2014, 41, 1476–1482. [Google Scholar] [CrossRef]
- Sivakami, K.; Saraswathi, N. Mining big data: Breast cancer prediction using DT-SVM hybrid model. Int. J. Sci. Eng. Appl. Sci. 2015, 1, 418–429. [Google Scholar]
- Hall, M.; Frank, E.; Holmes, G.; Pfahringer, B.; Reutemann, P.; Witten, I.H. The WEKA data mining software: An update. ACM SIGKDD Explor. Newsl. 2009, 11, 10–18. [Google Scholar] [CrossRef]
- Quinlan, R.J. C4.5: Programs for Machine Learning, 1st ed.; Morgan Kaufmann: Burlington, MA, USA, 1992. [Google Scholar]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Cohen, W.W. Fast effective rule induction. In Proceedings of the Twelfth International Conference on Machine Learning, Tahoe City, CA, USA, 9–12 July 1995; pp. 115–123. [Google Scholar]
- Aha, D.W.; Kibler, D.; Albert, M.K.; Quinian, J.R. Instance-based learning algorithms. Mach. Learn. 1991, 6, 37–66. [Google Scholar] [CrossRef]
- Cleary, J.G.; Trigg, L.E. K*: An Instance-based Learner Using an Entropic Distance Measure. In Proceedings of the Twelfth International Conference on Machine Learning, Tahoe City, CA, USA, 9–12 July 1995; pp. 108–114. [Google Scholar]
- Haykin, S. Neural Networks: A Comprehensive Foundation, 2nd ed.; Prentice Hall: Hamilton, ON, Canada, 1994. [Google Scholar]
- Platt, J. Fast Training of Support Vector Machines using Sequential Minimal Optimization. In Advances in Kernel Methods—Support Vector Learning; MIT Press: Cambridge, MA, USA, 1999; pp. 185–208. [Google Scholar]
- le Cessie, S.; Van Houwelingen, J.C. Ridge Estimators in Logistic Regression. Appl. Stat. 1992, 41, 191–201. [Google Scholar] [CrossRef]
- George, H.J.; Langley, P. Estimating Continuous Distributions in Bayesian Classifiers. In Proceedings of the Eleventh Conference on Uncertainty in Artificial Intelligence, Montreal, QC, Canada, 18–20 August 1995; pp. 338–345. [Google Scholar]
- Breiman, L. Bagging predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef]

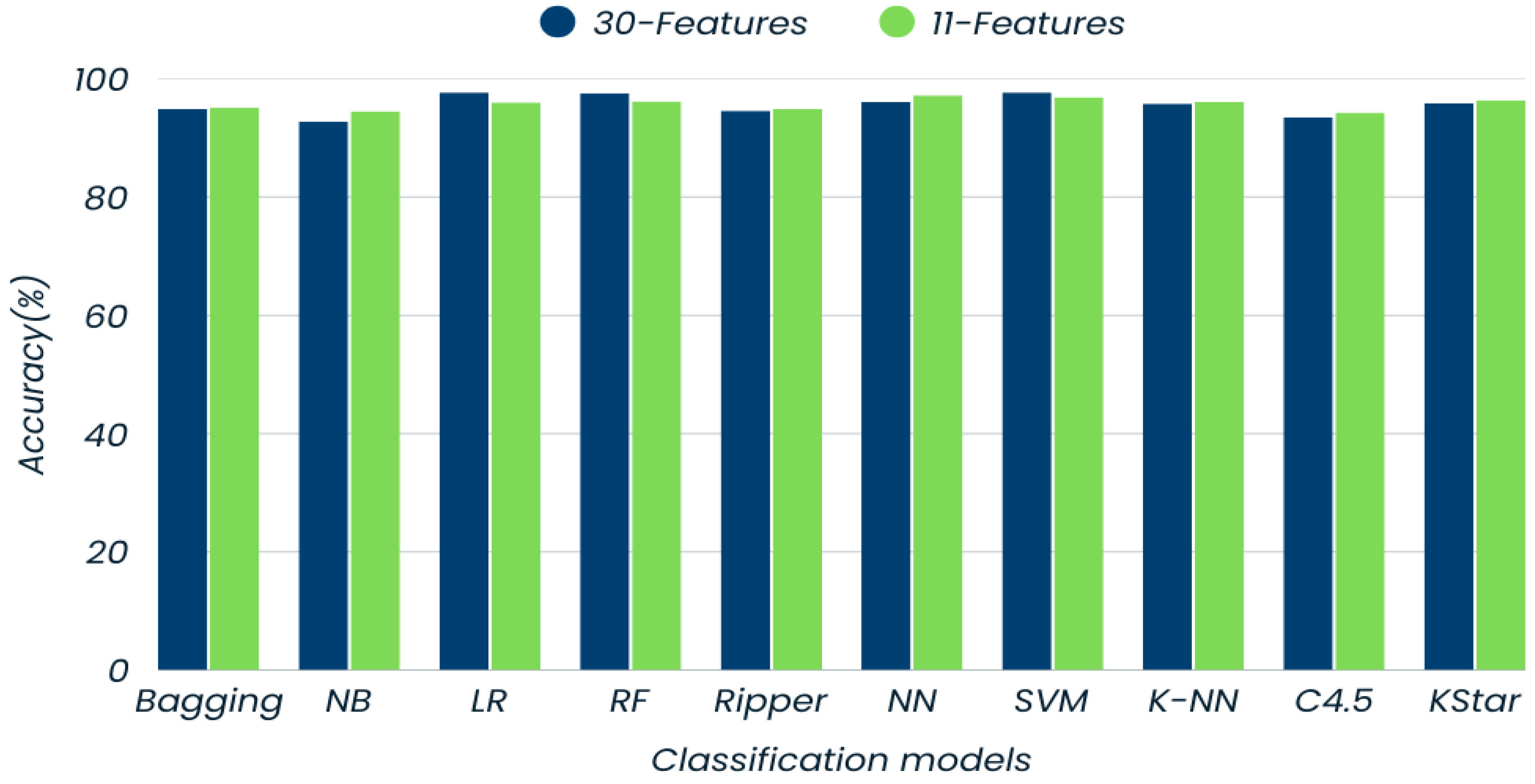
| Models | Accuracy (%) | Precision (%) | Recall (%) | F-Measure (%) | |||
|---|---|---|---|---|---|---|---|
| Class (M) | Class (B) | Class (M) | Class (B) | Class (M) | Class (B) | ||
| Bagging | 94.9 | 94.0 | 95.6 | 93.7 | 95.8 | 93.9 | 95.7 |
| Naïve Bayes | 92.8 | 93.0 | 92.7 | 89.3 | 95.3 | 91.1 | 94.0 |
| Logistic Regression | 97.7 | 99.2 | 96.6 | 95.3 | 99.4 | 97.2 | 98.1 |
| Random Forest | 97.6 | 97.2 | 97.8 | 96.8 | 98.1 | 97.0 | 97.9 |
| Ripper | 94.6 | 93.0 | 95.8 | 94.1 | 95.0 | 93.5 | 95.4 |
| Neural Network | 96.1 | 96.7 | 95.7 | 93.7 | 97.8 | 95.2 | 96.7 |
| SVM | 97.7 | 99.2 | 96.8 | 95.3 | 99.4 | 97.2 | 98.1 |
| K-NN | 95.8 | 94.2 | 96.9 | 95.7 | 95.8 | 94.9 | 96.4 |
| C4.5 | 93.5 | 91.1 | 95.2 | 93.3 | 93.6 | 92.2 | 94.4 |
| Kstar | 95.9 | 95.6 | 96.2 | 94.5 | 97.0 | 95.0 | 96.6 |
| Models | Bagging | Naive Bayes | Logistic Regression | Random Forest | Ripper | Neural Network | SVM | K-NN | C4.5 | KStar |
|---|---|---|---|---|---|---|---|---|---|---|
| Bagging | – | W | 0 | L | 0 | L | L | 0 | W | L |
| Naïve Bayes | L | – | L | L | 0 | L | L | L | 0 | L |
| Logistic Regression | 0 | W | – | 0 | W | 0 | 0 | 0 | W | 0 |
| Random Forest | W | W | 0 | – | W | 0 | 0 | W | W | W |
| Ripper | 0 | 0 | L | L | – | L | L | 0 | W | 0 |
| Neural Network | W | W | 0 | 0 | W | – | 0 | W | W | W |
| SVM | W | W | 0 | 0 | W | 0 | – | W | W | W |
| K-NN | 0 | W | 0 | L | 0 | L | L | – | W | 0 |
| C4.5 | L | 0 | L | L | L | L | L | L | – | 0 |
| Kstar | 0 | W | 0 | L | 0 | L | L | 0 | W | – |
| Feature | Description | Importance |
|---|---|---|
| concavity_mean | Measures the average severity of concave portions of the contour. | Malignant tumors tend to have more irregular, concave shapes. |
| concave_points_mean | Average number of concave portions in the contour. | A higher number of concave points is typical in malignant cells. |
| area_se | Standard error of the area covered by the nucleus. | Captures variability; malignant nuclei often have larger, more irregular areas. |
| symmetry_se | Standard error of symmetry. | Malignant masses are generally more asymmetric. |
| radius_worst | Largest value of the radius across all nuclei. | Malignant nuclei tend to be larger. |
| texture_worst | Variation in texture (e.g., smoothness, granularity) of the nucleus. | Textural irregularity is higher in malignant cells. |
| perimeter_worst | Largest perimeter value found among nuclei. | Longer perimeters reflect more irregular, possibly cancerous shapes. |
| area_worst | Largest area found among nuclei. | High values are associated with malignancy. |
| smoothness_worst | Smoothness of the border (worst case). | Malignant tumors tend to have fewer smooth edges. |
| concavity_worst | Maximum concavity observed. | Deep concavities are linked with malignancy. |
| concave_points_worst | Maximum number of concave points detected. | More concave points typically indicate cancerous lesions. |
| Models | Accuracy (%) | Precision (%) | Recall (%) | F-Measure (%) | |||
|---|---|---|---|---|---|---|---|
| Class (M) | Class (B) | Class (M) | Class (B) | Class (M) | Class (B) | ||
| Bagging | 95.1 | 94.4 | 95.6 | 93.7 | 96.1 | 94.0 | 95.9 |
| Naïve Bayes | 94.5 | 94.7 | 94.3 | 91.7 | 96.4 | 93.2 | 95.3 |
| Logistic Regression | 96.6 | 96.0 | 97.0 | 95.7 | 97.2 | 95.8 | 97.1 |
| Random Forest | 96.2 | 95.3 | 96.9 | 95.7 | 96.7 | 95.5 | 96.8 |
| Ripper | 94.9 | 94.4 | 95.3 | 93.3 | 96.1 | 93.8 | 95.7 |
| Neural Network | 97.2 | 97.2 | 97.3 | 96.0 | 98.1 | 96.6 | 97.7 |
| SVM | 96.9 | 98.0 | 96.2 | 94.5 | 98.6 | 96.2 | 97.4 |
| K-NN | 96.1 | 94.9 | 96.9 | 95.7 | 96.4 | 95.3 | 96.7 |
| C4.5 | 94.3 | 92.6 | 95.5 | 93.7 | 94.7 | 93.1 | 95.1 |
| Kstar | 96.4 | 96.4 | 96.4 | 94.9 | 97.5 | 95.6 | 97.0 |
| Models | Bagging | Naive Bayes | Logistic Regression | Random Forest | Ripper | Neural Network | SVM | K-NN | C4.5 | KStar |
|---|---|---|---|---|---|---|---|---|---|---|
| Bagging | – | 0 | 0 | 0 | 0 | L | L | 0 | 0 | 0 |
| Naïve Bayes | 0 | – | L | L | 0 | L | L | 0 | 0 | 0 |
| Logistic Regression | 0 | W | – | 0 | W | 0 | 0 | 0 | 0 | 0 |
| Random Forest | 0 | W | 0 | – | 0 | 0 | 0 | 0 | 0 | 0 |
| Ripper | 0 | 0 | L | 0 | – | 0 | 0 | 0 | 0 | 0 |
| Neural Network | W | W | 0 | 0 | W | – | 0 | 0 | 0 | 0 |
| SVM | W | W | 0 | 0 | W | 0 | – | 0 | 0 | 0 |
| K-NN | 0 | 0 | 0 | 0 | 0 | 0 | 0 | – | 0 | 0 |
| C4.5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | – | 0 |
| Kstar | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | W | – |
| Models | Train Time on 30-Feature Dataset | Train Time on 11-Feature Dataset |
|---|---|---|
| Bagging | 0.03 | 0.01 |
| Naïve Bayes | 0.01 | 0.01 |
| Logistic Regression | 0.02 | 0.01 |
| Random Forest | 0.08 | 0.07 |
| Ripper | 0.03 | 0.01 |
| Neural Network | 1.67 | 0.32 |
| SVM | 0.01 | 0.01 |
| K-NN | 0.01 | 0.01 |
| C4.5 | 0.01 | 0.01 |
| Kstar | 0.01 | 0.01 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Baloyi, V.; Mattiev, J.; Mokwena, S. Importance of Data Preprocessing for Accurate and Effective Prediction of Breast Cancer: Evaluation of Model Performance in Novel Data. Big Data Cogn. Comput. 2025, 9, 266. https://doi.org/10.3390/bdcc9100266
Baloyi V, Mattiev J, Mokwena S. Importance of Data Preprocessing for Accurate and Effective Prediction of Breast Cancer: Evaluation of Model Performance in Novel Data. Big Data and Cognitive Computing. 2025; 9(10):266. https://doi.org/10.3390/bdcc9100266
Chicago/Turabian StyleBaloyi, Vekani, Jamolbek Mattiev, and Sello Mokwena. 2025. "Importance of Data Preprocessing for Accurate and Effective Prediction of Breast Cancer: Evaluation of Model Performance in Novel Data" Big Data and Cognitive Computing 9, no. 10: 266. https://doi.org/10.3390/bdcc9100266
APA StyleBaloyi, V., Mattiev, J., & Mokwena, S. (2025). Importance of Data Preprocessing for Accurate and Effective Prediction of Breast Cancer: Evaluation of Model Performance in Novel Data. Big Data and Cognitive Computing, 9(10), 266. https://doi.org/10.3390/bdcc9100266








