A Real-Time Vehicle Speed Prediction Method Based on a Lightweight Informer Driven by Big Temporal Data
Abstract
1. Introduction
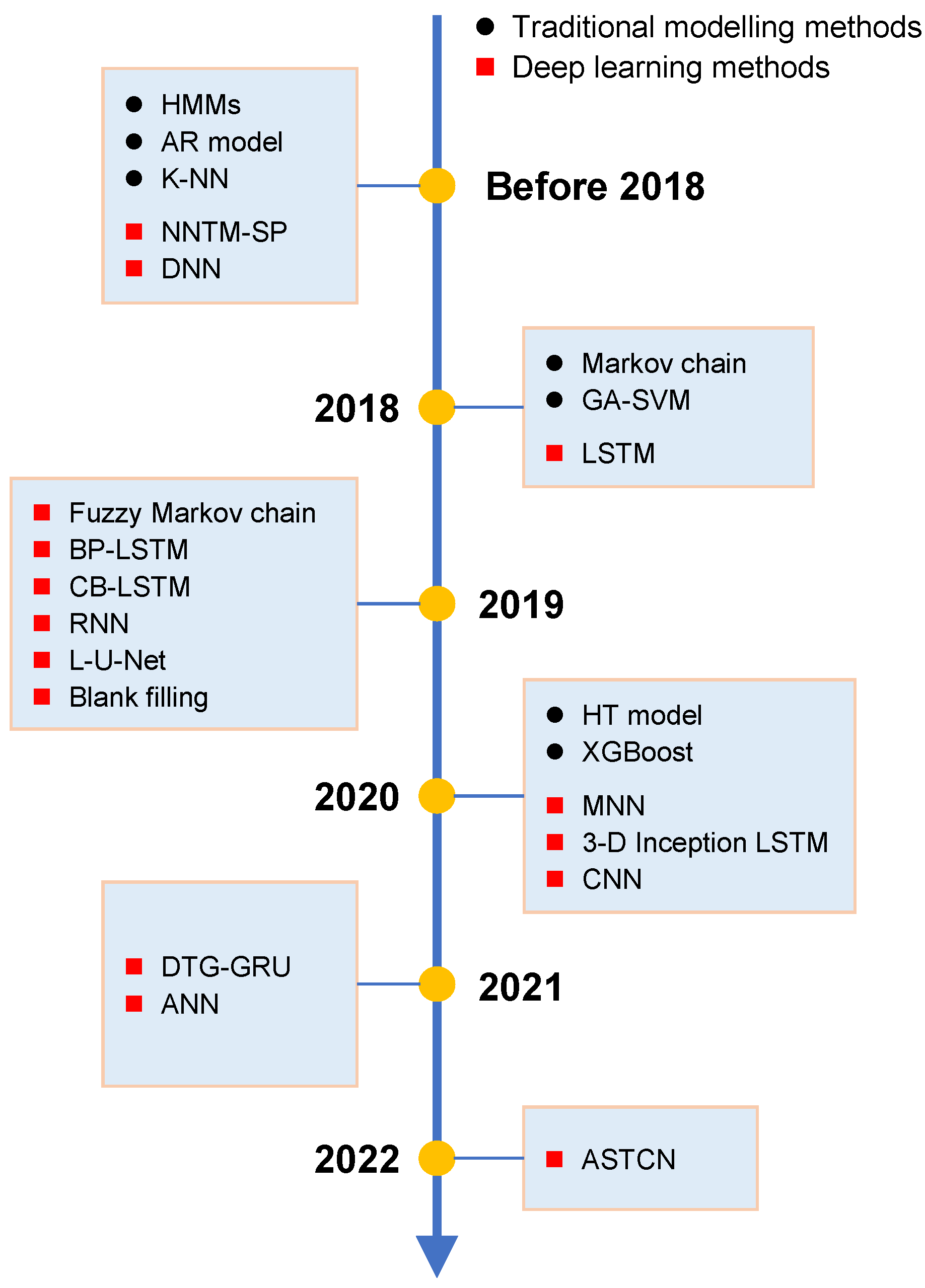
2. Related Work
2.1. Traditional Modelling Methods
2.2. Modern Deep Learning Methods
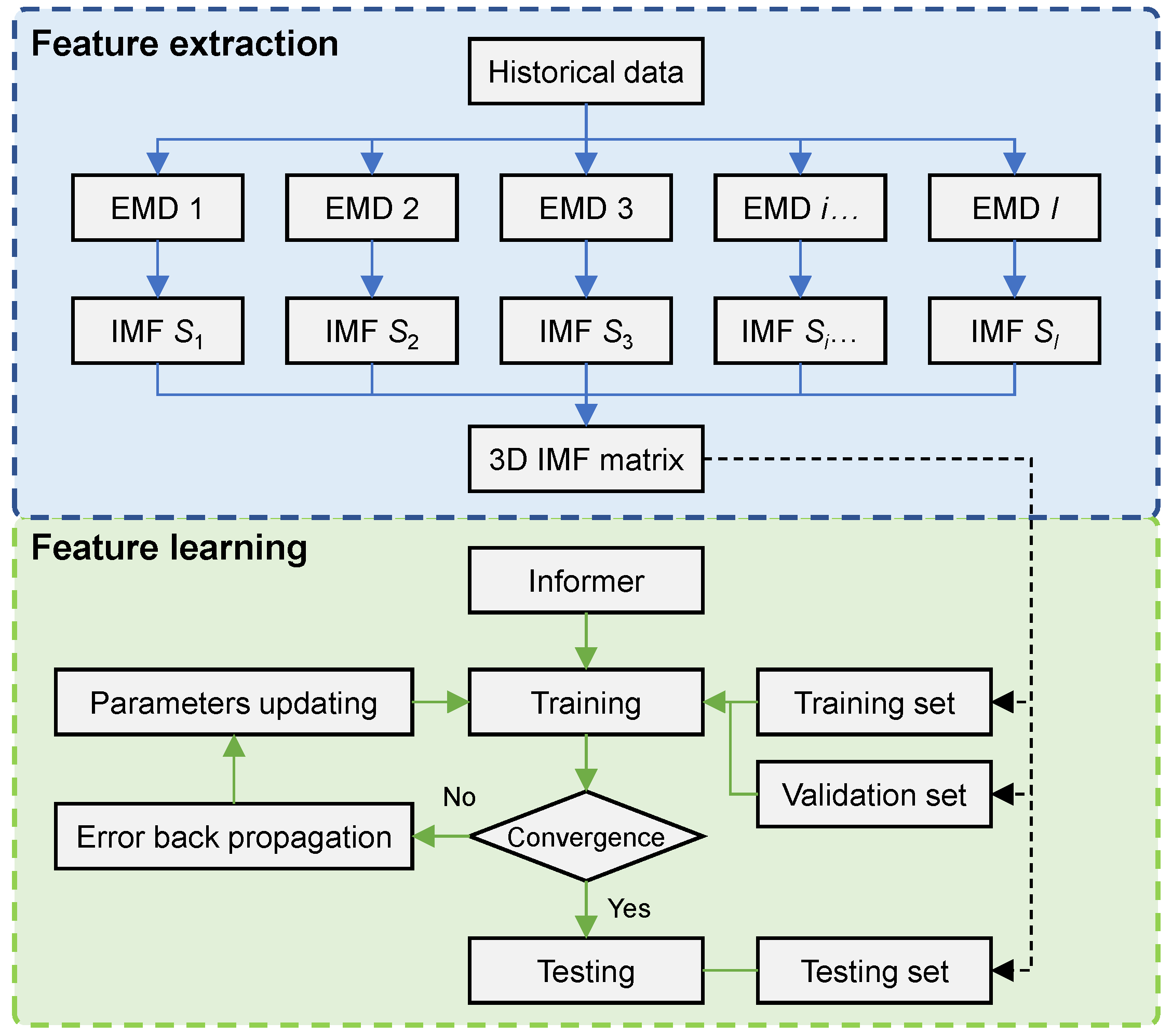
3. EMD-Based Informer for Vehicle Speed Prediction
3.1. EMD Analysis
3.1.1. Signal Decomposition
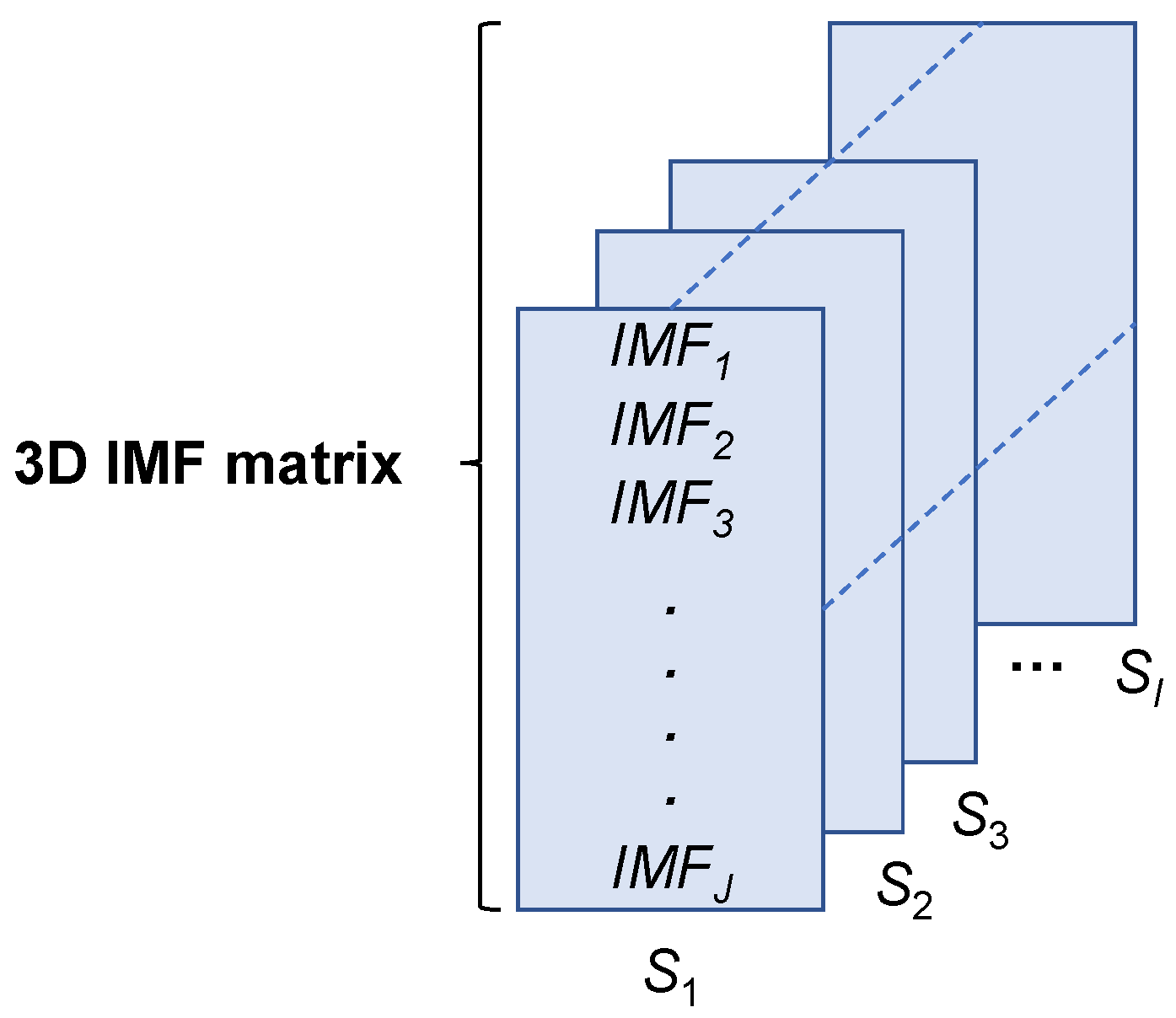
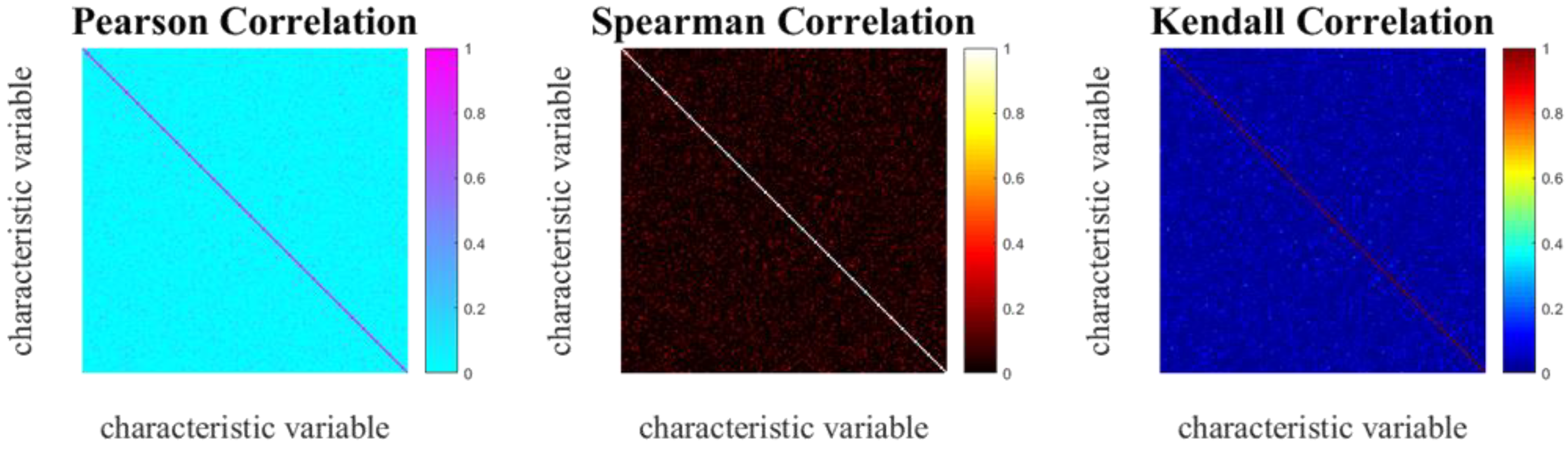
3.1.2. Representation Construction
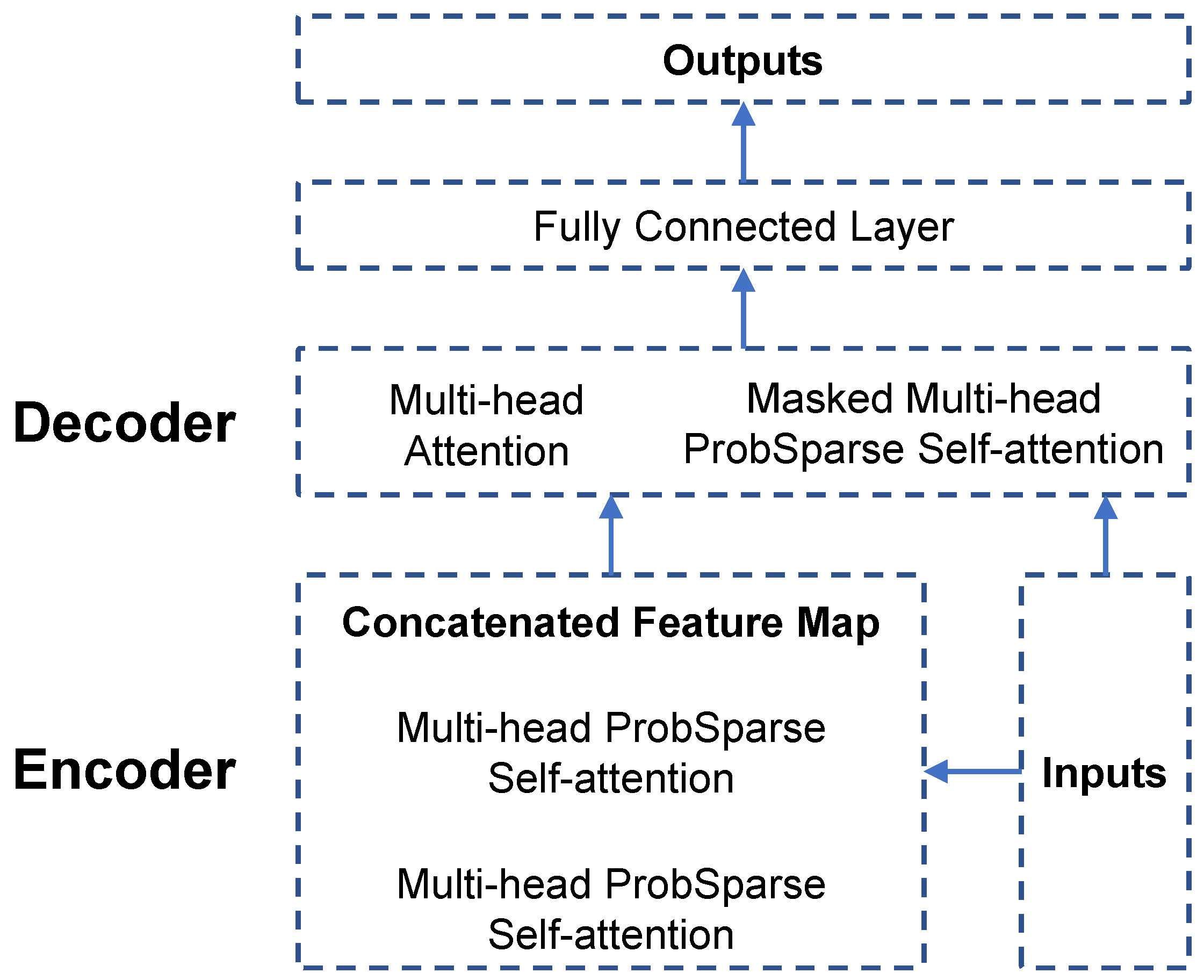
3.2. Informer Model
3.2.1. Model Structure
3.2.2. Parameters Learning
| Algorithm 1 Asynchronous SGD optimization process. |
| Input: Data sequence X |
| Initialization: Step size, initial parameters, and batch size. |
| Compute the batch gradient of D0. |
| for t = 1, 2, … do |
| Gradient arrives from batch set Dt; |
| Update the parameters; |
| Send θt to batch set Dt; |
| Compute the batch gradient of Dt. |
| end for |
| Output: Convergent deep learning model. |
- The learning rate controls the magnitude of parameter updates at each step; too fast of a learning rate may lead to model oscillation and non-convergence, while too slow of a learning rate will make the model converge slowly.
- The batch size controls the amount of data for each parameter update. Too large of a batch size may lead to insufficient memory, and too small of a batch size may make the model converge slowly.
- The SGD algorithm is sensitive to parameter initialization. Different initialization methods may lead to differences in model convergence speed and location. Considering that data from multiple scenarios are used for the experiments, random samples obeying a standard normal distribution were used to export the model parameters.
- Gradient explosion or gradient disappearance is a common problem faced by deep learning, which can be mitigated using gradient cropping techniques.
3.2.3. Vehicle Speed Prediction
| Algorithm 2 Entire process for vehicle speed prediction. |
| Input: Data sequence X. |
| Initialization: The number of EMD, step size, initial model |
| parameters, and batch size. |
| Construct the 3D IMF matrix. |
| Initialize the deep learning model. |
| Train the model using the asynchronous SGD. |
| Crop the model to the lightweight structure. |
| Reasoning based on the forward propagation. |
| Output: Predicted vehicle speed at T + 1 moment. |
4. Experimental Results and Analysis
4.1. Experimental Settings
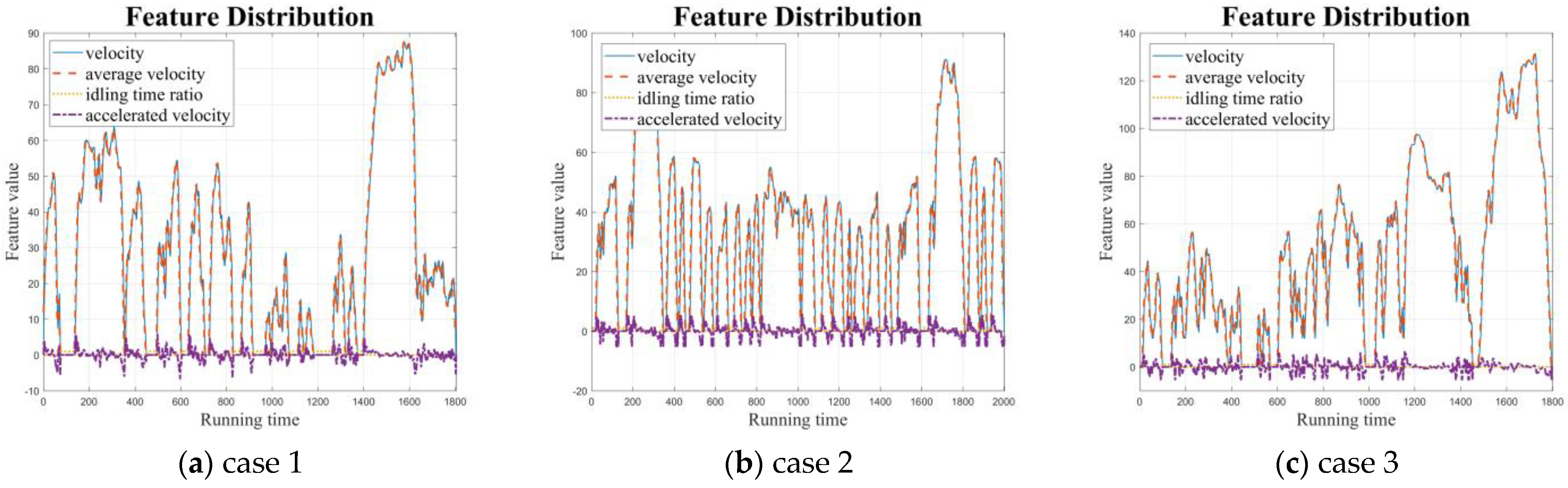
4.1.1. Experimental Data
4.1.2. Experimental Hyper-Parameters
4.1.3. Experimental Platform
4.1.4. Evaluation Metrics
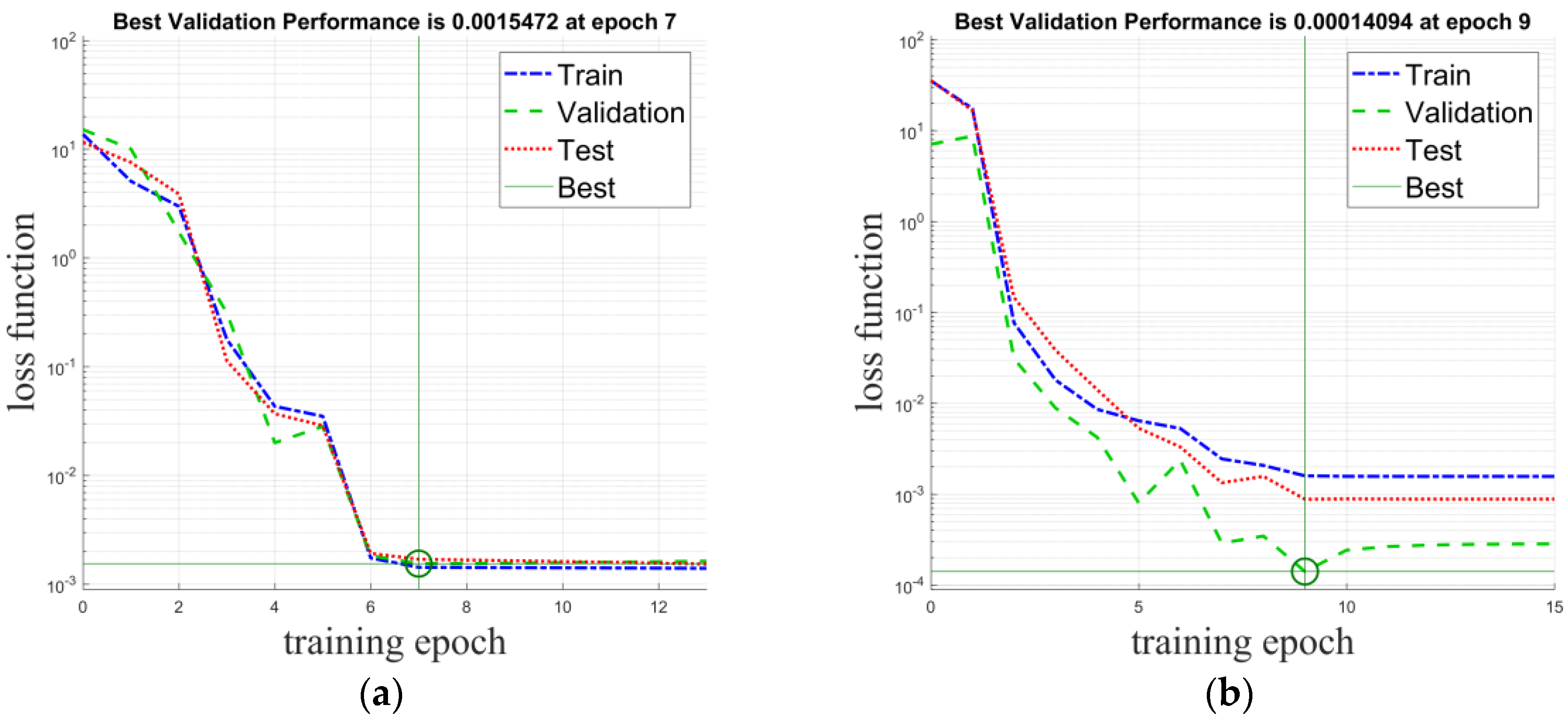
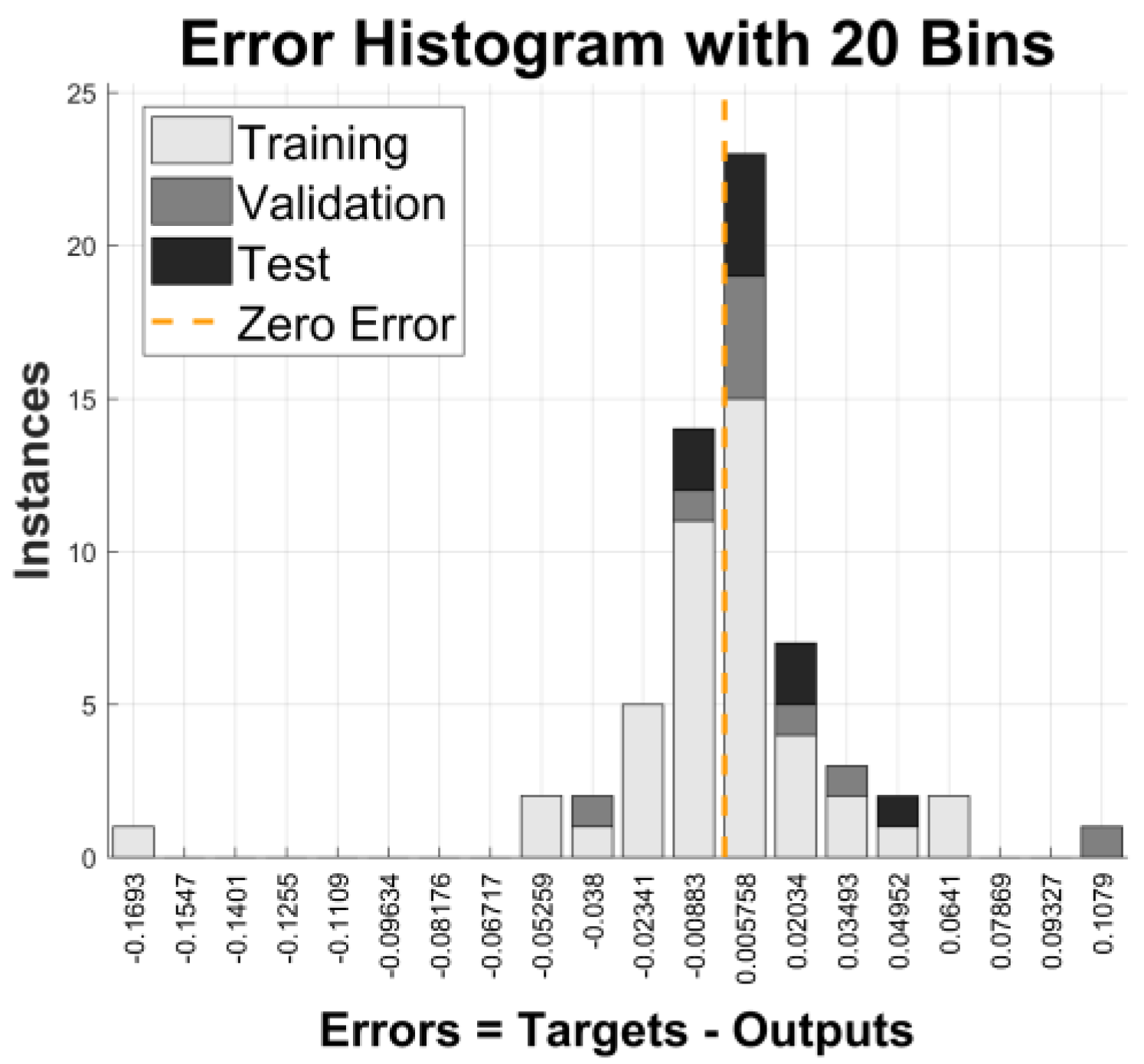
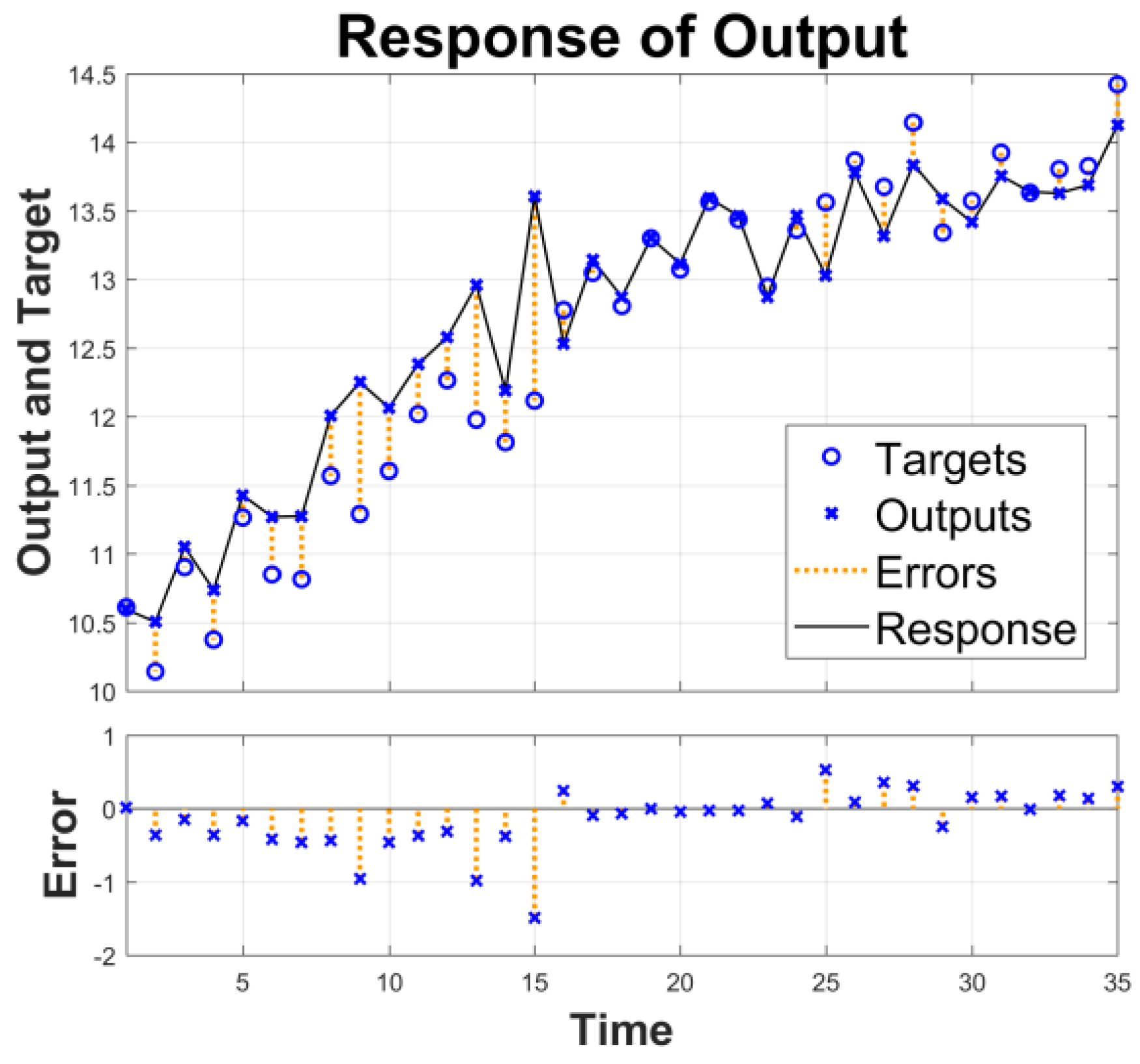
4.2. Prediction Performance
4.3. Ablation Studies
4.4. Robustness Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, Y.; Gui, G.; Gacanin, H.; Ohtsuki, T.; Dobre, O.; Poor, H. An efficient specific emitter identification method based on complex-valued neural networks and network compression. IEEE J. Sel. Areas Commun. 2021, 39, 2305–2317. [Google Scholar] [CrossRef]
- Wang, Y.; Gui, G.; Lin, Y.; Wu, H.-C.; Yuen, C.; Adachi, F. Few-Shot Specific Emitter Identification via Deep Metric Ensemble Learning. IEEE Internet Things J. 2022, 9, 24980–24994. [Google Scholar] [CrossRef]
- Zheng, Q.; Tian, X.; Yang, M.; Wu, Y.; Su, H. CLMIP: Cross-layer manifold invariance based pruning method of deep convolutional neural network for real-time road type recognition. Multidimens. Syst. Signal Process. 2021, 32, 239–262. [Google Scholar] [CrossRef]
- Li, Q.; Cheng, R.; Ge, H. Short-term vehicle speed prediction based on BiLSTM-GRU model considering driver heterogeneity. Phys. A Stat. Mech. Its Appl. 2023, 610, 128410. [Google Scholar] [CrossRef]
- Peng, Y.; Hou, C.; Zhang, Y.; Lin, Y.; Gui, G.; Gacanin, H.; Mao, S.; Adachi, F. Supervised Contrastive Learning for RFF Identification with Limited Samples. IEEE Internet Things J. 2023. Early access. [Google Scholar] [CrossRef]
- Pulvirenti, L.; Rolando, L.; Millo, F. Energy management system optimization based on an LSTM deep learning model using vehicle speed prediction. Transp. Eng. 2023, 11, 100160. [Google Scholar] [CrossRef]
- Zhang, Y.; Peng, Y.; Sun, J.; Gui, G.; Lin, Y.; Mao, S. GPU-Free Specific Emitter Identification Using Signal Feature Embedded Broad Learning. IEEE Internet Things J. 2023, 10, 13028–13039. [Google Scholar] [CrossRef]
- Fu, X.; Peng, Y.; Liu, Y.; Lin, Y.; Gui, G.; Gacanin, H.; Adachi, F. Semi-Supervised Specific Emitter Identification Method Using Metric-Adversarial Training. IEEE Internet Things J. 2023, 10, 10778–10789. [Google Scholar] [CrossRef]
- Zheng, Q.; Yang, M.; Zhang, Q.; Yang, J. A bilinear multi-scale convolutional neural network for fine-grained object classification. IAENG Int. J. Comput. Sci. 2018, 45, 340–352. [Google Scholar]
- Xu, T.; Xu, P.; Zhao, H.; Yang, C.; Peng, Y. Vehicle running attitude prediction model based on Artificial Neural Network-Parallel Connected (ANN-PL) in the single-vehicle collision. Adv. Eng. Softw. 2023, 175, 103356. [Google Scholar] [CrossRef]
- Yuan, H.; Li, G. A Survey of Traffic Prediction: From Spatio-Temporal Data to Intelligent Transportation. Data Sci. Eng. 2021, 6, 63–85. [Google Scholar] [CrossRef]
- Yin, X.; Wu, G.; Wei, J.; Shen, Y.; Qi, H.; Yin, B. Deep learning on traffic prediction: Methods, analysis, and future directions. IEEE Trans. Intell. Transp. Syst. 2021, 23, 4927–4943. [Google Scholar] [CrossRef]
- Tian, X.; Zheng, Q.; Jiang, N. An abnormal behavior detection method leveraging multi-modal data fusion and deep mining. IAENG Int. J. Appl. Math. 2021, 51, 92–99. [Google Scholar]
- Tedjopurnomo, D.A.; Bao, Z.; Zheng, B.; Choudhury, F.; Qin, A.K. A Survey on Modern Deep Neural Network for Traffic Prediction: Trends, Methods and Challenges. IEEE Trans. Knowl. Data Eng. 2020, 34, 1544–1561. [Google Scholar] [CrossRef]
- Boukerche, A.; Wang, J. Machine Learning-based traffic prediction models for Intelligent Transportation Systems. Comput. Netw. 2020, 181, 107530. [Google Scholar] [CrossRef]
- Zheng, Q.; Yang, M.; Tian, X.; Wang, X.; Wang, D. Rethinking the role of activation functions in deep convolutional neural networks for image classification. Eng. Lett. 2020, 28, 80–92. [Google Scholar]
- Zhang, Q.; Yang, M.; Zheng, Q.; Zhang, X. Segmentation of hand gesture based on dark channel prior in projector-camera system. In Proceedings of the IEEE/CIC International Conference on Communications in China (ICCC), Qingdao, China, 22–24 October 2017; pp. 1–6. [Google Scholar]
- Guo, K.; Hu, Y.; Qian, Z.; Liu, H.; Zhang, K.; Sun, Y.; Gao, J.; Yin, B. Optimized Graph Convolution Recurrent Neural Network for Traffic Prediction. IEEE Trans. Intell. Transp. Syst. 2020, 22, 1138–1149. [Google Scholar] [CrossRef]
- Zheng, Q.; Zhao, P.; Wang, H.; Elhanashi, A.; Saponara, S. Fine-Grained Modulation Classification Using Multi-Scale Radio Transformer With Dual-Channel Representation. IEEE Commun. Lett. 2022, 26, 1298–1302. [Google Scholar] [CrossRef]
- Zhao, L.; Song, Y.; Zhang, C.; Liu, Y.; Wang, P.; Lin, T.; Deng, M.; Li, H. T-GCN: A Temporal Graph Convolutional Network for Traffic Prediction. IEEE Trans. Intell. Transp. Syst. 2019, 21, 3848–3858. [Google Scholar] [CrossRef]
- Goyani, J.; Chaudhari, P.; Arkatkar, S.; Joshi, G.; Easa, S.M. Operating Speed Prediction Models by Vehicle Type on Two-Lane Rural Highways in Indian Hilly Terrains. J. Transp. Eng. Part A: Syst. 2022, 148, 04022001. [Google Scholar] [CrossRef]
- Niu, X.; Zhu, Y.; Zhang, X. DeepSense: A novel learning mechanism for traffic prediction with taxi GPS traces. In Proceedings of the IEEE Global Communications Conference, Austin, TX, USA, 8–12 December 2014; pp. 2745–2750. [Google Scholar]
- Kuang, L.; Hua, C.; Wu, J.; Yin, Y.; Gao, H. Traffic Volume Prediction Based on Multi-Sources GPS Trajectory Data by Temporal Convolutional Network. Mob. Netw. Appl. 2020, 25, 1405–1417. [Google Scholar] [CrossRef]
- Yang, H.; Zhang, X.; Li, Z.; Cui, J. Region-Level Traffic Prediction Based on Temporal Multi-Spatial Dependence Graph Convolutional Network from GPS Data. Remote. Sens. 2022, 14, 303. [Google Scholar] [CrossRef]
- Ma, X.; Dai, Z.; He, Z.; Ma, J.; Wang, Y.; Wang, Y. Learning Traffic as Images: A Deep Convolutional Neural Network for Large-Scale Transportation Network Speed Prediction. Sensors 2017, 17, 818. [Google Scholar] [CrossRef]
- Akolkar, H.; Ieng, S.H.; Benosman, R. Real-time high speed motion prediction using fast aperture-robust event-driven visual flow. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 44, 361–372. [Google Scholar] [CrossRef] [PubMed]
- Yu, B.; Chen, Y.; Bao, S. Quantifying visual road environment to establish a speeding prediction model: An examination using naturalistic driving data. Accid. Anal. Prev. 2019, 129, 289–298. [Google Scholar] [CrossRef] [PubMed]
- Guan, Q.; Bao, H.; Xuan, Z. The research of prediction model on intelligent vehicle based on driver’s perception. Clust. Comput. 2017, 20, 2967–2979. [Google Scholar] [CrossRef]
- Malaghan, V.; Pawar, D.S.; Dia, H. Speed prediction models for heavy passenger vehicles on rural highways based on an instrumented vehicle study. Transp. Lett. 2022, 14, 39–48. [Google Scholar] [CrossRef]
- Zheng, Q.; Zhao, P.; Li, Y.; Wang, H.; Yang, Y. Spectrum interference-based two-level data augmentation method in deep learning for automatic modulation classification. Neural Comput. Appl. 2021, 33, 7723–7745. [Google Scholar] [CrossRef]
- Mehdi, M.Z.; Kammoun, H.M.; Benayed, N.G.; Sellami, D.; Masmoudi, A.D. Entropy-based traffic flow labeling for CNN-based traffic congestion prediction from meta-parameters. IEEE Access 2022, 10, 16123–16133. [Google Scholar] [CrossRef]
- George, M.A.; Kamat, D.V.; Kurian, C.P. Electric vehicle speed tracking control using an ANFIS-based fractional order PID controller. J. King Saud Univ. Eng. Sci. 2022. early access. [Google Scholar] [CrossRef]
- Pan, Z.; Zhang, W.; Liang, Y.; Zhang, W.; Yu, Y.; Zhang, J.; Zheng, Y. Spatio-Temporal Meta Learning for Urban Traffic Prediction. IEEE Trans. Knowl. Data Eng. 2020, 34, 1462–1476. [Google Scholar] [CrossRef]
- Diao, C.; Zhang, D.; Liang, W.; Li, K.-C.; Hong, Y.; Gaudiot, J.-L. A Novel Spatial-Temporal Multi-Scale Alignment Graph Neural Network Security Model for Vehicles Prediction. IEEE Trans. Intell. Transp. Syst. 2022, 24, 904–914. [Google Scholar] [CrossRef]
- Tian, X.; Ruan, F.; Cheng, H.; Zheng, Q. A signal timing model for improving traffic condition based on active priority control strategy. Eng. Lett. 2020, 28, 235–242. [Google Scholar]
- Zheng, Q.; Tian, X.; Yang, M.; Wu, Y.; Su, H. PAC-Bayesian framework based drop-path method for 2D discriminative convolutional network pruning. Multidimens. Syst. Signal Process. 2020, 31, 793–827. [Google Scholar] [CrossRef]
- Tian, X.; Su, H.; Wang, F.; Zhang, K.; Zheng, Q. A electric vehicle charging station optimization model based on fully electrified forecasting method. Eng. Lett. 2019, 27, 731–743. [Google Scholar]
- Zheng, Q.; Tian, X.; Liu, S.; Yang, M.; Wang, H.; Yang, J. Static hand gesture recognition based on Gaussian mixture model and partial differential equation. IAENG Int. J. Comput. Sci. 2018, 45, 569–583. [Google Scholar]
- Shin, J.; Sunwoo, M. Vehicle Speed Prediction Using a Markov Chain With Speed Constraints. IEEE Trans. Intell. Transp. Syst. 2018, 20, 3201–3211. [Google Scholar] [CrossRef]
- Jiang, B.; Fei, Y. Vehicle Speed Prediction by Two-Level Data Driven Models in Vehicular Networks. IEEE Trans. Intell. Transp. Syst. 2016, 18, 1793–1801. [Google Scholar] [CrossRef]
- Jing, J.; Filev, D.; Kurt, A.; Ozatay, E.; Michelini, J.; Ozguner, U. Vehicle speed prediction using a cooperative method of fuzzy Markov model and auto-regressive model. In Proceedings of the IEEE Intelligent Vehicles Symposium (IV), Los Angeles, CA, USA, 11–14 June 2017; pp. 881–886. [Google Scholar]
- Li, Y.; Chen, M.; Lu, X.; Zhao, W. Research on optimized GA-SVM vehicle speed prediction model based on driver-vehicle-road-traffic system. Sci. China Technol. Sci. 2018, 61, 782–790. [Google Scholar] [CrossRef]
- Amini, M.R.; Feng, Y.; Yang, Z.; Kolmanovsky, I.; Sun, J. Long-term vehicle speed prediction via historical traffic data analysis for improved energy efficiency of connected electric vehicles. Transp. Res. Rec. 2020, 2674, 17–29. [Google Scholar] [CrossRef]
- Lv, F.; Wang, J.; Cui, B.; Yu, J.; Sun, J.; Zhang, J. An improved extreme gradient boosting approach to vehicle speed prediction for construction simulation of earthwork. Autom. Constr. 2020, 119, 103351. [Google Scholar] [CrossRef]
- Shin, J.; Kim, S.; Sunwoo, M.; Han, M. Ego-vehicle speed prediction using fuzzy Markov chain with speed constraints. In Proceedings of the IEEE Intelligent Vehicles Symposium (IV), Paris, France, 9–12 June 2019; pp. 2106–2112. [Google Scholar]
- Rasyidi, M.A.; Kim, J.; Ryu, K.R. Short-term prediction of vehicle speed on main city roads using the k-nearest neighbor algorithm. J. Intell. Inf. Syst. 2014, 20, 121–131. [Google Scholar] [CrossRef]
- Yan, M.; Li, M.; He, H.; Peng, J. Deep Learning for Vehicle Speed Prediction. Energy Procedia 2018, 152, 618–623. [Google Scholar] [CrossRef]
- Park, J.; Li, D.; Murphey, Y.L.; Kristinsson, J.; McGee, R.; Kuang, M.; Phillips, T. Real time vehicle speed prediction using a neural network traffic model. In Proceedings of the IEEE International Joint Conference on Neural Networks (IJCNN), San Jose, CA, USA, 31 July–5 August 2011; pp. 2991–2996. [Google Scholar]
- Lemieux, J.; Ma, Y. Vehicle speed prediction using deep learning. In Proceedings of the IEEE Vehicle Power and Propulsion Conference (VPPC), Montreal, QC, Canada, 19–22 October 2015; pp. 1–5. [Google Scholar]
- Li, Y.; Chen, M.; Zhao, W. Investigating long-term vehicle speed prediction based on BP-LSTM algorithms. IET Intell. Transp. Syst. 2019, 13, 1281–1290. [Google Scholar]
- Han, S.; Zhang, F.; Xi, J.; Ren, Y.; Xu, S. Short-term vehicle speed prediction based on convolutional bidirectional lstm networks. In Proceedings of the IEEE Intelligent Transportation Systems Conference (ITSC), Auckland, NZ, USA, 27–30 October 2019; pp. 4055–4060. [Google Scholar]
- Shih, C.-S.; Huang, P.-W.; Yen, E.-T.; Tsung, P.-K. Vehicle speed prediction with RNN and attention model under multiple scenarios. In Proceedings of the IEEE Intelligent Transportation Systems Conference (ITSC), Auckland, NZ, USA, 27–30 October 2019; pp. 369–375. [Google Scholar]
- Madhan, E.S.; Neelakandan, S.; Annamalai, R. A Novel Approach for Vehicle Type Classification and Speed Prediction Using Deep Learning. J. Comput. Theor. Nanosci. 2020, 17, 2237–2242. [Google Scholar] [CrossRef]
- Niu, K.; Zhang, H.; Zhou, T.; Cheng, C.; Wang, C. A Novel Spatio-Temporal Model for City-Scale Traffic Speed Prediction. IEEE Access 2019, 7, 30050–30057. [Google Scholar] [CrossRef]
- Zhang, Y.; Huang, Z.; Zhang, C.; Lv, C.; Deng, C.; Hao, D.; Chen, J.; Ran, H. Improved Short-Term Speed Prediction Using Spatiotemporal-Vision-Based Deep Neural Network for Intelligent Fuel Cell Vehicles. IEEE Trans. Ind. Informatics 2020, 17, 6004–6013. [Google Scholar] [CrossRef]
- Li, Y.; Wu, C.; Yoshinaga, T. Vehicle speed prediction with convolutional neural networks for ITS. In Proceedings of the IEEE/CIC International Conference on Communications in China (ICCC Workshops), Chongqing, China, 9–11 August 2020; pp. 41–46. [Google Scholar]
- Jeong, M.-H.; Lee, T.-Y.; Jeon, S.-B.; Youm, M. Highway Speed Prediction Using Gated Recurrent Unit Neural Networks. Appl. Sci. 2021, 11, 3059. [Google Scholar] [CrossRef]
- Zhao, J.; Gao, Y.; Bai, Z.; Wang, H.; Lu, S. Traffic Speed Prediction Under Non-Recurrent Congestion: Based on LSTM Method and BeiDou Navigation Satellite System Data. IEEE Intell. Transp. Syst. Mag. 2019, 11, 70–81. [Google Scholar] [CrossRef]
- Maczyński, A.; Brzozowski, K.; Ryguła, A. Analysis and Prediction of Vehicles Speed in Free-Flow Traffic. Transp. Telecommun. J. 2021, 22, 266–277. [Google Scholar] [CrossRef]
- Zhang, A.; Liu, Q.; Zhang, T. Spatial–temporal attention fusion for traffic speed prediction. Soft Comput. 2022, 26, 695–707. [Google Scholar] [CrossRef]
- Lin, T.; Horne, B.; Tino, P.; Giles, C. Learning long-term dependencies in NARX recurrent neural networks. IEEE Trans. Neural Netw. 1996, 7, 1329–1338. [Google Scholar] [PubMed]



| Hyper-Parameters | Values | |
|---|---|---|
| EMD | decomposition times I | 6 |
| decomposition series J | 5 | |
| Informer | step size | 0.01 |
| batch size | 16 | |
| L2-regularization | 0.0005 | |
| dropout rate | 0.5 | |
| Methods | AE | MSE | Speed (s) |
|---|---|---|---|
| XGBoost | 0.144 | 0.090 | 0.20 |
| Markov | 0.157 | 0.097 | 0.14 |
| NARX | 0.133 | 0.057 | 0.83 |
| LSTM | 0.118 | 0.039 | 1.30 |
| 1D CNN | 0.127 | 0.052 | 0.22 |
| CNN-LSTM | 0.113 | 0.035 | 1.78 |
| EMD-Informer | 0.094 | 0.021 | 0.96 |
| Input Types | AE | MSE | Speed (s) |
|---|---|---|---|
| Time series input | 0.133 | 0.069 | 0.15 |
| Single IMF input | 0.107 | 0.026 | 0.24 |
| 3D IMF matrix input | 0.094 | 0.021 | 0.96 |
| Hyper-Parameters | AE | MSE | |
|---|---|---|---|
| Types | Values | ||
| Decomposition times I | 3 | 0.112 | 0.034 |
| 4 | 0.110 | 0.032 | |
| 5 | 0.103 | 0.027 | |
| 6 | 0.094 | 0.021 | |
| Decomposition series J | 2 | 0.104 | 0.024 |
| 3 | 0.101 | 0.023 | |
| 4 | 0.096 | 0.021 | |
| 5 | 0.094 | 0.021 | |
| Step size | 0.001 | 0.103 | 0.024 |
| 0.005 | 0.092 | 0.019 | |
| 0.01 | 0.094 | 0.021 | |
| 0.05 | 0.128 | 0.060 | |
| Batch size | 8 | 0.113 | 0.034 |
| 16 | 0.094 | 0.021 | |
| 32 | 0.098 | 0.022 | |
| 64 | 0.090 | 0.017 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, X.; Zheng, Q.; Yu, Z.; Yang, M.; Ding, Y.; Elhanashi, A.; Saponara, S.; Kpalma, K. A Real-Time Vehicle Speed Prediction Method Based on a Lightweight Informer Driven by Big Temporal Data. Big Data Cogn. Comput. 2023, 7, 131. https://doi.org/10.3390/bdcc7030131
Tian X, Zheng Q, Yu Z, Yang M, Ding Y, Elhanashi A, Saponara S, Kpalma K. A Real-Time Vehicle Speed Prediction Method Based on a Lightweight Informer Driven by Big Temporal Data. Big Data and Cognitive Computing. 2023; 7(3):131. https://doi.org/10.3390/bdcc7030131
Chicago/Turabian StyleTian, Xinyu, Qinghe Zheng, Zhiguo Yu, Mingqiang Yang, Yao Ding, Abdussalam Elhanashi, Sergio Saponara, and Kidiyo Kpalma. 2023. "A Real-Time Vehicle Speed Prediction Method Based on a Lightweight Informer Driven by Big Temporal Data" Big Data and Cognitive Computing 7, no. 3: 131. https://doi.org/10.3390/bdcc7030131
APA StyleTian, X., Zheng, Q., Yu, Z., Yang, M., Ding, Y., Elhanashi, A., Saponara, S., & Kpalma, K. (2023). A Real-Time Vehicle Speed Prediction Method Based on a Lightweight Informer Driven by Big Temporal Data. Big Data and Cognitive Computing, 7(3), 131. https://doi.org/10.3390/bdcc7030131











