Digital Twin Four-Dimension Fusion Modeling Method Design and Application to the Discrete Manufacturing Line

Abstract

With the development of new-generation information technologies, such as big data and artificial intelligence, digital twins have become a key technology in intelligent manufacturing. The introduction of digital twin technology has addressed many problems in discrete manufacturing lines, including low visualization and difficult cyber–physical integration. However, the application of digital twin technology to discrete manufacturing lines still faces problems of low modeling accuracy, response delay, and insufficient production line control accuracy. Therefore, this paper proposes a digital twin four-dimension fusion modeling method to solve the above problems. First, a digital twin system architecture for a discrete manufacturing production line is designed. Then, the information control dimension is integrated into traditional digital twin modeling methods. Further, a digital twin geometry–physics–behavior–information control four-dimension fusion modeling method is proposed. This method can describe the geometric and physical characteristics of a physical entity and map its behavior mechanism. More importantly, it reveals the control logic and virtual–real mapping rules, which provides important support for the virtual–real intelligent mutual control. Finally, the feasibility and effectiveness of the proposed method are verified by experiments on a fidget spinner discrete manufacturing line, and a digital twin operation and maintenance management system is developed. The results presented in this study could provide ideas for the digital transformation of discrete manufacturing enterprises.

1. Introduction

With the deep integration of new-generation information technology and the manufacturing industry, intelligent manufacturing with cyber–physical integration as a core has become the dominant paradigm in the future manufacturing industry [1,2,3]. Discrete manufacturing is characterized by multiple varieties and small batches, and customization has been the general trend in this field [4,5,6]. However, due to a lack of transparent and efficient production line control means, current discrete manufacturing production faces certain problems, such as a low visualization degree, an unbalanced production cycle, and untimely decision making, and it is also difficult to meet the requirements for production flexibility [7]. Therefore, discrete manufacturing production lines urgently need to be transformed toward a more digital, networked, and intelligent direction. As an enabling technology and one of the key means to practice the concept of intelligent manufacturing [8,9,10], digital twin technology can replicate the behavior and state of physical entities in a virtual environment. In addition, it can help to identify potential problems and improve production line performance and production efficiency [11]. Moreover, it can achieve the symbiosis of physical entities and virtual environments to a certain extent [12,13].

Every high-fidelity virtual model is a cornerstone of the digital twin [14] and an important prerequisite for realizing the function of the digital twin [15]. Bordeleau et al. [16] reviewed various model-driven engineering techniques, tools, and methods in digital twin modeling to address the challenges in model development, maintenance, and evolution of the digital twin modeling process. Malik et al. [17] proposed a digital twin modeling method for a full life cycle of a complex system in a human–machine collaborative intelligent factory and applied the digital twin virtual–real fusion method to the system design, manufacturing, and operation. Tao et al. [18] defined the construction criteria and proposed a theoretical system for digital twin modeling. They also analyzed the construction of a digital twin workshop model. Leng et al. [19] proposed a digital twin-driven automated production line modeling and rapid reconfiguration method, which can effectively improve model reusability. Hu et al. [20] proposed a digital twin geometry–mechanism–data high-fidelity modeling method for the spinning-forming manufacturing process of thin-walled parts and introduced a digital twin model fidelity evaluation method. Zhang et al. [21] proposed a digital twin stamping production line modeling method based on physical data, where the information interaction between physical and digital spaces of the stamping production line was realized by constructing a physical data model and a digital information model.

Although there have been many studies on digital twin modeling, there has been less research on a virtual–real mapping strategy of control logic in a digital twin modeling method for discrete manufacturing lines. In addition, discrete manufacturing digital twin modeling still faces certain challenges, such as insufficient precision and characterization of multi-dimensional and multi-domain characteristics of physical objects. Therefore, it is necessary to establish a high-fidelity virtual model of multi-dimension fusion and improve the precision of production line regulation to realize a real and complete mirror image of physical and digital twin spaces.

The main contributions in this study can be summarized as follows:

• A digital twin system architecture for discrete manufacturing production lines is proposed to address the digital twin requirements and characteristics of discrete manufacturing production lines;
• A digital twin geometry-physics-behavior-information control four-dimension fusion modeling method is developed. Compared to the traditional modeling methods, this method reveals the control logic and virtual–real mapping rules of physical entities and virtual models. Furthermore, it creates necessary conditions for the virtual–real intelligent mutual control of a production line;
• The feasibility and effectiveness of the proposed method are verified through examples. A digital twin operation and maintenance management system is developed, which can provide ideas for the digital transformation of discrete manufacturing enterprises.

The rest of this paper is structured as follows. Section 2 presents a digital twin system architecture for a discrete manufacturing production line. Section 3 proposes a digital twin geometry–physics–behavior–information control four-dimension fusion modeling method. Section 4 presents a specific application case of the proposed method. Section 5 concludes the paper.

2. Digital Twin Architecture for a Discrete Manufacturing Line

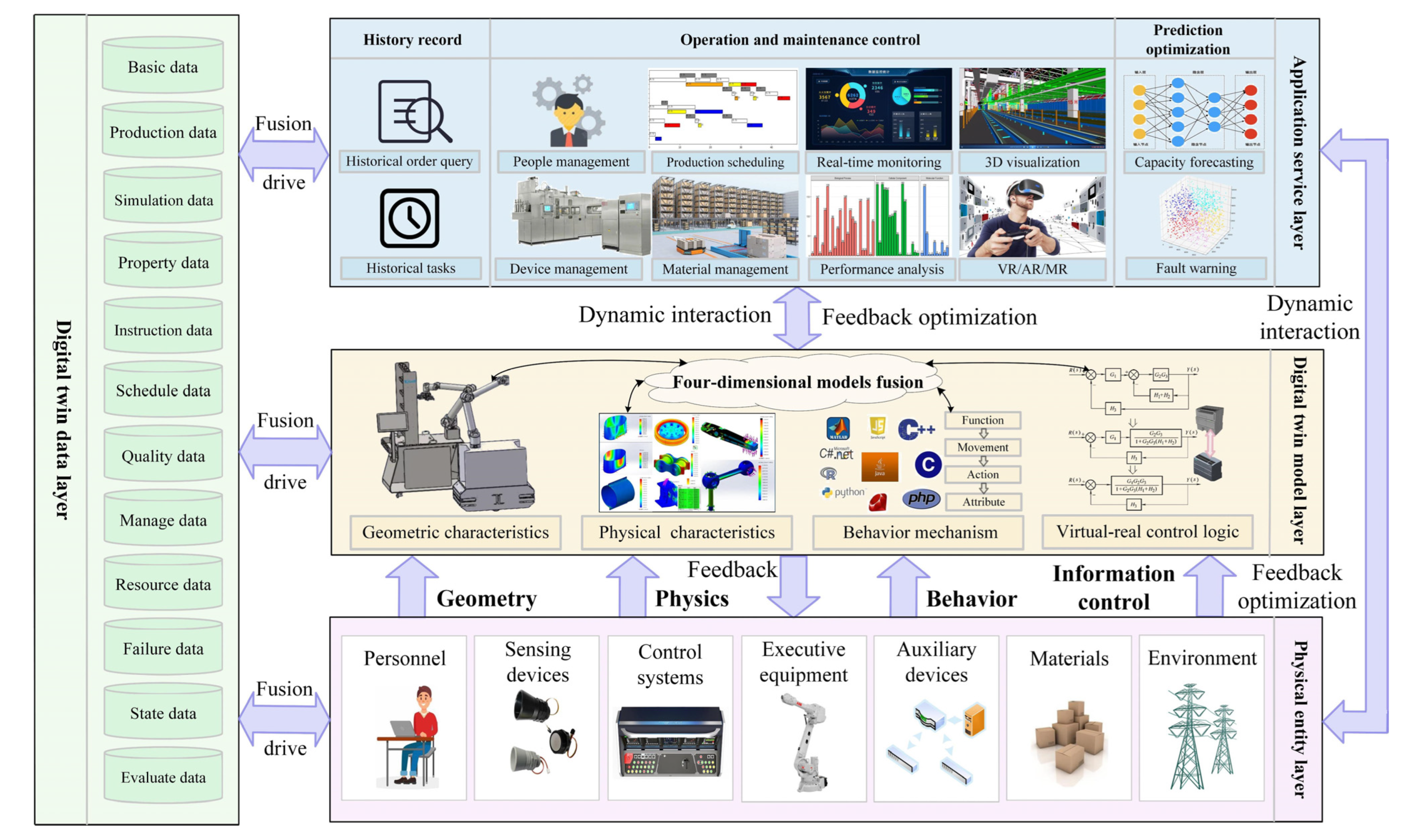
Referring to the five-dimensional conceptual digital twin model proposed by Tao et al. [22], this paper designs a digital twin system architecture for a discrete manufacturing production line. This architecture addresses the digital twin requirements and characteristics of discrete manufacturing production lines, as shown in Figure 1. Specifically, the proposed architecture includes a physical entity layer, a digital twin model layer, a digital twin data layer, an application service layer, and a data transmission mechanism between layers. The main structural parts of the proposed architecture are presented in detail in the following paragraphs.

The physical entity layer represents a collection of all elements of the production process in the real physical world. It mainly includes personnel, sensing devices, control systems, executive equipment, auxiliary devices, materials, and an environment. Among them, the sensing devices, control systems, and executive equipment together constitute the main facilities of the discrete manufacturing line. The auxiliary devices mainly include network communication devices and displays. The environment mainly includes energy supply, temperature, and humidity. The physical layer is the basis not only for normal production activities but also for the construction and operation of the other layers.

The digital twin model layer represents a digital mirror image of the physical entity layer. Namely, by building a digital twin geometry model, physics model, behavior model, and information control model, and then conducting multi-disciplinary and multi-scale fusion between the same-dimensional models and different-dimensional models, it is possible to achieve an exact depiction of the physical entity layer.

The application service layer is supported by the digital twin model layer and the digital twin data layer, thus allowing the services of historical retrospect, operation and maintenance management, and forecast optimization. Through the development and combination of real-time monitoring, performance analysis, and other functional modules, the needs of personalized management are met. Virtual reality (VR)/augmented reality (AR)/mixed reality (MR) technologies can also be used to realize human–machine interaction and multi-directional immersive participation in production management and control [23,24]. This layer provides a platform for intelligent control of a production line, which is an objective embodiment of twin data management and application.

The digital twin data layer is the data center of the physical entity layer, digital twin model layer, and application service layer. This layer includes not only physical entity data, digital twin model data, and application service data, but also fusion-derived data. The data cover the historical state, real-time dynamics, and predictive optimization schemes of the physical entity. In this layer, the information storage, processing, sharing, and value-added functions in a digital twin system are realized.

As an information interaction bridge between layers, a data transmission mechanism provides data flow between layers, ensures real-time transmission of information, and realizes interconnection between layers. It also provides the necessary prerequisites for the optimal control of a real production process, the dynamic correction of a digital twin model, and the digitization of application services.

3. Digital Twin Modeling for a Discrete Manufacturing Line

A digital twin model represents a high-fidelity digital image of a physical entity [25,26], which plays an important role in expressing a physical entity’s geometric and physical characteristics, describing its behavioral logic, revealing control rules, and monitoring the operational status. Aiming to construct a high-fidelity digital twin virtual model for a discrete manufacturing production line, this study proposes a digital twin geometry–physics–behavior–information control four-dimension fusion modeling method, which enables accurate mapping of physical entities in a virtual space.

A digital twin model can be defined as follows:

$$\mathrm{VM}=\left\{\mathrm{G}\mathrm{M},\mathrm{P}\mathrm{M},\mathrm{B}\mathrm{M},\mathrm{I}\mathrm{C}\mathrm{M}\right\}$$

(1)

where GM denotes the geometry model, PM is the physics model, BM represents the behavior model, and ICM is the information control model.

The geometry model is used to describe the geometric attributes of physical entities, such as the size, shape, and structure of each component. In this way, the visual expression of the positional relationship between components and assembly attributes can be obtained.

The physics model is used to describe the static state, mechanical evolution, and multi-physics coupling attributes of physical entities in a human–equipment–material–environment system. In addition, this model expresses the internal mechanism of the evolution of multi-discipline and multi-physical quantities.

The behavior model is used to map the behavioral characteristics and mechanisms of different physical objects, as well as to reveal the internal logic between various moving parts.

Aiming at realizing the mapping of digital twin models to physical entities with more dimensions and higher fidelity, this paper develops the information control model based on the aforementioned dimensional model, which is used to describe the control logic of physical entities and digital twin models, establish virtual–real interaction channels, and reveal virtual–real mapping rules.

3.1. Geometry Model Construction

In this study, a geometry model is constructed from a multi-level perspective, considering the part level, component level, standalone equipment level, and multi-machine system level. The specific definition of the geometry model is as follows:

$$\mathrm{GM}=\left\{\mathrm{P}\mathrm{G}\mathrm{M},\mathrm{C}\mathrm{G}\mathrm{M},\mathrm{E}\mathrm{G}\mathrm{M},\mathrm{S}\mathrm{G}\mathrm{M}\right\}$$

(2)

where PGM refers to the geometry model at the part level, CGM indicates the geometry model at the component level, EGM is the geometry model at the standalone equipment level, and SGM represents the geometry model at the multi-machine system level.

The establishment of geometric attributes is the key task in the geometry model construction process. The geometric attributes of each level are defined in

Table 1. Definition table of geometric attributes at each level.

Level	Geometric Attribute Sets	Main Attributes
Part level	Shape attribute (SA)	Dimensions, angles, radians, curvature
	Location attribute (LA)	Hole-position relation, sinking-surface position, slot position, wrench space, coordinate origin
	Transition attribute (TRA)	Round chamfer, transition plane, transition bevel, transition arc
	Manufacturing technology attribute (MTA)	Turning, milling, planing, grinding, drilling, boring
	Dimensional tolerance attribute (DTA)	Basic size, limit size
	Geometric tolerance attribute (GTA)	Flatness, cylindricity, coaxiality
Component level	Location attribute (LA)	Contact, embedding, separation
	Hierarchical relationship attribute (HRA)	Parent–child relationship
	Assembly attribute (AA)	Slip, concentricity, clearance fit, interference fit
	Connection technology attribute (CTA)	Screw connection, key connection, pin connection, glue connection
	Motion type attribute (MTA)	Translation, rotation
Standalone equipment level	Location attribute (LA)	Contact, embedding, separation
	Assembly attribute (AA)	Slip, concentricity, clearance fit, interference fit
	Hierarchical relationship attribute (HRA)	Parent–child relationship
Multi-machine system level	Space attribute (SPA)	Coordinate origin, position, posture
	Function attribute (FA)	Processing, assembly, packaging, loading, unloading

, and the geometry models of the four levels can be expressed as follows:

$$\mathrm{PGM}=\left\{\mathrm{S}\mathrm{A},\mathrm{L}\mathrm{A},\mathrm{T}\mathrm{R}\mathrm{A},\mathrm{M}\mathrm{T}\mathrm{A},\mathrm{D}\mathrm{T}\mathrm{A},\mathrm{G}\mathrm{T}\mathrm{A}\right\}$$

(3)

$$\mathrm{CGM}=\left\{\mathrm{L}\mathrm{A},\mathrm{H}\mathrm{R}\mathrm{A},\mathrm{A}\mathrm{A},\mathrm{C}\mathrm{T}\mathrm{A},\mathrm{M}\mathrm{T}\mathrm{A}\right\}$$

(4)

$$\mathrm{EGM}=\left\{\mathrm{L}\mathrm{A},\mathrm{A}\mathrm{A},\mathrm{H}\mathrm{R}\mathrm{A}\right\}$$

(5)

$$\mathrm{SGM}=\left\{\mathrm{S}\mathrm{P}\mathrm{A},\mathrm{F}\mathrm{A}\right\}$$

(6)

where SA is the shape attribute; LA denotes the location attribute; TRA represents the transition attribute; MTA is the manufacturing technology attribute; DTA is the dimensional tolerance attribute; GTA denotes the geometric tolerance attribute; HRA is the hierarchical relationship attribute; AA represents the assembly attribute; CTA denotes the connection technology attribute; MTA is the motion type attribute; SPA represents the space attribute; and FA is the function attribute.

The construction method of the digital twin geometry model of a discrete manufacturing production line is presented in Figure 2. Considering the overall function of a discrete manufacturing production line, the specific function of each of the sub-modules is analyzed from the aspects of part, component, and standalone equipment levels. Based on the above geometric attribute sets, the required geometric attributes are analyzed in detail. With the help of 3D modeling software, including SolidWorks, Creo, and CATIA, the corresponding characteristics are obtained by stretching, rotating, cutting, and other operations. Then each sub-module is imported from the child level to the parent level in turn, the concentric, coincidence and other assembly relations are set, and the nested relationship between multiple modules are set. Finally, simulation is carried out to realize the geometric and topological feature mapping of the part, component, and standalone equipment level. Further, a multi-machine system-level geometry model is constructed by integrating the geometry models of the standalone equipment level. Based on the real production and logistics relationships of discrete manufacturing lines, the origin position is converted, and spatial constraints such as size limits are added to build a multi-machine system-level geometry model. The mapping of physical entities’ spatial and functional attributes is completed. In addition, lightweight model processing facilitates fast parsing of model files [27,28]. Finally, the file format is converted to a cross-platform common intermediate format, such as the STEP format.

Before using the intermediate format to construct a digital twin physics model, preprocessing should be performed. The layout is reconstructed based on the optimization of manufacturing resource allocation. Specifically, the optimal layout scheme is designed based on the key factors affecting production efficiencies, such as facility layout, process planning, personnel allocation, and material flow, to ensure the collaborative and efficient operation of all manufacturing resources. After that, the assembly is split into components according to the hierarchy. Finally, all components are colored and rendered. Compared with the model without preprocessing, the preprocessed model can more accurately express the spatial position information and color information of physical entities, which is closer to the real production scene.

Using the above method, the digital twin geometry model for a discrete manufacturing production line is constructed, which provides intuitive 3D visual representation of physical entities in terms of size, shape, structure, and topological relationships.

3.2. Physics Model Construction

The digital twin physics model of a discrete manufacturing production line is composed of a human physics model, an equipment physics model, a material physics model, and an environment physics model, which can be expressed as follows:

$$\mathrm{PM}=\left\{\mathrm{H}\mathrm{P}\mathrm{M},\mathrm{E}\mathrm{Q}\mathrm{P}\mathrm{M},\mathrm{M}\mathrm{P}\mathrm{M},\mathrm{E}\mathrm{N}\mathrm{P}\mathrm{M}\right\}$$

(7)

where HPM stands for the human physics model; EQPM is for the equipment physics model; MPM denotes the material physics model; and ENPM represents the environment physics model.

The digital twin physics model contains many elements and attributes, and the physical attribute mapping represents a core task of the physics model construction. A sub-physics model of a discrete manufacturing production line can be formalized as follows:

$$\mathrm{HPM}=\left\{\mathrm{N}\mathrm{A},\mathrm{W}\mathrm{H}\mathrm{A},\mathrm{W}\mathrm{R}\mathrm{A},\mathrm{L}\mathrm{B}\mathrm{A}\right\}$$

(8)

$$\mathrm{DPM}=\left\{\mathrm{I}\mathrm{A},\mathrm{D}\mathrm{S}\mathrm{A}\right\}=\left\{\left\{\mathrm{M}\mathrm{A},\mathrm{S}\mathrm{A},\mathrm{W}\mathrm{A},\mathrm{I}\mathrm{N}\mathrm{A}\right\},\left\{\mathrm{M}\mathrm{E}\mathrm{A},\mathrm{M}\mathrm{P}\mathrm{C}\mathrm{A}\right\}\right\}$$

(9)

$$\mathrm{MPM}=\left\{\mathrm{I}\mathrm{A},\mathrm{Q}\mathrm{N}\mathrm{A},\mathrm{Q}\mathrm{L}\mathrm{A}\right\}=\left\{\left\{\mathrm{M}\mathrm{A},\mathrm{S}\mathrm{A},\mathrm{W}\mathrm{A},\mathrm{I}\mathrm{N}\mathrm{A}\right\},\mathrm{Q}\mathrm{N}\mathrm{A},\mathrm{Q}\mathrm{L}\mathrm{A}\right\}$$

(10)

$$\mathrm{EPM}=\left\{\mathrm{L}\mathrm{O}\mathrm{A},\mathrm{T}\mathrm{A},\mathrm{H}\mathrm{A},\mathrm{E}\mathrm{A}\right\}$$

(11)

where NA represents the number attribute; WHA is the working hour attribute; WRA denotes the working range attribute; LBA is the load bearing attribute; IA represents the intrinsic attribute; DSA is the dynamic attribute; MA denotes the material attribute; SA is the surface attribute; WA denotes the weight attribute; INA is the inertia attribute; MEA stands for the mechanical evolution attribute; MPCA is the multi-physics coupling attribute; QNA denotes the quantity attribute; QLA represents the quality attribute; LOA is the layout attribute; TA stands for the temperature attribute; HA is the humidity attribute; and EA denotes the energy attribute.

The entity-relationship (E-R) diagram of a digital twin physics model is established to describe the attribute data of each category intuitively, as shown in Figure 3. This model aims at human–equipment–material–environment integration.

In the characterization of the above-mentioned attributes, the most critical task is to describe the static intrinsic attributes and dynamic attributes of key equipment. Intrinsic attributes reflect the most basic characteristics of physical entities, including material information and surface information, whereas dynamic attributes reveal the laws of mechanical evolution and multi-physics coupling. The mechanical evolution attribute characterizes the changes in physical quantities during the mechanical evolution processes, such as stacking, collision, and falling. The multi-physics coupling attribute covers complex scenarios such as electromagnetic heat, electric liquid force, and heat force. In the coupling evolution process of multi-field, multi-disciplinary, and multi-physical quantities, the changing laws of each physical quantity can be characterized.

First, the key data on the above-mentioned attributes are collected and preprocessed. Then, the mathematical formula derivation, finite element simulation calculation, secondary development of a physical engine software platform, and other modeling and analysis methods are used. In this way, the integration of various elements of the digital twin physics model is promoted, and the inherent laws of physical phenomena can be deduced. Finally, a digital twin physics model integrating human–equipment–material–environment is developed, which can perform the simulation and description of static and dynamic, and macro and micro scales of the physical entity.

3.3. Behavior Model Construction

The fidelity of the behavior model of a digital twin is a key indicator of the digital twin model. The digital twin behavior model can be formally described as follows:

$$\mathrm{BM}=\left\{\mathrm{B}\mathrm{A}\mathrm{T},\mathrm{B}\mathrm{A}\mathrm{L},\mathrm{B}\mathrm{F}\right\}$$

(12)

where BAT is the behavior attribute, BAL denotes the behavior algorithm, and BF represents the behavior function.

The core of a digital twin behavior model is the behavior function. The construction process of the behavior function includes behavior attribute configuration and behavior algorithm compilation. Particularly, the behavior attributes are configured according to the function–motion–action derivation result of each component of a physical entity. Then, a behavior algorithm is developed according to the behavior logic of a specific discrete manufacturing production line. Further, the behavior attribute and behavior algorithm are encapsulated as a behavior function. In addition, the processes of a discrete manufacturing production line are arranged in series to form a process flow. The process flow drives the control system to call the corresponding behavior function at a specific time node. The construction process of a digital twin behavior model of a discrete manufacturing production line is presented in Figure 4.

3.3.1. Behavior Attribute Configuration

In this study, the idea of the function–motion–action (FMA) theory [29] is introduced into the digital twin behavior model design, and a construction method of the function–motion–action–attribute (FMAA) digital twin behavior attribute is proposed. Namely, based on the function of each component of the physical entity, the motion and meta-action are decomposed, in turn, and the corresponding behavior attributes are deduced and configured.

Considering the commonly used industrial robots in discrete manufacturing scenarios, it can be concluded that industrial robots have multiple functions, such as picking up and placing workpieces. However, performing these functions requires the coordination of multiple joints and motions. For instance, the waist joint rotation motion is composed of the waist motor drive, harmonic reducer rotation, and other elements. The meta-actions reflect the spatial attributes of physical entities, such as displacement, attitude transformation, and dynamic behavior attributes (e.g., velocity and acceleration), but they are restricted by certain constraint attributes, such as travel singularity. After modeling and characterization of the above-mentioned behavior attributes, the basic behavior characteristics and rules of physical entities can be accurately mapped to a virtual space.

3.3.2. Behavior Algorithm Development

A digital twin behavior model of a discrete manufacturing production line is based on various mathematical methods and artificial intelligence algorithms. For instance, using the Denavit–Hartenberg (D–H) parameter method, expression (13) is derived, and then the forward-inverse kinematics algorithm is used to model and solve the joint attitude transformation of industrial robots.

$${}_i{}^{i-1}T=\left[\begin{array}{cccc}\cos {\theta }_i& -\sin {\theta }_i& 0& a_{i-1}\\ \sin {\theta }_i\cos {\alpha }_{i-1}& \cos {\theta }_i\cos {\alpha }_{i-1}& -\sin {\alpha }_{i-1}& -\sin {\alpha }_{i-1}{d}_i\\ \sin {\theta }_i\sin {\alpha }_{i-1}& \cos {\theta }_i\sin {\alpha }_{i-1}& \cos {\alpha }_{i-1}& \cos {\alpha }_{i-1}{d}_i\\ 0& 0& 0& 1\end{array}\right]$$

(13)

In (13), ${}_i{}^{i-1}T$ represents the pose transformation matrix of the connecting rod pair; $a_{i-1}$ is the length of the connecting rod; ${\alpha }_{i-1}$ denotes the torque of the connecting rod; $d_i$ is the offset of the connecting rod; ${\theta }_i$ represents the joint rotation angle.

For another example, by using the interpolation method to simulate the generation of linear trajectories in the Cartesian space of a five-axis machining center, the following expression is obtained:

$$\left\{\begin{array}{c}{x}_i=x_s+i\times [(x_e-x_s)÷n]\\ y_i=y_s+i\times [(y_e-y_s)÷n]\\ z_i=z_s+i\times [(z_e-z_s)÷n]\\ {\alpha }_i={\alpha }_s+i\times [({\alpha }_e-{\alpha }_s)÷n]\\ {\beta }_i={\beta }_s+i\times [({\beta }_e-{\beta }_s)÷n]\end{array}\right.$$

(14)

where $i$ denotes the number of current interpolation segments, and $i=0,1,\cdots ,n$; $n$ represents the total number of interpolation segments; $(x_i,y_i,z_i,{\alpha }_i,{\beta }_i)$ denotes the pose of the tool center point in an interpolation cycle; $(x_s,y_s,z_s,{\alpha }_s,{\beta }_s)$ represents the pose of the interpolation’s starting point; $(x_e,y_e,z_e,{\alpha }_e,{\beta }_e)$ is the pose of the interpolation’s end point.

Furthermore, an autonomous-path-planning algorithm is used to enable the autonomous navigation and intelligent obstacle avoidance of virtual AGVs. The depth-first search algorithm is employed to traverse the parent–child nodes and promote the dependency switch of the workpieces in different scenarios. In addition, by continuously adjusting the algorithm parameters to promote the iteration of the model, thus optimizing the model, the fidelity and maturity of the model are improved [30]. Finally, behavioral algorithms integrate behavioral attributes and encapsulate them into behavioral functions that can be called by the control system to ensure flexible and changeable process flows.

3.3.3. Behavior Function Call

The process flow of discrete manufacturing objects should be planned reasonably. The processes are organized and arranged according to the relationship of series, parallel, and stratification, and the interdependence between the work steps is analyzed correctly. Finally, an appropriate production rhythm is determined, and a process flow is defined so as to meet the requirements for process flexibility. It should be noted that each work step triggers a call to the behavior function in the behavior model. In this way, a digital twin model can simulate the actual production process of a physical production line more accurately and in real-time, which is beneficial to optimizing the production rhythm and realizing auxiliary decision making.

According to the above-mentioned behavior model construction method, the moving parts of a production line of the digital twin model can perform specific actions according to the set mode and program. This can not only map the behavior characteristics of a physical object but also reveal the operating mechanism and internal logic of a physical production line. Therefore, a digital twin production line can accurately simulate the whole process of a physical production line.

3.4. Information Control Model Construction

In this study, a digital twin information control model is constructed to realize an accurate simulation of the operational rules, control logic, and dynamic production process of physical entities, as shown in Figure 5.

The digital twin information model mainly includes three parts: physical entity control logic analysis, virtual model control mechanism reappearance, and virtual–real interaction channel construction, which can be expressed as follows:

$$\mathrm{ICM}=\left\{\mathrm{P}\mathrm{C}\mathrm{L},\mathrm{V}\mathrm{C}\mathrm{M},\mathrm{V}\mathrm{R}\mathrm{C}\right\}$$

(15)

where PCL represents the physical entity control logic, VCM is the virtual model control mechanism, and VRC denotes the virtual–real interaction channel.

3.4.1. Physical Entity Control Logic Analysis

Based on the aforementioned process flow and actual production needs, the control logic of a discrete manufacturing production line is analyzed in this study. Particularly, the data transmission mechanism and control strategy of each component module in the hardware system, such as the information acquisition module, execution module, and auxiliary module, are deeply analyzed to establish a physical entity control system framework. Next, the function and performance of the control system are analyzed, and through continuous debugging and optimization, an integrated control mechanism of a physical production line is established. Then, the physical production line can produce the required workpieces in an orderly manner, according to the established logic and rules.

The PLC performs data interaction with the upper computer via a communication protocol, such as TCP/IP. It performs data transmission and communication with each PLC slave station using a communication protocol, such as Modbus. After the upper computer and PLC analyze and process the information obtained by the information acquisition module, they drive the components of the execution module to complete the corresponding actions using a specific control strategy. The dynamic data of a production line are fed back to the control terminal in real time. In addition, closed-loop control is realized to ensure the orderly and stable production of a production line.

3.4.2. Virtual Model Control Mechanism Reappearance

Based on the above-presented analysis of the control mechanism of physical entities, using the automation control theory, mathematical optimization method, and control algorithm, the input and output transfer relationship, interference characteristics, and other mathematical models of the control system are abstracted. The key parameters are calibrated and adjusted. By using the control system modeling and simulation tools, as well as developing control programs, the control mechanism model of a virtual model is established. The control logic and integrated control mechanism of physical entities are characterized.

The PLC has the advantages of powerful functions, high reliability, and convenient use and has been widely used in discrete manufacturing production lines. In the digital twin model of a production line using the PLC as the main controller, the virtual PLC also serves as a master controller of the digital twin model. According to the real control mechanism of a physical production line, the same control program as the physical PLC is written in the virtual model. Then, the key variable signal points are virtually connected according to the corresponding physical connection. Combining the configured physical and behavioral attributes and behavioral scripts, the virtual production line becomes consistent with the physical production line. The virtual production line will produce the target workpieces in an orderly manner, according to the established logic and rules, simulating a real production rhythm.

3.4.3. Virtual–Real Interaction Channel Construction

There are two ways to construct a virtual–real interaction channel between physical entities and digital twin models:

• Create virtual and actual key variables and correlate them into the corresponding pairs;
• Simultaneously access data in the same address in an external database.

The OPC UA technology has many advantages and features: namely, it provides an open unified interface, which ensures favorable conditions for information integration and multi-source heterogeneous data fusion [31]. Moreover, most manufacturers of controllers and industrial equipment on the market support the OPC UA communication functions. In addition, all attributes of a physical entity can correspond to each other in the digital twin model. Therefore, this paper adopts the method of associating virtual–real key variable pairs and builds a virtual–real interaction channel based on the OPC UA communication protocol. In this way, the dynamic interaction of key variables and characteristics between virtual and physical spaces is achieved.

For large-scale discrete manufacturing lines, the amount of data generated during the line operation is massive and diverse. According to their functions, these data can be roughly divided into sensor signals, action signals, status data, and command data and organized in a tree structure. The PLC is associated with the address of the OPC UA server. After that, a client uses the subscription mode to access and traverse the server node data to achieve the objective of high-volume and continuous read-and-write operations.

Aiming to improve the response speed of the digital twin model and reduce the state delay between the physical entity and the digital twin model, this study adopts the principle of function-preference pairing of virtual–real variables. That is, variable signals at key nodes are selected as the carriers of virtual–real interaction information, while signals at the other non-key nodes are not used as listening objects. The critical node is determined depending on whether the node state has a direct impact on the function and performance of a production line. Particularly, the key virtual input and output variables of each information control object are paired with the corresponding input and output variables of the real PLC, keeping the key variable pairs updated dynamically. The other indicators, such as data type, data range, and the number of variables, remain consistent and unchanged.

A large amount of data are generated and collected during the operation of the digital twin models in a simulation environment, including instruction signals, state information, simulation results, and optimization schemes. These data are then transmitted to the physical entity in real time via communication protocols. After analyzing the data, the upper computer and the physical PLC drive the execution module to complete the corresponding action, thus realizing the intelligent control of the physical production line. In addition, the field data collected from the physical production line using the information acquisition module are also transmitted and stored in the digital twin model in real time. After data analysis and processing, the dynamic correction of the digital twin model is driven. The virtual and real two-way information flow promotes the feedback optimization of production activities, process control, and manufacturing resource management of the production lines.

Driven by key variables and real-time data, the digital twin information control model maps the control strategy from the physical space to the twin space. It provides important support for dynamic interaction, accurate synchronization, and intelligent mutual control between the digital twin models and the physical entities in discrete manufacturing production lines.

3.5. Geometry–Physics–Behavior–Information Control Four-Dimensional Model Fusion

The digital twin geometry models, physics models, behavior models, and information control models of discrete manufacturing lines are not isolated from each other. Namely, they all promote the mapping of physical objects from the physical space to the virtual space. In these types of models, a geometry model is used to describe the geometric characteristics and topological relationship between the parts of a physical entity; a physics model is adopted to describe the internal laws of multi-disciplinary and multi-physical quantity evolution; a behavior model is used to map behavior characteristics and mechanisms; finally, an information control model is employed to reveal control logic and virtual–real mapping rules.

The aforementioned four-dimensional model involves the characteristics and data of each level structure of a production system, as well as the coupling relationship of the key production factors [32]. In addition, these models consider internal connections, such as energy, information, and material flows. These models cover data and knowledge of electrical, mechanical, hydraulic, pneumatic, and other multi-disciplinary systems. It should be noted that a production line may be affected by both explicit and implicit disturbances, which cause certain errors in the modeling process. Therefore, to ensure the interaction and information sharing between the four models and improve their accuracy, a fusion method of the four-dimensional models for a discrete manufacturing production line is proposed. This method promotes the above four-dimensional models’ fusion from the following five aspects:

(1)

Interface Matching

Each digital twin model has its specific connotation and function. Therefore, a single model can be abstracted into a single-function module, and then a unified standard interface can be configured in each functional module [33]. Then, a dynamic coupling mechanism of key elements between models can be sorted out and analyzed, and the model interface information can be matched accordingly. The multi-dimensional and multi-field digital twin models form various combinations, thus reflecting the hierarchy and logic of a manufacturing line.

(2)

File Format Exchange

When multiple simulation tools are used for cross-platform joint modeling and fusion, there is a problem of inconsistent file formats that cannot be parsed. Therefore, converting multi-type files containing multi-source heterogeneous data into file formats that can be recognized by other dimensional digital twin models represents the key practice. It is also possible to use unified modeling language to represent multi-dimensional and multi-domain models according to the unified rules. The mutual conversion of file formats is beneficial to model expansion and improves the interoperability between models.

(3)

Data Fusion

The key task in the digital twin model-fusion process is the fusion of multi-time-scale, multi-dimensional, and multi-source heterogeneous data [34]. This task is related to the digital twin data layer and data transmission in the digital twin system architecture. In addition, the information control model can provide logical operation and signal interaction guarantee for the interconnection between the four models of different dimensions. Moreover, big data technology can be used to remove redundant data, correct inaccurate data, and extract deeper levels of data value [35], which is accomplished through combining a variety of techniques, such as data classification, cleansing, feature extraction, and parsing. Additionally, data fusion methods, such as weighted averaging, Kalman filtering, Bayesian estimation, neural networks, and support vector machines, can be employed.

(4)

Model Parameter Update

To achieve real-time reproduction of physical entities, it is necessary to update digital twin models’ parameters dynamically, based on the physical entities’ operational state. For this purpose, site-data intelligent perception, data value extraction, model interface calls, and database operations, such as addition, deletion, and querying, are used to extract and put the updated data into the corresponding parameter input position, thus dynamically updating the model parameters.

(5)

Model Logical Relationship Update

When the actual production scenario of a discrete manufacturing line changes or the production plan is adjusted (for instance, production equipment is replaced or the original process flow is changed), the logical relationship between the virtual models needs to be updated accordingly. The relationship between the related models is reorganized by adding, deleting, and adjusting digital twin models. Then, with the help of virtual simulation tools, the twin production lines are initialized, and the trial is run; the coupling relationship between the key production factors is updated, and the internal correlations, such as the energy, information, and material flows, are updated. Finally, the logical relations of the digital models are reconstructed dynamically.

Geometry–physics–behavior–information control digital twin four-dimensional model fusion realizes information integration and sharing, which promotes multi-dimensional and multi-domain model iteration updating and feedback optimization. Moreover, the connectivity and integrity of the digital models are further enhanced [36]. The high-fidelity digital twin models are established to achieve the comprehensive and accurate characterization of complex physical entities in all dimensions and fields.

4. Case Study

A fidget spinner is a kind of leisure toy that can be idled on the fingers for a long time. Its manufacturing process included feeding, mechanical processing, assembly, packaging, storage, and other processes. Figure 6 shows the different shapes of a fidget spinner from raw materials to finished products. A fidget spinner discrete manufacturing line was designed to produce fidget spinner toys of different types and specifications. It was mainly composed of a three-dimensional warehouse unit, an unattended five-axis processing unit, a press-fit unit, a packaging unit, a composite mobile robot unit, and an intelligent control unit, which represented a typical discrete manufacturing scenario.

Based on the proposed digital twin modeling method and digital twin system architecture, digital twin models were constructed. The fidget spinner discrete manufacturing line was used as an example for verification. In addition, a digital twin operation and maintenance management system was developed. The digital twin system architecture of the fidget spinner discrete manufacturing line is presented in Figure 7.

Taking the spatial and temporal accuracy of the digital twin modeling as indices, the real-time tracking of a robot’s running trajectory and the processing time of each process in the whole manufacturing cycle of the fidget spinner were selected as examples to verify the modeling method mentioned above. The experimental equipment mainly included each unit of the physical production line, Visual Components modeling and simulation software, and the upper computer.

(1)

Spatial Accuracy

In the manufacturing process of fidget spinners, the real-time tracking of a robot’s trajectory in the three-dimensional warehouse unit of the ABB was selected as an example, and the spatial accuracy of the action of the digital twin model was taken as the index to verify the proposed modeling method. Through the above modeling methods, the geometry–physics–behavior–information control four-dimensional fusion digital twin models for a fidget spinner discrete manufacturing line were constructed in Visual Components. Then the real-time joint-angle values of each axis of the ABB 1200 industrial robot digital twin model were obtained from the simulation environment, and the joint-angle values at the corresponding time were derived from the physical controller of the physical robot. As shown in Figure 8a, when the digital twin model of the six-axis industrial robot stored the finished fidget spinner box from 119 s to 126 s in the fidget spinner manufacturing cycle, the angle values of each joint changed with time. At this time, as shown in Figure 8b, the joint-angle values were sent by the controller when the physical entity robot performed the corresponding warehousing task. For the purpose of a more intuitive presentation, the joint values of the six axes of the digital twin robot and the physical entity robot were compared,. Moreover, local magnification of joint values was performed at 121 s, as shown in Figure 9.

During 119–126 s of the fidget spinner manufacturing cycle, the digital twin robot and the physical robot were performing the finished product box-loading task, and their six axis joints performed corresponding actions according to the programmed program. The comparison of the joint-angle values of the digital twin robot and the physical robot showed that the average error was 0.127%, and the maximum error was 0.288%. This error was caused by the influence of environmental factors and transmission delay. Both errors were within the reasonable range, indicating that the actions of the digital twin robot and the physical robot were highly consistent and synchronized.

(2)

Temporal Accuracy

In the whole manufacturing process of a fidget spinner, the start time and end time of each process of the digital twin production line and physical production line were obtained and recorded from the simulation environment and upper computer, respectively. The process duration and error were obtained by calculation. The temporal accuracy of the production process was used as the index to verify the digital twin modeling method.

Table 2. The comparison of process duration between the digital twin model and physical entity.

Process Name	Process Duration of the Digital Twin Model (s)	Process Duration of the Physical Entity (s)
Logistics 1 (AGV in situ; three-dimensional warehouse)	22.759	22.981
Raw material delivery	7.636	7.625
Logistics 2 (three-dimensional warehouse; five-axis processing unit)	21.815	21.965
Five-axis processing unit machining	18.388	18.513
Logistics 3 (five-axis processing unit; press-fit unit)	11.798	11.924
Bearing assembly	46.400	46.138
Logistics 4 (press-fit unit; packaging unit)	12.218	12.331
Fidget spinner packaging	29.655	29.521
Logistics 5 (packaging unit; three-dimensional warehouse)	28.388	28.221
Finished fidget spinner box storage	7.159	7.113
Logistics 6 (three-dimensional warehouse; AGV in situ)	26.299	26.525

shows the comparison between the process duration of 11 processes of the digital twin model and the physical entity of the fidget spinner manufacturing cycle.

There was a small deviation between the digital twin fidget spinner discrete manufacturing line and the physical one in the process duration of each process. For the purpose of a more intuitive presentation, the process duration errors are shown in Figure 10.

The first process was the composite mobile robot’s receiving the start signal and starting to move to the raw material grabbing position in the three-dimensional warehouse. Taking this process as an example, it took 22.759 s for the digital twin composite mobile robot to perform this task and 22.981 s for the physical composite mobile robot. The time deviation between the two is 0.222 s, and the error is 0.976%. Similarly, the processing duration errors of other processes were calculated and analyzed in the same way. It could be concluded that the average error was 0.724%, and the maximum error was 1.173%, when the digital twin model and the physical entity were executing the same process. This error was caused by the impact of data transmission delay. Both errors were within the reasonable range, indicating that the digital twin fidget spinner discrete manufacturing line can effectively reproduce the whole production process of the physical manufacturing line and achieve the purpose of virtual–real dynamic interaction and synchronous evolution.

Through the verification of spatial and temporal accuracy, the feasibility and effectiveness of the proposed method were proved. Using this method, the high-fidelity digital twin models for the discrete manufacturing line could be effectively constructed. Moreover, the production transparency and production feedback timeliness could be improved.

In order to further realize precise control of a production line, a digital twin operation and maintenance management system was designed and developed, and the system home page is shown in Figure 11. The system included modules for data monitoring, planning and scheduling, equipment management, error handling, and other operations. It could provide users with various functions, such as authority management, 3D real-time visual monitoring, lean production scheduling, and yield analysis. The data monitoring module is shown in Figure 12. This module had several functions, including real-time visual monitoring of digital twin models, production progress feedback, product quality evaluation, and equipment status monitoring.

The digital twin operation and maintenance management system is convenient for production managers to monitor the production status of a fidget spinner discrete manufacturing line and manage the production data. It can perform the production plan adjustment and equipment maintenance in a timely manner and improve production efficiency. In this way, problems of an unbalanced production beat and delayed production line maintenance can be avoided. The system can help a fidget spinner discrete manufacturing line to transform in a more intelligent direction.

5. Conclusions

In this paper, common problems in discrete manufacturing, including low accuracy of digital twin modeling, response delay, and insufficient precision of the production line control are studied. First, a digital twin system architecture for discrete manufacturing production lines is proposed. Then, using digital twin modeling technology as an entry point and adding the information control dimension, a digital twin geometry–physics–behavior–information control four-dimension fusion modeling method is developed. The digital twin model constructed based on the proposed method can effectively describe the geometric and physical characteristics of physical entities, map the behavior mechanism, and reveal the control logic and virtual–real mapping rules. The proposed method is verified by tests on a fidget spinner discrete manufacturing line. Finally, a digital twin operation and maintenance management system is developed to meet the requirements for real-time visual monitoring and operation and maintenance management of fidget spinner production.

The results presented in this study can effectively solve the problems of low accuracy and response delay in digital twin modeling as well as insufficient accuracy of production line control in discrete manufacturing lines. Furthermore, it can improve production transparency, ensure timely production-dynamic feedback, and promote the deep integration of information and physical spaces, in addition to providing ideas for the digital transformation of discrete manufacturing enterprises. In the future, digital twin modeling technology could be explored from more aspects, and high-fidelity models with more dimensions, fields, and scales could be constructed. In addition, more digital twin operation and maintenance management services could be considered.