Abstract
In information systems research, the advantages of Customer Experience (CX) and its contribution to organizations are largely recognized. The CX analytics evaluate how customers perceive products, ranging from their functional usage to their cognitive states regarding the product, such as emotions, sentiment, and satisfaction. The most recent research in psychology reveals that cognition analytics research based on Classical Probability Theory (CPT) and statistical learning, which is used to evaluate people’s cognitive states, is limited due to their reliance on rational decision-making. However, the cognitive attitudes of customers are characterized by uncertainty and entanglement, resulting in irrational decision-making bias. What is captured by traditional CPT-based data science in the context of cognition aspects of CX analytics is only a small portion of what should be captured. Current CX analytics efforts fall far short of their full potential. In this paper, we set a novel research direction for CX analytics by Quantum Probability Theory (QPT). QPT-based analytics have been introduced recently in psychology research and reveal better cognition assessment under uncertainty, with a high level of irrational behavior. Adopting recent advances in the psychology domain, this paper develops a vision and sets a research agenda for expanding the application of CX analytics by QPT to overcome CPT shortcomings, identifies research areas that contribute to the vision, and proposes elements of a future research agenda. To stimulate debate and research QPT-CX analytics, we attempt a preliminary characterization of the novel method by introducing a QPT-based rich mathematical framework for CX cognitive modeling based on quantum superposition, Bloch sphere, and Hilbert space. We demonstrate the implementation of the QPT-CX model by the use case of customers’ emotional motivator assessments while implementing quantum vector space with a set of mathematical axioms for CX analytics. Finally, we outline the key advantages of quantum CX over classical by supporting theoretical proof for each key.
1. Introduction
The Customer Experience (CX) on digital platforms is becoming increasingly crucial to organizations due to the rapid growth of digital environments and the need to develop personal customer relationships [1]. It highly depends on context, subjectivity, and dynamics [2]. Digital CX emphasizes the significance of interactive, impactful, useful, and valuable human–computer interaction and product ownership and considers pragmatic aspects such as utility, functionality, and aesthetics [3]. CX is the term used to describe how customers perceive a company based on their interactions and perceptions of the brand. A CX incorporates the customers’ cognitive states of feelings, including emotions, sentiment, and satisfaction [4].
Artificial Intelligence (AI) may revolutionize the interactions between organizations and customers by supporting CX analytics [5,6,7,8,9,10,11,12,13,14]. In the case of customers’ interactions in online environments, businesses must collect and analyze data from multiple digital touchpoints to better understand customer preferences, minimize friction in digital journeys, and identify opportunities to enhance user and customer experiences with digital products. Businesses can realize substantial returns by carefully employing AI technology at crucial digital client touchpoints [14]. AI advancements could improve customers’ impressions of a company’s brand, their thoughts about online purchasing experiences, and their ability to operate technology-related components of digital commerce platforms. Additionally, CX analytics must focus on customers’ cognitive states and assessment of feelings, including emotions, sentiment, and satisfaction [4]. Current CX analytics research focuses on evaluating functional and usage aspects rather than the cognitive states of customers regarding the product or service [7,8,9,10]. These studies analyzed over 800 research papers related to CX analytics and identified a clear research gap in the field of customer cognition analytics. Only a few studies have presented customer sentiment analysis based on various CPT-based techniques for analyzing customer reviews [11,12,13]. There are no identified studies that analyze the customers’ emotion analytics. Our research’s primary objective is to define the research direction for customer cognition analytics as part of a comprehensive evaluation of CX analytics.
The latest cognition research in psychology focuses on what type of probability theory best describes how humans make judgments under uncertainty and decisions under conflict. Psychology research considers three main theories regarding the relevance of probability theory to cognition. The first is Bayesian/Classical Probability Theory (CPT) [15]. CPT axioms embody rational decision-making. Second, there are heuristics and biases, a toolbox of rules which offer fast and frugal accounts that describe numerous behavioral findings [16]. Third, there is Quantum Probability Theory (QPT), a newer direction, suggested by psychology research for decision-making analytics under uncertainty [17]. Like CPT, QPT is a general probability theory, that is, a set of rules for how to combine and update probabilities. Although rational CPT models of cognition have become prominent and have achieved much success, they adhere to the laws of classical probability theory even though human reasoning does not always conform to these laws. For this reason, the recent emergence of QPT models based on an alternative probabilistic framework is drawn from quantum theory.
QPT has provided a novel, rich mathematical framework for cognitive modeling, especially for use cases that appear paradoxical from classical perspectives. CX analytics is one of the paradoxical use cases in that CPT could fail in evaluation. Customers’ decision-making process is characterized by uncertainty, which is well studied in the cognition domain [18,19]. Existing CX analytics research presumes the cognitive states of customers to be rational decision-making processes, employing data science methodologies based on CPT, assuming rational decision-making to evaluate CX probabilities and change their preferences. CPT-based CX analytics cannot reach its full potential due to an insufficient grasp of cognitive fallacies and illogical user decision-making.
Quantum theory can alleviate the difficulties of CPT in characterizing human cognition [20,21,22,23]. As a result of recent advances in quantum cognition research, we offer a novel quantum paradigm based on QPT for the CX analytics domain to impose the constraints of the conventional method. While traditional CPT-based data science implies a customer is always in a specific state, the QPT-based data science implies a customer could be in multiple cognitive states simultaneously considering each system feature. To this end, quantum probability presents a mathematical model in which a customer can exist in an unlimited state at any given time, with the capacity to express all possible states, implementing the quantum total-probability approach.
At the time of our current research (February–September 2022), we could not locate any studies on implementing QPT for CX analytics. Consequently, this study highlights the novel theoretical direction for future CX analytics research. Our contribution to theory is the formalizing of a QPT-CX analytics method that has the potential to improve the evaluation of customers’ cognition states significantly. Our research demonstrates the benefits of QPT-based analytics for customers’ cognition analytics over CPT. We demonstrate how some of the distinctive principles of QPT can facilitate CX cognitive event representation and capture cognitive biases that CPT cannot. We expose and explore the fundamental axioms and definitions of CPT and QPT, discuss the theoretical advantages of the QPT over the CPT for CX analytics and present substantial theoretical evidence to support our vision. Using a customer’s emotional motivator analytics use case, we demonstrate how the QPT-based mathematical formalism can be used to model observed deviations from classicality for CX assessment.
The remaining sections are organized as follows. The second section describes the state of the art. It provides a theoretical foundation for the QPT-based CX approach, providing the theoretical evidence why QPT is superior to CPT for CX cognitive analytics. The third section introduces the established QPT-based method for CX analytics: QPT-CX. The concluding section addresses a discussion of research findings, research limitations, and future directions.
2. State of the Art
In recent years, numerous studies have been conducted on applying quantum theory to cognitive science [21,22,23,24,25,26,27]. Researchers have recognized the significance of quantum theory in mitigating cognitive bias, particularly when analyzing human cognition. Recent research has demonstrated that QPT predicts human emotional states more accurately than CPT [21,22]. QPT provides a simple conceptual paradigm for expressing human cognitive science concepts. This theory is based on the idea that psychological and quantum processes are conceptually similar [21]. While CPT assumes that a human is in a specific state relative to all potential states at any given time, the QPT assumes that until a system is measured, all conceivable definite user’s cognitive states have the potential to become actual. The actual quantum state is a combination of all user states’ possibilities, where a complex number specifies the proportion of each.
CX is similar to quantum theory. Most customers perceive system features differently. Despite the simplicity of rational decision-making, customer decision problems have many potential outcomes correlated with each action [20]. Similarities between CX and quantum theory suggest a rich research area, especially for CX cognitive analytics challenges involving context and uncertainty. QPT has the potential to enhance CX analytics evaluation, as previous studies have acknowledged the importance of quantum theory in mitigating bias, especially when analyzing customers’ cognitive abilities.
Classical vs. Quantum Approach for Human Cognition Analytics
Our world is composed of particles that assemble into objects. Within the quantum theory, quantum mechanics allows a particle to simultaneously occupy multiple locations, a phenomenon known as quantum superposition. Quantum mechanics can explain the behavior of systems with multiple particles in any position. Quantum particles do not have a defined velocity but a velocity distribution; they do not have defined energy but an energy distribution. When one of these properties is measured, the particle collapses into one of the possibilities. It is challenging to make a precise prediction for measurements of its position, velocity, and energy simultaneously because measuring one of them can affect the results of measuring the others.
Quantum mechanics was adopted to explain the human cognitive state that could not be explained by classical theories [21,22,23]. Previously, cognitive studies relied on classical probability theory and classical mechanics principles. Recent research has revealed, however, that certain experimental data on human cognition, such as violations of the sure-thing principle, conjunction fallacies, disjunction fallacies, and order effects, cannot be investigated using classical theory [22,23].
Quantum cognition is a new cognitive field resulting from applying quantum theory to cognitive science research. According to certain aspects of quantum theory, such as complementarity, superposition, contextuality, and entanglement, QPT appears to be an effective framework for describing a vast array of human behavior. The brain is biologically complex; its operation and interactions with the external environment are not yet fully understood. It is commonly asserted that human behavior is irrational [28].
At the theoretical level, our vision for pursuing a total CX formulation by the QPT is to bring greater insight into the design of CX analytics, which is associated with high irrationality in humans’ decision-making. Specifically, an underlying mathematical basis that provides a quantitative characterization of quantum theory, but in the context of a classical CX use case, would help bridge the gap between the quantum nature of multidimensional data science based on QPT and the classical nature of existing data science methods based on CPT.
Classical data science based on CPT, like classical physics, assumes that a CX is always in a particular state. However, the CX may be in multiple cognitive states regarding each system feature, technical support, training efforts, and system roadmap issues. To this end, quantum probability provides a mathematical model in which a user can exist in an indefinite state at any given time, with the potential to express all possible “superposition states”. The quantum theory allows a person to be in an indefinite state (utilized by a quantum superposition) at any given time. In contrast, the classical model assumes that a person is always in a certain state. As a result, a person can exist in an indefinite state in which all possible states (utilized by probability amplitudes) have the potential to be expressed at any given time. People’s disputes, uncertainty, and confusion are better represented in a superposition state [22]. As the Born rule specifies, quantum formalism allows for an interference term in the law of total probability, allowing probabilities to be calculated as squared norms of ψ-function projections.
A quantum system is modeled mathematically by a vector space equipped with an inner product over complex numbers, known as Hilbert space [23]. The central idea is that a neuron’s state space must have the Hilbert space structure. A single neuron must “operate” with probabilistic superpositions of states, including cognitive information. At the same time, a neuron is viewed as an open system whose superposition state is influenced by information flows from the electrochemical environment, composed of signals generated by other neurons [17].
CPT implies that a system is in a particular state regarding all potential states at any given time. This actual state can change randomly over time, but it is still definite at any time, and the system generates a definite sample path. On the other hand, QPT assumes that until a system is measured, it is always in an indeterminate superposition state [21]. In a superposed condition, all conceivable definite states have the potential to become actual, but only one of them will when they are measured. That actual state is a combination of all these possibilities, where the amount of each one is specified by a complex number. Many psychological phenomena are characterized by fuzzy, ambiguous, and uncertain feelings, which are reflected in the idea of superposition [23,24,25]. The ability to simultaneously exist in multiple states is achieved by qubits that can simultaneously represent a variety of 1 and 0 combinations. More formally, a qubit state is a mathematical entity that provides a probability distribution for the outcomes of each possible measurement on a system. According to quantum superposition theory, any two (or more) qubits can be joined together (“superposed”) to form a further viable quantum state.
In contrast, each quantum state can be represented as the sum of two or more separate states, which clarifies the explainability of the model. This vector space is created (span) by a set of basis state vectors, each representing some property of the particle we wish to measure. For example, a quantum logical qubit state is a quantum superposition of the “basis states” 0 and 1. A qubit, unlike a traditional bit, which can only be in one of two states: 0 or 1, can be in a state that is a superposition of both. It indicates that the probability of a qubit being measured as 0 or 1 is rarely 0.0 or 1.0 and that multiple measurements on identical qubits will not always yield the same result. For example, three independent basis vectors will represent the three-particle properties of position, velocity, and energy. A vector in the Hilbert space represents a particle, usually called a pure state vector or a superposition state, which is a linear combination of all the basis states. Note that we obtain different linear combinations for the same pure state for different basis states. To measure our particle’s current position, velocity, and energy, we must project its state vector onto each of the three basis vectors. The projection is a mathematical operation that multiplies the state vector with some matrix. Each basis vector has its projection matrix.
CPT starts with an event sample space, where a subset of the sample space represents a possible question outcome. A combination of events is calculated by the relevant interaction of some subsets, which is also a subset, representing the result of a combination of questions. Its probability is calculated and derived according to the probabilities of each of the original equations participating in that combination.
On the other hand, QPT starts with a vector space span by a set of pure (basic) vectors, where a vector is a line with a defined direction and length. All possible outcomes for our inquiries are contained in such a vector space. Orthogonal vectors rotated by an angle represent a question’s possible responses. The and axes for various queries are linked together by simple rotations. A ray is a one-dimensional subspace that a vector representing a question outcome traverses (see Figure 1). A (unit length) state vector represents a person’s collection of views concerning these issues, i.e., some sampled data. The probability of a question outcome on a state vector can be calculated by projecting that state vector onto the corresponding subspace and determining the squared length. CPT inference is considered rational, forcing us to follow the axioms of CPT, which are founded on set theory. In particular, the probability that two events will happen simultaneously equals the probability of their intersection.
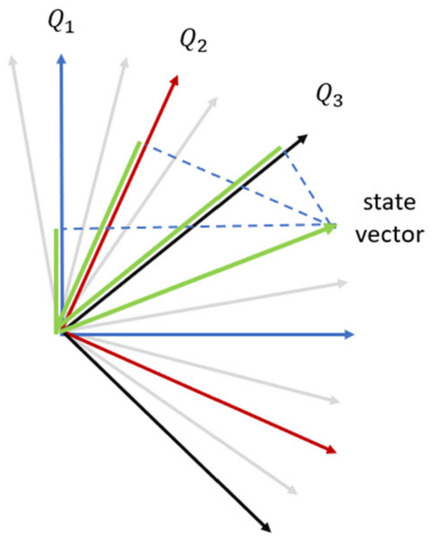
Figure 1.
There are three questions, , , and , each with its own basis state together with their corresponding orthogonal vectors , where each pair spans a two-dimensional plane. are colored blue, are colored red, and are colored black. The gray vectors, together with their orthogonal vectors, can potentially represent some additional other questions rather than the ones we presented before. The green vector represents the customer data during their digital purchases, and the dashed lines represent the projection on each of the three questions, which indicates the probability of each of these questions’ outcomes.
3. QPT-CX Visionary Method for CX Cognitive Analytics
3.1. Customer Emotional Motivator Model
Digital customer emotions are feelings mainly affected, augmented, formed, or conveyed by digital technology. Contextual content and experiences trigger digital emotions and services online platforms provide, while customer activity data can be stored, edited, and analyzed at scale, revealing CX’s emotional state [29]. Consequently, the digital emotions evaluation has the potential to offer a novel perspective on CX on online platforms. CX emotional analytics will be able to illuminate what influences customers’ decisions and why by recognizing and interpreting the new and constantly evolving digital communication tools underlying digital emotion, as well as how customers’ online behaviors reflect their emotional state [30].
Since online platforms provide a virtual abstraction from reality, most digital customers are more at ease expressing feelings online that they might be uncomfortable expressing in person. According to research from hundreds of brands across multiple industries, emotional needs are a key driver of digital CX, leading to engagement, conversion, and loyalty [30]. Hundreds of “emotional motivators” influence digital customer behavior, ranging from ideas of safety and collectivism to freedom and excitement. Implementing a digital CX strategy based on emotional connection reduced attrition rates by 23.8 percent, increased customer advocacy by 10.8 percent, increased the number of active customers by 15 percent, and increased same-store sales by 50 percent [30]. The top emotional motivators for digital customers are outlined in Table 1, which will aid QPT-CX model development.

Table 1.
Top 10 customers’ emotional motivators (adopted from Magidis, 2015 [30]).
Understanding digital CX emotional motivators is essential because most businesses fail to align themselves with the emotions that drive their customers’ most valuable actions. As a result, emotional motivators can reveal where businesses should focus, revealing that they frequently invest in the wrong areas, such as focusing on changing dissatisfied consumers into satisfied customers. Mobile app browsing and purchasing, visits to the retailer’s social media pages, e-commerce site navigation, feedback, and in-store returns of online products are omnichannel touchpoints that digital customers use to interact with the retailer. Each touchpoint can influence a subset of the emotional motivators differently [31]. The following section examines the current state of the art in digital CX experience analytics.
As depicted in Figure 2, we have identified four primary data sources for customers’ emotional motivators. Most AI-based emotion analytics research currently focuses on text, audio, and image signals. Businesses can check the online reviews their customers leave after a transaction but determining the key drivers of consumer satisfaction can become complicated and time-consuming as reviews grow [32]. Organizations use big data, text mining, and analytics to detect trends, patterns, and major topics that customers create on digital platforms for customer analytics. Online feedback can be obtained through reviews, quizzes, social media, and direct messaging [33]. Whereas basic text data analysis can recognize subjects based on keywords or rules, machine learning techniques improve text analytics accuracy. The ability of algorithms to label data (supervised learning), find patterns in data (unsupervised learning), and learn from their own experience and results (reinforcement learning) increased the possibility of transforming raw data into useful information and analyzing the relationship between touchpoints such as services, product features, descriptions, calls, and customer experience, among other things.
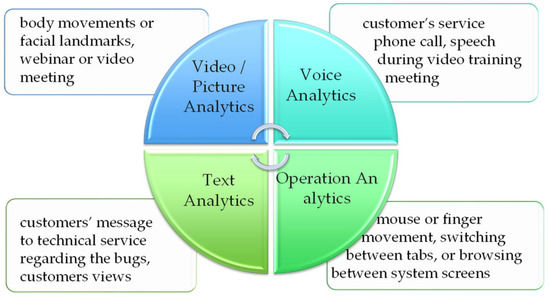
Figure 2.
Data sources for customer’s emotional motivator analytics.
3.2. Mathematical Framework for Quantum-Based Costumer Emotional Motivator Analytics
In our vision model, a particle represents a customer, and the particle properties we wish to measure represent the ten customers’ emotional motivators as presented in Table 1. Each motivator contains two positive and negative emotions in the same range. Thus, we will have twenty basis vectors that can be divided into pairs of positive and negative emotions of the same class. These vectors of the same pair, i.e., the same emotional class, are orthogonal (which means mathematically that their inner product is zero). Every pair of orthogonal basis state vectors spans a two-dimensional Hilbert space (i.e., a subspace of the entire Hilbert space representing the full quantum mechanical system), known as the Bloch sphere. The north and south poles of the Bloch sphere are typically chosen to correspond to the basis vectors, and the points on the surface of the sphere correspond to the pure states of the system, whereas the interior points correspond to the mixed states. The Bloch sphere can be generalized to an n-level quantum system, but it is harder to think about it visually.
Quantum superposition, which describes the uncertainty of a single particle (a photon, for example), is expressed by a probability distribution of mutually exclusive basis states. Let be a basis state which spans the Hilbert space as an orthogonal basis. Each is a vector of dimension over the real numbers, i.e., for every . A pure state , in that space, can be represented as a linear combination of the basis states, together with probability amplitudes , i.e., Notice that each coefficient is a complex number, such that , where is the absolute value of a complex number. If for all , then that pure state is called a superposition state. Denote by a two-dimentional Hilbert space, also known as the Bloch sphere, and let and be its orthogonal basis. A familiar way to represent a pure state in that special sphere uniquely involves the parameters as follows:
where is the imaginary number, and both set the degrees of that pure vector state. In particular, stands for the degrees between the and axes (i.e., up and down), and stands for the degrees between the and axes on the sphere (i.e., left to right), as shown in Figure 3.
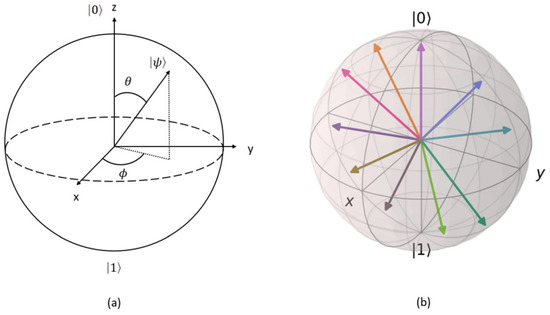
Figure 3.
(a) Bloch sphere illustrated visually with two basis states |0⟩ and |1⟩ and a state vector |ψ⟩. (b) Bloch sphere with ten vectors representing all ten emotional motivator classes. Note that all their ten orthogonal vectors are omitted for simplicity.
The measurement concept, which is used to calculate quantum probabilities, is also included in quantum cognition. The Projection-Valued Measure (PVM) in quantum mechanics transforms an uncertain system state into a specific event by projecting a state to its equivalent basis state. The state is uncertain in the absence of measurement because it takes all possible measurement values at the same time.
Following measurement, the state collapses to a specific basis state. Because PVMs cannot represent subsystems of a larger system, the Positive-Operator Valued Measure (POVM) can be used to solve this problem by assigning a positive probability to each measurement outcome while ignoring the post-measurement condition [34], i.e., POVM is an extension of PVM that provides mixed state information for the entire ensemble of subsystems. A POVM is composed of a collection of Hermitian positive semidefinite matrices on Hilbert space whose sum equals the identity matrix. Each matrix is of dimension over the real numbers, i.e., for every , where . These matrices are known as orthogonal projectors in the simplest instance of the POVM, and they project a given pure state on each one of the selected events by computing (i.e., calculating the inner product of the resulting vector—matrix multiplication) in order to determine the probability that our mixed state is in that specific event.
Incompatibility is a concept that applies exclusively to a Hilbert space. Each basis state that defines a probability event includes a projector that evaluates the event. The combination of two events is not always commutative [35]. In quantum cognition, the joint probability distribution of two events which are represented by the basis vectors and , correspondingly for some , equals the product of the two projectors . If
then the two events are called compatible, and is a projector of a basis state vector which is in the intersection (middle) between , where .
Otherwise, their product is not a projector, and the two events do not commute. Incompatibility means that the two measurements cannot be obtained parallelly without interfering with one another. Classical probability, which assumes that measurements are always consistent, is incapable of accounting for such a disturbance. However, the mathematical framework of quantum probability allows for both compatible and incompatible measurements to exist [36].
Recall that the most common models of human decision-making have been based on classical probability theory, although there is strong evidence (by experiences in psychology) that the way people tend to make decisions is irrational and more compatible with quantum probability theory. To be able to compare our quantum model with a similar one that uses classical probability, we define ten events for each of the emotional motivators listed above. In particular, let stand for “feel a sense of freedom” and for “feel secure”. Similarly, let be the basis vectors in Hilbert space, where represents the emotion motivator in our model, and is its orthogonal vector. For example, is the basis vector for “feel a sense of freedom” while is its orthogonal vector, which stands for “not feeling freedom”, and is the basis vector for “feel secure” while is its orthogonal vector, which stands for “not feeling secure”. Consider now asking a customer whether they feel a sense of freedom or not. Before asking the question, they might be in an indefinite (superposition) state
Notice that Equation (3) symbolizes that the customer is in an indefinite state regarding freedom, simultaneously entertaining both possibilities but uncommitted to either. In classical probability, one cannot represent that uncertainty state regarding feeling freedom or not. Asking the question is equivalent to measuring the state on the “freedom basis”, which is carried out by the two projectors:
The probability that the customer responds “feeling freedom” is:
As in quantum mechanics, questions can be compatible or incompatible. For example, we can ask our customers two questions, whether they feel free and feel secure. In classic probability, it is always possible to specify a joint probability distribution over the four possible pairs of answers, i.e., , and . In applying QPT in psychology, we can ask whether one decision is likely to affect the other. It is plausible that freedom and security are related. The angle between the two bases and reflects the fact that freedom is likely to be correlated to security. Notice that once we get an answer regarding freedom, we will be in an indefinite state regarding security, and vice versa. Suppose we first ask the customer if they feel secure and then ask if they feel free. The probability that they answer “yes” to both questions is given by
The rules of QPT give the probability:
Meanwhile, asking these two questions in the opposite order gives the probability:
which might be equal to or different from the result of Equation (7). Moreover, as can be seen in Figure 4, the probability of answering positively to one question may be smaller than answering positively to two or more questions, as opposed to classical probability, i.e.,
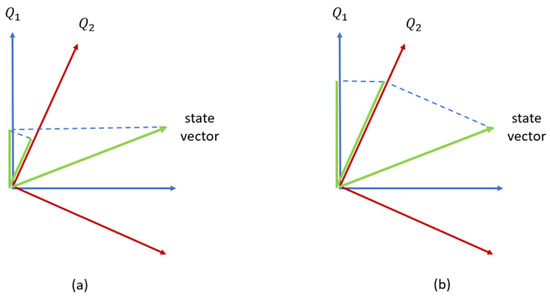
Figure 4.
Denote by the state vector, and let be two questions with their corresponding basis vectors , and denote by their projectors. (a) The outcome when first asking and then on the state vector, i.e., . (b) The outcome when first asking and then on the state vector, i.e.,. In that case, .
Equation (9) holds since feeling secure denotes the feeling of freedom, while in CPT
The complex exponent is a periodic function repeating itself after every radians. It defines the circular topology of the phase dimension, suitable for mapping relationships between emotions. In this scheme, the quantum (Bloch) sphere contains the following ten pure vectors, where each one of them represents one emotional class out of all the ten emotional motivators. The uncertainty between pure states (i.e., emotions) is expressed as mixed vectors of the ten emotional motivators. All these vectors span the quantum vector space (up to different vector classes). The following are the ten fundamental emotional classes:
- Stand out from the crowd
Highlights a unique social identity of the customer to make customers to feel special, for example, by personal customization in a digital platform, offering unique personalized value preposition.
- 2.
- Have confidence in the future
Digital services give customers a long-term feeling of trust in the brand’s future interconnection and a clear picture of what is to come.
- 3.
- Enjoy a sense of well-being
Customers feel that life is living up to expectations, and a sense of balance has been obtained. For example, customers seek a stress-free environment free of dispute and risks.
- 4.
- Feel a sense of freedom
Customers feel the act without being bound by any commitments or prohibitions. For example, customers can add as many names and phrases to a tag as they want by going to an online platform.
- 5.
- Feel a sense of thrill
Customers feel that they participate in exciting, fun events; experience visceral emotions, such as overwhelming pleasure and excitement.
- 6.
- Feel a sense of belonging
Customers feel a sense of belonging to a customer group they relate to or aspire to be part of. If a customer shared a review, for example, customers felt like they were part of a group of people who had made a genuine connection with one another and could also create their review.
- 7.
- Protect the environment
Customers feel that the digital environment is sacred; for example, customers should feel safe and secure when thinking about security and privacy concerns.
- 8.
- Be the person I want to be
During the operation of the digital platform, customers were able to fulfill their desire for continuous self-improvement; they were able to live up to their ideal self-image.
- 9.
- Feel secure
Customers feel that digital businesses that serve them today will be there tomorrow. For example, customers should have faith that the company will fulfill all obligations related to the digital product.
- 10.
- Succeed in life
Customers feel they live meaningful lives; they value themselves in ways that go beyond financial or socioeconomic considerations.
The process structure holds for both pure and mixed qubit states. The circular process dimension associated with the basic behavioral alternativeis a key difference from classical probability space describing binary uncertainty. The similarity metric indicates that the distinction between different emotions becomes less distinct as one moves from the sphere’s surface to its center. Any new sample with features is a state vector which is usually a mixed one, i.e., a combination of our ten basis vectors (emotional classes) defined above. That state vector can be projected to any of the ten pure vectors. Probabilities are calculated as the squared length of the state vector’s projection onto the appropriate axis. Furthermore, one can add up to different pure vectors (emotion classes), each representing a subset of the ten emotional motivators. For example, let be the vector with that represents the event that a customer feels secure and successful in life (i.e., emotion numbers 9 and 10) simultaneously. This vector class differs from the superposition of both emotional motivators. In that case, the meaning is that we are uncertain whether the customer feels secure or successful. It is expressed by the probability that the customer feels exactly one out of these two different emotion classes.
4. Discussion
This article aims to formulate a novel research direction and develop a vision for expanding the application of CX analytics by QPT to address CPT limitations. Additionally, it identifies research areas that contribute to the vision and proposes future research agenda elements to stimulate discussion and research on QPT-CX analytics. We introduce a QPT-based rich mathematical framework for CX cognitive modeling and a set of mathematical axioms for CX analytics in an attempt to characterize the novel method. We illustrate the implementation of the QPT-CX model by analyzing customers’ emotional drivers.
As a new theoretical approach to CX analytics, we employed the quantum cognition method first proposed by Bruza [17] to achieve this goal. We recognize the rich value of quantum theory for CX analytics and consider QPT to enable emotional analytics for customers during product usage. As a result, we developed the QPT-CX method. We demonstrated the QPT-CX through emotional customer analytics, a subset of the broader QPT-CX analytics domain. The method could also analyze user emotions, engagement, and motivation throughout the product usage experience.
The current era is known as “The Age of the Customer”, in which customers, not companies, drive business decisions [37]. For this reason, it is more important than ever for businesses to gain a deeper understanding of their customers, and they are beginning to utilize big data for this purpose. Increasing smartphone usage and internet penetration generate massive amounts of data daily. Also known as a data lake or big data, they consist of structured and unstructured data. In an era where online businesses must truly comprehend their customers’ experiences and behaviors to succeed (or survive), it is imperative that they have access to big data sources and can leverage these data to gain crucial insight. Everyone knows those analytics are only as good as the data they are based on. Still, organizational roadblocks and technological constraints have made it difficult for many brands to feed their analytics with quality data. This paper demonstrates that classical probability models alone are insufficient for revealing crucial customer behavior insights. Consequently, their analytics are frequently misleading, insufficient, or inaccessible. Based on likes, shares, search history, and more, the capability of high-quality quantum CX analytics allows for a more accurate evaluation of customers’ needs. It is effective to utilize a recommendation engine that employs data filtering tools that collect data and then filter them using algorithms. The techniques, tools, and frameworks that result from big data analytics make this possible. Our research reveals three advantages of the quantum approach over the classical one for the QPT-CX.
The first advantage is the disjunction effect phenomenon. It was discovered while testing a rational axiom of decision theory called the sure-thing principle [38]. According to the sure-thing principle, if under a state of the world individual feels emotion over , and if under the complementary state of the world individual also feels emotion A over , then the individual should feel emotion over even when an individual does not know the state of the world. Usually, people do not behave according to the sure-thing principle. Consider, for example, asking a person whether they are happy or sad. Before asking the question, they might be in an indefinite (superposition) state. It is not just that we do not know whether the person is happy or sad; rather, the person “is in an indefinite state regarding happiness and sadness, simultaneously entertaining both possibilities, but being uncommitted to either” [39]. Followed by superposition, one can model users’ uncertainty in different emotional states. Measurement (decision) turns indefinite into definite. The state-based judgment or decision disambiguates the superposition state.
The second advantage is the conjunction fallacy [40]. In classical probability, we have a strong dependency between the probabilities of intersections of events. In general, the probability of any subset of events is derived from a set of classical probability rules. For example, the probability that two events, and , occur is smaller or equal to the probability that occurs and the probability that occurs separately, i.e., and . Other stiff inequalities hold for union and conditional events. Yet, these rules are not always compatible with real-world events. For instance, the probability of feeling both anxious and scared might be bigger than the probability of feeling only anxiety, i.e., . Quantum probability can be used to tackle this problem by defining a new basis vector for every subset of events (emotions). The direction of each such new basis vector can be set independently of all the previous basis vectors, which implies degrees of freedom. See Figure 5 for illustration. Notice that this problem might be overcome via very complex and big classic machine learning models requiring enormous CPU and memory resources and a huge amount of data to train these models.
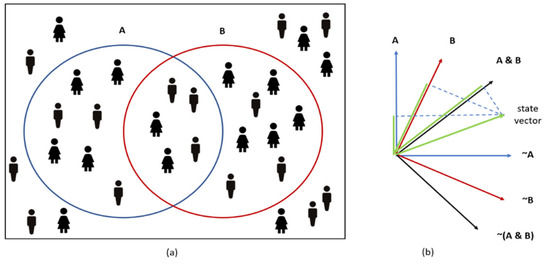
Figure 5.
(a) The probabilities of the events and in classical probability: , whereas (b) presents the same three events, but in terms of quantum probability, the length of the projection of the state vector (colored in green) onto each of the basis vectors and indicates the probability of each of them occurring according to the state vector.
The third advantage is the incompatibility property or asymmetric similarity. In classical probability, it does not matter which event you measure; first, the probability will always be the same, i.e., . However, Moore [41] proved that the order might affect the probability of an outcome in real-world events. Since classical probability cannot describe and model such events, it seems more suitable to use quantum probability theory in that case, which enables us to model and represent the following inequality: .
5. Conclusions
Followed by quantum theory’s progress in psychological research to evaluate humans’ cognitive state, we argue that quantum theory has great potential for CX analytics. We theoretically show how QPT can improve CX cognitive analytics using a customer’s emotional evaluation use case. Finally, we reflect on quantum theory’s current limitations using CX use cases and sketch research activities needed to realize our vision. This paper guides academia and industry in quantum theory research and CX analytics applications.
The proposed QPT-CX could account for uncertain or irrational elements in customers’ decision-making processes, more accurately reflecting customers’ true emotional states. We introduce Hilbert space and quantum cognition to CX analytics. Some key axioms and definitions of classical AI and quantum data science are discussed. The incompatibility captures cognitive biases in decision-making that would be impossible to measure using traditional probability. We show how some of the Hilbert space’s and quantum cognition’s unique principles, such as compatibility, can help in event representation and capture cognitive biases that classical probability cannot. We demonstrate how the quantum probability mathematical formalism can be used to model observed deviations from classicality for CX assessment through an emotion analytics case study.
Although the QPT-CX method improves emotion prediction, it does have some drawbacks. The analytical framework’s obvious flaw is its lack of empirical validation. To turn the framework and its underlying definition into useful tools for researchers and practitioners, the framework and its underlying definition must be studied conceptually and empirically. However, it does open up possibilities for future research. We recommend empirical studies to validate the QPT-CX and evaluate the analytical framework, either in its entirety or in parts, when attempting to identify, understand, and explain flawed QPT-CX adoptions such as users’ sentiments, engagement, motivation, and emotions. Suppose the analytical framework is found to be useful. In that case, future empirical work can include empirical experiments while implementing new information systems or open source validated data sources. The experiment will evaluate the correctness of QPT-CX results by observing real-time users’ experiences and deploying quantum-based algorithms. As quantum CX research progresses, it is tempting to set more ambitious goals to treat many-particle CX phenomena where quantum behavior is a significant or dominant contribution. Future research on quantum CX analytics could place emphasis on the domain of customer loyalty. Customer relationships are characterized by their loyalty. Customers with a high level of loyalty can have a higher average spend and make more repeat purchases than those with a low level of loyalty. In some instances, a loyal customer can be more valuable than a new customer who makes a single purchase; therefore, the greater the number of loyal customers and the greater their loyalty, the better. Improving customer loyalty can have a substantial impact on a company’s bottom line, which justifies making it a primary marketing initiative. In addition to enhancing customer understanding, quantum CX has the potential to improve the accuracy of personalized recommendations that contribute to enhanced customer experiences. By personalizing each micro-moment of the customer experience, businesses can deliver the right offer or interaction at the right time throughout the customer journey and for each customer.
This study’s findings have both theoretical and practical implications. First, this paper provides a summary of quantum cognition research regarding the evolution and application of the term within the context of CX analytics. We provide complete theoretical proof of the superiority of the QPT-CX method over the conventional method. Second, researchers can use the QPT-CX presented in this study to expand the broad user experience domain, thereby enhancing the information system management research. Through the analysis of the case study, this research validates that practitioners can use QPT-CX to understand the customer decision-making process better, clarify the customer service delivery process, and consequently improve their service design process and customer service experience, as well as their service sustainability.
Author Contributions
Conceptualization, H.R., I.A. and R.W.; methodology, H.R., I.A. and I.A.; formal analysis, H.R., I.A. and I.A.; investigation, H.R., I.A. and I.A.; writing—original draft preparation, H.R., I.A. and R.W.; writing—review and editing, H.R., I.A. and I.A.; visualization, H.R., I.A. and I.A.; project administration, I.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Becker, L.; Jaakkola, E. Customer experience: Fundamental premises and implications for research. J. Acad. Mark. Sci. 2020, 48, 630–648. [Google Scholar] [CrossRef]
- Levy, M.; Hadar, I.; Aviv, I. Agile-Based Education for Teaching an Agile Requirements Engineering Methodology for Knowledge Management. Sustainability 2021, 13, 2853. [Google Scholar] [CrossRef]
- Silvennoinen, J.M.; Jokinen, J.P.P. Aesthetic Appeal and Visual Usability in Four Icon Design Eras. In Proceedings of the 2016 CHI Conference on Human Factors in Computing Systems, San Jose, CA, USA, 7–12 May 2016; Association for Computing Machinery: San Jose, CA, USA, 2016; pp. 4390–4400. [Google Scholar]
- Méndez-Aparicio, M.D.; Jiménez-Zarco, A.; Izquierdo-Yusta, A.; Blazquez-Resino, J.J. Customer Experience and Satisfaction in Private Insurance Web Areas. Front. Psychol. 2020, 11, 581659. [Google Scholar] [CrossRef]
- Chen, J.-S.; Le, T.-T.; Florence, D. Usability and responsiveness of artificial intelligence chatbot on online customer experience in e-retailing. Int. J. Retail Distrib. Manag. 2021, 49, 1512–1531. [Google Scholar] [CrossRef]
- Batra, M.M. Strengthening customer experience through artificial intelligence: An upcoming trend. Compet. Forum Am. Soc. Compet. 2019, 17, 223–231. [Google Scholar]
- Ledro, C.; Nosella, A.; Vinelli, A. Artificial intelligence in customer relationship management: Literature review and future research directions. J. Bus. Ind. Mark. 2022, 37, 48–63. [Google Scholar] [CrossRef]
- Pesta, P.; Peters, C. Artificial Intelligence-driven Customer Experience: Status Quo and a Framework for Future Research. In Proceedings of the International Conference on Wirtschaftsinformatik (WI), Duisburg/Essen, Germany, 9 March 2021. [Google Scholar]
- Nicolescu, L.; Tudorache, M.T. Human-Computer Interaction in Customer Service: The Experience with AI Chatbots—A Systematic Literature Review. Electronics 2022, 11, 1579. [Google Scholar] [CrossRef]
- Mariani, M.M.; Perez-Vega, R.; Wirtz, J. AI in marketing, consumer research and psychology: A systematic literature review and research agenda. Psychol. Mark. 2021, 39, 755–776. [Google Scholar] [CrossRef]
- Aviv, I.; Barger, A.; Pyatigorsky, S. Novel Machine Learning Approach for Automatic Employees’ Soft Skills Assessment: Group Collaboration Analysis Case Study. In Proceedings of the 2021 Fifth International Conference On Intelligent Computing in Data Sciences (ICDS), Fez, Morocco, 20–22 October 2021; pp. 1–7. [Google Scholar] [CrossRef]
- Wankhade, M.; Rao, A.C.S.; Kulkarni, C. A survey on sentiment analysis methods, applications, and challenges. Artif. Intell. Rev. 2022, 55, 5731–5780. [Google Scholar] [CrossRef]
- Aviv, I.; Hadar, I.; Levy, M. Knowledge Management Infrastructure Framework for Enhancing Knowledge-Intensive Business Processes. Sustainability 2021, 13, 11387. [Google Scholar] [CrossRef]
- Aviv, I. The Distributed Ledger Technology as Development Platform for Distributed Information Systems. In Proceedings of the International Conference on Intelligent Vision and Computing (ICIVC 2021), Online, 24 March 2022; pp. 344–355. [Google Scholar] [CrossRef]
- Henson, J.; Lal, R.; Pusey, M.F. Theory-independent limits on correlations from generalized Bayesian networks. New J. Phys. 2014, 16, 113043. [Google Scholar] [CrossRef]
- Lockton, D. Cognitive biases, heuristics and decision-making in design for behaviour change. Heuristics and Decision-Making in Design for Behaviour Change. SSRN Electron. J. 2012. [Google Scholar] [CrossRef]
- Bruza, P.D.; Wang, Z.; Busemeyer, J.R. Quantum cognition: A new theoretical approach to psychology. Trends Cogn. Sci. 2015, 19, 383–393. [Google Scholar] [CrossRef]
- Sniazhko, S. Uncertainty in decision-making: A review of the international business literature. Cogent Bus. Manag. 2019, 6, 1650692. [Google Scholar] [CrossRef]
- Aljazzazen, S.; Balawi, A. Risk and uncertainty in consumer decision-making: An overview of principles and perspectives. Mod. Manag. Rev. 2022, 27, 7–19. [Google Scholar] [CrossRef]
- Polman, E.; Wu, K. Decision making for others involving risk: A review and meta-analysis. J. Econ. Psychol. 2019, 77, 102184. [Google Scholar] [CrossRef]
- Pothos, E.M.; Busemeyer, J.R. Quantum cognition. Annu. Rev. Psychol. 2020, 73, 749–778. [Google Scholar] [CrossRef]
- Song, Q.; Wang, W.; Fu, W.; Sun, Y.; Wang, D.; Gao, Z. Research on quantum cognition in autonomous driving. Sci. Rep. 2022, 12, 1–16. [Google Scholar] [CrossRef]
- Rika, H.; Aviv, I.; Aviv, B. AI Methods for Emotion Analytics from Machine Learning to Quantum Cognition. In Proceedings of the IEEE World Conference on Applied Intelligence and Computing (AIC2022), Virtual Conference, 17–19 June 2022. [Google Scholar]
- Gunji, Y.-P.; Haruna, T. Concept Formation and Quantum-like Probability from Nonlocality in Cognition. Cogn. Comput. 2022, 14, 1328–1349. [Google Scholar] [CrossRef]
- Fell, L.; Dehdashti, S.; Bruza, P.; Moreira, C. An experimental protocol to derive and validate a quantum model of decision-making. arXiv 2019, arXiv:1908.07935. [Google Scholar]
- Gkoumas, D.; Li, Q.; Dehdashti, S.; Melucci, M.; Yu, Y.; Song, D. Quantum Cognitively Motivated Decision Fusion for Video Sentiment Analysis. Proc. Conf. AAAI Artif. Intell. 2021, 35, 827–835. [Google Scholar] [CrossRef]
- Khrennikov, A. Quantum-like modeling of cognition. Front. Phys. 2015, 3, 77. [Google Scholar] [CrossRef]
- Gilovich, T.; Griffin, D.; Kahneman, D. Heuristics and Biase: The Psychology of Intuitive Judgment; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Mensio, M.; Rizzo, G.; Morisio, M. The rise of emotion-aware conversational agents: Threats in digital emotions. In Proceedings of the Companion Proceedings of the The Web Conference 2018, Lyon, France, 23–27 April 2018; pp. 1541–1544. [Google Scholar]
- Magids, S.; Zorfas, A.; Leemon, D. The new science of customer emotions. Harv. Bus. Rev. 2015, 76, 66–74. [Google Scholar]
- De Keyser, A.; Verleye, K.; Lemon, K.N.; Keiningham, T.L.; Klaus, P. Moving the Customer Experience Field Forward: Introducing the Touchpoints, Context, Qualities (TCQ) Nomenclature. J. Serv. Res. 2020, 23, 433–455. [Google Scholar] [CrossRef]
- Sujata, J.; Aniket, D.; Mahasingh, M. Artificial intelligence tools for enhancing customer experience. Int. J. Recent Technol. Eng. 2019, 8, 700–706. [Google Scholar]
- Lan, Y.-T.; Liu, W.; Lu, B.-L. Multimodal Emotion Recognition Using Deep Generalized Canonical Correlation Analysis with an Attention Mechanism. In Proceedings of the 2020 International Joint Conference on Neural Networks (IJCNN), Glasgow, UK, 19–24 July 2020. [Google Scholar] [CrossRef]
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information: 10th Anniversary Edition, 10th ed.; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Busemeyer, J.R.; Wang, Z. Hilbert space multidimensional theory. Psychol. Rev. 2018, 125, 572–591. [Google Scholar] [CrossRef] [PubMed]
- Hughes, R.I. The Structure and Interpretation of Quantum Mechanics; Harvard University Press: Cambridge, MA, USA, 1989. [Google Scholar]
- Aviv, I.; Levy, M.; Hadar, I. Knowledge-Intensive business process audit: The practical aspect. In Proceedings of the 9th International Conference on Knowledge Management and Knowledge Technologies (I-KNOW), Graz, Austria, 2–4 September 2009. [Google Scholar]
- Tversky, A.; Shafir, E. The Disjunction Effect in Choice under Uncertainty. Psychol. Sci. 1992, 3, 305–310. [Google Scholar] [CrossRef]
- Pothos, E.M.; Busemeyer, J.R.; Trueblood, J.S. A quantum geometric model of similarity. Psychol. Rev. 2013, 120, 679–696. [Google Scholar] [CrossRef]
- Tversky, A.; Kahneman, D. Extensional versus intuitive reasoning: The conjuctive fallacy in probability judgment. Psychol. Rev. 1983, 90, 293–315. [Google Scholar] [CrossRef]
- Moore, R. The restructuring of higher education curricula: Contrasting models of interpretation. J. Educ. 2002, 27, 33–58. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).