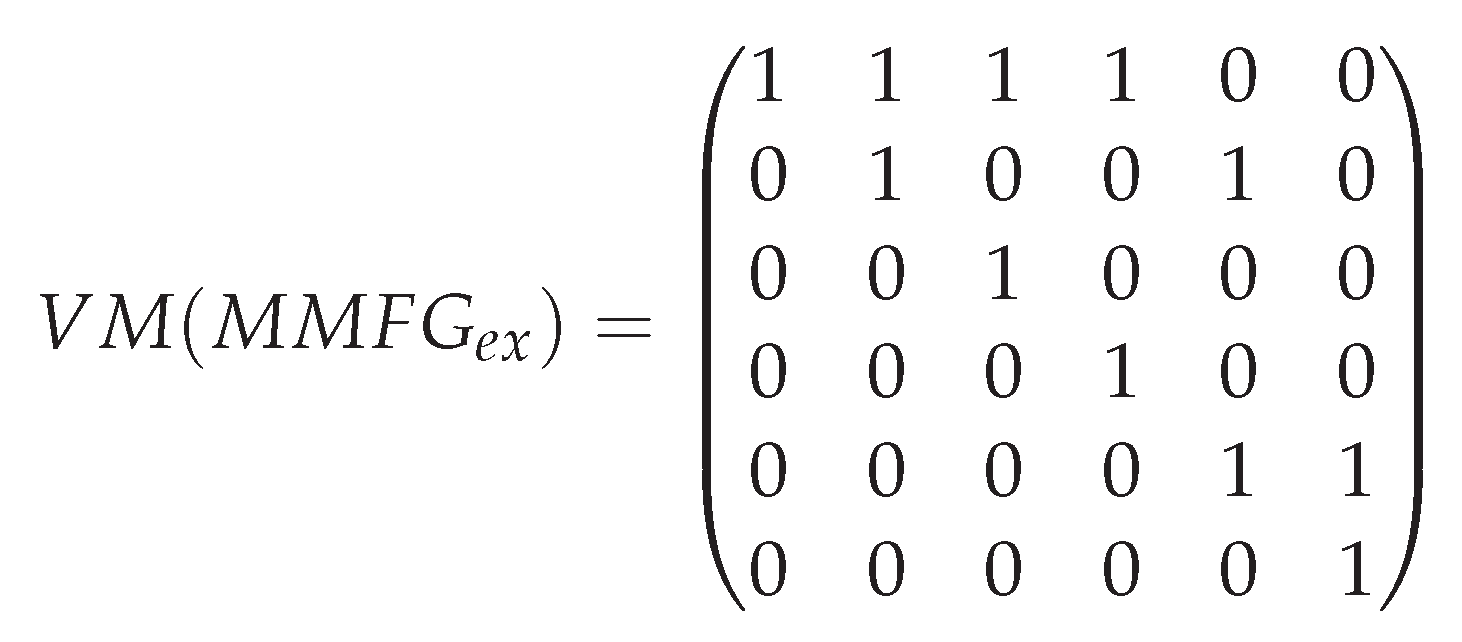3.1. Graph Code Feature Vocabularies and Dictionaries
Here, we will introduce the definitions for vocabularies, their dictionaries, and therefore feature term vocabulary representations of Graph Codes. Based on these definitions, a metric for similarity calculations going beyond node and edge types, based on Graph Codes can be defined. Summarizing our current example, matrices can represent only node and edge types so far. In each MMFG, the set of
n nodes representing distinct feature terms can be regarded as unique identifiers for the MMFG’s feature term vocabulary
:
This set of a MMFG’s vocabulary terms thus represents the elements of a corresponding Graph Code’s Dictionary, i.e., the set of all individual feature vocabulary terms of a Graph Code. However, it is important to uniquely identify the feature vocabulary term assigned to a field of a Graph Code. Thus, we introduce a Graph Code Dictionary for each Graph Code, which is represented by a vector
and provides a ordered representation of the set
with uniquely defined positions for each MMFG’s feature vocabulary term. The elements in
can be ordered according to the corresponding MMFG, e.g., by applying a breadth-first-search, but also other ordering strategies could be applied. As the ordering does not effect the Graph Code algorithms and concepts as such, in the following examples, we chose a manual ordering to maximize illustration. In the Graph Code matrix representation, each node field (in the diagonal) of a Graph Code can now be unambiguously mapped to an entry of its Graph Code Dictionary vector, which can be represented as follows:
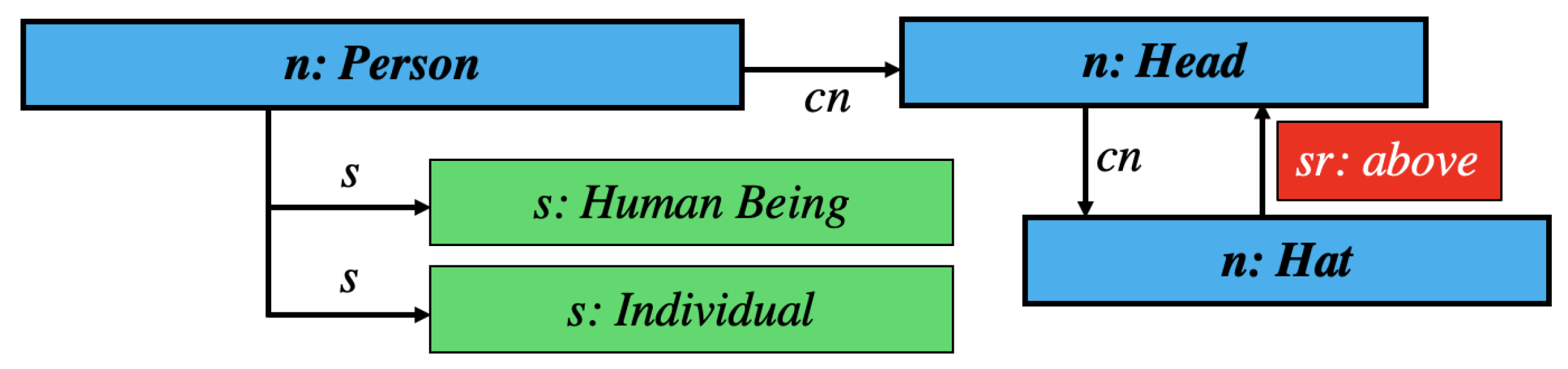
Applied to the Graph Code of the previous example, the set of feature vocabulary terms
would be {Person, Head, Human Being, Individual, Hat, above}, in which the elements do not have any order. The corresponding vector
would be:
and—in contrast to the set representation—uniquely identifies each vocabulary term by its position within the vector. Thus,
can also be regarded as a indexed list:
| Index i | 1 | 2 | 3 | 4 | 5 | 6 |
| Person | Head | Human Being | Individual | Hat | above |
When comparing the similarity of two Graph Codes, it is important to compare only feature-equivalent node fields in the diagonal of each matrix to each other. Each Graph Code has its own, individual dictionary-vector
, and another Graph Code will have a different dictionary-vector according to the content of its represented MMFG, typically
. Feature-equivalent node fields of Graph Codes can be determined through their corresponding Graph Code Dictionaries, as these fields will have positions represented by an equal feature vocabulary term of each corresponding dictionary. For comparison, only the set of intersecting feature vocabulary terms of e.g., two Graph Codes is relevant, as non-intersecting feature vocabulary terms would represent non-common MMFG feature nodes, which cannot be similar. Thus, the set of intersecting feature vocabulary terms
of e.g., two MMFGs can be defined as:
The methodology of intersecting sets can be also applied to Graph Code dictionaries. The intersection of two vectors
can be defined correspondingly as:
To illustrate the calculation of
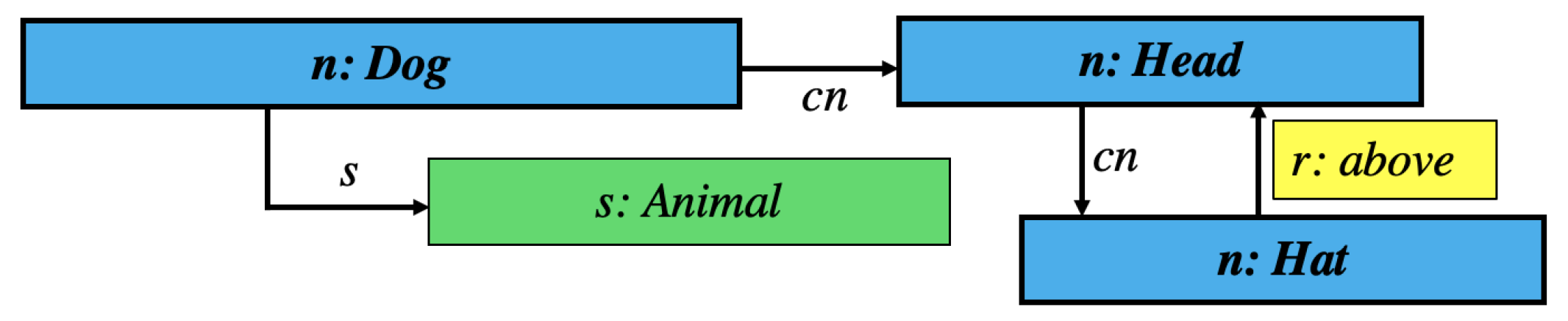
, we introduce a second exemplary Graph Code
based on a
as shown in
Figure 5 and the corresponding
Table 3.
The set
in this case is above, Dog, Head, Animal, Hat} and the set
of intersecting feature vocabulary terms is above, Head, Hat}. The dictionary-vector
thus is:
illustrated as a indexed list,
would be:
| Index i | 1 | 2 | 3 | 4 | 5 |
| above | Dog | Head | Animal | Hat |
The vector
represents the dictionary of intersecting vocabulary terms and only contains the subset of vocabulary terms of
, where a equal vocabulary term can be found in
. The order of intersecting vocabulary terms in
is given by the order of
:
From an algorithmic perspective, this means that all elements of
are deleted that cannot be found in
. Typically, the index position of
is different from both
and
. For our example, the indexed list representation of
would be:
| Index i | 1 | 2 | 3 |
| above | Head | Hat |
Based on these dictionary-vectors, a translation of equivalent Graph Code positions can be performed, as each feature vocabulary term has a unique position within each of the Graph Code’s dictionaries.
Applications will typically utilize a collection of MMFGs and their corresponding Graph Codes. The overall feature term vocabulary
containing
c vocabulary terms of such a collection of
n MMFGs can be defined as the union of all MMFG’s feature term vocabularies and also be represented by the union of all Graph Code Dictionaries
:
In this dictionary-union-vector, the ×-operation for calculating the union of dictionary-vectors is implemented by traversing all the collection’s dictionaries and collecting unique dictionary vocabulary terms into a single dictionary-vector. In case of our example with and , the calculated (Person, Head, Human Being, Individual, Hat, above, Dog, Animal). If a is calculated for the complete collection of Graph Codes, it can be regarded as a global dictionary-vector with collection-wide unique positions for each feature vocabulary term.
As we will show in the remainder of this paper, an exemplary MMFG could contain about 500 feature nodes and 2000 edges, thus the resulting Graph Code matrix would contain 500 rows and columns and 2500 non-zero entries (500 for the nodes in one diagonal, 2000 for edges between these nodes). Processing many different MMFGs will result in many different Graph Codes having about similar size, but different vocabulary terms, leading to an increase of
. The Oxford English Dictionary [
39] e.g., contains 170,000 English words (Note: translation and multilingual support is not in scope of this paper and does not affect the general concept of Graph Codes). If we assume, that applications exist, which produce English terms as representations for feature-nodes, MMFGs representing the overall vocabulary would result in matrices of size 170,000 × 170,000 resulting in 28.9 billion matrix fields. Calculations on this large number of fields will be no longer efficient enough for MMIR.
Of course, in some use cases, an application-wide dictionary can be required. However, in some other applications, it would be better to apply a much smaller dictionary. Hence, two major approaches of modeling dictionaries can be proposed:
Application-wide dictionary: in this scenario, we assume that any Graph Code will be processed with the dictionary-vector terms . If in an MMIR application all images are almost similar, a processing and re-processing approach can automatically increase or decrease the collection’s vocabulary terms according to the analysis of new content. All existing Graph Codes have to be adjusted whenever new indexing terms are detected (the size of increases) or whenever existing multimedia feature content is removed from the collection (the size of decreases). The key advantage of this approach is, that all Graph Codes have exactly the same size and identical positions represented by their dictionary-vectors. This makes comparisons easier as no further transformation is required. It also simplifies the employment of Machine Learning algorithms. However, a permanent re-processing of all existing Graph Codes can be computationally expensive. In this case, the following scenario should be preferred.
Dictionaries for smaller combinations of individual vocabularies: if images from many different areas (i.e., with many different feature vocabulary terms) have to be processed, two Graph Codes can be compared based on the intersection of their individual Graph Code’s dictionary vectors . In this case, a mapping of corresponding feature vocabulary terms by their position within each dictionary-vector can be performed and equivalent node matrix fields can be calculated by a simple transformation (i.e., re-ordering) of one of the dictionary-vectors. As this also eliminates lots of unnecessary operations (e.g., comparing unused fields of ), this approach can be very efficient, when Graph Codes vary a lot within a collection.
Applied to
and
of our above example, the application-wide dictionary
would result Graph Codes with a size of
matrix fields, whereas
would result in a intersection matrix of
fields. This intersection matrix
can be calculated of a
by removing any rows and columns, that are not part of
.
Table 4 shows the intersection matrices of
and
.
For the comparison of these intersection matrices, we would like to apply the standard matrix subtraction. However, due to the different orders of and , the matrix field positions of the matrices do not represent the same feature vocabulary terms. For example, the field (2,1)of represents the relationship between Hat and Head, but the equivalent relationship in is located in field (3,2). To solve this, we introduce a equivalence function , which transforms a Graph Code intersection matrix or the corresponding dictionary-vector in a way, that the corresponding dictionary-vector is ordered according to .
Thus, equivalence of a matrix field
in
and a matrix field
in
and corresponding dictionary vectors
and
can be defined as:
:
In the case of comparing only two Graph Codes,
is automatically ordered according to the first Graph Code. Thus, in this case, the second dictionary-vector would be re-ordered to match the order of the first one. This reordering is applied to the corresponding intersection matrix of the Graph Code. In our example,
would be reordered to match
. Thus, the resulting reordered intersection matrix would be as shown in
Table 5.
Based on this description of the representation of MMFGs as on the definition of Graph Code feature vocabularies, we will now define a metric to calculate similarity of Graph Codes as a basis for MMIR retrieval applications.
3.2. Graph Code Similarity
In this section, we define a metric, that enables MMIR application to compare Graph Codes and thus utilize them for retrieval. In case of Graph Codes and their matrix-based representation, the calculation of similarity requires the consideration of rows, columns and fields representing nodes and edges (i.e., node relationships) of a MMFG. These nodes and relationships have to be of equivalent node or relationship type for comparison. This means, that it is important to compare the correct matrix field position to each other, which typically is different in e.g., two Graph Codes. Matrix field positions employed for the definition of a metric represent nodes (i.e., detected features) or edges (i.e., detected node-relationships), edge-types (i.e., detected node relationship types), and their type values. The definition of a metric for Graph Codes has to be applicable for matrices, where rows and columns represent MMFG nodes and the corresponding feature vocabulary terms. Matrix cells represent node types (in one diagonal) and all other non-zero matrix fields represent edge types and their values. Based on these characteristics of Graph Code we can define a metric:
as a triple of metrics containing a feature-metric
, a feature-relationship-metric
and a feature-relationship-type-metric
.
The Graph Code Feature Metric
The feature-metric
can be employed to calculate the similarity of Graph Codes according to the intersecting set of dictionary vocabulary terms.
is defined as the ratio between the cardinality of
the intersecting dictionary vocabulary terms and the cardinality
a Graph Code’s dictionary vector. In the following formulas, the notation
for vectors denotes the cardinality of a vector
v, i.e., the number of elements in this vector:
Thus, the more features are common in e.g., two MMFGs, the higher the similarity value based on
- independent of the relationships between these corresponding MMIR features. In case of the example above, the numerical distance between
and
based on the metric
is:
The Graph Code Feature Relationship Metric
The feature-relationship-metric
is the basis for the similarity calculation of MMFG-edges, i.e., the non-diagonal and non-zero fields (representing edges of deliberate types) of the Graph Code’s matrix representation. This metric is only applied to equivalent fields (i.e., relationships with the same source and target node) of intersection matrices
of two Graph Codes. We base this metric on the non-diagonal fields of the Adjacency Matrix
(i.e., the matrix containing only the values 1 and 0). Then,
can be defined as ratio between the sum of all non-diagonal fields and the cardinality of all non-diagonal fields. Sum and cardinality of all non-diagonal fields are calculated by subtracting the number of nodes
n from the sum or cardinality of all fields:
Thus, represents the ratio between the number of non-zero edge-representing matrix fields and the overall number of equivalent and intersecting edge-representing matrix fields of e.g., two Graph Codes. Note, that in this way, the metric counts all edges existing between source and target nodes, independent of the equivalence of the edges’ types.
Applied to our example, the
and the equivalent matrix
is shown in
Table 6 and
Table 7.
Looking at the two Graph Codes in
Table 6 and
Table 7, there are six potential positions representing edges: three fields in the upper right of the diagonal and three fields in the lower left. Out of these possible positions, only two contain edges. These are located in matrix positions (2,1) and (3,2). Thus, only two out of six possible edge representing matrix field positions have a non-zero value. Thus, the numerical distance of the metric
:
Note, that currently only the existence of an edge—independent from its type—is employed for the metric . However, also the type of each relationship can indicate additional similarity. Hence, we will introduce an edge-type-based metric in the next section.
The Graph Code Feature Relationship Type Metric
The metric
is based on the feature-relationship-types of Graph Codes. As the Graph Code encoding function
encodes different MMFG edge-types with different base values (see
Section 2.4), feature-relationship-type-similarity can only exist, when the edge-types represented by equivalent matrix fields of Graph Codes are equal. In case of
, calculations are performed no longer on the adjacency matrices of Graph Codes, but on the
matrices of the Graph Codes (see
Table 8).
A matrix field is equal to another, if the subtraction of their values returns zero. If all equivalent fields are equal, the sum of these fields is zero. While
is based on the pure existence of a non-zero edge representing matrix field,
additionally employs the value of this matrix field (representing the relationship type) and hence represents the ratio between the sum of all non-diagonal matrix fields and their cardinality:
In our example, the difference of these two intersection matrices for non-diagonal fields (i.e.,
) is calculated as:
Thus, the mathematical sum of this matrix is 1. This means, that one out of six possible fields had a different edge type value. The numerical distance of the metric
for these two Graph Codes can be calculated as:
Thus, in terms of our example, the overall similarity
between
and
is:
This means, that the similarity based on common vocabulary terms is 0.5, the similarity based on common edge positions is 0.33, and the similarity of equal edge types is 0.16.
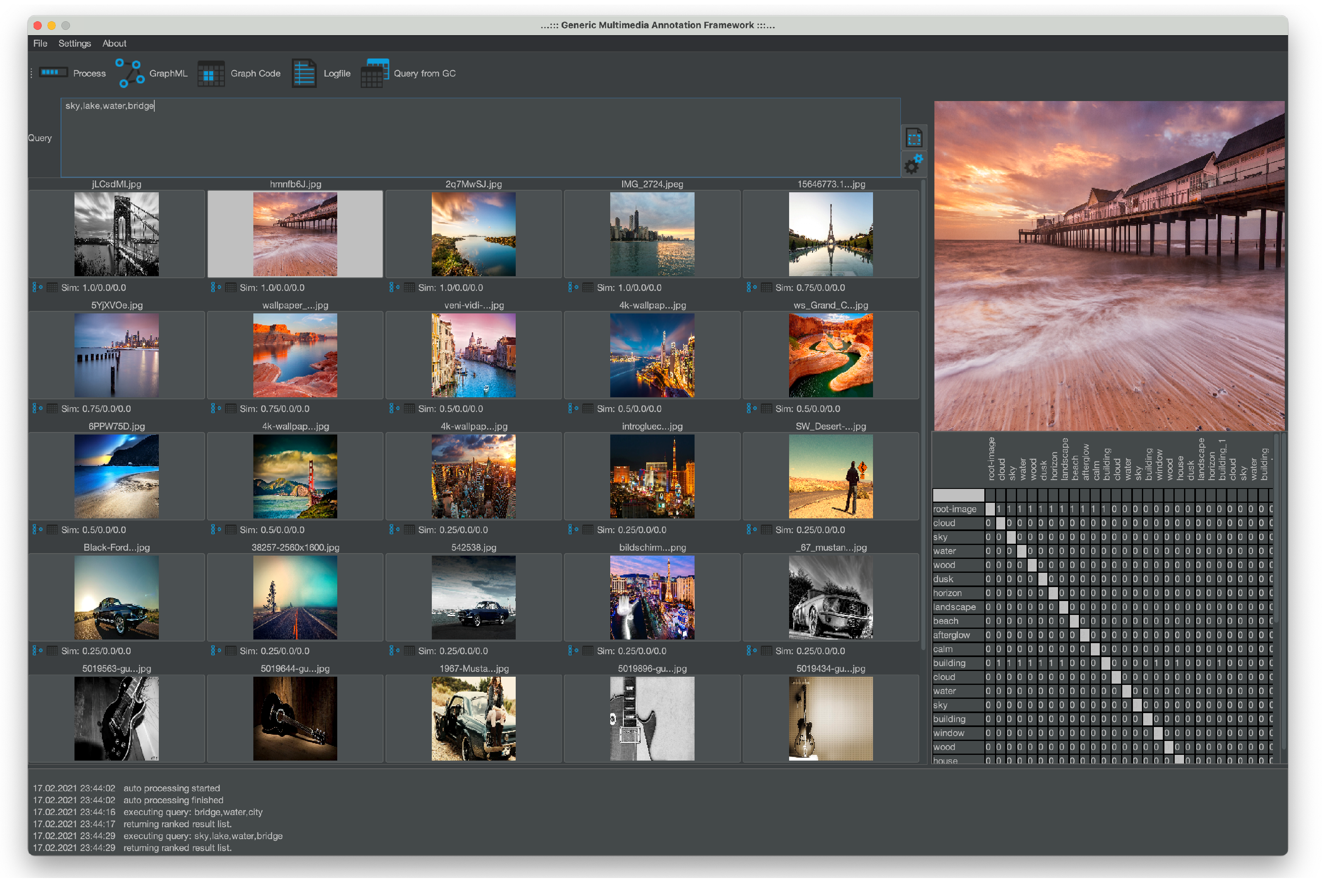
Based on the metrics for Graph Codes, MMIR retrieval can utilize comparison functions to calculate a ranked list of results. In the next and subsequent part, we will illustrate the Graph Code query construction and retrieval execution algorithms.
3.3. Querying with Graph Codes
Query Construction based on Graph Codes is possible in three ways: a manual construction of a query Graph Code , the application of the Query by Example paradigm, or an adaptation of existing Graph Codes. These three options are described in this section.
A manual construction of a
by users can result in a
Graph Code, which then is employed for querying. This manual construction could be performed by entering keywords, structured queries (e.g., in a query language like SPARQL [
40]), or also natural language based commands [
41] into a MMIR application’s query user interface. The
and corresponding
in this case is created completely from scratch.
Query construction can be based on the Query by Example paradigm [
42]. In this case, a
is represented by an already existing Graph Code, which typically is selected by the user to find similar assets in the collection of a MMIR application.
An adaptation of an existing Graph Code can lead to a as well. A refinement in terms of Graph Codes means, that e.g., some non-zero fields are set to zero, or that some fields get new values assigned according to the Graph Code encoding function . From a user’s perspective, this can be performed by selecting detected parts of corresponding assets and choosing, if they should be represented in the query or not.
A prototype for all three options of Graph Code querying is illustrated in [
22] and available on GitHub [
20]. The adaptation of existing MMFGs in terms of the Graph Code matrices is shown in
Table 9, which shows an exemplary
and an exemplary adapted version
.
To further optimize the execution of such a query, we construct a compressed Graph Code
by deleting all rows and columns with zero values from an adapted Graph Code. This
provides an excellent basis for comparison algorithms, as it typically contains very few entries. In the previous sections, we showed, that this would also reduce the number of required matrix comparison operations. In our example,
would semantically represent a search for images containing a red watch (see
Table 10).
Instead of traversing feature graphs to match sub-graphs, a comparison based on Graph Codes employs matrix-operations to find relevant Graph Codes based on their similarity to the implemented by the metric . This approach facilitates the use of Machine Learning, Pattern Matching, and specialized hardware for parallelization of query execution, which is described in more detail in the next section.
3.4. Information Retrieval Based on Graph Codes
In
Section 3, we have already introduced the retrieval function:
which returns a list of Graph Codes ordered by relevance implemented on basis of the similarity metric:
and thus directly represents the retrieval result in form of a ranked list. The calculation of this ranked list can be performed in parallel, if special hardware is available. In many MMIR applications, this calculation can also be done in advance. For a given query Graph Code
, a similarity calculation with each Graph Code
of the collection is performed, based on the Graph Code metric
. Compared to graph-based operations, matrix-based algorithms can be highly parallelized and optimized. In particular, modern GPUs are designed to perform a large number of independent calculations in parallel [
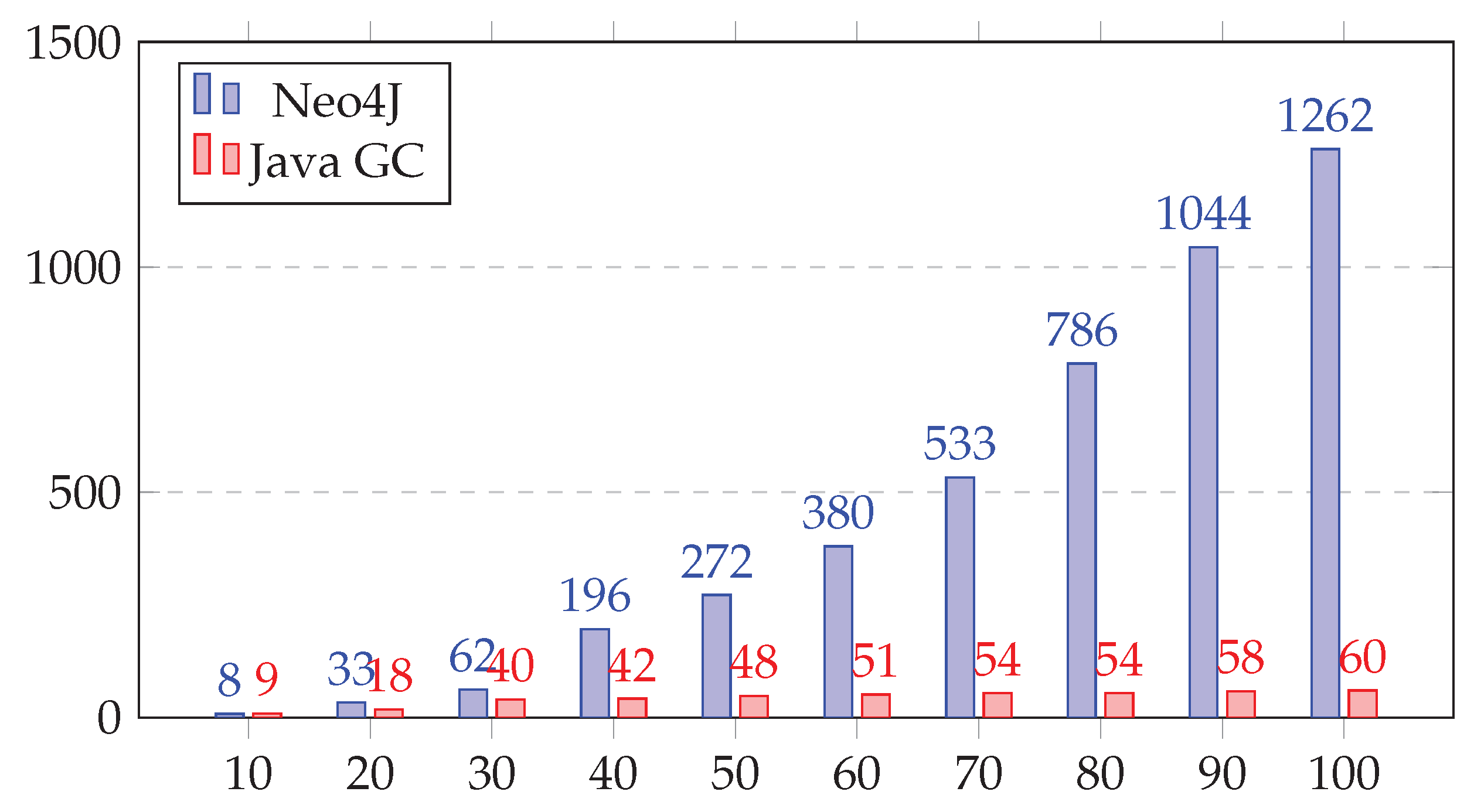
43]. Thus, the comparison of two Graph Codes can be performed in
on appropriate hardware, which means that the execution of a complete matrix comparison can be fully parallelized and thus be performed in a single processing step. It is notable, that even current smartphones or tablets are produced with specialized hardware for parallel execution and ML tasks like Apple’s A14 bionic chip [
44]. Hence, the Graph Encoding Algorithm performs well also on smartphones or tablets. In the evaluation section of this paper (
Section 5), we give detailed facts and figures. The basic algorithm for this comparison and ordering is outlined in pseudocode below:
for each GC in collection
|
--- parallelize ---
|
calculate the intersection matrices
|
of GC_Query and~GC
|
|
--- parallelize each ---
|
calculate M_F of GC_Query and GC
|
calculate M_FR of GC_Query and GC
|
calculate M_RT of GC_Query and GC
|
--- end parallelize each ---
|
compare
|
--- end parallelize~---
|
|
order result list according to
|
value of M_F
|
value of M_FR where M_F is equal
|
value of M_RT where M_F and M_FR are equal
|
return result list
|
To calculate the ranked result list, this algorithm employs the three metrics , and in such a way, that first, the similarity according to (i.e., equal vocabulary terms) is calculated. For those elements, that have equal vocabulary terms, additionally the similarity value of for similar feature relationships is applied for ordering. For those elements with similar relationships (i.e., edges), we also apply the metric , which compares edge types. So, the final ranked result list for a Graph Code is produced by applying all three Graph Code metrics to the collection.
3.5. Discussion
In this section, we presented the conceptual details, their mathematical background and formalization, a conceptual description of the and algorithms for processing Graph Codes and their application for MMIR. We introduced Graph Code feature vocabularies and dictionaries as a foundation for further modeling. Particularly Graph Code dictionary vectors are the basis for several operations and provide a clearly defined, indexed list of vocabulary terms for each Graph Code. The design of MMIR applications can employ application-wide dictionaries or dictionaries for smaller or individual vocabularies, which provides high flexibility in the application design when using Graph Codes.
Hence, we also introduced an example to illustrate the corresponding matrix operations, which is also employed as a basis for the calculation of Graph Code similarity. Similarity of Graph Codes is defined by a metric , which addresses different properties of the underlying MMFG. Firstly, provides a measure for similarity based on the vocabulary terms of Graph Codes. Secondly, checks, if equal edge relationships exist between the two Graph Codes and thirdly, compares the relationship type of existing edges. With this metric-triple, a comprehensive comparison of Graph Codes can be implemented. Based on this metric, we discussed the construction of Graph Code queries, which can be performed manually, as Query by Example, or in terms of a adaptation of existing Graph Codes and will result in a query Graph Code. This query object can be compressed and will provide an excellent basis for comparison algorithms based on the metric . We also showed, that MMIR retrieval based on Graph Codes can be highly parallelized.
In general, all these introduced concepts show, that it is possible to perform calculations in a 2D matrix space instead of traversing graph structures and to integrate features of various sources into a single feature graph. However, to demonstrate that these calculations provide the expected advantages compared to graph-based operations, a proof-of-concept implementation and corresponding evaluation is required. Hence, we will now outline the most important facts and show, that by using Graph Codes a significant improvement of efficiency and effectiveness in MMIR applications can be achieved in the following sections of this paper.