Unscented Kalman Filter Based on Spectrum Sensing in a Cognitive Radio Network Using an Adaptive Fuzzy System
Abstract
:1. Introduction
| Algorithm 1 In the proposed scheme based on the UKF, all CUs are calculated the UKF gain and the estimated covariance. |
Input: Select appropriate segma points, Output: Calculate the UKF gain, K and the estimated covariance,
|
2. Related Work
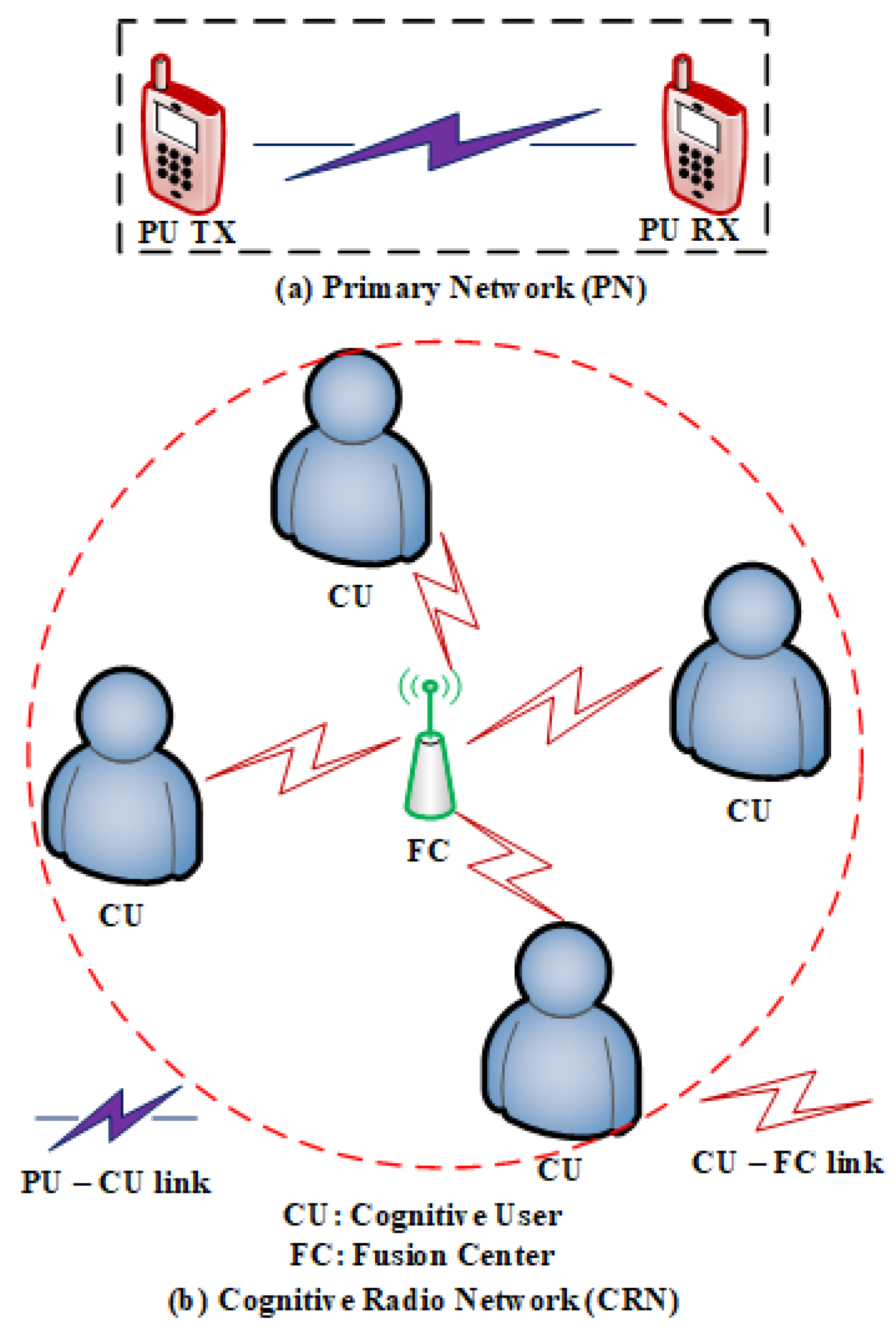
3. System Model
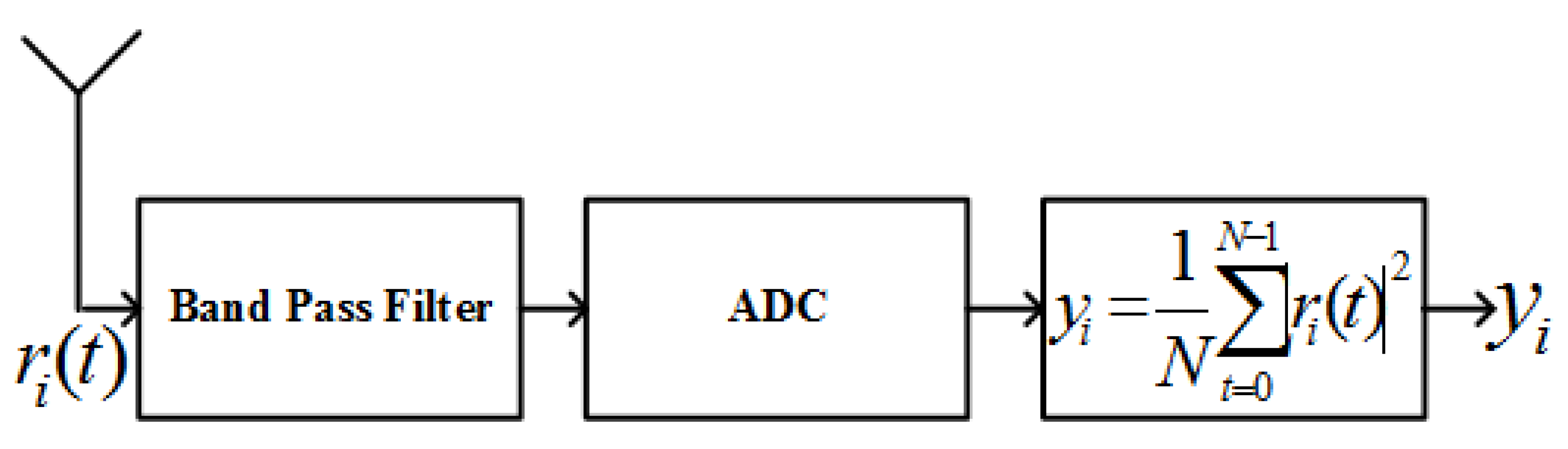
4. Energy Detection Technique
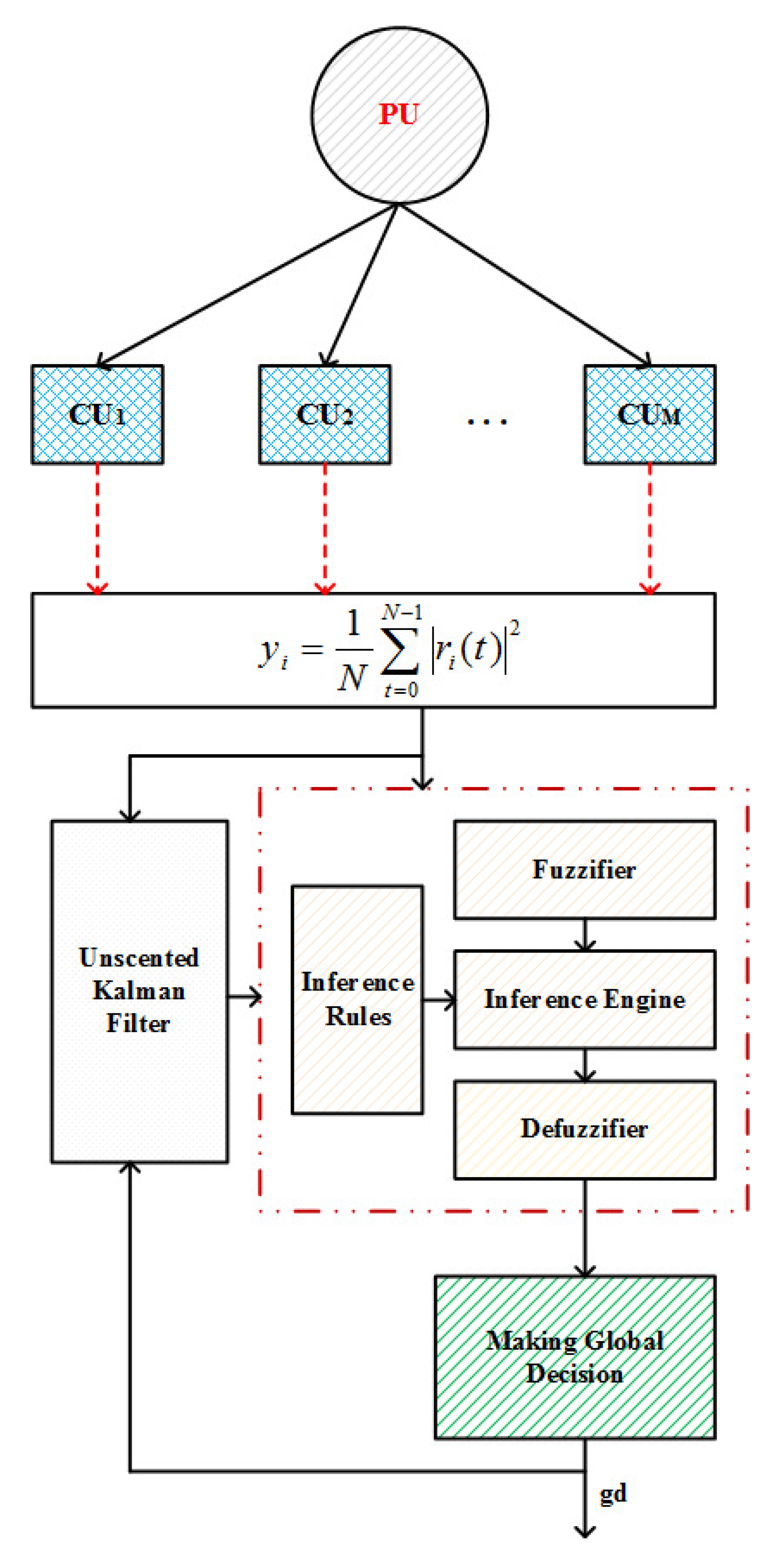
5. Proposed Scheme Based on Unscented Kalman Filter Using an Adaptive Fuzzy System
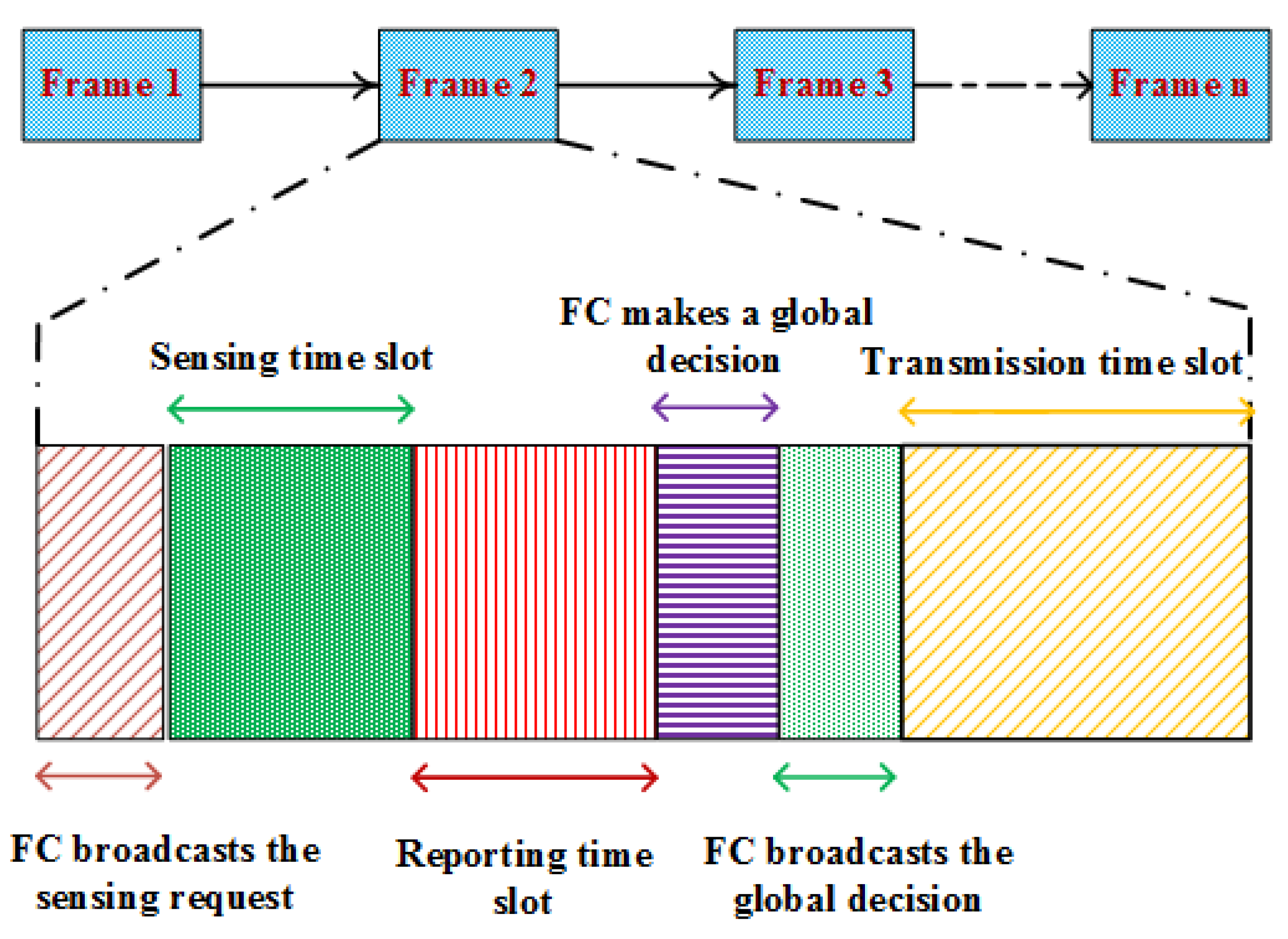
5.1. Cooperative Spectrum Sensing (CSS)
5.2. Kalman Filter (KF)
5.3. Unscented Kalman Filter (UKF)
5.4. Fuzzy Set
5.5. Fuzzy Logic
5.6. Fuzzifier
5.7. Fuzzy Inference Rules
- Rule 1: If ( is Low), then ( = ).
- Rule 2: If ( is High), then ( = ).
5.8. Defuzzification
5.9. Global Decision
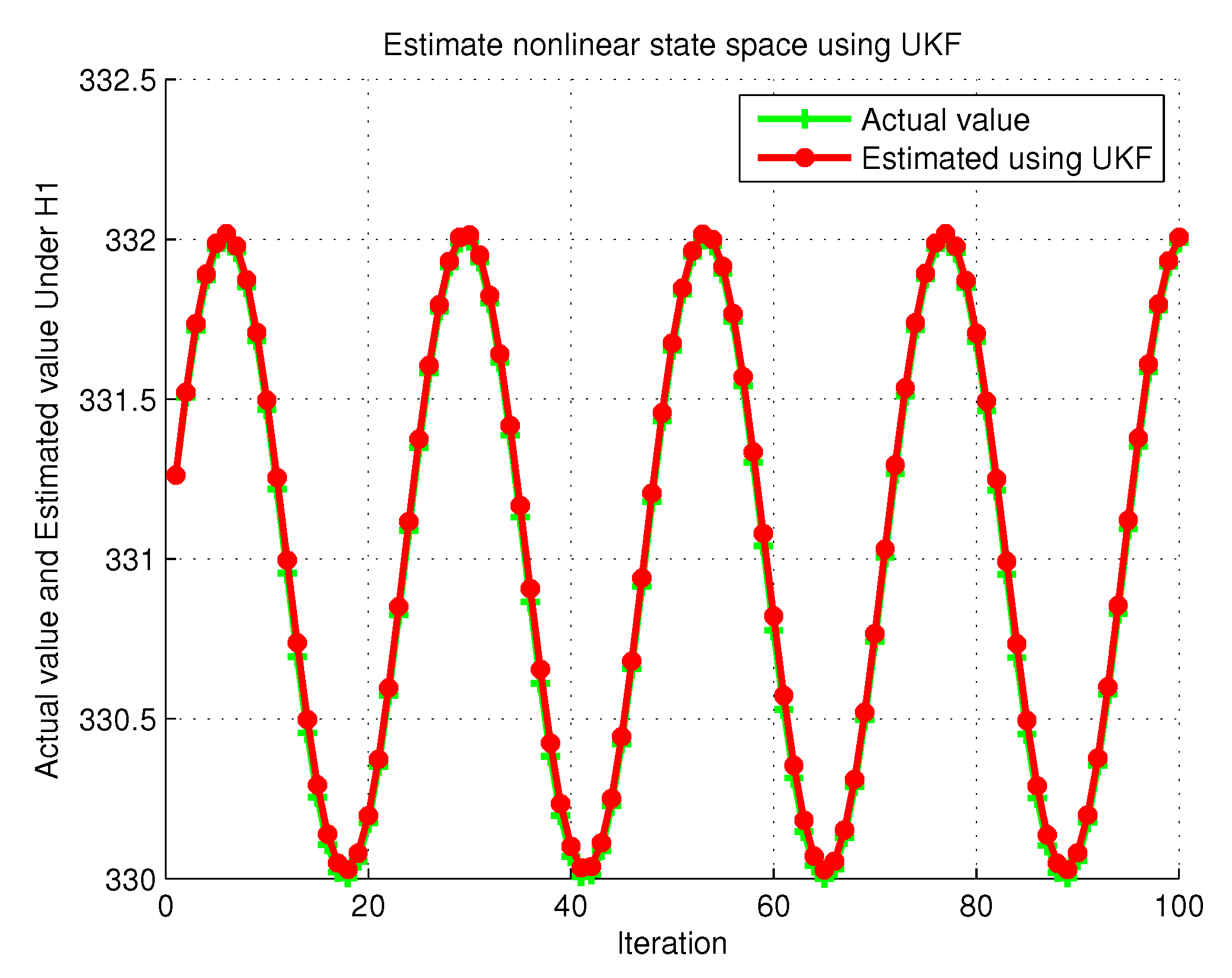
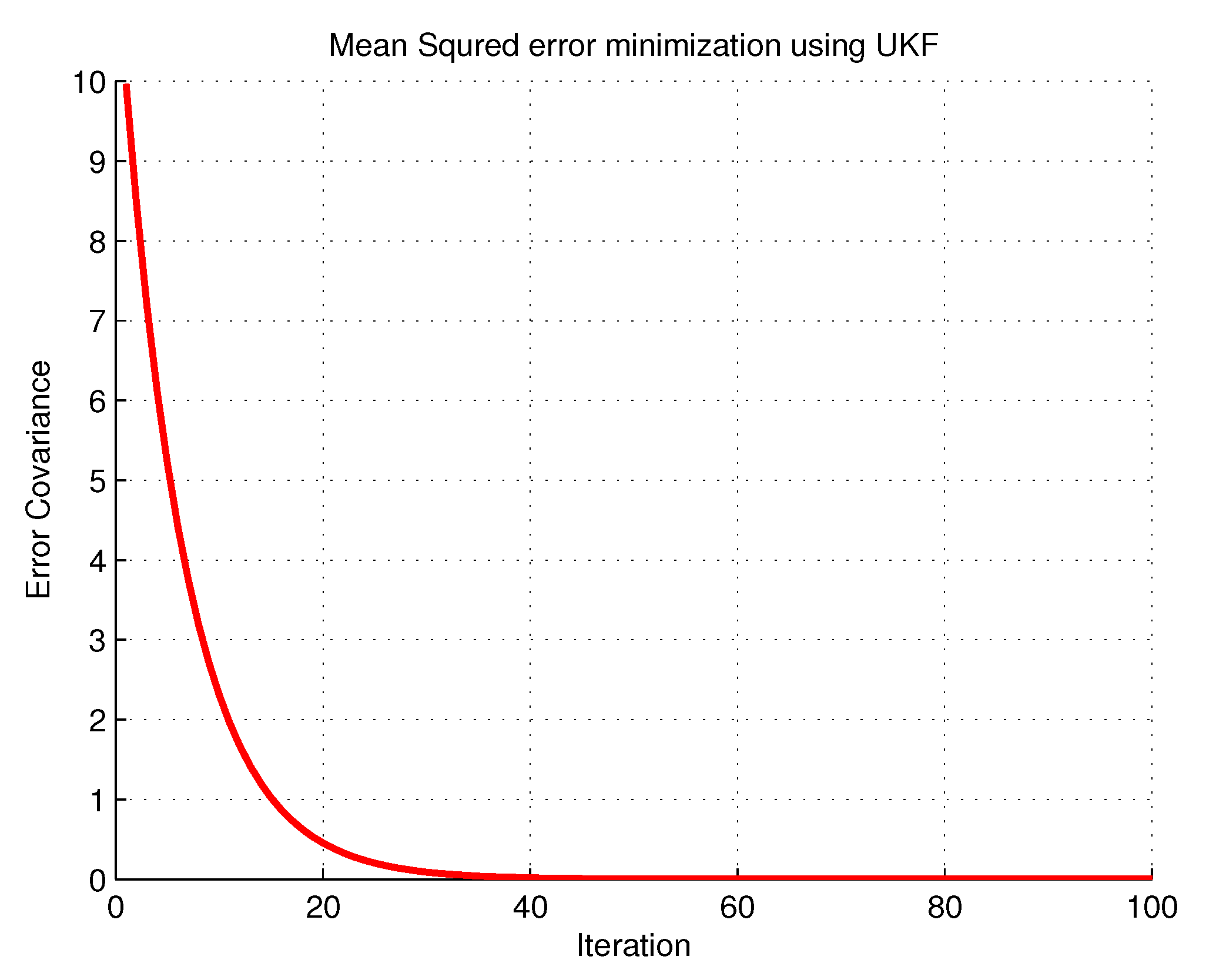
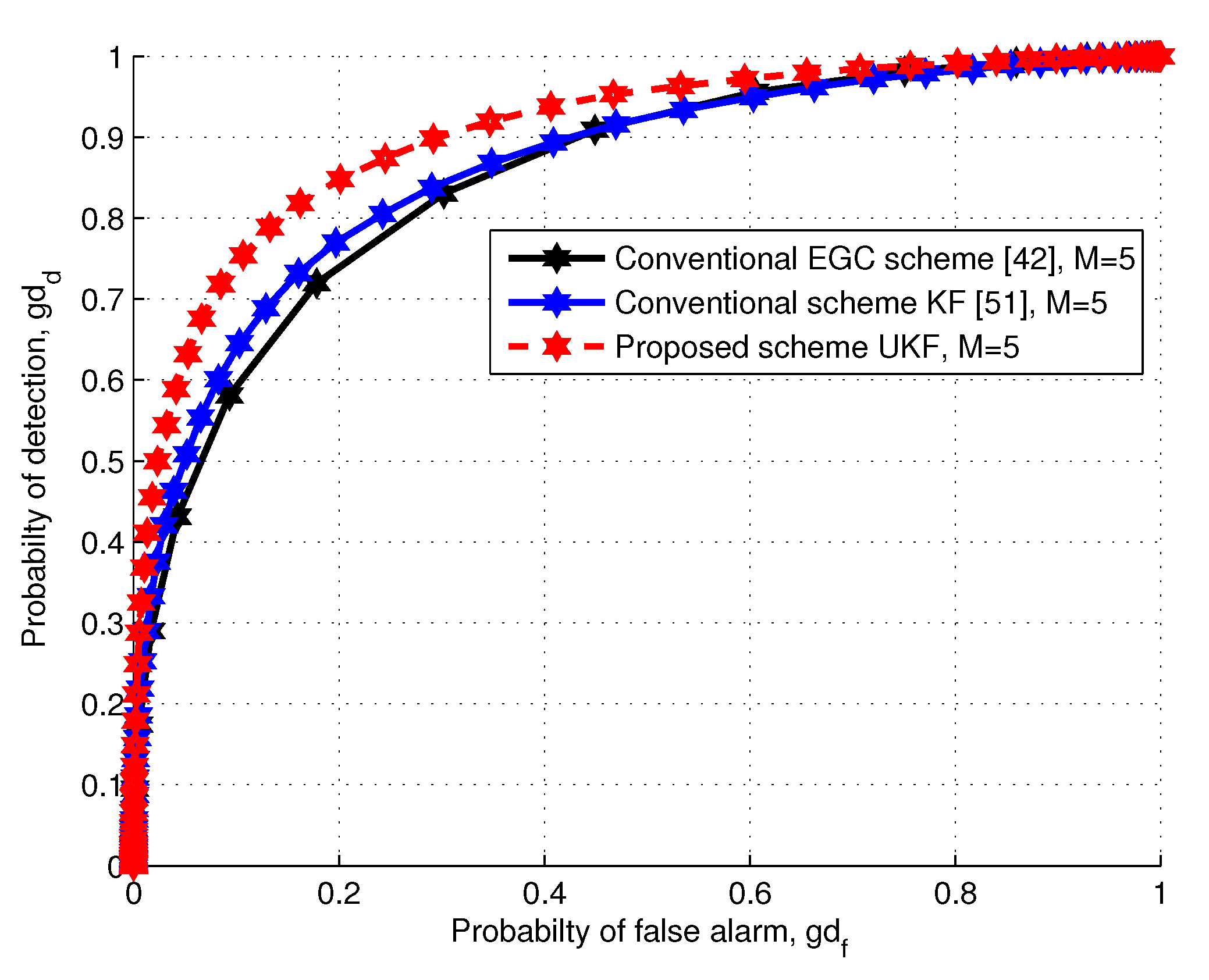
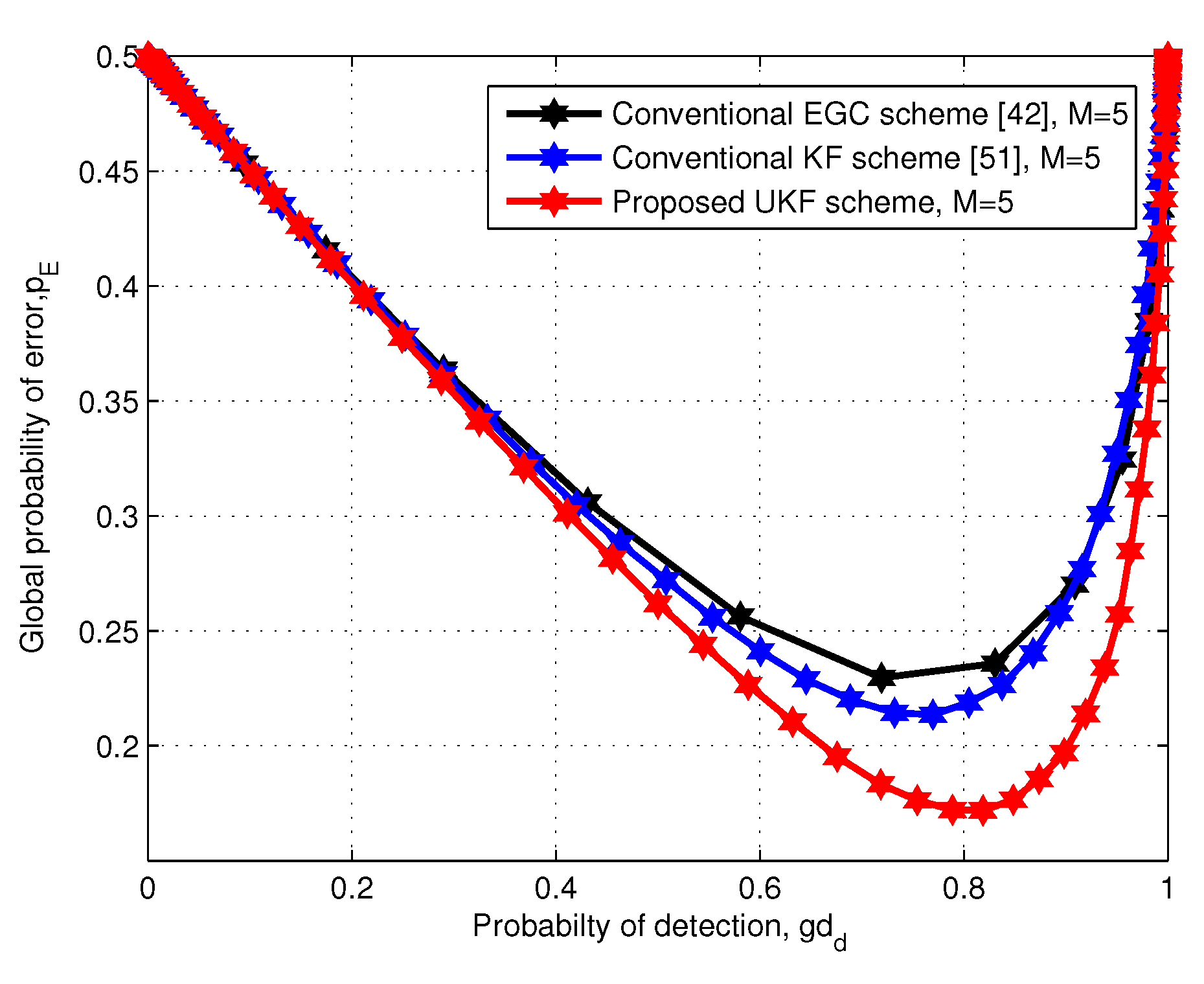
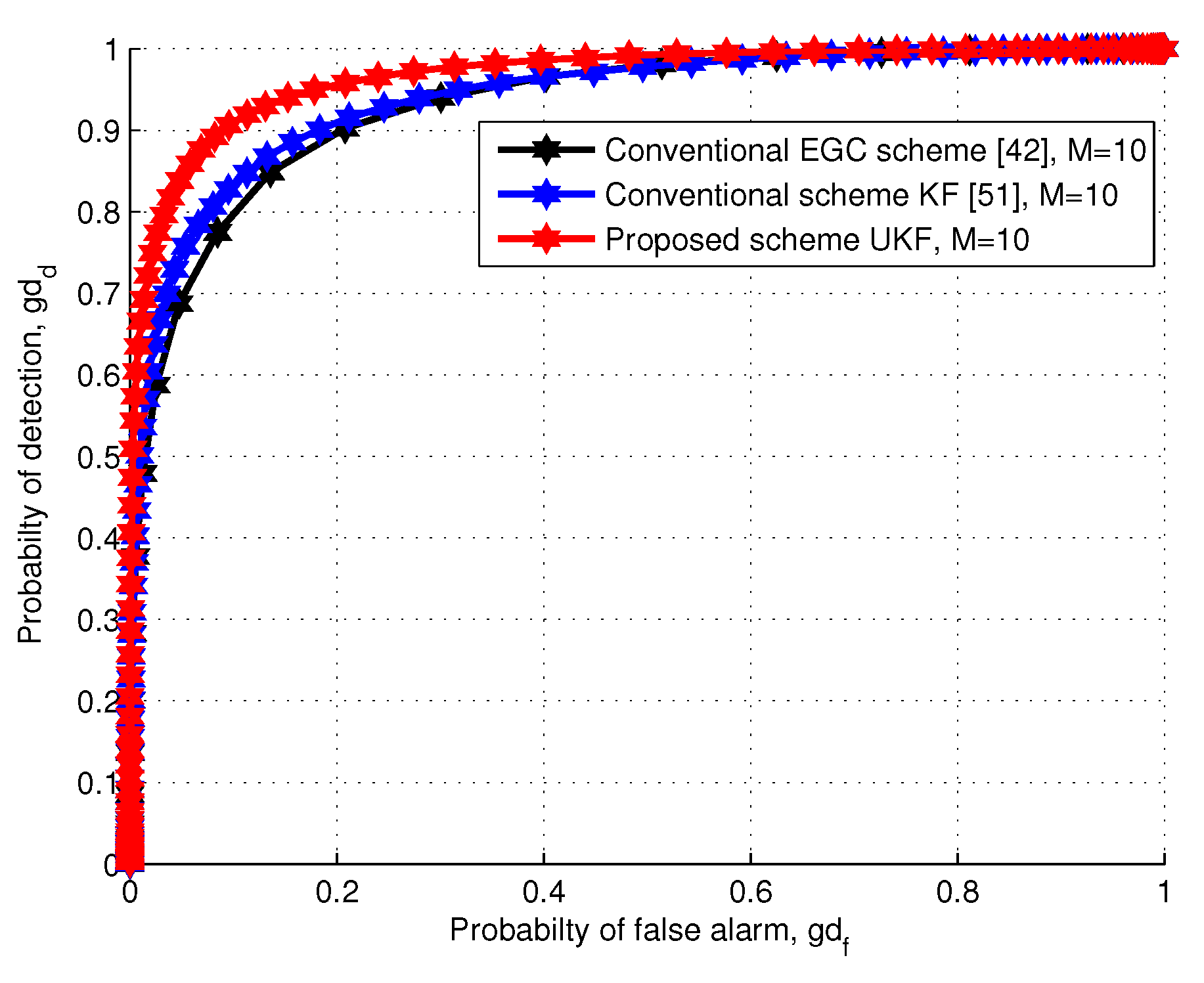
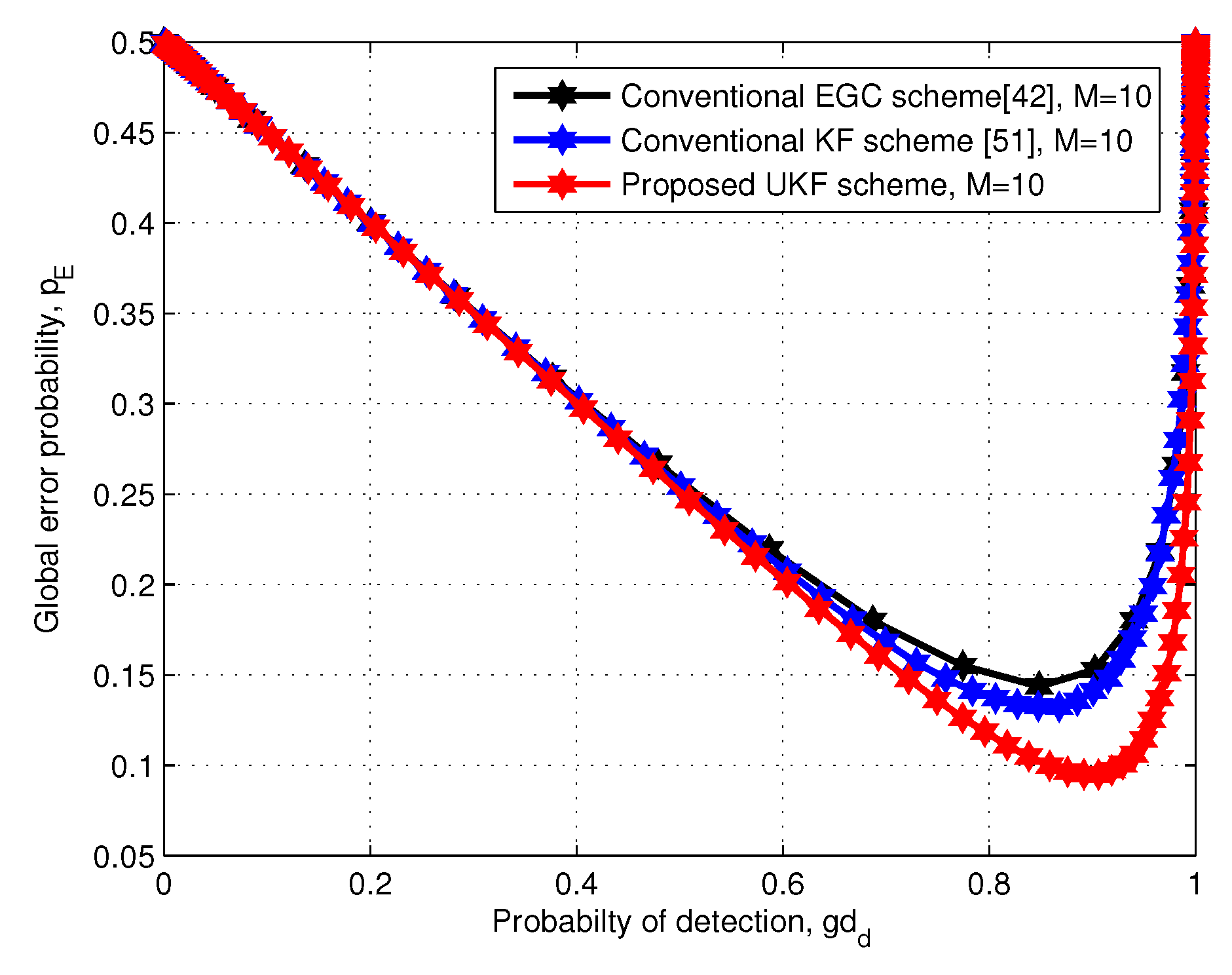
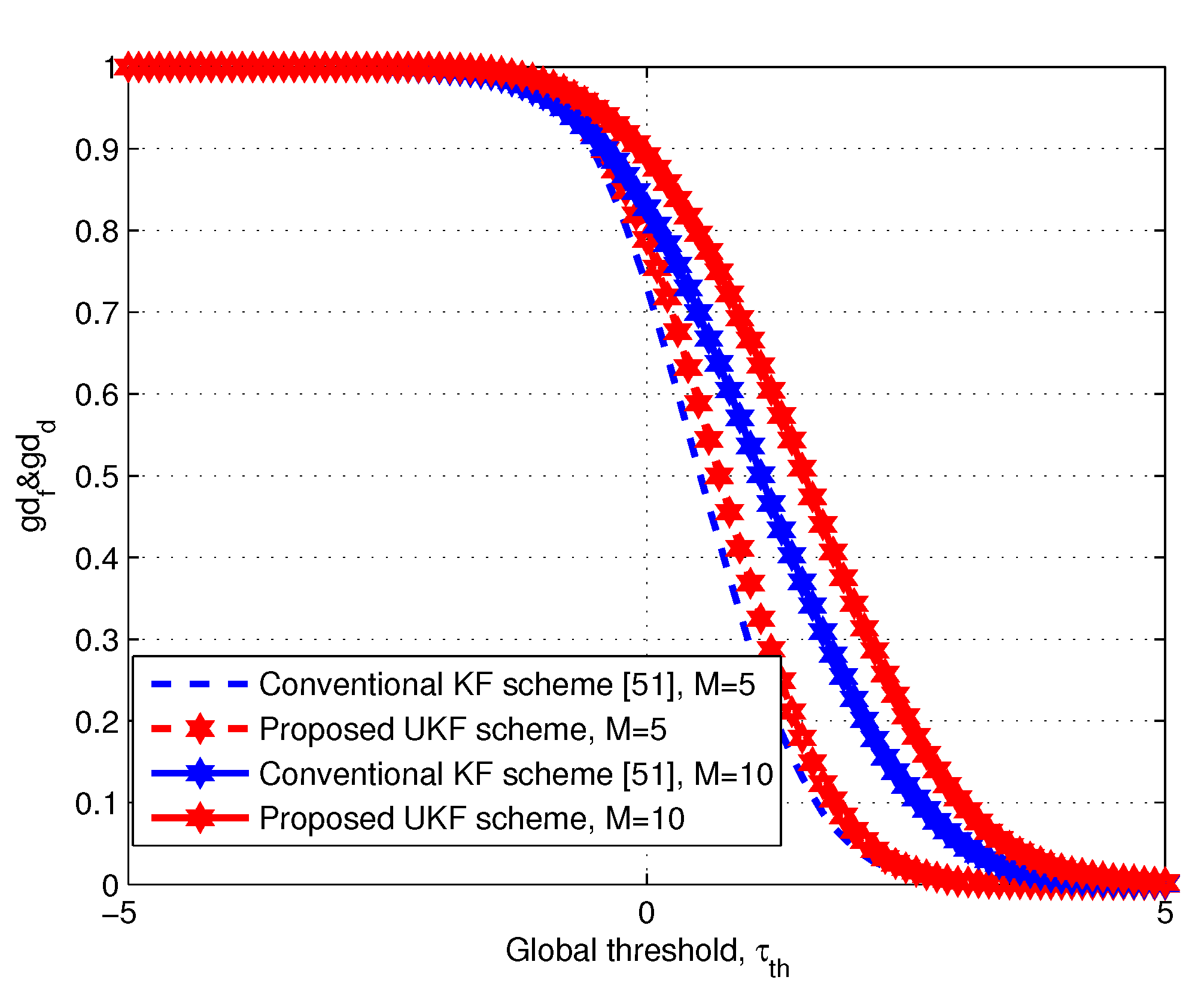
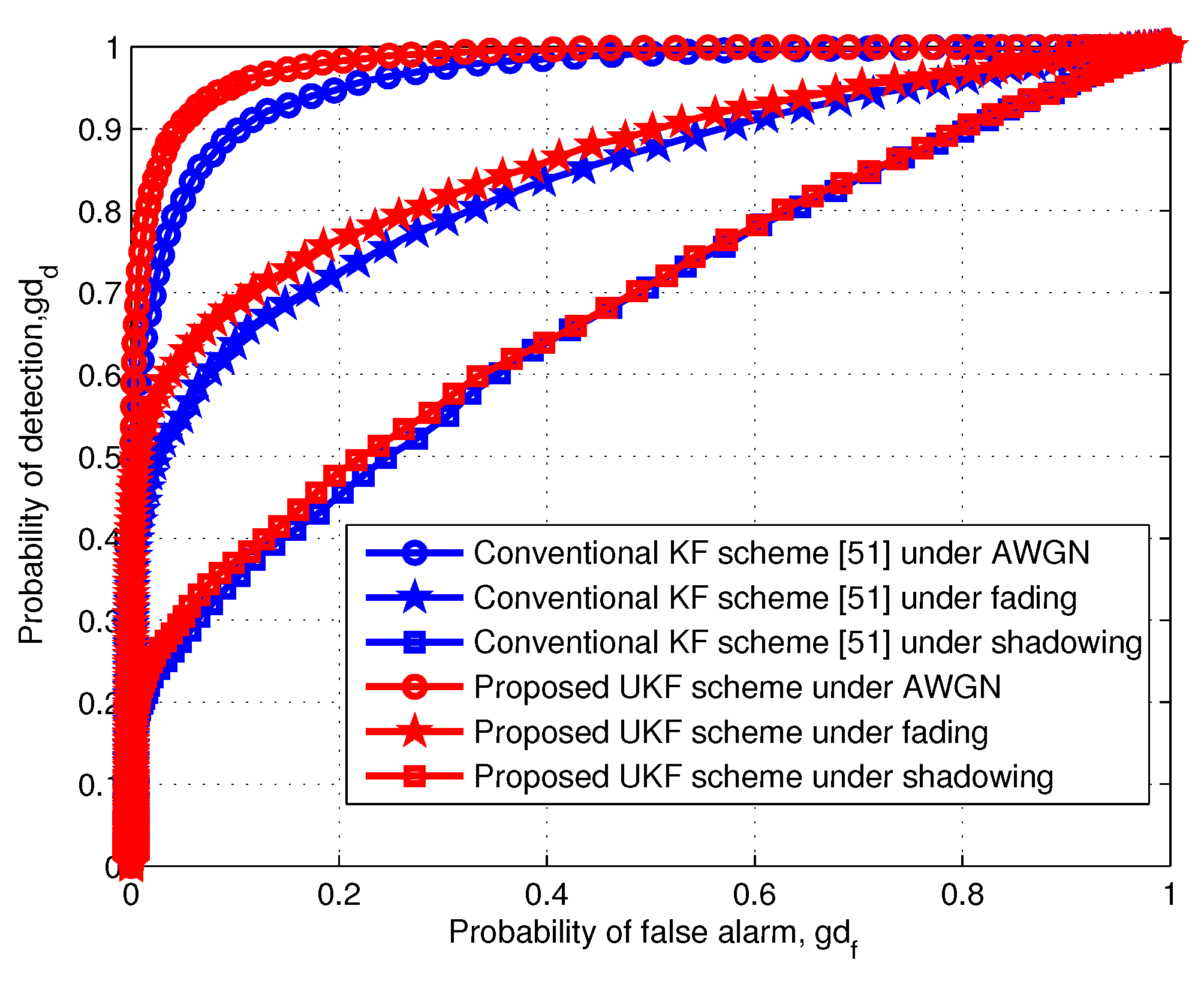
6. Simulation Results and Discussion
7. Conclusions and Future Work
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| UKF | Unscented Kalman Filter |
| CSS | Cooperative Spectrum Sensing |
| CRN | Cognitive Radio Network |
| PU | Primary User |
| FC | Fusion Center |
| EGC | Equal Gain Combining |
| KF | Kalman Filter |
| WSN | Wireless Sensor Network |
| FCC | Federal Communication Commission |
| CR | Cognitive Radio |
| CRN | Cognitive Radio Network |
| CU | Cognitive User |
| ED | Energy Detection |
| SNR | Signal-to-Noise Ratio |
| EKF | Extended Kalman Filter |
| AWGN | Additive White Gaussian Noise |
| PN | Primary Network |
| TDMA | Time Division Multiplexig Access |
| ADC | Analog-to-Digital converter |
| CLT | Central Limit Theory |
| MSEM | Mean Squared Error Minimization |
| ROC | Receiver Operating Characteristics |
References
- Zhang, C.; Hu, Z.; Guo, T.N.; Qiu, R.; Currie, K. Cognitive radio network as wireless sensor network (III): Passive target intrusion detection and experimental demonstration. In Proceedings of the 2012 IEEE Radar Conference (RADAR), Atlanta, GA, USA, 7–11 May 2012; pp. 293–298. [Google Scholar]
- Nakayama, Y.; Maruta, K. Analysis of Nonlinear Bypass Route Computation for Wired and Wireless Network Cooperation Recovery System. Big Data Cogn. Comput. 2018, 2, 28. [Google Scholar] [CrossRef]
- Stevenson, C.R.; Chouinard, G.; Lei, Z.; Hu, W.; Shellhammer, S.J.; Caldwell, W. IEEE 802.22: The first cognitive radio wireless regional area network standard. IEEE Commun. Mag. 2009, 47, 130–138. [Google Scholar] [CrossRef]
- Oh, D.C.; Lee, Y.H. Energy detection based spectrum sensing for sensing error minimization in cognitive radio networks. Int. J. Commun. Netw. Inf. Secur. 2009, 1, 1–5. [Google Scholar]
- Chen, M.; Yang, J.; Hao, Y.; Mao, S.; Hwang, K. A 5G cognitive system for healthcare. Big Data Cogn. Comput. 2017, 1, 2. [Google Scholar] [CrossRef]
- Miah, M.S.; Schukat, M.; Barrett, E. An enhanced sum rate in the cluster based cognitive radio relay network using the sequential approach for the future Internet of Things. Hum.-Centric Comput. Inf. Sci. 2018, 8, 16. [Google Scholar] [CrossRef]
- Zhang, L.; Xiao, Z. Performance analysis of cooperative spectrum sensing algorithm for cognitive radio networks. In Proceedings of the 2010 International Conference on Computer Design and Applications (ICCDA), Qinhuangdao, China, 25–27 June 2010; Volume 4, pp. V4–V557. [Google Scholar]
- Mingchuan, Y.; Yuan, L.; Xiaofeng, L.; Wenyan, T. Cyclostationary feature detection based spectrum sensing algorithm under complicated electromagnetic environment in cognitive radio networks. China Commun. 2015, 12, 35–44. [Google Scholar]
- Upadhyay, S.; Deshmukh, S. Blind parameter estimation based matched filter detection for cognitive radio networks. In Proceedings of the 2015 International Conference on Communications and Signal Processing (ICCSP), Melmaruvathur, India, 2–4 April 2015; pp. 904–908. [Google Scholar]
- Dos Santos Costa, L.; Bomfin, R.C.D.V.; Guimarães, D.A.; de Souza, R.A.A. Performance of Blind Cooperative Spectrum Sensing under Nonuniform Signal and Noise Powers. J. Commun. Inf. Syst. 2018, 33. [Google Scholar] [CrossRef]
- Politis, C.; Maleki, S.; Tsinos, C.G.; Liolis, K.P.; Chatzinotas, S.; Ottersten, B. Simultaneous sensing and transmission for cognitive radios with imperfect signal cancellation. IEEE Trans. Wirel. Commun. 2017, 16, 5599–5615. [Google Scholar] [CrossRef]
- Gahane, L.; Sharma, P.K.; Varshney, N.; Tsiftsis, T.A.; Kumar, P. An Improved Energy Detector for Mobile Cognitive Users Over Generalized Fading Channels. IEEE Trans. Commun. 2018, 66, 534–545. [Google Scholar] [CrossRef]
- Wei, L.; Tirkkonen, O. Cooperative spectrum sensing of OFDM signals using largest eigenvalue distributions. In Proceedings of the 2009 IEEE 20th International Symposium on Personal, Indoor and Mobile Radio Communications, Tokyo, Japan, 13–16 September 2009; pp. 2295–2299. [Google Scholar]
- Miah, M.S.; Rahman, M.M.; Yu, H. Superallocation and Cluster-Based Cooperative Spectrum Sensing in 5G Cognitive Radio Network. In Towards 5G Wireless Networks—A Physical Layer Perspective; InTech: London, UK, 2016. [Google Scholar]
- Miah, M.S.; Yu, H.; Godder, T.K.; Rahman, M.M. A cluster-based cooperative spectrum sensing in cognitive radio network using eigenvalue detection technique with superposition approach. Int. J. Distrib. Sens. Netw. 2015, 11, 207935. [Google Scholar] [CrossRef]
- Ma, J.; Zhao, G.; Li, Y. Soft combination and detection for cooperative spectrum sensing in cognitive radio networks. IEEE Trans. Wirel. Commun. 2008, 7, 4502–4507. [Google Scholar]
- Miah, M.S.; Schukat, M.; Barrett, E. Maximization of sum rate in AF-cognitive radio networks using superposition approach and n-out-of-k rule. In Proceedings of the 2017 28th Irish Signals and Systems Conference (ISSC), Killarney, Ireland, 20–21 June 2017; pp. 1–6. [Google Scholar]
- Captain, K.; Joshi, M. SNR wall for generalized energy detector in the presence of noise uncertainty and fading. Phys. Commun. 2018, 32, 172–184. [Google Scholar] [CrossRef]
- Swetha, N.; Sastry, P.N.; Rao, Y.R.; Sabat, S.L. Parzen window entropy based spectrum sensing in cognitive radio. Comput. Electr. Eng. 2016, 52, 379–389. [Google Scholar] [CrossRef]
- Oubabas, H.; Djennoune, S.; Bettayeb, M. Interval sliding mode observer design for linear and nonlinear systems. J. Process Control 2018, 61, 12–22. [Google Scholar] [CrossRef]
- Jacob, J.; Jose, B.R.; Mathew, J. A fuzzy approach to decision fusion in cognitive radio. Procedia Comput. Sci. 2015, 46, 425–431. [Google Scholar] [CrossRef]
- Bharatula, S.; Murugappan, M. An intelligent fuzzy based energy detection approach for cooperative spectrum sensing. Circuits Syst. 2016, 7, 1042. [Google Scholar] [CrossRef]
- Wang, L. Adaptive Fuzzy Systems and Control: Design and Stability Analysis; PTR Prentice Hall: Englewood Cliffs, NJ, USA, 1994. [Google Scholar]
- Digham, F.F.; Alouini, M.S.; Simon, M.K. On the energy detection of unknown signals over fading channels. In Proceedings of the IEEE International Conference on Communications (ICC’03), Anchorage, AK, USA, 11–15 May 2003; Volume 5, pp. 3575–3579. [Google Scholar]
- St-Pierre, M.; Gingras, D. Comparison between the unscented Kalman filter and the extended Kalman filter for the position estimation module of an integrated navigation information system. In Proceedings of the IEEE Intelligent Vehicles Symposium, Parma, Italy, 14–17 June 2004; pp. 831–835. [Google Scholar]
- Julier, S.J.; Uhlmann, J.K. New extension of the Kalman filter to nonlinear systems. In Signal Processing, Sensor Fusion, and Target Recognition VI; International Society for Optics and Photonics: Bellingham, WA, USA, 1997; Volume 3068, pp. 182–194. [Google Scholar]
- Chandrasekar, J.; Ridley, A.; Bernstein, D. A comparison of the extended and unscented Kalman filters for discrete-time systems with nondifferentiable dynamics. In Proceedings of the American Control Conference (ACC’07), New York, NY, USA, 9–13 July 2007; pp. 4431–4436. [Google Scholar]
- Yawada, P.S.; Wei, A.J. Comparative study of spectrum sensing techniques base on techniques non-cooperative in cognitive radio networks. In Proceedings of the 2016 5th International Conference on Computer Science and Network Technology (ICCSNT), Changchun, China, 10–11 December 2016; pp. 517–520. [Google Scholar]
- Suseela, B.; Sivakumar, D. Non-cooperative spectrum sensing techniques in cognitive radio—A survey. In Proceedings of the 2015 IEEE Technological Innovation in ICT for Agriculture and Rural Development (TIAR), Chennai, India, 10–12 July 2015; pp. 127–133. [Google Scholar]
- Tsinos, C.G.; Berberidis, K. Decentralized adaptive eigenvalue-based spectrum sensing for multiantenna cognitive radio systems. IEEE Trans. Wirel. Commun. 2015, 14, 1703–1715. [Google Scholar] [CrossRef]
- Ali, S.S.; Liu, C.; Liu, J.; Jin, M.; Kim, J.M. On the Eigenvalue Based Detection for Multiantenna Cognitive Radio System. Mob. Inf. Syst. 2016, 2016, 3848734. [Google Scholar] [CrossRef]
- Nguyen, V.D.; Shin, O.S. Cooperative prediction-and-sensing-based spectrum sharing in cognitive radio networks. IEEE Trans. Cogn. Commun. Netw. 2018, 4, 108–120. [Google Scholar] [CrossRef]
- Mu, J.; Jing, X.; Huang, H.; Gao, N. Subspace-based method for spectrum sensing with multiple users over fading channel. IEEE Commun. Lett. 2018, 22, 848–851. [Google Scholar] [CrossRef]
- Kyperountas, S.; Correal, N.; Shi, Q.; Ye, Z. Performance analysis of cooperative spectrum sensing in Suzuki fading channels. In Proceedings of the 2nd International Conference on Cognitive Radio Oriented Wireless Networks and Communications (CrownCom 2007), Orlando, FL, USA, 1–3 August 2007; pp. 428–432. [Google Scholar]
- Sun, M.; Zhao, C.; Yan, S.; Li, B. A novel spectrum sensing for cognitive radio networks with noise uncertainty. IEEE Trans. Veh. Technol. 2017, 66, 4424–4429. [Google Scholar] [CrossRef]
- Erceg, V.; Greenstein, L.J.; Tjandra, S.Y.; Parkoff, S.R.; Gupta, A.; Kulic, B.; Julius, A.A.; Bianchi, R. An empirically based path loss model for wireless channels in suburban environments. IEEE J. Sel. Areas Commun. 1999, 17, 1205–1211. [Google Scholar] [CrossRef]
- Liu, X.; Zeng, Z.; Guo, C. Robust Cooperative Spectrum Sensing in Dense Cognitive Vehicular Networks. In Proceedings of the 2017 IEEE/CIC International Conference on Communications in China (ICCC), Qingdao, China, 22–24 October 2017; pp. 1–6. [Google Scholar]
- Jia, M.; Zhang, G.; Gu, X. Optimal primary-user mobility aware parameters design of spectrum sensing in cognitive radio networks. In Proceedings of the 2015 International Conference on Information and Communication Technology Convergence (ICTC), Jeju, Korea, 28–30 October 2015; pp. 1237–1239. [Google Scholar]
- Hossain, M.K.; El-Saleh, A.A.; Ismail, M. A comparison between binary and continuous genetic algorithm for collaborative spectrum optimization in cognitive radio network. In Proceedings of the 2011 IEEE Student Conference on Research and Development (SCOReD), Cyberjaya, Malaysia, 19–20 December 2011; pp. 259–264. [Google Scholar]
- Cacciapuoti, A.S.; Caleffi, M.; Paura, L.; Savoia, R. Decision maker approaches for cooperative spectrum sensing: Participate or not participate in sensing? IEEE Trans. Wirel. Commun. 2013, 12, 2445–2457. [Google Scholar] [CrossRef]
- Salam, A.O.A.; Sheriff, R.E.; Al-Araji, S.R.; Mezher, K.; Nasir, Q. Adaptive threshold and optimal frame duration for multi-taper spectrum sensing in cognitive radio. ICT Express 2018, in press. [Google Scholar]
- Deka, S.K.; Chauhan, P.; Sarma, N. Dynamic Threshold based Cooperative Spectrum Sensing using Coalitional Game for CRNs. In Proceedings of the 2018 5th International Conference on Signal Processing and Integrated Networks (SPIN), Noida, Delhi, 22–23 February 2018; pp. 49–55. [Google Scholar]
- Cacciapuoti, A.S.; Caleffi, M.; Paura, L. On the impact of primary traffic correlation in TV White Space. Ad Hoc Netw. 2016, 37, 133–139. [Google Scholar] [CrossRef]
- Anand, J.; Buttar, A.S.; Kaur, R. Fuzzy Logic Based Spectrum Handover Approach in Cognitive Radio Network: A Survey. In Proceedings of the 2018 Second International Conference on Electronics, Communication and Aerospace Technology (ICECA), Coimbatore, Tamilnadu, India, 29–31 March 2018; pp. 775–780. [Google Scholar]
- Wang, Y.; Li, Y.; Yuan, F.; Yang, J. A cooperative spectrum sensing scheme based on trust and fuzzy logic for cognitive radio sensor networks. Int. J. Comput. Sci. Issues 2013, 10, 275. [Google Scholar]
- Vijayakumar, P.; Malarvizhi, S. Fuzzy Logic Based Decision System for Context Aware Cognitive Waveform Generation. Wirel. Pers. Commun. 2017, 94, 2681–2703. [Google Scholar] [CrossRef]
- Kieu-Xuan, T.; Koo, I. A Cooperative Spectrum Sensing Scheme Using Fuzzy Logic for Cognitive Radio Networks. KSII Trans. Internet Inf. Syst. 2010, 4, 289–304. [Google Scholar] [CrossRef]
- Kieu-Xuan, T.; Koo, I. Cooperative Spectrum Sensing using Kalman Filter based Adaptive Fuzzy System for Cognitive Radio Networks. KSII Trans. Internet Inf. Syst. 2012, 6, 287–304. [Google Scholar] [CrossRef]
| Parameters | Meaning |
|---|---|
| K | The Kalman gain |
| The effective weights | |
| Hypotheses (absent/present) | |
| The global error probability | |
| The global decision threshold at the fusion center (FC) | |
| The posterior estimate at the kth element | |
| The posterior covariance at the kth element | |
| The posterior observations at the kth element | |
| The nonlinearity function in the process model | |
| The nonlinearity function in the measurement model | |
| The signal-to-noise ratio (SNR) at the ith cognitive user (CU) | |
| The local decision based on the observation at the ith CU | |
| The global decision at the FC where the subscript, f is the probability of false alarm | |
| The global decision at the FC where the subscript, d is the probability of detection |
| Parameters | Value |
|---|---|
| The number of samples, N | 300 |
| The number of iteration, L | 5000 |
| The sensing time, | 1 ms |
| The time slot length, T | 10 ms |
| The channel bandwidth, W | 300 kHz |
| The number of CUs, M | [5, 10] |
| The primary user signal, | BPSK |
| The channel noise in CU, | AWGN |
| The minimum SNR, | −30 dB |
| The maximum SNR, | 20 dB |
| The channels | AWGN fading |
| The global decision threshold, | [−5, 5] |
| The probability of the absence of the PU, | 0.5 |
| The probability of the presence of the PU, | 0.5 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Amin, M.R.; Rahman, M.M.; Hossain, M.A.; Islam, M.K.; Ahmed, K.M.; Singh, B.C.; Miah, M.S. Unscented Kalman Filter Based on Spectrum Sensing in a Cognitive Radio Network Using an Adaptive Fuzzy System. Big Data Cogn. Comput. 2018, 2, 39. https://doi.org/10.3390/bdcc2040039
Amin MR, Rahman MM, Hossain MA, Islam MK, Ahmed KM, Singh BC, Miah MS. Unscented Kalman Filter Based on Spectrum Sensing in a Cognitive Radio Network Using an Adaptive Fuzzy System. Big Data and Cognitive Computing. 2018; 2(4):39. https://doi.org/10.3390/bdcc2040039
Chicago/Turabian StyleAmin, Md Ruhul, Md Mahbubur Rahman, Mohammad Amazad Hossain, Md Khairul Islam, Kazi Mowdud Ahmed, Bikash Chandra Singh, and Md Sipon Miah. 2018. "Unscented Kalman Filter Based on Spectrum Sensing in a Cognitive Radio Network Using an Adaptive Fuzzy System" Big Data and Cognitive Computing 2, no. 4: 39. https://doi.org/10.3390/bdcc2040039
APA StyleAmin, M. R., Rahman, M. M., Hossain, M. A., Islam, M. K., Ahmed, K. M., Singh, B. C., & Miah, M. S. (2018). Unscented Kalman Filter Based on Spectrum Sensing in a Cognitive Radio Network Using an Adaptive Fuzzy System. Big Data and Cognitive Computing, 2(4), 39. https://doi.org/10.3390/bdcc2040039






