NREL-5MW Wind Turbine Noise Prediction by FWH-LES †
Abstract
:1. Introduction
2. Methodology
2.1. Large Eddy Simulation
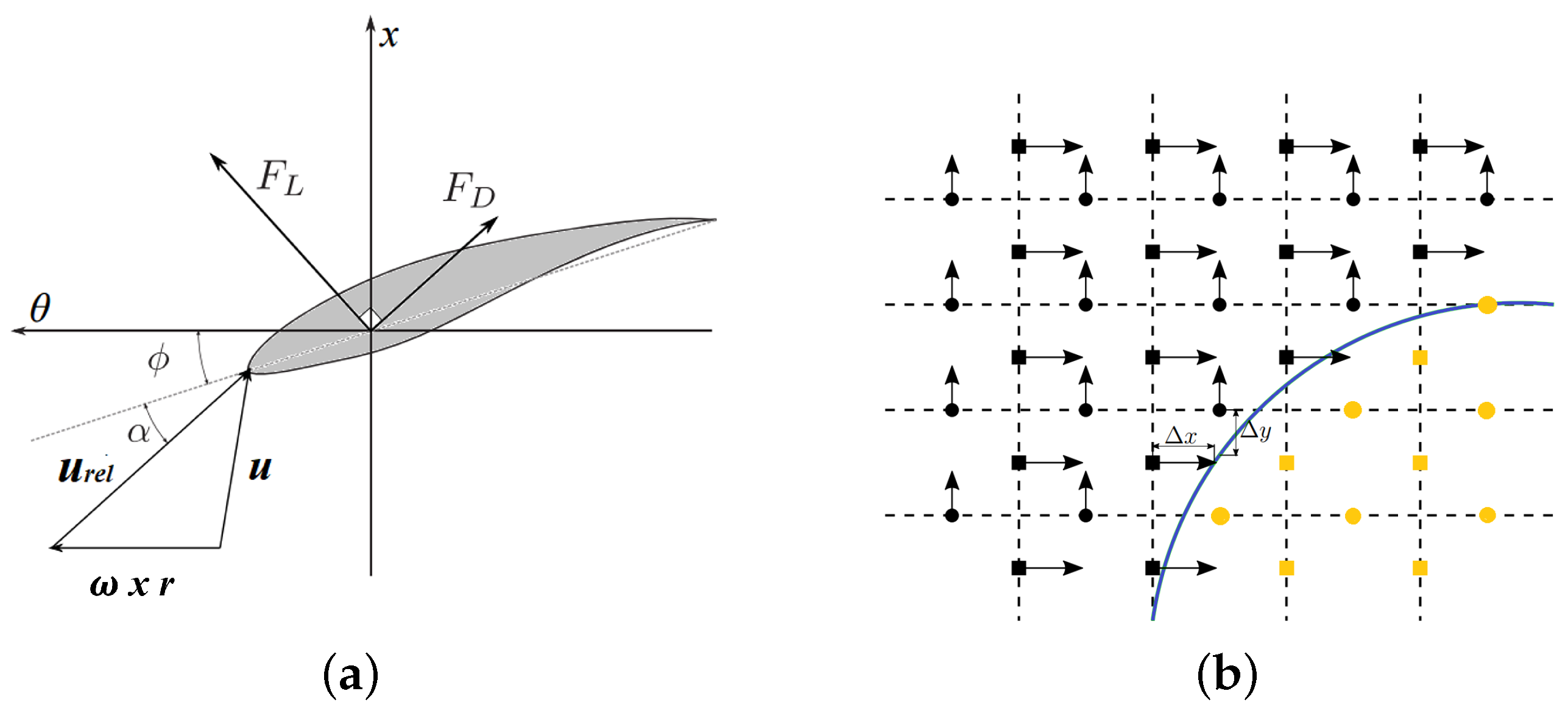
2.2. Actuator Line Model and Immersed Boundary Method
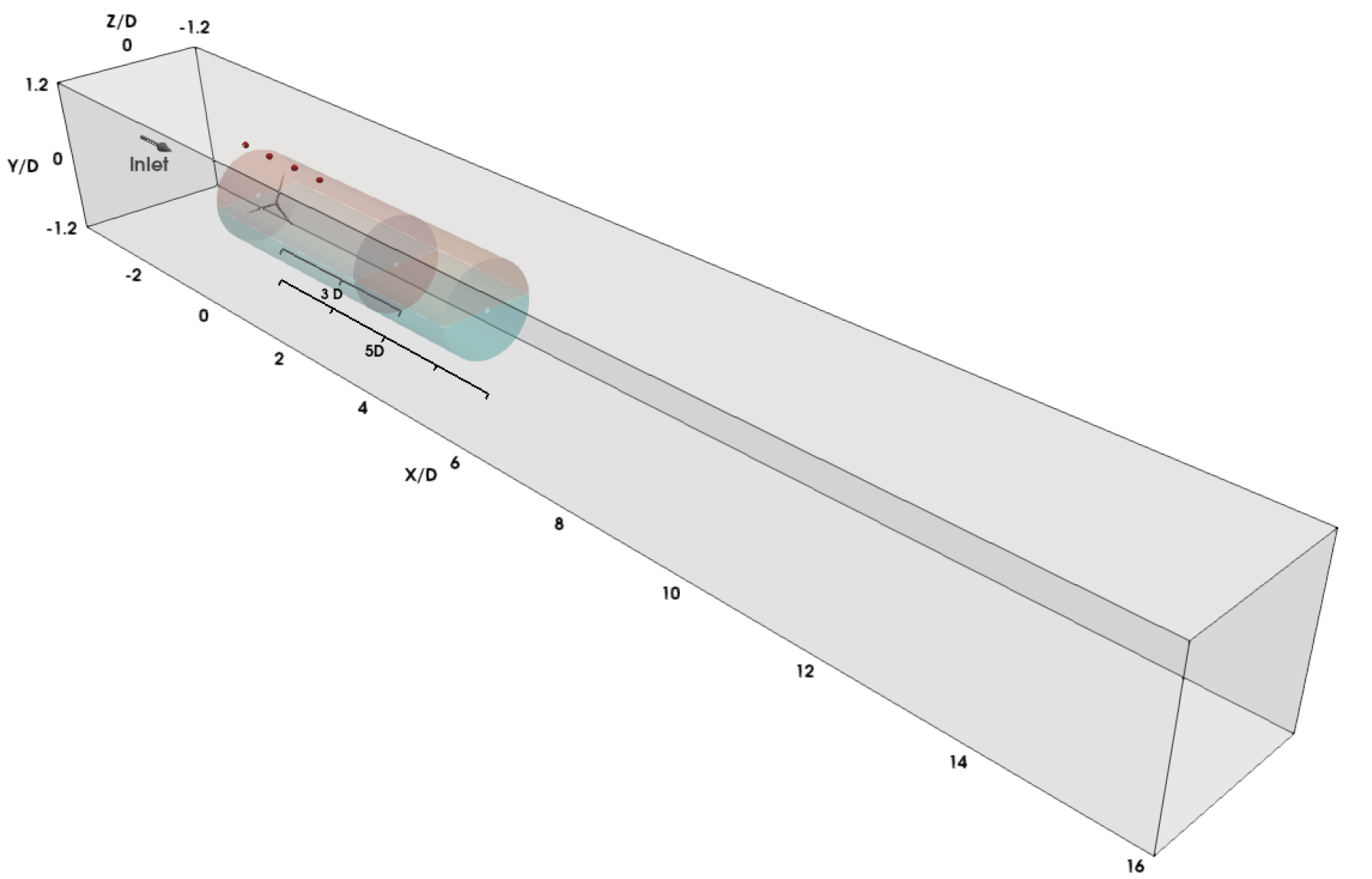
2.3. Simulation Setup
2.4. FWH Acoustic Analogy
2.5. Sound Computation Procedure
2.5.1. Interpolation
2.5.2. Outflow Disk Averaging
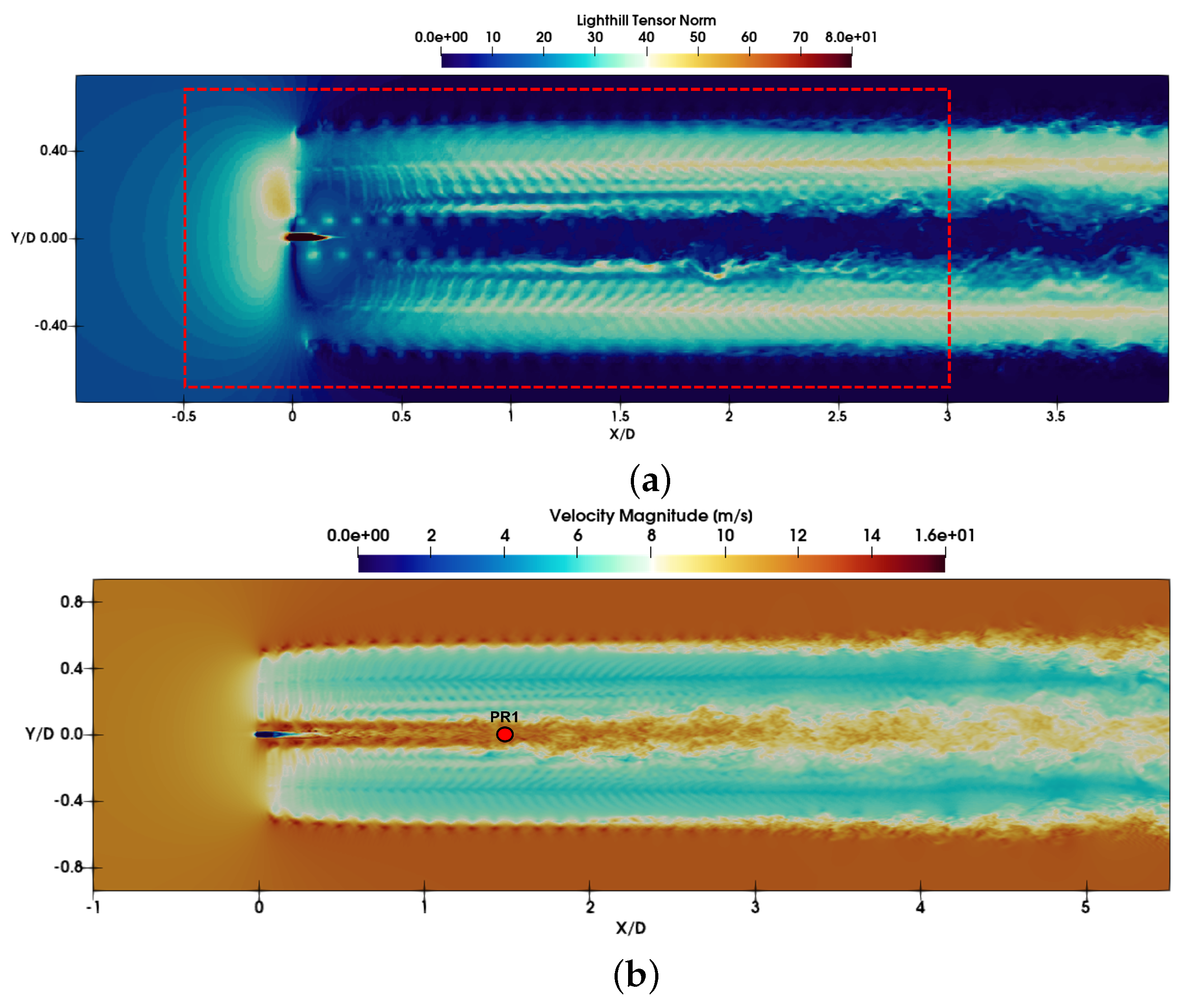
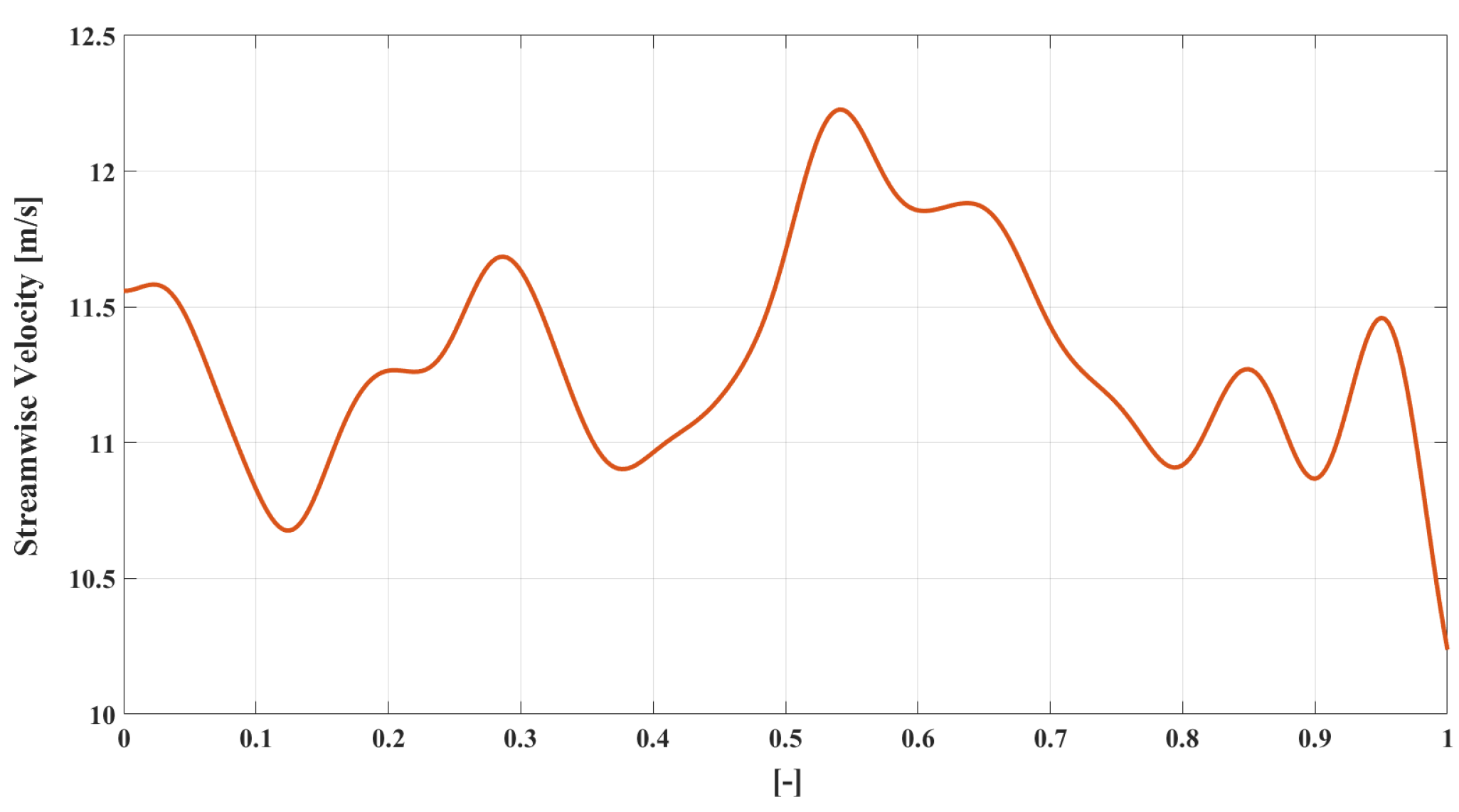
3. Numerical Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| LES | Large-Eddy Simulation |
| ALM | Actuator Line Method |
| IBM | Immersed Boundary Method |
| FWH-P | Ffowcs Williams–Hawkings equation for porous surface |
| OASPL | Overall Sound Pressure Level |
| Acoustic Permeable Surface | |
| BEM | Boundary Element Method |
| SGS | Sub-Grid Scale |
| CFD | Computational Fluid Dynamics |
| OBS | Acoustic Observer |
| PSD | Power Spectral Density |
| FFT | Fast Fourier Transform |
| BPF | Blade Passage Frequency |
References
- Bolinger, M.; Wiser, R. Understanding wind turbine price trends in the US over the past decade. Energy Policy 2012, 42, 628–641. [Google Scholar] [CrossRef]
- Tonin, R. Sources of wind turbine noise and sound propagation. Acoust. Aust. 2012, 40. [Google Scholar]
- Jimenez, A.; Crespo, A.; Migoya, E.; García, J. Advances in large-eddy simulation of a wind turbine wake. J. Phys. Conf. Ser. 2007, 75, 012041. [Google Scholar] [CrossRef]
- Porté-Agel, F.; Wu, Y.T.; Lu, H.; Conzemius, R.J. Large-eddy simulation of atmospheric boundary layer flow through wind turbines and wind farms. J. Wind Eng. Ind. Aerodyn. 2011, 99, 154–168. [Google Scholar] [CrossRef]
- Delorme, Y.; Stanly, R.; Frankel, S.H.; Greenblatt, D. Application of actuator line model for large eddy simulation of rotor noise control. Aerosp. Sci. Technol. 2021, 108, 106405. [Google Scholar] [CrossRef]
- Bontempo, R.; Manna, M. Effects of the approximations embodied in the momentum theory as applied to the nrel phase vi wind turbine. Int. J. Turbomach. Propuls. Power 2017, 2, 9. [Google Scholar] [CrossRef]
- Bernardi, C.; Porcacchia, F.; Testa, C.; De Palma, P.; Leonardi, S.; Cherubini, S. Wind Turbine Aeroacustics by Large-Eddy Simulation—Acoustic Analogy Approach. In Proceeding of the 15th European Turbomachinery Conference, Budapest, Hungary, 24–28 April 2023; Paper n. ETC2023-333. Available online: https://www.euroturbo.eu/publications/conference-proceedings-repository/ (accessed on 15 November 2023).
- De Cillis, G.; Cherubini, S.; Semeraro, O.; Leonardi, S.; De Palma, P. POD-based analysis of a wind turbine wake under the influence of tower and nacelle. Wind Energy 2021, 24, 609–633. [Google Scholar] [CrossRef]
- Sotiropoulos, F.; Yang, X. Immersed boundary methods for simulating fluid–structure interaction Prog. Aerosp. Sci. 2014, 65, 1–21. [Google Scholar]
- De Cillis, G.; Cherubini, S.; Semeraro, O.; Leonardi, S.; De Palma, P. The influence of incoming turbulence on the dynamic modes of an NREL-5MW wind turbine wake. Renew. Energy 2022, 183, 601–616. [Google Scholar] [CrossRef]
- Ffowcs Williams, J.; Hawkings, D. Sound Generation by Turbulence and Surfaces in Arbitrary Motion. Phil. Trans. R. Soc. A 1969, 264, 321–342. [Google Scholar]
- di Francescantonio, P. A new boundary integral formulation for the prediction of sound radiation. J. Sound Vib. 1997, 202, 491–509. [Google Scholar] [CrossRef]
- De Cillis, G.; Semeraro, O.; Leonardi, S.; De Palma, P.; Cherubini, S. Dynamic-mode-decomposition of the wake of the NREL-5MW wind turbine impinged by a laminar inflow. Renew. Energy 2022, 199, 1–10. [Google Scholar] [CrossRef]
- Ciri, U.; Salvetti, M.; Carrasquillo, K.; Santoni, C.; Iungo, G.; Leonardi, S. Effects of the subgrid-scale modeling in the large-eddy simulations of wind turbines. In Direct and Large-Eddy Simulation X; Springer: Berlin/Heidelberg, Germany, 2018; pp. 109–115. [Google Scholar]
- Sarlak, H.; Meneveau, C.; Sørensen, J.N. Role of subgrid-scale modeling in large eddy simulation of wind turbine wake interactions. Renew. Energy 2015, 77, 386–399. [Google Scholar] [CrossRef]
- Sørensen, J.N.; Shen, W.Z. Computation of wind turbine wakes using combined Navier-Stokes/actuator-line Methodology. In Proceedings of the 1999 European Wind Energy Conference and Exhibition, Nice, France, 1–5 March 1999; pp. 156–159. [Google Scholar]
- Troldborg, N. Actuator Line Modeling of Wind Turbine Wakes; Technical University of Denmark: Lyngby, Denmark, 2009. [Google Scholar]
- Orlandi, P.; Leonardi, S. DNS of turbulent channel flows with two-and three-dimensional roughness. J. Turbul. 2006, 7, N73. [Google Scholar] [CrossRef]
- Jonkman, J.; Butterfield, S.; Musial, W.; Scott, G. Definition of a 5-MW Reference Wind Turbine for Offshore System Development; Technical report; National Renewable Energy Lab. (NREL): Golden, CO, USA, 2009.
- Lighthill, M. On sound generated aerodynamically. I. General theory. Proc. R. Soc. A 1952, 211, 564–587. [Google Scholar]
- Brentner, K.; Farassat, F. An Analytical Comparison of the Acoustic Analogy and Kirchhoff Formulation for Moving Surfaces. AIAA J. 1997, 36, 1379–1386. [Google Scholar] [CrossRef]
- Testa, C.; Poggi, C.; Bernardini, G.; Gennaretti, M. Pressure-field permeable-surface integral formulations for sound scattered by moving bodies. J. Sound Vib. 2019, 459, 114860. [Google Scholar] [CrossRef]
- Testa, C.; Porcacchia, F.; Zaghi, S.; Gennaretti, M. Study of a FWH-based permeable-surface formulation for propeller hydroacoustics. Ocean Eng. 2021, 240, 109828. [Google Scholar] [CrossRef]
- Nitzkorski, Z.; Mahesh, K. A Dynamic end cap Technique for Sound Computation Using the Ffowcs Williams and Hawkings Equations. Phys. Fluids 2014, 26. [Google Scholar] [CrossRef]
- Uzun, A.; Lyrintsis, A.S.; Blaisdell, G.A. Coupling of integral acoustics methods with LES for jet noise prediction. Int. J. Aeroacous. 2004, 3, 297–346. [Google Scholar] [CrossRef]
- Rahier, G.; Prieur, J.; Vuillot, F.; Lupoglazoff, N.; Biancherin, A. Investigation of integral surface formulations for acoustic predictions of hot jets starting from unsteady aerodynamic simulations. In Proceedings of the AIAA 2003–3164, 9th AIAA/CEAS Aeroacoustics Conference, Hilton Head, SC, USA, May 12–14 2003. [Google Scholar]
- Eastwood, S.; Tucker, P.; Xia, H. High-Performance Computing in Jet Aerodynamics, Parallel Scientific Computing and Optimization; York, S.N., Ed.; Springer Optimization and Its Applications; Springer: Berlin/Heidelberg, Germany, 2009; Volume 27, pp. 193–206. [Google Scholar]
- Shur, M.L.; Spalart, P.R.; Strelets, M.K. Noise prediction for increasingly complex jets. Part I: Methods and tests. Int. J. Aeroacous. 2005, 4, 213–246. [Google Scholar] [CrossRef]
- Greschner, B.; Thiele, F.; Jacob, M.C.; Casalino, D. Prediction of sound generated by a rod-airfoil configuration using EASM DES and the generalised Lighthill/FW-H analogy. Comput. Fluids 2008, 37, 402–413. [Google Scholar] [CrossRef]

| Name | |||
|---|---|---|---|
| Obs 1 | −0.65D | 0.71D | 0.0 |
| Obs 2 | 0.0 | 0.71D | 0.0 |
| Obs 3 | 0.65D | 0.71D | 0.0 |
| Obs 4 | 1.3D | 0.71D | 0.0 |
| Name | Not—Cured | Cured | |
|---|---|---|---|
| Obs 2 | 69.72 dB | 65.07 dB | 69.71 dB |
| Obs 3 | 63.10 dB | 60.97 dB | 64.13 dB |
| Obs 4 | 56.43 dB | 56.44 dB | 55.93 dB |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY-NC-ND) license (https://creativecommons.org/licenses/by-nc-nd/4.0/).
Share and Cite
Bernardi, C.; Porcacchia, F.; Testa, C.; De Palma, P.; Leonardi, S.; Cherubini, S. NREL-5MW Wind Turbine Noise Prediction by FWH-LES. Int. J. Turbomach. Propuls. Power 2023, 8, 54. https://doi.org/10.3390/ijtpp8040054
Bernardi C, Porcacchia F, Testa C, De Palma P, Leonardi S, Cherubini S. NREL-5MW Wind Turbine Noise Prediction by FWH-LES. International Journal of Turbomachinery, Propulsion and Power. 2023; 8(4):54. https://doi.org/10.3390/ijtpp8040054
Chicago/Turabian StyleBernardi, Claudio, Federico Porcacchia, Claudio Testa, Pietro De Palma, Stefano Leonardi, and Stefania Cherubini. 2023. "NREL-5MW Wind Turbine Noise Prediction by FWH-LES" International Journal of Turbomachinery, Propulsion and Power 8, no. 4: 54. https://doi.org/10.3390/ijtpp8040054
APA StyleBernardi, C., Porcacchia, F., Testa, C., De Palma, P., Leonardi, S., & Cherubini, S. (2023). NREL-5MW Wind Turbine Noise Prediction by FWH-LES. International Journal of Turbomachinery, Propulsion and Power, 8(4), 54. https://doi.org/10.3390/ijtpp8040054








