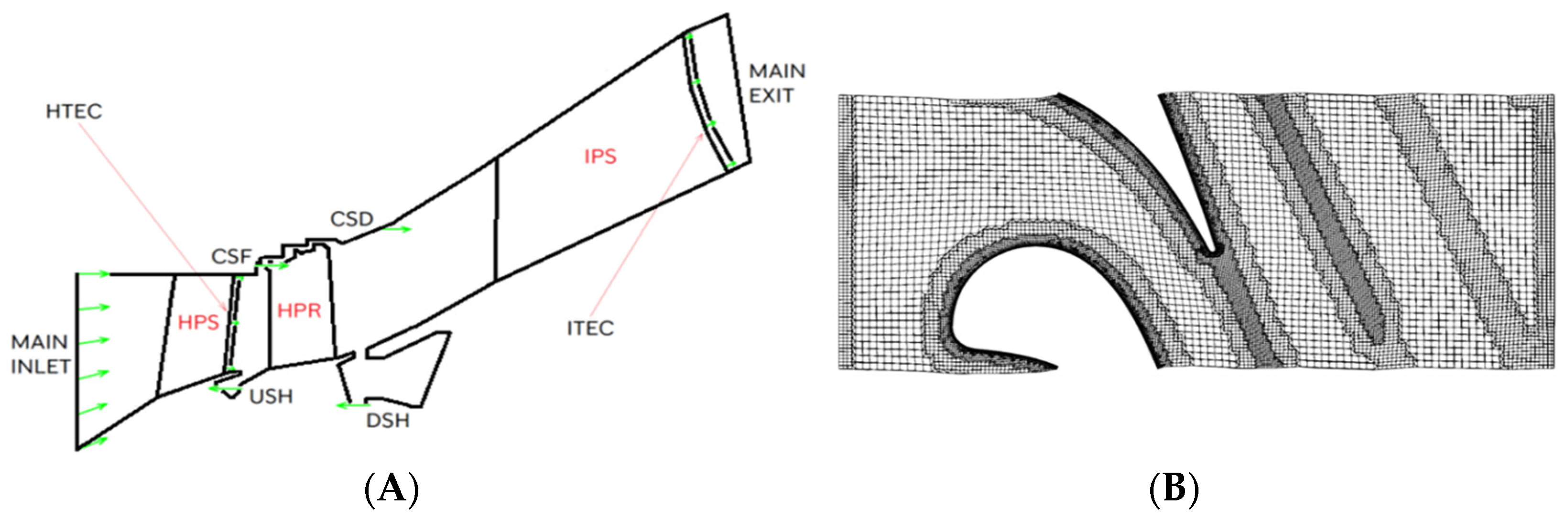
1. Introduction
To achieve high cycle efficiencies and to maximize power outputs, modern gas turbine engines employ increasingly high turbine inlet temperatures, exceeding 2000 K [
1]. These temperatures are significantly higher than the metal’s melting point, which is around 1400 K [
2]. A prolonged overheating of the blade surface, even by a relatively low value in the order of the tens of Kelvins, can lead to a dramatic acceleration of thermal barrier coating (TBC) erosion and melting of the metal alloy. High-pressure turbine (HPT) rotors are known to experience the most arduous thermal conditions, particularly towards the tip region [
3]. Higher-than-nominal temperatures may accelerate the creep process locally [
4], and have been shown to degrade the metal alloy on a microstructural level [
5]. For these reasons, the temperature of the HP components must be managed carefully through the use of sophisticated internal and external cooling mechanisms. The amount of coolant that is injected must be kept to a minimum, to limit mixing losses and overall cycle losses due to the compressor bleed. Therefore, the heat transfer systems need to be highly efficient and finely optimized to fulfil their purpose.
These systems are conceived around the nominal “running” geometries, and a set of operating conditions (usually takeoff and cruise), where they operate at peak performance. There are, however, a number of factors that may lead to deviations from the nominal. These include geometric modifications due to manufacturing variations [
6,
7], defects and handling damage, fouling near the film-cooling holes, as well as variations in operating conditions such as outboard traverse bias [
8], or engine over-throttling due to an overall performance deficit. The ‘aim’ of the present analysis was to study the correlation between the geometric deviation from the design intent and the distribution of surface heat transfer coefficient, for a large set of in-service shrouded HP turbine rotor blades of a modern jet engine resulting from high-resolution 3D-structured light optical scans. Thermal results were obtained through the use of a CFD methodology published by Maffulli and He (Maffulli and He, 2013, 2014), which calculates the heat transfer coefficient (HTC) by fitting a quadratic relation between the local wall temperature and heat flux. This technique is described in further detail in the Methodology section of this paper. This three-point non-linear fitting process requires three CFD simulations of the flow around the same blade geometry, with prescribed wall temperatures. Previous work [
9] has focused on studying the correlation between aerodynamic efficiency loss and parametrized geometric deviation, and understanding the main loss mechanisms that characterize the flow field around in-service HP turbine blades. The objective of this analysis was to determine whether in-service deterioration, by virtue of inducing a modification in the geometry of the blades and the flow conditions, can cause an increase in the heat transfer coefficient in critical areas such as the blade shroud, leading the blades to experience a consequential acceleration of their degradation process.
3. Results
The scanned blades displayed notable differences from the nominal, both in terms of geometry and heat transfer, particularly in the shroud region.
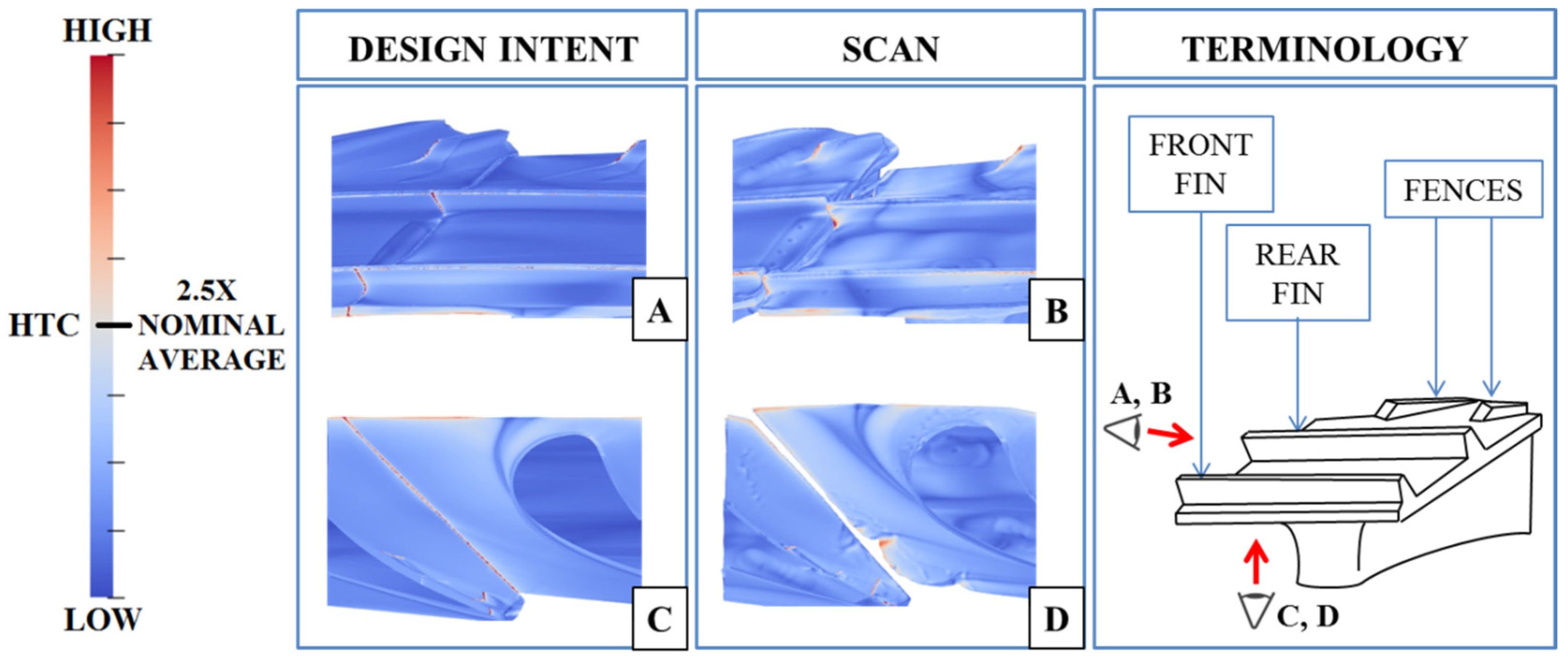
Figure 4 shows a comparison of the heat transfer patterns on the design intent rotor and on a typical in-service scans from the present set. By visual inspection of the HTC results from flow simulations carried out on the scans, it can be seen that higher-than-nominal heat transfer zones formed due to the deterioration and modification of the flow conditions. It can be seen in
Figure 4A that the many sharp corners on the design intent geometry are marked as high-HTC areas, which is expected since heat transfer is usually higher in stagnation and sharp-turning points. The same corners appear to have been rounded off by erosion in the in-service component. In the baseline design, the inter-platform shroud gap is near zero, and there is no significant amount of flow passing through it.
The figures show that there was a notable overall increase in shroud HTC due to damage. It was found that the overall shroud HTC (calculated as the average HTC on the whole shroud region) on the scanned blades was approximately 11% higher than the corresponding nominal value. The damaged geometry shown in
Figure 4B,D also displays a high-HTC patch in the rear part of the shroud gap, where erosion has carved the aforementioned V-shaped opening in the suction-side platform. This patch is clearly visible when looking at the shroud from below (
Figure 4D). The contours of
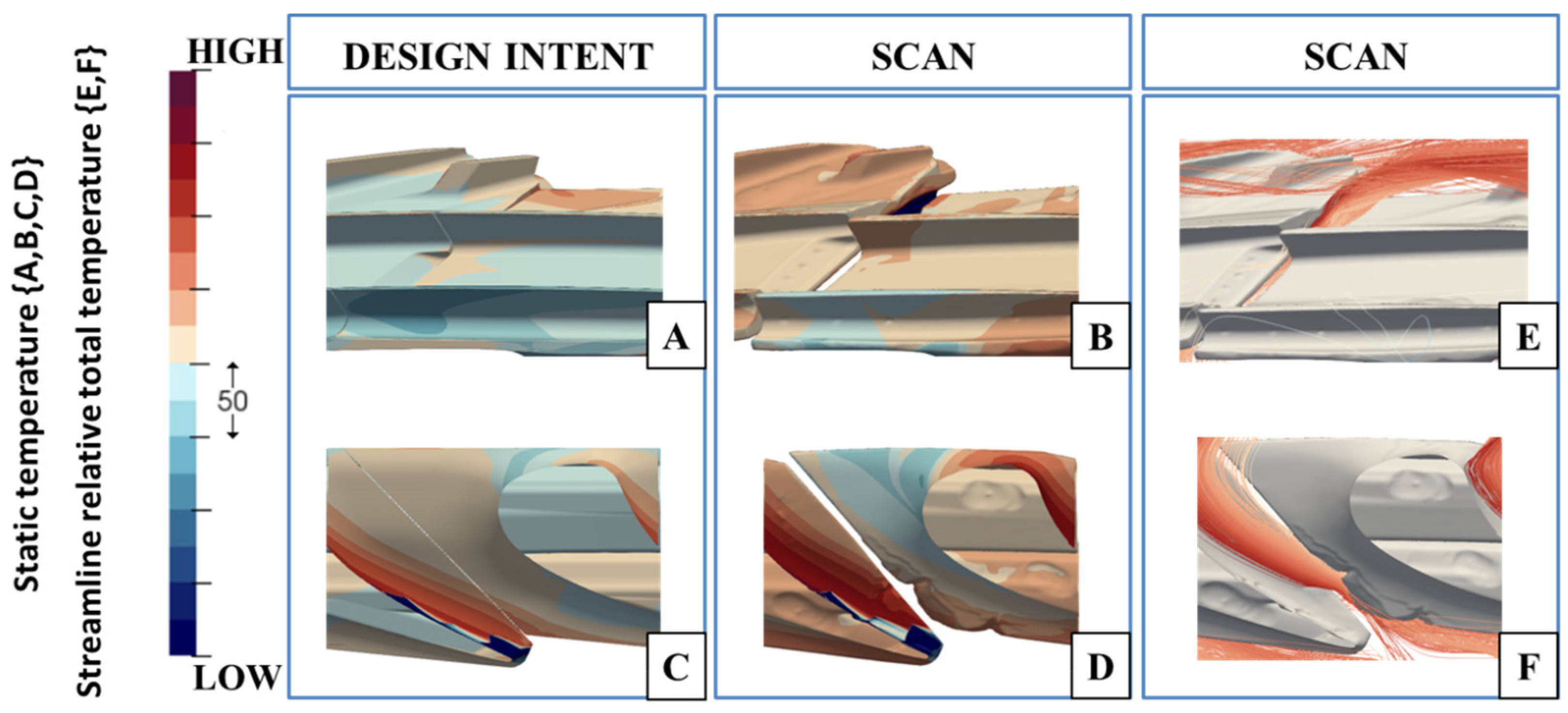
Figure 5 show the near-wall gas static temperatures for the same blades used in
Figure 4. In the scanned rotor case (
Figure 5B,D), the gas that comes in contact with the upper face of the shroud platform is 25 K to 50 K hotter with respect to the nominal case.
By looking at the contours on the lower face (
Figure 5A,C), it can be seen that a stream of high-temperature gas from the main passage reaches and crosses the aft portion of the inter-platform shroud gap, where most of the erosion is taking place. This is confirmed by the streamline visualization of
Figure 5E,F, showing the trajectories of the stream particles passing through the rear shroud gap opening. This particular region of the shroud sees a combination of high HTC and high near-wall gas temperatures, which can accelerate the erosion process.
The progressive erosion and formation of the opening can be seen from the views of the bottom face of the shroud displayed in
Figure 6, where HTC contours are shown for three in-service blades named “A”, “B”, and “C”, representing the low, medium, and high HTC levels of the set, respectively. HTC levels increasingly worsen with damage, as the amount of hot passage flow that is able to cross the opening in the gap increases. This, for the current set of blades and flow conditions, indicates a degenerative process.
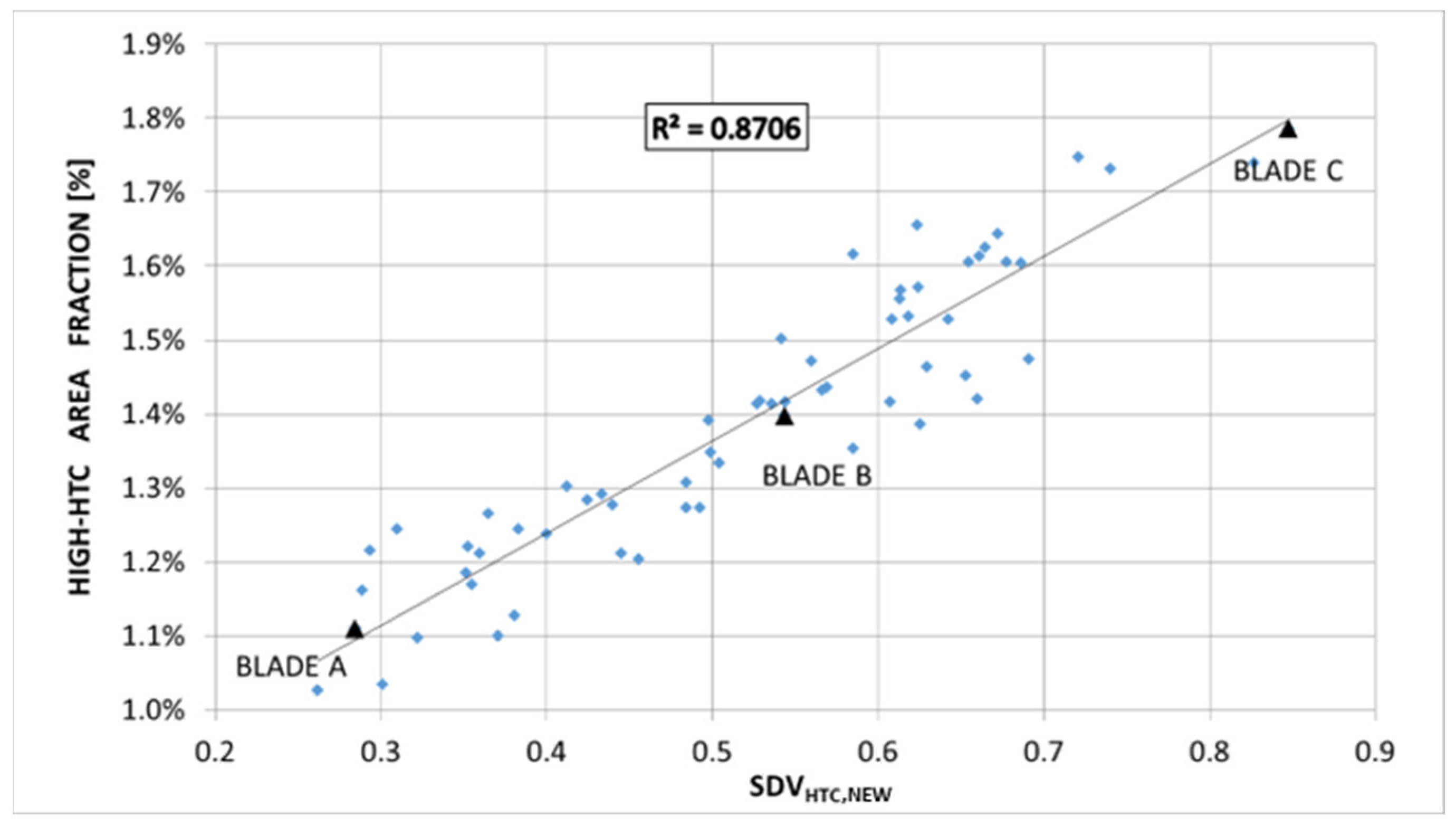
A linear correlation analysis was conducted to determine the effect of the parameters listed in
Table 1 on shroud heat transfer. The metric used to quantify the level of HTC on the shroud platforms of the in-service blades is the fraction of surface area with an HTC value exceeding 2.5 times the average value on the nominal shroud. A linear correlation between this metric and the parameters in
Table 1 was sought through multiple runs of a random-search algorithm. A linear combination variable was formulated with the set of coefficients achieving the best
R2. The resulting best-fit linear combination called “
SDVHTC” (shroud damage variable for HTC correlation) achieved good correlation (
R2 = 0.8706) and is reported in Equation (5), where the terms that ended up having a near-zero (<0.01) coefficient are removed.
The results shown in
Figure 7 indicate that there is significant linear correlation between the combination variable
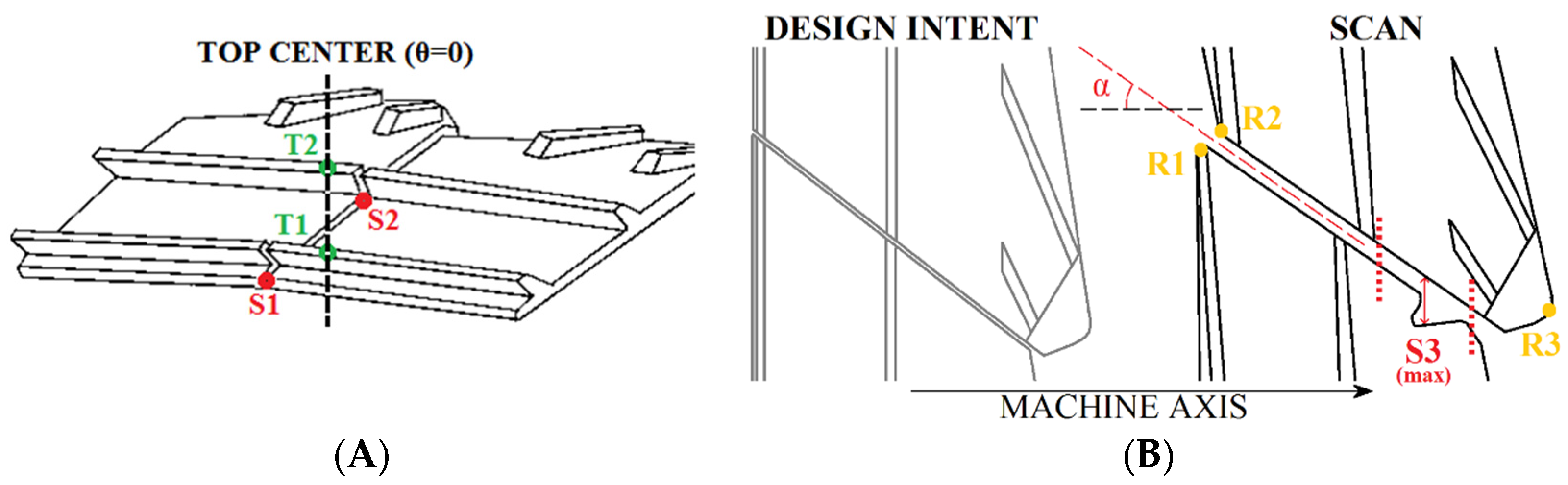
SDVHTC and the shroud surface area with high HTC. The values of the coefficients also indicate which parameters are more associated with the formation of high-HTC regions on the shroud surface. The maximum shroud gap amplitude in the rear half of the platform (
S3max) and the volume loss (
V) are the most important parameters with coefficients equal to 0.33 and 0.2, respectively. This is in agreement with what can be seen from the contours of
Figure 6, where the highest HTC levels are associated with large amounts of erosion in the rear portion of the inter-platform shroud gap, both in terms of depth of the V-shaped opening and metal volume loss.
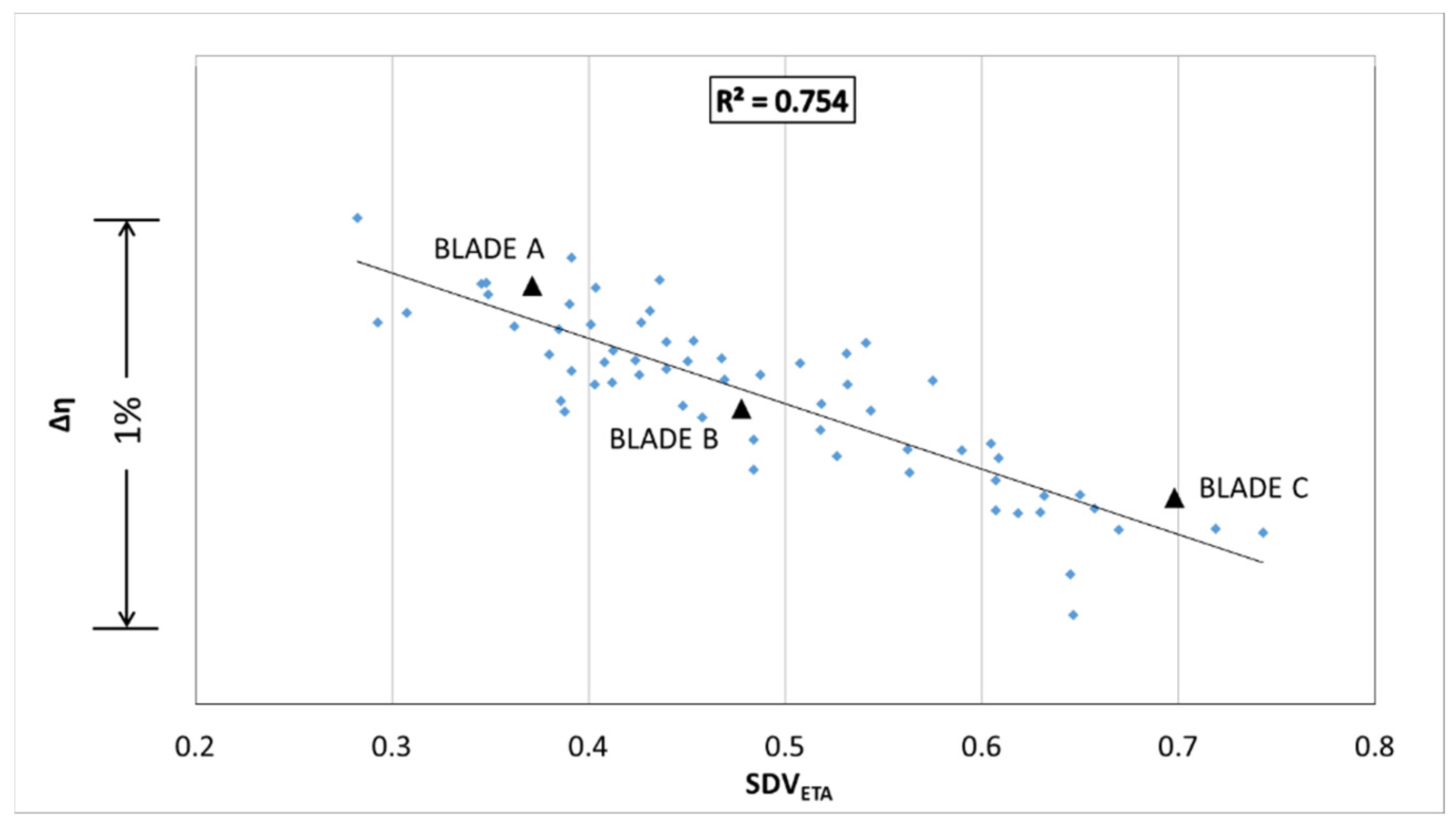
The scanned geometries used in the present analysis also suffered from different degrees of aerodynamic performance loss. Isentropic stage efficiency (Equation (1)) for the present set of blades was correlated against the shroud damage, employing the same parametrization used in the previous section for the HTC analysis. Likewise, a linear combination variable was constructed through a combination of the damage parameters with a set of best-fit coefficients, as reported in Equation (6).
Figure 8 presents the distribution of isentropic stage efficiency for the scanned geometries as a function of the “
SDVETA” variable. Similarly to what was observed with the HTC correlation study, there was significant correlation between the variable
SDVETA and the isentropic stage efficiency loss with respect to the nominal, with an
R2 of 0.754. In this case, however, the most relevant parameter to aerodynamic performance is the mid-chord shroud gap “
S2”. This finding is in line with that observed in previous work conducted by the authors: a large pressure differential can be found at that particular position between the passage and top cavity flows. This creates a large amount of leakage through the inter-platform shroud gap, which is severely detrimental to aerodynamic performance. A more detailed description of this loss mechanism can be found in [
9].
The trailing edge elongation,
R3, and rear fin tip gap are also associated with a relatively high impact on efficiency for this set of blades. In contrast with what was presented in the previous section for heat transfer, it appears that the depth of the V-shaped opening (
S3max parameter) has a low impact when looking at aerodynamic performance. In
Figure 8, the points pertaining to the three blades, “A”, “B”, and “C”, shown in
Figure 6 are also highlighted. It is interesting to note that the SDV combination variables (
Figure 7 and
Figure 8) rank these blades in the same order in terms of parametric damage vs. performance, indicating that a low aerodynamic performance is also associated with high heat transfer. It is hypothesized that the twisting of the blades is what causes the initial rotation of the shrouds, which, in turn, results in a wider inter-platform shroud gap. At that point, the blades that display the highest values of the heat transfer coefficient (HTC) are those where flow leaking through the gap was able to carve an opening in the sides of the platforms, through progressive erosion of the metal. The impact of blade twist, and its effect on the component’s aerodynamics, was assessed in a previous study [
9]. A parameter expressing the amount of twist measured on the blades was included in the present work under the name of “shroud angle”. This represents the angle formed by the shroud platform with the machine axis, and this parameter is directly affected by the rotation (twisting) of the blade sections below the shroud. In the present study, it was found that the twist itself has a negligible impact on the HTC on the blade shroud, as demonstrated by the fact that the corresponding correlation coefficient was near-zero and was thus omitted in Equation (5).
4. Conclusions
This work represents the extended version of the paper presented by the authors at the 15th European Turbomachinery Conference (ETC15) in Budapest, Hungary [
18].
A series of CFD simulations was conducted on a set of blue-light optical scans of in-service HP turbine rotor geometries from a modern jet engine, with the objective of identifying the damage modes that are associated with increased heat transfer in the shroud region. All the blades belonging to this set display overall higher (+11%) HTC values on the shroud when compared with the average value measured on the nominal shroud region. All the sharp corners originally present in the nominal design appear to have been rounded off in the in-service blades, as a result of erosion. Furthermore, significant HTC increases were observed locally, particularly in the shroud gap region. Shroud damage levels on the present set of blades have been measured in terms of a set of parameters including shroud gaps, tip gaps, elongation, and volumetric loss. A correlation analysis was then conducted to assess the impact of each parameter on HTC levels, intended as the fraction of shroud surface area with an HTC 2.5 times greater than the average value on the nominal shroud surface. A linear correlation between this measure and the set of parameters was sought, obtaining an R2 of 0.871, with the largest coefficients being those pertaining to the amplitude of the shroud gap in the rear platform part, and the metal volume loss due to erosion in the same region. A notable isentropic stage efficiency loss was observed with a 1% variability within the set. A linear correlation study was conducted between efficiency and the set of parameters, achieving an R2 of 0.754, with the highest-ranking coefficient being the S2 inter-platform shroud gap at the mid-chord. This finding is in line with the results of previous work conducted by the authors on a similar set of scanned geometries.
It is interesting to note that the thermal and aerodynamic aspects are markedly sensitive to damage in different areas of the shroud: the mid-chord gap for the aerodynamic performance and maximum rear platform gap for the thermal exchange performance. It is hypothesized that, due to an initial twist of the shroud platforms due to blade turning, the blades experience an increase in inter-platform shroud gap. Consequently, a stream of hot passage gas is able to cross the shroud gap, reaching the top cavity. Over time, the leakage flow through the rear portion of the shroud gap carves a V-shaped opening in the suction side of the shroud platform, exposing a larger surface of the internal alloy to the erosion process. Analysis of the CFD results revealed that an increase in the size of the opening causes higher local HTC values, which further increases heat exchange and can lead to degenerative acceleration of the erosion process. This study focused on a specific industrial case; however, it describes a process that can be found in modern jet engine turbines in general, by virtue of the extremely high turbine entry temperatures that characterize these engines, and the tendency of modern blades to experience a steep loss in performance during real-world operation.
Due to multi-disciplinary interactions between teams within Rolls-Royce plc, the authors have discovered that many HPT blades from different engines were experiencing what can be defined as a “vicious circle”, where deterioration of the HPT blades (deformation and erosion) translates into even faster deterioration rates during the upcoming operation cycles of the engine. For instance, initial geometric deviations from the nominal of the components can cause aerodynamic performance loss (and thus, a thrust deficit), which is compensated by over-throttling the engine to achieve the desired thrust, but this causes higher temperatures on the hot end, which accelerates deterioration rates by causing further damage and geometric deviation. The trigger of this aero-thermal deterioration mechanism was identified to be the initial blade twist below the shroud platform; therefore, it is recommended to periodically monitor this parameter during service. This could be achieved with less-invasive techniques (e.g., borescope analysis). The temperature distribution provided by the combustor also plays a key role in this phenomenon. By shifting the distribution peak towards the inner radii, the temperature of the flow streams that end up crossing the shroud gap may be reduced. This will be the subject of further optimization studies.