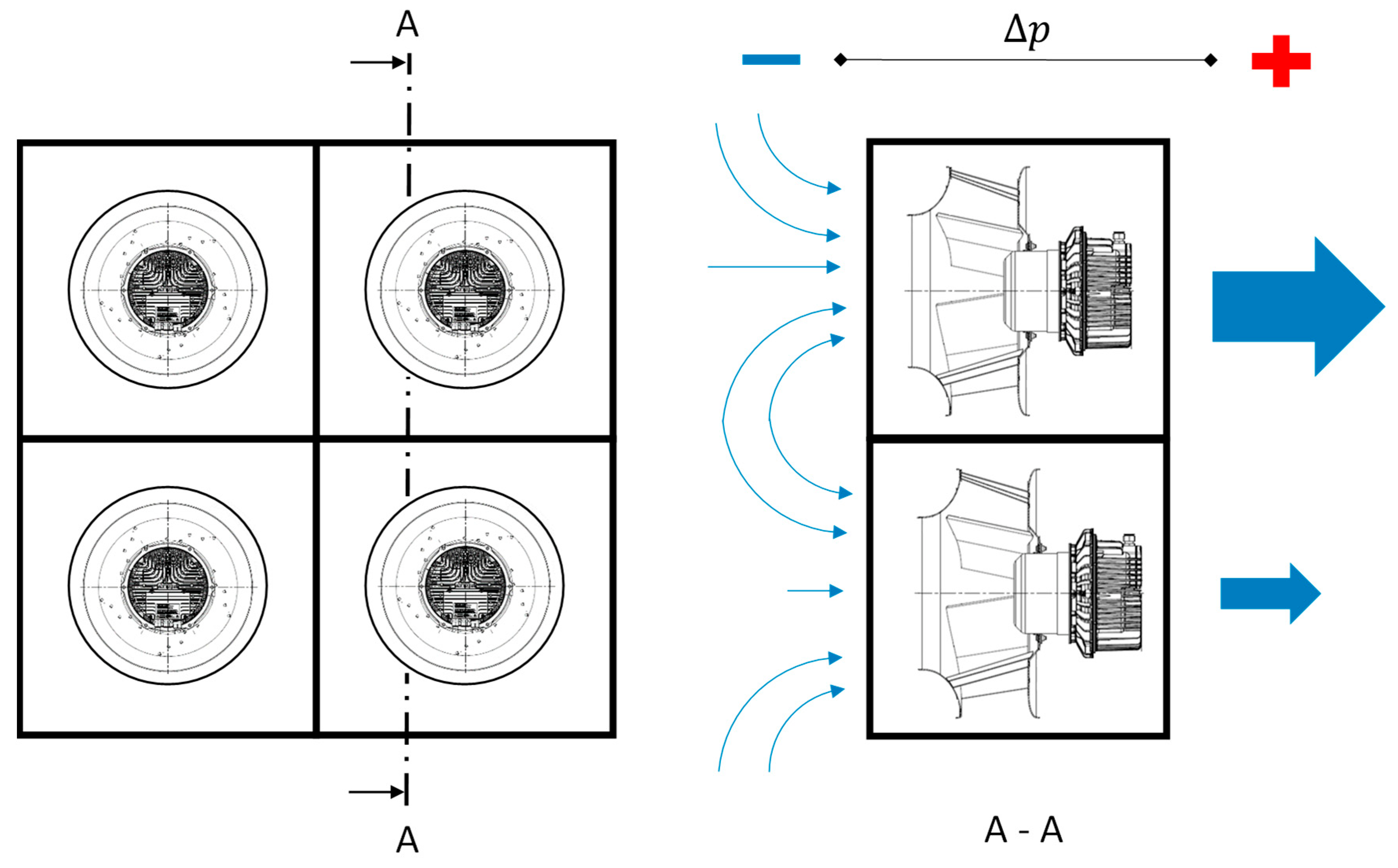
The A fan array of size
is defined as
(not necessarily identical) fans operating in parallel. That is, all fans in the array deliver the same static pressure rise. However, depending on their individual speed, their individual contribution to the overall volume flow rate might be different. This is depicted schematically in
Figure 1 with four ebm-papst R3G500 centrifugal fans in a 2 × 2 setup.
There are only two prerequisites present in the theoretical derivation of our method:
The non-dimensional fan power for each individual fan in the array, denoted by index
i, is given by:
with the well known pressure number
flow number
, and the efficiency
. The dimensional power is thus given by:
with diameter
D and operating speed
n of the
i-th fan in the array and density
ρ.
2.1. Fixed Array Size with identical Fans
Now, we consider the fan array with a fixed number and fixed type of fans. That is, in the following, the are set to a constant value and the operating speeds become the sole free variables in the system. The goal of our method is to find the optimal speed for each individual fan.
The optimality condition for an array with size
k and given operating point
and
is the minimization of the total power consumption of the array:
where
is the volume flow rate for the
i-th individual fan in the array. As this is a continuous non-linear programming problem (NLP) with a single equality constraint, we choose the method of Lagrange multipliers for its solution [
5]. This formulation of the optimization problem leads to a non-linear system of equations with
unknowns (
k speeds plus one Lagrange multiplier
λ for the volume flow rate constraint):
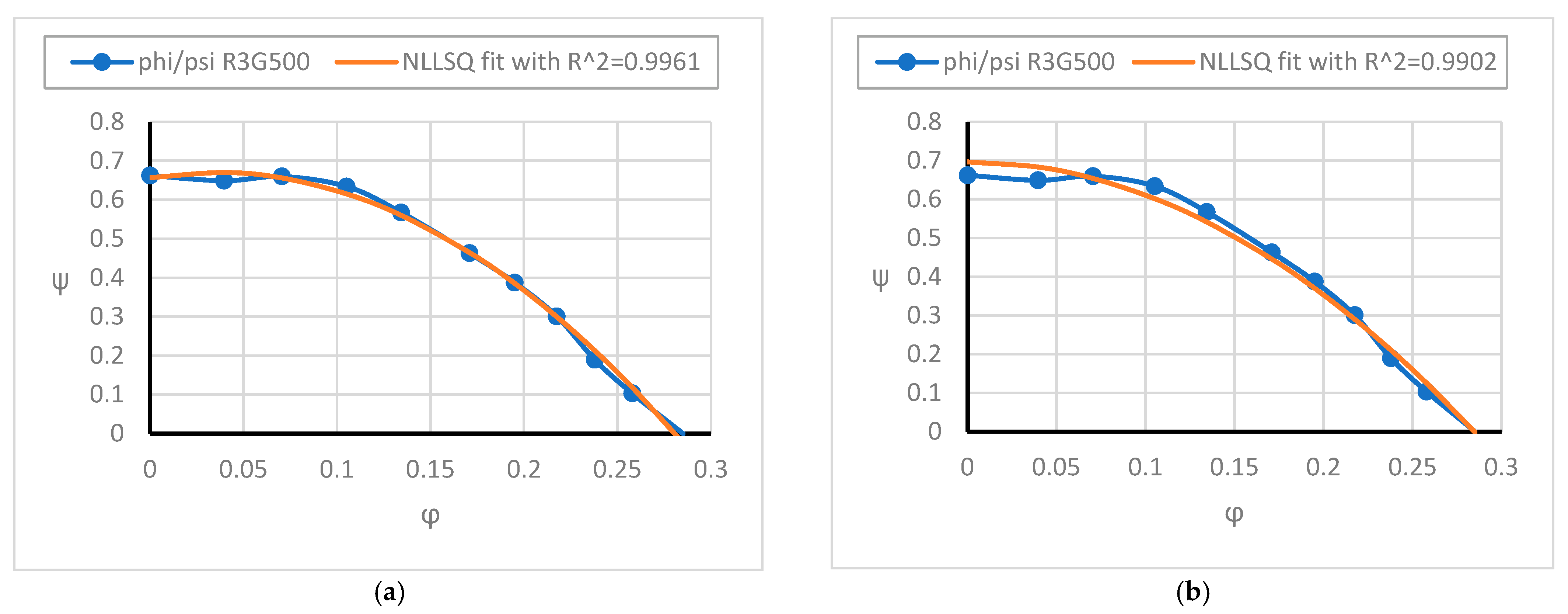
For the solution of this system of equations, the partial derivatives of the dimensional power with respect to the operating speed are required. In order to make the optimization problem accessible to a calculation, the power and the volume flow rate are transformed in such a way that they are pure functions of the speed. At this point, the dimensionless pressure and efficiency curves of the fans used in an array are introduced. In the following, we stick to the special case of an ebmpapst R3G500 centrifugal fan characteristic shown in
Figure 2. However, this is for demonstration purposes and does not restrict the validity of our approach. The overall shape of the performance and efficiency characteristic curves will always be similar for all conventional fans due to well-known loss mechanisms [
6,
7].
From Equation (3) it is obvious that we need to approximate the fan characteristics using continuously differentiable functions. The respective dimensionless pressure characteristic of a fan is approximated with a second-order polynomial Equation (4). Preference is given here to the approximation with a quadratic approach Equation (5), since the approximation function is then strictly monotonic in the considered range
> 0. This is an idealization because in reality, the fan stalls for low
and the operation becomes unstable. One would have to define a minimum
, but we opt for this approach to demonstrate the method.
With this description of the pressure number, the flow number can be expressed as a function of the constant coefficients of the polynomial approximation, diameter, density, speed, and pressure increase. Resolving the quadratic Equation (4) for the flow number yields:
The derivative of the flow number with respect to the fan speed is given by:
Accordingly, the efficiency characteristics need to be approximated. Preference is given here to a fourth order polynomial:
Likewise, deriving Equation (7) yields:
Both Equations (7) and (9) are needed in the chain rule for the computation of the derivative of the non-dimensional power
:
Finally, we are able to compute the derivative of the dimensional fan power with respect to the fan speed:
In a last step, we derive the dimensional volume flow rate with respect to the fan speed:
At this point, we acquired all expressions needed in Equation (3). All approximations used are continuously differentiable by construction through polynomials. The solution of this system of equations yields the optimal operating speeds for each fan such that the array adheres to the operating point given by and .
By variation in the operating point specification and subsequent solving of the system of equations, we obtain a map of optimal operating speeds in the boundaries Δ and for the fan array.
In reality, the fan speed has an upper limit given by the motor and/or the material. There is also a lower fan speed limit, which is determined by the maximum pressure number for the considered operating point (i.e., the individual fan needs to be able to generate the operating pressure). Both limits are considered as a non-linear inequality constraint.
2.2. Variable Array Size with Identical Fans
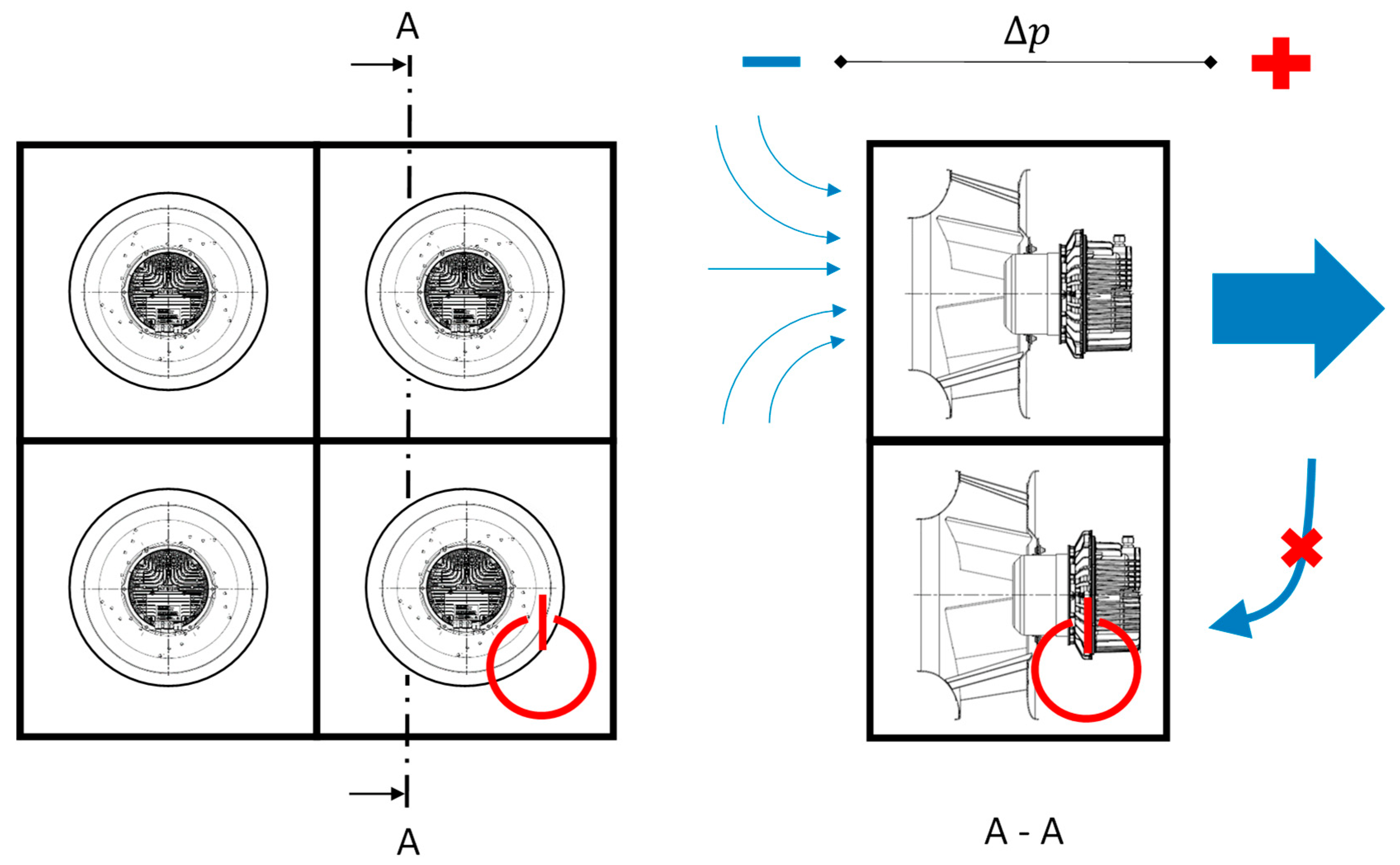
So far, we assumed that all fans of an array with size are actively in operation. Now, we investigate possible benefits of selectively turning off one or more fans in such an array. With this modification, the optimization problem becomes a mixed-integer nonlinear programming problem (MINLP).
We solve this by applying our method to different array sizes . That means, instead of solving the MINLP directly, we resort to solving a series of NLPs and choose the best configuration in a postprocessing step. In the case of , we turn off fans in the array. As stated above, we assume that there is no backflow for turned off fans.
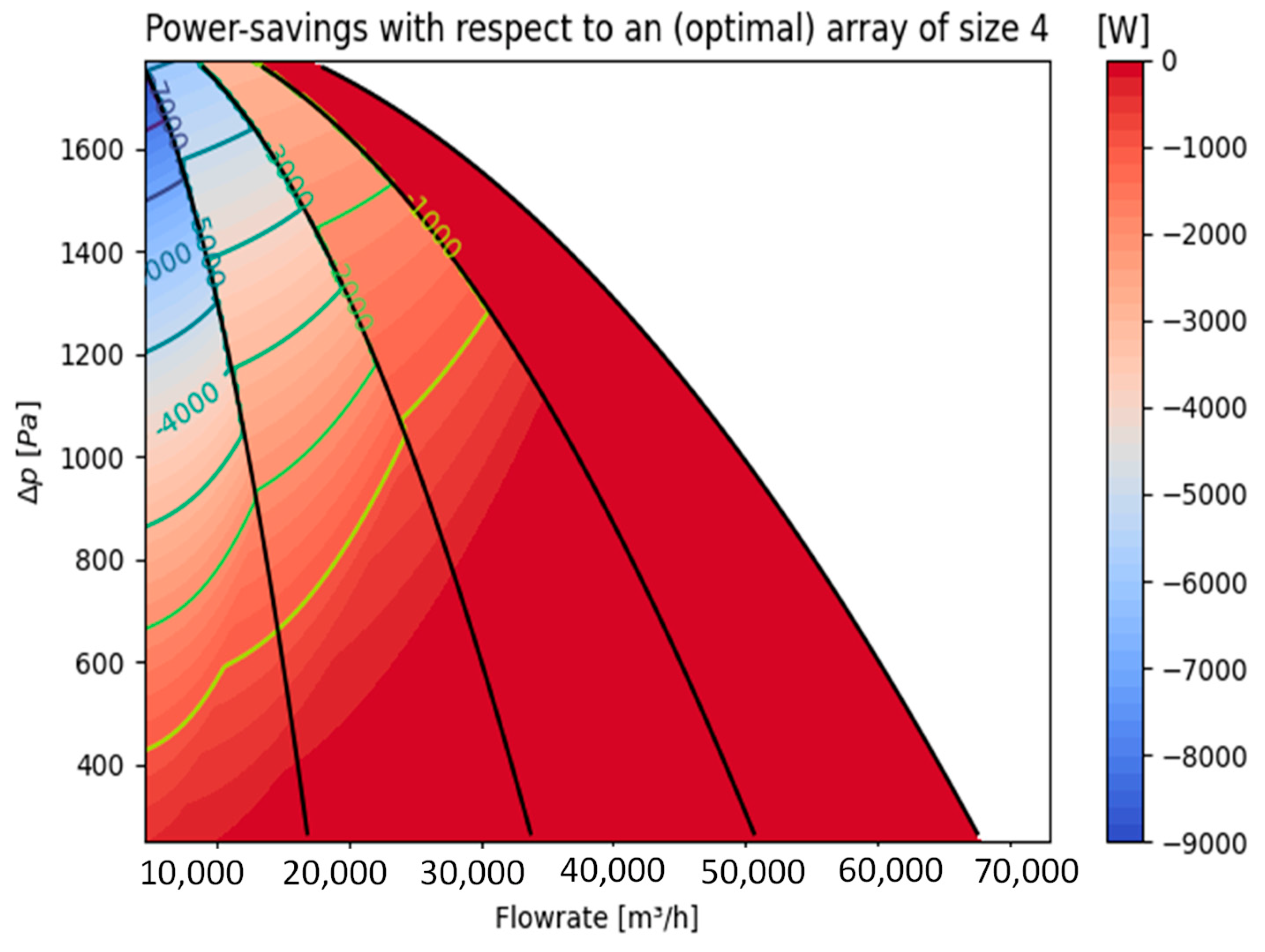
This approach yields the optimal fan speeds along with the corresponding overall power consumption for each of the different arrays sizes. Picking the array size with minimum power consumption yields the optimal array size, i.e., the number of fans to turn off while operating the active fans using their optimal fan speeds.
2.3. Variable Array Size with Different Fan Sizes and/or Fan Types
The fans in a parallel setting do not need to be from the same type or size. A possible scenario for an array with different fans is shown in
Figure 3:
Our approach is able to account for arrangements where we mix, for example, different sizes of centrifugal fans with different sizes of axial fans. In order to describe this more formally, the fans can vary in their size (Di) as well as their non-dimensional characteristics described with the coefficients and in Equations (4), (5), and (8).
In contrast to the approach used for varying array sizes with identical fans, we now have to distinguish between different settings of the array when one or more fans are turned off. This is a problem of unordered sampling without replacement. When shutting down fans, there are unique possible combinations for the operation of the fan array of size .
For a given operating point, we need to vary the array size and additionally calculate all possible combinations of active fans. This approach yields optimal fan speed combinations, power consumptions, and fan combinations, respectively. The minimum of these power consumptions determines the optimal array size and corresponding fan speeds, as well as the corresponding fan combinations. With this approach, we can assign every operating point in the map with Δ and a -tuple of optimal fan speeds and the corresponding optimal combination of active fans, which maximizes the system efficiency, where fans are turned off, respectively.