Inlet Gap Effect on Tonal Noise Generated from a Voluteless Centrifugal Fan
Abstract
1. Introduction
2. Configuration
3. Numerical Methodology
3.1. CFD Method
3.2. Numerical Settings
3.3. FW-H Equation
4. Mesh
5. Results and Discussion
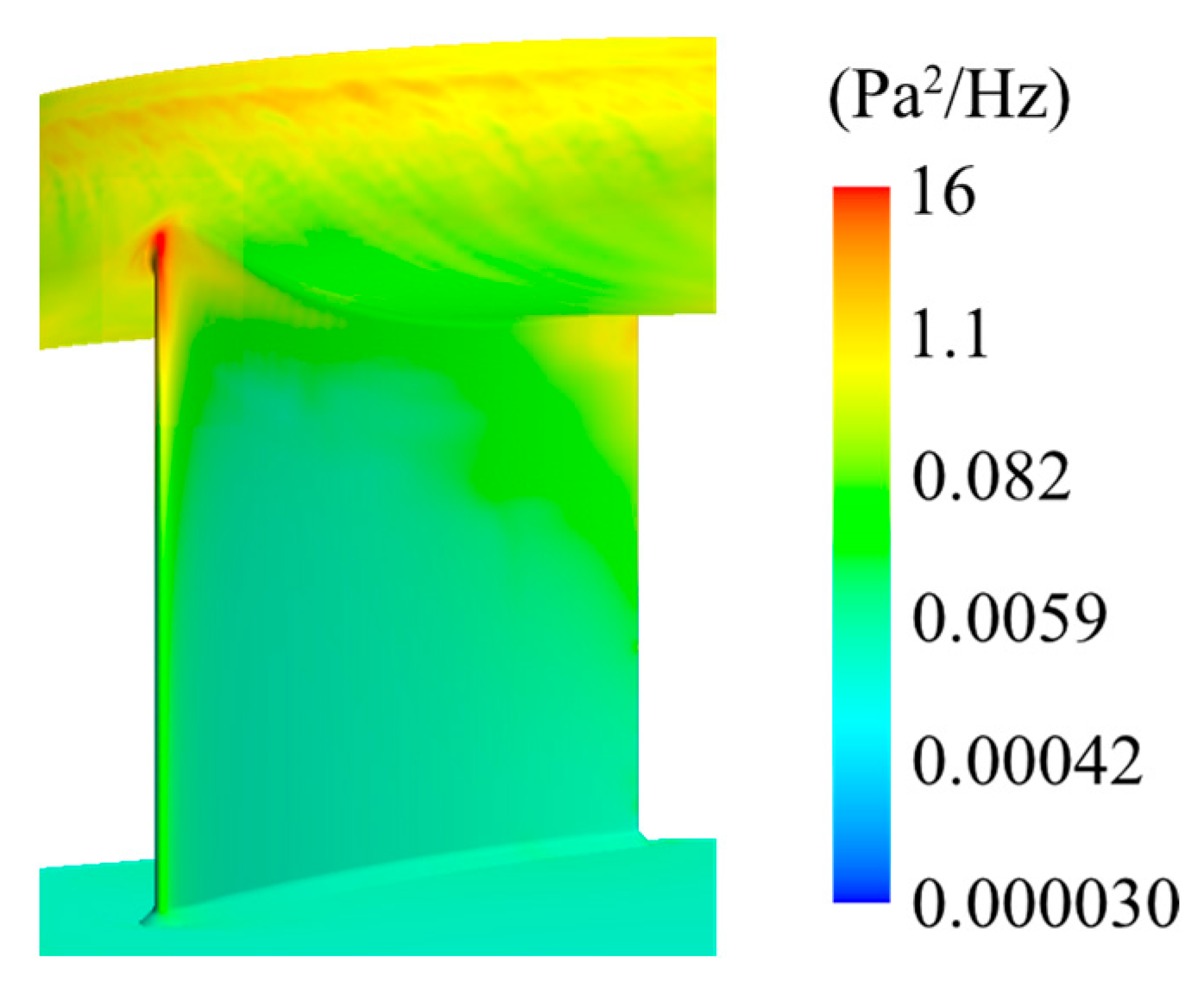
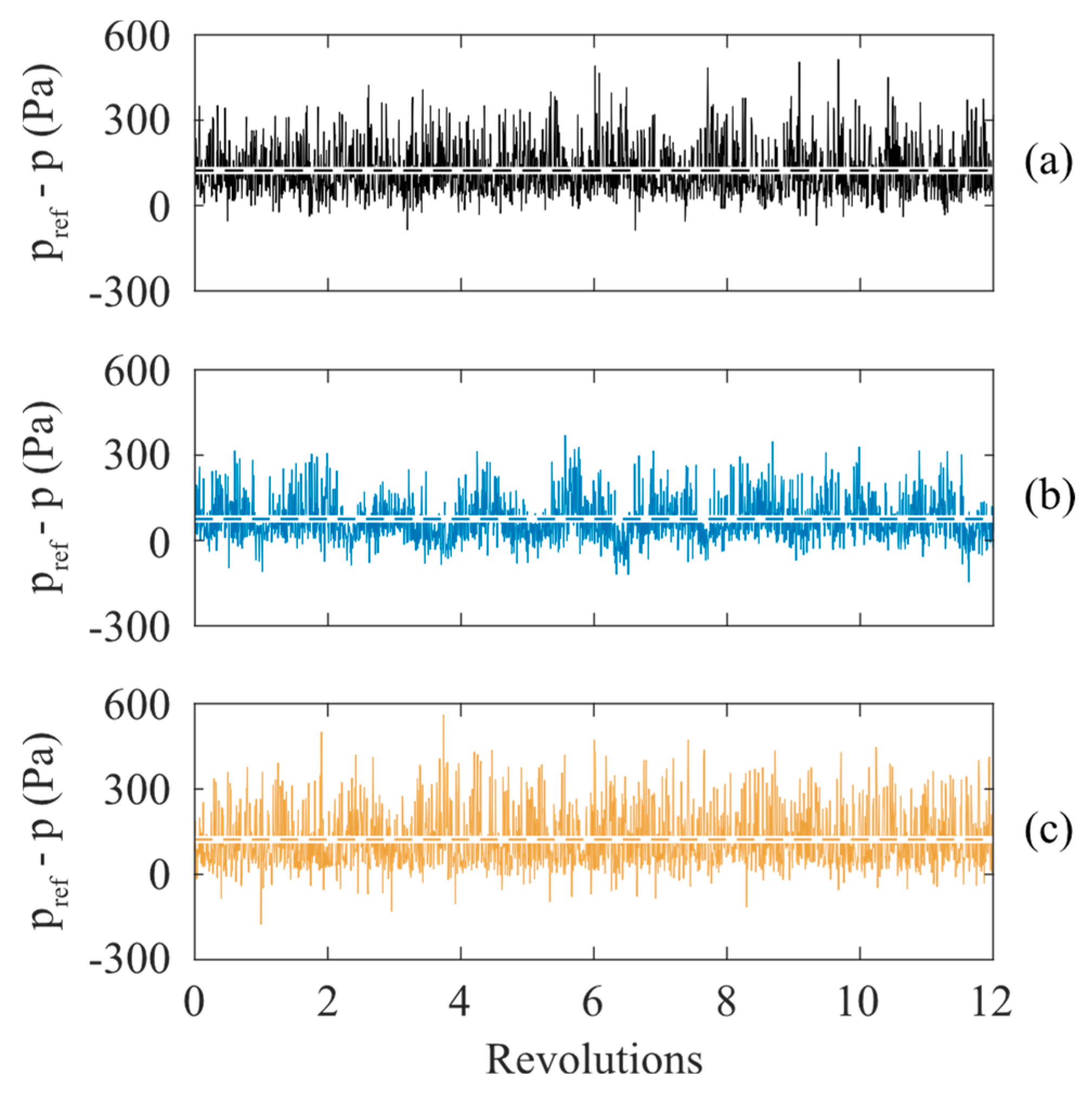
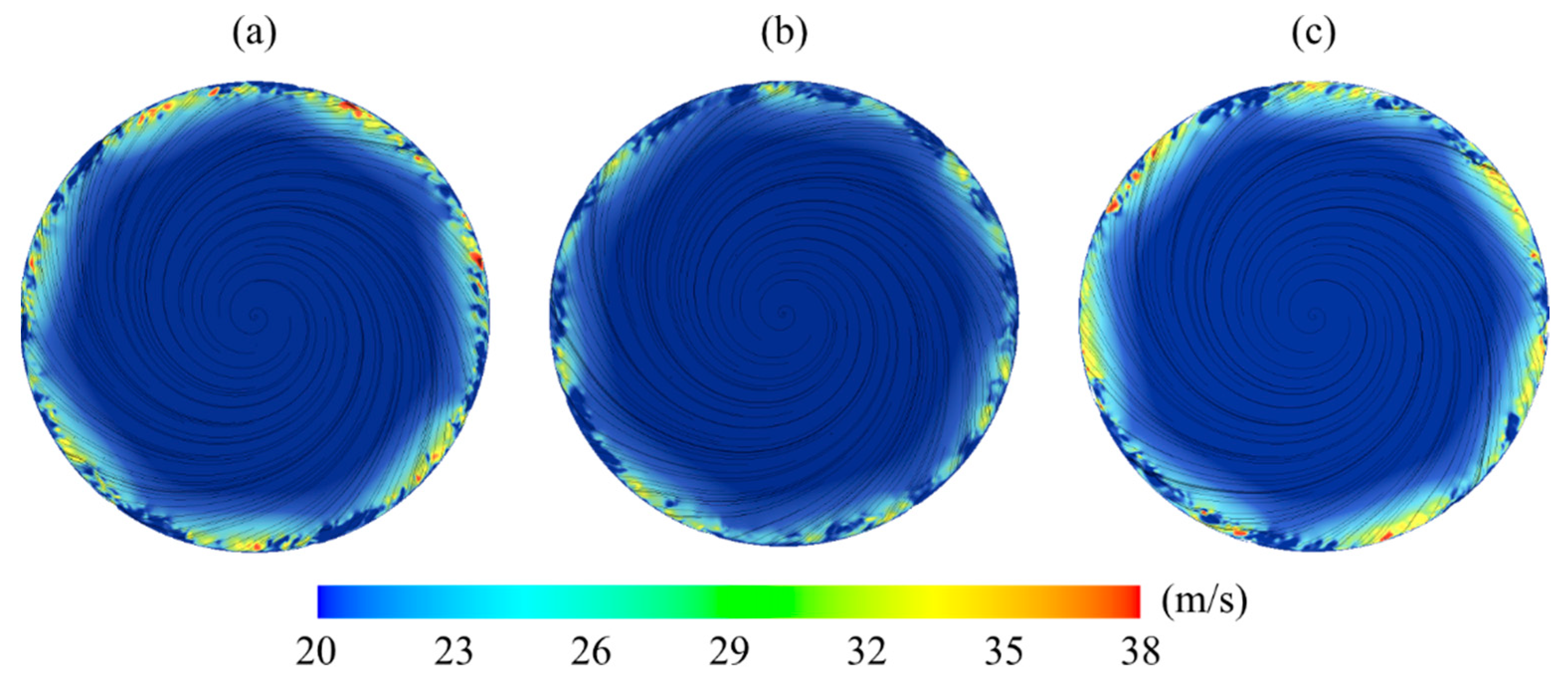
5.1. Identifying Sources for Tonal Noise for Case 1
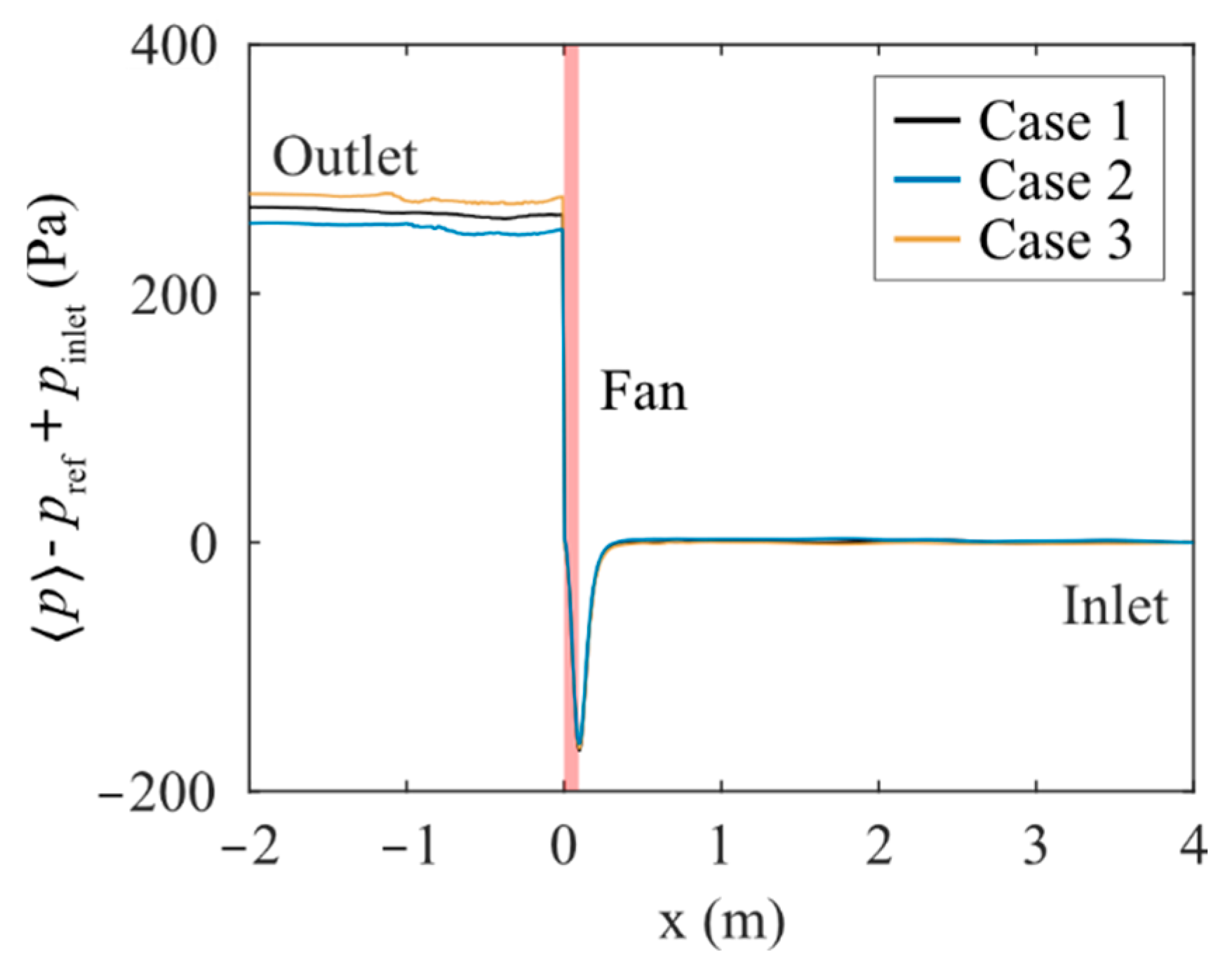
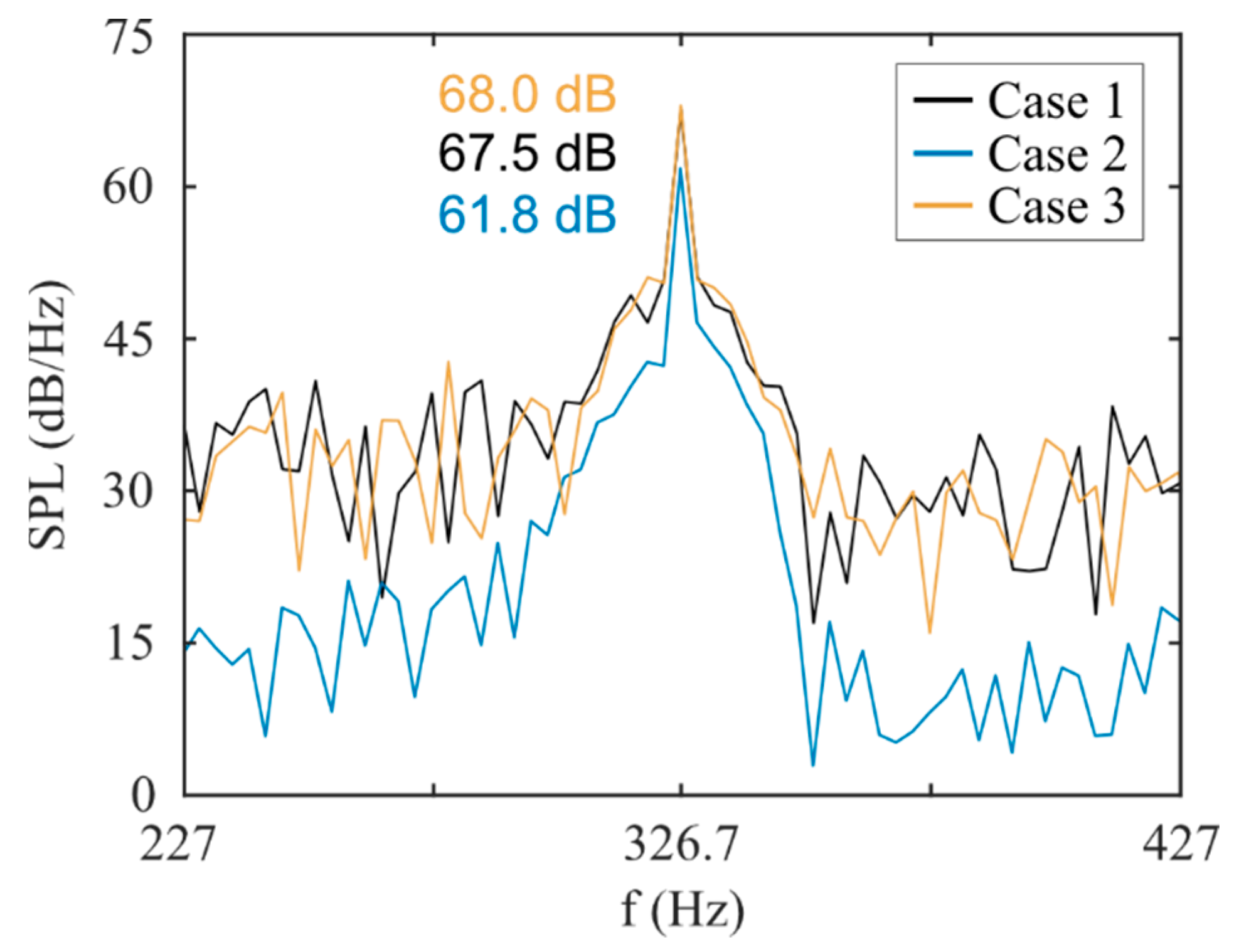
5.2. Fan Performance Comparison
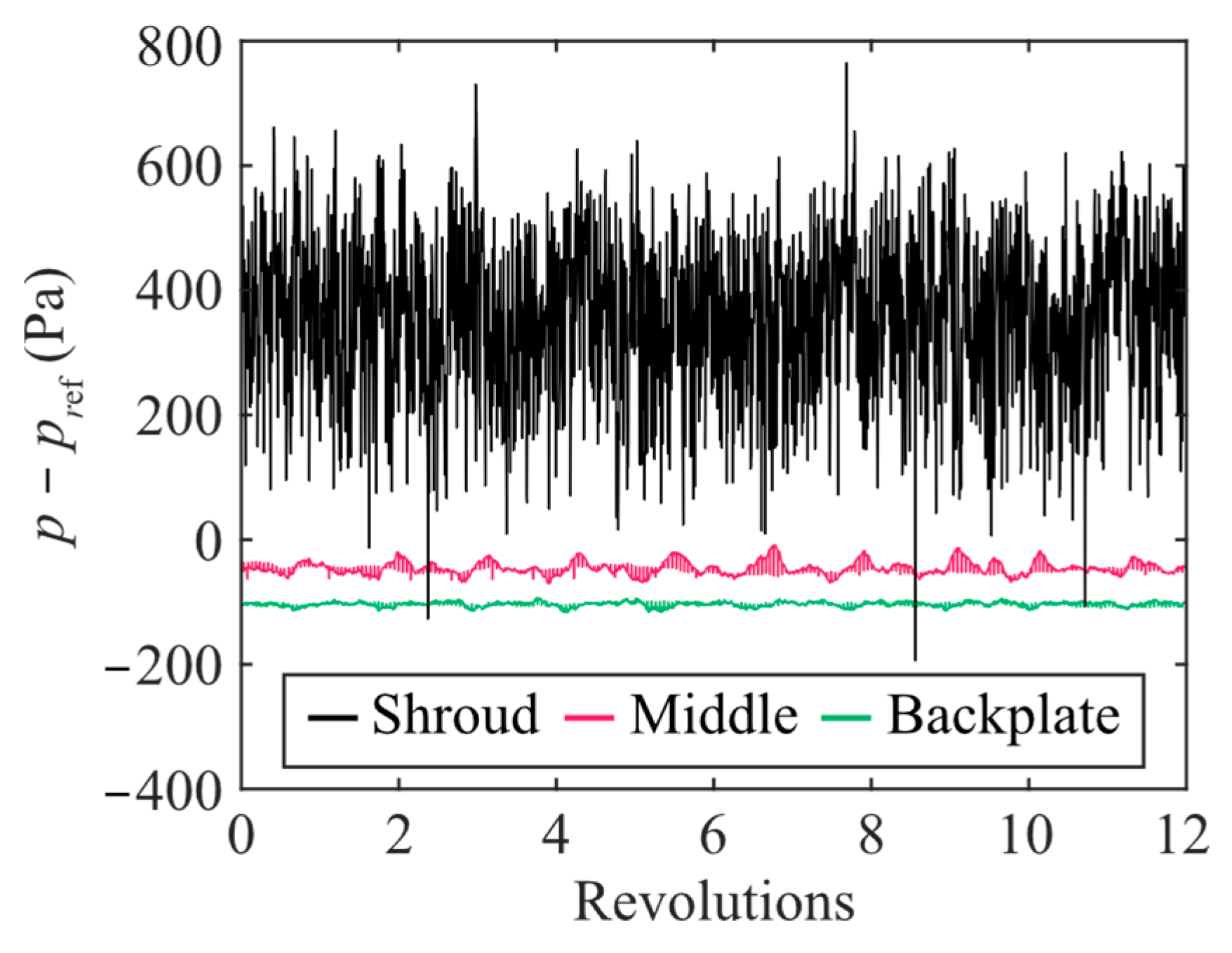
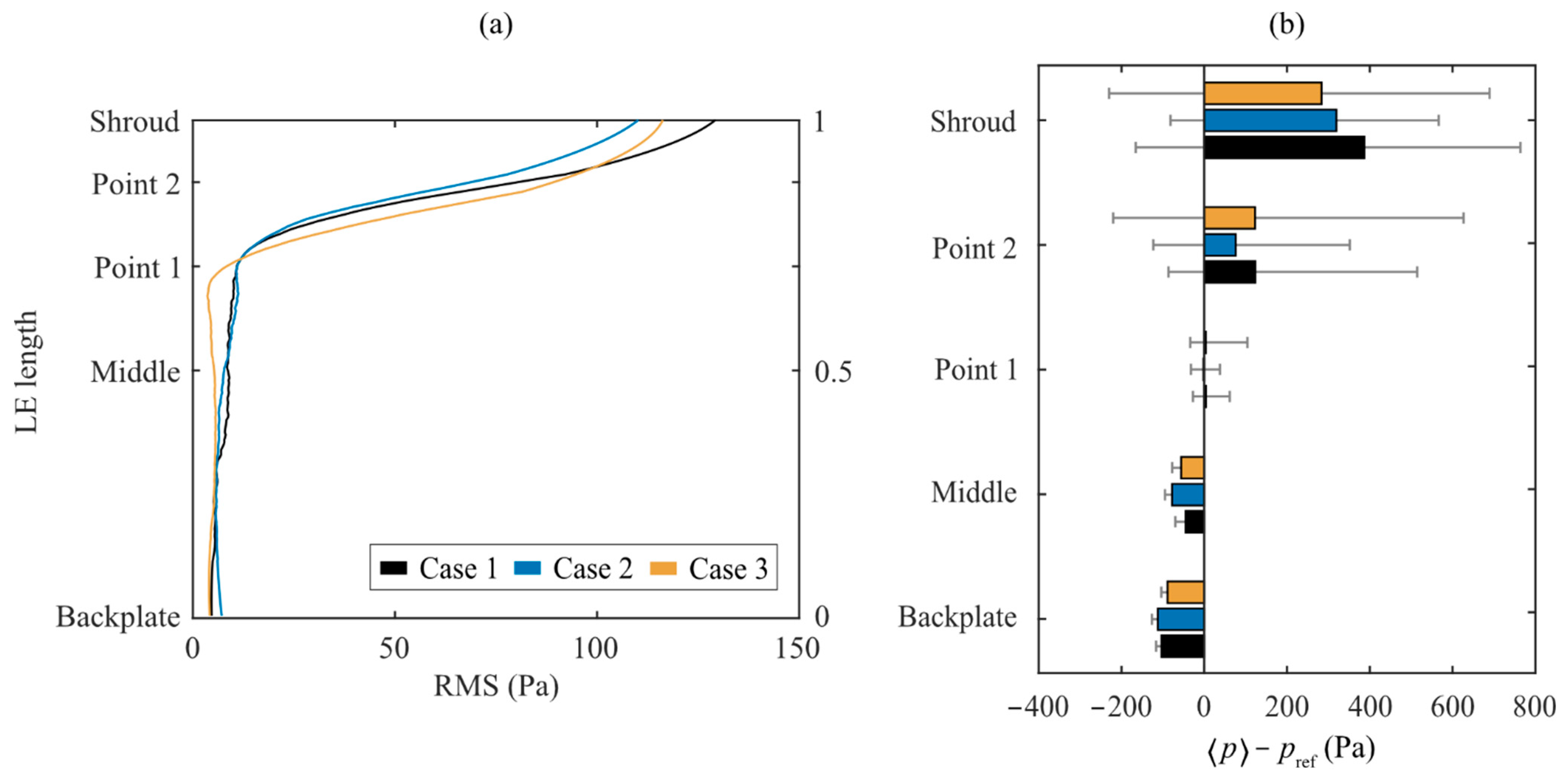
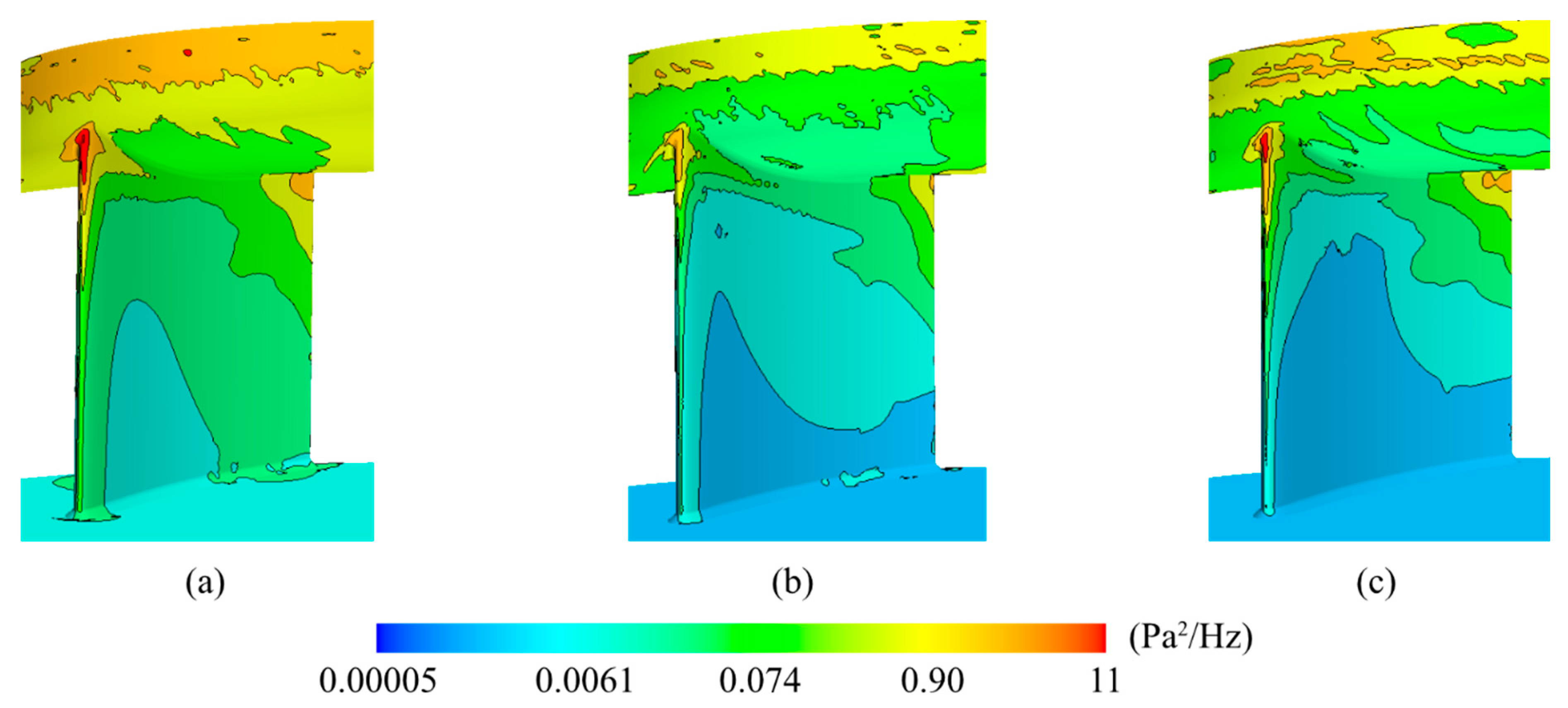
5.3. Wall Pressure Fluctuations Comparison
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Berglund, B.; Lindvall, T.; Schwela, D. New Guidelines for Community Noise. Noise Vib. Worldw. 2000, 31, 24–29. [Google Scholar] [CrossRef]
- Azimi, M. Noise Reduction in Buildings Using Sound Absorbing Materials. J. Archit. Eng. Technol. 2017, 6, 198. [Google Scholar]
- Hariharan, C.; Govardhan, M. Effect of inlet clearance on the aerodynamic performance of a centrifugal blower. Int. J. Turbo Jet Engines 2016, 33, 215–228. [Google Scholar] [CrossRef]
- Wolfram, D.; Carolus, T.H. Experimental and numerical investigation of the unsteady flow field and tone generation in an isolated centrifugal fan impeller. J. Sound Vib. 2010, 329, 4380–4397. [Google Scholar] [CrossRef]
- Sanjose, M.; Moreau, S. Direct noise prediction and control of an installed large low-speed radial fan. Eur. J. Mech. 2017, 61, 235–243. [Google Scholar] [CrossRef]
- Pérot, F.; Kim, M.S.; Goff, V.L.; Carniel, X.; Goth, Y.; Chassaignon, C. Numerical optimization of the tonal noise of a backward centrifugal fan using a flow obstruction. Noise Control. Eng. J. 2013, 61, 307–319. [Google Scholar] [CrossRef]
- Schaefer, R.; Boehle, M. Influence of the mesh size on the Aerodynamic and Aeroacoustics of a Centrifugal Fan using Lattice-Boltzmann Method. In Proceedings of the 23rd Internatinoal Congress on Acoustics, Aachen, Germany, 9–13 September 2019; pp. 1882–1889. [Google Scholar]
- Ottersten, M.; Yao, H.-D.; Davidson, L. Tonal noise of voluteless centrifugal fan generated by turbulence stemming from upstream inlet gap. Phys. Fluids 2021, 33, 75110. [Google Scholar] [CrossRef]
- Shur, M.L.; Spalart, P.R.; Strelets, M.K.; Travin, A.K. A Hybrid RANS-LES Approach with Delayed-DES and Wall-Modelled LES Capabilities. Int. J. Heat Fluid Flow 2008, 29, 1638–1649. [Google Scholar] [CrossRef]
- Ffowcs Williams, J.E.; Hawkings, D.L. Theory relating to the noise of rotating machinery. J. Sound Vib. 1969, 10, 10–21. [Google Scholar] [CrossRef]
- Siemens PLM Software. STAR-CCM+ User Guide (Version 12.04); Siemens PLM: Plano, TX, USA, 2017. [Google Scholar]
- Salunkhe, S.; Fajri, O.E.; Bhushane, S.; Thompson, D.; O’Dohety, D.; O´Dohety, T.; Mason-Jones, A. Validation of tidal stream turbine wake predictions and analysis of wake recovery mechanism. J. Mar. Sci. Eng. 2019, 7, 362. [Google Scholar] [CrossRef]
- Rynell, A.; Efraimsson, G.; Chevalier, M.; Åbom, M. Inclusion of Upstream Turbulent Inflow Statistics to Numerically Acquire Proper Fan Noise Characteristics; SAE Technical Paper 2016-01-1811; SAE International: Warrendale, PA, USA, 2016. [Google Scholar]
- Rynell, A.; Chevalier, M.; Åbom, M.; Efraimsson, G. A numerical study of noise characteristics originating from a shrouded subsonic automotive fan. Appl. Acoust. 2018, 140, 110–121. [Google Scholar] [CrossRef]
- Brentner, K.S.; Farassat, F. Analytical comparison of the acoustic analogy and Kirchhoff formulation for moving surfaces. AIAAA J. 1998, 36, 1379–1386. [Google Scholar] [CrossRef]
- Neise, W. Review of fan noise generation mechanisms and control methods. In Proceedings of the Fan Noise 1992 International Symposium, Senlis, France, 1–3 September 1992; pp. 45–56. [Google Scholar]
- Ottersten, M.; Yao, H.-D.; Davidson, L. Unsteady Simulation of tonal noise from isolated centrifugal fan. In Proceedings of the Fan Noise 2018 Symposium, Darmstadt, Germany, 18–20 April 2018. [Google Scholar]
- Baris, O.; Mendonça, F. Automotive turbocharger compressor CFD and extension towards incorporating installation effects. In Proceedings of the ASME Turbo Expo 2011: Power for Land, Sea and Air, Vancouver, BC, Canada, 6–10 June 2011. [Google Scholar]
- Yao, H.-D.; Davidson, L.; Eriksson, L.E. Surface integral analogy approaches for predicting noise from 3D high-lift low-noise wings. Acta Mech. Sin. 2014, 30, 326–338. [Google Scholar] [CrossRef]
- Lee, Y. Impact of fan gap flow on the centrifugal impeller aerodynamics. J. Fluids Eng. 2010, 132, 091103. [Google Scholar] [CrossRef]
- Ottersten, M.; Yao, H.-D.; Davidson, L. Numerical and experimental study of tonal noise sources at the outlet of an isolated centrifugal fan. arXiv 2020, arXiv:2011.13645. [Google Scholar]
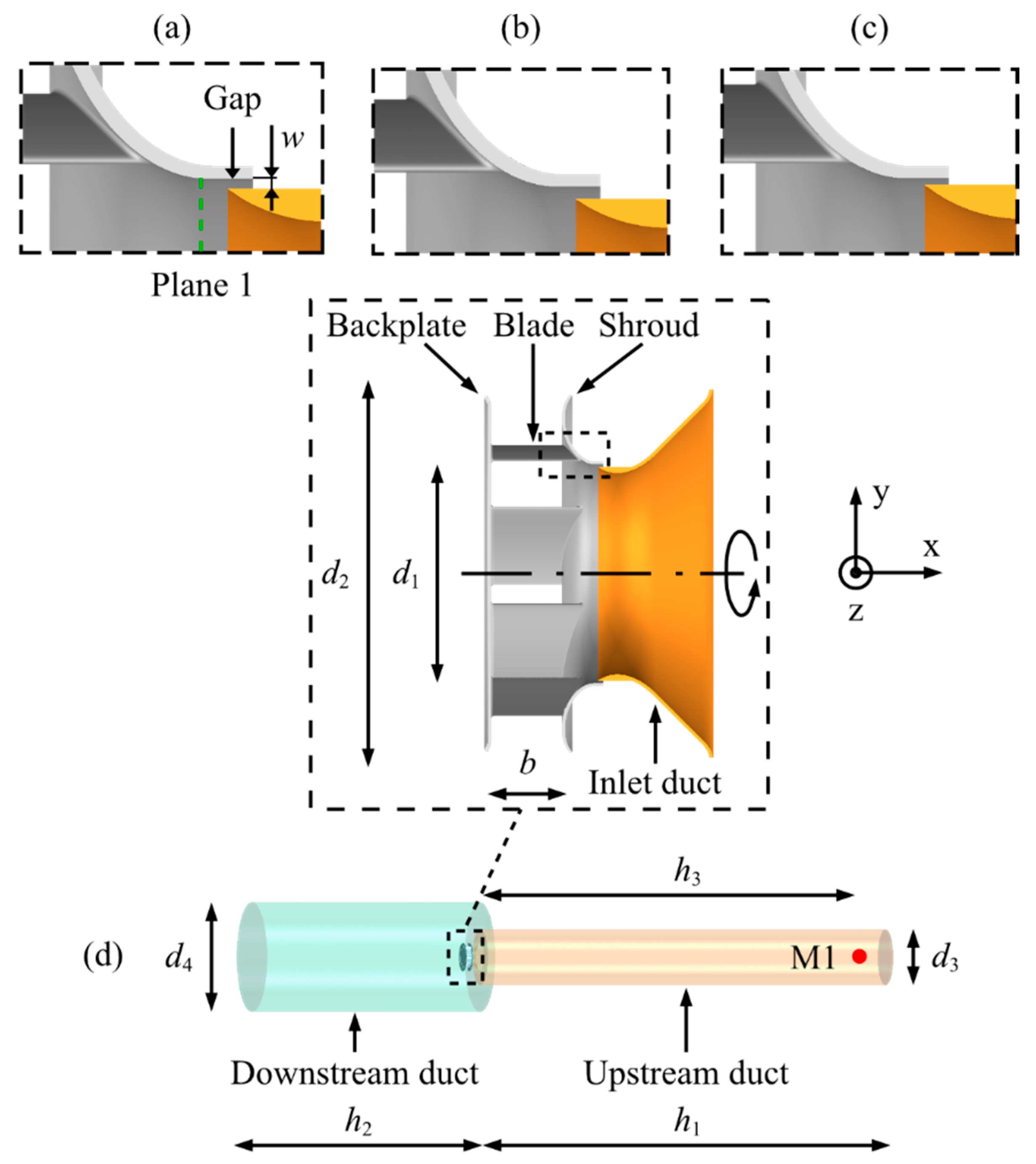
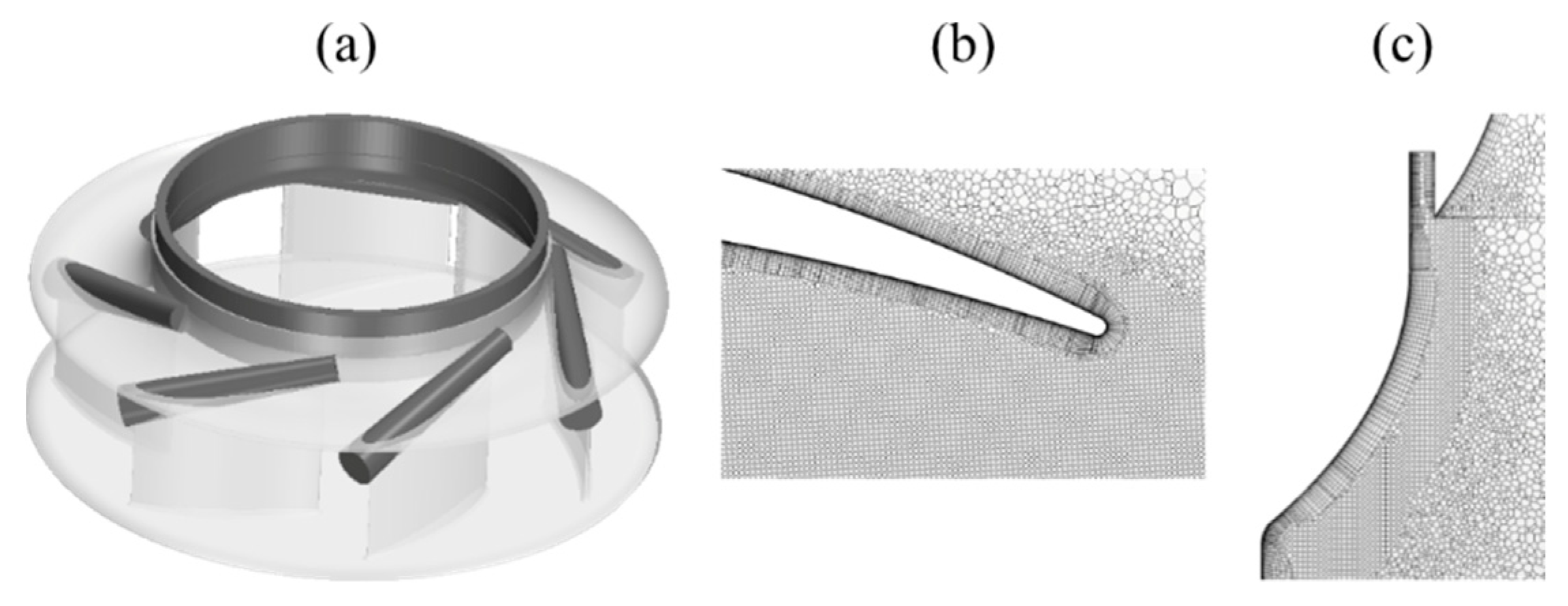

| d1 | d2 | d3 | d4 | b | h1 | h2 | h3 | wcase1 | wcase2 | wcase3 |
|---|---|---|---|---|---|---|---|---|---|---|
| 0.165 m | 0.268 m | 0.6 m | 1.1 m | 0.053 | 4.0 m | 2.3 m | 3.2 m | 1.5 mm | 2.0 mm | 1.0 mm |
| Cases 1–3 | |
|---|---|
| Total number of cells | |
| Number of cells in the rotating zone | |
| Maximum first cell height near blade walls | 0.73 |
| Cell growth ratio | 1.05 |
| Comparative Features | Case 1 | Case 2 | Case 3 |
|---|---|---|---|
| Gap width (mm) | 1.5 | 2.0 | 1.0 |
| Static pressure rise (Pa) | 268 | 261 | 281 |
| SPL at BPF (dB) | 67.5 | 61.8 | 68.0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY-NC-ND) license (https://creativecommons.org/licenses/by-nc-nd/4.0/).
Share and Cite
Ottersten, M.; Yao, H.-D.; Davidson, L. Inlet Gap Effect on Tonal Noise Generated from a Voluteless Centrifugal Fan. Int. J. Turbomach. Propuls. Power 2022, 7, 33. https://doi.org/10.3390/ijtpp7040033
Ottersten M, Yao H-D, Davidson L. Inlet Gap Effect on Tonal Noise Generated from a Voluteless Centrifugal Fan. International Journal of Turbomachinery, Propulsion and Power. 2022; 7(4):33. https://doi.org/10.3390/ijtpp7040033
Chicago/Turabian StyleOttersten, Martin, Hua-Dong Yao, and Lars Davidson. 2022. "Inlet Gap Effect on Tonal Noise Generated from a Voluteless Centrifugal Fan" International Journal of Turbomachinery, Propulsion and Power 7, no. 4: 33. https://doi.org/10.3390/ijtpp7040033
APA StyleOttersten, M., Yao, H.-D., & Davidson, L. (2022). Inlet Gap Effect on Tonal Noise Generated from a Voluteless Centrifugal Fan. International Journal of Turbomachinery, Propulsion and Power, 7(4), 33. https://doi.org/10.3390/ijtpp7040033







