Abstract
Non-synchronous blade vibrations have been observed in an experimental multi-stage high-speed compressor setup at part-speed conditions. A detailed numerical study has been carried out to understand the observed phenomenon by performing unsteady full-annulus Reynolds-Averaged Navier–Stokes (RANS) simulations of the whole setup using the solver elsA. Several operating conditions have been simulated to observe this kind of phenomena along a speedline of interest. Based on the simulation results, the physical source of the non-synchronous blade vibration is identified: An aerodynamic disturbance appears in a highly loaded downstream rotor and excites a spinning acoustic mode. A “lock-in” phenomenon occurs between the blade boundary layer oscillations and the spinning acoustic mode. The establishment of axially propagating acoustic waves can lead to a complex coupling mechanism and this phenomenon is highly relevant in understanding the multi-physical interactions appearing in modern compressors. It is shown that aerodynamic disturbances occurring downstream can lead to critical excitation of rotor blades in upstream stages due to an axially propagating acoustic wave. The paper includes the analysis of a relevant transient test and a detailed analysis of the numerical results. The study shows the capability and necessity of a full-annulus multistage simulation to understand the phenomenon.
1. Introduction
Non-Synchronous Vibrations (NSV) have received much attention since the 1990s [1,2,3,4,5,6]. The term of ‘NSV’ is used to describe a specific aeroelastic phenomenon where the characteristic frequency is not related to the shaft frequency. Unfortunately, a multitude of phenomena can lead to non-synchronous blade vibrations in turbomachinery, as flutter [7], buffeting, or rotating stall. The term of ‘NSV’ has been widely used to identify an aeroelastic phenomenon where blade vibrations are measured without a precise terminology.
According to cases of ‘NSV’ reported in literature, a characterization can be derived:
- Blade vibrations caused by convective phenomena: This type of ‘NSV’ is typically driven by small-scale aerodynamic disturbances that are convected around the circumference and may adapt their phase to blade vibration [8]. Before the establishment of blade vibrations, it was observed that these aerodynamic disturbances were already present with a random azimuthal distribution and a characteristic circumferential phase velocity. Once ‘NSV’ is established, this characteristic phase velocity is slightly altered to enable the coincidence of the aerodynamic disturbances with the coherent blade eigenmode. Generally, phenomena of this kind occur in modern transonic compressor rotors under highly throttled conditions close to the stall boundary.
- Acoustic resonance: In this specific case, several spinning modes of zeroth radial order can originate and propagate only in one axial direction due to the change of acoustic propagation conditions upstream and downstream of a blade row [8,9,10,11,12]. This change of acoustic propagation conditions enables only a series of resonant modes with a certain circumferential wave number and circumferential phase velocity [13]. Unstable aerodynamic flow structures can phase-lock to the acoustic mode, and thus serve as a periodic energy source. If it coincides with a structural mode, it may cause damaging effects. In this particular case, it is important to note that a backward traveling acoustic mode originating in a downstream stage of the compressor can be coincident with a specific structural mode of an upstream rotor. This type of phenomena can occur far from the stability limit of the compressor.
Both mechanisms can lead to severe blade vibrations and damage the structure. These phenomena are highly relevant to engine manufacturers since modern compressor stages can develop sensitive flow structures, such as flow separations or small-scale disturbances at off-design conditions. The characterization of such phenomena requires special attention to consider the interdependency between aerodynamics, structure dynamics, and acoustics. Safran Helicopter Engines conducted complex experiments with synchronized aerodynamic and blade vibration measurements to improve the understanding and interaction mechanisms of the observed ‘NSV’ occurring in a research axial compressor.
As will be shown in this paper, pressure modes observed in the experiment and the numerical simulations are cut-on only in one axial direction (upstream or downstream). This paper represents a synthesis of previous publications on the phenomenon [14,15,16,17]. The main objective is to clarify the mechanism behind the non-synchronous phenomena observed experimentally and to give a coherent explanation through comparison with numerical simulations.
Non-synchronous activity has been observed at different operating conditions, but in one specific transient test, an acoustic mode coincides with a structural mode and leads to significant blade vibration. This paper will describe the test case and experimental observations concerning this non-synchronous phenomenon. Full annulus unsteady simulations are carried out for two operating conditions to understand the establishment of this phenomenon. To post-process numerical results in detail, a spatial Fourier transform is calculated to determine dominant circumferential wave numbers. Then, a temporal Fourier transform is computed to derive frequencies and velocities in both frames of reference.
2. Fundamentals
In this study, only non-synchronous frequencies are relevant. To isolate these non-synchronous fluctuations, the deviation of temporal signals is calculated by subtracting an ensemble average of the preceding r revolutions from the instantaneous value at sample i and revolution n [18]:
In this work, a sliding ensemble average of 4 rotations is subtracted from experimental and numerical data to keep only the non-synchronous part of the raw data. All frequencies in this paper are normalized by the shaft rotation frequency () using Equation (2), yielding to Engine Order (EO).
Figure 1 presents two frequency spectra of unsteady wall pressure signal (a) and associated non-synchronous wall pressure fluctuations (b), in the stationary frame of reference. Synchronous and non-synchronous activity is observed in the frequency spectrum (a). The frequency peak corresponding to the blade passing frequency of rotor blades (EO) is clearly visible in the raw data. This peak is not observed after isolating the non-synchronous part as shown in the frequency spectrum (b). Regarding the non-synchronous frequencies ( close to 6 and 12EO), their amplitudes are equal in both spectra. By applying this method, non-synchronous frequencies are thus well isolated. All data presented in the following only contain the non-synchronous part of raw data.
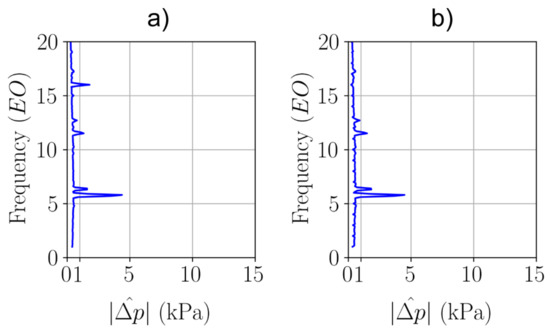
Figure 1.
Frequency spectra in the stationary frame of reference of: (a) unsteady wall pressure signal; (b) non-synchronous wall pressure fluctuations after subtracting a sliding ensemble average of 4 rotations.
A pressure wave can be described in the stationary frame of reference as series of space-time harmonics as shown in Equation (3), where is the amplitude, is the normalized frequency in the stationary frame of reference, and represents the phase:
For a specific spinning pressure wave in the stationary frame of reference with normalized frequency , which is traveling around the circumference with circumferential propagating speed , it is possible to derive the circumferential wave number using Equation (4) [19]. Term represents the blade velocity at radius r.
It is also possible to established the circumferential organization from Equation (5), where and correspond respectively to normalized frequency and circumferential propagating speed measured in the rotating frame of reference:
The relation between frequencies in both frames of reference is given by Equation (6):
Regarding a structural vibration mode based on blade eigenfrequency , the term Nodal Diameter () is used instead of the circumferential wave number. In contrast to aerodynamic modes, the nodal diameter has to be less than half the number of blades (). If the structure is in resonance with an aerodynamic mode of , a structural mode traveling in the opposite circumferential direction with develops.
3. Test Case and Experimental Results
3.1. Experimental Setup
The research axial compressor under investigation designed by Safran Helicopter Engines is representative of a modern high-speed multi-stage compressor of helicopter engines. The purpose of the test campaign was to study vibrations in each blade row at off-design operating conditions. The compressor rig is composed of struts, variable Inlet Guide Vanes (IGVs), and three stages, as shown in Figure 2. The stagger angle of IGVs and Stators-1 are varying according to the shaft speed. The presented transient test was conducted at constant part-speed. Thus, stagger angles of both rows are held at fixed position during the experiment. Regarding some specifics of the compressor, the tip clearance of all rotors is lower than of chord, the hub-to-tip ratio lies between 0.6 and 0.8, and the blades aspect ratio evolves between 0.8 and 1.0.
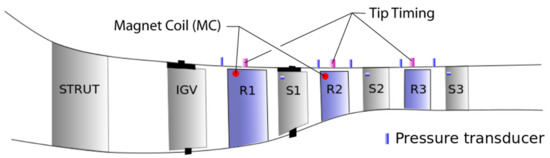
Figure 2.
Schematic of Safran Helicopter Engines research compressor.
Different measurement systems are available on this test rig. Unsteady pressure measurements are carried out using case-mounted and stator-mounted Kulite transducers. These data are measured in the stationary frame of reference. Blade vibrations of the three rotors are also measured in the rotating frame of reference by using a magnet-coil system [20] and tip-timing technology [21]. The magnet-coil system consists in a small magnet mounted at the rotor tip and a coil installed along the rotor circumference where the voltage induced by the relative motion between both components is measured. Compared to the tip-timing technology, which measures the tip displacement of each rotor blade, vibrations of one blade per row only, is derived by this technique. To derive the circumferential wave number of the vibration pattern (nodal diameter), conventional tip-timing is used. The temporal Fourier transform of the measurement signal of circumferentially distributed optical sensors is calculated to obtain the amplitude of vibration related to structural eigenfrequencies for each blade. Then, a spatial Fourier transform is calculated to obtain the nodal diameter decomposition.
3.2. Experimental Compressor Characteristic
Non-synchronous phenomena were observed in repeated transient tests at a certain speedline [14,15]. Figure 3 shows the relevant compressor characteristic for the entire rig. Experimental data measured at stabilized operating points are depicted as purple squares. During several transient tests where the throttle is slowly closed towards low mass flow rates, non-synchronous pressure oscillations were observed. The operating conditions where these significant pressure oscillations were measured are shown in Figure 3 (pink and yellow operating points). It is important to notice that these non-synchronous phenomena occur far from the stability limit, unlike the rotating stall or surge. The highest level of amplitude related to the non-synchronous activity was measured in the transient test from operating point OP-A towards the stability limit, thus its analysis is presented in detail in Section 3.3. OP-B and OP-C are two particular operating points, OP-B representing a frequency switch of non-synchronous modes and OP-C representing the onset of significant blade vibration, occurring close to numerical condition OP2. Unsteady full-annulus simulations at OP0, OP1, and OP2 are detailed in the numerical of Section 4.
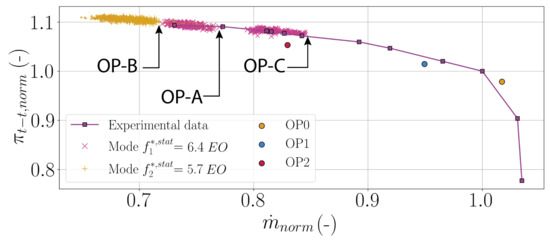
Figure 3.
Full compressor characteristic from experiment; indicators for non-synchronous activity in transient experiment (× and + symbols) and mean averaged performance from unsteady simulations (OP0, OP1, and OP2).
3.3. Transient Test from OP-A to Stability Limit
Figure 4 presents an overview of experimental data measured during the considered transient test at the casing near the leading edge of Rotor-2. The frequency spectrogram of pressure fluctuations (upper part of the figure) reveals several non-synchronous frequencies in the stationary frame of reference. Two phases can be identified in this spectrogram and they are named Phase I and Phase II. Mean average frequency spectra are also plotted in the lower part of the figure for each phase. The change of phase occurs at OP-B, which is identified in Figure 3. During Phase I, a dominant non-synchronous peak at is clearly visible. This peak switches from to at the normalized mass flow rate of . Thus, the pressure peak at is observed in Phase II. The respective second harmonics of each dominant non-synchronous frequency are also visible in the spectra, as well as the modulation with the blade passing frequency of Rotor-2 (). In Phase I, the second harmonic has a frequency of and the modulation peaks are observed at . During Phase II, the second harmonic of the aerodynamic disturbance presents a frequency of . Both peaks resulting of the modulation with the blade passing frequency are identified at . The amplitude of the non-synchronous pressure oscillations is significant in both phases with a level higher than 8 kPa at the casing near the leading edge of Rotor-2. The switch does not occur instantly, but transiently within a few hundred revolutions, representing a fraction of a second.
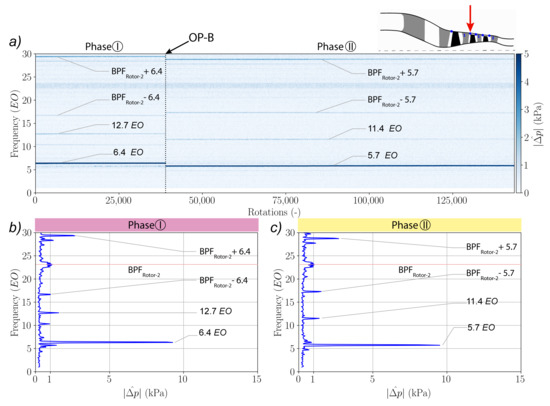
Figure 4.
Spectrum analysis of pressure fluctuations measured at the casing near the leading edge of Rotor-2: (a) frequency spectrogram during the transient test; (b) mean averaged frequency spectrum during Phase I; (c) mean averaged frequency spectrum during Phase II.
This spectral analysis shows that an aerodynamic disturbance identified as a non-synchronous pressure wave of high amplitude, is established in the compressor. During the presented transient test, its frequency changes at operating point OP-B. Moreover, its second harmonic and modulations with the blade passing frequency are still observed. This indicates that the phenomenon is stable and does not change its physical nature between the different phases but its circumferential wave number.
These non-synchronous pressure oscillations are observed in the whole compressor, as shown by Figure 5. It presents the axial evolution of the mean averaged amplitude of the dominant pressure waves for each respective phase. When two wall pressure probes are available at the same axial position, an average of the two probes is computed. The trend between both axial evolutions is identical in Phase I and Phase II. The highest amplitude of around ≈13 kPa is reached at Stage-2 and a rapid decay is observed downstream. The lower level of amplitude is measured at the casing near the leading edge of Rotor-1, but it is still a significant level of more than 1 kPa. The sharp drop in amplitude downstream Stator-2 is discussed in Section 5.
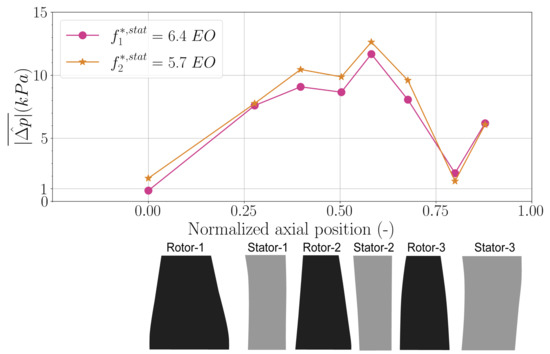
Figure 5.
Axial evolution of the mean averaged amplitude of the non-synchronous pressure peak during Phase I and Phase II.
As a conclusion, the considered test reveals the establishment of stable non-synchronous pressure waves of high amplitude in the whole compressor. During the test, two phases are distinguished. The frequency of the non-synchronous pressure mode switches from (Phase I) to (Phase II). However, the axial evolution of the associated amplitude remains the same between both phases. It is important to note that a non-synchronous pressure mode similar to the one established during Phase I has been observed at higher mass flow rates from OP-C towards OP-A (see Figure 3).
Tip-timing technology and magnet-coil system enable to measure the rotor blade vibration in the rotating frame of reference. Figure 6 shows the temporal evolution of the vibrating amplitude of three representative blades of Rotor-2. Phase I and Phase II can also be distinguished. A change of behavior occurs at OP-B. A significant level of vibration is measured during Phase I with a mean displacement of of the axial chord (≈0.1 mm). In contrast, it decreases rapidly in Phase II and remains at a constant level during this phase. Since the rotor blades are vibrating with a lower amplitude in Phase II while the pressure mode remains at constant level, a self-excited flutter-like phenomenon can be excluded.
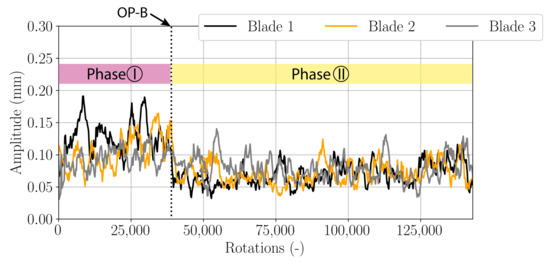
Figure 6.
Temporal evolution of the vibrating amplitude for three representative blades of Rotor-2.
Figure 7 presents the frequency spectrogram of the magnet-coil signal of Rotor-2. The frequencies observed in this dataset are measured in the rotating frame of reference. Large amplitudes are clearly observed during the entire test for the first blade eigenmode of Rotor-2 indicated as Mode-1. Its frequency is equal to . Considering the mean averaged frequency spectra, the amplitude of the structural mode Mode-1 decreases slightly from Phase I to Phase II. It is important to note that a non-synchronous activity is also visible in this spectrogram. A very low amplitude peak at in Phase I disappears in Phase II. A peak at is clearly visible in Phase II. This frequency switch occurs at the same instant of the frequency switch observed in the stationary frame of reference (see Figure 4) at OP-B. In Figure 7, a clear frequency peak is also observed at during the entire transient test. The signature resembles that of a rotating stall cell traveling around the circumference with a speed of of rotor speed, however this same signature is not observed in the unsteady wall pressure measurements. Since its amplitude remains constant between both phases, it is not investigated in this work and the peak cannot be explained based on available data. This non-synchronous activity is not related to an eigenmode and its source must be sought in the flow dynamics. At this time, it is necessary to derive the nodal diameter of the structural mode Mode-1 to identify a potential interaction between a pressure mode and blade eigenmode.
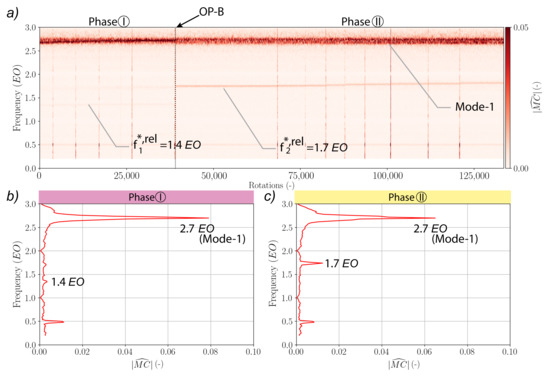
Figure 7.
Spectrum analysis of magnet-coil signal of Rotor-2: (a) frequency spectrogram during the transient test; (b) mean averaged frequency spectrum during Phase I; (c) mean averaged frequency spectrum during Phase II.
The nodal diameter of Mode-1 can be derived from the tip-timing data, which records the tip displacement of each rotor blade. Knowing the tip blade displacement and the vibrating frequency, the nodal diameter of the structural mode is determined. Figure 8 presents the nodal diameter decomposition at the 1st blade eigenfrequency of Rotor-2 (Mode-1) for both phases. The amplitude of the tip-timing decomposition is normalized by the highest amplitude reached during Phase I, in order to compare both phases. It is obvious that the dominant pattern of the structural mode Mode-1 is equivalent to a nodal diameter of during Phase I. A planar pattern () is also observed. In Phase II, the vibration of Rotor-2 blades decreases significantly (comp. Figure 6). The maximal normalized amplitude is strongly reduced by . The nodal diameter decomposition is not conclusive then. However a dominant pattern of during this phase could be determined.
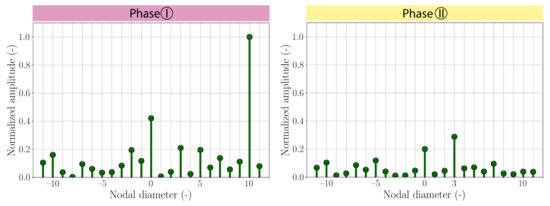
Figure 8.
Nodal diameter decomposition, estimated from tip-timing results in Rotor-2 for its 1st blade eigenfrequency during Phase I and Phase II.
Tip-timing data are also post-processed to get the nodal diameter decomposition for and . As the amplitude of the non-synchronous pressure mode is the highest in Stator-2 (see Figure 5), the tip-timing data of downstream Rotor-3 are used. Figure 9 presents the nodal diameter decomposition at the non-synchronous frequency observed in each phase. The amplitude is normalized as in Figure 8 by the value for the 1st blade eigenmode during Phase I. A clear nodal diameter of appears in Phase I and it switches to a nodal diameter of in Phase II with a similar amplitude.
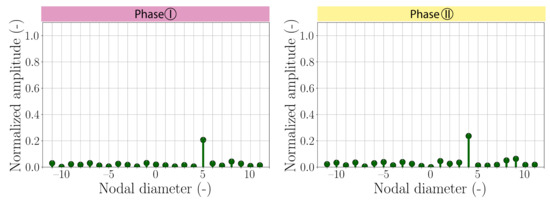
Figure 9.
Nodal diameter decomposition, estimated from tip-timing results in Rotor-3 for the dominant non-synchronous frequency in Phase I () and Phase II ().
The circumferential wave number can be derived from a comparison between the stationary and rotating frames of reference regarding Equation (6). Non-synchronous activities have been measured in both frames of reference (see Figure 4 and Figure 7). The comparison is presented for both phases in Figure 10 and Figure 11. The frequency spectrum in the stationary frame of reference (blue curve) is computed using the unsteady wall pressure signal recorded at the leading edge of Stator-2 at of channel height. The frequency spectrum in the rotating frame of reference (red curve) is derived from the magnet-coil signal measured in Rotor-2.
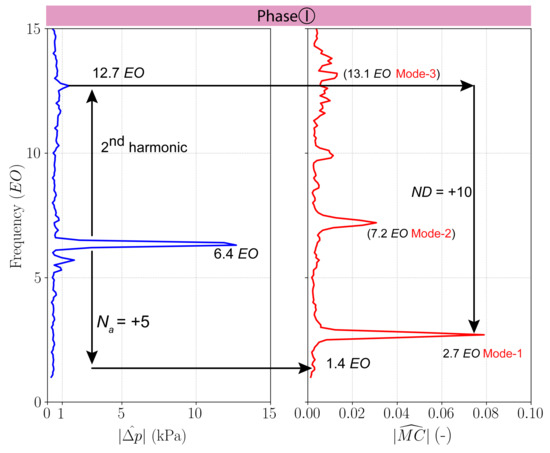
Figure 10.
Frequency spectra during Phase I of pressure fluctuations measured at the leading edge of Stator-2 at of channel height in the stationary frame of reference and magnet-coil signal of Rotor-2 measured in the rotating frame of reference.
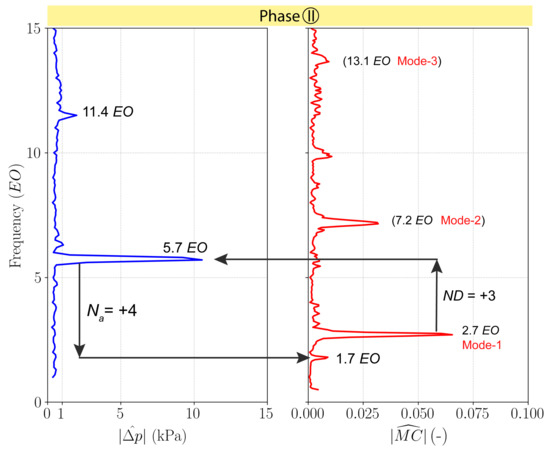
Figure 11.
Frequency spectra during Phase II of pressure fluctuations measured at the leading edge of Stator-2 at of channel height in the stationary frame of reference and magnet-coil signal of Rotor-2 measured in the rotating frame of reference.
Several observations from aerodynamic and mechanical data can be dressed from Figure 10:
- A non-synchronous pressure frequency at ;
- Its 2nd harmonic at ;
- The 1st blade eigenfrequency of Rotor-2 indicated by Mode-1 at ;
- The 2nd blade eigenfrequency of Rotor-2 indicated by Mode-2 at ;
- The 3rd blade eigenfrequency of Rotor-2 indicated by Mode-3 at .
Using Equation (6) and Figure 8, the frequency of Mode-1 in the stationary frame of reference can be derived and is equal to . This frequency is visible in the spectrum of unsteady wall pressure signal (blue curve). It is coincident with the 2nd harmonic of the non-synchronous aerodynamic disturbance at . The non-synchronous excitation of presents a pattern of (see Figure 9) which corresponds to a frequency in the stationary frame of reference of . Hence during Phase I, the pressure wave with a dominant wave number of leads to a non-resonant excitation of the rotor blades at and its second harmonic of to a resonant excitation of Mode-1 at , causing the high vibration amplitudes (see Figure 6).
From Phase I to Phase II at OP-B, the occurring aerodynamic disturbance changes its circumferential wave number from to (see Figure 9), and a sharp drop of the vibrating amplitude of Rotor-2 is observed (see Figure 6).
Similar observations noticed in Phase I can be also dressed in Phase II according to Figure 11:
- A non-synchronous pressure frequency at ;
- Its 2nd harmonic at ;
- a non-synchronous vibrating frequency at ;
- The 1st blade eigenfrequency of Rotor-2 indicated by Mode-1 at ;
- The 2nd blade eigenfrequency of Rotor-2 indicated by Mode-2 at ;
- The 3rd blade eigenfrequency of Rotor-2 indicated by Mode-3 at .
The frequency of Mode-1 in the stationary frame of reference for the most dominant nodal diameter of (see Figure 8) is also equal to . The non-synchronous excitation of presents a pattern of (see Figure 9) which corresponds to a frequency in the stationary frame of reference of . Even though this frequency corresponds to the frequency of the occurring aerodynamic disturbance, the circumferential wave number is not coherent between the aerodynamic disturbance () and structural mode ().
Table 1 summarizes the characteristics of experimental modes observed as coupled in the transient test. Both the structural mode and pressure mode (2nd harmonic of the acoustic mode) are spinning in the same direction as the rotor with a circumferential speed at the casing higher than the rotor blade speed. This observation indicates that the pressure wave is of an acoustic nature, as the convective phenomena cannot propagate faster than the rotor. The 1st harmonic of this acoustic mode corresponds to a pressure mode with a circumferential wave number of and a frequency in the stationary frame of reference of .

Table 1.
Experimentally observed coupled non-synchronous modes during Phase I.
Reconsidering Figure 3, it appears that for pink operating points that a co-rotating acoustic mode with and its 2nd harmonic established in the entire machine. Based on tip-timing analysis and magnet-coil data, Rotor-2 develops a structural vibration pattern based on its 1st blade eigenmode, which is coherent with the 2nd harmonic of the acoustic mode. Throttling further (yellow operating points), the circumferential wave number of the acoustic mode changes to . Thus, the previous coherence of its 2nd harmonic is lost. As a consequence, the blade vibration of Rotor-2 (see Figure 6) diminishes at the same time while the amplitude of the aerodynamic disturbance remains constant (see Figure 5). Based on this interpretation, the phenomenon is denoted as “Non-Synchronous Forced Response”.
4. Numerical Investigation
4.1. Numerical Setup
To reproduce the acoustic resonance observed in the transient test, a numerical investigation is performed at the relevant speedline (see Figure 3). As acoustic modes are observed in the entire compressor, the computational domain includes the IGVs and the three stages, as presented in Figure 12. The downstream experimental nozzle is extended by a convergent nozzle in order to improve numerical stability.
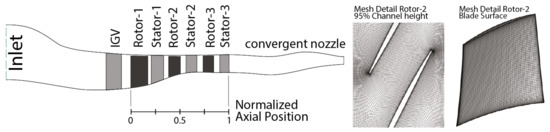
Figure 12.
Computational domain for steady and unsteady simulations and detail of Rotor-2 mesh.
The axial and azimuthal wavelengths of observed spinning modes in this work are large: Around 0.8 times the axial length of the compressor and close to 0.2 times the compressor circumference. It has been observed that the circumferential wave number of the acoustic mode is not fixed (it changes from to in the experiment). It is essential not to constrain it by periodic boundary conditions. Thus, full-annulus simulations are required. Moreover pressure modes have to be axially propagative between rows. Hence, sliding meshes are used between stationary and rotating domains instead of mixing planes. Non-reflective 1-D boundary conditions that specify conservative and turbulent variables are applied at the inlet and outlet of the computational domain.
Numeca AutoGrid5 is used to mesh the domain. The full compressor without struts is modeled with a total number of cells of . Each blade passage of each rotor is meshed with approximately cells. Mesh visualizations of Rotor-2 are also shown in Figure 12.
All simulations are performed using the flow solver elsA, an unsteady Reynolds-Average Navier–Stokes (URANS) solver developed by ONERA (Paris, France) [22]. The Roe scheme is used with 2nd order accuracy in space and the turbulence model used is the Smith model. Wall functions are applied to all surfaces (). Comparison between results wall resolved versus wall modeled was performed to validate the approach [19]. Simulations are time-accurate using a dual-time stepping scheme with 10 sub-iterations and 1000 physical time steps per rotation. This corresponds to 40 physical time steps per minimal blade passing period. The highest frequency captured according to this temporal discretization is , which is more than sufficient for this case. Unsteady full-annulus simulations are initialized with steady single passage simulations with mixing planes. Each calculation is distributed on 700 processors and 40 rotations are calculated to reach a periodic convergence. The computational cost amounts to 385,000 CPU hours for one operating point.
4.2. Simulation Results
Simulations were performed at three operating points, depicted in Figure 3 as OP0, OP1, and OP2. They are respectively located near choke (OP0), near peak efficiency (OP1), and at a mass flow rate where strong non-synchronous pressure oscillations have been measured in the experiment (OP2). The performance of the entire compressor is well predicted by the unsteady simulations but shows a tendency towards a reduced total-pressure rise. Simulations at higher loaded conditions than OP2 diverge due to the establishment of rotating stall cells.
4.2.1. Mean Averaged Results
In [15], steady results were briefly discussed. Figure 13 presents the contours of the average relative Mach number calculated over the four last computed rotations in the whole compressor for the unsteady full-annulus results at OP0, OP1, and OP2. The flow condition in Rotor-3 is transonic. For OP1 and OP2, the relative velocity in Rotor-1 is very low due to the IGV setting, and Rotor-2 is running transonic. The loading of Rotor-2 strongly increases between OP1 and OP2. A thickened boundary layer appears on the suction side of Rotor-2 for OP2. Rotor-3 is highly loaded with far detached shocks. A thickened boundary layer is also observed on the suction side of Rotor-3.
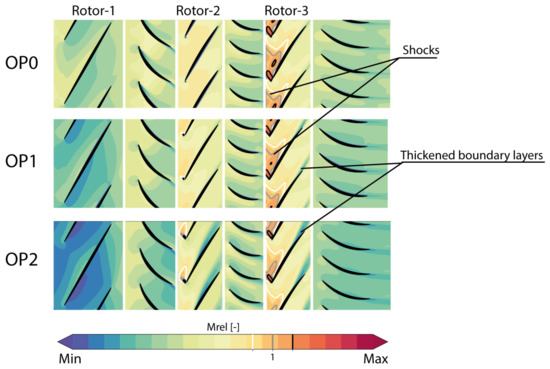
Figure 13.
Relative Mach number contours at of channel height for the whole compressor, the mean average of the URANS simulations for OP0, OP1, and OP2. The gray isocontours at low supersonic velocity visualize the shock structure.
4.2.2. Modal Decomposition
To determine all the non-synchronous modes established in the compressor for the three operating points, it is necessary to derive the axial evolution of circumferential wave number . The following procedure is applied on the static pressure field at of channel height in order to remain in the tip gap but out of the influence region of the wall function. The ensemble average of the four last computed rotations is subtracted from the instantaneous signal to remove rotor periodic phenomena.
According to Equation (3), non-synchronous pressure waves are described as a series of space-time harmonic. To derive circumferential wave numbers , a spatial Fourier transform is calculated around the circumference at different axial positions for each time step over 4 rotations. The average value of these instantaneous spectra is analyzed to determine the azimuthal organization of non-synchronous pressure modes.
The modal decomposition at OP0 reveals small traces of non-synchronous pressure modes between Stage-2 and Stage-3 with an amplitude much lower than 1 kPa. It is considered that OP0 does not experience significant non-synchronous pressure activity.
Figure 14 and Figure 15 shows, respectively, this axial evolution for OP1 and OP2. The leading edge and trailing edge of each rotor are represented by two vertical lines. At OP1, a strong non-synchronous activity is observed in Stage-3. A pressure mode with (indicated by letter “A”) is clearly identified with a peak in Rotor-3. The associated amplitude is high (≈2 kPa) near Rotor-3 and slightly decays downstream. This pressure mode is not observed upstream of this rotor. Significant peaks at and are also present in Rotor-3, as indicated respectively by the letters “B” and “C”. The pressure mode is propagating upstream of the rotor until it reaches the leading edge of Stator-2. The mode is only visible in Rotor-3. Both modes indicate a modulation of the non-synchronous pressure mode with the number of blades of Rotor-3 () to yielding 20 and 26. A last peak is observed at located downstream of Rotor-3 and indicated by letter “D”. It will not be discussed in this paper.
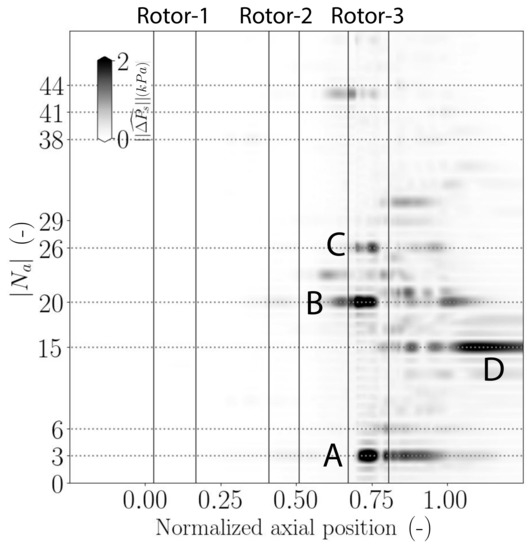
Figure 14.
Axial evolution of the circumferential wave number () based on the static pressure signal at of channel height for OP1.
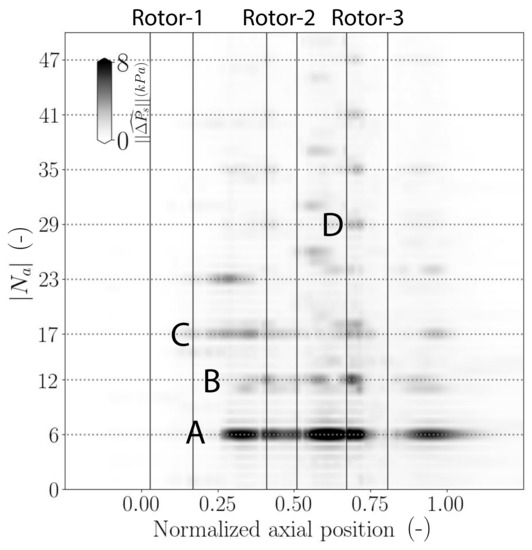
Figure 15.
Axial evolution of the circumferential wave number () based on the static pressure signal at of channel height for OP2.
Figure 15 shows the axial evolution of the circumferential wave number based on a non-synchronous pressure signal at OP2 where strong non-synchronous blade vibrations were measured experimentally (see Figure 3). It is important to note that the pressure scale is 4 times higher than the scale in Figure 14. A clearly dominant circumferential wave number at is fully established in the compressor from Stator-1 to Stator-3. This dominant peak is indicated by letter “A”. Its 2nd harmonic (letter “B”) and its modulations with the number of blades of Rotor-3 (letters “C” and “D”) are also visible. The amplitude of the non-synchronous mode at is high in Stage-2 and Stage-3.
4.2.3. Characteristics of Non-Synchronous Dominant Modes
To derive frequencies of established modes in both frames of reference, the following decomposition of the non-synchronous pressure field at of channel height is applied. First, a spatial filter of the circumferential signal for each individual time step depending on the targeted circumferential wave number () is applied. Hence, the temporal evolution of the spatially filtered amplitude is extracted (see Equation (3)). Secondly, the temporal Fourier transform of this amplitude over 8 rotations is used. The number of 8 rotations improves the frequency resolution. This decomposition applied in a rotor (resp. stator) gives the frequency in the rotating (resp. stationary) frame of reference (resp. ).
Figure 16 and Figure 17 presents the axial evolution of the frequency associated to each dominant mode depending on the operating point: Pressure mode with for OP1 (see Figure 14) and for OP2 (see Figure 15). At OP1, the dominant non-synchronous mode with has a frequency of in the stationary frame of reference (highest in Stator-3), as indicated by letter “A” in Figure 16. This dominant mode has also a frequency of in the rotating frame of reference (highest in Rotor-3) as indicated by letter “B”. Since , is equal to according to Equation (6). According to Figure 17, the dominant pressure mode at OP2 with presents a frequency in the stationary frame of reference equal to (highest in Stator-2, indicated by letter “A”) and a frequency of in the rotating frame of reference (highest in Rotor-3, indicated by letter “B”). In this case , so is equal to .
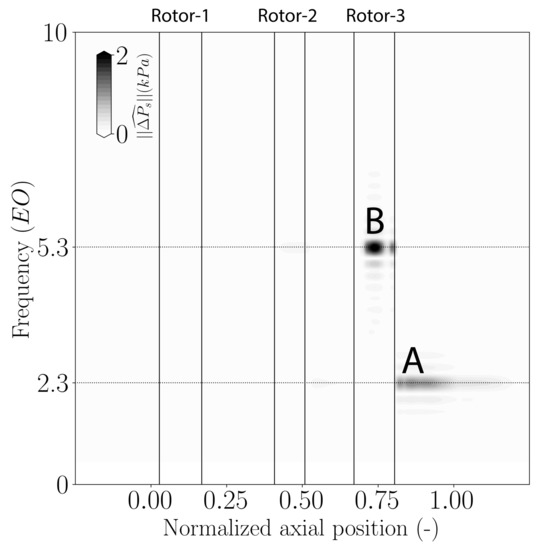
Figure 16.
Axial evolution of the frequency of the dominant mode based on static pressure signal at of channel height for OP1: Mode at ( in rotors, in stators).
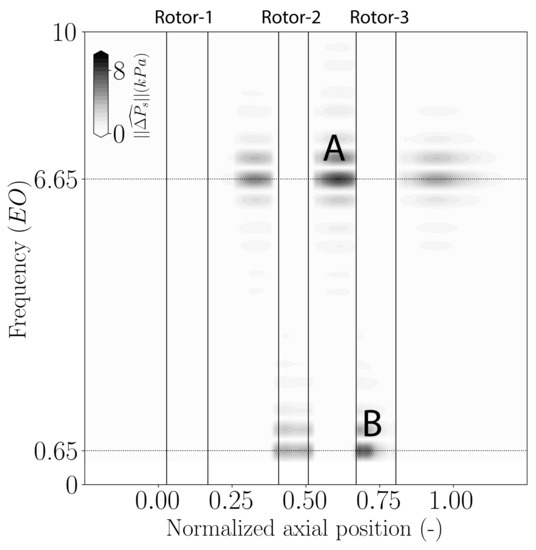
Figure 17.
Axial evolution of the frequency of the dominant mode based on static pressure signal at of channel height for OP2: Mode at ( in rotors, in stators).
Thus, both unsteady full-annulus simulations at OP1 and OP2 develop a dominant non-synchronous pressure mode. Table 2 summarizes the relevant characteristics of each. As the frequencies in both frames of reference are known as well as the circumferential wave number, the circumferential propagating speed can be derived according to Equations (4) and (5). For OP1, a pressure mode with 3 lobes contra-rotating in the stationary frame of reference is observed in the simulations as illustrated in Figure 18 which represents a snapshot of the simulation after reaching periodic convergence. This 3-lobes pressure mode stronger in Rotor-3 is visible at each time instant of the simulation in Stage-3. No significant non-synchronous activity is observed upstream at this stage in the pressure signal. At OP2, the dominant pressure mode corresponds to 6 lobes which are co-rotating in the stationary frame of reference. This 6-lobes pressure mode is clearly distinguished in Figure 19 over Stator-1, Stage-2, and Stage-3. It is highest in Stage-2. Both modes do not propagate with a typical convective speed but are of an acoustic nature since they travel with a speed, which is opposite or higher than the rotor speed in the stationary frame of reference. Thus, the circumferential speed exceeds the speed of sound relative to the mean flow , according to Table 2.

Table 2.
Numerical dominant non-synchronous modes.
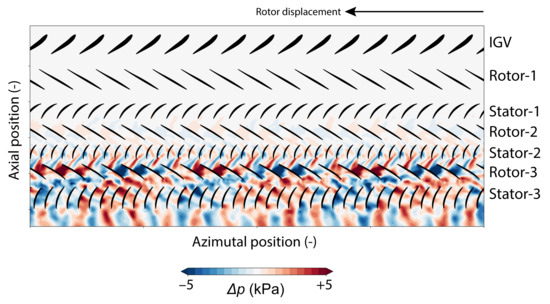
Figure 18.
Snapshot of unsteady non-synchronous pressure fluctuations at OP1 at one time instant after periodic convergence at of span.
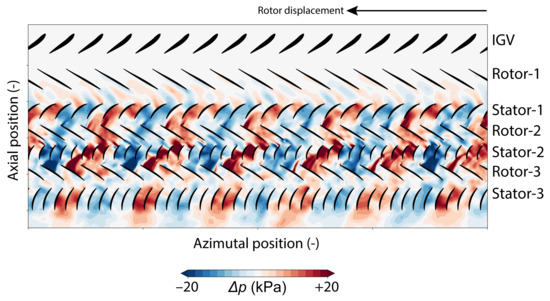
Figure 19.
Snapshot of unsteady non-synchronous pressure fluctuations at OP2 at one time instant after periodic convergence at of span.
4.2.4. Lock-In between Aerodynamic Disturbances and Acoustic Modes
As the two operating points reveal the establishment of high amplitude acoustic modes, it is relevant to observe how these modes affect the flow field in Stage-2 and Stage-3. Figure 20 compares the axial Mach number in the axial plane at of chord in Rotor-2 and Rotor-3 for the two operating points at a representative instant. It clearly shows how the flow is mostly undisturbed at OP1, compared to OP2. For OP1, the dominant circumferential wave number of is invisible in Rotor-2 and only slightly observed in Rotor-3. A weak flow separation is present on the suction side of Rotor-3. At the higher loaded operating point OP2, the dominant circumferential wave number of is much stronger. It is radially extended from the hub to the casing in both rotors. In Rotor-3, a large separation zone on the suction side is observed near the hub. Hence, the lock-in phenomenon can be interpreted as a resonance between a swirling acoustic mode, which reaches high amplitudes in the axial gap between the rotor and stator, and a fluctuating boundary layer in the highly loaded rotor, which serves as an energy source. Thus, the dominant circumferential wave number depends on the acoustic propagation conditions.
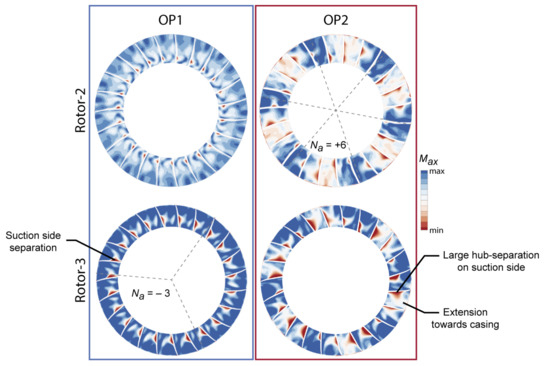
Figure 20.
Axial Mach number at of chord in Rotor-2 and Rotor-3 for OP1 and OP2.
5. Comparison and Discussion
The axial evolution of the modal amplitude of the dominant pressure mode at OP2 is presented in Figure 21 for the experiment (, , see Figure 10) and the simulation (, , see Figure 17), along the amplitude of the dominant mode (, , see Figure 16) observed at OP1. These evolutions are determined at the casing. The coherence between experimental and numerical results at OP2 is remarkable. The circumferential wave number is not the same (experiment and simulation ), nevertheless the modal amplitude extracted from simulation is in good agreement with the experiment. At OP1, the non-synchronous activity appears only in Stage-3.
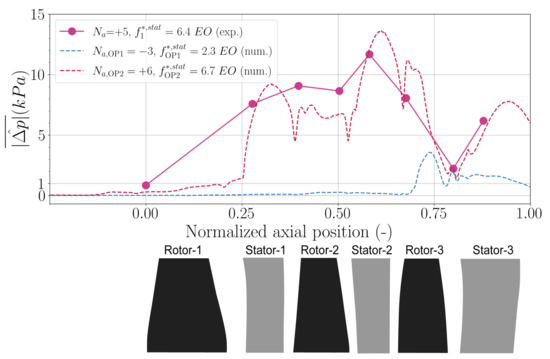
Figure 21.
Axial evolution of the amplitude associated to dominant non-synchronous pressure mode, experimental results during Phase I and numerical results at OP1 and OP2.
As Rotor-3 is the most sensitive rotor, Figure 22 presents the evolution of the cut-on frequency depending on the circumferential wave number [23]. Flow conditions used to compute this frequency are derived from simulations. This evolution is given upstream (blue curve) and downstream (red curve) of this rotor. Experimental and numerical acoustic modes are depicted with symbols. The evolution of the 1st eigenfrequency of Rotor-2 blades in the stationary frame of reference according to Equation (6) is drawn as a black curve.
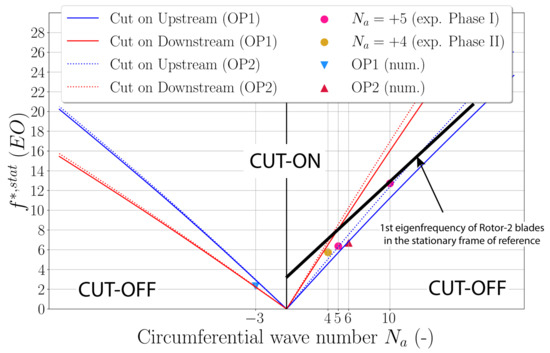
Figure 22.
Frequency and circumferential wave number of acoustic modes in the experiment and simulation, as well as the cut-on conditions upstream and downstream of Rotor-3.
Three important observations can be made:
- All occurring modes, both experimentally and in simulations, are propagative only in one axial direction. Co-rotating modes () are cut-on only upstream, while contra-rotating modes () are cut-on only downstream;
- At highly-loaded conditions OP2, the modes in the experiment and simulations are clustered in the wave-number and frequency ( and );
- Coincidence of the second harmonic at of an acoustic mode at with the structural blade-eigenfrequency leads to significant non-synchronous forced response in the experiment during Phase I. As soon as the mode switches to in Phase II, the vibration amplitude drops as the excitation at is far off resonance.
It is impossible that a self-excited phenomenon (as flutter) is present, as the bladed disk vibration cannot excite a sub-harmonic acoustic mode. This is confirmed in the experiment by the fact that after the wave number changes, the acoustic pressure amplitude remains constant however the vibration diminishes. The reason behind the inaccurate prediction of the wave number of the acoustic mode ( versus ) cannot be explained clearly from the results. The first assumption is that the numerical resolution (spatial and temporal) is not sufficiently accurate to predict the correct wave number. Secondly, a specific wave number can be preferred in the experiment due to geometrical asymmetry and structural mistuning. As the cut-on conditions are sensitive to the flow field in Rotor-2 and Rotor-3, a slight inaccuracy in the simulation can shift the critical frequencies and also enforce the development of the next integer wave number.
Nevertheless, these observations are of importance for the interpretation of experiments, the setup of simulations, and the development of countermeasures. The acoustic propagation conditions upstream and downstream of a rotor that is highly loaded and sensitivity to external feedback determine the development of critical modes. These propagation conditions can be estimated from averaged flow values from experiments or RANS simulations, which are usually performed during the design phase of a multistage compressor. Typically the range of modes, which are propagative only in one axial direction is narrow as depicted in Figure 22. If structural vibration occurs and the eigenfrequency is known, possible interaction can be assessed as presented. Obviously, harmonics of dominant-trapped modes need to be taken into account if amplitudes are significant. Countermeasures must primarily aim to reduce the sensitivity of the rotor-aerodynamics. Typical measures, such as mistuning, will not be efficient for the observed case, as it is not a coupled phenomenon, like flutter or convective NSV [5]. Mistuning is generally considered detrimental for forced-response problems. For this configuration, a full annulus multistage setup was required to reproduce the phenomenon in simulations. Special attention needs to be laid on boundary conditions interacting with acoustic modes. The presented results indicate that the mismatching of the compressor with significant overloading of Rotor-3 is responsible for the emergence of unsteadiness. The actual process observed leading to trapped acoustic modes is then a symptom that cannot be avoided; there will always be room for cut-on/cut-off modes and coincidence with structural eigenmodes is always possible. Design must focus on the avoidance of operating conditions and lead to the excitation of trapped acoustic modes. The focus of the presented study was on the physical explanation of what happens if these conditions occur. Typical procedures to stabilize part-speed operation focus on IGV scheduling, however the study shows that very complex phenomena can occur at a stable aerodynamic performance.
6. Conclusions
During repeated test campaigns, significant non-synchronous activity was measured in a research axial multi-stage compressor at part-speed for moderately loaded operating points.
High-amplitude acoustic modes were observed in multiple stages of the machine. The source for the acoustic mode was identified in a highly loaded downstream stage, in which the phase of local flow separations lock-in with an upstream-propagating acoustic mode.
In the experiment, coincidence between the second harmonic of the dominant acoustic mode and a structural vibration eigenmode leads to a severe non-synchronous forced response.
Using unsteady full-annulus simulations, the phenomenon is reproduced. Slight differences in the wave number are observed, however amplitude and frequency of the dominant mode are well captured. Results indicate that an estimation of critical modes can be made based on acoustic propagation conditions derived from experiments or steady RANS calculations.
Author Contributions
Conceptualization, A.-L.F. and C.B.; methodology, A.-L.F. and C.B.; validation, S.A., N.B.; formal analysis, investigation, A.-L.F., C.B. and A.V.; writing—original draft preparation, A.-L.F.; writing—review and editing, S.A. and C.B.; visualization, A.-L.F.; supervision, N.B., S.A. and C.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Safran Helicopter Engines.
Data Availability Statement
Not applicable.
Acknowledgments
The authors thank Safran Helicopter Engines (Safran Goup) for permission to publish these results. We are truly grateful for the technical advice and the comments of Jacques Demolis of Safran Helicopter Engines during the preparation of this paper. We would also like to thank Nick Cumpsty of the Imperial College London for the helpful discussions on this work. This work was granted access to the HPC resources of CINES under the allocation 2019-A0052A07410 made by GENCI and to the HPC resources of CCRT.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| IGV | Inlet Guide Vane |
| MC | Magnet-coil |
| NSV | Non-Synchronous Vibrations |
| ND | Nodal diameter |
| EO | Engine Order |
| c | Speed of sound [m·s] |
| Circumferential propagating speed [m·s] | |
| Shaft rotation frequency [Hz] | |
| Pressure fluctuations [Pa] | |
| Axial Mach number | |
| Relative Mach number | |
| Circumferential wave number | |
| Number of blades | |
| Rotational speed [rad·s] | |
| r | Radius [m] |
| Absolute tangential velocity [m·s] | |
| Fourier coefficient | |
| Stationary frame of reference | |
| Rotating frame of reference |
References
- Baumgartner, M.; Kameier, F.; Hourmouziadis, J. Non-Engine Order Blade Vibration in a High Pressure Compressor. In Proceedings of the Twelfth International Symposium on Airbreathing Engines, Melbourne, Australia, 10–15 September 1995. [Google Scholar]
- Jüngst, M.; Holzinger, F.; Leichtfuss, S.; Schiffer, H.-P. Analysing non-synchronous blade vibrations in a transonic compressor rotor. In Proceedings of the 11th European Conference on Turbomachinery, Madrid, Spain, 23–27 March 2015. [Google Scholar]
- Kielb, R.E.; Barter, J.W.; Thomas, J.P.; Hall, K.C. Blade Excitation by Aerodynamic Instabilities: A Compressor Blade Study. In Turbo Expo: Power for Land, Sea, and Air; American Society of Mechanical Engineers: Atlanta, GA, USA, 2003. [Google Scholar]
- Möller, D.; Jüngst, M.; Holzinger, F.; Brandstetter, C.; Schiffer, H.-P.; Leichtfuss, S. Mechanism of Nonsynchronous Blade Vibration in a Transonic Compressor Rig. J. Turbomach. 2017, 139, 011002. [Google Scholar] [CrossRef]
- Stapelfeldt, S.; Brandstetter, C. Non-synchronous vibration in axial compressors: Lock-in mechanism and semi-analytical model. J. Sound Vib. 2020, 488, 115649. [Google Scholar] [CrossRef]
- Brandstetter, C.; Paoletti, B.; Ottavy, X. Acoustic and Convective Mechanisms Contributing to Non-Synchronous-Vibrations in a Multistage Compressor. In Turbo Expo: Power for Land, Sea, and Air; American Society of Mechanical Engineers: Phoenix, AZ, USA, 2019. [Google Scholar]
- Marshall, J.G.; Imregun, M. A review of aeroelasticity methods with emphasis on turbomachinery applications. J. Fluids Struct. 1996, 10, 237–267. [Google Scholar] [CrossRef]
- Brandstetter, C.; Jüngst, M.; Schiffer, H.-P. Measurements of Radial Vortices, Spill Forward, and Vortex Breakdown in a Transonic Compressor. J. Turbomach. 2018, 140, 061004. [Google Scholar] [CrossRef]
- Cooper, A.J.; Peake, N. Trapped acoustic modes in aeroengine intakes with swirling flow. J. Turbomach. 2000, 419, 151–175. [Google Scholar] [CrossRef]
- Hellmich, B.; Seume, J. Causes of Acoustic Resonance in a High-Speed Axial Compressor. In Turbo Expo: Power for Land, Sea, and Air; American Society of Mechanical Engineers: Barcelona, Spain, 2006. [Google Scholar]
- Holzinger, F.; Wartzek, F.; Schiffer, H.-P.; Leichtfuss, S.; Nestle, M. Self-Excited Blade Vibration Experimentally Investigated in Transonic Compressors: Acoustic Resonance. J. Turbomach. 2015, 138, 041001. [Google Scholar] [CrossRef]
- Parker, R. Acoustic resonances and blade vibration in axial flow compressors. J. Sound Vib. 1984, 92, 529–539. [Google Scholar] [CrossRef]
- Tyler, J.M.; Sofrin, T.G. Axial Flow Compressor Noise Studies; SAE Technical Paper; University of Leeds: Leeds, UK, 1962; Volume 620532. [Google Scholar]
- Fiquet, A.-L.; Brandstetter, C.; Aubert, S.; Philit, M. Non-Engine Order oscillations in an axial multi-stage compressor—Aeroacoustic interaction. In Proceedings of the 15th International Symposium on Unsteady Aerodynamics, Aeroacoustics and Aeroelasticity of Turbomachines, Oxford, UK, 24–27 September 2018. [Google Scholar]
- Fiquet, A.-L.; Brandstetter, C.; Aubert, S.; Philit, M. Non-Synchronous Aeroacoustic Interaction in an Axial Multi-Stage Compressor. J. Turbomach. 2019, 141, 101013. [Google Scholar] [CrossRef]
- Fiquet, A.-L.; Buffaz, N.; Vercoutter, A.; Aubert, S.; Brandstetter, C. Acoustic resonance in an axial multistage compressor leading to non-synchronous blade vibration. In Proceedings of the 14th European Conference on Turbomachinery Fluid dynamics and Thermodynamics, Gdansk, Poland, 12–16 April 2021. [Google Scholar]
- Fiquet, A.-L.; Buffaz, N.; Vercoutter, A.; Aubert, S.; Brandstetter, C. Non-synchronous forced response due to trapped acoustic modes in an axial multi-stage compressor. In Proceedings of the ASME Turbo Expo 2020, London, UK, 22–26 September 2020. [Google Scholar]
- Brandstetter, C.; Paoletti, B.; Ottavy, X. Compressible Modal Instability Onset in an Aerodynamically Mistuned Transonic Fan. J. Turbomach. 2019, 141, 031004. [Google Scholar] [CrossRef]
- Fiquet, A.-L. Analyse et Modélisation de Phénomènes Aéroélastiques Non-Synchrones dans un Compresseur Axial Multi-étages. Ph.D. Thesis, École Centrale de Lyon, Lyon, France, 2021. [Google Scholar]
- Garnier, J.; Vercoutter, A.; Talon, A. Magnet-Coil measurement technology for analyzing turbomachine blade vibrations. In Proceedings of the Surveillance-8, Roanne, France, 20–21 October 2015. [Google Scholar]
- Bouchain, A.; Picheral, J.; Lahalle, E.; Vercoutter, A.; Burgardt, B.; Talon, A. New Possibilities for Analyzing Complex Asynchronous Blade Vibrations From Tip-Timing Data Using a Sparse Spectral Analysis Method. In Turbo Expo: Power for Land, Sea, and Air; American Society of Mechanical Engineers: Phoenix, AZ, USA, 2019. [Google Scholar]
- Cambier, L.; Heib, S.; Plot, S. The Onera elsA CFD software: Input from research and feedback from industry. Mech. Ind. 2013, 14, 159–174. [Google Scholar] [CrossRef] [Green Version]
- Camp, T.R. A Study of Acoustic Resonance in a Low-Speed Multistage Compressor. J. Turbomach. 1999, 121, 36–43. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY-NC-ND) license (https://creativecommons.org/licenses/by-nc-nd/4.0/).