Abstract
Results from an experimental profile loss study are presented of an additive manufactured linear turbine cascade placed in the test section of a closed-loop organic vapor wind tunnel. This test facility at Muenster University of Applied Sciences allows the investigation of high subsonic and transonic organic vapor flows under ORC turbine flow conditions at elevated pressure and temperature levels. An airfoil from the open literature was chosen for the cascade, and the organic vapor was Novec 649TM. Pitot probes measured the flow field upstream and downstream of the cascade. The inflow turbulence level was 0.5%. The roughness parameters of the metal-printed blades were determined, and the first set of flow measurements was performed. Then, the blade surfaces were further finished, and the impact of roughness on profile losses was assessed in the second flow measurement set. Although the Reynolds number level was relatively high, further surface treatment reduces the profile loss noticeably in organic vapor flows through the printed cascade.
1. Introduction
Additive manufacturing (also known as 3D printing technology) offers excellent potential for many turbomachinery applications because it can realize intricate blade designs (see, for instance, Magerramova et al. [1], Albright [2], or Adair et al. [3]). Faced with complex internal cooling channel designs, all leading gas turbine companies have considered this technology. Additive manufacturing is also a promising approach for organic Rankine cycle (ORC) turbines. Firstly, suitable additive manufacturing materials are widely available for the temperature and pressure levels in ORC turbines. Secondly, several ORC turbines are compact devices, and sophisticated three-dimensional blades might help to optimize their aerodynamics. Additive manufacturing could be a cost-efficient way to realize such highly efficient blading. However, the high surface roughness levels of printed blades can cause severe profile losses. For many decades, it has been well known that roughness is of significant importance for cascade and turbine performance (Speidel [4], Scholz [5], and Bammert and Sandstede [6]). Although considerable progress can be observed in additive manufacturing technology, substantial rework is still necessary to achieve roughness levels comparable to conventionally manufactured blades. The relatively high roughness level of printed objects makes it questionable how much rework and additional production cost would be required to create competitive blades. This severe issue might reduce the broader acceptance of this technology in the turbomachinery industry. Furthermore, the open literature reports virtually nothing about additive manufactured cascade’s loss and aerodynamic performance in organic vapor flows. In the following, the outcome of an experimental investigation of profile losses of a printed linear turbine cascade is presented. The cascade was placed in the test section of a closed-loop organic vapor wind tunnel (CLOWT). This test facility at Muenster University of Applied Sciences enables the investigation of high subsonic and transonic organic vapor flows under ORC turbine flow conditions at elevated pressure and temperature levels. Before presenting the experimental setup and procedure and before discussing the results, the following remarks might help. The present study focused only on cascade aerodynamics and profile losses, and manufacturing or other technology items were explicitly out of scope. Although additive manufacturing offers its full potential for creating complex three-dimensional blades and nozzles, the present study only considered two-dimensional profile losses because roughness issues are especially relevant for that kind of loss.
2. Test Case
The so-called VKI-Sieverding blade profile, shown in Figure 1, was chosen for the cascade because for this airfoil, as many reliable data and results are available for the subsonic and transonic flow of an ideal gas in the open literature (see Sieverding [7], Lehthaus [8], Kiock et al. [9]). The airfoil was designed following Dejc’s method, and the suction side is derived from one basic lemniscate, while the pressure side is composed of both a circular arc and a lemniscate.

Figure 1.
Geometric dimensions of the blade profiles and printed final design cascade.
Although the VKI-Sieverding profile represents a classical gas turbine airfoil design, it has been widely recognized as suitable for general transonic testing purposes. The airfoil is typical for cooled gas turbine rotor sections, and the trailing edge radius is relatively large compared to steam turbine profiles. For the present purpose, the large trailing edge radius was advantageous because it enabled the inclusion of trailing edge losses which are highly relevant for ORC turbines, as discussed by Baumgärtner et al. [10].
Based on this airfoil, a linear cascade, Figure 1, was designed to fit the test section of the employed closed-loop organic vapor wind tunnel (see section “Description of Test Facility”). Table 1 shows all determined dimensions of the blade profile. The cross-section of the test section was 100 mm × 50 mm. The test section height H = 50 mm of the airfoils corresponded to the transonic wind tunnel facility of VKI Rhode-St. Genese (Kiock et al. [9]) and was found to be appropriate for investigating profile loss. However, the present test section permitted only an axial inflow and an axial outflow. The maximum channel height was 100 mm, which was much smaller than at the VKI transonic wind tunnel facility. Since an airfoil with a significant deflection was employed; these severe design constraints led to a cascade configuration with only three entirely free-standing airfoils (and additional guiding profiles at the cascade’s boundaries see Figure 2 and Figure 3). The cascade’s final design, including its guiding profile and its outflow region, was defined after a numerical optimization procedure, employing compressible CFD analyses using a perfect gas model for air. During numerical optimization, the main objective was to meet the flow’s salient features through the central test blade passage.

Table 1.
Determined dimensions of the blade profile.
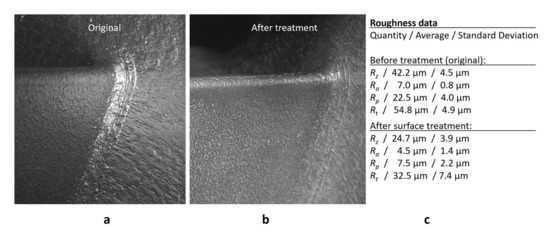
Figure 2.
Position: trailing edge, original state (a); treatment state (b); and measured roughness data (c).
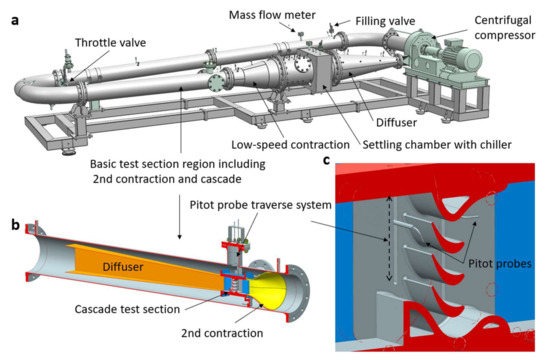
Figure 3.
Position: Closed-loop organic vapor wind tunnel CLOWT (Close-loop organic vapor Wind tunnel) (a); test section (b); and cascade (c).
2.1. Roughness and Blade Manufacturing
The quality of a surface is defined as the height of the peaks, the roughness structure, and its waviness. A single roughness parameter was usually prescribed in traditional workshop practice, including the roughness height Rt, defined as the largest height of the roughness peaks or the center-line-average CLA value. In the German industry standard DIN4767, the relationship was quoted for traditionally mechanically manufactured surfaces. Today, the arithmetic mean deviation of the assessed surface, Ra, or the average value over the assessment length, Rz, using the maximum peak to valley height, or the maximum profile peak height, Rp, are frequently used in the turbomachine industry.
The impact of roughness on the flow is a complicated topic because flow roughness and manufacturing roughness are not the same. If the viscous sublayer fully envelops peaks, there is no influence on the skin friction, and the surface is hydraulically smooth. If the peaks reach out of the viscous sublayer, shearing stress typically increases and additional loss occurs. A common approach is using an equivalent sand grain roughness ks [5]. A milled surface with roughness Rt behaves like a surface with sand grains of size ks = Rt/2.56 for a flow perpendicular to the milling grooves. On the other hand, it was also observed that a surface with sharp regular steps of height Rt could be hydraulically much rougher than a sand grain surface with the same peak level. Here, a relation ks = Rt/0.08 = 12.5·Rt was experimentally observed [5]. For blades, it is frequently quoted (Scholz [5], Bammert and Sandstede [6]) that the admissible sand grain roughness ks,adm normalized by the chord length l is a function of the Reynolds number Re = clρ/µ and can be correlated by
In ORC turbine applications, the Reynolds number Re can be relatively high due to the substantial density ρ of organic vapors consisting of complex molecules. Hence, the admissible roughness ks,adm might be relatively small for ORC turbines, posing considerable manufacturing challenges. Most of our knowledge on roughness on the flow past blades has been collected in light of conventional manufacturing methods. Much less is known regarding the surface quality of additive manufactured blades. Adair et al. [3] reported surface roughness measurements of electronic beam melting (EBM) blade artifacts in the as-printed and post-electrochemical machining conditions.
They found values of order Ra ≈ 80 µm (Rz ≈ 90 µm) in as-printed condition for the pressure and the suction side of gas turbine blades. After pulsed electrochemical machining (PECM), the roughness values were reduced to levels of Ra ≈ 1.3 µm (Rz ≈ 7.2 µm).
The present cascade was manufactured using the selective laser melting (SLM) method. Figure 2a shows the printed part when the supplier provided it. The printing direction was normal to the main flow direction and, after printing, the supplier did a first surface treatment. This surface is hence called “original”. After the first set of flow measurements, the printed part’s surface was treated using vibratory finishing. The improvement due to the second finishing process can be seen in Figure 2. Figure 2b compares the surfaces of the blades (leading edge region) before and after finishing. Figure 2c provides some roughness data. The deviation between the roughness levels measured in stream-wise direction and measured in printing direction was noticeable; however, it is not further elaborated in this contribution. The roughness data and relation (1) indicated that both the original and finished parts are rough in aerodynamics: the inflow Reynolds number was of order Re = 106 yielding ks,adm/l = 10−4. The admissible roughness, Rt,adm, would hence be of order 8 µm, which was easily not achieved after the applied standard finishing process, as displayed in Figure 2c. Thus, a different finishing process would be required to achieve hydraulically smooth blades. In principle, this is possible (see Adair et al. [3]), but is not covered within the present study.
2.2. Description of the Test Facility
The present experiments were performed in the closed-loop organic vapor wind tunnel (CLOWT) test section using the perfluorinated ketone Novec™ 649 and dry air as working fluids. The wind tunnel test facility CLOWT is shown in Figure 3. More details on CLOWT and its design features and its control system can be found in previous publications (Reinker et al. [11,12]).
After passing the centrifugal compressor, the working fluid was decelerated in the diffuser and entered the settling chamber, where the stagnation pressure p0 and temperature T0 were recorded. The mass flow rate through the wind tunnel was measured utilizing a device in the return of the wind tunnel. The compressor running speed n controlled the flow rate. The wind tunnel’s temperature level was controlled using an electrical heating system (not shown in Figure 3) and the coolant mass flow through the chiller. In combination with the inventory forward control (i.e., the amount of working fluid mass in the closed wind tunnel), stable operation conditions were achieved during the tests (for further details see Reinker et al. [12]). In CLOWT, a two-stage contraction zone accelerates the flow. The first subsonic axisymmetric nozzle (standard diameter DN500 to DN250) offers a moderate contraction ratio of about 3.7. The second nozzle accelerated the fluid up to the desired inflow conditions (see Figure 3b). In the present study, the second contraction was established by a three-dimensional nozzle based on additive manufacturing.
The second nozzle provided a three-dimensional cross-section change from round to rectangular contraction (standard diameter DN250 to a rectangular cross-section of 50 mm × 100 mm), leading to a total contraction ratio of 39. After passing the two-stage contraction zone, the fluid entered the cascade’s high-speed test section, as shown in Figure 3b,c. Different inflow turbulence intensities could be achieved through variable screen sets in the settling chamber. Still, during the present study, no additional screen was implemented to provide a moderate inflow turbulence intensity of order Tu = 0.5% for cascade testing. The turbulence level was experimentally confirmed by hot-wire anemometry, as explained by Reinker and aus der Wiesche [13]. The inflow turbulence Taylor micro length scale was of order λ = 4 up to 6 mm.
For the experiments, Novec 649TM by 3M was used primarily as working fluid. The typical pressure and temperature values at inlet stagnation conditions were 2.5 bar and 97 °C. In addition to the organic vapor, some cascade tests were also performed using dry air at atmospheric conditions (1 bar and 25 °C). In Table 2, some relevant thermodynamic data are listed for typical process conditions during the present cascade tests. Thermodynamic data of Novec 649 and air were calculated by employing REFPROP and its underlying equation of states (see McLinden et al. [14]) using actual pressure and temperature measurements. As pointed out by Baumgärtner et al. [10], the isentropic exponent κ is expected to be of some relevance for profile loss. Table 2 shows that the isentropic exponent κ was significantly lower for Novec 649TM than for air. Due to the high-density ρ of Novec 649TM, high inflow Reynolds numbers Re1 = c1lρ1/µ1 were achieved for the cascade flow.
The total enthalpy h0 was determined using the wall pressure p0, the (total) temperature T0 was measured at the settling chamber (denoted by subscript 0) and the mass flow rate obtained in the return of the wind tunnel. Since incompressible flow was involved in the settling chamber (with Mach number of order M0 = 10−2), the density ρ0 in the settling chamber was simply calculated using p0 and T0. During steady-state operation, the total enthalpy h0 was assumed to be constant for the contraction and test section; however, a slight temporal drift of system pressure and the temperature was taken into account during the long-term operation of the wind tunnel.

Table 2.
Thermophysical properties of dry air and Novec 649TM at typical pressure and temperature levels (calculated using REFPROP 9.0).
Table 2.
Thermophysical properties of dry air and Novec 649TM at typical pressure and temperature levels (calculated using REFPROP 9.0).
| Fluid | Air | Novec 649 |
|---|---|---|
| Pressure level p [MPa] | 0.10 | 0.25 |
| Temperature level T [K] | 298 | 370 |
| Density ρ [kg/m3] | 1.17 | 28.46 |
| Isentropic exponent κ [−] | 1.40 | 1.05 |
| Compressibility factor Z [−] | 1.000 | 0.903 |
| Speed of sound a [m/s] | 346.2 | 90.8 |
| Dynamic viscosity η [Pas] | 1.848 × 10−5 | 1.389 × 10−5 |
At the beginning of the high-speed test section, far upstream, the inflow static wall pressure p1 was obtained through a static pressure tap placed centrally at the entrance of the test section. Further static end-wall pressure taps were located close to the cascade wall downstream (p1) and upstream of the cascade (p2) at planes where the total pressures p01 and p02 were measured employing traversing Pitot probes, as displayed in Figure 3c. In addition to the static pressure measurements close to the cascade trailing edge plane, the static pressure p2 far downstream was measured independently. The employed Pitot probes had a stem diameter of 3 mm, and the probe head diameter was 1 mm. A prior calibration study indicated that the employed Pitot probes were robust against the flow angle within ±10°. Hence, the probes were insensitive to the expected flow angle changes, as in the case of the study of Shelton et al. [15]. Since the cascade test section’s outflow zone was anything than optimal, as shown in Figure 2, it was decided to carry out the wake traverse measurements relatively close to the trailing edge plane (at a distance of about 2 mm). Regarding mixing losses, it was not possible to traverse at a downstream plane (p02) sufficiently far away from the cascade, as recommended by Scholz [5] and Kiock et al. [9]. However, that issue was of minor importance for the present purpose (i.e., a comparison of rough and smooth blades).
The accurate determination of pressures for the organic vapor flow requires special attention. In the case of dry air, measurements of static and total pressures can be performed by standard instrumentation using pressure transducers or manometers. In the case of organic vapor flows, condensation issues in pressure lines outside of the hot stream domain can substantially affect the measurements. For scanning the cascade test section pressures (i.e., p1, p2, p01, and p02), a rotatable switching device mounted at a side flange of the test tube was designed and employed for the involved valves. All connecting lines and valves for cascade pressure scanning were mounted inside the hot wind tunnel test tube.
Furthermore, a thermal decoupling device described in detail by Reinker et al. [16] was employed to avoid condensation issues at the pressure transducer mounted outside. Although previous functionality tests suggested that the leaking effect seemed to be negligible for the rotatable switching device, experiments at higher Mach numbers indicated that some systematic errors occurred during the measurements of the static pressure taps p2. Therefore, the static pressure p2* measured independently far downstream of the cascade was employed for data reduction.
2.3. Data Reduction
The inflow Mach number M1 was the primary flow input parameter since the angle of incidence (or inflow angle β1) was fixed for the present study (see Figure 1. The inflow Mach number M1 was calculated through an isentropic relation M1 = f(p01, p1) for a given stagnation enthalpy h0 and static pressure p1. The isentropic relation f for the inflow Mach number was provided by a separate routine implemented in REFPROP (see McLinden et al. [14] for details). In non-perfect gas dynamics, the isentropic relations f are not universal functions as in the case of perfect gas dynamics; instead, they depend on the given initial state h0 and p0. Following Shelton et al. [15], the isentropic exit Mach number M2is was calculated through an isentropic relation M2is = f(p01, p2avg) with the inflow total pressure p01 and the average exit static pressure p2avg. In the case of a perfect gas, the isentropic relation f for the exit Mach number can be given as analytical formulas. Substantially more efforts are required for non-perfect gas flows. For the present study, Passmann et al. [17] proposed a method using REFPROP data of Novec 649. For the total downstream pressure in supersonic flow, a bow shock occurs upstream of a Pitot probe. In supersonic flow, the total pressure p02m measured by the Pitot probe is related to the actual total pressure p02 through a normal shock relation. In the case of a perfect gas, the analytical Rayleigh–Pitot equation can be used for calculating the actual exit Mach number M2 using the static pressure data p2 and the Pitot probe signal p02. In supersonic organic vapor flows, it is necessary to solve the coupled set of balance equations (mass, energy, and impulse) numerically for stations upstream and downstream of the normal shock using appropriate equations of states [17]. Even in the case of high subsonic organic vapor flow, the deviations between a perfect gas expression and a correct thermodynamic treatment of the Pitot probe can be significant [16]. In the present study, the deviations between the Rayleigh–Pitot Equation (2) and the numerically obtained Mach number M2 were of order 4 up to 8%.
In an ideal cascade experiment, p01 would not depend on the traverse coordinate y; however, a weak mal-distribution might occur in actual tests. In the present cascade test section, no noticeable inflow total pressure mal-distribution p01 was found. An example of upstream total and downstream total pressure distributions for a typical run is shown in Figure 4. Whereas the inflow total pressure po1 was nearly constant over the normalized traverse coordinate y/s, the specific wake flow distribution became visible in the exit total pressure distribution p02(y).
A serious question is how to average flow quantities for a given purpose (see, Cumpsty and Horlock [18] for a discussion of the “correct” averaging procedure). Exit static pressures have to be arithmetically averaged over spacing s to get p2avg. In the case of total pressures, the so-called mass-weighted average is typically preferred (Dixon and Hall [19]); however, experimentalists frequently use area-averaged total pressures as well [18]. The latter approach was chosen in the present treatment, similar to Scholz [5] or Speidel [4]. In addition to that averaging issue, different ways for expressing cascade performance and losses are in use. Following Shelton et al. [15], a total pressure loss coefficient Y = (p01 − p02)/p01 was defined using averaged total exit pressures p02 (the inlet total pressure p01 was practically constant, Figure 4).
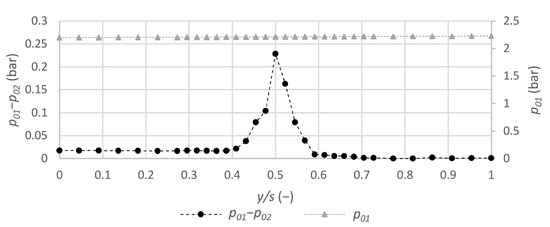
Figure 4.
Examples of total upstream and total downstream pressure difference distributions (Novec 649, M2is = 0.68).
Kiock et al. [9] preferred an energy loss coefficient ζ = 1 − c22/c2is2 defined by the actual exit and the isentropic exit velocities c2 and c2is, respectively. For the present purpose, the profile loss performance study reported by Kiock et al. [9] was of significant relevance because this study compared measurements performed independently at four different leading research facilities. Moffat [20] distinguished between three levels of replication: Nth order, first order, and zeroth order. The Nth order includes variations between different researchers with physically other test facilities. The first order includes variation due to changes in the instrumentation’s calibration and changes in ambient conditions at a particular test facility. In the zeroth-order replication, the process is steady at a specific test facility, and the chief source of error is the inaccuracy of the instrument readings. In validating analytical tools or computational fluid dynamics (CFD) simulation methods, it is desirable to evaluate the magnitudes of the errors occurring in Nth-order replication. It is also useful to know these errors in order to assess non-perfect gas effects on cascade performance for the present study. Kiock et al. [9] reported significant deviations for the loss results between the four test facilities by considering the same configuration using air. That observation has to be kept in mind when new loss results are presented for an organic vapor.
2.4. Uncertainty Analysis
Experiments with organic vapor flow at elevated pressure and temperature levels require special efforts. The uncertainty of the flow variables can have two uncertainty sources: bias and precision. The total uncertainty of a variable is a combination of both. Although the employed pressure transducers’ uncertainty level was of order 0.1 up to 0.2% (depending on the actual pressure level), a much higher total uncertainty level (of order Δp/p = 0.5 up to 1.6%) was developed. This substantially higher uncertainty level was mainly given by bias errors caused by condensation in the pressure lines [16]. In the present case, the condensation issue was the primary source of uncertainty for the pressure measurements. The contribution due to precision was nearly negligible (the precision error was of order 0.01 up to 0.05%). The absolute uncertainty of the temperature measurements (using temperature sensors PT100 1/10 DIN B) was of order ΔT = 0.1 K (nearly independent on the actual temperature level), yielding to a total relative uncertainty level of ΔT/T = 0.06 up to 0.1%, including the data logger and precision contributions. The contribution due to precision was only of order 0.01% regarding temperature measurements.
In addition to the above general uncertainty sources for the primary variables pressure and temperature, the thermodynamic properties’ calculation uncertainty due to the selected equation of states and fluid database and the scattering of wind tunnel operation during a measurement run had to be considered for data reduction.
The thermodynamic variables calculation utilized the REFPROP database with the appropriate equation of states for a given fluid [14]. REFPROP provided information about the uncertainty range of thermodynamic variables, and these uncertainties were treated as bias errors in the uncertainty analysis. For example, REFPROP quoted that the uncertainty in vapor speed of sound was only 0.05%. This value was used as a corresponding bias error contribution to calculate the uncertainty of the Mach number. A substantial level of uncertainty resulted in density calculations. Without considering the systematic error due to the finite accuracy of the thermodynamic equation of states, the total relative uncertainty level for the density was of order Δρ/ρ = 0.7 up to 2.0% (depending on the pressure and temperature level). Considering the systematic uncertainty due to the thermodynamic equation of states led to Δρ/ρ = 1.6 up to 3.0%. The uncertainty level of the density affected the total uncertainty of the mass flow rate, and the total relative uncertainty of order Δm/m = 1.6 up to 4.5% resulted in that quantity. That uncertainty directly affected the Mach and the Reynolds number uncertainty levels for which similar figures were obtained.
The scattering of the wind tunnel operation (i.e., pressure, temperature, and mass flow rate) was within the experimental uncertainty level of the involved instrumentation (see above). The transient temperature drift did not exceed 10−3 K/s.
3. Results and Discussion
In the present closed-loop wind tunnel facility, a nearly linear relationship between the inflow Mach number M1 and Reynolds number Re1 existed, as seen in Figure 5. Close to the choking Mach number at about M1,ch = 0.27, the dependency on the pressure of the sound speed for Novec 649 caused a nonlinear behavior. The exit Reynolds number level was of order 106 up to 3 × 106, which was slightly higher than in the literature studies reported by Kiock et al. [9], where Re2 did not exceed 0.9 × 106. The relationship between the inlet and exit Mach numbers agreed with the literature data obtained for air (Figure 6). Using the cascade data of Figure 1 and employing the perfect gas expression quoted by Scholz [5], a theoretical value of M1,ch = 0.27 resulted in the choking Mach number, which is in excellent agreement with the observed choking Mach number. Kiock et al. [9] reported that choking conditions would be achieved for air at M2 = 0.9. This behavior was also observed for the organic vapor flow through the cascade. Obviously, the isentropic exponent value or other real gas effects were not relevant for the choking behavior in the present study conducted in the dilute gas regime of an organic vapor. No impact of roughness on the overall choking behavior was found.
The energy loss coefficient ζ against exit Mach number M2 can be compared with literature data reported by Kiock et al. [9], although the present study used Novec 649 as working fluid instead of air. In Figure 7, the loss coefficient ζ against the exit Mach number M2 is shown and compared with literature data. The loss coefficients obtained for the organic vapor flow through the finished printed cascade were in good agreement with literature data obtained for air and a smooth cascade at higher subsonic Mach numbers. A somewhat higher value than in literature was observed at lower exit Mach numbers. The reason for that deviation remained unclear, possibly resulting in residual roughness and a lower Reynolds number. Since the Mach and the Reynolds numbers were strongly related in the present study, a low Mach number corresponded to a lower Reynolds number. It is likely that flow separation occurred at lower Reynolds numbers leading to higher profile losses. A somewhat similar picture was also observed by Yuan and Kind [21]. They suspected that the flow was separating rather upstream of the suction-surface trailing edge of the rough blades, at least at lower Mach numbers (i.e., lower Reynolds numbers). The loss coefficient ζ at M2 = 0.68 was noticeably higher for the original, roughly printed cascade than for the treated cascade (see Figure 8). In Table 3, three different coefficient results are listed. The level of the local pressure loss coefficient Y, used by Shelton et al. [15], is typically much lower than the energy loss coefficient ζ preferred by Kiock et al. [9]. In nearly the same order of magnitude as the energy losses are the losses YP. This loss definition is used by Yuan and Kind [21] in their investigations. The reduction due to surface treatment was comparable for all three definitions. Table 3 shows that the loss reduction for the three different definitions is in an area of about 32 ± 2%.
Corresponding details of the two local loss coefficient distributions in the wakes are shown in Figure 8, where the local energy loss coefficient ζ is plotted against the normalized traverse coordinate y/s for an exit Mach number M2 = 0.68.

Figure 5.
Inflow Reynolds number ReInflow against inlet Mach number M1.
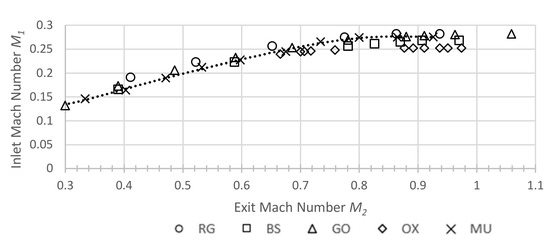
Figure 6.
Inlet Mach number M1 against exit Mach number M2 and choking behavior (MU = new data obtained at Muenster and literature data adapted from Kiock et al. [9]; RG = von Karman Institute for Fluid Dynamics, GO = German Aerospace Centre (DLR) Göttingen, BS = TU Braunschweig, OX = Oxford University).
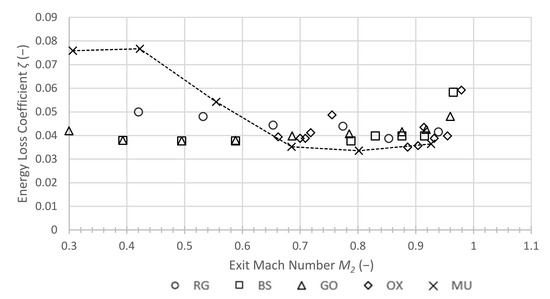
Figure 7.
Loss coefficient ζ against exit Mach number M2 for NOVEC 649 and literature data obtained for air and smooth blades (adapted from Kiock et al. [9]; RG = von Karman Institute for Fluid Dynamics, GO = German Aerospace Centre (DLR) Göttingen, BS = TU Braunschweig, OX = Oxford University).
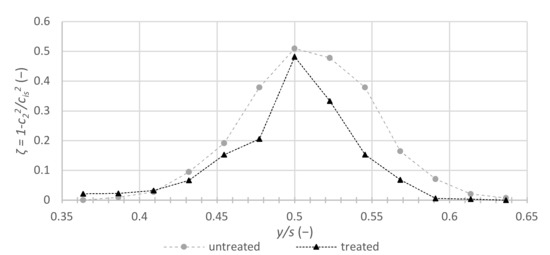
Figure 8.
Energy loss coefficient ζ against traverse/space ratio coordinate (M2 = 0.68).

Table 3.
Three different approaches for the loss coefficient and average loss coefficients obtained for Novec 649 at M2 = 0.68.
Table 3.
Three different approaches for the loss coefficient and average loss coefficients obtained for Novec 649 at M2 = 0.68.
| Loss Coefficient | Untreated State * (Original) | Treated State * (Finished) | Percentage Improvement |
|---|---|---|---|
| Y = | 1.1% | 0.747% | 32.1% |
| YP = | 5.71% | 4% | 30% |
| ζ = | 5.3% | 3.51% | 33.8% |
* Roughness Rt: original 54.8 ± 4.9 µm, finished 32.5 ± 7.4 µm.
The local loss distributions indicated a thicker boundary layer and, hence, a higher profile loss in the case of the rougher cascade. Both pressure and suction side boundary layer thicknesses were reduced due to the surface treatment; however, the impact seemed to be stronger for the suction side. This effect of roughness is not uncommon in cascade aerodynamics.
The wake flow observations in Figure 8 indicate that a turbulent boundary layer flow past the airfoils was established for an exit Mach number of M2 = 0.68. Hence, it is interesting to compare the loss reduction due to finishing with the predictions of boundary layer theory. The ratios Yfinished/Yoriginal, YP,finished/YP,original and ζfinished/ζoriginal were 0.68 and 0.65, respectively (see Table 3). During the present experiments at M2 = 0.68, the corresponding inlet and exit Reynolds numbers were of order Re1 = 1 × 106 and Re2 = 2.8 × 106, respectively. The relative roughness of the finished surface was ks/l = 10−3 and ks/l = 1.8 × 10−3 for the original part. Then, the ratio of the skin friction coefficients of the finished and the original surface would be of order 0.75 (see Scholz [5], especially page 402). This value is relatively close to the observed loss coefficient ratios. This agreement supports the hypothesis that surface roughness affected the profile loss in the usual boundary layer theory framework. Due to the moderate Mach number level, the skin friction and loss coefficients were not significantly affected by compressibility effects. For smaller Reynolds numbers, there is a significant increase in the profile losses. These are no longer comprehensible with the theory of Scholz [5]. Therefore, it is assumed that in the lower velocity range (see Figure 7), friction losses at the airfoils occur and the local detachment of the center blade contributes to the losses. In this context, it is further interesting to note that the empirical profile loss correlation by Traupel [22] would predict a value of ζ = 3.6% for the finished blade. This value is very close to the measured value ζ = 3.51%, as displayed in Table 3.
4. Conclusions
Profile loss results were reported of an experimental study using an additive manufactured linear turbine cascade placed in the test section of a closed-loop organic vapor wind tunnel. A blade profile from the open literature was chosen for the cascade, and the organic vapor was Novec 649. Pitot probes were employed to measure the flow field upstream and downstream of the cascade. The original roughness parameters of the metal-printed blades, as delivered by the manufacturer, were determined, and the first set of flow measurements was performed. Then, the printed part was finished, and the second set of flow measurements enabled an assessment of the impact of roughness on profile losses.
Although the Reynolds number level was relatively high, it was found that further surface treatment noticeably reduces the profile loss, as in the case of organic vapor flows through the printed cascade. After an additional finishing process, a similar profile loss behavior could be achieved, as reported for smooth blades. In addition, it was shown that the residual roughness has a massive influence on profile losses in the lower subsonic velocity range. This phenomena that the losses increase in the lower speed range was also detected in a study on the roughness effect. The reduction in the profile losses was nearly in the same area for all three loss approaches. Therefore, it is confirmed that the loss considerations are equivalent to each other in terms of velocity or pressure.
No significant new non-perfect gas dynamics effects were observed for the global cascade performance in this high subsonic up to transonic dilute gas flow regime.
Author Contributions
Conceptualization, S.a.d.W. and L.H.; methodology, L.H.; software, L.H.; validation, M.S., S.a.d.W. and L.H.; formal analysis, L.H.; investigation, F.R., R.W. and L.H.; resources, S.a.d.W.; data curation, L.H.; writing—original draft preparation, S.a.d.W.; writing—review and editing, L.H.; visualization, L.H.; supervision, F.R.; project administration, S.a.d.W.; funding acquisition, S.a.d.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research work was funded by the program “progress.nrw-Research” of the State of Northrhine-Westfalia, Germany, under the grant number 005-2003-0076_037/PtJ 2003pr006. The support by J. Hollekamp for obtaining the surface roughness data is also acknowledged.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| a | speed of Sound | m/s |
| c | flow velocity | m/s |
| f | isentropic relation | - |
| h | specific enthalpy | J/kg |
| ks | sand grain roughness | µm |
| l | chord length | mm |
| lx | axial chord | mm |
| M | Mach number | - |
| o | narrowing | mm |
| p | static pressure | bar |
| p0 | total pressure | bar |
| Ra | mean roughness | µm |
| Re | Reynolds number | - |
| Rp | average peak-to-valley height | µm |
| Rt | maximum surface roughness | µm |
| Rz | peak-to-valley height | µm |
| s | spacing | mm |
| s | specific entropy | J/(kg·K) |
| s/l | space chord ratio | - |
| T | temperature | K |
| y | vertical traversing line | mm |
| y/s | traversing spacing ratio | - |
| Y | total pressure loss coefficient | - |
| YP | pressure loss coefficient | - |
| Z | compressibility factor | - |
| Greek Symbols | ||
| β1 | inflow angle | ° |
| β2 | exit angle | ° |
| ζ | energetic loss coefficient | - |
| η | dynamic viscosity | Pa·s |
| к | isentropic exponent | - |
| µ | micro | µ |
| ρ | density | kg/m3 |
| Subscripts | ||
| 1 | inflow | |
| 2 | exit | |
| avg | average | |
| ch | choke | |
| t | total | |
| is | isentropic | |
References
- Magerramova, L.; Vasilyev, B.; Kinzburskiy, V. Novel Designs of Turbine Blades for Additive Manufacturing. In Proceedings of the ASME Turbo Expo 2016: Turbomachinery Technical Conference and Exposition, (GT2016-56084). Seoul, Korea, 13–17 June 2016. [Google Scholar]
- Albright, B. Siemens 3D Prints Power Turbine Blades. Digital Engineering. 12 June 2017. Available online: www.digitalengineering247.com/article/siemens-3d-prints-power-turbine-blades (accessed on 25 May 2020).
- Adair, D.; Kirka, M.; Ryan, D. Additive Manufacture of Prototype Turbine Blades for Hot-Fired Engine Performance Validation Trials. In Proceedings of the ASME Turbo Expo 2019, (GT2019-90966). Phoenix, AZ, USA, 17–21 June 2019. [Google Scholar]
- Speidel, L. Einfluss der Oberflächenrauhigkeit auf die Strömungsverluste in ebenen Schaufelgittern. Forschung. Ing. 1954, 20, 129–140. [Google Scholar] [CrossRef]
- Scholz, N. Aerodynamik der Schaufelgitter; G. Braun: Karlsruhe, Germany, 1965. [Google Scholar]
- Bammert, K.; Sandstede, H. Influences of Manufacturing Tolerances and Surface Roughness of Blades on the Performance of Turbines. ASME J. Eng. Power Jan. 1976, 98, 29–36. [Google Scholar] [CrossRef]
- Sieverding, C.H. Experimental Data on Two Transonic Turbine Blade Sections and Comparison With Various Theoretical Methods. VKI Lecture Series 59 - Volume 3 (Transonic Flows in Turbomachinery); 21–25 May 1973; Part 3. VKI PP 1972-05.
- Lehthaus, F. Berechnung der transsonischen Strömung durch ebene Turbinengitter nach dem Zeit-Schritt-Verfahren. VDI-Forsch. 1978, 586, 5–24. [Google Scholar]
- Kiock, R.; Lehthaus, F.; Baines, N.C.; Sieverding, C.H. The Transonic Flow Through a Plane Turbine Cascade as Measured in Four European Wind Tunnels. ASME J. Eng. Gas Turbines Power 1986, 108, 277–284. [Google Scholar] [CrossRef]
- Baumgärtner, D.; Otter, J.J.; Wheeler, A.P.S. The Effect of Isentropic Exponent on Transonic Turbine Performance. In Proceedings of the ASME Turbo Expo 2019, Phoenix, AZ, USA, 17–21 June 2019. (GT2019-90251). [Google Scholar]
- Reinker, F.; Kenig, E.Y.; aus der Wiesche, S. CLOWT: A Multifunctional Test Facility for the Investigation of Organic Vapor Flows. In In Proceedings of the ASME 2018 5th Joint US-European Fluids Engineering Division Summer Meeting, (V002T14A004). Montreal, QC, Canada, 15 July 2018. [Google Scholar]
- Reinker, F.; Kenig, E.Y.; aus der Wiesche, S. Closed Loop Organic Vapor Wind Tunnel CLOWT: Commissioning and Operational Experience. In In Proceedings of the ORC, Athens, Greece, 9–11 September 2019; p. 47. [Google Scholar]
- Reinker, F.; aus der Wiesche, S. Application of Hot-Wire Anemometry in the High Subsonic Organic Vapor Flow Regime. In In Proceedings of the 3rd International Seminar on Non-Ideal Compressible Fluid Dynamics for Propulsion and Power, Delft, The Netherlands, 29–30 October 2020. [Google Scholar]
- McLinden, M.O.; Perkins, R.A.; Lemmon, E.W.; Fortin, T.J. Thermodynamic Properties of 1,1,1,2,2,4,5,5,5-Nonafluoro-4(trifluoromethyl)-3-pentanone: Vapor Pressure, (p, ρ, T) Behavior, and Speed of Sound Measurements, and an Equation of State. J. Chem. Eng. Data 2015, 60, 3646–3659. [Google Scholar] [CrossRef]
- Shelton, M.L.; Gregory, B.A.; Doughty, R.L.; Kiss, T.; Moses, H.L. A Statistical Approach to the Experimental Evaluation of Transonic Turbine Airfoils in a Linear Cascade. ASME J. Turbomach. 1993, 115, 366–375. [Google Scholar] [CrossRef]
- Reinker, F.; Wagner, R.; Passmann, M.; Hake, L.; aus der Wiesche, S. Performance of a Rotatable Cylinder Pitot Probe in High Subsonic Non-Ideal Gas Flows. In In Proceedings of the 3rd International Seminar on Non-Ideal Compressible Fluid Dynamics for Propulsion and Power, Delft, The Netherlands, 29–30 October 2020. [Google Scholar]
- Passmann, M.; aus der Wiesche, S.; Joos, F. A one-dimensional analytical calculation method for obtaining normal shock losses in supersonic real gas flows. IOP Conf. Ser. J. Phys. Conf. Ser. 2017, 821, 012004. [Google Scholar] [CrossRef]
- Cumpsty, N.A.; Horlock, J.H. Averaging Nonuniform Flow for a Purpose. ASME J. Turbomach. 2006, 128, 120–129. [Google Scholar] [CrossRef]
- Dixon, S.L.; Hall, C.A. Fluid Mechanics and Thermodynamics of Turbomachinery, 6th ed.; Butterworth-Heinemann: Burlington, MA, USA, 2010. [Google Scholar]
- Moffat, R.J. Contributions to the Theory of Uncertainty Analysis of Single-Sample Experiments. In Proceedings of the 1980–81 AFOSR-HTTM-Stanford Conference on Complex Turbulent Flows, Stanford, CA, USA, 1 February 1982 ; Volume 1, pp. 40–56. [Google Scholar]
- Yuan, L.Q.; Kind, R.J. Measurements and computations of compressible flow through a turbine cascade with surface roughness. In Proceedings of the ASME Turbo Expo 2006, (GT2006-90018). Barcelona, Spain, 8–11 May 2006. [Google Scholar]
- Traupel, W. Thermische Turbomaschinen, Erster Band; Springer: Berlin/Heidelberg, Germany, 1966. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY-NC-ND) license (https://creativecommons.org/licenses/by-nc-nd/4.0/).