Transport of Swirling Entropy Waves through an Axial Turbine Stator †
Abstract
:1. Introduction
2. Materials and Methods
2.1. Test Rig and Entropy Wave Generator
2.2. Measuring Devices
2.2.1. Turbine and EWG Set-Up
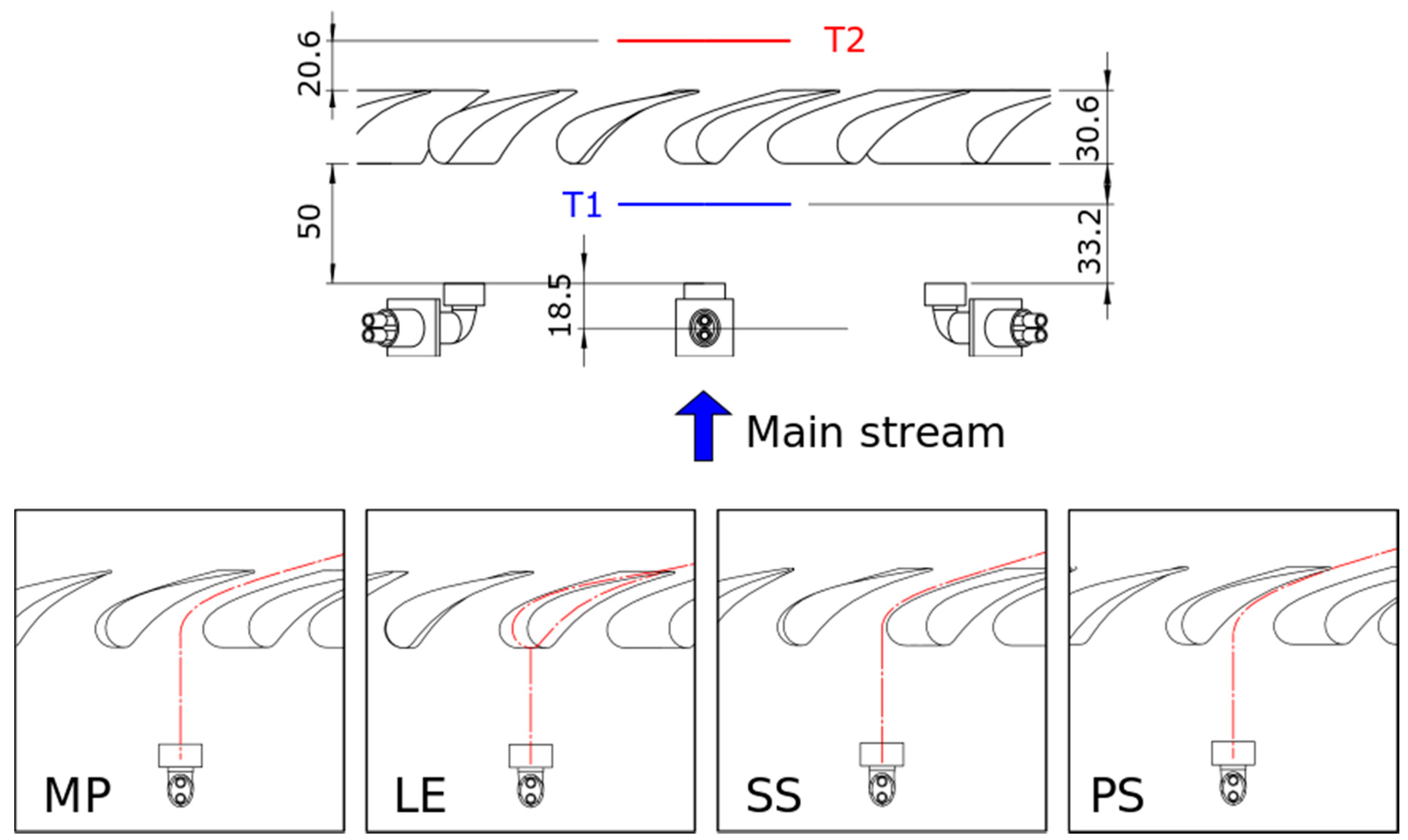
2.2.2. Flow Field Measurements
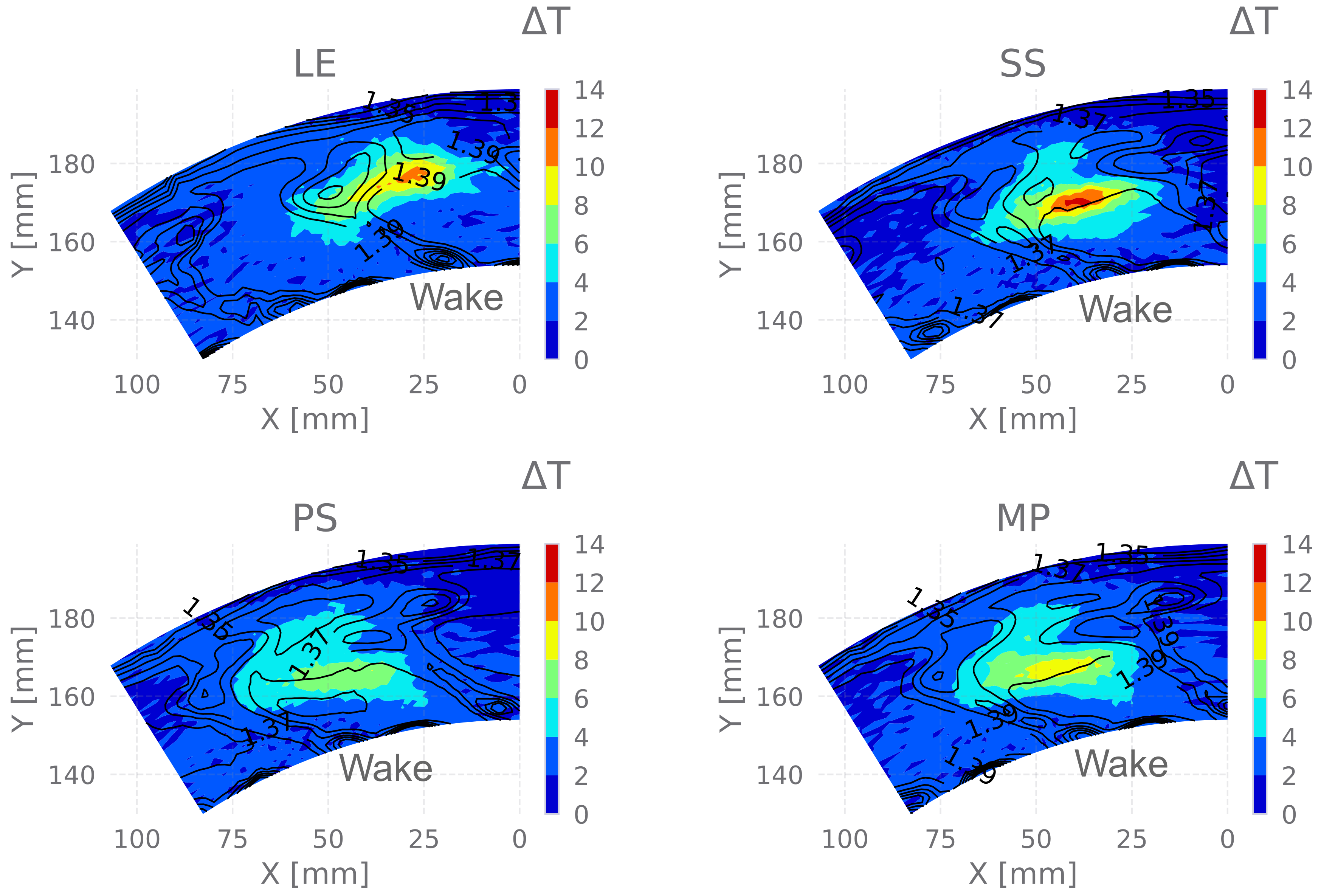
- LE: aligned to the stator leading edge;
- PS: at 1/3 of the pitch close to the pressure side;
- MP: at mid pitch;
- SS: at 1/3 of the pitch close to the suction side.
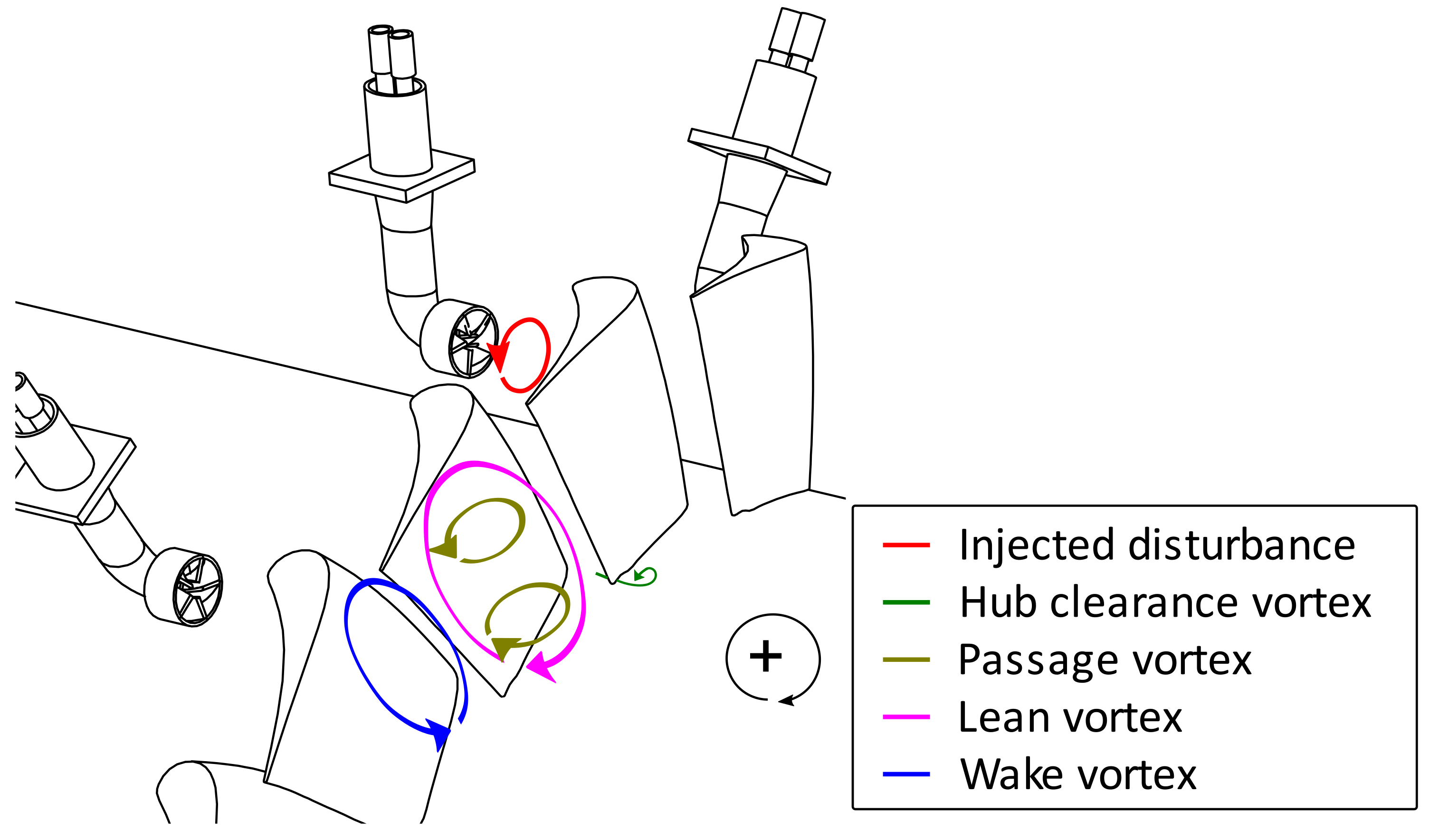
3. Results and Discussion
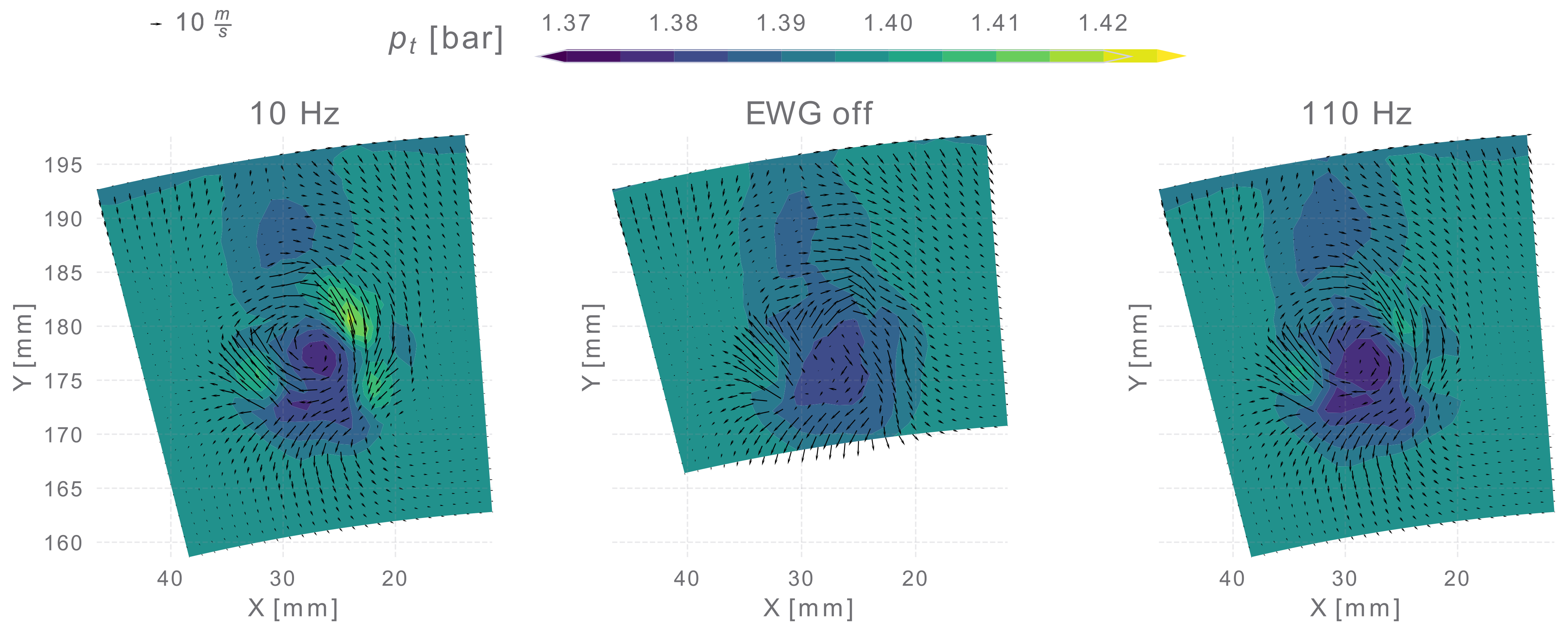
3.1. Generated Disturbance
3.2. Downstream Stator Measurements
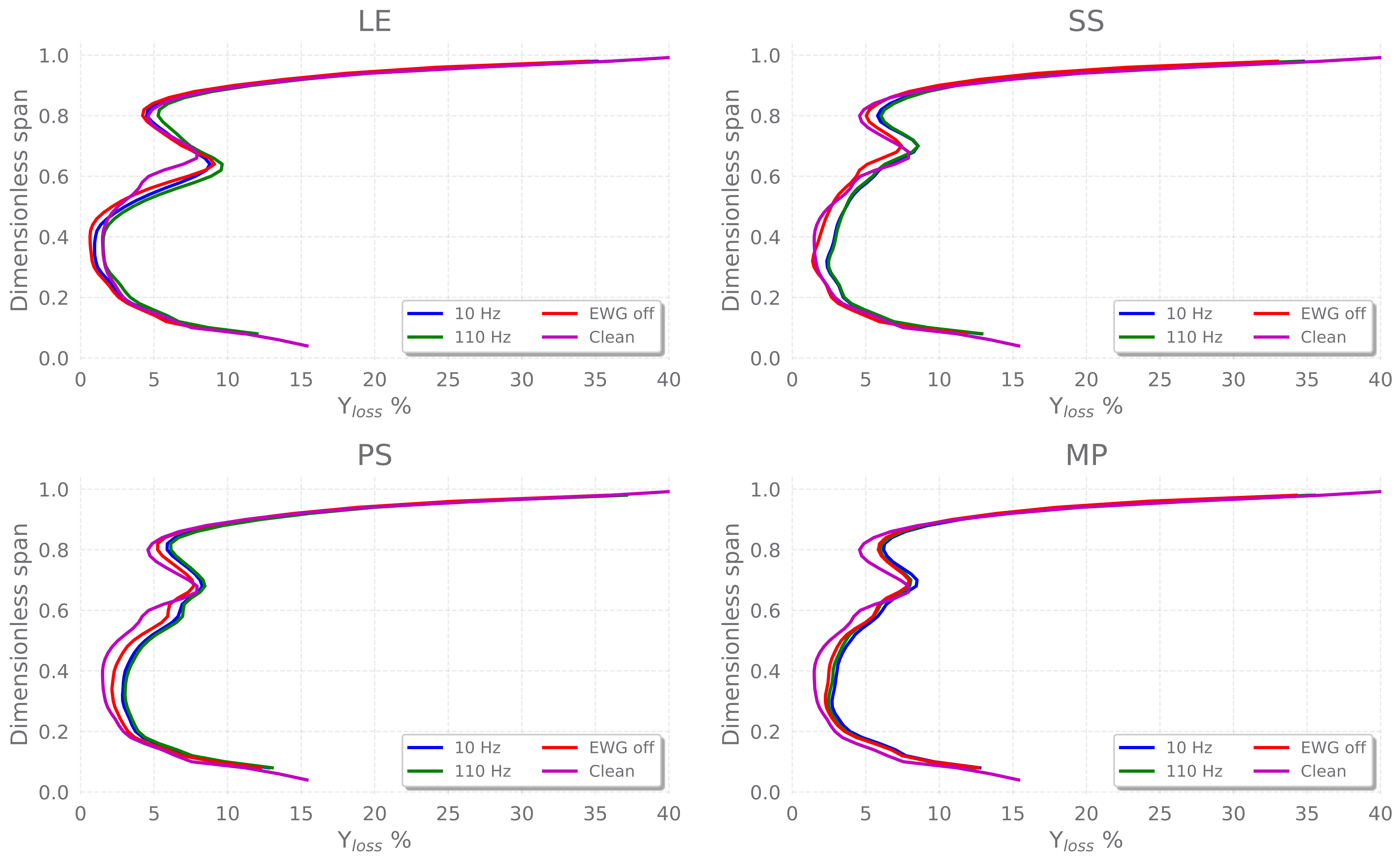
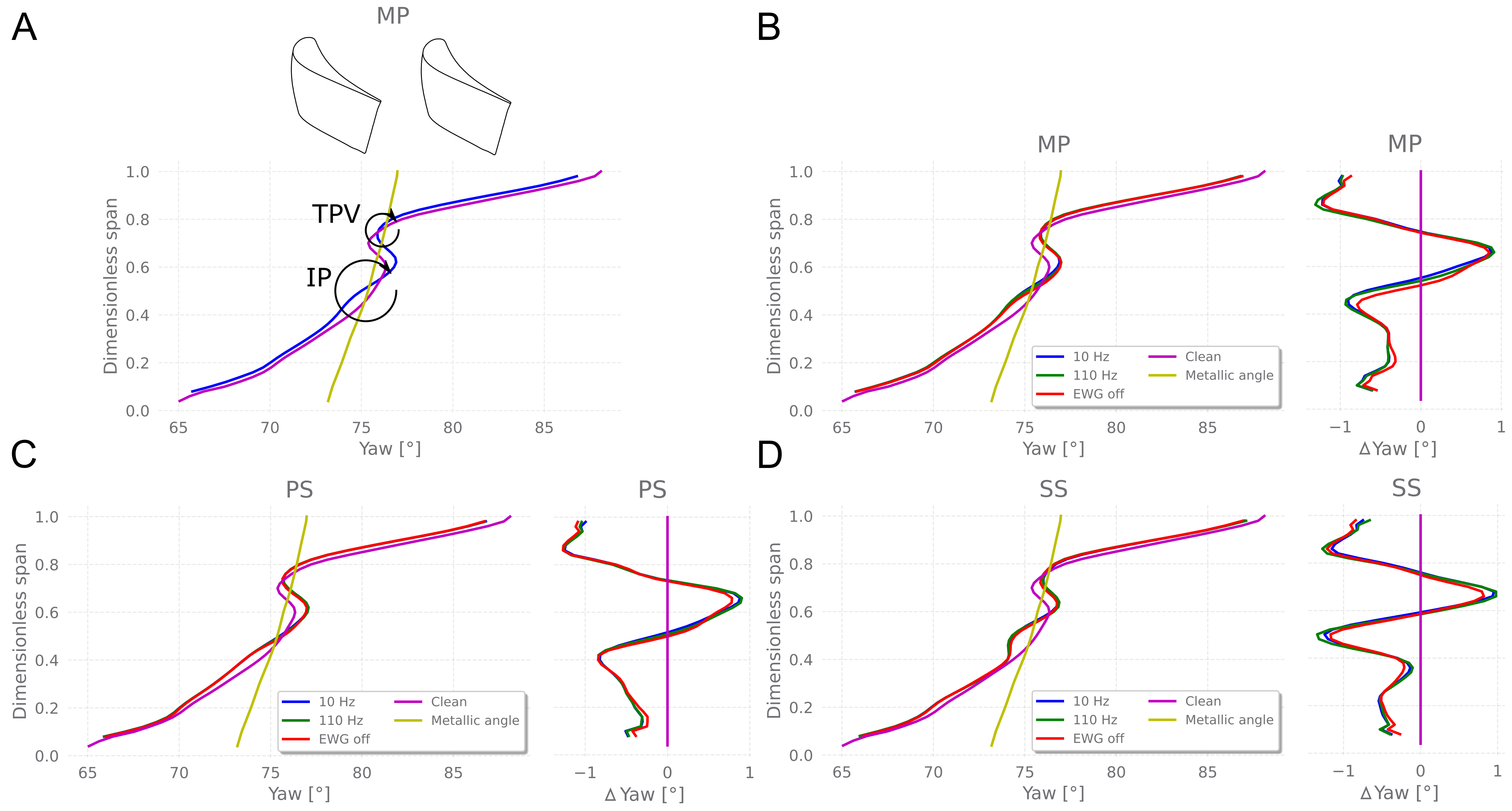
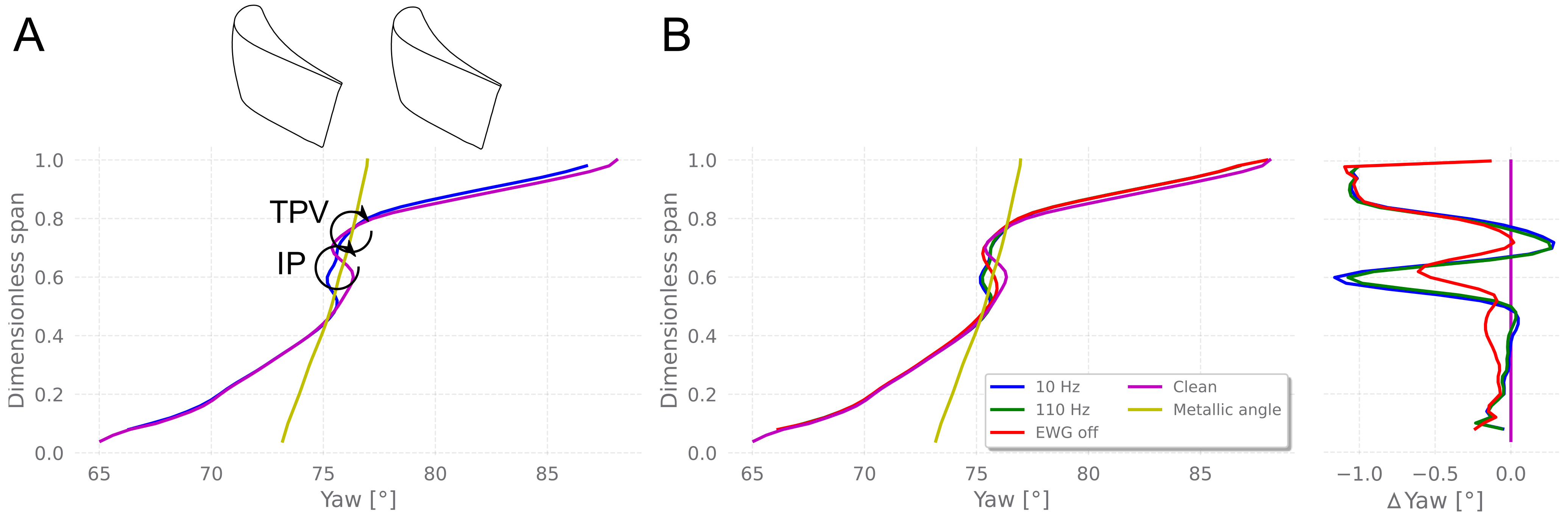
3.2.1. 5-Hole Pressure Probe
3.2.2. Fast-Thermocouple
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Morgans, A.S.; Duran, I. Entropy noise: A review of theory, progress and challenges. Int. J. Spray Combust. 2016, 8, 285–298. [Google Scholar] [CrossRef] [Green Version]
- Dowling, A.N.; Mahmoudi, Y. Combustion noise. Proc. Combust. Inst. 2015, 35, 65–100. [Google Scholar] [CrossRef] [Green Version]
- Morgans, A.S.; Goh, C.S.; Dahan, J.A. The dissipation and shear dispersion of entropy waves in combustor thermoacoustic. J. Fluid Mech. 2013, 733, R2. [Google Scholar] [CrossRef]
- Sattelmayer, T. Influence of the combustor aerodynamics on combustion instabilities from equivalence ratio fluctuations. J. Eng. Gas Turb. Power 2003, 125, 11–19. [Google Scholar] [CrossRef]
- Beard, P.F.; Smith, A.; Povey, T. Impact of severe temperature distortion on turbine efficiency. J. Turbomach. 2013, 135, 011018. [Google Scholar] [CrossRef]
- Jacobi, S.; Mazzoni, C.; Chana, K.; Rosic, B. Investigation of unsteady flow phenomena in first vane caused by combustor flow with swirl. J. Turbomach. 2017, 139, 041006. [Google Scholar] [CrossRef]
- Beard, P.F.; Smith, A.; Povey, T. Effect of combustor swirl on transonic high pressure turbine efficiency. J. Turbomach. 2014, 136, 011002. [Google Scholar] [CrossRef]
- Gundy-Burlet, K.L.; Dorney, D.J. Influence of 3D Hot Streak on Turbine Heat Transfer. Int. J. Turbo Jet Eng. 1997, 14, 123–131. [Google Scholar]
- Cumpsty, N.A.; Marble, F.E. The interaction of entropy fluctuations with turbine blade rows; A mechanism of turbojet engine noise. Proc. R. Soc. Lond. 1997, 357, 323–344. [Google Scholar]
- Qureshi, I.; Smith, A.D.; Povey, T. HP Vane Aerodynamics and Heat Transfer in the Presence of Aggressive Inlet Swirl. J. Turbomach. 2013, 135, 021040. [Google Scholar] [CrossRef]
- Butler, T.L.; Sharma, O.P.; Joslyn, H.D.; Dring, R.P. Redistribution of an Inlet Temperature Distortion in an Axial Flow Turbine Stage. J. Propuls. Power 1989, 5, 64–71. [Google Scholar] [CrossRef]
- Basol, A.M.; Jenny, P.; Ibrahim, M.; Kalfas, A.I.; Abhari, R.S. Hot Streak Migration in a Turbine Stage: Integrated Design to Improve Aerothermal Performance. J. Eng. Gas Turb. Power 2011, 133, 061901. [Google Scholar] [CrossRef]
- Gaetani, P.; Persico, G. Transport of Entropy Waves Within a High Pressure Turbine Stage. J. Turbomach. 2019, 141, 031006. [Google Scholar] [CrossRef]
- Pinelli, L.; Marconcini, M.; Pacciani, R.; Gaetani, P.; Persico, G. Computational and Experimental Study of the Unsteady Convection of Entropy Waves Within a High Pressure Turbine Stage. J. Turbomach. 2021, 143, 091011. [Google Scholar] [CrossRef]
- Adams, M.G.; Povey, T.; Hall, B.F.; Cardwell, D.N.; Chana, K.S.; Beard, P.F. Commissioning of a combined hot-streak and swirl profile generator in a transonic turbine test facility. J. Eng. Gas Turb. Power 2020, 142, 031008. [Google Scholar] [CrossRef] [Green Version]
- Adams, M.G.; Beard, P.F.; Stokes, M.R.; Wallin, F.; Chana, K.S.; Povey, T. Effect of a Combined Hot-Streak and Swirl Profile on Cooled 1.5-Stage Turbine Aerodynamics: An Experimental and Computational Study. J. Turbomach. 2021, 143, 021011. [Google Scholar] [CrossRef]
- Khanal, B.; He, L.; Northall, J.; Adami, P. Analysis of Radial Migration of Hot-Streak in Swirling Flow Through High-Pressure Turbine Stage. J. Turbomach. 2013, 135, 041005. [Google Scholar] [CrossRef]
- Giusti, A.; Worth, N.A.; Mastorakos, E.; Dowling, A.P. Experimental and Numerical Investigation into the Propagation of Entropy Waves. AIAA J. 2017, 55, 446–458. [Google Scholar] [CrossRef]
- Christodoulou, L.; Karimi, N.; Cammarano, A.; Paul, M.; Navarro-Martinez, S. State prediction of an entropy wave advecting through a turbulent channel flow. J. Fluid Mech. 2020, 882, A8. [Google Scholar] [CrossRef]
- Notaristefano, A.; Gaetani, P. Design and commissioning of a Combustor Simulator combining Swirl and Entropy Wave generation. Int. J. Turbomach. Propuls Power 2020, 5, 27. [Google Scholar] [CrossRef]
- Gaetani, P.; Persico, G.; Spinelli, A. Coupled effect of expansion ratio and blade loading on the aerodynamics of a high-pressure gas turbine. Appl. Sci. 2017, 7, 259. [Google Scholar] [CrossRef] [Green Version]
- Notaristefano, A.; Gaetani, P.; Dossena, V.; Fusetti, A. Uncertainty evaluation on multi-hole aerodynamic pressure probes. J. Turbomach. 2021, 143, 091001. [Google Scholar] [CrossRef]
- Ruith, M.R.; Chen, P.; Meiburg, E.; Maxworthy, T. Three-dimensional vortex breakdown in swirling jets and wakes: Direct numerical simulation. J. Fluid Mech. 2003, 486, 331–378. [Google Scholar] [CrossRef] [Green Version]
- Gupta, A.K.; Lilley, D.G.; Syred, N. Swirl Flows; Energy and Engineering Science Series; Abacus Press: Kent, UK, 1985. [Google Scholar]
- Andreini, A.; Bacci, T.; Insinna, M.; Mazzei, L.; Salvadori, S. Hybrid RANS-LES modeling of the aerothermal field in an annular hot streak generator for the study of combustor—Turbine interaction. J. Eng. Gas Turb. Power 2016, 139, 021508. [Google Scholar] [CrossRef]
- Werschnik, H.; Schneider, M.; Herrmann, J.; Ivanov, D.; Schiffer, H.P.; Lyko, C. The influence of combustor swirl on pressure losses and the propagation of coolant flows at the Large Scale Turbine Rig (LSTR): Experimental and numerical investigation. Int. J. Turbomach. Propuls. Power 2017, 2, 12. [Google Scholar] [CrossRef]
- D’Ippolito, G.; Dossena, V.; Mora, A. The Influence of Blade Lean on Straight and Annular Turbine Cascade Flow Field. J. Turbomach. 2011, 133, 011013. [Google Scholar] [CrossRef]
- Harrison, S. The Influence of Blade Lean on Turbine Losses. J. Turbomach. 1992, 114, 184–190. [Google Scholar] [CrossRef]
- Denton, J.D.; Xu, L. The exploitation of three-dimensional flow in turbomachinery design. Proc. Inst. Mech. Eng. Part C J. Mec. 1999, 213, 125–137. [Google Scholar] [CrossRef]
- Persico, G.; Gaetani, P.; Dossena, V.; D’Ippolito, G.; Osnaghi, C. On the definition of the secondary flow in three-dimensional cascades. Proc. Inst. Mech. Eng. Part A J. Power Energy 2003, 223, 667–676. [Google Scholar] [CrossRef]



| Operating Condition | β | n (rpm) | (kg/s) | |
|---|---|---|---|---|
| 3.78 | 313 | |||
| Geometry | h (mm) | tc/h | Dm (mm) | Gap/Cx,v |
| 50 | 0.02 | 350 | 1.00 | |
| Blade rows | σ | AR | Δθ | |
| Vane | 22 | 1.20 | 0.83 | 75.2 |
| Rotor | 25 | 1.25 | 0.91 | 115.3 |
| Frequency (Hz) | 10 Hz | 110 Hz |
|---|---|---|
| Duty cycle | 40–60 | 35–65 |
| Feeding pressure (barG) | 1.2 | 0.7 |
| Heater power (W) | 600 | 600 |
| Position | 10 Hz | 110 Hz | EWG off | Clean |
|---|---|---|---|---|
| MP | 6.0 | 5.7 | 5.6 | 4.5 |
| LE | 5.0 | 5.7 | 4.7 | |
| PS | 6.1 | 6.3 | 5.4 | |
| SS | 5.6 | 5.7 | 4.7 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY-NC-ND) license (https://creativecommons.org/licenses/by-nc-nd/4.0/).
Share and Cite
Notaristefano, A.; Gaetani, P. Transport of Swirling Entropy Waves through an Axial Turbine Stator. Int. J. Turbomach. Propuls. Power 2021, 6, 45. https://doi.org/10.3390/ijtpp6040045
Notaristefano A, Gaetani P. Transport of Swirling Entropy Waves through an Axial Turbine Stator. International Journal of Turbomachinery, Propulsion and Power. 2021; 6(4):45. https://doi.org/10.3390/ijtpp6040045
Chicago/Turabian StyleNotaristefano, Andrea, and Paolo Gaetani. 2021. "Transport of Swirling Entropy Waves through an Axial Turbine Stator" International Journal of Turbomachinery, Propulsion and Power 6, no. 4: 45. https://doi.org/10.3390/ijtpp6040045
APA StyleNotaristefano, A., & Gaetani, P. (2021). Transport of Swirling Entropy Waves through an Axial Turbine Stator. International Journal of Turbomachinery, Propulsion and Power, 6(4), 45. https://doi.org/10.3390/ijtpp6040045







